Элементы корреляционного анализа в MQL5: Критерий независимости хи-квадрат Пирсона и корреляционное отношение

Введение

Сегодня хотелось бы коснуться такого важного раздела математической статистики как корреляционный анализ, в чьи задачи входит обнаружение и оценка зависимостей между случайными величинами. Самым популярным инструментом в арсенале корреляционного анализа, безусловно, является коэффициент корреляции. Однако для оценки зависимостей в данных, особенно таких, как приращения биржевых цен, вычисления одного коэффициента корреляции совершенно недостаточно. Во-первых, он оценивает только линейную зависимость. Во-вторых, нулевые значения коэффициента корреляции вовсе не означают отсутствие зависимости, если выборка данных, по которой он рассчитывается, имеет распределение отличное от нормального. Для ответа на вопрос, являются ли данные зависимыми, отмечают критерии независимости. Мы поговорим о самом известном из них — критерии независимости хи-квадрат Пирсона. Также поговорим о такой числовой характеристике, как коэффициент корреляционного отношения, который помогает определить, является ли исследуемая зависимость нелинейной.

Гипотеза независимости

Предполагается, что данные представляют собой наблюдения над некоторой двумерной случайной величиной (X, Y) с неизвестной функцией распределения F(X, Y), о которой требуется проверить гипотезу независимости H0 : F(X, Y) = F(X)*F(Y), где F(X) и F(Y) одномерные функции распределения.

Под случайными величинами X и Y в данной статье я буду подразумевать или приращения логарифмов цен разных финансовых инструментов, или приращения цен одного инструмента, но взятые с лагом один.

Критерий независимости хи-квадрат Пирсона

Критерий независимости хи-квадрат применяют как для дискретных случайных величин с конечным числом исходов, так и для непрерывных случайных величин, но с обязательным условием их предварительной группировки. При этом множество всех возможных значений случайной величины X разбивается на i непересекающихся интервалов A1,A2,Ai, а множество всех значений Y на множество j непересекающихся интервалов B1,B2,Bj. Таким образом, множество значений двумерной величины (X, Y) разбивается на i*j прямоугольников (ячеек). Для наглядности эти данные представляют в виде так называемой таблицы сопряженности признаков (корреляционной таблицы, таблицы распределения вероятностей двумерной случайной величины и т.п.).

                              

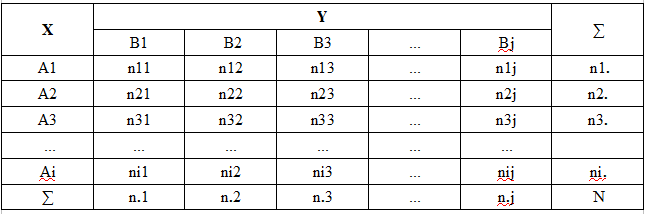
В этой таблице:

• Ai = (Xi-1, Xi) - i-й интервал группировки случайной величины Х

• Bj = (Yj-1,Yj) – j-й интервал группировки случайной величины Y

• nij - фактическая групповая частота ячейки (количество тех пар наблюдений (X, Y) значения которых попали в интервал Ai и Bj)

• ni. - число наблюдений в i-й строке

• n.j – число наблюдений в j-м столбце

• N – объем выборки

В качестве критерия независимости хи-квадрат используется статистика:

CHI2 = (Actual – Expected) ^2 / Expected,

где

• Actual - фактическая групповая частота ячейки nij,

• Expected – ожидаемая групповая частота ячейки nij

Данная статистика распределена по закону хи-квадрат с v = (j-1)(i-1) степенями свободы.

Нулевая гипотеза независимости отвергается, если расчетная статистика CHI2 превышает критические значения распределения хи-квадрат с v степенями свободы на некотором уровне значимости alpha.

Фактические частоты мы рассчитаем по данным выборки, а принцип построения ожидаемых частот следующий: если случайные величины X и Y независимы, тогда справедлива следующая формула:

P {Ai, Bj} = P {Ai}*P{Bj},

то есть, вероятность одновременного осуществления событий Ai и Bj равна произведению вероятности появления событий Ai на вероятность появления события Bj.

Для того, чтобы найти математические ожидания событий {Ai, Bj}, {Ai} и {Bj}, умножим обе части данного равенства на N*N, то есть на квадрат количества наблюдений.

N*N * P {Ai, Bj} = N *P{Ai} * N* P{Bj}

Тогда получаем:

• N *P{Ai} - математическое ожидание числа наблюдений в i-й строке

• N* P{Bj} - математическое ожидание числа наблюдений в j-м столбце

• N * P {Ai, Bj} = (N *P{Ai} * N* P{Bj})/N - математическое ожидание числа попаданий в ячейку на пересечении i-й строки и j-го столбца

Тогда, подставляя вместо математических ожиданий N *P{Ai} и N* P{Bj} их оценки ni. и n.j (то есть фактические частоты из корреляционной таблицы), мы получим искомую оценку ожидаемых частот

Expected = (ni. * n.j)/N

Таким образом, в предположении гипотезы независимости ожидаемая частота попадания в ячейку на пересечении i-й строки и j-го столбца равна произведению сумм числа наблюдений в i-й строке и j-м столбце, деленном на объем выборки.

Поэтому при расчете критерия естественно ожидать, что чем больше фактические частоты отличаются от ожидаемых частот, тем больше вероятность  того, что данные не являются независимыми.

Индикатор Chi2Test

Расчет критерия независимости хи-квадрат Пирсона реализован в индикаторе Chi2Test. Индикатор проверяет гипотезу независимости на каждом баре между соседними приращениями цен для одного финансового инструмента.

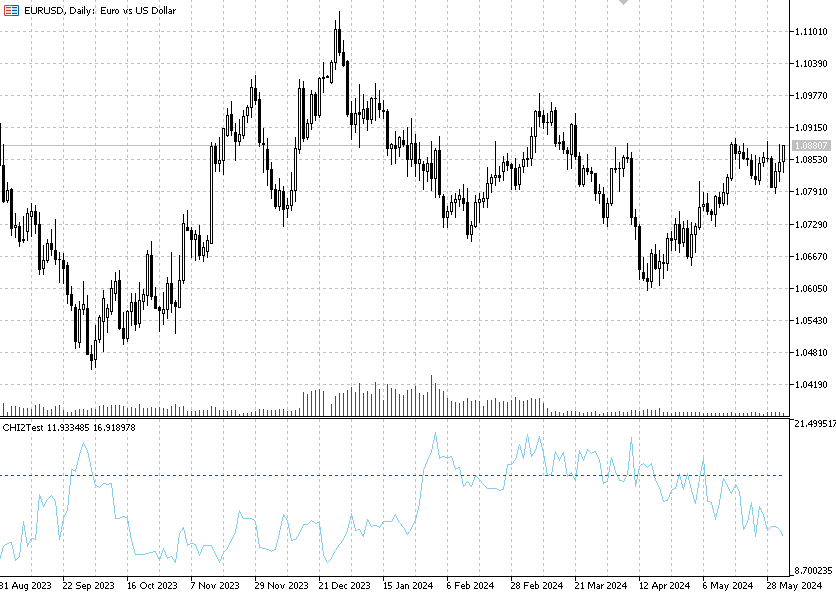
В данном индикаторе четыре входных параметра:

• alpha – уровень значимости

• Data – окно данных для расчета

• Tails - количество стандартных отклонений

• Contingency coefficient – коэффициент сопряженности

Для того, что бы посчитать статистику хи-квадрат, нам в первую очередь необходимо рассчитать фактические частоты в таблице сопряженности признаков. Для этого используется функция crosstab.

//+------------------------------------------------------------------+
//|  Функция рассчитывает таблицу сопряженности двух СВ (X,Y)        |
//+------------------------------------------------------------------+
bool Crosstab(const double &dataX[],const double &dataY[],const double &bins[],matrix &freq)
  {

   int datasizeX=ArraySize(dataX);
   int datasizeY=ArraySize(dataY);
   int binssize=ArraySize(bins);
   if(datasizeX==0 || datasizeY==0 || binssize==0)
      return(false);
   if(datasizeX != datasizeY)
      return(false);

   for(int i=0; i<datasizeX; i++)
     {
      if(!MathIsValidNumber(dataX[i]) || !MathIsValidNumber(dataY[i]))
         return(false);
     }

   matrix m_freq=matrix::Zeros(binssize, binssize);
   
   for(int x=0; x<binssize; x++)
     {
      for(int i=0; i<datasizeX; i++)
        {
         for(int y=0; y<binssize; y++)
           {
            if(dataX[i]<=bins[x] && dataY[i]<=bins[y]) 
              {
               m_freq[x,y]=m_freq[x,y]+1;
               break;
              }
           }
        }
     }
     
   matrix Actual = m_freq;
   vector p1,p2,diffp;
   for (int j=1; j<binssize; j++)
   {
   p1 = m_freq.Row(j-1);
   p2 = m_freq.Row(j);
   diffp = p2-p1;
   Actual.Row(diffp,j);   
   }
   freq = Actual; 
   
   return(true);
  }

Так как данные, с которыми мы работаем, непрерывны, то в первую очередь нам следует их сгруппировать. При этом можно встретить такие рекомендации, что для корректного расчета критерия желательно, чтобы минимальное значение ожидаемой частоты в ячейках было не меньше единицы, а количество тех ячеек, в которых ожидаемая частота меньше пяти, не должно быть большим (например, допускается две таких ячейки, если общее количество ячеек меньше 10). Так как распределения биржевых данных, как мы все хорошо знаем, обладают тяжелыми хвостами, то возникает определенная сложность с построением интервалов группировки, которые смогут соответствовать вышеописанным требованиям.

Я предлагаю сгруппировать данные, предварительно проведя их стандартизацию. После чего, урезать тяжелые хвосты распределения до 2-3-4 сигма, в зависимости от объема данных, которые анализируются. В индикаторе за это отвечает параметр Tails. Так, например, если объем данных небольшой (200-300 значений), тогда следует выбирать значение Tails равное 2 сигма, в результате чего, получим интервалы группировки: (-2,-1),(-1,0),(0,1),(1,2) и, следовательно, таблицу сопряженности признаков 4x4. Таким образом, чтобы корректно рассчитать статистику хи-квадрат, мы будем объединять соседние интервалы группировки с малыми ожидаемыми частотами.

Contingency coefficient (Коэффициент сопряженности Крамера)

Статистика CHI2, к сожалению, не может служить численной мерой вероятностной зависимости, поэтому для этой цели используют коэффициент сопряженности Крамера. Его значения меняются от нуля до единицы. Ноль означает отсутствие зависимости между данными, единица — функциональную зависимость.

Коэффициент сопряженности Крамера, основан на статистике хи-квадрат:

Contingency coefficient = sqrt (CHI2 / N*(Bins_count-1)),

где Bins_count – количество строк (или столбцов) в таблице сопряженности признаков.

Таким образом в одном индикаторе реализовано фактически две статистики – основная статистика хи-квадрат и, рассчитанный на этой статистике, коэффициент сопряженности (Contingency coefficient).

Если вы хотите проверить на независимость два различных финансовых инструмента, используйте скрипт Crosstab. Для этого активируйте параметр X vs Y (true). В противном случае, скрипт рассчитывает статистику по данным текущего символа. Выборочные данные для расчета отсчитываются с предпоследнего бара на графике.

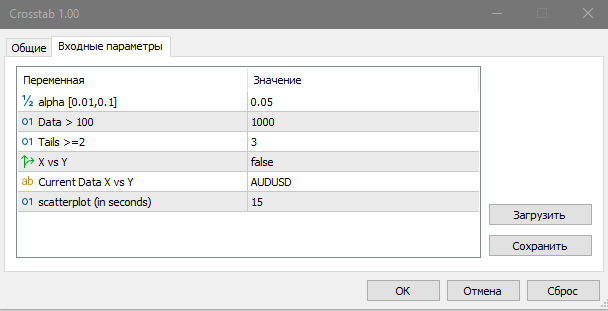
Скрипт Crosstab рассчитывает и выводит в журнал следующую информацию:

• матрицу фактических (Actual ) и ожидаемых (Expected) частот

• коэффициент корреляции r, рассчитанный по сгруппированным данным

• коэффициент корреляции Pearson, рассчитанный по несгруппированным данным (для сравнения точности расчетов, ведь статистика, посчитанная по сгруппированным данным, менее точна)

• корреляционное отношение Nxy, Nyx (Correlation ratio)

• проверяет гипотезу об отсутствии корреляционной зависимости ( f statistic correl independence)

• проверяет гипотезу о линейности корреляционной зависимости (f statistic Linear/Nonlinear),

• статистику хи-квадрат CHI2

• коэффициент сопряженности Крамера (Contingency coefficient)

На экран выводится также диаграмма рассеивания (корреляционное поле) для визуальной оценки парной зависимости (scatterplot).

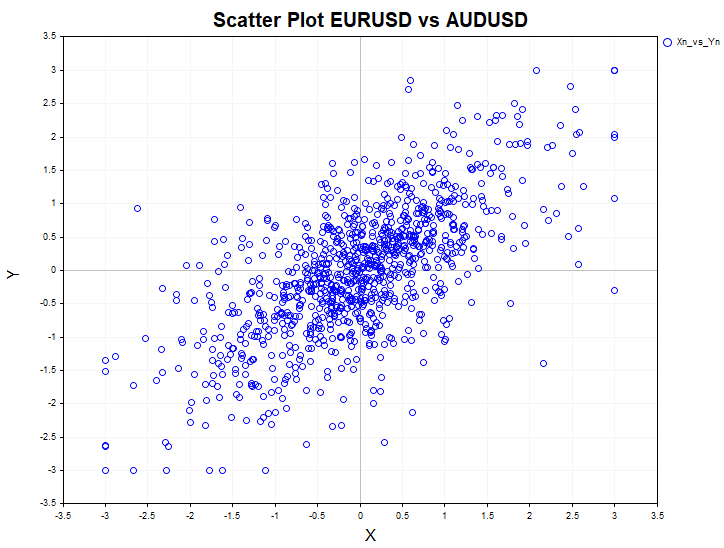
Чтобы протестировать на независимость модельные данные, используйте скрипт Crosstab_Models. В качестве моделей выступают равномерное распределение, авторегрессия первого порядка, авторегрессионная условная гетероскедастичность ARCH и логистическое отображение.

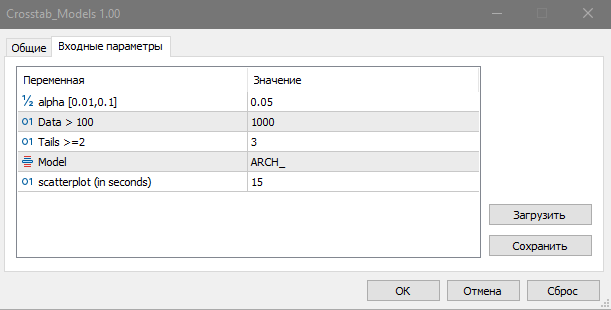
Модельные данные служат своего рода неким шаблоном, с которым можно сравнивать результаты, полученные на реальных данных. Например, вот так выглядит нелинейная зависимость в одномерной нелинейной динамической системе — логистическом отображении:

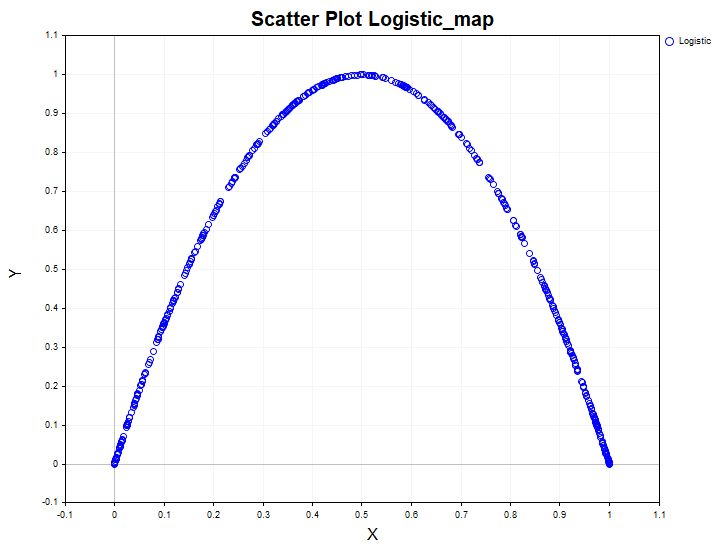
Проанализировав данные такой системы только с помощью линейного коэффициента корреляции, можно было сделать ошибочный вывод, что данный процесс является белым шумом. Вместе с тем, критерий независимости хи-квадрат с легкостью обнаруживает, что данные зависимы, а корреляционное отношение подтверждает, что зависимость имеет нелинейный характер.

Корреляционное отношение

Для оценки нелинейноcти корреляционной зависимости используют корреляционное отношение (Correlation ratio) :

Nyx = sqrt (D[E(Y|X)]/Sy)

Nxy = sqrt (D[E(X|Y)])/Sx)

где:

• E(Y|X) — условное математическое ожидание случайной величины Y

• E(X|Y) — Условное математическое ожидание случайной величины X

• D[E(Y|X)] – дисперсия УМО случайной величины Y

• D[E(X|Y)] – дисперсия УМО случайной величины X

• Sy, Sx – безусловные дисперсии случайных величин Y и X

Вспомним, что:

• условное математическое ожидание E(Y|X) является случайной величиной.

• E[E(Y|X)] = E[Y] (математическое ожидание от УМО случайной величины Y равно безусловному математическому ожиданию Y).

• дисперсия Y это - D[Y] = E[(Y – E(Y) )^2)] математическое ожидание квадрата отклонения случайной величины Y от математического ожидания E[Y].

• И тогда D[E(Y|X)] = E{[ E(Y|X) – E[Y] ] ^ 2}, то есть дисперсия УМО E(Y|X) равна математическому ожиданию квадрата отклонения УМО E(Y|X) от безусловного математического ожидания E[Y].

Другими словами, корреляционное отношение — это корень квадратный из отношения двух дисперсий — условной и безусловной. Корреляционное отношение можно вычислить только на основании корреляционной таблицы, то есть по сгруппированным данным. Перечислим свойства которыми он обладает:

• корреляционное отношение несимметрично относительно X и Y, то есть Nxy != Nyx.

• 0 ≤ | r | ≤ Nxy ≤ 1, 0 ≤ | r | ≤ Nyx ≤ 1, значения показателя лежат в пределах [0,1] и всегда больше или равно линейного коэффициента корреляции r, взятого по модулю.

• если данные независимы, то Nxy=Nyx=0. Обратное не верно, то есть из некоррелированности не следует независимость.

• если | r | = Nyx =Nyx <1, тогда корреляция между X и Y линейна, то есть, для уравнения регрессии нельзя найти лучшей кривой, чем прямая линия.

• если корреляция между X и Y нелинейна, то | r | < min (Nxy, Nyx). Чем меньше разность между коэффициентом корреляции и корреляционным отношением, тем ближе к линейной зависимость между X и Y.

Рассчитав выборочное корреляционное отношение, можно проверить гипотезу об отсутствии корреляционной зависимости между двумя случайными величинами (H0: Nyx = 0).

Для этого рассчитывают статистику:

F = Nyx^2 * (N-Bins_count) / (1- Nyx^2) *(Bins_count-1)

Если проверяемая гипотеза верна, то статистика F распределена по закону Фишера с v1= Bins_count-1 и v2 = N-Bins_count степенями свободы.

Нулевая гипотеза отклоняется на уровне значимости alpha, если расчетное значение статистики F превышает критическое значение этой статистики (тогда принимается альтернатива H1: Nyx >0)

Допустим, мы убедились, что корреляционная зависимость присутствует. Возникает вопрос — эта зависимость линейная или нелинейная ? На этот вопрос отвечает гипотеза о линейности корреляционной зависимости между двумя случайными величинами.

При проверке гипотезы о линейности корреляционной зависимости Y от X (H0: Nyx^2 = r^2) используют статистику:

F = (Nyx^2 - r^2) * (N-Bins_count) / (1- Nyx^2) *(Bins_count-2)

Если проверяемая гипотеза верна, то статистика F распределена по закону Фишера с v1= Bins_count-2 и v2 = N-Bins_count степенями свободы.

Нулевая гипотеза о линейности корреляции отклоняется на уровне значимости alpha, если расчетное значение статистики F превышает критическое значение этой статистики (тогда принимается альтернатива H1: Nyx^2 != r^2 )

Заключение

В данной статье были рассмотрены такие важные инструменты корреляционного анализа, как критерий независимости хи-квадрат Пирсона и корреляционное отношение. С их помощью можно гораздо точнее оценить наличие скрытых взаимосвязей в данных. Индикатор CHI2Test выполняет проверку гипотезы независимости, позволяя получать статистически обоснованные выводы о наличии взаимосвязей в данных.

Скрипты Crosstab и Crosstab_Models, кроме статистики хи-квадрат, также рассчитывают корреляционное отношение и проверяют гипотезу о корреляционной зависимости и линейности этой зависимости, в том числе и для модельных данных. Дополнительно на экран выводится график корреляционного поля для визуальной оценки парной зависимости. Точность статистических тестов пользователь может регулировать самостоятельно, выбирая желаемый уровень значимости alpha. Чем меньше уровень значимости, тем меньше вероятность получить ложный ответ.