Нейросети — это просто (Часть 84): Обратимая нормализация (RevIN)

Введение

В предыдущей статье мы познакомились с методом Conformer, который был разработан для прогнозирования погоды. Довольно интересный метод. И при тестировании обученной модели мы получили не плохой результат. Но все ли мы сделали правильно? Или можно получить результат лучше? Давайте посмотрим на процесс обучения. Легко заметить, что модель прогнозирования последующих наиболее вероятных показателей временных рядов мы явно использование не по прямому назначению. Подавая на вход модели исходные данные из временной последовательности, мы обучали её, спуская градиент ошибки от моделей, использующих результаты прогнозирования. Сначала от Критика.

         if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) ||
            !Encoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

А затем от Актера.

         if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder)) ||
            !Encoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

И ещё раз от Актера, при корректировке его политики с учетом доходности операций.

         Critic.TrainMode(false);
         if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) ||
            !Actor.backPropGradient((CNet *)GetPointer(Encoder), -1, -1, false) ||
            !Encoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

В этом, конечно, нет ничего плохого. И является широко используемой практикой при обучении различных моделей. Однако в данном случае мы делаем акцент при обучении модели Энкодера исходного состояния окружающей среды не на прогнозировании последующих состояний, а на выделении отдельных признаков, позволяющих оптимизировать работу последующих моделей.

Конечно, нашей основной задачей является поиск оптимальной политики Актера. И на первый взгляд нет ничего плохого в адаптации модели Энкодера под цели Актера. Но в таком случае Энкодер решает несколько иную задачу. Практически он становится блоком последующих моделей. И его архитектура может быть не оптимальной для решения поставленных задач.

Более того, при обучении Энкодера градиентами ошибки 3 различных задач мы модем столкнуться с проблемой, когда градиенты отдельных задач будут разнонаправленными. И модель в таком случае будет искать "золотую середину", максимально удовлетворяющую всем поставленным задачам. И вполне вероятно, что такое решение может быть довольно далеким от оптимального.

Думаю очевидно, что структурированную логику использования моделей следует реализовать и в процессе обучения. И в такой парадигме нам необходимо научить Энкодера прогнозировать последующие состояния окружающей среды. Именно в Энкодере используются подходы Conformer. А затем мы обучим политику Актера с учетом прогнозных состояний окружающей среды.

Теоретически все ясно. А при практической реализации мы сталкиваемся со значительным разрывом распределений отдельных признаков описания состояния окружающей среды. Получая на вход модели подобные "сырые" данные описания состояния окружающей среды мы нормализуем их для приведения в сопоставимый вид. Но как нам получить столь отличающиеся значения на выходе модели?

Я хочу напомнить, что с подобной проблемой мы уже сталкивались при обучении различных моделей автоэнкодеров. Тогда мы нашли выход в использовании исходных данных после нормализации в качестве целей. Однако в данном случае нам нужны данные описания последующих состояний окружающей среды, которые отличны от исходных данных. Один из методов решения данной проблемы был предложен в статье "Reversible Instance Normalization for Accurate Time-Series Forecasting against Distribution Shift".

Авторы статьи предлагают простой, но эффективный метод нормализации и денормализации — обратимая инстантная нормализация (RevIN), который сначала нормализует исходные последовательности, а затем денормализует выходные последовательности модели для решения проблем прогнозирования временных рядов, связанных со сдвигом распределения. RevIN симметрично структурирована для возвращения исходной информации о распределении к выходу модели путем масштабирования и сдвига выхода в слое денормализации на величину, эквивалентную сдвигу и масштабированию исходных данных в слое нормализации.

RevIN — это гибкий, обучаемый слой, который может быть применен к любым произвольно выбранным слоям, эффективно подавляя нестационарную информацию (среднее и дисперсию экземпляра) в одном слое и восстанавливая ее в другом слое практически симметричного положения, например, входных и выходных слоев. 

1. Алгоритм RevIN

Для знакомства с алгоритмом RevIN рассмотрим задачу многомерного прогнозирования временных рядов в дискретном времени для набора исходных данных X = {xi}i=[1..N] и соответствующих целевых данных Y = {yi}i=[1..N], где N обозначает количество элементов в последовательности.

Пусть K, Tx и Ty обозначают количество переменных, длину входной последовательности и длину прогноза модели соответственно. Учитывая входную последовательность Xi ∈ RK*Tx, наша цель состоит в решении задачи прогнозирования временных рядов, которая заключается в прогнозировании последующих значений Yi ∈ RK*Ty. В RevIN длина входной последовательности Tx и длина прогноза Ty могут различаться, поскольку наблюдения нормализуются и денормализуются по временному измерению. Предложенный метод, RevIN, состоит из симметрично структурированных слоев нормализации и денормализации. Сначала мы нормализуем исходные данные Xi с использованием их среднего значения и стандартного отклонения, что широко принято, как инстантная нормализация. Среднее и стандартное отклонение вычисляются для каждого экземпляра Xi исходных данных следующим образом:

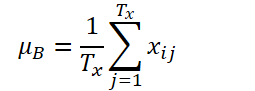
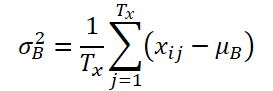
Нормализованные последовательности могут иметь более согласованное среднее и стандартное отклонение, где уменьшается нестационарная информация. В результате слой нормализации позволяет модели точно прогнозировать локальную динамику внутри последовательности при получении входных данных с согласованными распределениями по среднему и стандартному отклонению.

Модель получает трансформированные данные на входе и прогнозирует их будущие значения. Однако исходные данные имеют различную статистику по сравнению с исходным распределением, и наблюдая только нормализованный вход, трудно захватить исходное распределение входных данных. Таким образом, чтобы упростить эту задачу для модели, мы явно возвращаем нестационарные свойства, удаленные из входных данных, в выход модели, обратив нормализацию на симметричном позиционировании, выходном слое. Шаг денормализации может вернуть выход модели к исходному значению временного ряда. Соответственно, мы денормализуем выход модели, применяя обратные нормализации операции:

Те же статистические показатели, которые использовались на этапе нормализации, применяются для масштабирования и сдвига. Теперь ŷi является окончательным прогнозом модели.

Просто добавленный в виртуально симметричные позиции в сети, RevIN может эффективно уменьшить расхождение распределения в данных временных рядов. Аналогично обучаемому слою нормализации, который применим к произвольным глубоким нейронным сетям. Действительно, предложенный метод является гибким, обучаемым слоем, который может быть применен к любым произвольно выбранным слоям, даже к нескольким слоям. Авторы метода подтверждают его эффективность как гибкого слоя, добавляя его к промежуточным слоям в различные модели. Однако RevIN наиболее эффективен, когда применяется к виртуально симметричным слоям структуры Энкодер-Декодер. В типичной модели прогнозирования временных рядов граница между Энкодером и Декодером часто неясна. Поэтому авторы метода применяют RevIN к входному и выходному слоям модели, так как их можно рассматривать как структуру Энкодер-Декодер, генерирующую последующие значения на основе входных данных.

Авторская визуализация метода RevIN представлена ниже.

2. Реализация средствами MQL5

После рассмотрения теоретических аспектов метода мы переходим к практической реализации предложенных подходов средствами MQL5.

Из  представленного выше теоретического описания метода легко заметить, что предложенная авторами метода нормализация исходных данных полностью повторяет алгоритм реализованного нами ранее слоя пакетной нормализации CNeuronBatchNormOCL. Следовательно, мы вполне можем использовать имеющийся класс для нормализации данных. А вот для денормализации данных нам предстоит создать новый нейронный слой CNeuronRevINDenormOCL.

2.1 Создание нового слоя Денормализации

Вполне очевидно, что в процессе денормализации данных будут использоваться объекты, применяемые при нормализации данных. Поэтому и новый слой CNeuronRevINDenormOCL мы создадим наследником от слоя нормализации CNeuronBatchNormOCL.

class CNeuronRevINDenormOCL   :  public CNeuronBatchNormOCL
  {
protected:
   int               iBatchNormLayer;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   {  return true;   }

public:
                     CNeuronRevINDenormOCL(void)   :  iBatchNormLayer(-1) {};
                    ~CNeuronRevINDenormOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, int NormLayer, 
                          CNeuronBatchNormOCL *normLayer);
   virtual int       GetNormLayer(void)   {  return iBatchNormLayer; }
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronRevInDenormOCL;    }
   virtual CLayerDescription* GetLayerInfo(void);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau)   {  return true;   }
  };

Сразу следует обратить внимание, что в алгоритме метода RevIN предусмотрено использование для денормализации параметров, обучаемых на стадии нормализации. Здесь логика такова, что на стадии нормализации мы изучаем распределение исходных данных. После чего приводим исходные данные в сопоставимый вид, удаляя "разрывы". И далее модель работает с нормализованными данными. На выходе модели мы денормализуем данные, возвращая им параметры распределения исходных данных. Таким образом, мы ожидаем на выходе модели прогнозные данные в "природном" распределении исходных данных.

Очевидно, что на стадии денормализации обновление параметров модели не происходит. Поэтому в структуре класса мы переопределяем методы обновления параметров модели "пустыми заглушками". Однако, алгоритм прямого прохода и распределения градиента ошибки нам ещё предстоит реализовать. Но обо всем по порядку.

В данном классе мы не объявляем дополнительных внутренних объектов. Следовательно, конструктор и деструктор класса остаются пустыми. Однако мы создадим переменную для записи идентификатора слоя нормализации в модели iBatchNormLayer. И тут же мы создадим публичный метод для получения значения данной переменной GetNormLayer(void).

Инициализация объекта нашего нового класса осуществляется в методе CNeuronRevINDenormOCL::Init. В параметрах метод получает всю необходимую информацию для успешной инициализации внутренних объектов и переменных. И тут надо сказать есть весьма существенное отличие от аналогичных методов ранее рассмотренных нейронных слоев. Дело в том, что в параметрах методу, помимо констант, мы будем передавать указатель на объект слоя пакетной нормализации CNeuronBatchNormOCL.

bool CNeuronRevINDenormOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, 
                                 int NormLayer, CNeuronBatchNormOCL *normLayer)
  {
   if(NormLayer > 0)
     {
      if(!normLayer)
         return false;
      if(normLayer.Type() != defNeuronBatchNormOCL)
         return false;
      if(BatchOptions == normLayer.BatchOptions)
         BatchOptions = NULL;
      if(!CNeuronBatchNormOCL::Init(numOutputs, myIndex, open_cl, numNeurons, normLayer.iBatchSize, normLayer.Optimization()))
         return false;
      if(!!BatchOptions)
         delete BatchOptions;
      BatchOptions = normLayer.BatchOptions;
     }

Еще одно кардинальное отличие кроется в теле метода. Здесь мы создаем разветвление алгоритма в зависимости от полученного идентификатора слоя пакетной нормализации. Если он больше "0", то мы проверяем и полученный указатель на слой пакетной нормализации. Кроме того, мы проверяем тип полученного объекта. После чего вызываем одноименный метод родительского класса. И только после успешного прохождения всех указанных точек контроля мы осуществляем подмену буфера параметров оптимизации.

Обратите внимание, что мы не копируем данные. А полностью меняем указатель на объект буфера. Таким образом в процессе обучения модели мы будем работать с всегда актуальными параметрами нормализации.

Вторая ветка алгоритма предназначена для инициализации пустого объекта класса в процессе загрузки ранее сохраненной модели. Здесь мы лишь вызываем одноименный метод родительского класса с минимальными параметрами

   else
      if(!CNeuronBatchNormOCL::Init(numOutputs, myIndex, open_cl, numNeurons, 0, ADAM))
         return false;

И далее, вне зависимости от выбранного пути, мы сохраняем полученный идентификатор слоя пакетной нормализации и завершаем работу метода.

   iBatchNormLayer = NormLayer;
//---
   return true;
  }

2.2 Организация прямого прохода

Реализацию алгоритма прямого прохода мы начнем с создания кернела RevInFeedForward на стороне OpenCL программы. По аналогии с реализацией алгоритма слоя пакетной нормализации, данный кернел мы планируем запускать в 1 мерном пространстве задач.

В параметрах кернела мы будем передавать указатели 3 буфера данных: исходных данных, параметров нормализации и результатов. А так же 2 константы: размер буфера параметров пакета нормализации и тип оптимизации параметров.  

__kernel void RevInFeedForward(__global float *inputs, __global float *options,
                               __global float *output, int options_size,
                               int optimization)
  {
   int n = get_global_id(0);

Напомню, что от выбранного алгоритма оптимизации параметров зависит размер буфера параметров нормализации. Данный буфер имеет ниже следующую структуру.

В теле кернела мы идентифицируем анализируемый поток в пространстве задач. И сразу определяем смещение в буферах до анализируемых данных. В буферах исходных данных и результатов смещение равно идентификатору потока. А смещение в буфере параметров оптимизации мы определяем в соответствии с приведенной структурой буфера и указанным методом оптимизации параметров.

int shift = (n * optimization == 0 ? 7 : 9) % options_size;

Кроме того, здесь мы должны учесть, что количество анализируемых состояний окружающей среды может отличаться от глубины нашего прогноза. В данном случае мы исходим из предположения сохранения структуры анализируемых и прогнозируемых состояний окружающей среды. Иными словами, количество и порядок анализируемых параметров описания 1 состояния окружающей среды полностью сохраняется при прогнозировании последующих состояний. Таким образом, для определения смещения в буфере параметров нормализации мы берем остаток от деления смещения рассчитанного смещения с учетом анализируемого потока и структуры буфера на размер буфера параметров нормализации.

Следующим шагом мы извлечем данные из глобальных буферов в локальные переменные.

   float mean = options[shift];
   float variance = options[shift + 1];
   float k = options[shift + 3];

Вычислим денормализованное значение прогнозируемого параметра.

   float res = 0;
   if(k != 0)
      res = sqrt(variance) * (inputs[n] - options[shift + 4]) / k + mean;
   if(isnan(res))
      res = 0;

Результат операций запишем в соответствующий элемент буфера результатов.

   output[n] = res;
  }

После реализации алгоритма денормализации данных на стороне OpenCL программы нам предстоит организовать вызов созданного кернела из основной программы. Для этого мы переопределим метод CNeuronRevINDenormOCL::feedForward. 

bool CNeuronRevINDenormOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;
//---
   PrevLayer = NeuronOCL;
//---
   if(!BatchOptions)
      iBatchSize = 0;
   if(iBatchSize <= 1)
     {
      activation = (ENUM_ACTIVATION)NeuronOCL.Activation();
      return true;
     }

Как и одноименный метод родительского класса, в параметрах метод получат казатель на объект предыдущего слоя, который содержит для нас исходные данные.

В теле метода мы сразу проверяем полученный указатель и сохраняем его в соответствующую переменную.

Затем мы проверяем размер пакета нормализации. И если он не превышает "1", мы оцениваем это как отсутствие нормализации и передаем данные предыдущего слоя без изменений. Мы, конечно, не будем полностью копировать данные. А только скопируем идентификатор функции активации. И при обращении к буферу результатов или градиентов вернем указатели на буферы предыдущего слоя. Данный функционал уже был реализован в родительском классе.

Далее мы реализуем алгоритм непосредственной постановки кернела в очередь выполнения. Здесь мы сначала определим пространство задач.

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Neurons()};

После чего передадим необходимые параметры кернелу.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_RevInFeedForward, def_k_revffinputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

   if(!OpenCL.SetArgumentBuffer(def_k_RevInFeedForward, def_k_revffoptions, BatchOptions.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

   if(!OpenCL.SetArgumentBuffer(def_k_RevInFeedForward, def_k_revffoutput, Output.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

   if(!OpenCL.SetArgument(def_k_RevInFeedForward, def_k_revffoptions_size, (int)BatchOptions.Total()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

   if(!OpenCL.SetArgument(def_k_RevInFeedForward, def_k_revffoptimization, (int)optimization))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

И отправим кернел в очередь выполнения.

   if(!OpenCL.Execute(def_k_RevInFeedForward, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

При этом не забываем на каждом шаге контролировать процесс выполнения операций.

2.3 Алгоритм распределения градиента ошибки

После реализации прямого прохода нам предстоит реализовать алгоритм обратного прохода. Как уже было сказано выше, данный слой не содержит обучаемых параметров. Точнее он использует параметры, обучаемые на стадии нормализации. Следовательно, все методы обновления параметров заменены "заглушками".

Тем не менее, слой участвует в алгоритмах обратного прохода и через него передается градиент ошибки на предыдущий нейронный слой. Как и ранее, сначала мы создаем кернел RevInHiddenGraddient на стороне OpenCL программы. На этот раз количество параметров кернела увеличилось. Мы будем передавать 4 указатели на буферы данных: буферы результаты и градиентов ошибки предыдущего слоя, параметров оптимизации и градиент ошибки на уровне результатов текущего слоя. И 3 константы: размер буфера параметров нормализации, тип оптимизации параметров и функция активации предыдущего слоя.

__kernel void RevInHiddenGraddient(__global float *inputs, __global float *inputs_gr,
                                   __global float *options, __global float *output_gr,
                                   int options_size,
                                   int optimization,
                                   int activation)
  {
   int n = get_global_id(0);
   int shift = (n * optimization == 0 ? 7 : 9) % options_size;

В теле кернела мы сначала идентифицируем анализируемый поток и определяем смещения в буферах данных. Алгоритм определения смещения в буферах описан выше при построении кернела прямого прохода.

Далее мы загружаем данные из глобальных буферов данных в локальные переменные.

   float variance = options[shift + 1];
   float inp = inputs[n];
   float k = options[shift + 3];

И скорректируем градиент ошибки на производную функции денормализации. Здесь следует обратить внимание, что на этапе денормализации все параметры нормализации являются константами и производная функции заметно упрощается.

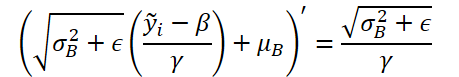
Реализуем в коде представленную функцию.

   float res = 0;
   if(k != 0)
      res = sqrt(variance) * output_gr[n] / k;
   if(isnan(res))
      res = 0;

После чего мы скорректируем градиент ошибки на производную функции активации предыдущего нейронного слоя.

   switch(activation)
     {
      case 0:
         res = clamp(res + inp, -1.0f, 1.0f) - inp;
         res = res * (1 - pow(inp == 1 || inp == -1 ? 0.99999999f : inp, 2));
         break;
      case 1:
         res= clamp(res + inp, 0.0f, 1.0f) - inp;
         res = res * (inp == 0 || inp == 1 ? 0.00000001f : (inp * (1 - inp)));
         break;
      case 2:
         if(inp < 0)
            res *= 0.01f;
         break;
      default:
         break;
     }

Результат операций сохраним в соответствующем элементе буфера градиентов ошибки предыдущего нейронного слоя.

//---
   inputs_gr[n] = res;
  }

Следующим этапом нам предстоит реализовать вызов данного кернела на стороне основной программы. Этот функционал выполняется в методе CNeuronRevINDenormOCL::calcInputGradients. А сам алгоритм постановки кернела в очередь выполнения полностью повторяет описанный выше для метода прямого прохода. Поэтому мы не будем сейчас останавливаться на его детальном рассмотрении.

Мы так же не будем подробно рассматривать вспомогательные методы класса. Их алгоритм довольно прост и доступен для самостоятельного ознакомления во вложении, где Вы найдете полный код всех методов нового класса и ранее созданных. Там же Вы можете самостоятельно ознакомиться со всеми программами, используемыми при подготовке статьи.

2.4 Точечные правки в классах более высокого уровня

Несколько слов надо сказать о внесении точечных правок в методы классов более высокого уровня, которые вызваны спецификой нашего нового класса CNeuronRevINDenormOCL. И прежде всего это касается инициализации и загрузки объектов данного класса.

При описании метода инициализации объекта нашего класса CNeuronRevINDenormOCL мы упоминали об особенности передачи указателя на объект слоя нормализации данных. Здесь надо понимать, что на момент описания архитектуры модели мы у нас нет указателя на данный объект по одной простой причине — данный объект ещё не создан. Мы можем лишь указать порядковый номер слоя. Его мы знаем исходя из описываемой архитектуры модели.

Однако мы четко знаем, что слой нормализации стоит перед слоем денормализации. При этом между ними еще может быть произвольное количество нейронных слоев. Значит, на момент создания объекта слоя денормализации в модели уже должен быть создан слой нормализации. И мы можем получить к нему доступ, но только внутри модели. Так как доступ к отдельным нейронным слоям закрыт для внешних программ.

Следовательно, в методе CNet::Create мы создаем отдельный блок для инициализации объекта слоя денормализации CNeuronRevINDenormOCL.

            case defNeuronRevInDenormOCL:
               if(desc.layers>=layers.Total())
                 {
                  delete temp;
                  return false;
                 }

Здесь мы сначала проверяем, чтобы слой с указанным идентификатором уже был создан в нашей модели.

Затем мы проверяем тип указанного слоя. Он должен быть слоем пакетной нормализации.

               if(((CLayer *)layers.At(desc.layers)).At(0).Type()!=defNeuronBatchNormOCL)
                 {
                  delete temp;
                  return false;
                 }

И только после успешного прохождения указанных контролей мы создаем новый объект.

               revin = new CNeuronRevINDenormOCL();
               if(!revin)
                 {
                  delete temp;
                  return false;
                 }

Инициализируем его.

               if(!revin.Init(outputs, 0, opencl, desc.count, desc.layers, 
                                  ((CLayer *)layers.At(desc.layers)).At(0)))
                 {
                  delete temp;
                  delete revin;
                  return false;
                 }

И добавляем в массив объектов.

               if(!temp.Add(revin))
                 {
                  delete temp;
                  delete revin;
                  return false;
                 }
               break;

Кроме того, есть нюанс и при загрузке ранее обученной модели. Как Вы знаете, в методе инициализации нашего нового класса мы создали разветвление алгоритма в зависимости от идентификатора слоя нормализации. Это было сделано с оглядкой на процесс загрузки предварительно обученной модели. Дело в том, что перед загрузкой объекта нам необходимо создать его "болванку". Это функционал выполняется в методе CLayer::CreateElement. И сложность момента заключается в том, что до загрузки данных мы не знаем идентификатор слоя нормализации. Поэтому мы указываем "-1" в качестве идентификатора и "NULL" вместо указателя на объект.

         case  defNeuronRevInDenormOCL:
            if(CheckPointer(OpenCL) == POINTER_INVALID)
               return false;
            revin = new CNeuronRevINDenormOCL();
            if(CheckPointer(revin) == POINTER_INVALID)
               result = false;
            if(revin.Init(iOutputs, index, OpenCL, 1, -1, NULL))
              {
               m_data[index] = revin;
               return true;
              }
            delete revin;
            break;

И далее в процессе загрузки загружаются уже все данные во внутренние объекты и переменные нашего класса. Но и тут есть нюанс. В процессе загрузки данных мы получим параметры нормализации, сохраненные после предварительного обучения модели. Но нас это не устраивает. Для дальнейшего обучения модели и её эксплуатации нам необходима синхронизация параметров между слоями нормализации и денормализации. Иначе у нас возникнет разрыв между распределениями исходных данных и наших прогнозов. Поэтому мы переходим в метод CNet::Load и после загрузки очередного нейронного слоя проверяем его тип.

bool CNet::Load(const int file_handle)
  {
........
........
//--- read array length
   num = FileReadInteger(file_handle, INT_VALUE);
//--- read array
   if(num != 0)
     {
      for(i = 0; i < num; i++)
        {
         //--- create new element
         CLayer *Layer = new CLayer(0, file_handle, opencl);
         if(!Layer.Load(file_handle))
            break;
         if(Layer.At(0).Type() == defNeuronRevInDenormOCL)
           {
            CNeuronRevINDenormOCL *revin = Layer.At(0);
            int l = revin.GetNormLayer();
            if(!layers.At(l))
              {
               delete Layer;
               break;
              }

В случае обнаружения слоя денормализации CNeuronRevINDenormOCL мы запрашиваем указатель на слой нормализации и проверяем наличие загруженного такого слоя.

Мы так же проверяем тип этого слоя.

            CNeuronBaseOCL *neuron = ((CLayer *)layers.At(l)).At(0);
            if(neuron.Type() != defNeuronBatchNormOCL)
              {
               delete Layer;
               break;
              }

И после успешного прохождения указанных точек контроля мы инициализируем объект слоя с передачей указателя на соответствующий слой нормализации.

            if(!revin.Init(revin.getConnections(), 0, opencl, revin.Neurons(), l, neuron))
              {
               delete Layer;
               break;
              }
           }
         if(!layers.Add(Layer))
            break;
        }
     }
   FileClose(file_handle);
//--- result
   return (layers.Total() == num);
  }

И далее по ранее созданному алгоритму.

С полным кодом всех классов и их методов, а так же всех программ, используемых при подготовке статьи, Вы можете ознакомиться во вложении.

2.5 Архитектура обучаемых моделей

Выше мы реализовали подходы, предложенные авторами метода RevIN средствами MQL5. И теперь пришло время включить их в архитектуру наших моделей. Как и обсуждалось ранее, денормализацию мы будем использовать в модели Энкодере с целью реализации возможности обучения его для прямого прогнозирования последующих состояний окружающей среды. Количество прогнозируемых состояний окружающей среды (в нашем случае последующих свечей) мы определим константой NForecast.

#define        NForecast               6             //Number of forecast

Так как мы планируем обучать Энкодер отдельно от Актера и Критика, то и описание архитектуры Энкодера мы вынесем в отдельный метод CreateEncoderDescriptions. В параметры которому мы передадим лишь один указатель на динамический массив для сохранения архитектуры создаваемой модели. Здесь следует обратить внимание, что наша реализация класса CNeuronRevINDenormOCL не позволяет выделить Декодер в отдельную модель.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

В теле метода мы проверяем полученный указатель и, при необходимости, создаем новый экземпляр объекта динамического массива.

На вход модели мы, как и ранее, подаем "сырые" исходные данные описания состояния окружающей среды.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Полученные данные проходят первичную обработку в слое пакетной нормализации, и мы запомним порядковый номер слоя.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = MathMax(1000, GPTBars);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

После нормализации исходных данных мы создаем их эмбединг с добавлением во внутренний стек.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
     {
      int temp[] = {4, 1, 1, 1, 2};
      ArrayCopy(descr.windows, temp);
     }
   prev_count = descr.count = GPTBars;
   int prev_wout = descr.window_out = EmbeddingSize / 2;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * 5;
   descr.step = descr.window = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Затем добавляем позиционное кодирование данных.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPEOCL;
   descr.count = prev_count;
   descr.window = prev_wout * 5;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Подготовленные таким образом данные мы подаем на вход блока из 5 слоев CNeuronConformer.

//--- layer 5-10
   for(int i = 0; i < 5; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronConformerOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 4;
      descr.window_out = EmbeddingSize;
      descr.layers = 5;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }
     }

Для целей проверки метода в качестве декодера мы используем полносвязный слой с соответствующим количеством элементов. Однако для повышения качества прогнозирования рекомендуется использовать Декодер с более сложной архитектурой.

//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NForecast*BarDescr;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Так как мы работаем с нормализованными данными и предполагаем, что их дисперсия близка к "1", а среднее значение к "0". То в качестве функции активации на выходе Декодера используем гиперболический тангенс (tanh). Как известно, диапазон его значений от "-1" до "1".

И в завершении денормализуем прогнозные значения.

//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   prev_count = descr.count = prev_count;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers=1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Чтобы уже завершить работу по описанию архитектуры моделей, предлагаю сразу рассмотреть построение Актера и Критика. Архитектура указанных моделей описывается в методе CreateDescriptions. Она во многом заимствована из предыдущей статьи, но есть нюанс.

В параметрах метод получает указатели на 2 динамических массива.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

В теле метода мы проверяем полученные указатели и, при необходимости, создаем новые экземпляры объектов.

На вход Актера мы подаем тензор описания состояния счета и открытых позиций.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Генерируем эмбединг данного представления.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

И далее идет блок Кросс-Внимания, в котором анализируется текущее состояние счета в свете прогнозных состояний окружающей среды.

//--- layer 2-4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, NForecast};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, BarDescr};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 16;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }

И завершает модель Актера блок принятия решений со стохастической политикой.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Аналогичным образом мы строим и модель Критика. Только вместо описания состояния счета, Критик анализирует действия Актера в контексте прогнозных состояний окружающей среды.

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 2-4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, NForecast};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, BarDescr};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 16;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!critic.Add(descr))
        {
         delete descr;
         return false;
        }
     }

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

И на выходе Критика мы получаем четкую, а не стохастическую, оценку действий Агента.

2.6 Программы обучения моделей

После описания архитектуры обучаемых моделей мы переходим к созданию программ непосредственного их обучения. Для обучения Энкодера мы создадим советник "...\Experts\RevIN\StudyEncoder.mq5". Архитектура построения советника заимствована из предыдущих работ и была уже не раз рассмотрена в рамках статей данной серии. Поэтому мы остановимся лишь на методе непосредственного обучения модели Train.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

В теле метода мы, как обычно, генерируем вектор вероятностей выбора траекторий в зависимости от их доходности. Надо сказать, что для прогнозирования будущих состояний окружающей среды все проходы одинаковы. Ведь Энкодер не анализирует состояние счета и открытые позиции. Тем не менее мы оставили данный функционал на случай наличия в буфере воспроизведения опыта проходов на различных исторических промежутках.

Затем мы подготавливаем локальные переменные и организовываем систему циклов обучения модели.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int batch = GPTBars + 48;
      int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - batch));
      if(state <= 0)
        {
         iter--;
         continue;
        }
      Encoder.Clear();
      int end = MathMin(state + batch, Buffer[tr].Total - NForecast);

В теле внешнего цикла мы сэмплируем траекторию из буфера воспроизведения опыта и состояние начала обучения на ней. Затем определяем конечное состояние пакета обучения и очищаем внутренний стек модели. После чего организовываем вложенный цикл обучения на выбранном отрезке исторических данных.

      for(int i = state; i < end && !IsStopped() && !Stop; i++)
        {
         bState.AssignArray(Buffer[tr].States[i].state);
         //--- State Encoder
         if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Здесь мы сначала загружаем анализируемое состояние из обучающей выборки. Переносим его в буфер данных. И осуществляем прямой проход Энкодера путем вызова соответствующего метода нашей модели.

На следующем этапе нам предстоит подготовить целевые данные. Для этого мы организуем еще один вложенный цикл, в котором возьмем из обучающей выборки необходимое количество последующих состояний и добавим их в буфер данных.

         //--- Collect target data
         bState.Clear();
         for(int fst = 1; fst <= NForecast; fst++)
           {
            if(!bState.AddArray(Buffer[tr].States[i + fst].state))
               break;
           }

После сбора целевых значений мы можем осуществить обратный проход Энкодера с целью минимизации ошибки между прогнозными и целевыми значениями.

         if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

И далее нам остается лишь проинформировать пользователя о ходе процесса обучения и перейти к следующей итерации.

         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, 
                                                                          Encoder.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

После успешного завершения всех итераций обучения мы очищаем поле комментариев.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Выводим в журнал информацию о достигнутых результатах обучения и инициализируем завершение работы советника.

Обучение модели прогнозирования будущих состояний окружающей среды полезно. Но наша цель — обучение политики Актера. И следующим этапом мы переходим к созданию советника обучения Актера и Критика "...\Experts\RevIN\Study.mq5". Советник строится по той же архитектуре, поэтому мы коснемся лишь точечных изменений.

Первое, в процессе инициализации советника отсутствие предварительно обученного Энкодера генерирует ошибку не корректной инициализации программы.

int OnInit()
  {
//---
........
........
//--- load models
   float temp;
   if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true))
     {
      PrintFormat("Error of load Encoder: %d", GetLastError());
      return INIT_FAILED;
     }
........
........
//---
   return(INIT_SUCCEEDED);
  }

Второе, Энкодер в данной модели не обучается и, соответственно, не сохраняется.

void OnDeinit(const int reason)
  {
//---
   if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE))
     {
      Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true);
      Critic.Save(FileName + "Crt.nnw", 0, 0, 0, TimeCurrent(), true);
     }
   delete Result;
   delete OpenCL;
  }

Кроме того, есть нюанс при использовании Энкодера в качестве источника исходных данных для Актера и Критика. В начале статьи мы говорили о важности использования нормализованных данных для обучения и эксплуатации моделей. Слой Денормализации на выходе Энкодера напротив возвращает наши прогнозы в распределение исходных данных, что делает их несопоставимыми.

Однако, мы уже давно реализовали функционал обращения к скрытым слоям модели для извлечения данных. И мы воспользуемся этим функционалом для получения нормализованных прогнозных данных из предпоследнего слоя Энкодера. Именно эти данные мы будем использовать в качестве исходных данных для Актера и Критика. Указатель на необходимый слой мы укажем в константе LatentLayer.

#define        LatentLayer             11

Тогда вызов прямого прохода Критика примет вид:

         if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder),LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

или

         if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder),LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Соответственно, вызов прямого прохода Актера мы запишем как

         if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder),LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

И не забудем указать идентификатор слоя при вызове методов обратного прохода наших моделей.

         if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder),LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder),LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         Critic.TrainMode(false);
         if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder),LatentLayer) ||
            !Actor.backPropGradient((CNet *)GetPointer(Encoder), LatentLayer, -1, true))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Такие же точечные изменения были внесены в советники взаимодействия с окружающей средой. Но с ними я предлагаю Вам ознакомиться самостоятельно. Полный код всех программ, используемых при подготовке статьи, Вы можете найти во вложении.

3. Тестирование

После создания всех необходимых программ мы можем перейти к обучению и тестированию моделей, что позволит оценить нам эффективность предложенных решений.

Как обычно, обучение и тестирование моделей мы осуществляем на реальных исторических данных инструмента EURUSD тайм-фрейм H1.

Время не стоит на месте. А вместе с ним и пополняется наша база исторических данных. При подготовке данной статьи я решил расширить исторический интервал обучающей выборки до всего 2023 года. При этом проверять обученные модели мы будем на данных Января 2024 года.

Для создания первичной обучающей выборки воспользовался фреймворком Real-ORL. Его подробное описание вы найдете по ссылке. Я загрузил данные о сделках с 20 реальных сигналов. И запустил советник "...\Experts\RevIN\ResearchRealORL.mq5" в режиме медленной оптимизации.

В результате я получил 20 траекторий. И не все из них прибыльные.

На этом этапе мы сначала запускаем обучение Энкодера. А после его завершение осуществляем первичное обучение Актера и Критика. Первичное потому, что 20 траекторий очень мало для получения оптимальной политики Актера.

Следующим этапом мы пополняем нашу обучающую выборку. Для этого в режиме медленной оптимизации запускам советник "...\Experts\RevIN\Research.mq5", который проверит на реальных исторических данных обучающего периода текущую политику Актера и добавит проходы в нашу обучающую выборку.

На данном этапе не стоит ожидать каких-то выдающихся результатов. Отрицательный результат тоже результат. И хороший опыт для дальнейшего обучения моделей. Кроме того, подобная итерация позволяет лучше узнать окружающую среду в области действий текущей политики Актера.

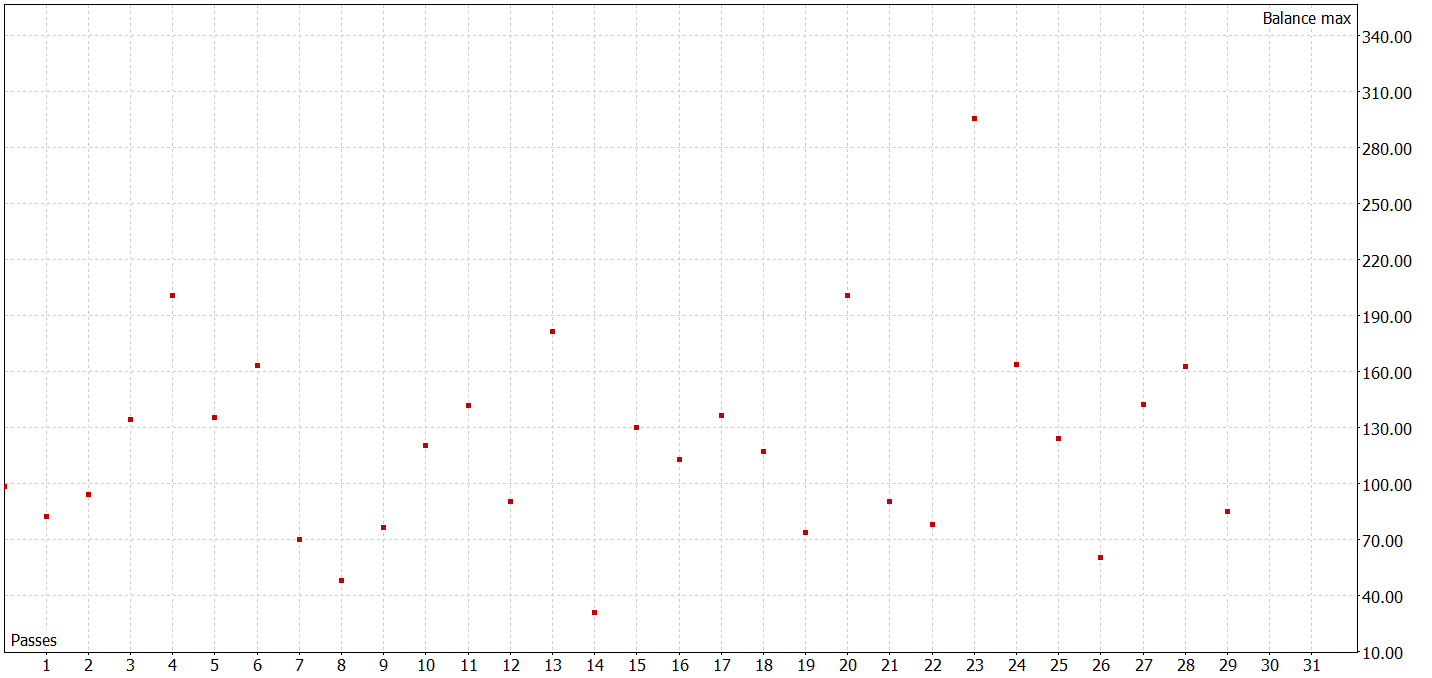
После нескольких итераций обучения политики Актера и сбора дополнительных данных в обучающую выборку мне удалось обучить модель способную генерировать прибыль как на обучающей, так и на тестовой выборке.

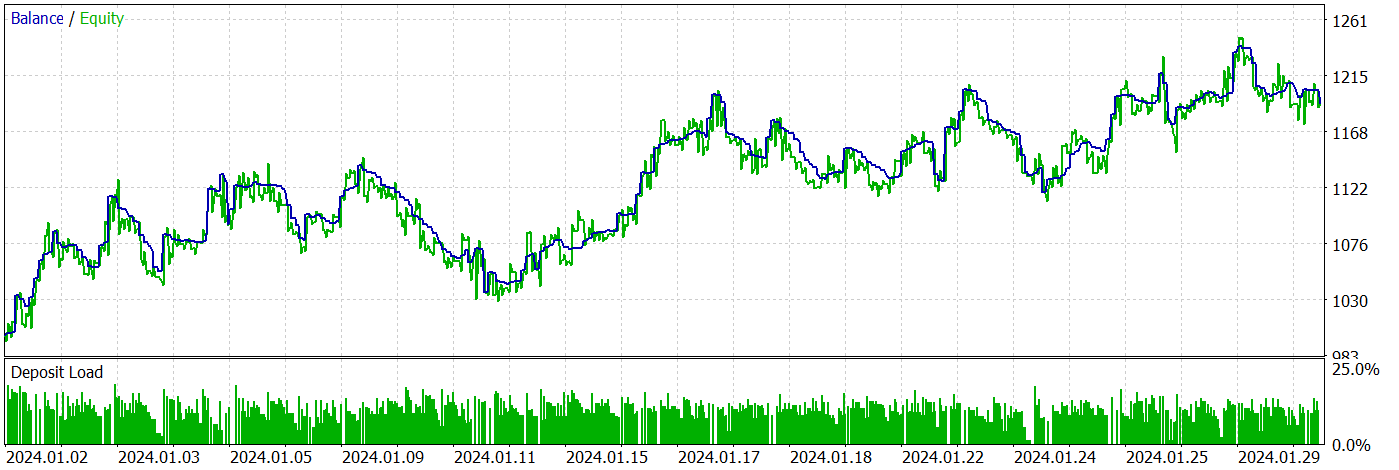
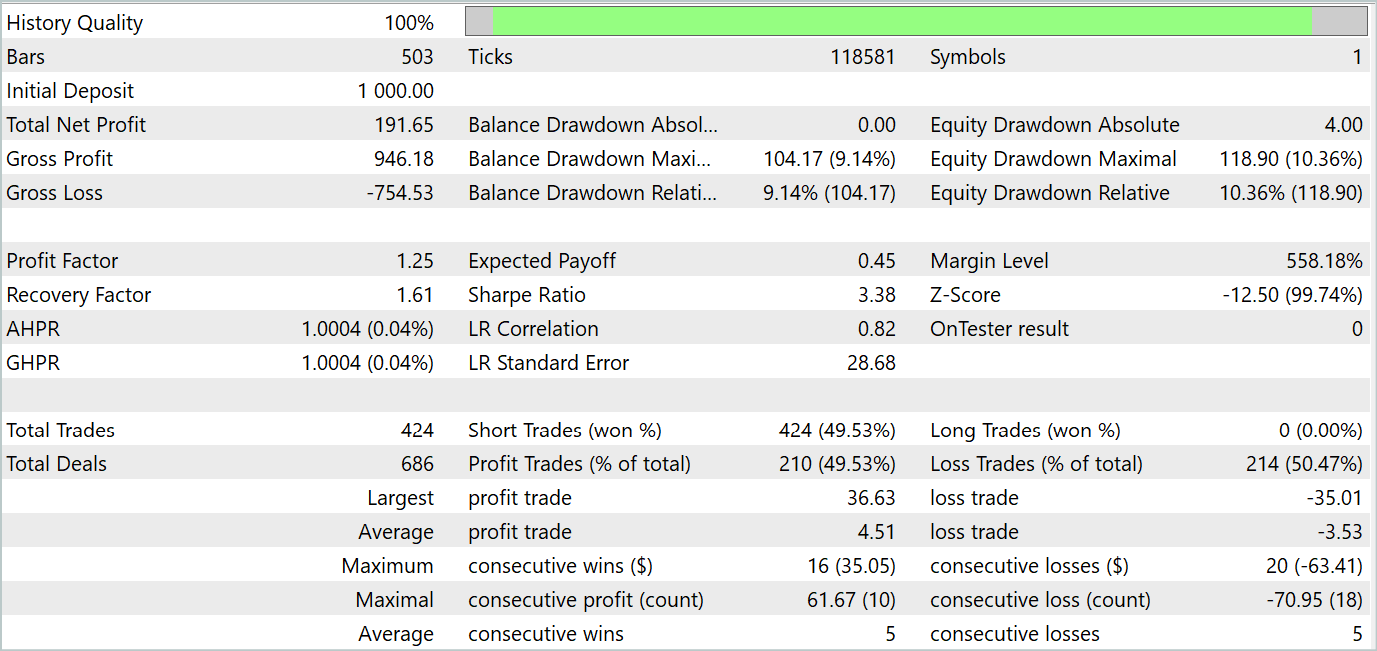
За период тестирования советник совершил 424 сделки, 210 из них были закрыты с прибылью. Что составило 49.53%. Однако, благодаря превышению максимальной и средней прибыльной сделки над аналогичными показателями убыточных сделок позволило в целом за период тестирования получить прибыль. При этом максимальная просадка по балансу и эквити показали близкие результаты (9.14% и 10.36% соответственно). Профит-фактор за период тестирования составил 1.25. А коэффициент Шарпа достиг отметки 3.38.

Заключение

В данной статье мы познакомились с методом RevIN, который представляет собой важный шаг в развитии техник нормализации и денормализации. Особенно для моделей глубокого обучения в контексте прогнозирования временных рядов. Он позволяет сохранять и восстанавливать статистическую информацию о временных рядах, что является критическим для точного прогнозирования. RevIN демонстрирует устойчивость к изменению динамики данных со временем. Это делает его эффективным инструментом для решения проблемы сдвига распределения во временных рядах.

Одним из важных преимуществ RevIN является его гибкость и применимость к различным моделям глубокого обучения. Он может быть легко внедрен в различные архитектуры нейронных сетей и даже применен к нескольким слоям, обеспечивая стабильное качество прогнозирования.

В практической части статьи мы реализовали предложенные подходы средствами MQL5. Обучили модели на реальных исторических данных. И протестировали их на новых данных, не входящих в обучающую выборку.

Результаты тестирования показали способность обученных моделей обобщать данные обучающей выборки и генерировать прибыль как на исторических данных обучающей выборки, так и за её пределами.

Однако следует напомнить, что все программы, представленные в статье, носят демонстрационный характер и предназначены только для проверки предложенных подходов.

Ссылки

Reversible Instance Normalization for Accurate Time-Series Forecasting against Distribution Shift

Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	StudyEncoder.mq5	Советник	Советник обучения Энкодера
5	Test.mq5	Советник	Советник для тестирования модели
6	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
7	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
8	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL