Нейросети в трейдинге: Transformer с относительным кодированием

Введение

Прогнозирование цен и рыночных трендов — центральная задача для успешной торговли и управления рисками. Качественные прогнозы ценовых движений помогают трейдерам своевременно принимать решения и избегать финансовых потерь. Однако в условиях высокой волатильности рынков традиционные модели машинного обучения могут оказаться ограниченными в своих возможностях.

Переход от обучения моделей с нуля к предварительному обучению на больших наборах неразмеченных данных, с последующей тонкой настройкой для конкретных задач, позволяет достичь высокой точности прогнозирования без необходимости сбора огромных объемов новых данных. К примеру, модели на основе архитектуры Transformer, адаптированные для финансовых данных, могут использовать информацию о корреляциях между активами, временными зависимостями и другими факторами для построения более точных прогнозов. Внедрение альтернативных механизмов внимания помогает учитывать важные рыночные зависимости, что существенно повышает производительность моделей. Это открывает новые возможности для создания торговых стратегий, минимизируя ручные настройки и сложные модели, опирающиеся на правила.

Один из таких альтернативных алгоритмов внимания был представлен в работе "Relative Molecule Self-Attention Transformer". Авторы статьи разработали новую формулу Self-Attention для молекулярных графов, которая тщательно обрабатывает различные входные функции для получения повышенной точности и надежности во многих химических областях. Relative Molecule Attention Transformer (R-MAT) является предварительно обученной моделью на основе Transformer. Это новый вариант относительного Self-Attention, который позволяет эффективно объединять информацию о расстоянии и окрестностях. R-MAT обеспечивает современную и конкурентоспособную производительность в широком спектре задач.

1. Алгоритм R-MAT

При обработке естественного языка ванильный слой Self-Attention не учитывает позиционную информацию входных токенов, то есть, при перестановке исходных данных результат останется прежним. Для того чтобы добавить позиционную информацию в исходные данные, ванильный Transformer обогащает ее кодированием абсолютного положения. С другой стороны, относительное позиционное кодирование добавляет относительное расстояние между каждой парой токенов, что приводит к существенному выигрышу в некоторых задачах. В алгоритме R-MAT используется относительное кодирование позиции токенов.

Основная идея заключается в повышении гибкости обработки информации о графах и расстояниях. Авторы метода R-MAT адаптировали позиционное относительное кодирование с целью обогащения блока Self-Attention информацией эффективного представления относительных позиций элементов в исходной последовательности.

Взаимное расположение двух атомов в молекуле характеризуется тремя взаимосвязанными факторами:

• их относительным расстоянием,
• расстоянием в молекулярном графе,
• их физико-химическим отношением.

Два атома представлены векторами 𝒙i, 𝒙j размерностью D. Авторы предлагают кодировать их отношение с помощью эмбединга отношений атомов 𝒃ij размерности D′. Это вложение затем будет использоваться в модуле Self-Attention после проекционного слоя.

Вначале осуществляется кодирование порядка окрестности между двумя атомами с информацией о том, сколько других вершин находится между узлами i и j в исходном молекулярном графе. Затем используется радиальное базисное кодирование расстояний. И в завершении выделяется каждая связь, чтобы отразить физическое отношение между парами атомов.

Авторы метода отмечают, что, хотя эти функции могут быть легко изучены в ходе предварительного обучения, такое конструирование может быть очень полезным для обучения R-MAT на небольших наборах данных.

Полученный токен 𝒃ij для каждой пары атомов в молекуле используется для определения нового слоя Self-Attention, который авторы метода называли относительным Self-Attention молекулы (Relative Molecule Self-Attention).

В новой архитектуре авторы метода зеркально отражают дизайн Query-Key-Value ванильного Self-Attention, токен 𝒃ij преобразуется в векторы, специфичные для ключа и значения 𝒃ijV, 𝒃ijK с использованием двух нейронных сетей φV и φK. Каждая нейронная сеть состоит из двух слоев. Скрытый слой, общий для всех голов внимания и выходного слоя, который создает отдельный относительный эмбединг для разных голов внимания. Относительное Self-Attention можно выразить следующим образом:

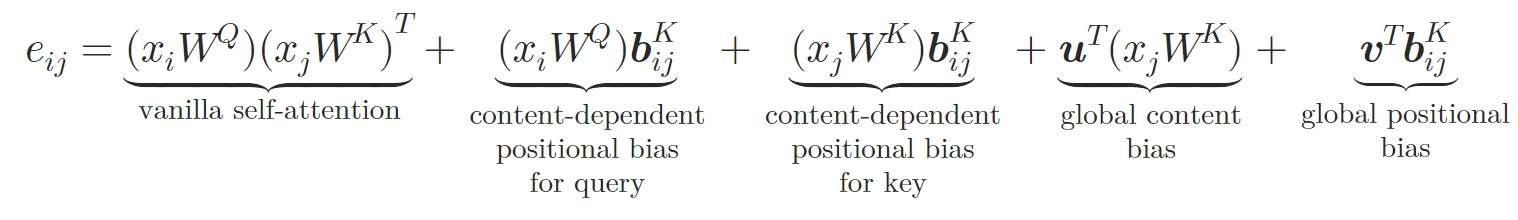
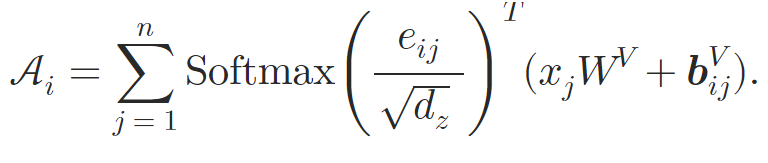
где 𝒖, 𝒗 являются обучаемыми векторами.

Таким образом, авторы метода обогащают блок Self-Attention за счет встраивания атомных отношений. На этапе вычисления весов внимания добавляется зависимое от содержания позиционное смещение, глобальное смещение контекста и глобальное позиционное смещение, которые рассчитываются на основе 𝒃ijK. Затем, во время расчета средневзвешенного внимания, авторы метода так же включают информацию о другом эмбединге 𝒃ijV.

Блок относительного Self-Attention используется для создания архитектуры Transformer относительного молекулярного внимания (Relative Molecule Attention Transformer — R-MAT).

Исходные данные передаются в виде матрицы размера Nатом×36, которые обрабатываются с помощью стека из N слоев внимания Relative Molecule Self-Attention. За каждым слоем внимания следует MLP с остаточной связью, аналогично ванильной модели Transformer.

После обработки исходных данных с использованием слоев внимания, авторы метода объединяют представление в вектор фиксированного размера. Для этого используется пулинг Self-Attention.

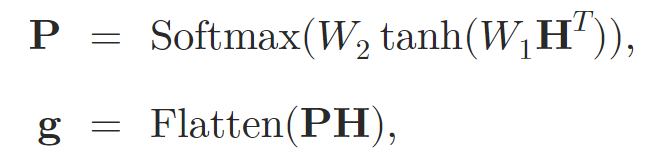
где 𝐇 — это скрытое состояние, полученное из слоев Self-Attention, W1 и W2 — объединяющие веса внимания.

Встраивание графов 𝐠 затем передается в двухуровневый MLP с функцией активации leaky-ReLU, на выходе которой мы получаем прогнозные значения.

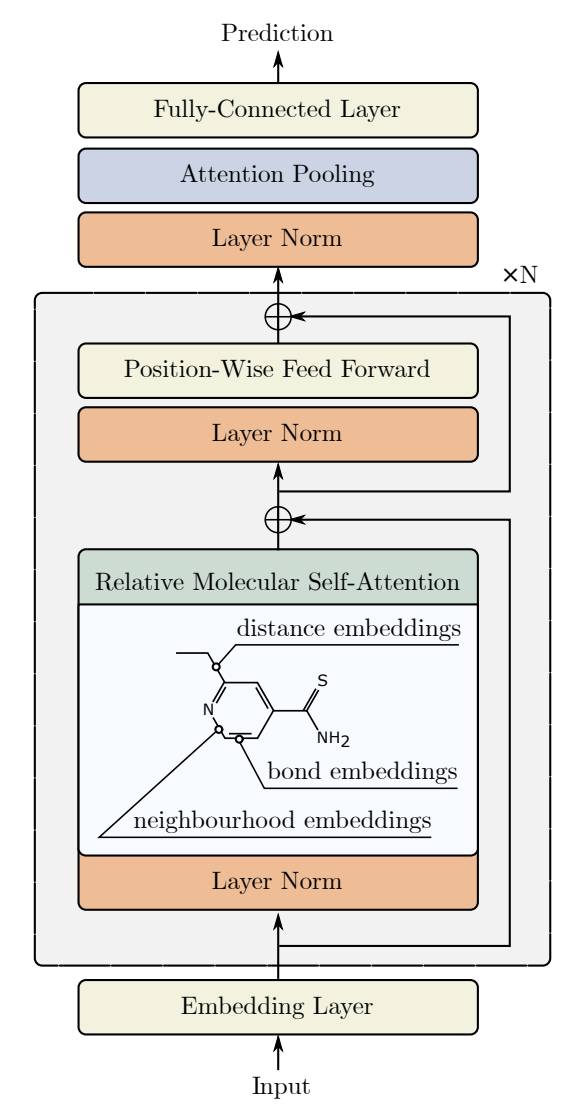
Авторская визуализация метода представлена ниже.

2. Реализация средствами MQL5

После рассмотрения теоретических аспектов предложенного метода Relative Molecule Attention Transformer (R-MAT), мы переходим к построению своего видения предложенных подходов средствами MQL5. И сразу хочу сказать, что построение предложенного алгоритма я решил разделить на блоки. Вначале мы создадим отдельный объект для реализации алгоритма относительного Self-Attention, а затем соберем модель R-MAT в отдельном классе верхнего уровня.

2.1 Модуль относительного Self-Attention

Как вы знаете, основной объем вычислений мы вынесли в контекст OpenCL. Следовательно, приступая к реализации нового алгоритма, мы должны добавить недостающие кернелы в нашу OpenCL-программу. Первым мы создадим кернел прямого прохода MHRelativeAttentionOut. Хотя данный кернел мы создавали на базе ранее рассмотренных реализаций алгоритма Self-Attention, здесь легко заметить значительное увеличение числа глобальных буферов, с назначением которых мы познакомимся в процессе построения алгоритма.

__kernel void MHRelativeAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                     __global const float *k,         ///<[in] Matrix of Keys
                                     __global const float *v,         ///<[in] Matrix of Values
                                     __global const float *bk,        ///<[in] Matrix of Positional Bias Keys
                                     __global const float *bv,        ///<[in] Matrix of Positional Bias Values
                                     __global const float *gc,        ///<[in] Global content bias vector
                                     __global const float *gp,        ///<[in] Global positional bias vector
                                     __global float *score,           ///<[out] Matrix of Scores
                                     __global float *out,             ///<[out] Matrix of attention
                                     const int dimension              ///< Dimension of Key
                                    )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k_id = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Данный кернел мы планируем выполнять в трехмерном пространстве задач, каждое из которых соответствует размерностям Query, Kye и Heads. В рамках второго измерения мы создаем рабочие группы.

В теле кернела мы сразу идентифицируем текущей поток во всех измерениях пространства задач, а так же определяем его границы. После чего определяем константы смещения в буферах данных для доступа к необходимым элементам.

   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Тут же мы создаем массив в локальной памяти, для обмена информацией внутри рабочей группы.

   __local float temp[LOCAL_ARRAY_SIZE];

Далее, согласно алгоритма относительного Self-Attention, нам предстоит вычислить коэффициенты внимания. Для этого нам предстоит вычислить скалярное произведение нескольких векторов и суммировать полученные результаты. Здесь мы воспользуемся тем свойством, что размерности всех умножаемых векторов равны. Следовательно, нам достаточно одного цикла для умножения всех необходимых векторов.

//--- score
   float sc = 0;
   for(int d = 0; d < dimension; d++)
     {
      float val_q = q[shift_q + d];
      float val_k = k[shift_kv + d];
      float val_bk = bk[shift_kv + d];
      sc += val_q * val_k + 
	    val_q * val_bk + 
            val_k * val_bk + 
            gc[shift_q + d] * val_k + 
            gp[shift_q + d] * val_bk;
     }

Следующим шагом нам предстоит нормализовать полученные коэффициенты зависимости в разрезе отдельных Query. Для нормализации мы используем функцию SoftMax аналогично ванильному алгоритму. Поэтому и алгоритм нормализации перекочевал из имеющихся наработок без изменений. Здесь мы сначала вычисляем экспоненциальное значение коэффициента.

   sc = exp(sc / koef);
   if(isnan(sc) || isinf(sc))
      sc = 0;

А затем суммируем полученные коэффициенты в рамках рабочей группы с использованием массива, созданного ранее в локальной памяти.

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   uint count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Теперь мы можем разделить ранее полученный коэффициент на общую сумму и сохранить нормализованное значение в соответствующий глобальный буфер.

//--- score
   float sum = temp[0];
   if(isnan(sum) || isinf(sum) || sum <= 1e-6f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

После вычисления нормализованных коэффициентов зависимости, мы можем вычислить результат операции внимания. Здесь алгоритм очень близок к ванильному. Мы лишь добавляем суммирование векторов Value и bijV перед умножением на коэффициент внимания.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = sc * (val_v + val_bv);
      if(isnan(val) || isinf(val))
         val = 0;
      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      if(k_id == 0)
         out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]);
     }
  }

Наверное стоит еще раз напомнить об аккуратности использования барьеров для синхронизации операций между потоками рабочей группы. Их расстановка по коду кернела должна быть осуществлена таким образом, чтобы каждый отдельный поток рабочей группы подошел к барьеру одинаковое количество раз. В коде не должно быть обходов барьеров и ранних выходов до посещения всех точек синхронизации. В противном случае, мы рискуем получить зависание работы кернела, когда отдельные потоки будут ждать подхода к барьеру потока, завершившего свои операции ранее.

Алгоритм обратного прохода реализован в кернеле MHRelativeAttentionInsideGradients. Его реализация полностью инверсирует операции рассмотренного выше кернела прямого прохода и во многом заимствована из ранее рассмотренных реализаций. Поэтому я предлагаю вам ознакомиться с ним самостоятельного. Полный код всех OpenCL-программы приведен во вложении.

А мы переходим к работе над основной программой. Здесь мы создадим класс CNeuronRelativeSelfAttention, в котором и реализуем алгоритм относительного Self-Attention. Но прежде чем приступить к его реализации, необходимо обсудить некоторые аспекты относительного позиционного кодирования.

Авторы фреймворка R-MAT предложили свой алгоритм для решения задач в химической промышленности. И строили алгоритм позиционного описания атомов молекул, исходя из специфики решаемых задач. Для нас расстояние между свечами и их признаками также имеет значение, но есть нюанс. Помимо расстояния, нам так же важно направление. Только однонаправленное ценовое движение формирует тенденции, переходящие в тренды.

Второй момент — это размер анализируемой последовательности. Количество атомов в молекуле часто ограничено довольно небольшим числом. И в таком случае можно вычислить вектор отклонения для каждой пары атомов. В нашем же случае груда анализируемой истории может быть довольно большой. И в таком случае вычисление и хранение отдельных векторов отклонений для каждой пары анализируемых свечей может оказаться довольно ресурсоемкой задачей.

Поэтому было принято решение отказаться от предложенной авторами методологии вычисления отклонений между отдельными элементами последовательности. В поисках альтернативного механизма, мы воспользовались довольно простым решением — умножением матрицы исходных данных на свою транспонированную копию. С математической точки зрения, умножение 2 векторов равно произведению скалярных длин данных векторов на косинус угла между ними. Таким образом, произведение перпендикулярных векторов равно 0. При этом однонаправленные вектора дают положительное значение, а разнонаправленные — отрицательное. Следовательно, при сопоставлении одного вектора с рядом других, значение произведения векторов растет при уменьшении угла между векторами и ростом длины второго вектора.    

И теперь, когда мы определились с методологией, можно переходить к построению нашего нового объекта, структура которого приведена ниже.

class CNeuronRelativeSelfAttention   :  public CNeuronBaseOCL
  {
protected:
   uint                    iWindow;
   uint                    iWindowKey;
   uint                    iHeads;
   uint                    iUnits;
   int                     iScore;
   //---
   CNeuronConvOCL          cQuery;
   CNeuronConvOCL          cKey;
   CNeuronConvOCL          cValue;
   CNeuronTransposeOCL     cTranspose;
   CNeuronBaseOCL          cDistance;
   CLayer                  cBKey;
   CLayer                  cBValue;
   CLayer                  cGlobalContentBias;
   CLayer                  cGlobalPositionalBias;
   CLayer                  cMHAttentionPooling;
   CLayer                  cScale;
   CBufferFloat            cTemp;
   //---
   virtual bool      AttentionOut(void);
   virtual bool      AttentionGraadient(void);

   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRelativeSelfAttention(void) : iScore(-1) {};
                    ~CNeuronRelativeSelfAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRelativeSelfAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Как можно заметить, в представленной структуре нового класса довольно много внутренних объектов. С их функционалом мы познакомимся в процессе реализации алгоритмов методов класса. А сейчас для нас важно, что все объекты объявлены статично. Значит, мы можем оставить пустыми конструктор и деструктор класса. Инициализация всех объявленных и унаследованных объектов, как всегда, осуществляется в методе Init. В параметрах данного метода мы получаем константы, которые позволяют нам точно определить архитектуру создаваемого объекта. Легко заметить, что все параметры метода перекочевали из ванильного Multi-Head Self-Attention без изменений. Только параметр указания числа внутренних слоев "потерялся по дороге". Это намеренный шаг, так как в данной реализации количество слоев будет определяться объектом верхнего уровня путем создания достаточного количества внутренних объектов.

bool CNeuronRelativeSelfAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                        uint window, uint window_key, uint units_count, uint heads, 
                                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

В теле метода мы сразу вызываем одноименный метод родительского класса с передачей ему части полученных параметров. Как вы знаете, в методе родительского класса уже реализованы алгоритмы минимального контроля полученных параметров и инициализация унаследованных объектов. Мы лишь проверяем логический результат выполнения этих операций.

Затем мы сохраним полученные константы во внутренние переменные класса для последующего использования.

   iWindow = window;
   iWindowKey = window_key;
   iUnits = units_count;
   iHeads = heads;

И приступаем к инициализации объявленных внутренних объектов. Вначале мы инициализируем сверточные слои генерации сущностей Query, Key и Value в одноименных внутренних объектах. Параметры всех трех слоев мы используем идентичные.

   int idx = 0;
   if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;

Далее нам предстоит подготовить объекты для вычисления нашей матрицы расстояний. Для этого мы сначала создадим объект транспонирования исходных данных.

   idx++;
   if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

А затем создадим объект для записи результатов. Сама операция умножения матриц уже реализована в родительском классе.

   idx++;
   if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnits, optimization, iBatch))
      return false;

Далее нам предстоит организовать процесс генерации тензоров BK и BV. Как было сказано в теоретическом описании метода, для их генерации используется MLP, содержащая 2 слоя. Первый слой общий для всех голов внимания, а второй генерирует отдельные токены для каждой головы внимания. В своей реализации мы воспользуемся двумя последовательными сверточными слоями для каждой сущности. И установим гиперболический тангенс для создания нелинейности между слоями.

   idx++;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;

Ещё нам необходимы обучаемые вектора глобального смещения контекста и позиции. Для их создания мы воспользуемся подходом, которым пользовались в предыдущих работах. Я говорю о создании MLP из двух слоев. Один из них статичен и содержит "1", а второй обучаемый и генерирует необходимый тензор. Указатели на создаваемые объекты мы сохраним в массивах cGlobalContentBias и cGlobalPositionalBias.

   idx++;
   CNeuronBaseOCL *neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;
   idx++;
   CBufferFloat *buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;
   idx++;
   buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;

На этом этапе мы подготовили все объекты для корректной подготовки исходных данных нашего модуля относительного внимания. На следующем этапе мы переходим к объектам обработки результатов внимания. Вначале создадим объект записи результатов многоголового внимания и добавим его указатель в массив cMHAttentionPooling.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(neuron)
     )
      return false;

Далее мы добавим MLP операций пулинга.

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, 
                                                                       optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iHeads, iUnits, 1, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;

И добавим слой SoftMax на выходе.

   idx++;
   conv.SetActivationFunction(None);
   CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   softmax.SetHeads(iUnits);

Обратите внимание, что на выходе MLP пулинга мы получаем нормализованные коэффициенты влияния голов внимания для каждого отдельного элемента последовательности. Теперь нам достаточно умножить полученные вектора на соответствующие результаты блока многоголового внимания для получения итоговых результатов. Только вот размер вектора описания одного элемента последовательности будет равен нашей внутренней размерности. Поэтому мы добавляем ещё объекты масштабирования результатов до уровня исходных данных.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iUnits, optimization, iBatch) ||
      !cScale.Add(neuron)
     )
      return false;
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(LReLU);
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(None);

Теперь нам остается осуществить подмену буферов данных, для исключения излишних операций копирования, и вернуть логический результат выполнения операций метода вызывающей программе.

//---
   if(!SetGradient(conv.getGradient(), true))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Обратите внимание, что в данном случае мы осуществляем подмену только на указатель буфера градиентов. Это вызвано созданием остаточных связей внутри блока внимания. Но этот вопрос мы обсудим при реализации метода прямого прохода feedForward.

В параметрах метода прямого прохода мы получаем указатель на объект исходных данных, который сразу передаем в одноименный метод внутренних объектов для генерации сущностей Query, Key и Value.

bool CNeuronRelativeSelfAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cQuery.FeedForward(NeuronOCL) ||
      !cKey.FeedForward(NeuronOCL) ||
      !cValue.FeedForward(NeuronOCL)
     )
      return false;

Обратите внимание, что мы не проверяем актуальность полученного от внешней программы указателя на объект исходных данных. Ведь эта операция уже реализована в методах внутренних объектов. Следовательно, такая точка контроля в данном случае излишня.

Далее мы переходим к генерации сущностей определения расстояний между анализируемыми объектами. Мы транспонируем тензор исходных данных.

   if(!cTranspose.FeedForward(NeuronOCL) ||
      !MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnits, iWindow, iUnits, 1)
     )
      return false;

И тут же осуществляем матричное умножение тензора исходных данных на свою транспонированную копию. Результат операции мы используем для генерации сущностей BK и BV. Для этого организуем циклы перебора слоев соответствующих внутренних моделей.

   if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) ||
      !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject())
     )
      return false;
   for(int i = 1; i < cBKey.Total(); i++)
      if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1]))
         return false;
   for(int i = 1; i < cBValue.Total(); i++)
      if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1]))
         return false;

Затем организуем циклы генерации сущностей глобального смещения.

   for(int i = 1; i < cGlobalContentBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1]))
         return false;
   for(int i = 1; i < cGlobalPositionalBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1]))
         return false;

И на этом подготовительный этап работы завершен. Мы вызываем метод-обертку вышесозданного кернела прямого прохода относительного внимания.

   if(!AttentionOut())
      return false;

После чего приступаем к обработке результатов. Сначала воспользуемся MLP пулинга для генерации тензора влияния голов внимания.

   for(int i = 1; i < cMHAttentionPooling.Total(); i++)
      if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1]))
         return false;

А затем умножим полученные вектора на результаты многоголового внимания.

   if(!MatMul(((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).getOutput(),
              ((CNeuronBaseOCL*)cMHAttentionPooling[0]).getOutput(),
              ((CNeuronBaseOCL*)cScale[0]).getOutput(),
              1, iHeads, iWindowKey, iUnits)
     )
      return false;

Теперь нам остается масштабировать полученные значения с помощью MLP масштабирования.

   for(int i = 1; i < cScale.Total(); i++)
      if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1]))
         return false;

А полученные результаты суммируем с исходными данными, а результат запишем в буфер результатов верхнего уровня, унаследованный от родительского класса. Именно для выполнения этой операции нам потребовалось оставить без подмены указатель на буфер результатов.

   if(!SumAndNormilize(NeuronOCL.getOutput(), 
                       ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), 
                       Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

После реализации метода прямого прохода, мы обычно переходим к построению алгоритмов обратного прохода, которые организуем в методах calcInputGradients и updateInputWeights. В первом — осуществляется распределение градиентов ошибки до всех элементов модели, в соответствии с их влиянием на конечный результат. А во втором — корректируются параметры модели в сторону уменьшения ошибки модели. Я предлагаю вам самостоятельно ознакомиться с указанными методами во вложении. Там же вы найдете полный код данного класса и всех его методов. А мы переходим к следующему этапу нашей работы — построению объекта верхнего уровня с реализацией фреймворка R-MAT.

2.2 реализацией фреймворка R-MAT

Для организации алгоритма верхнего уровня фреймворка R-MAT, мы создадим новый класс CNeuronRMAT. Его структура представлена ниже.

class CNeuronRMAT :  public CNeuronBaseOCL
  {
protected:
   CLayer               cLayers;
   //---
   virtual bool         feedForward(CNeuronBaseOCL *NeuronOCL)
   override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRMAT(void) {};
                    ~CNeuronRMAT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRMAT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

И в отличие от предыдущего класса, он содержит лишь один вложенный объект динамического массива. На первый взгляд, этого может быть недостаточно для реализации столь комплексной архитектуры. Тем не менее, мы объявили динамический массив, в который будем записывать указатели на объекты, необходимые для построения алгоритма.

Динамический массив мы объявили статичным, и это позволяет нам оставить пустыми конструктор и деструктор класса. Инициализация внутренних и унаследованных объектов осуществляется в методе Init.

bool CNeuronRMAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                       uint window, uint window_key, uint units_count, uint heads, 
                       uint layers, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

В параметрах метода инициализации мы получаем константы, позволяющие нам однозначно интерпретировать пожелания пользователя касательно создаваемого объекта. И здесь мы видим привычный набор параметров блока внимания, включая количество внутренних слоев.

И первая операция, которую мы выполняем, — уже привычный вызов одноименного метода родительского класса. Затем мы подготовим локальные переменные.

   cLayers.SetOpenCL(OpenCL);
   CNeuronRelativeSelfAttention *attention = NULL;
   CResidualConv *conv = NULL;

И организуем цикл с числом итераций, равным количеству создаваемых внутренних слоев.

   for(uint i = 0; i < layers; i++)
     {
      attention = new CNeuronRelativeSelfAttention();
      if(!attention ||
         !attention.Init(0, i * 2, OpenCL, window, window_key, units_count, heads, optimization, iBatch) ||
         !cLayers.Add(attention)
        )
        {
         delete attention;
         return false;
        }

В теле цикла мы сначала создаем новый экземпляр выше реализованного объекта относительного внимания и инициализируем его, с передачей констант, полученных от внешней программы.

Как вы помните, в методе прямого прохода класса относительного внимания мы организовали поток остаточных связей. Поэтому мы можем опустить данную операцию на этом уровне и двигаться дальше.

Следующим шагом нам предстоит создать блок FeedForward аналогично ванильному Transformer. Однако для создания видимой простоты объекта верхнего уровня мы решили немного изменить архитектуру блока. И инициализируем вместо него сверточный блок с остаточной связью CResidualConv. Как можно догадаться из названия, данный блок также содержит остаточные связи и исключает необходимость их реализации в классе верхнего уровня.

      conv = new CResidualConv();
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window, window, units_count, optimization, iBatch) ||
         !cLayers.Add(conv)
        )
        {
         delete conv;
         return false;
        }
     }

Таким образом, нам достаточно создать лишь 2 объекта для организации одного слоя относительного внимания. Мы добавляем указатели на созданные объекты в наш динамический массив в порядке их последующего вызова и переходим к следующей итерации цикла генерации внутренних слоев внимания.

После успешного выполнения всех итераций цикла, мы осуществляем подмену указателей на буфера данных из нашего последнего внутреннего слоя в соответствующие буфера верхнего уровня.

   SetOutput(conv.getOutput(), true);
   SetGradient(conv.getGradient(), true);
//---
   return true;
  }

После чего передадим вызывающей программе логический результат выполнения операций и завершим работу метода.

Как можно заметить, благодаря разделению алгоритма фреймворка R-MAT на отдельные блоки, нам удалось построить довольно лаконичный объект верхнего уровня.

Здесь надо сказать, что подобная лаконичность прослеживается и в других методах класса. Возьмем, к примеру, метод прямого прохода feedForward. В параметрах метод получает указатель на объект исходных данных.

bool CNeuronRMAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *neuron = cLayers[0];
   if(!neuron.FeedForward(NeuronOCL))
      return false;

В теле метода мы сначала вызываем одноименный метод первого вложенного объекта. А затем организуем цикл последовательного перебора всех вложенных объектов с вызовом одноименных методов. При этом, в качестве исходных данных мы передаем указатель на предыдущий объект.

   for(int i = 1; i < cLayers.Total(); i++)
     {
      neuron = cLayers[i];
      if(!neuron.FeedForward(cLayers[i - 1]))
         return false;
     }
//---
   return true;
  }

А после завершения всех итераций цикла нам даже нет необходимости копировать данные, так как ранее мы организовали подмену буферов данных. Поэтому просто завершаем работу метода с передачей логического результата выполнения операций вызывающей программе.

Аналогичная ситуация и с методами обратного прохода, которые я предлагаю вам изучить самостоятельно. А мы на этом завершаем рассмотрение алгоритмов реализации фреймворка R-MAT средствами MQL5. Полный код представленных в данной статье классов  и всех их методов вы можете найти во вложении.

Там же вы найдете и полный код программ взаимодействия с окружающей средой и обучения моделей. Они полностью перенесены из предыдущих работ без изменений. Что же касается архитектуры моделей, то в нее внесены лишь точечные правки по замене одного слоя в Энкодере состояния окружающей среды.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRMAT;
   descr.window=BarDescr;
   descr.count=HistoryBars;
   descr.window_out = EmbeddingSize/2;                // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Полное описание архитектуры обучаемых моделей вы можете найти во вложении.

3. Тестирование

Мы провели серьезную работу по реализации фреймворка R-MAT средствами MQL5. И теперь переходим к заключительной части нашей работы — обучению моделей и тестированию полученной политики. В данной работе мы придерживаемся ранее описанного алгоритма обучения моделей. В данном случае мы одновременно обучаем все 3 модели: Энкодер состояния счета, Актер и Критик. Первая модель выполняет подготовительную работу по интерпретации рыночной ситуации. Актер принимает решение о совершении торговых операций на основе выученной политики. А Критик оценивает действия Актера и указывает направление корректировки политики.

Как и ранее, обучение моделей осуществляется на реальных исторических данных финансового инструмента EURUSD таймфрейм H1 за весь 2023 год. Параметры всех анализируемых индикаторов используются по умолчанию.

Обучение моделей проводится итерационно с периодическим обновлением обучающей выборки.

Эффективность обученной политики мы проверяем на исторических данных января 2024 года. Результаты тестов представлены ниже.

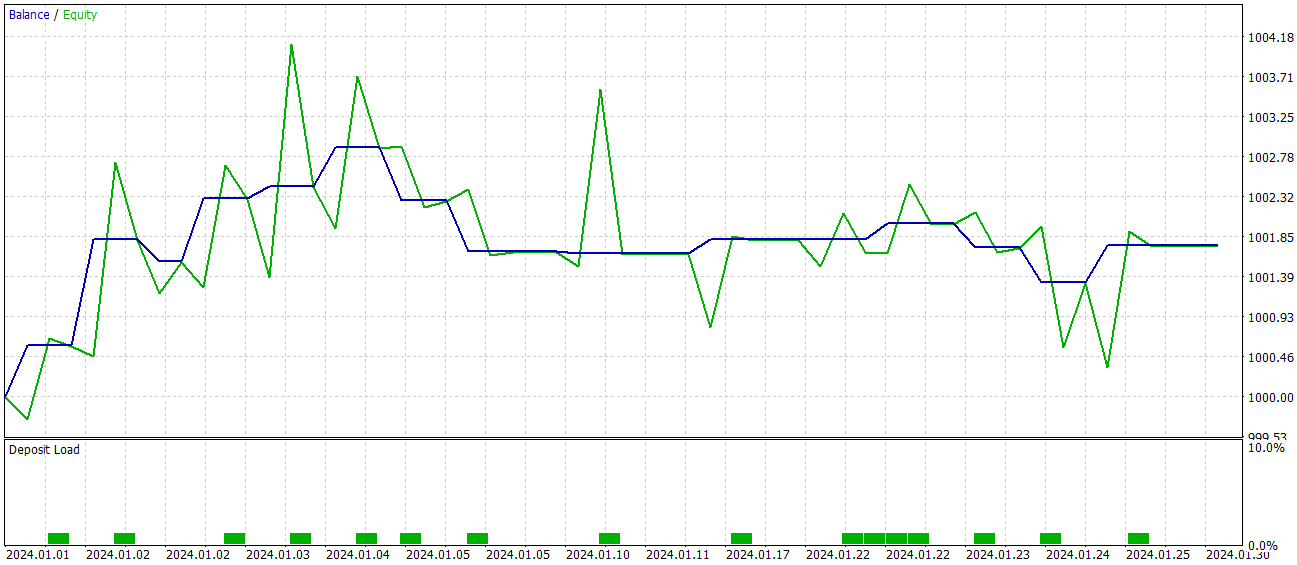
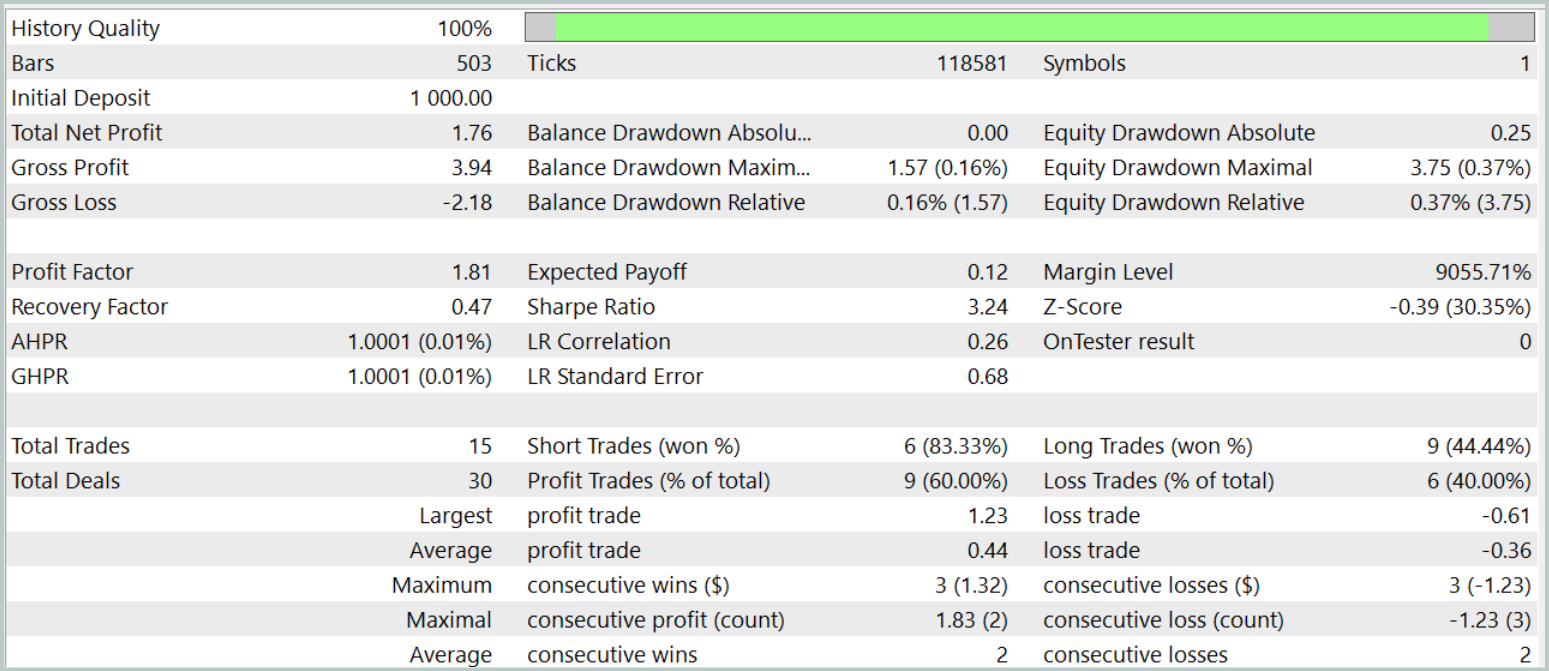
Как можно заметить, по результатам тестирования модель достигла уровня в 60% прибыльных операций. При этом наблюдается превышение как средней, так и максимальной прибыльной позиции над аналогичным показателем убыточных операций.

Тем не менее в данной "бочке меда есть ложка дегтя". За период тестирования модель совершила всего 15 торговых операций. А на графике баланса видно, что основной доход получен в начале месяца. А далее наблюдается флет. Поэтому в данном случае, мы можем говорить лишь о потенциале модели, но для работы на более длительном временном интервале с ней надо еще поработать.

Заключение

Модель Relative Molecule Attention Transformer (R-MAT) представляет собой значительный шаг вперёд в области прогнозирования сложных свойств. В контексте трейдинга R-MAT можно рассматривать как мощный инструмент для анализа сложных взаимосвязей между различными рыночными факторами, учитывая как их относительные расстояния, так и временные зависимости.

В практической части мы реализовали свое видение предложенных подходов средствами MQL5 и обучили полученные модели на реальных данных. Результаты тестирования позволяют говорить о потенциале предложенного решения. Однако модель требует еще доработок перед использованием в реальной торговле.

Ссылки

• Relative Molecule Self-Attention Transformer
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL