Как опередить любой рынок (Часть V): Альтернативные данные FRED EURUSD

MetaTrader 5 — Примеры | 23 апреля 2025, 13:12

293

Цель этой серии статей — помочь вам сориентироваться в постоянно расширяющемся потоке альтернативных финансовых данных. Современный инвестор, живущий в эпоху больших данных, может не обладать достаточными ресурсами, чтобы решить, какие альтернативные наборы данных ему следует включить в свою торговлю. Наша цель — предоставить вам необходимую информацию, чтобы вы могли принять обоснованное решение о том, какие альтернативные наборы данных вам, вероятно, следует рассмотреть, а без каких можно обойтись.

Обзор торговой стратегии

Корреляция является краеугольным принципом аналитического подхода к финансам. Если два актива коррелируют, то инвесторы, стремящиеся либо диверсифицировать свои портфели, либо максимально воспользоваться ожидаемыми изменениями цен, могут разумно использовать этот показатель для формирования своего портфеля.

Федеральная резервная система ведет набор индексов, которые служат обобщенными показателями валютной стоимости доллара. Из всех доступных нам индексов нас особенно интересовал номинальный обобщенный дневной индекс доллара (Nominal Broad Dollar Daily Index, NBDD). Индекс был создан в январе 2006 года со значением 100 пунктов. На момент написания статьи индекс достигал рекордно низких значений — около 86 пунктов — во время рецессии 2008 года и исторический максимум — около 128 пунктов — в 2022 году. Индекс находится в восходящем тренде с конца 2011 года и в настоящее время колеблется около 121 пункта. Это очень близко к историческому максимуму.

На графике ниже мы наложили обобщенный индекс доллара и курс пары EURUSD. Практически невозможно увидеть какую-либо существенную взаимосвязь между двумя временными рядами данных. Курс доллара США практически не виден и напоминает почти ровную линию в нижней части графика, в то время как обобщенный индекс доллара представлен четко красной линией.

Немасштабированные данные FRED

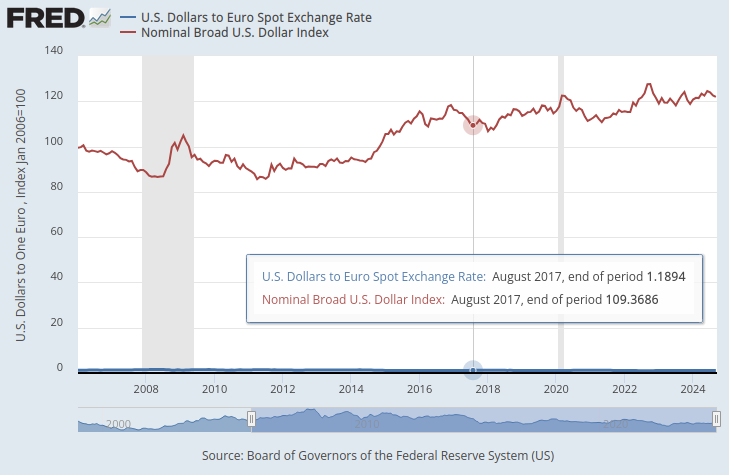
Рис. 1. Спотовый обменный курс доллара к евро и обобщенный индекс доллара

Если бы оба временных ряда данных находились в одинаковом масштабе, то проявилась бы очевидная закономерность. Мы изменим нашу ось Y так, чтобы она отражала процентное изменение данных временного ряда за 1 год. Сделав это, мы ясно видим, что индекс демонстрирует почти идеальную отрицательную корреляцию с курсом EURUSD.

Данные FRED EURUSD

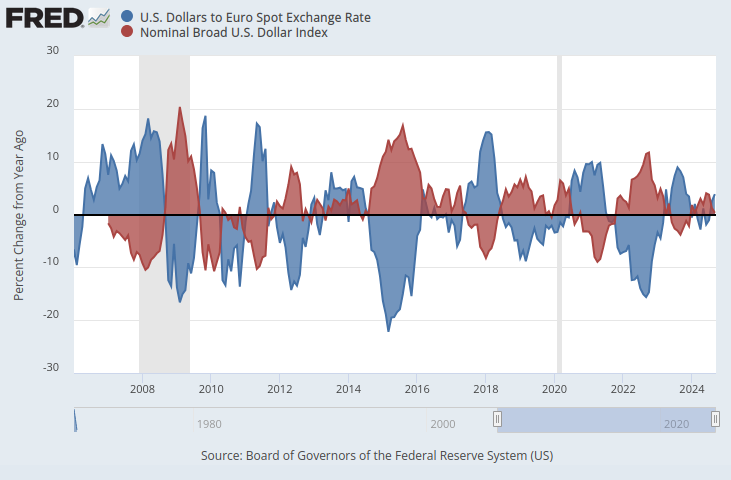
Рис. 2. Спотовый обменный курс доллара к евро и обобщенный индекс доллара в процентном отношении

Мы изучим возможность алгоритмического обучения торговой стратегии, которая использует эти наборы данных для прогнозирования будущего обменного курса EURUSD. Учитывая идеальную отрицательную корреляцию, потенциально наша модель могла бы получить некоторую информацию об обменном курсе, учитывая макроэкономические показатели из Экономической базы данных Федеральной резервной системы (Federal Reserve Economic Database, FRED).

Обзор методологии

Чтобы проверить обоснованность нашего предложения, мы начали с извлечения ежедневных исторических курсов обмена EURUSD из терминала MetaTrader 5 и объединили эти данные с тремя макроэкономическими наборами данных, которые мы получили из API FRED Python. Три набора данных временных рядов FRED регистрировали:

Процентные ставки по американским облигациям
Ожидаемые темпы инфляции в США
Обобщенный индекс доллара

Это позволило нам создать 3 набора данных для построения нашей модели ИИ:

Обычные рыночные котировки OHLC.
Альтернативные данные FRED
Расширенный набор из первых двух.

После объединения всех рассматриваемых наборов данных и преобразования масштабов для воспроизведения данных с сайта FRED, мы обнаружили, что уровни корреляции между ценами обменного курса EURUSD и обобщенным индексом доллара составили почти -0,9. Это почти идеальный результат! Более того, мы также наблюдали, что корреляция между текущим значением широкого индекса доллара и будущим значением закрытия EURUSD через 20 дней составила -0,7.

После визуализации нам удалось на удивление хорошо разделить данные временных рядов, с таким уровнем точности, который мы вряд ли демонстрировали ранее в этой серии статей. Похоже, что использование процентного изменения данных за относительно более длительные периоды времени позволяет нам очень хорошо разделять данные. Наши трехмерные диаграммы рассеяния еще раз подтвердили, насколько хорошо были разделены данные, и мы смогли определить явные бычьи и медвежьи зоны. Более того, когда мы построили диаграммы рассеяния данных с официального сайта FRED, мы смогли четко проследить тенденцию в данных. Тенденция на диаграмме рассеяния была четко определена даже без необходимости использования нашего обычного набора продвинутых аналитических инструментов в Python. Это дало нам уверенность в том, что в двух наборах данных временных рядов может содержаться некоторая потенциальная информация, которую, как мы надеемся, наша модель сможет усвоить.

Данные FRED показывают тенденцию

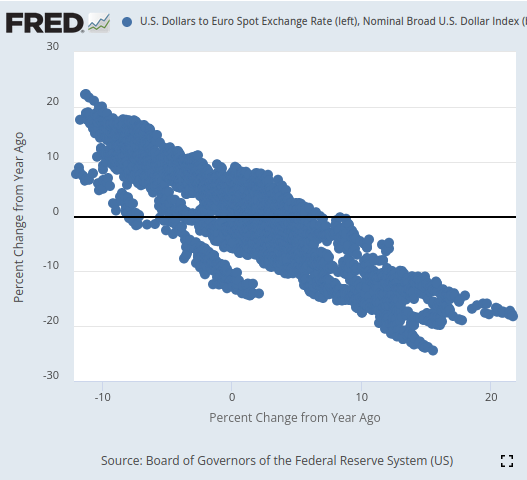
Рис. 3. Визуализация диаграммы рассеяния двух интересующих нас наборов данных

Как бы многообещающе все это ни звучало, ничто из этого не привело к улучшению нашей способности прогнозировать будущее значение обменного курса EURUSD. На самом деле наши результаты только ухудшились, и, похоже, нам было бы лучше использовать первый набор данных, содержащий только обычные рыночные котировки.

Мы обучили 3 идентичных регрессора глубокой нейронной сети (DNN), чтобы изучить взаимосвязь между нашими тремя наборами данных и общей целью, которую они все разделяют. Первая модель DNN показала самый низкий уровень ошибок. Более того, ни один из наших алгоритмов выбора признаков не был впечатлен наборами данных FRED, выбранных нами для анализа. Нам удалось успешно настроить параметры нашей модели DNN с использованием обучающего набора данных, не допуская переобучения под обучающие данные. Об этом свидетельствует тот факт, что мы превзошли модель DNN по умолчанию на невидимых проверочных данных. Для принятия этих решений в ходе обучения и проверки мы использовали перекрестную проверку временных рядов без случайного перемешивания.

Перед экспортом нашей модели в формат ONNX мы проверили остатки нашей модели, чтобы убедиться, что она находится в хорошем состоянии. К сожалению, остатки, которые мы наблюдали в нашей модели, вели себя крайне некорректно, что может указывать на то, что наша модель не смогла эффективно обучаться.

Наконец, мы экспортировали нашу модель в формат ONNX и создали интегрированный советник на базе искусственного интеллекта с использованием Python и MQL5.

Извлечение данных

Для начала мы импортировали необходимые нам библиотеки Python.

#Import the libraries we need
from   fredapi           import Fred
import seaborn           as sns
import numpy             as np
import pandas            as pd
import MetaTrader5       as mt5
import matplotlib.pyplot as plt

Затем мы определили, какие временные ряды мы хотели бы получить из FRED.

#Define important variables
fred_api                = "ENTER YOUR API KEY"
fred_broad_dollar_index = "DTWEXBGS"
fred_us_10y             = "DGS10"
fred_us_5y_inflation    = "T5YIFR"

Входим в систему FRED.

#Login to fred
fred = Fred(api_key=fred_api)

Получаем необходимые данные.

#Fetch the data
dollar_index    = fred.get_series(fred_broad_dollar_index)
us_10y          = fred.get_series(fred_us_10y)
us_5y_inflation = fred.get_series(fred_us_5y_inflation)

Наименование серий позволит нам впоследствии объединить их.

#Name the series so we can merge the data
dollar_index.name    =  "Dollar Index"
us_10y.name          =  "Bond Interest"
us_5y_inflation.name =  "Inflation"

Заполним все недостающие значения с помощью скользящего среднего.

#Fill in any missing values
dollar_index.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)
us_10y.fillna(us_10y.rolling(window=5,min_periods=1).mean(),inplace=True)
us_5y_inflation.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)

Прежде чем мы сможем извлечь данные из терминала MetaTrader 5, нам необходимо его инициализировать.

#Initialize the terminal
mt5.initialize()

True

Мы хотели бы получить исторические данные за 4 года.

#Define how much data to fetch
amount = 365 * 4
#Fetch data
eur_usd = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",mt5.TIMEFRAME_D1,0,amount))
eur_usd

Преобразуем столбец времени из формата секунд в фактические даты.

#Convert the time column
eur_usd['time'] = pd.to_datetime(eur_usd.loc[:,'time'],unit='s')

Убедимся, что столбец времени является индексом наших данных.

#Set the column as the index
eur_usd.set_index('time',inplace=True)

Определим, насколько далеко в будущее мы хотели бы заглянуть.

#Define the forecast horizon
look_ahead = 20

Теперь уточним наши предикторы и цели.

#Define the predictors
predictors = ["open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
ohlc_predictors = ["open","high","low","close","tick_volume"]
fred_predictors = ["Dollar Index","Bond Interest","Inflation"]
target = "Target"
all_data = ["Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
all_data_binary = ["Binary Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]

Объединим данные.

#Merge our data
merged_data = eur_usd.merge(dollar_index,right_index=True,left_index=True)
merged_data = merged_data.merge(us_10y,right_index=True,left_index=True)
merged_data = merged_data.merge(us_5y_inflation,right_index=True,left_index=True)

Маркируем данные.

#Define the target
target         = merged_data.loc[:,"close"].shift(-look_ahead)
target.name    =  "Target"

Отформатируем данные так, чтобы они показывали годовое процентное изменение, как данные, которые мы проанализировали на сайте FRED.

#Convert the data to yearly percent changes
merged_data = merged_data.loc[:,predictors].pct_change(periods = 365) * 100
merged_data = merged_data.merge(target,right_index=True,left_index=True)
merged_data.dropna(inplace=True)
merged_data

Добавим бинарную цель для построения графика.

#Add binary targets for plotting purposes
merged_data["Binary Target"] = 0
merged_data.loc[merged_data["close"] < merged_data["Target"],"Binary Target"] = 1

Сбросим индекс данных.

#Reset the index
merged_data.reset_index(inplace=True,drop=True)
merged_data

Разведочный анализ данных

Начнем с воссоздания графика, который мы сгенерировали по данным с сайта Федерального резерва Сент-Луиса. Это подтвердит, что мы выполнили все этапы предварительной обработки так, как предполагалось.

#Plotting our data set
plt.title("EURUSD Close Against FRED Broad Dollar Index")
plt.plot(merged_data.loc[:,"close"])
plt.plot(merged_data.loc[:,"Dollar Index"])

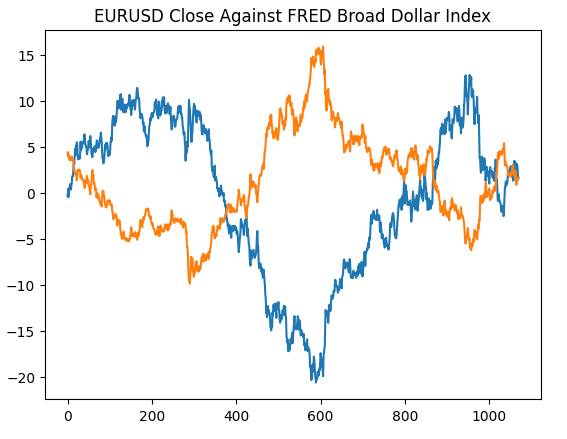
Рис. 4. Воссоздание наших наблюдений на сайте FRED на Python

Давайте теперь проанализируем уровни корреляции в нашем наборе данных. Как мы можем видеть, набор данных по инфляции имеет самые слабые уровни корреляции из всех трех альтернативных наборов данных FRED, которые мы получили. Однако мы не добились никаких улучшений производительности, хотя два оставшихся альтернативных набора данных, казалось, имели огромный потенциал.

#Exploratory data analysis
sns.heatmap(merged_data.loc[:,all_data].corr(),annot=True)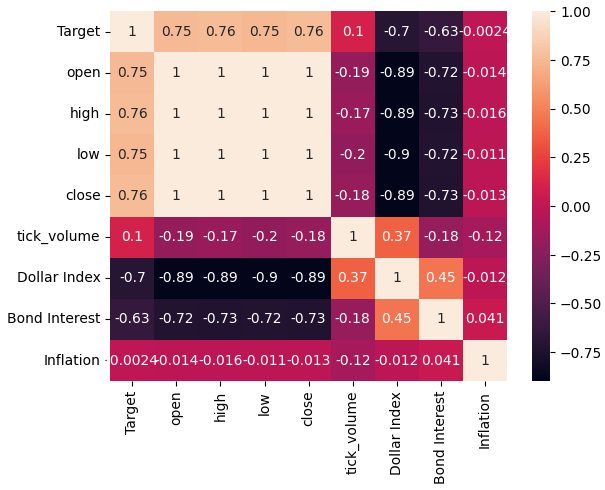

Рис. 5. Тепловая карта корреляции

При одновременном просмотре большого количества наборов данных парные графики могут помочь нам быстро увидеть взаимосвязи, которые могут существовать между всеми имеющимися у нас данными. Мы ясно видим, что оранжевые и синие точки на удивление хорошо разделены. Более того, у нас есть графики оценки плотности ядра (kernel-density estimation, KDE), расположенные вдоль главной диагонали этого графика. Графики KDE помогают нам визуализировать распределение данных в каждом столбце. Тот факт, что мы наблюдаем нечто похожее на две холмообразные формы, которые накладываются друг на друга на небольшом участке, означает, что данные по большей части хорошо разделены.

sns.pairplot(merged_data.loc[:,all_data_binary],hue="Binary Target")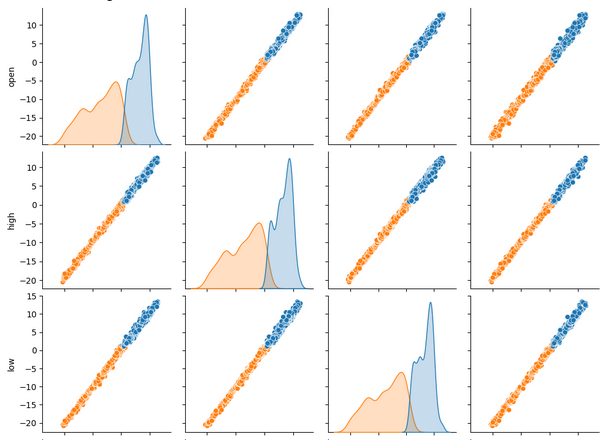

Рис. 6. Визуализация наших данных с использованием парных графиков

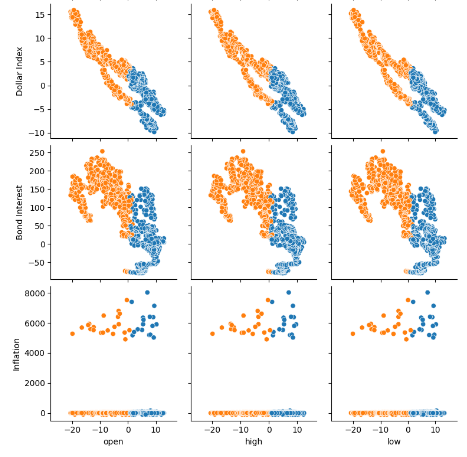
Рис. 7. Визуализация альтернативных данных FRED и их взаимосвязи с парой EURUSD

Теперь построим трехмерные диаграммы рассеяния, используя широкий индекс доллара и процентную ставку по облигациям по осям X и Y, а также цену закрытия EURUSD по оси Z. Данные, по-видимому, разделены на два отдельных кластера, которые мало пересекаются. Это, естественно, подразумевает, что может существовать граница принятия решений, которую наша модель могла бы изучить на основе данных. К сожалению, я считаю, что нам не удалось эффективно продемонстрировать это в нашей модели.

#Define the 3D Plot
fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection="3d")
ax.scatter(merged_data["Dollar Index"],merged_data["Bond Interest"],merged_data["close"],c=merged_data["Binary Target"])
ax.set_xlabel("Dollar Index")
ax.set_ylabel("Bond Interest")
ax.set_zlabel("EURUSD close")

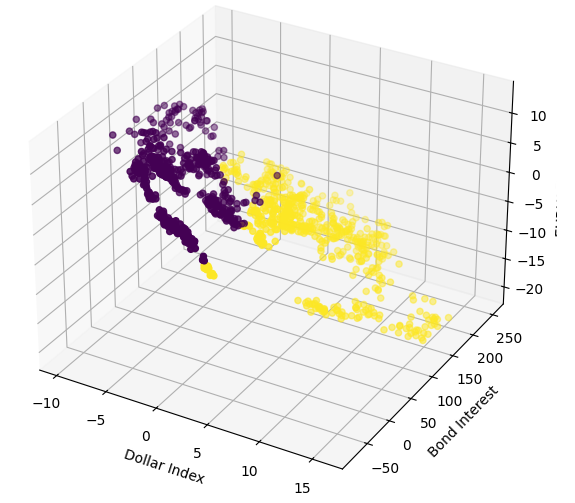
Рис. 8. Визуализация наших рыночных данных в 3D

Подготовка к моделированию данных

Давайте теперь подготовимся к моделированию имеющихся у нас финансовых данных. Начнем с определения входных данных и цели нашей модели.

#Let's define our set of predictors
X = merged_data.loc[:,predictors]
y = merged_data.loc[:,"Target"]

Импортируем нужную нам библиотеку.

#Import the libraries we need
from sklearn.model_selection import train_test_split

Теперь разделим наши данные на три группы, которые мы обозначили ранее.

#Partition the data
ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,test_size=0.5,shuffle=False)
fred_train_X,fred_test_X,_,_            = train_test_split(X.loc[:,fred_predictors],y,test_size=0.5,shuffle=False)
train_X,test_X,_,_                      = train_test_split(X.loc[:,predictors],y,test_size=0.5,shuffle=False)

Создадим фрейм данных для хранения точности перекрестной проверки нашей модели.

#Prepare the dataframe to store our validation error
validation_error = pd.DataFrame(columns=["MT5 Data","FRED Data","ALL Data"],index=np.arange(0,5))

Моделирование данных

Импортируем библиотеки, необходимые для моделирования данных.

#Let's cross validate our models
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import cross_val_score

Определим три нейронные сети, которые мы описали ранее.

#Define the neural networks
ohlc_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
fred_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
all_nn  = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)

Протестируем каждую модель.

#Let's obtain our cv score
ohlc_score = cross_val_score(ohlc_nn,ohlc_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
fred_score = cross_val_score(fred_nn,fred_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
all_score = cross_val_score(all_nn,train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)

Сохраним результаты перекрестной проверки.

for i in np.arange(0,5):
    validation_error.iloc[i,0] = ohlc_score[i]
    validation_error.iloc[i,1] = fred_score[i]
    validation_error.iloc[i,2] = all_score[i]

Визуализируем ошибку проверки.

#Our validation error
validation_error

Данные MetaTrader 5	Альтернативные данные FRED	Все данные
-0.147973	-0.79131	-4.816608
-0.103913	-2.073764	-0.655701
-0.211833	-0.276794	-0.838832
-0.094998	-1.954753	-0.259959
-1.233912	-2.152471	-3.677273

Анализ наших средних показателей по всем 5 позициям показывает, что наши обычные рыночные данные из MetaTrader 5 могут быть нашим лучшим вариантом.

#Our mean performane across all groups
validation_error.mean()

Входные данные	Средняя 5-кратная ошибка
MetaTrader 5	-0.358526
FRED	-1.449818
ВСЕ	-2.049675

При построении графика эффективности наших моделей мы можем заметить, что данные MetaTrader 5 давали более стабильные уровни ошибок.

#Plotting our performance
validation_error.plot()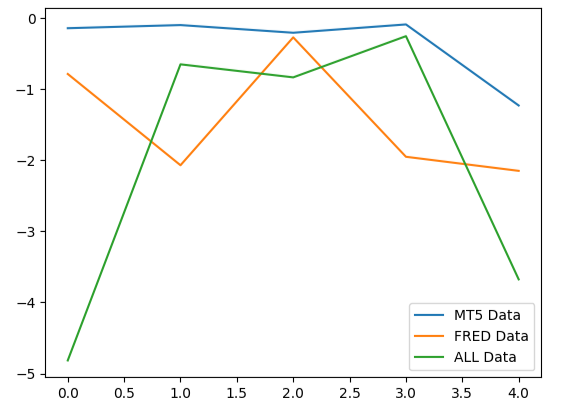

Рис. 9. Визуализация 3 различных уровней ошибок, полученных с помощью 3 наборов данных, из которых нам пришлось выбирать

Сплющенная форма диаграммы ошибок MetaTrader 5 предпочтительна, поскольку она показывает, что модель демонстрирует свою эффективность посредством стабильной работы.

#Creating box-plots of our performance
sns.boxplot(validation_error)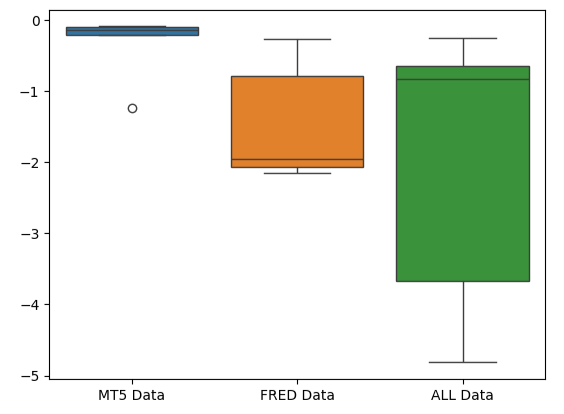

Рис. 10. Визуализация показателей ошибок модели в виде блочной диаграммы

Значимость признаков

Давайте рассмотрим, какие характеристики могут быть наиболее важными для нашей модели DNN. Будем надеяться, что выбранные нами альтернативные данные окажутся полезными, что будет отмечено нашими алгоритмами оценки важности признаков. К сожалению, наш анализ показывает, что колебания рыночных данных MetaTrader 5 сами по себе, по-видимому, достаточно хорошо объясняют целевой показатель. Таким образом, во временном ряду FRED не содержалось никакой дополнительной информации, которую наша модель не могла бы извлечь из имеющихся у нее данных.

Для начала импортируем необходимые библиотеки.

#Feature importance
from alibi.explainers import ALE, plot_ale

Графики накопленных локальных эффектов (Accumulated Local Effects, ALE) помогают нам визуализировать влияние каждого входного параметра модели на целевой показатель. Графики ALE популярны благодаря своей надежной способности объяснять модели, обученные на данных с высокой степенью корреляции, таких как наши. Классические академические методы, такие как графики частичной зависимости (Partial Dependency, PD), просто не были надежными при объяснении предикторов с сильными уровнями корреляции. Оригинальную спецификацию алгоритма можно прочитать в статье (на английском) 2016 года Дэниела Эпли (Daniel W. Apley) и Цзинъюя Чжу (Jingyu Zhu).

Рис. 11. Дэниел Эпли, один из создателей алгоритма ALE

Давайте подгоним объяснение ALE к нашему регрессору DNN.

#Explaining our deep neural network
model = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
model.fit(train_X,train_y)
dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["Target"])

Теперь мы можем получить объяснение каждого эффекта предиктора на цель. Графики ALE имеют интуитивно понятную визуальную интерпретацию, что делает их хорошей отправной точкой. Проще говоря, если полученный нами график ALE представляет собой ровную линию, то с точки зрения нашей модели DNN наблюдаемый предиктор практически не оказывает влияния на цель. Аналогично, чем дальше график ALE от линейности, тем дальше, как усвоила наша модель, связь между целью и предиктором может быть от простой линейной зависимости.

График ALE цены открытия и цели в верхнем левом углу рис. 12 говорит нам о том, что по мере роста цены открытия EURUSD модель усвоила, что будущая цена закрытия также увеличится. Обратите внимание, как графики ALE цены открытия и закрытия изменяются в противоположных направлениях. Это может указывать нам на то, что только эти два предиктора могут объяснить значительную дисперсию целевого показателя.

#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)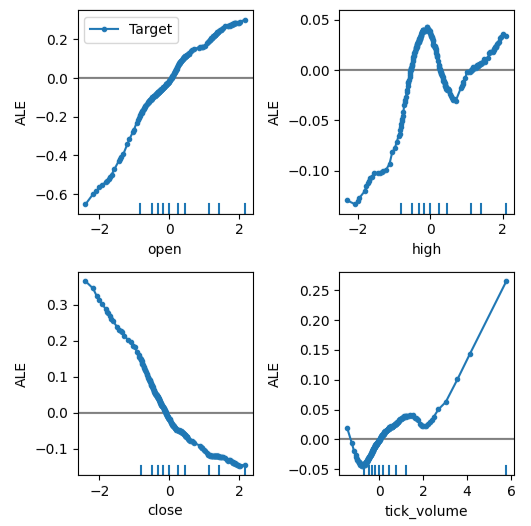

Рис. 12. Визуализация графиков ALE на наших рыночных данных MetaTrader 5

Теперь выполним прямой отбор. Алгоритм начинается с нулевой модели и итеративно добавляет 1 признак, который максимально улучшит производительность модели, до тех пор, пока производительность модели не станет невозможной для дальнейшего повышения.

#Forward selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs

Инициализируем модель.

#Reinitialize the model
all_nn  = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)

Теперь нам нужно указать нужный нам объект прямого выбора. Мы дадим указание этому экземпляру алгоритма выбрать столько переменных, сколько он сочтет важными.

#Define the feature selector
sfs1 = SFS(all_nn,
           k_features=(1,X.shape[1]),
           forward=True,
           scoring='neg_mean_squared_error',
           cv=5,
           n_jobs=-1
          )

Ни один из временных рядов FRED не был выбран алгоритмом.

#Best features we identified
sfs1.k_feature_names_

('open', 'high', 'low')

Мы можем визуализировать процесс выбора алгоритма. Наш график ясно показывает, что эффективность нашей модели снизилась по мере увеличения параметров модели.

#Fit the forward selection algorithm
fig1 = plot_sfs(sfs1.get_metric_dict(), kind='std_dev')

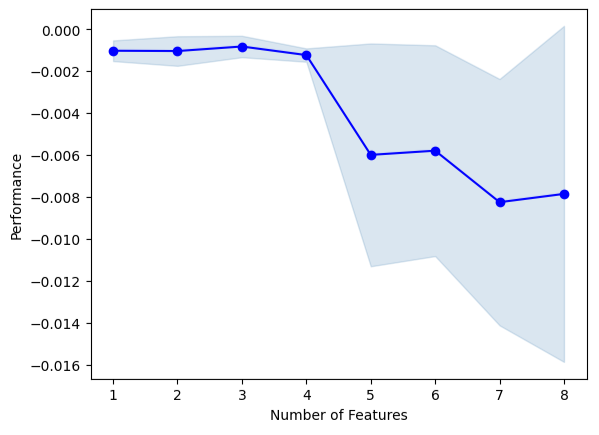
Рис. 13. Визуализация производительности нашей модели при последовательном добавлении дополнительных предикторов

Настройка параметров

Давайте выполним настройку параметров нашей модели DNN, используя случайный поиск. Сначала нам нужно инициализировать нашу модель.

#Reinitialize the model
model  = MLPRegressor(max_iter=500)

Теперь определим параметры нашей настройки.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "hidden_layer_sizes":[(10,20,40),(10,20,40,80),(5,10,20,100),(100,50,10),(20,20,10),(1,5,10,20),(20,10,5,1)],
        "early_stopping":[True,False],
        "warm_start":[True,False],
        "shuffle": [True,False]
        },
        n_iter=500,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Установим объект настройки.

#Fit the tuner
tuner.fit(train_X,train_y)

Давайте посмотрим на лучшие параметры, которые нам удалось найти.

#The best parameters we found
tuner.best_params_

{'warm_start': False,
'tol': 1e-05,
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 0.01,
'learning_rate': 'invscaling',
'hidden_layer_sizes': (10, 20, 40, 80),
'early_stopping': True,
'alpha': 0.1,
'activation': 'relu'}

Более глубокая оптимизация параметров

Давайте поищем лучшие параметры модели, используя библиотеку SciPy. Мы можем представить себе процессы оптимизации как задачу поиска - почти как детскую игру в прятки. Видите ли, идеальные параметры для нашей модели, которые обеспечат наилучший уровень ошибок на данных, которые модель ранее не видела, скрыты в бесконечном пространстве возможных значений, которые мы могли бы присвоить каждому из наших непрерывных параметров.

Импортируем необходимые библиотеки.

#Deeper optimization
from scipy.optimize import minimize
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import TimeSeriesSplit

Определите объект разделения временного ряда.

#Define the time series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Создадим фрейм данных для возврата текущей стоимости и список для хранения прогресса нашей модели для визуализации.

#Create a dataframe to store our accuracy
current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
algorithm_progress = []

Теперь определим нашу функцию затрат. Библиотека SciPy Minimize предлагает нам различные алгоритмы для поиска входных данных для любой функции, которые приведут к минимальному выходному значению функции. Мы будем использовать среднее значение 5-кратного уровня ошибки модели на обучающих данных в качестве величины, которую необходимо минимизировать, при этом все остальные параметры DNN будут оставаться постоянными.

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=x[0],
                         tol=x[1],
                         learning_rate_init=x[2]
                         )
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(train_X)):
        #Train the model
        model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
        #Measure the RMSE
        current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
    #Store the algorithm's progress
    algorithm_progress.append(current_error_rate.iloc[:,0].mean())
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Давайте определим начальные точки процедуры, а также укажем границы для параметров. Для этой задачи наше единственное ограничение заключается в том, что все параметры модели должны быть положительными.

#Define the starting point
pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]]
bnds = ((10.00 ** -100,10.00 ** 100),
        (10.00 ** -100,10.00 ** 100),
        (10.00 ** -100,10.00 ** 100))

Для оптимизации параметров нашей модели мы будем использовать усеченный метод Ньютона (Truncated Newton Constrained, TNC). Это семейство методов, подходящих для решения больших нелинейных задач оптимизации с учетом ограничений. Библиотека SciPy предоставляет нам оболочку для реализации алгоритма на языке C.

#Searching deeper for parameters
result = minimize(objective,pt,method="TNC",bounds=bnds)

Давайте убедимся в успешном завершении.

#The result of our optimization
result

message: Linear search failed
success: False
status: 4
     fun: 0.001911232280110637
       x: [ 1.000e-100 1.000e-100 1.000e-100]
     nit: 0
     jac: [ 2.689e+06 9.227e+04 1.124e+05]
    nfev: 116

Похоже, у нас возникли трудности с поиском оптимальных входных данных. Давайте визуализируем эффективность нашей процедуры оптимизации.

#Store the optimal coefficients
optimal_weights = result.x
optima_y = min(algorithm_progress)
optima_x = algorithm_progress.index(optima_y)
inputs = np.arange(0,len(algorithm_progress))

#Plot the performance of our optimization procedure
plt.scatter(inputs,algorithm_progress)
plt.plot(optima_x,optima_y,'ro',color='r')
plt.axvline(x=optima_x,ls='--',color='red')
plt.axhline(y=optima_y,ls='--',color='red')
plt.xlabel("Iterations")
plt.ylabel("Training MSE")
plt.title("Minimizing Training Error")

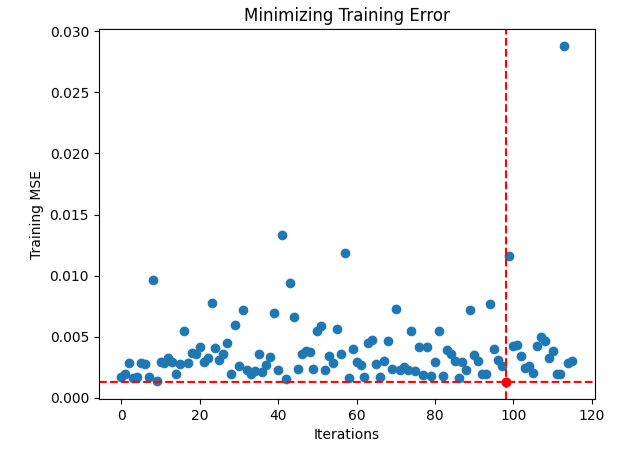
Рис. 14. Красная точка представляет оптимальные входные значения, рассчитанные нашим оптимизатором TNC.

Проверка на переобучение

Инициализируем все три наши модели и посмотрим, сможем ли мы обучить их на обучающем наборе и превзойти модель по умолчанию на тестовых данных. Напомним, что до сих пор мы не использовали тестовые данные в процессе принятия решений.

#Testing for overfitting
default_nn = MLPRegressor(max_iter=500)

#Randomized NN
random_search_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"]
                         )

#TNC NN
tnc_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=result.x[0],
                         tol=result.x[1],
                         learning_rate_init=result.x[2]
                         )

Поместим каждую из моделей в тренировочный набор.

#Store the models in a list
models = [default_nn,random_search_nn,tnc_nn]

#Fit the models
for model in models:
    model.fit(train_X,train_y)

Создадим фрейм данных для хранения уровней ошибок проверки.

#Create a dataframe to store our validation error
validation_error = pd.DataFrame(columns=["Default","Randomized","TNC"],index=np.arange(0,5))

Протестируем каждую модель и запишем полученные результаты.

#Let's obtain our cv score
default_score = cross_val_score(default_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
random_score = cross_val_score(random_search_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
tnc_score = cross_val_score(tnc_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)

#Store the model error in a dataframe
for i in np.arange(0,5):
    validation_error.iloc[i,0] = default_score[i]
    validation_error.iloc[i,1] = random_score[i]
    validation_error.iloc[i,2] = tnc_score[i]

Посмотрим на ошибку проверки.

#Let's see the validation error
validation_error

Модель по умолчанию	Случайный поиск	TNC
-0.362851	-0.029476	-0.054709
-0.323601	-0.053967	-0.087707
-0.064432	-0.024282	-0.026481
-0.121226	-0.019693	-0.017709
-0.064801	-0.012812	-0.016125

Расчет средней эффективности по всем 5 параметрам ясно показывает, что наша модель случайного поиска является наилучшим вариантом.

#Our best performing model
validation_error.mean()

Модель	Средняя ошибка проверки
Модель по умолчанию	-0.187382
Случайный поиск	-0.028046
TNC	-0.040546

Блочные диаграммы позволяют быстро увидеть, в какой степени варьировалась эффективность модели по умолчанию. Наши индивидуальные модели смогли продемонстрировать эффективность в узком диапазоне уровней погрешности, что дало нам большую уверенность в выборе параметров настройки.

#Let's create box-plots
sns.boxplot(validation_error)

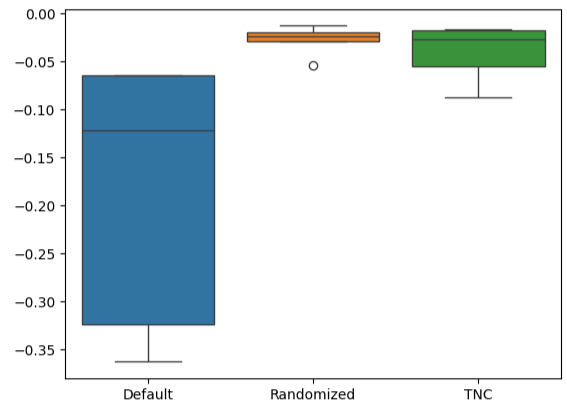
Рис. 15. Визуализация эффективности нашей модели в виде блочных диаграмм

Создание линейных графиков данных перекрестной проверки подчеркивает несоответствие между моделью по умолчанию и нашими настроенными моделями. Мы видим, что между синей линией, представляющей производительность модели по умолчанию, и остальными цветными графиками имеется значительная погрешность.

#We can also visualize model performance through a line plot
validation_error.plot()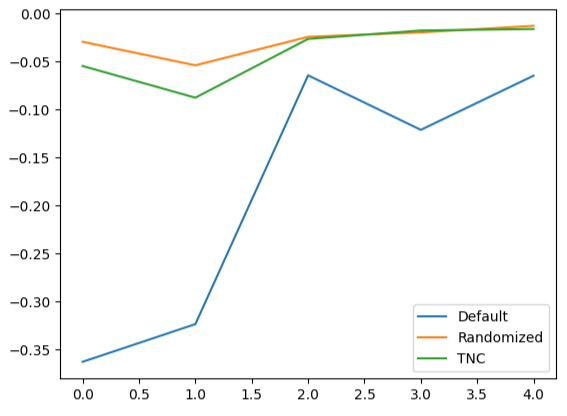

Рис. 16. Построение графика пятикратной производительности наших различных моделей на основе тестовых данных

Анализ остатков

Мы не можем слепо доверять нашей модели и сразу же внедрять ее. Давайте попробуем убедиться, что наша модель действительно эффективно обучилась, проверив ее остатки. В идеале модель, которая идеально аппроксимирует функцию, будет иметь остатки, представляющие собой ровную линию. Это означает, что в прогнозе модели нет ошибки. Кроме того, это также означает, что величина ошибки в прогнозе модели не меняется.

Следовательно, чем дальше эффективность нашей модели от идеала, тем больше искажений мы увидим в идеальном линейном и стационарном графике остатков. Остаточные значения нашей модели демонстрировали различную величину ошибки, которая порой коррелировала с предыдущей величиной ошибки. Это вероятная причина для беспокойства, и ее можно потенциально устранить путем преобразования предиктора или цели.

Инициализируем модель.

#Resdiuals analysis
model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"]
                         )

Подгоните модель под обучающие данные, а затем запишите остатки, используя тестовые данные.

#Fit the model
model.fit(train_X,train_y)

#Record the residuals
residuals = test_y - model.predict(test_X)

Наш график остатков далек от идеала, и нам, возможно, придется изучить другие этапы предварительной обработки, чтобы решить эту проблему.

#Residuals analysis
residuals.plot()

Рис. 17. Визуализация остатков нашей модели на тестовых данных

Измерение автокорреляции — надежный подход к обнаружению возможных ложных регрессий. К сожалению, остатки нашей модели также не прошли этот тест и, возможно, могли бы служить индикатором того, что мы можем получить дополнительные улучшения, если лучше трансформируем наши предикторы или цель.

#Autocorrelation plot
from statsmodels.graphics.tsaplots import plot_acf
acf = plot_acf(residuals,lags=40)

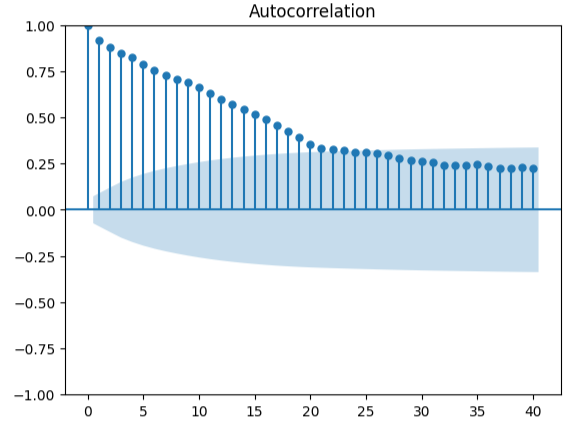
Рис. 18. Визуализация остатков нашей модели

Подготовка к экспорту в ONNX

Прежде чем экспортировать наши данные в формат ONNX, давайте сначала сохраним средние значения и стандартные отклонения каждого столбца в фрейме данных. Обратите внимание: поскольку мы не получили никаких улучшений от преобразования данных в процентные изменения, мы вместо этого будем использовать данные в их исходной форме и использовать их для расчетов z-оценки.

#Prepare to convert the model to ONNX format
scale_factors = pd.DataFrame(columns=X.columns,index=["mean","std"])
for i in X.columns:
    scale_factors.loc["mean",i] = merged_data.loc[:,i].mean()
    scale_factors.loc["std",i]  = merged_data.loc[:,i].std()
    merged_data.loc[:,i] = (merged_data.loc[:,i] - scale_factors.loc["mean",i]) / scale_factors.loc["std",i]

scale_factors

Рис. 19. Фрейм данных с z-оценками

Запишем данные в формат CSV.

#Save the scale factors to CSV format
scale_factors.to_csv("FRED EURUSD D1 scale factors.csv")

Экспорт в ONNX

ONNX — это протокол с открытым исходным кодом, который позволяет разработчикам создавать и развертывать модели машинного обучения на любом языке программирования, поддерживающем API ONNX. Сначала импортируем необходимые библиотеки.

# Import the libraries we need
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Инициализируйте модель в последний раз.

#Initialize the model
model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"]
                         )

Подгоним модель под все имеющиеся у нас данные.

# Fit the model on all the data we have
model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])

Определим выходную форму нашей модели.

# Define the input type
initial_types = [("float_input",FloatTensorType([1,X.shape[1]]))]

Создадим графическое представление нашей модели в формате ONNX.

# Create the ONNX representation
onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)

Сохраним модель ONNX.

# Save the ONNX model
onnx.save_model(onnx_model,"FRED EURUSD D1.onnx")

Визуализация модели в Netron

Визуализация нашей модели поможет нам убедиться, что она создана в соответствии с нашими спецификациями. Мы хотим убедиться, что формы входных и выходных данных соответствуют нашим ожиданиям. Netron — библиотека с открытым исходным кодом для визуализации моделей машинного обучения. Для начала импортируем библиотеку.

import netron

Теперь мы можем легко визуализировать наш DNN-регрессор.

netron.start("FRED EURUSD D1.onnx")

Визуализация модели ONNX

Рис. 20. Визуализация нашего регрессора DNN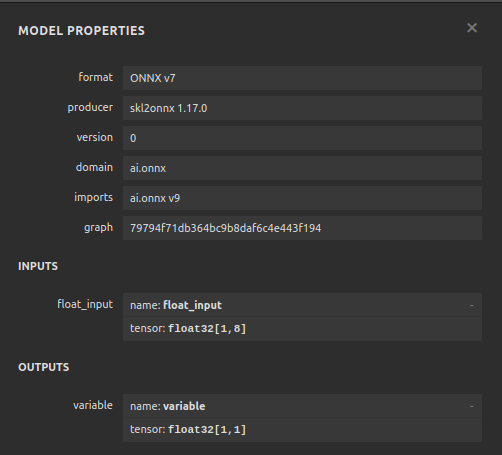

Спецификации моделей

Рис. 21. Визуализация входных и выходных форм нашей модели

Реализация средствами MQL5

Первым компонентом, который нам необходимо интегрировать в наш советник, будет ONNX-модель. Мы просто включим файл ONNX в качестве ресурса для нашего советника.

//+------------------------------------------------------------------+
//|                                               FRED EURUSD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Require the ONNX file                                            |
//+------------------------------------------------------------------+
#resource "\\Files\\FRED EURUSD D1.onnx" as const uchar onnx_buffer[];

Теперь давайте загрузим торговую библиотеку, которая нам нужна для управления нашими позициями.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Создание глобальных переменных, которые нам понадобятся на протяжении всей нашей программы.

//+------------------------------------------------------------------+
//| Define global variables                                          |
//+------------------------------------------------------------------+
long    model;
double  mean_values[5] = {1.1113568153310105,1.1152603484320558,1.1078179790940768,1.1114909337979093,65505.27177700349};
double  std_values[5]  = {0.05467420688685988,0.05413287747761819,0.05505429755411189,0.054630920048519924,26512.506288360997};
vectorf model_output   = vectorf::Zeros(1);
vectorf model_inputs   = vectorf::Zeros(8);
int     model_sate     = 0;
int     system_sate    = 0;
double  bid,ask;

Всякий раз, когда наша модель загружается в первый раз, давайте сначала попробуем загрузить нашу ONNX-модель, а затем проверим, работает ли она.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX model
   if(!load_onnx_model())
     {
      //--- We failed to load the ONNX model
      return(INIT_FAILED);
     }

//--- Test if we can get a prediction from our model
   model_predict();

//--- Eveything went fine
   return(INIT_SUCCEEDED);
  }

Если нашу модель удалить из графика, мы также освободим ресурсы, которые больше не используем.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we no longer need
   release_resources();
  }

Всякий раз, когда мы получаем новые цены, мы обновляем переменные, назначенные нами для хранения текущих рыночных цен. Аналогично, если у нас нет открытых позиций, мы будем следовать нашей модели. Если у нас уже есть открытые позиции, мы позволим нашей модели предупредить нас о возможных разворотах и закроем наши позиции соответствующим образом.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update our bid and ask prices
   update_market_prices();

//--- Fetch an updated prediction from our model
   model_predict();

//--- If we have no trades, follow our model's directions.
   if(PositionsTotal() == 0)
     {
      //--- Our model is predicting price levels will appreciate
      if(model_sate == 1)
        {
         Trade.Buy(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI");
         system_sate = 1;
        }
      //--- Our model is predicting price levels will deppreciate
      if(model_sate == -1)
        {
         Trade.Sell(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI");
         system_sate = -1;
        }
     }

//--- Otherwise Manage our open positions
   else
     {
      if(system_sate != model_sate)
        {
         Alert("AI System Detected A Reversal! Closing All Positions on EURUSD");
         Trade.PositionClose("EURUSD");
        }
     }

  }
//+------------------------------------------------------------------+

Функция обновит наши переменные, отслеживающие текущие рыночные цены.

//+------------------------------------------------------------------+
//| Update market prices                                             |
//+------------------------------------------------------------------+
void update_market_prices(void)
  {
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

Теперь мы определим, каким образом должны быть высвобождены наши ресурсы.

//+------------------------------------------------------------------+
//| Release the resources we no longer need                          |
//+------------------------------------------------------------------+
void release_resources(void)
  {
   OnnxRelease(model);
   ExpertRemove();
  }

Определим функцию, отвечающую за создание нашей ONNX-модели из буфера, который мы создали выше. Если эта функция в какой-либо момент даст сбой, она вернет false, что остановит нашу процедуру инициализации.

//+------------------------------------------------------------------+
//| Create our ONNX model from the buffer we defined above           |
//+------------------------------------------------------------------+
bool load_onnx_model(void)
  {
//--- Create the ONNX model from the buffer we defined
   model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Validate the model was not illdefined
   if(model == INVALID_HANDLE)
     {
      //--- We failed to define our model
      Comment("We failed to create our ONNX model: ",GetLastError());
      return false;
     }

//---- Define the model I/O shape
   ulong input_shape[] = {1,8};
   ulong output_shape[] = {1,1};
//--- Validate our model's I/O shapes
   if(!OnnxSetInputShape(model,0,input_shape) || !OnnxSetOutputShape(model,0,output_shape))
     {
      Comment("Failed to define our model I/O shape: ",GetLastError());
      return(false);
     }
//--- Everything went fine!
   return(true);
  }

Это функция, отвечающая за получение прогноза из нашей модели. Функция сначала извлечет и нормализует котировки EURUSD, а затем вызовет процедуру, отвечающую за чтение текущих альтернативных данных FRED.

//+------------------------------------------------------------------+
//| This function will fetch a prediction from our model             |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Get the input data ready
   for(int i =0; i < 6; i++)
     {
      //--- The first 5 inputs will be fetched from the market
      matrix eur_usd_ohlc = matrix::Zeros(1,5);
      eur_usd_ohlc[0,0] = iOpen(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,1] = iHigh(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,2] = iLow(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,3] = iClose(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,4] = iTickVolume(Symbol(),PERIOD_D1,0);
      //--- Fill in the data
      if(i<4)
        {
         model_inputs[i] = (float)((eur_usd_ohlc[0,i] - mean_values[i])/ std_values[i]);
        }
      //--- We have to read in the fred alternative data
      else
        {
         read_fred_data();
        }
     }
  }
//+------------------------------------------------------------------+

Функция будет считывать альтернативные данные FRED из нашего каталога MQL5\Files. Напомним, что CSV-файл будет обновляться каждый день нашим скриптом Python.

//+------------------------------------------------------------------+
//| This function will read in our FRED data                         |
//+------------------------------------------------------------------+
bool read_fred_data(void)
  {
//--- Read in the file
   string file_name = "FRED EURUSD ALT DATA.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file

      int counter = 0;
      string value = "";
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {
         if(counter > 20)   //if you aim to read 10 values set a break point after 10 elements have been read
            break;          //stop the reading progress

         value = FileReadString(result);
         Print("Counter: ");
         Print(counter);
         Print("Trying to read string: ",value);

         if(counter == 3)
           {
            model_inputs[5] = (float) value;
           }

         if(counter == 5)
           {
            model_inputs[6] = (float) value;
           }

         if(counter == 7)
           {
            model_inputs[7] = (float) value;
           }

         if(FileIsLineEnding(result))
           {
            Print("row++");
           }

         counter++;
        }

      //--- Show the input and Fred data
      Print("Input Data: ");
      Print(model_inputs);
      //---Close the file
      FileClose(result);
      //--- Store the model prediction
      OnnxRun(model,ONNX_DEFAULT,model_inputs,model_output);
      Comment("Model Forecast: ",model_output[0]);
      if(model_output[0] > iClose(Symbol(),PERIOD_D1,0))
        {
         model_sate = 1;
        }

      else
        {
         model_sate = -1;
        }

      //--- Everything went fine
      return(true);
     }

//--- We failed to find the file
   else
     {
      //--- Give the user feedback
      Print("We failed to find the file with the FRED data");
      return false;
     }

//--- Something went wrong
   return false;
  }

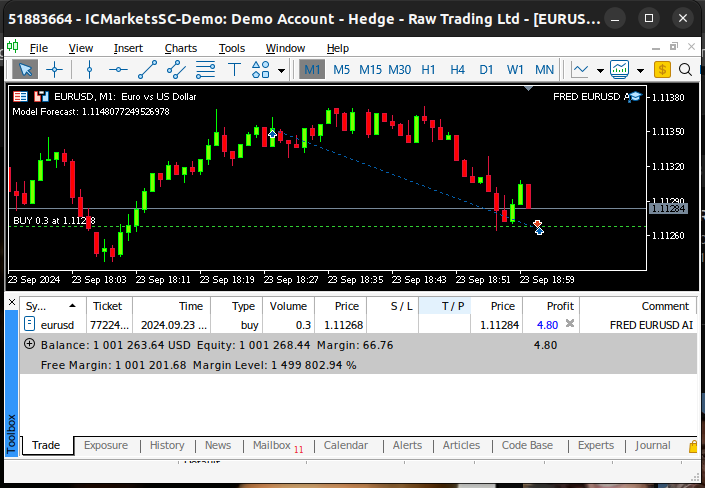
Рис. 22. Форвард-тестирование нашего алгоритма

Заключение

Мы продемонстрировали, что номинальный обобщенный дневной индекс бесполезен при прогнозировании пары EURUSD или же символ может потребовать дополнительных преобразований, прежде чем можно будет эффективно изучить истинную взаимосвязь. Мы также можем протестировать более широкий спектр моделей, чтобы максимально повысить вероятность правильного определения взаимосвязи. Такие модели, как метод опорных векторов (Support Vector Machines), как правило, хорошо работают в задачах, требующих изучения границы принятия решений в многомерном пространстве. Существуют сотни тысяч наборов данных, доступных для изучения. Но, к сожалению, на этот раз мы не получили преимущества над рынком.

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15949

Прикрепленные файлы |

Загрузить ZIP

FRED_EURUSD_AI.mq5 (8.61 KB)

FRED_EURUSD_D1.onnx (18.9 KB)

Alternative_Data_EURUSD.ipynb (2502.45 KB)

Fetch_Fred_Data.ipynb (3.75 KB)

Visualizing_The_Deep_Neural_Network.ipynb (1.31 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Классы таблицы и заголовка на базе модели таблицы в MQL5: Применение концепции MVC

Это вторая часть статьи, посвященной реализации модели таблицы в MQL5 с использованием архитектурной парадигмы MVC (Model-View-Controller). В статье рассматривается разработка классов таблицы и её заголовка, основанных на ранее созданной модели таблицы. Разработанные классы станут основой для дальнейшей реализации компонентов представления (View) и управления (Controller), которые будут рассмотрены в следующих статьях.

Одномерный сингулярный спектральный анализ

Статья рассматривает теоретические и практические аспекты метода сингулярного спектрального анализа (SSA), который представляет собой эффективный метод анализа временных рядов, позволяющий представить сложную структуру ряда в виде разложения на простые компоненты, такие как тренд, сезонные (периодические) колебания и шум.

Парный трейдинг: Алготорговля с автооптимизацией на разнице Z-оценки

В этой статье разберем, что такое парный трейдинг и как происходит торговля на корреляциях. Также создадим советник для автоматизации парного трейдинга и добавим возможность автоматической оптимизации такого торгового алгоритма на исторических данных. Кроме того, в рамках проекта узнаем, как рассчитывать расхождения двух пар с помощью z-оценки.

Совместное использование PSAR, Хейкин-Аши и глубокого обучения для трейдинга

В настоящем проекте исследуется сочетание глубокого обучения и технического анализа для тестирования торговых стратегий на рынке Форекс. Для быстрого экспериментирования используется скрипт на Python, использующий модель ONNX наряду с традиционными индикаторами, такими как PSAR, SMA и RSI, для прогнозирования движения пары EUR/USD. Затем скрипт MetaTrader 5 переносит эту стратегию в реальную среду, используя исторические данные и технический анализ для принятия обоснованных торговых решений. Результаты тестирования на исторических данных свидетельствуют об осторожном, но последовательном подходе, направленном на управление рисками и устойчивый рост, а не на агрессивную погоню за прибылью.