
Estimation de la densité de noyau de la fonction de densité de probabilité inconnue
Introduction
L'amélioration des performances MQL5 et la croissance constante de la productivité du PC permettent aux utilisateurs de la plate-forme MetaTrader 5 d'appliquer des méthodes mathématiques assez sophistiquées et avancées pour l'analyse du marché. Ces méthodes peuvent appartenir à divers domaines de l'économie, de l'économétrie ou de la statistique mais dans tous les cas, nous aurons à traiter le concept de fonction de densité de probabilité lors de leur utilisation.
De nombreuses méthodes d'analyse courantes ont été développées sur la base de l'hypothèse de la normalité de la distribution des données ou de la normalité des erreurs dans le modèle utilisé. Par ailleurs, il est souvent nécessaire de connaître la distribution des différentes composantes du modèle utilisé pour estimer les résultats de l'analyse. Dans les deux cas, nous avons pour tâche de créer un « outil » (universel, dans un cas idéal) permettant d'estimer la fonction de densité de probabilité inconnue.
Dans cet article, on tente de créer une classe réalisant un algorithme plus ou moins universel pour estimer la fonction de densité de probabilité inconnue. L'idée originale était qu'aucun moyen externe ne serait utilisé pendant l'estimation, c'est-à-dire que tout devait être réalisé au moyen de MQL5 uniquement. Mais finalement l'idée originale a été modifiée dans une certaine mesure. Il est clair que la tâche d'estimation visuelle de la fonction de densité de probabilité se compose de deux parties indépendantes.
À savoir, le calcul de l'estimation elle-même et sa visualisation, c'est-à-dire son affichage sous forme de graphique ou de diagramme. Bien entendu, les calculs ont été réalisés à l'aide de MQL5, tandis que la visualisation doit être mise en œuvre par la création d'une page HTML et son affichage dans un navigateur web. Cette solution a finalement été utilisée pour obtenir des graphiques sous forme vectorielle.
Mais comme la partie calcul et l'affichage des résultats sont réalisés séparément, un lecteur peut, bien sûr, visualiser en utilisant toute autre méthode disponible. En outre, nous nous attendons à ce que diverses bibliothèques, y compris graphiques, apparaissent dans MetaTrader 5 (les travaux sont en cours, à notre connaissance). Il ne sera pas difficile de modifier la partie affichage dans la solution proposée, dans le cas où MetaTrader 5 fournit des moyens avancés pour construire des graphiques et des diagrammes.
Il convient de noter au préalable que la création d'un algorithme véritablement universel pour l'estimation de la fonction de densité de probabilité des séquences s'est avérée être un objectif irréalisable. Bien que la solution proposée ne soit pas hautement spécialisée, elle ne peut pas non plus être qualifiée de complètement universelle. Le problème est que les critères d'optimalité s'avèrent assez différents lors de l'estimation de la densité, par exemple, pour les distributions en cloche, telles que les normales et les exponentielles.
Par conséquent, il est toujours possible de choisir la solution la plus adaptée à chaque cas spécifique, si l'on dispose de quelques informations préliminaires concernant la distribution estimée. Mais, néanmoins, nous supposerons que nous ne savons rien de la nature de la densité estimée. Une telle approche affectera sûrement la qualité des estimations, mais espérons qu'elle sera payante en offrant la possibilité d'estimer des densités très différentes.
Étant donné que nous devons souvent traiter des séquences non stationnaires lors de l'analyse des données du marché, nous sommes surtout intéressés par l'estimation de la densité des séquences courtes et moyennes. C'est un moment critique qui détermine le choix de la méthode d'estimation utilisée.
Les histogrammes et les P-splines peuvent être utilisés avec succès pour les très longues séquences contenant plus d'un million de valeurs. Mais certains problèmes apparaissent lorsque nous essayons de construire efficacement les histogrammes pour des séquences contenant 10-20 valeurs. Par conséquent, nous nous concentrerons principalement sur les séquences ayant approximativement de 10 à 10 000 valeurs pour la suite.
1. Méthodes d'estimation de la fonction de densité de probabilité
On connaît aujourd'hui un grand nombre de méthodes plus ou moins populaires d'estimation de la fonction de densité de probabilité. Ils peuvent être facilement trouvés sur Internet, par exemple, en utilisant des expressions clés telles que « estimation de la densité de probabilité », « densité de probabilité », « estimation de la densité », etc. Mais, malheureusement, nous n'avons pas réussi à choisir le meilleur d'entre eux. Tous présentent des avantages et des inconvénients.
Les histogrammes sont traditionnellement utilisés pour l'estimation de la densité [1]. L'utilisation des histogrammes (y compris les histogrammes lisses) permet d'obtenir des estimations de densité de probabilité de haute qualité, mais uniquement dans le cas de longues séquences. Comme il a été mentionné précédemment, il n'est pas possible de diviser une courte séquence en un grand nombre de groupes, alors qu'un histogramme composé de 2-3 barres ne peut pas illustrer la loi de distribution de densité de probabilité d'une telle séquence. Par conséquent, nous avons dû abandonner l'utilisation des histogrammes.
Une autre méthode d'estimation assez connue est l'estimation par densité de noyau [2]. L'idée d'utiliser le lissage du noyau est assez bien illustrée en [3]. C'est pourquoi nous avons choisi cette méthode, malgré tous ses inconvénients. Certains aspects liés à la mise en œuvre de cette méthode seront brièvement abordés ci-dessous.
Il est également nécessaire de mentionner une méthode d'estimation de la densité très intéressante, qui utilise l'algorithme « Expectation–maximization » [4]. Cet algorithme permet de diviser une séquence en composantes distinctes ayant, par exemple, une distribution normale. Il est possible d'obtenir une estimation de la densité en additionnant les courbes de distribution obtenues après avoir déterminé les paramètres des composants séparés. Cette méthode est mentionnée en [5]. Cette méthode n'a pas été mise en œuvre et testée lors du travail sur cet article, ainsi que sur de nombreux autres. Le grand nombre de méthodes d'estimation de la densité décrites dans diverses sources empêche de toutes les examiner en pratique.
Passons maintenant à la méthode d'estimation de la densité du noyau qui a été choisie pour la mise en œuvre.
2. Estimation par densité de noyau de la fonction de densité de probabilité
L'estimation par la densité du noyau de la fonction de densité de probabilité est basée sur la méthode de lissage de noyau. Les principes de cette méthode peuvent être trouvés, par exemple, à [6], [7].
L'idée de base dulissage de noyau est assez simple. Les utilisateurs de MetaTrader 5 sont familiers avec l'indicateur de moyenne mobile (MA). Cet indicateur peut être facilement représenté comme une fenêtre glissant le long d'une séquence avec ses valeurs pondérées lissées à l'intérieur. La fenêtre peut être rectangulaire, exponentielle ou avoir une autre forme. Nous pouvons facilement voir la même fenêtre glissante lors du lissage du noyau (par exemple, [3]). Mais dans ce cas, il est symétrique.
Des exemples des fenêtres les plus fréquemment utilisées dans le lissage du noyau peuvent être trouvés dans [8]. Si une régression d'ordre zéro est utilisée pour le lissage du noyau, les valeurs pondérées de la séquence qui ont atteint la fenêtre (noyau) sont simplement lissées, comme dans MA. Nous pouvons voir le même type d'application de la fonction fenêtre lorsque nous traitons des questions de filtrage. Mais aujourd'hui, la même procédure est présentée un peu différemment. Les caractéristiques amplitude-fréquence et phase-fréquence sont utilisées, tandis que le noyau (fenêtre) est appelée caractéristique d'impulsion de filtre.
Ces exemples montrent qu'une même chose peut souvent être représentée de différentes manières. Cela contribue à l'appareil mathématique, bien sûr. Mais cela peut également prêter à confusion lorsque l'on discute de ce genre de questions.
Bien que l'estimation de la densité du noyau utilise les mêmes principes que le lissage du noyau déjà mentionné, son algorithme diffère un peu.
Passons à l'expression définissant l'estimation de la densité en un point.
![]()
où
- x - séquence de longueur n ;
- K - noyau symétrique;
- h - intervalle, paramètre de lissage.
Seul le noyau gaussien sera utilisé par la suite pour les estimations de densité :
![]()
Comme il ressort de l'expression ci-dessus, la densité au point X est calculée comme la somme des valeurs du noyau pour les quantités définies par les différences entre les valeurs du point X et la séquence. De plus, les points X utilisés pour le calcul de la densité peuvent ne pas coïncider avec les valeurs de la séquence elle-même.
Voici les étapes de base de la mise en œuvre de l'algorithme d'estimation de la densité du noyau.
- Évaluation de la valeur moyenne et de l'écart type de la séquence d'entrée.
- Normalisation de la séquence d'entrée. Déduire la moyenne précédemment obtenue de chacune de ses valeurs et diviser par la valeur de l'écart type. Après une telle normalisation, la séquence d'origine aura une moyenne nulle et un écart type égal à un. Une telle normalisation n'est pas nécessaire pour calculer la densité mais elle permet d'unifier les graphiques résultants, car pour toute séquence sur l'échelle X, il y aura des valeurs exprimées en unités d'écart-type.
- Trouver les valeurs hautes et basses dans la séquence normalisée.
- Création de deux tableaux, dont les tailles correspondent au nombre souhaité de points affichés sur le graphique résultant. Par exemple, si le graphique doit être construit en utilisant 200 points, la taille des tableaux doit inclure de manière appropriée 200 valeurs chacun.
- Réserver l'un des tableaux créés pour stocker le résultat. Le second est utilisé pour former les valeurs des points, pour lesquels l'estimation de densité a été effectuée. Pour ce faire, nous devons former 200 (dans ce cas) valeurs équidistantes entre les valeurs hautes et basses préalablement préparées et enregistrez-les dans le tableau que nous avons préparé.
- En utilisant l'expression présentée ci-dessus, nous devons effectuer l'estimation de la densité en 200 (dans notre cas) points de test en sauvegardant le résultat dans le tableau que nous avons préparé à l'étape 4.
La mise en œuvre logicielle de cet algorithme est illustrée ci-dessous.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
La méthode NTpoints() permet de définir le nombre requis de points d'essai également espacés, pour lesquels l'estimation de la densité sera effectuée. Cette méthode doit être appelée avant d'appeler la méthode Density(). Le lien vers le tableau contenant les données d'entrée et la valeur de l’intervalle (paramètre de lissage) est transmis à la méthode Density() en tant que paramètres lorsque la méthode est appelée.
La méthode Density() renvoie zéro en cas de réussite, tandis que les valeurs des points de test et les résultats des estimations sont situés dans les tableaux T[] et Y[] de cette classe, respectivement.
Les tailles des tableaux sont définies lors de l'accès à NTpoints(), tout en étant égales à 200 valeurs par défaut.
L'exemple de script suivant montre l'utilisation de la classe CDens présentée.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
Les tableaux pour stocker la séquence d'entrée des points de test et les résultats de l'estimation sont préparés dans cet exemple. Ensuite, le tableau X[] est rempli de valeurs aléatoires, à titre d'exemple. La copie de la classe CDens est créée après que toutes les données aient été préparées.
Ensuite, le nombre de points de test nécessaire est défini (npoint=300 dans notre cas) par l'invocation de la méthode NTpoints(). S'il n'est pas nécessaire de modifier le nombre de points par défaut, l'invocation de la méthode NTpoints() peut être exclue.
Les valeurs calculées sont copiées dans les tableaux prédéfinis après l'invocation de la méthode Density(). Ensuite, la copie précédemment créée de la classe CDens est supprimée. Cet exemple ne montre que l'interaction avec la classe CDens. Aucune autre action avec les résultats obtenus (tableaux T[] et Y[]) n'est effectuée.
Si ces résultats sont destinés à être utilisés pour créer un graphique, cela peut être facilement fait en plaçant les valeurs du tableau T[] sur l'échelle du graphique X, tandis que les valeurs appropriées du tableau Y[] doivent être placées sur l'échelle Y.
3. Sélection de gamme optimale
La figure 1 présente les graphiques d'estimation de la densité pour la séquence ayant la loi de distribution normale et différentes valeurs de l'intervalle h.
Les estimations sont effectuées en utilisant la classe CDens décrite ci-dessus. Les graphiques ont été construits sous forme de pages HTML. La méthode de construction de ces graphiques sera présentée à la fin de l'article. La création de graphiques et de diagrammes au format HTML peut être trouvée à [9].
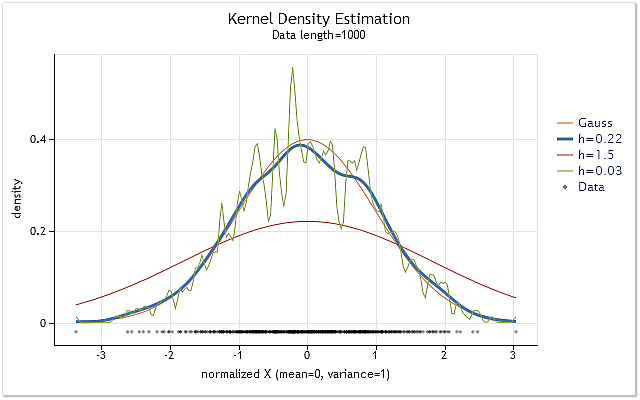
Fig. 1. Estimation de la densité pour diverses valeurs de l’intervalle h
La figure 1 affiche également la vraie courbe de densité de distribution normale (distribution gaussienne) ainsi que trois estimations de densité. On peut facilement voir que le résultat d'estimation le plus approprié a été obtenu avec h=0,22 dans ce cas. Dans deux autres cas, on peut observer un « sur-lissage » et un « sous-lissage » définis.
La figure 1 montre clairement l'importance d'une sélection correcte de l'intervalle h lors de l'utilisation de l'estimation de la densité du noyau. Dans le cas où la valeur h a été choisie de manière incorrecte, une estimation sera fortement décalée par rapport à la densité réelle ou considérablement dispersée.
De nombreux travaux sont consacrés à la sélection optimale de l'intervalle h. La règle empirique de Silverman, simple et éprouvée, est souvent utilisée pour la sélection des h (voir [10]).
![]()
Dans ce cas, A est la valeur la plus basse parmi les valeurs de l'écart-type de la séquence et l'écart interquartile divisé par 1,34.
Considérant que la séquence d'entrée a un écart-type égal à un dans la classe CDens mentionnée ci-dessus, il est assez facile de mettre en œuvre cette règle en utilisant le fragment de code suivant :
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Cette estimation convient aux séquences dont la fonction de densité de probabilité est proche de la normale par sa forme.
Dans de nombreux cas, la prise en compte de l'écart interquartile permet d'ajuster la valeur h vers le bas lorsque la forme de la densité évaluée s'écarte de la normale. Cette méthode d'évaluation est donc assez polyvalente. Par conséquent, cette règle empirique vaut la peine d'être utilisée comme estimation initiale de la valeur h de base. En outre, elle ne nécessite pas de longs calculs.
Outre les estimations asymptotiques et empiriques de la valeur de l'intervalle h, il existe également diverses méthodes basées sur l'analyse de la séquence d'entrée elle-même. Dans ce cas, la valeur optimale de h est déterminée en considérant l'estimation préliminaire de la densité inconnue. On trouvera une comparaison de l'efficacité de certaines de ces méthodes dans [11], [12].
Selon les résultats des tests publiés dans diverses sources, la méthode du plug-in Sheather-Jones (SJPI) est l'une des méthodes d'estimation de portée les plus efficaces. Optons pour cette méthode. Afin de ne pas surcharger l'article par de longues expressions mathématiques, seules certaines des caractéristiques de la méthode seront abordées plus loin. Si nécessaire, la base mathématique de cette méthode peut être trouvée dans [13].
Nous utilisons un noyau gaussien, qui est un noyau à support non borné (c'est-à-dire qu'il est spécifié lorsque son paramètre passe de moins à plus l'infini). Comme il résulte de l'expression ci-dessus, nous aurons besoin d'opérations O(M*N) pour estimer la densité en M points de la séquence ayant N longueur en utilisant la méthode de calcul direct et le noyau à support non borné. Dans le cas où nous devons faire des estimations à chacun des points de séquence, cette valeur augmente jusqu'à O(N*N) opérations et le temps consacré au calcul augmentera proportionnellement au carré de la longueur de la séquence.
Une telle demande de ressources de calcul est l'un des inconvénients majeurs de la méthode de lissage par noyau. Si nous passons à la méthode SJPI, nous verrons que ce n'est pas mieux en termes de quantité de calcul requise. En bref, nous devons d'abord calculer deux fois la somme de deux dérivées de densité sur toute la longueur de la séquence d'entrée lorsque nous mettons en œuvre la méthode SJPI.
Ensuite, nous devons calculer l'estimation de manière répétée en utilisant les résultats obtenus. La valeur d'estimation doit être égale à zéro. La méthode de Newton-Raphson [14] peut être utilisée pour trouver l'argument auquel cette fonction est égale à zéro. Dans le cas du calcul direct, l'application de la méthode SJPI pour déterminer la valeur de l’intervalle optimale peut nécessiter environ dix fois plus de temps que le calcul des estimations de densité.
Il existe plusieurs méthodes pour accélérer les calculs dans le lissage par noyau et l'estimation de la densité par noyau. Dans notre cas, on utilise le noyau gaussien, dont on peut supposer que les valeurs sont négligeables pour les valeurs d'argument supérieures à 4. Ainsi, si la valeur de l'argument est supérieure à 4, il n'est pas nécessaire de calculer les valeurs du noyau. Par conséquent, nous pouvons réduire partiellement le nombre de calculs requis. Nous ne verrons pratiquement aucune différence entre le graphique basé sur une telle estimation et la version entièrement calculée.
Un autre moyen simple d'accélérer les calculs est de réduire le nombre de points pour lesquels l'estimation est effectuée. Comme il a été mentionné ci-dessus, si M est inférieur à N, le nombre d'opérations requises sera réduit de O(N*N) à O(M*N). Si nous avons une longue séquence, par exemple, N=100 000, nous ne pouvons effectuer des estimations que sur M=200 points. Nous pouvons donc réduire considérablement le temps de calcul.
Aussi, des méthodes plus complexes peuvent être utilisées pour réduire le nombre de calculs nécessaires, par exemple, les estimations utilisant un algorithme de transformée de Fourier rapide ou des transformées en vaguelettes. Les méthodes basées sur la réduction de la dimension de la séquence d'entrée (par exemple, « Data binning » [15]) peuvent être appliquées avec succès pour les très longues séquences.
La transformation gaussienne rapide [16] peut également être appliquée pour accélérer les calculs en plus des méthodes mentionnées ci-dessus, dans le cas où le noyau gaussien est utilisé. Nous utiliserons l'algorithme basé sur la transformation gaussienne [17] pour mettre en œuvre la méthode SJPI d'estimation de la valeur de l’intervalle. Le lien mentionné ci-dessus mène aux documents contenant à la fois la description de la méthode et les codes de programme mettant en œuvre l'algorithme proposé.
4. Sheather-Jones plug-in (SJPI)
Comme dans le cas des expressions mathématiques déterminant l'essence de la méthode SJPI, nous ne copierons pas dans cet article la base mathématique de la mise en œuvre de l'algorithme que l'on peut trouver à [17]. Si nécessaire, vous pouvez consulter les publications à [17].
La classe CSJPlugin a été créée sur la base des matériaux situés dans [17]. Cette classe est destinée au calcul de la valeur optimale de l’intervalle h et comprend une seule méthode publique - double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
Les arguments suivants sont transmis à cette méthode lorsqu'elle est invoquée :
- double &px[] – le lien vers le tableau contenant la séquence originale ;
- double h est la valeur initiale de l'intervalle h, par rapport à laquelle la recherche est effectuée lors de la résolution des équations à l'aide de l'algorithme de Newton-Raphson. Il est souhaitable que cette valeur soit aussi proche que possible de la valeur recherchée. Cela peut réduire considérablement le temps consacré à la résolution des équations et diminuer la probabilité des cas où Newton-Raphson peut perdre sa fiabilité. La valeur trouvée en utilisant la règle empirique de Silverman peut être utilisée comme valeur h initiale ;
- double stdev=1 - la valeur de l'écart-type de la séquence originale. La valeur par défaut est un. Dans ce cas, il n'est pas nécessaire de modifier la valeur par défaut car cette méthode est destinée à être utilisée avec la classe CDens mentionnée précédemment, dans laquelle la séquence originale a déjà été normalisée et a un écart-type égal à un.
La méthode SelectH() renvoie la valeur optimale de l'intervalle h obtenue en cas de réussite. La valeur initiale h est renvoyée en paramètre en cas d'échec. Le code source de la classe CSJPlugin se trouve dans le fichier CSJPlugin.mqh.
Il est nécessaire de clarifier certaines caractéristiques de cette mise en œuvre.
La séquence source est transformée en une seule fois dans l'intervalle [0,1], tandis que la valeur initiale de l'intervalle h est normalisée proportionnellement à l'échelle de transformation de la séquence originale. Une normalisation inversée est appliquée à la valeur optimale de h obtenue au cours des calculs.
eps=1e-4 - la précision du calcul des estimations de la densité et de ses dérivés et P_UL=500 - le nombre maximum d'itérations internes de l'algorithme sont définis dans le constructeur de la classe CSJPlugin. Pour plus d'informations, voir [17].
IMAX=20 - nombre maximal d'itérations autorisé pour la méthode Newton-Raphson et PREC=1e-4 - précision de la résolution de l'équation à l'aide de cette méthode sont définis dans la méthode SelectH().
L'utilisation traditionnelle de la méthode Newton-Raphson nécessitait le calcul de la fonction cible et de sa dérivée au même point à chaque itération de valeur. Dans ce cas, le calcul de la dérivée a été remplacé par son estimation calculée en ajoutant un petit incrément à la valeur de son argument.
La figure 2 montre l'exemple d'utilisation de deux méthodes différentes d'estimation de la valeur optimale de l’intervalle h.
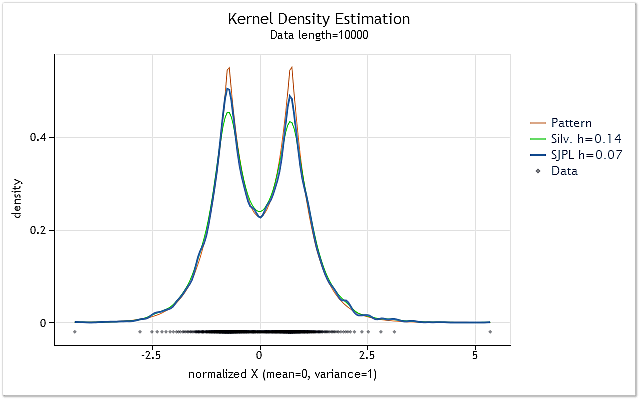
Fig. 2. Comparaison des estimations optimales de la valeur de l’intervalle h
La figure 2 affiche deux estimations pour la séquence aléatoire, dont la densité réelle est représentée par le graphique rouge (motif).
Les estimations ont été réalisées pour la séquence ayant une longueur de 10 000 éléments. La valeur de l'intervalle h de 0,14 a été obtenue pour cette séquence en utilisant la règle empirique de Silverman, alors qu'elle a été de 0,07 en utilisant la méthode SJPI.
En examinant les résultats de l'estimation de la densité de noyau pour ces deux valeurs de h présentées dans la figure 2, nous pouvons facilement voir que l'application de la méthode SJPI a permis d'obtenir une estimation de h plus intéressante par rapport à la règle de Silverman. Comme nous pouvons le voir, les sommets aigus sont beaucoup mieux formés, tandis qu'il n'y a presque pas d'augmentation de la dispersion aux creux inclinés dans le cas de h=0,07.
Comme prévu, l'utilisation de la méthode SJPI permet dans de nombreux cas d'obtenir des estimations d’intervalle h tout à fait satisfaisantes. Malgré le fait que des algorithmes assez rapides [17] aient été utilisés pour la création de classe CSJPlugin, l'estimation de la valeur h utilisant cette méthode peut encore prendre trop de temps pour de longues séquences.
Un autre inconvénient de cette méthode est sa tendance à surestimer la valeur h pour des séquences courtes constituées de seulement 10 à 30 valeurs. Les estimations faites à l'aide de la méthode SJPI peuvent dépasser h estimations faites par la règle empirique de Silverman.
Les règles suivantes seront utilisées dans la mise en œuvre ultérieure pour compenser ces inconvénients :
- L'estimation de Silverman sera l'estimation par défaut pour l'intervalle h, tandis qu'il sera possible d'activer la méthode SJPI par une commande séparée ;
- Lors de l'utilisation de la méthode SJPI, la valeur la plus faible parmi celles obtenues par les deux méthodes mentionnées sera toujours utilisée comme valeur finale h.
5. Effet de frontière
Le désir d'utiliser une valeur d'intervalle aussi optimale que possible dans l'estimation de la densité a conduit à la création de la classe CSJPlugin mentionnée ci-dessus et plutôt encombrante. Mais il y a un autre problème en plus de la spécification de la taille de l’intervalle et de l'intensité élevée des ressources de la méthode de lissage du noyau. C'est ce qu'on appelle l'effet de frontière.
Le problème est simple. Il sera affiché à l'aide du noyau défini sur l'intervalle [-1,1]. Un tel noyau est appelé noyau à support fini. Il est égal à zéro en dehors de l’intervalle spécifiée (n'existe pas).
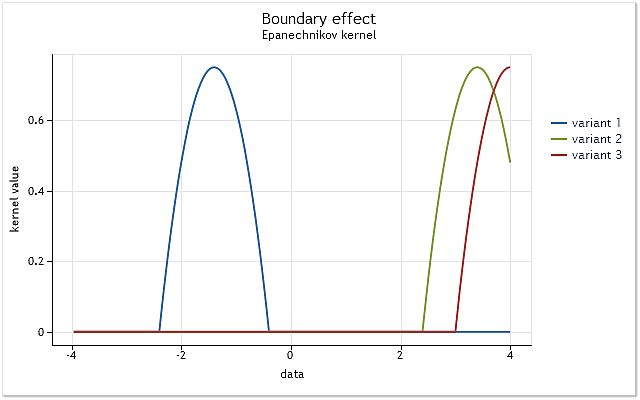
Fig. 3. La réduction du noyau à la limite de la frontière
Comme le montre la figure 3, dans le premier cas, le noyau couvre complètement les données originales situées sur l'intervalle [-1,1] par rapport à son centre. Lorsque le noyau se déplace (par exemple, vers la droite), la situation se présente lorsque les données ne sont pas suffisantes pour utiliser pleinement la fonction noyau sélectionnée.
Le noyau couvre déjà moins de données que dans le premier cas. Le pire des cas est lorsque le centre du noyau est situé à la limite de la séquence de données. La quantité de données couvertes par le noyau est réduite à 50 % dans ce cas. Une telle réduction du nombre de données utilisées pour l'estimation de la densité conduit à un décalage important des estimations et augmente leur dispersion dans les points proches des limites de l’intervalle.
La figure 3 montre un exemple de réduction pour un noyau à support fini (noyau d'Epanechnikov) à la limite de l'intervalle. Il est à noter que le noyau gaussien défini sur l'intervalle infinie (support non borné) a été utilisé lors de la mise en œuvre de la méthode d'estimation de densité à noyau. Théoriquement, la coupure d'un tel noyau doit toujours avoir lieu. Mais compte tenu du fait que la valeur de ce noyau est presque égale à zéro pour les grands arguments, les effets de frontière lui apparaissent de la même manière qu'aux noyaux à support fini.
Cette caractéristique ne peut pas affecter les résultats de l'estimation de la densité dans les cas présentés dans les figures 1 et 2, car dans les deux cas, l'estimation a été effectuée pour les distributions, dont la fonction de densité de probabilité a diminué aux frontières presque jusqu'à zéro.
Formons la séquence composée d'entiers positifs X=1,2,3,4,5,6,…n pour montrer l'influence de la coupure du noyau aux limites de l’intervalle. Une telle séquence a une loi paire de la distribution de densité de probabilité. Cela signifie que l'estimation de la densité de cette séquence doit être une ligne droite horizontale, situé à un niveau non nul.
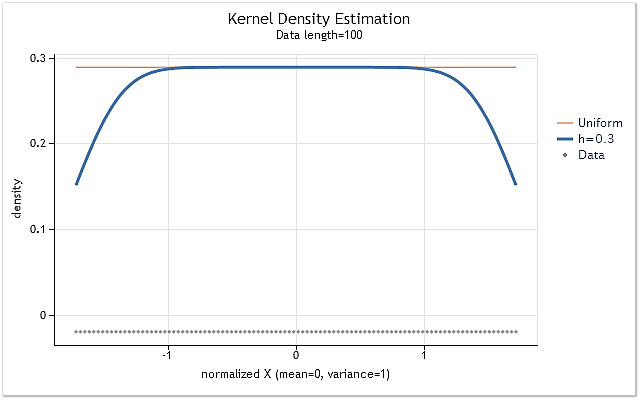
Fig. 4. Estimation de la densité pour la séquence ayant une loi de distribution paire
Comme prévu, la figure 4 montre clairement qu'il y a un décalage considérable des estimations de densité aux limites de l'intervalle. Il existe plusieurs méthodes permettant de réduire plus ou moins ce décalage. Ils peuvent être divisés en gros dans les groupes suivants :
- Méthodes de réflexion des données ;
- Méthodes de transformation des données ;
- Méthodes de pseudo-données ;
- Méthodes du noyau limite.
L'idée d'utiliser les données réfléchies est que la séquence d'entrée est intentionnellement augmentée en ajoutant les données, ce qui est une sorte de reflet miroir de cette séquence par rapport aux limites de l’intervalle de séquence. Après une telle augmentation, l'estimation de la densité est effectuée pour les mêmes points, comme pour la séquence originale, mais les données ajoutées intentionnellement sont également utilisées dans l'estimation.
Les méthodes impliquant la transformation de données sont axées sur la transformation de séquence près de ses limites d’intervalle. Par exemple, il est possible d'utiliser le logarithmique ou tout autre transformation permettant en quelque sorte de déformer l'échelle des données à l'approche de la limite de l’intervalle lors de l'estimation de la densité.
Les pseudo-données peuvent être utilisées pour l'extension intentionnelle (agrandissement) de la séquence originale. Il s'agit des données calculées sur la base des valeurs de la séquence originale. Ces données permettent d'envisager son comportement aux frontières et de le compléter de la manière la plus appropriée.
Il existe de nombreuses publications consacrées aux méthodes du noyau limite. Dans ces méthodes, le noyau modifie par certains moyens sa forme à l'approche de la frontière. La forme du noyau change pour compenser le décalage des estimations aux frontières.
Certaines méthodes dédiées à la compensation des distorsions apparaissant aux limites de l’intervalle, leur comparaison et l’évaluation de leur efficacité peuvent être trouvées dans [18].
La méthode de réflexion des données a été sélectionnée pour une utilisation ultérieure après quelques brèves expériences. Ce choix a été influencé par le fait que cette méthode n'implique pas de situations où l'estimation de la densité a une valeur négative. De plus, cette méthode ne nécessite pas de calculs mathématiques complexes. Le nombre total d'opérations augmente encore en raison de la nécessité d'effectuer chaque estimation de la séquence, dont la longueur est délibérément augmentée.
Il existe deux manières de mettre en œuvre cette méthode. Tout d'abord, il est possible de compléter la séquence originale par les données nécessaires et de multiplier sa taille par trois dans le processus. Ensuite, nous pourrons faire des estimations de la même manière, comme cela est montré dans le cours CDens présentée précédemment. Deuxièmement, il est possible de ne pas développer le tableau des données d'entrée. Nous pouvons simplement sélectionner à nouveau les données d'une certaine manière. La deuxième voie a été choisie pour la mise en œuvre.
Dans la classe CDens mentionnée ci-dessus, l'estimation de la densité a été mise en œuvre dans la fonction void kdens(double h). Modifions cette fonction en ajoutant la correction des distorsions de frontière.
La fonction augmentée peut se présenter comme suit.
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
La fonction est implémentée en supposant que les données source dans le tableau X[] avaient déjà été triées au moment où la fonction a été appelée. Cela permet d'exclure facilement deux éléments de séquence correspondant aux valeurs extrêmes de l’intervalle d'un autre traitement. Lors de la mise en œuvre de cette fonction, on a essayé de placer les opérations mathématiques en dehors des boucles chaque fois que cela était possible. Par conséquent, la fonction reflète moins bien l'idée de l'algorithme utilisé.
Il a déjà été mentionné précédemment qu'il est possible de réduire le nombre de calculs, au cas où nous ne calculerions pas de valeur de noyau pour les grandes valeurs des arguments. C'est exactement ce qui a été mis en œuvre dans la fonction ci-dessus. Dans ce cas, il est impossible de constater des changements après la création du graphique de densité évaluée.
Lors de l'utilisation de la version modifiée de la fonction kdens(), l'estimation de la densité illustrée à la figure 4 est transformée en une ligne droite et les creux des limites disparaissent complètement. Mais une telle correction idéale ne peut être obtenue que si la distribution près des frontières a un gradient nul, c'est-à-dire représenté par une ligne horizontale.
Si la densité de distribution estimée augmente ou diminue fortement près de la frontière, la méthode de réflexion des données sélectionnée ne sera pas en mesure d'ajuster complètement l'effet de frontière. Ceci est illustré par les figures suivantes.
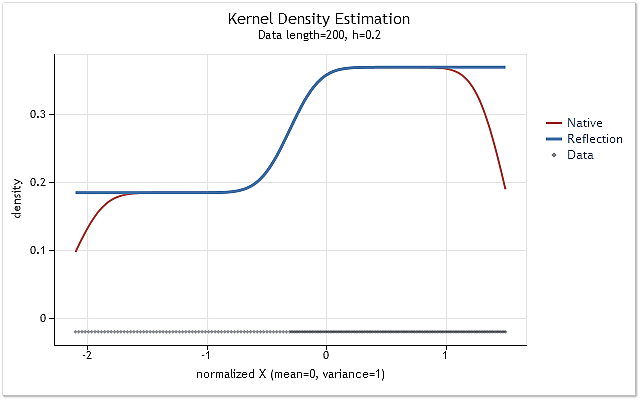
Fig. 5. Fig. 5. La densité de probabilité changeant par étapes
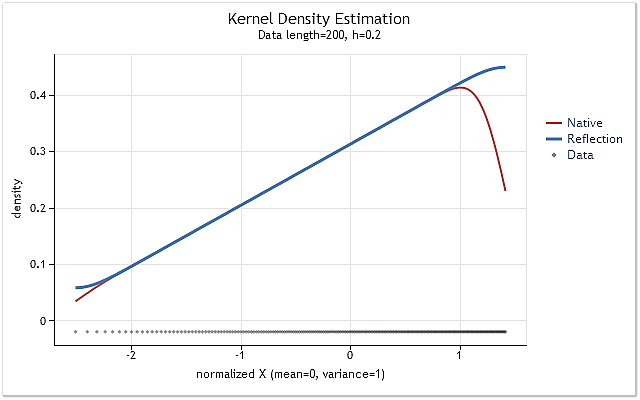
Fig. 6. La fonction de densité de probabilité augmente linéairement
Les figures 5 et 6 montrent l'estimation de la densité obtenue en utilisant la version originale de la fonction kdens() (rouge) et l'estimation obtenue en tenant compte des modifications appliquées qui mettent en œuvre la méthode de réflexion des données (bleu). L'effet de frontière a été entièrement corrigé dans la figure 5, tandis que le décalage près des frontières n'a pas été complètement éliminé dans la figure 6. Si la densité estimée augmente ou diminue fortement près de la frontière, alors elle semble être un peu plus lisse près de cette frontière.
La méthode de réflexion des données choisie pour ajuster l'effet de frontière n'est ni la meilleure ni la pire des méthodes connues. Bien que cette méthode ne puisse pas éliminer l'effet de frontière dans tous les cas, elle est suffisamment stable et facile à mettre en œuvre. Cette méthode permet d'obtenir un résultat logique et prévisible.
6. Mise en œuvre finale. Classe CKDensity
Ajoutons la possibilité de sélectionner automatiquement la valeur de l'intervalle h et la correction de l'effet de frontière à la classe CDens créée précédemment.
Vous trouverez ci-dessous le code source d'une telle classe modifiée.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
La méthode Density(double &x[],double hh=-1) est une méthode de base pour cette classe. Le premier argument est le lien vers le tableau x[], dans lequel la séquence d'entrée analysée doit être contenue. La longueur de la séquence d'entrée ne doit pas être inférieure à huit éléments. Le deuxième argument (facultatif) est utilisé pour le réglage forcé de la valeur de l’intervalle h.
Tout nombre positif peut être spécifié. La valeur h définie sera toujours limitée par 0,005 à partir du bas. Si ce paramètre a une valeur négative, la valeur de l’intervalle sera sélectionnée automatiquement. La méthode Density() renvoie zéro en cas de réussite et moins un en cas d'échec.
Après l'appel de la méthode Density() et son achèvement réussi, le tableau T[] contiendra les valeurs des points de test, pour lesquels l'estimation de la densité a été effectuée, tandis que le tableau Y[] contiendra les valeurs de ces estimations. Le tableau X[] contiendra la séquence d'entrée normalisée et triée. La valeur moyenne de cette séquence est égale à zéro, tandis que la valeur de l'écart type est égale à un.
Les valeurs suivantes sont contenues dans les variables qui sont des membres de classe :
- N – longueur de la séquence d'entrée ;
- Np - nombre de points de test pour lesquels l'estimation de la densité a été réalisée ;
- Moyenne – valeur moyenne de la séquence d'entrée ;
- Var – variance de séquence d'entrée ;
- StDev – écart type de la séquence d'entrée ;
- H - valeur de l'intervalle (paramètre de lissage) ;
- Pflag - indicateur de l'application de la méthode SJPI pour déterminer la valeur optimale de l’intervalle h.
La méthode NTpoints(int n) est utilisée pour définir le nombre de points de test auxquels l'estimation de la densité sera effectuée. Le réglage du nombre de points de test doit être effectué avant d'appeler la méthode de base Density(). Si la méthode NTpoints(int n) n'est pas utilisée, un nombre de points par défaut de 200 sera défini.
La méthode PluginMode(int m) autorise ou interdit l'utilisation de la méthode SJPI pour évaluer la valeur de l’intervalle optimale. Si le paramètre égal à un est utilisé lors de l'appel de cette méthode, la méthode SJPI sera appliquée pour spécifier l’intervalle h. Si la valeur de ce paramètre n'est pas égale à un, la méthode SJPI ne sera pas utilisée. Si la méthode PluginMode(int m) n'a pas été invoquée, la méthode SJPI sera désactivée par défaut.
7. Création de graphiques
La méthode que l'on peut trouver à [9] a été utilisée pour la rédaction de cet article. Cette publication portait sur l'application d'une page HTML prête à l'emploi comprenant la bibliothèque JavaScript highcharts [19] et la spécification complète de toutes ses invocations. Plus loin, un programme MQL forme un fichier texte contenant les données à afficher et ce fichier se connecte à la page HTML mentionnée ci-dessus.
Dans ce cas, il est nécessaire de modifier la page HTML en changeant le code JavaScript mis en œuvre pour apporter des corrections à la structure des graphiques affichés. Pour éviter cela, une interface simple a été développée permettant d'invoquer les méthodes JavaScript de la bibliothèque highcharts directement à partir du programme MQL.
Lors de la création de l'interface, il n'a pas été question de mettre en œuvre l'accès à toutes les possibilités de la bibliothèque highcharts. Ainsi, seules les possibilités permettant de ne pas modifier le fichier HTML préalablement créé lors de la rédaction de l'article ont été implémentées.
Le code source de la classe CLinDraw est affiché ci-dessous. Cette classe a été utilisée pour assurer la connexion avec les méthodes de la bibliothèque highcharts. Ce code ne doit pas être considéré comme une implémentation logicielle complète. Il s'agit juste d'un exemple montrant comment créer une interface ayant une bibliothèque graphique JavaScript.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Si nous voulons faire fonctionner cette classe correctement, nous avons besoin d'une page HTML prête à l'emploi ayant mis en œuvre les bibliothèques JavaScript. La taille et l'emplacement du champ pour le(s) diagramme(s) de construction doivent également être spécifiés. Vous trouverez un exemple de mise en œuvre d'une telle page dans les fichiers joints à cet article.
Lorsque la méthode AddGraph() est invoquée dans un fichier texte, un code JavaScript approprié est formé. Le fichier texte est ensuite inclus dans la page HTML précédemment créée. Le code mentionné fait référence à la bibliothèque graphique et permet de créer un graphique en utilisant les données soumises à la méthode AddGraph() comme argument. Un ou plusieurs graphiques supplémentaires peuvent être ajoutés sur le champ de sortie en invoquant à nouveau cette méthode.
Trois versions de la fonction surchargée AddGraph() sont incluses dans la classe CLinDraw. L'une des versions exige qu'un seul tableau avec les données affichées lui soit transféré en tant qu'argument. Il est conçu pour créer un diagramme séquentiel où l'indice de l'élément séquentiel est affiché sur l'axe des X.
La deuxième version reçoit deux tableaux en argument. Ces tableaux contiennent les valeurs affichées sur les axes X et Y, respectivement. La troisième version permet de définir une valeur constante pour l'axe Y. Il peut être utilisé pour construire une ligne horizontale. Les arguments restants de ces fonctions sont similaires :
- type de chaîne – type de graphique affiché. Peut avoir des valeurs « line », « spline » et « scatter » ;
- nom de chaîne – nom attribué au graphique ;
- int w=0 – largeur de ligne. Argument facultatif. Si la valeur est 0, la largeur par défaut de 2 est utilisée ;
- string col="" – définit la couleur de la ligne et sa valeur d'opacité. Argument facultatif.
La méthode LDraw() doit être invoquée en dernier. Cette méthode termine la sortie du code JavaScript et des données dans le fichier texte créé par défaut dans \MQL5\Files\. Ensuite, le fichier est déplacé vers le répertoire contenant les fichiers de la bibliothèque graphique et le fichier HTML.
La méthode LDraw() peut posséder un seul argument facultatif. Si la valeur de l'argument n'est pas définie ou est définie à un, un navigateur web par défaut sera invoqué et le graphique sera affiché après avoir déplacé le fichier de données dans un répertoire approprié. Si l'argument a une autre valeur, le fichier de données sera également complètement formé mais un navigateur Web ne sera pas invoqué automatiquement.
D'autres méthodes de classe CLinDraw disponibles permettent de définir des en-têtes de graphique et des étiquettes d'axes. Nous n'examinerons pas en détail les problèmes d'application de la bibliothèque highcharts et de la classe CLinDraw dans cet article. Des informations complètes sur la bibliothèque graphique highcharts sont disponibles dans [19], tandis que des exemples de son application pour la création de graphiques et de diagrammes sont disponibles dans [9], [20].
L'utilisation de bibliothèques externes doit être autorisée dans le terminal pour le fonctionnement normal de la classe CLinDraw.
8. Exemple d'estimation de la densité et de disposition des fichiers
Nous avons finalement obtenu trois classes - CKDensity, CSJPlugin et CLinDraw.
Vous trouverez ci-dessous le code source de l'exemple indiquant comment les classes peuvent être utilisées.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
Les données, pour lesquelles l'évaluation de la fonction de densité de probabilité sera effectuée, sont préparées au début du script KDE_Example.mq5. Pour ce faire, les valeurs « ouvertes » du symbole et de la période en cours sont copiées dans le tableau X[]. Les rendements logarithmiques sont ensuite calculés sur leur base.
L'étape suivante est la création d'une copie de la classe CKDensity. L'invocation de sa méthode PluginMode() permet d'utiliser la méthode SJPI pour l'évaluation de l’intervalle h. L'estimation de la densité est ensuite effectuée pour la séquence créée dans le tableau X[]. Le processus d'évaluation est terminé à cette étape. Toutes les étapes suivantes concernent la visualisation de l'estimation de densité obtenue.
Les estimations obtenues doivent être comparées à n'importe quelle loi de distribution connue. Pour ce faire, les valeurs correspondant à la loi de distribution de Laplace sont formées dans le tableau Z[]. Les données d'entrée normalisées et triées sont ensuite stockées dans le tableau Sc[]. Si la longueur de la séquence d'entrée dépasse 400 éléments, toutes ses valeurs ne seront pas incluses dans Sc[]. Certaines d'entre elles seront ignorées. Par conséquent, la taille du tableau Sc[] ne contiendra jamais plus de 400 éléments.
Une fois toutes les données nécessaires à l'affichage préparées, une copie de la classe CLinDraw est créée. Ensuite, les en-têtes sont spécifiés et les graphiques nécessaires sont ajoutés à l'aide de la méthode AddGraph().
Le premier est le graphique de loi de distribution de Laplace destiné à être un modèle. Il est suivi du graphique de l'estimation de la densité obtenue à partir des données d'entrée. Le graphique du bas affichant le groupe de données source est ajouté en dernier. Après avoir défini tous les éléments nécessaires à l'affichage, la méthode LDraw() est invoquée.
En conséquence, nous obtenons le graphique illustré à la figure 7.
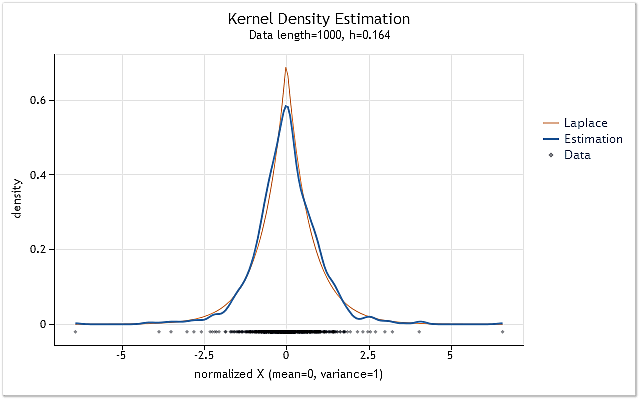
Fig. 7. Estimation de la densité pour les rendements logarithmiques (USDJPY, Quotidien)
L'estimation illustrée à la figure 7 a été effectuée pour 1 000 valeurs de rendements logarithmiques pour l'USDJPY, Quotidien. Comme on peut le voir, l'estimation est très similaire à la courbe correspondant à la distribution de Laplace.
Tous les fichiers nécessaires à l'estimation et à la visualisation de la densité se trouvent dans l'archive KDEFiles.zip ci-dessous. L'archive comprend les fichiers suivants :
- DensityEstimation\ChartTools\CLinDraw.mqh – classe pour l'interaction avec highcharts.js ;
- DensityEstimation\ChartTools\highcharts.js - Bibliothèque Highcharts JS v2.2.0 (2012-02-16);
- DensityEstimation\ChartTools\jquery.js – bibliothèque jQuery v1.7.1 ;
- DensityEstimation\ChartTools\LinDraw.htm – Page HTML destinée à l'affichage ;
- DensityEstimation\CKDensity.mqh – classe mettant en œuvre l'estimation de la densité ;
- DensityEstimation\CSJPlugin.mqh – classe mettant en œuvre la méthode SJPI de l'estimation de la valeur de l’intervalle optimale ;
- DensityEstimation\KDE_Example.mq5 – exemple d'estimation de densité pour les rendements logarithmiques.
Après avoir décompressé l'archive, le répertoire DensityEstimation\ avec tout son contenu doit être placé dans le répertoire Scripts (ou Indicateurs) du terminal. Il est ensuite possible de compiler et de lancer immédiatement KDE_Example.mq5. Le répertoire DensityEstimation peut être renommé, si nécessaire. Cela n'affectera pas le fonctionnement du programme.
Il convient de mentionner à nouveau que l'utilisation de bibliothèques externes doit être autorisée dans le terminal pour le fonctionnement normal de la classe CLinDraw.
Le répertoire DensityEstimation\ comprend le sous-répertoire ChartTools\ contenant tous les composants nécessaires pour visualiser les résultats de l'estimation. Les fichiers de visualisation sont situés dans un sous-répertoire distinct, afin que le contenu du répertoire DensityEstimation soit facilement visible. Le nom du sous-répertoire ChartTools\ est spécifié directement dans les codes sources. Par conséquent, il ne doit pas être renommé, sinon il sera nécessaire d'apporter des modifications aux codes sources.
Il a déjà été mentionné que le fichier texte est créé lors de la visualisation. Ce fichier contient les données nécessaires à la construction des graphiques. Ce fichier est à l'origine créé dans un répertoire Files spécial du terminal. Mais il est ensuite déplacé dans le répertoire ChartTools mentionné. Ainsi, il ne restera aucune trace de notre activité d'exemple de test dans Files\ ou dans tout autre répertoire de terminal. Par conséquent, vous pouvez simplement supprimer le répertoire DensityEstimation avec tout son contenu pour supprimer complètement les fichiers installés de cet article.
Conclusion
Les expressions mathématiques expliquant l'essence de certaines méthodes particulières ont été incluses dans l’ article. Cela a été fait délibérément dans le but de simplifier sa lecture. Si nécessaire, tous les calculs mathématiques peuvent être trouvés dans de nombreuses publications. Les liens de certains d'entre eux sont fournis ci-dessous.
Les codes sources fournis dans l'article n'ont pas fait l'objet de tests sérieux. Par conséquent, ils doivent être considérés uniquement comme des exemples, et non comme des applications entièrement fonctionnelles.
Références
- Histogramme.
- Estimation de la densité du noyau.
- Lissage du noyau.
- Expectation–algorithme de maximisation.
- А.V. Batov, V.Y. Korolyov, А.Y. Korchagin. Algorithme EM ayant un grand nombre de composants comme moyen de construire des estimations de densité non paramétriques (en russe).
- Hardle W. Régression non paramétrique appliquée.
- Noyau (statistiques).
- Graphiques et diagrammes en HTML.
- Simon J. Sheather. (2004). Estimation de la densité.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). Examen et comparaison des méthodes de sélection de la largeur de bande pour la régression du noyau.
- Clive R. Loader. (1999). Sélection de la bande passante : Classique ou Plug-In ?.
- S. J. Sheather, M. C. Jones. (1991). Une méthode fiable de sélection de bande passante basée sur les données pour l'estimation de la densité du noyau.
- Méthode de Newton.
- Regroupement des données.
- Changjiang Yang, Ramani Duraiswami et Larry Davis. (2004). Machines à noyau efficaces utilisant la transformée de Gauss rapide améliorée.
- Estimation rapide et optimale de la bande passante pour KDE univarié.
- R.J. Karunamuni et T. Alberts. (2005). Une méthode de transformation localement adaptative de la correction des limites dans l'estimation de la densité du noyau.
- Highcharts JS.
- Analyse des principales caractéristiques des séries chronologiques.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/396
 Obtenez 200 USD pour votre article sur le trading algorithmique !
Obtenez 200 USD pour votre article sur le trading algorithmique !
 Fondamentaux de la statistique
Fondamentaux de la statistique
 Application de la méthode des coordonnées propres à l'analyse structurelle de distributions statistiques non extensives
Application de la méthode des coordonnées propres à l'analyse structurelle de distributions statistiques non extensives
 Qui est qui dans MQL5.community ?
Qui est qui dans MQL5.community ?
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation