Aplicação da Teoria dos Jogos de Nash com Filtragem HMM em Trading

Introdução

Aplicar teorias matemáticas pode oferecer uma vantagem estratégica. Uma dessas teorias é o Equilíbrio de Nash, desenvolvido pelo renomado matemático John Forbes Nash Jr. Conhecido por suas contribuições à teoria dos jogos, o trabalho de Nash tem sido influente em diversos campos, incluindo economia e além. Este artigo explora como a teoria do equilíbrio de Nash pode ser efetivamente aplicada ao trading. Ao utilizar scripts em Python e modelos estatísticos avançados, buscamos aproveitar os princípios da teoria dos jogos de Nash para otimizar estratégias de negociação e tomar decisões mais informadas no mercado.

Nash

Quem é John Forbes Nash Jr.?

A Wikipédia diz sobre ele:

John Forbes Nash, Jr. (13 de junho de 1928 – 23 de maio de 2015), conhecido e publicado como John Nash, foi um matemático americano que fez contribuições fundamentais para a teoria dos jogos, geometria algébrica real, geometria diferencial e equações diferenciais parciais. Nash e os teóricos dos jogos John Harsanyi e Reinhard Selten receberam o Prêmio Nobel de Economia em 1994. Em 2015, ele e Louis Nirenberg receberam o Prêmio Abel por suas contribuições ao campo das equações diferenciais parciais.

Como estudante de pós-graduação no Departamento de Matemática da Universidade de Princeton, Nash introduziu uma série de conceitos (incluindo o equilíbrio de Nash e a solução de barganha de Nash), que agora são considerados centrais para a teoria dos jogos e suas aplicações em diversas ciências.

Há um filme baseado em sua vida intitulado "Uma Mente Brilhante". Vamos aplicar sua teoria dos jogos ao trading com MQL5.

Como vamos introduzir a Teoria dos Jogos de Nash no trading?

Teoria do Equilíbrio de Nash

O Equilíbrio de Nash é um conceito da teoria dos jogos onde se assume que cada jogador conhece as estratégias de equilíbrio dos outros jogadores, e nenhum jogador tem algo a ganhar mudando apenas sua própria estratégia.

Em um equilíbrio de Nash, a estratégia de cada jogador é ótima, dado as estratégias de todos os outros jogadores. Um jogo pode ter múltiplos equilíbrios de Nash ou nenhum.

O equilíbrio de Nash é um conceito fundamental na teoria dos jogos, nomeado em homenagem ao matemático John Nash. Ele descreve um estado em um jogo não cooperativo onde cada jogador escolheu uma estratégia, e nenhum jogador pode se beneficiar ao mudar unilateralmente sua estratégia enquanto os outros jogadores mantêm as suas inalteradas.

Definição formal:

Seja (N, S, u) um jogo com:

• N jogadores: N = {1, 2, ..., n}
• Conjuntos de estratégias para cada jogador: S = (S₁, S₂, ..., Sₙ)
• Funções utilitárias para cada jogador: u = (u₁, u₂, ..., uₙ)

Um perfil de estratégia s* = (s₁*, s₂*, ..., sₙ*) é um equilíbrio de Nash se, para cada jogador i e para todas as estratégias alternativas sᵢ ∈ Sᵢ:

uᵢ(s₁*, ..., sᵢ*, ..., sₙ*) ≥ uᵢ(s₁*, ..., sᵢ, ..., sₙ*)

Em outras palavras, nenhum jogador i pode melhorar unilateralmente sua utilidade ao desviar de sua estratégia de equilíbrio sᵢ* para qualquer outra estratégia sᵢ, dado que todos os outros jogadores mantêm suas estratégias de equilíbrio.

Para um jogo de dois jogadores, podemos expressar isso de forma mais concisa:

(s₁*, s₂*) é um equilíbrio de Nash se:

1. u₁(s₁*, s₂*) ≥ u₁(s₁, s₂*) para todo s₁ ∈ S₁
2. u₂(s₁*, s₂*) ≥ u₂(s₁*, s₂) para todo s₂ ∈ S₂Esta formulação enfatiza que a estratégia de cada jogador é a melhor resposta à estratégia do outro jogador no equilíbrio.

Esta formulação enfatiza que a estratégia de cada jogador é a melhor resposta à estratégia do outro jogador no equilíbrio.

É importante observar que:

1. Nem todos os jogos têm um equilíbrio de Nash em estratégias puras.
2. Alguns jogos podem ter múltiplos equilíbrios de Nash.
3. Um equilíbrio de Nash não é necessariamente pareto ótimo ou o resultado mais desejável para todos os jogadores coletivamente.

O conceito de equilíbrio de Nash tem aplicações abrangentes em economia, ciência política e outros campos onde interações estratégicas entre agentes racionais são estudadas.

Embora, em um equilíbrio de Nash, ninguém possa melhorar unilateralmente sua posição sem que os outros se adaptem, na prática, os mercados financeiros são dinâmicos e raramente estão em equilíbrio perfeito. Oportunidades de ganhar dinheiro surgem de ineficiências temporárias, vantagens informacionais, melhor gestão de riscos e a capacidade de reagir mais rapidamente do que outros jogadores. Além disso, fatores externos e imprevisíveis podem perturbar o equilíbrio, criando novas oportunidades para aqueles que estão preparados.

Primeiro de tudo, precisamos selecionar as moedas (vamos fazer o equilíbrio de Nash, então precisamos de dois símbolos, escolheremos símbolos negativamente correlacionados), usaremos o Python para isso. Este é o script usado:

import MetaTrader5 as mt5
import pandas as pd
from scipy.stats import pearsonr
from statsmodels.tsa.stattools import coint
import numpy as np
import datetime

# Connect with MetaTrader 5
if not mt5.initialize():
    print("Failed to initialize MT5")
    mt5.shutdown()

# Get the list of symbols
symbols = mt5.symbols_get()
symbols = [s.name for s in symbols if s.name.startswith('EUR') or s.name.startswith('USD') or s.name.endswith('USD')]  # Filter symbols by example

# Download historical data and save in dictionary
data = {}
for symbol in symbols:
    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    
    if rates is not None:
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        data[symbol] = df.set_index('time')['close']

# Close connection with MT5
mt5.shutdown()

# Calculate the Pearson coefficient and test for cointegration for each pair of symbols
cointegrated_pairs = []
for i in range(len(symbols)):
    for j in range(i + 1, len(symbols)):
        if symbols[i] in data and symbols[j] in data:
            common_index = data[symbols[i]].index.intersection(data[symbols[j]].index)
            if len(common_index) > 30:  # Ensure there are enough data points
                corr, _ = pearsonr(data[symbols[i]][common_index], data[symbols[j]][common_index])
                if abs(corr) > 0.8:  # Strong correlation
                    score, p_value, _ = coint(data[symbols[i]][common_index], data[symbols[j]][common_index])
                    if p_value < 0.05:  # P-value less than 0.05
                        cointegrated_pairs.append((symbols[i], symbols[j], corr, p_value))

# Filter and show only cointegrated pairs with p-value less than 0.05
print(f'Total pairs with strong correlation and cointegration: {len(cointegrated_pairs)}')
for sym1, sym2, corr, p_val in cointegrated_pairs:
    print(f'{sym1} - {sym2}: Correlation={corr:.4f}, P-Cointegration value={p_val:.4f}')

Este script inicializa o MetaTrader 5, depois obtém todos os símbolos que começam com EUR ou USD ou terminam em USD. Depois disso, ele baixa os dados desses símbolos e fecha o MetaTrader 5. Ele compara todos os símbolos e passa apenas os fortemente correlacionados e depois faz outro filtro para os pares fortemente cointegrados. Por fim, exibe no terminal os símbolos restantes.

Correlação mede como duas coisas estão relacionadas. Imagine que você e seu melhor amigo sempre vão ao cinema juntos aos sábados. Isso é um exemplo de correlação: quando você vai ao cinema, seu amigo também está lá. Se a correlação for positiva, significa que quando um aumenta, o outro também aumenta. Se for negativa, um aumenta enquanto o outro diminui. Se a correlação for zero, significa que não há conexão entre os dois.

Cointegração é um conceito estatístico usado para descrever uma situação em que duas ou mais variáveis têm alguma relação de longo prazo, mesmo que possam flutuar independentemente no curto prazo. Imagine dois nadadores amarrados juntos por uma corda: eles podem nadar livremente na piscina, mas não podem se afastar muito um do outro. A cointegração indica que, apesar de diferenças temporárias, essas variáveis sempre retornarão a um equilíbrio ou tendência de longo prazo comum.

Coeficiente de Pearson mede quão linearmente relacionadas duas variáveis estão. Se o coeficiente estiver próximo de +1, indica uma dependência direta: à medida que uma variável aumenta, a outra também aumenta. Um coeficiente próximo de -1 significa que, à medida que uma aumenta, a outra diminui, indicando uma relação inversa. Um valor de 0 significa nenhuma conexão linear. Por exemplo, medir a temperatura e o número de vendas de bebidas geladas pode ajudar a entender como esses fatores estão relacionados usando o Coeficiente de Pearson.

Os resultados do script devem parecer com estes (estes foram os resultados obtidos para as condições iniciais do script):

    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4

Total pairs with strong correlation and cointegration: 40
USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165
USDJPY - EURN.NASDAQ: Correlation=0.9153, P-Cointegration value=0.0008
USDCNH - USDZAR: Correlation=0.8474, P-Cointegration value=0.0193
USDRUB - USDRUR: Correlation=0.9993, P-Cointegration value=0.0000
AUDUSD - USDCLP: Correlation=-0.9012, P-Cointegration value=0.0280
AUDUSD - USDILS: Correlation=-0.8686, P-Cointegration value=0.0026
NZDUSD - USDNOK: Correlation=-0.9353, P-Cointegration value=0.0469
NZDUSD - USDILS: Correlation=-0.8514, P-Cointegration value=0.0110
...
EURSEK - XPDUSD: Correlation=-0.8200, P-Cointegration value=0.0269
EURZAR - USDP.NASDAQ: Correlation=-0.8678, P-Cointegration value=0.0154
USDMXN - EURCNH: Correlation=-0.8490, P-Cointegration value=0.0389
EURL.NASDAQ - EURSGD: Correlation=0.9157, P-Cointegration value=0.0000
EURN.NASDAQ - EURSGD: Correlation=-0.8301, P-Cointegration value=0.0358

Com todos os resultados, escolheremos esses dois símbolos (uma correlação negativa significa que quando um sobe, o outro desce e vice-versa, enquanto uma correlação positiva significa que os símbolos se movem juntos), escolherei o símbolo USDJPY, porque como explicado no equilíbrio de Nash, poderíamos aproveitar o USD sendo o motor do forex e os outros correlacionados poderiam se mover atrás dele:

USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165

Eu usei o MetaTrader 5 com uma conta demo para obter todos os dados e realizar o backtest do EA.

HMM (Modelo Oculto de Markov)

Um Modelo Oculto de Markov (HMM) é um modelo estatístico usado para descrever sistemas que mudam ao longo do tempo de uma maneira que é parcialmente aleatória e parcialmente dependente de estados ocultos. Imagine um processo onde podemos observar apenas certos resultados, mas esses resultados são influenciados por fatores subjacentes (ou estados) que não podemos ver diretamente.

O HMM é usado no trading para ter um modelo que prevê padrões do mercado usando dados passados.

Usaremos um script em Python para obter o modelo HMM. Precisamos levar em conta o período de tempo usado (deve ser o mesmo do EA), os Estados Ocultos e o número de dados para os quais fazer a previsão (quanto maior aqui, melhor).

O script Python retornará 3 matrizes (em um arquivo .txt) e três gráficos, que usaremos para o Expert Advisor.

Este é o script .py:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
from hmmlearn import hmm
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import datetime
import os
import sys

# Number of models to train
n_models = 10

# Redirect stdout to a file
def redirect_output(symbol):
    output_file = f"{symbol}_output.txt"
    sys.stdout = open(output_file, 'w')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Get and process data
def get_mt5_data(symbol, timeframe, start_date, end_date):
    """Get historical data from MetaTrader 5."""
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    return df

def calculate_features(df):
    """Calculate important features like returns, volatility, and trend."""
    df['returns'] = df['close'].pct_change()
    df['volatility'] = df['returns'].rolling(window=50).std()
    df['trend'] = df['close'].pct_change(periods=50)
    return df.dropna()

# Main script
symbol = "USDJPY"
timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"
current_date = datetime.datetime.now().strftime("%Y-%m-%d")

# Redirect output to file
redirect_output(symbol)

# Get historical data for training
df = get_mt5_data(symbol, timeframe, start_date, end_date)
df = calculate_features(df)

features = df[['returns', 'volatility', 'trend']].values
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# Lists to store the results of each model
state_predictions = np.zeros((scaled_features.shape[0], n_models))
strategy_returns = np.zeros((scaled_features.shape[0], n_models))
transition_matrices = np.zeros((10, 10, n_models))
means_matrices = np.zeros((n_models, 10, 3))
covariance_matrices = np.zeros((n_models, 10, 3, 3))

# Train multiple models and store the results
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-6, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)

    # Save the transition matrix, emission means, and covariances
    transition_matrices[:, :, i] = model.transmat_
    means_matrices[i, :, :] = model.means_
    covariance_matrices[i, :, :, :] = model.covars_

    # State prediction
    states = model.predict(scaled_features)
    state_predictions[:, i] = states

    # Generate signals and calculate strategy returns for this model
    df['state'] = states
    df['signal'] = 0
    for j in range(10):
        df.loc[df['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df['strategy_returns'] = df['returns'] * df['signal'].shift(1)
    strategy_returns[:, i] = df['strategy_returns'].values

# Average of matrices
average_transition_matrix = transition_matrices.mean(axis=2)
average_means_matrix = means_matrices.mean(axis=0)
average_covariance_matrix = covariance_matrices.mean(axis=0)

# Save the average matrices in the output file in appropriate format
print("Average Transition Matrix:")
for i, row in enumerate(average_transition_matrix):
    for j, val in enumerate(row):
        print(f"average_transition_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Means Matrix:")
for i, row in enumerate(average_means_matrix):
    for j, val in enumerate(row):
        print(f"average_means_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Covariance Matrix:")
for i in range(10):  # For each state
    for j in range(3):  # For each row of the covariance matrix
        for k in range(3):  # For each column of the covariance matrix
            print(f"average_covariance_matrix[{i}][{j}][{k}] = {average_covariance_matrix[i, j, k]:.8e};")

# Average of state predictions and strategy returns
average_states = np.round(state_predictions.mean(axis=1)).astype(int)
average_strategy_returns = strategy_returns.mean(axis=1)

# Store the average results in the original dataframe
df['average_state'] = average_states
df['average_strategy_returns'] = average_strategy_returns

# Calculate cumulative returns using the average strategy
df['cumulative_market_returns'] = (1 + df['returns']).cumprod()
df['cumulative_strategy_returns'] = (1 + df['average_strategy_returns']).cumprod()

# Plot cumulative returns (training)
plt.figure(figsize=(7, 6))
plt.plot(df.index, df['cumulative_market_returns'], label='Market Returns')
plt.plot(df.index, df['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_strategy_returns_{symbol}.png')
plt.close()

# Additional plots for averages
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(12, 15), sharex=True)

# Plot closing price and average HMM states
ax1.plot(df.index, df['close'], label='Closing Price')
scatter = ax1.scatter(df.index, df['close'], c=df['average_state'], cmap='viridis', s=30, label='Average HMM States')
ax1.set_ylabel('Price')
ax1.set_title('Closing Price and Average HMM States')
ax1.legend(loc='upper left')

# Add color bar for states
cbar = plt.colorbar(scatter, ax=ax1)
cbar.set_label('Average HMM State')

# Plot returns
ax2.bar(df.index, df['returns'], label='Market Returns', alpha=0.5, color='blue')
ax2.bar(df.index, df['average_strategy_returns'], label='Average Strategy Returns', alpha=0.5, color='red')
ax2.set_ylabel('Return')
ax2.set_title('Daily Returns')
ax2.legend(loc='upper left')

# Plot cumulative returns
ax3.plot(df.index, df['cumulative_market_returns'], label='Cumulative Market Returns')
ax3.plot(df.index, df['cumulative_strategy_returns'], label='Cumulative Average Strategy Returns')
ax3.set_ylabel('Cumulative Return')
ax3.set_title('Cumulative Returns')
ax3.legend(loc='upper left')

# Adjust layout
plt.tight_layout()
plt.xlabel('Date')

# Save figure
plt.savefig(f'average_returns_{symbol}.png')
plt.close()

# Calculate cumulative returns for each average state
state_returns = {}
for state in range(10):  # Assuming 10 states
    state_returns[state] = df[df['average_state'] == state]['returns'].sum()

# Create lists for states and their cumulative returns
states = list(state_returns.keys())
returns = list(state_returns.values())

# Create bar chart
plt.figure(figsize=(7, 6))
bars = plt.bar(states, returns)

# Customize chart
plt.title('Cumulative Returns by Average HMM State', fontsize=7)
plt.xlabel('State', fontsize=7)
plt.ylabel('Cumulative Return', fontsize=7)
plt.xticks(states)

# Add value labels above each bar
for bar in bars:
    height = bar.get_height()
    plt.text(bar.get_x() + bar.get_width()/2., height,
             f'{height:.4f}',
             ha='center', va='bottom')

# Add horizontal line at y=0 for reference
plt.axhline(y=0, color='r', linestyle='-', linewidth=0.5)

# Adjust layout and save chart
plt.tight_layout()
plt.savefig(f'average_bars_{symbol}.png')
plt.close()

# Get recent data to test the model
df_recent = get_mt5_data(symbol, timeframe, end_date, current_date)
df_recent = calculate_features(df_recent)

# Apply the same scaler to recent data
scaled_recent_features = scaler.transform(df_recent[['returns', 'volatility', 'trend']].values)

# Lists to store the results of each model for recent data
recent_state_predictions = np.zeros((scaled_recent_features.shape[0], n_models))
recent_strategy_returns = np.zeros((scaled_recent_features.shape[0], n_models))

# Apply the trained model to recent data
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-4, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)
    
    recent_states = model.predict(scaled_recent_features)
    recent_state_predictions[:, i] = recent_states

    df_recent['state'] = recent_states
    df_recent['signal'] = 0
    for j in range(10):
        df_recent.loc[df_recent['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df_recent['strategy_returns'] = df_recent['returns'] * df_recent['signal'].shift(1)
    recent_strategy_returns[:, i] = df_recent['strategy_returns'].values

# Average of state predictions and strategy returns for recent data
average_recent_states = np.round(recent_state_predictions.mean(axis=1)).astype(int)
average_recent_strategy_returns = recent_strategy_returns.mean(axis=1)

# Store the average results in the recent dataframe
df_recent['average_state'] = average_recent_states
df_recent['average_strategy_returns'] = average_recent_strategy_returns

# Calculate cumulative returns using the average strategy on recent data
df_recent['cumulative_market_returns'] = (1 + df_recent['returns']).cumprod()
df_recent['cumulative_strategy_returns'] = (1 + df_recent['average_strategy_returns']).cumprod()

# Plot cumulative returns (recent test)
plt.figure(figsize=(7, 6))
plt.plot(df_recent.index, df_recent['cumulative_market_returns'], label='Market Returns')
plt.plot(df_recent.index, df_recent['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy (Recent Data)')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_recent_strategy_returns_{symbol}.png')
plt.close()

# Close MetaTrader 5
mt5.shutdown()


# Assign descriptive names to the hidden states
state_labels = {}
for state in range(10):  # Assuming 10 states
    if state in df['average_state'].unique():
        label = f"State {state}: "  # You can customize this description based on your observations
        if state_returns[state] > 0:
            label += "Uptrend"
        else:
            label += "Downtrend"
        state_labels[state] = label
    else:
        state_labels[state] = f"State {state}: Not present"

# Print the states and their descriptive labels
print("\nDescription of Hidden States:")
for state, label in state_labels.items():
    print(f"{label} (State ID: {state})")

# Close MetaTrader 5 connection
mt5.shutdown()

# Finally, close the output file
sys.stdout.close()
sys.stdout = sys.__stdout__

Este script, com as condições iniciais, gerou os seguintes resultados:

timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"

Average Transition Matrix:
average_transition_matrix[0][0] = 0.15741321;
average_transition_matrix[0][1] = 0.07086962;
average_transition_matrix[0][2] = 0.16785905;
average_transition_matrix[0][3] = 0.08792403;
average_transition_matrix[0][4] = 0.11101073;
average_transition_matrix[0][5] = 0.05415263;
average_transition_matrix[0][6] = 0.08019415;
.....
average_transition_matrix[9][3] = 0.13599698;
average_transition_matrix[9][4] = 0.12947508;
average_transition_matrix[9][5] = 0.06385211;
average_transition_matrix[9][6] = 0.09042617;
average_transition_matrix[9][7] = 0.16088280;
average_transition_matrix[9][8] = 0.06588065;
average_transition_matrix[9][9] = 0.04559230;

Average Means Matrix:
average_means_matrix[0][0] = 0.06871601;
average_means_matrix[0][1] = 0.14572210;
average_means_matrix[0][2] = 0.05961646;
average_means_matrix[1][0] = 0.06903949;
average_means_matrix[1][1] = 1.05226034;
.....
average_means_matrix[7][2] = 0.00453701;
average_means_matrix[8][0] = -0.38270747;
average_means_matrix[8][1] = 0.86916742;
average_means_matrix[8][2] = -0.58792329;
average_means_matrix[9][0] = -0.16057267;
average_means_matrix[9][1] = 1.17106076;
average_means_matrix[9][2] = 0.18531821;

Average Covariance Matrix:
average_covariance_matrix[0][0][0] = 1.25299224e+00;
average_covariance_matrix[0][0][1] = -4.05453267e-02;
average_covariance_matrix[0][0][2] = 7.95036804e-02;
average_covariance_matrix[0][1][0] = -4.05453267e-02;
average_covariance_matrix[0][1][1] = 1.63177290e-01;
average_covariance_matrix[0][1][2] = 1.58609858e-01;
average_covariance_matrix[0][2][0] = 7.95036804e-02;
average_covariance_matrix[0][2][1] = 1.58609858e-01;
average_covariance_matrix[0][2][2] = 8.09678270e-01;
average_covariance_matrix[1][0][0] = 1.23040552e+00;
average_covariance_matrix[1][0][1] = 2.52108300e-02;
....
average_covariance_matrix[9][0][0] = 5.47457383e+00;
average_covariance_matrix[9][0][1] = -1.22088743e-02;
average_covariance_matrix[9][0][2] = 2.56784647e-01;
average_covariance_matrix[9][1][0] = -1.22088743e-02;
average_covariance_matrix[9][1][1] = 4.65227101e-01;
average_covariance_matrix[9][1][2] = -2.88257686e-01;
average_covariance_matrix[9][2][0] = 2.56784647e-01;
average_covariance_matrix[9][2][1] = -2.88257686e-01;
average_covariance_matrix[9][2][2] = 1.44717234e+00;

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

Para usá-lo, basta modificar o símbolo usado para obter os dados, o número de estados e as datas de onde obter os dados. Também precisaremos ajustar o EA e os dois scripts Python para usar o período de tempo (timeframe) (todos os scripts e o EA com o mesmo).

Este script terá 10 modelos e fará a média deles para obter um modelo robusto (se fizermos apenas dois modelos, ambos os grupos de matrizes seriam diferentes) (Levará algum tempo para fazer as matrizes). No final, você terá as matrizes, três gráficos (agora explicarei por que são importantes), uma descrição dos estados ocultos e um .txt com as matrizes.

Os Resultados

Na primeira imagem, vemos o resultado de um backtest com o modelo médio HMM. Você pode ver o valor do preço e a estratégia com os resultados do HMM para o backtest daquele período.

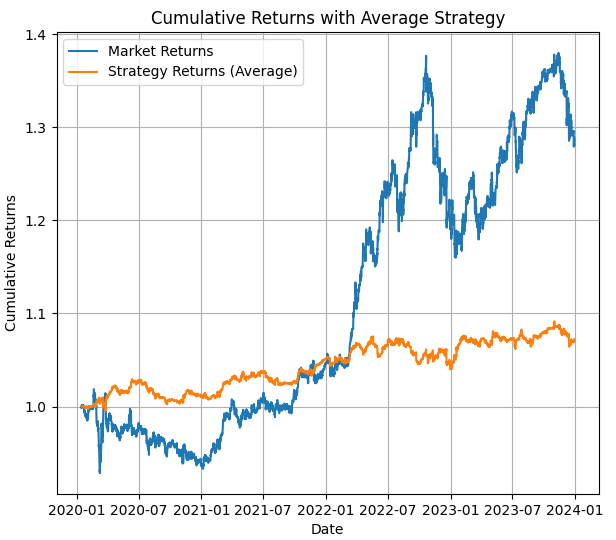
Na segunda imagem, vemos os resultados do backtest no período de teste e uma imagem importante que mostra onde os estados ocultos são usados (você pode ver onde eles indicam uma tendência de alta, tendência de baixa ou se estão em range ou neutros).

Na terceira imagem, você pode ver os ganhos para cada estado oculto em barras.

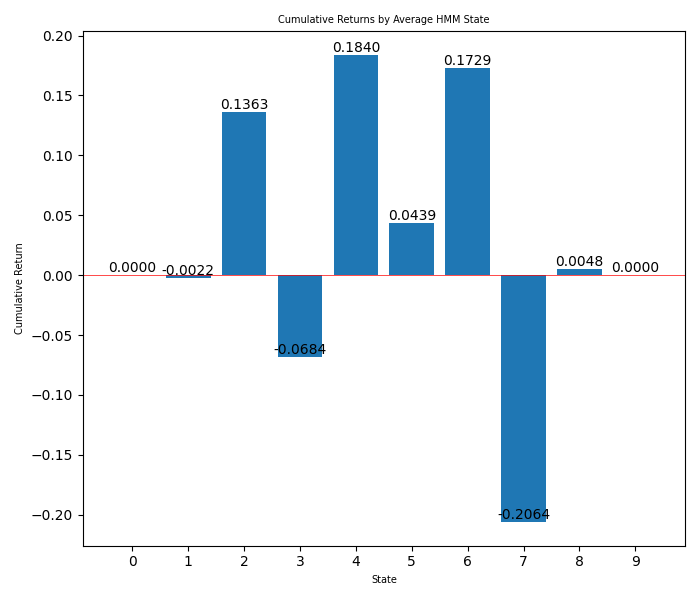
Há uma quarta imagem com os retornos médios para a estratégia durante o período entre a última data e hoje (isso é o que deveríamos esperar da estratégia no backtest do MetaTrader 5, se não ajustarmos os estados).

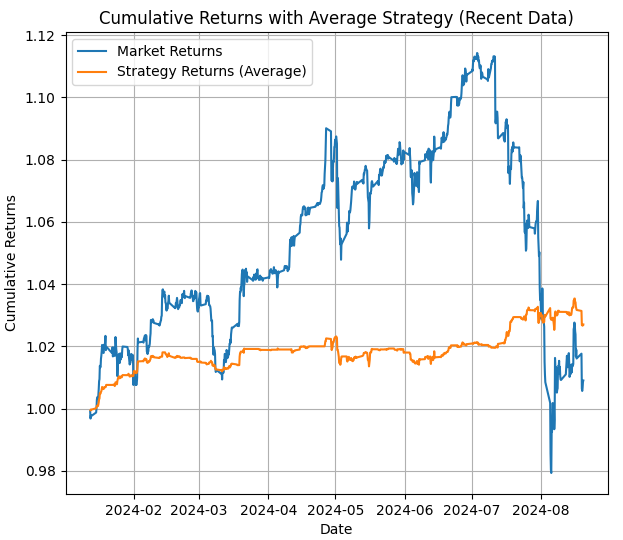
Agora que temos todas essas informações, podemos usá-las para selecionar quais estados ocultos usaremos e saber se um estado oculto indica tendência (com a segunda imagem) e também ganhos (com as barras). Então, com tudo isso, usaremos essas informações para alternar os estados no EA.

A partir das barras, podemos ver que os estados ocultos que queremos usar são: 2, 3 e 7, que provavelmente correspondem a range, tendência de alta e tendência de baixa, respectivamente. Pode ser uma tendência alta. Agora podemos configurar a estratégia no EA, levando em consideração que os outros estados ocultos não foram lucrativos (podemos fazer vários backtests para tentar ver qual é o melhor ajuste).

Todos os scripts Python usaram Python 3.10.

Poderíamos adicionar as matrizes ao EA (componente por componente, pois o Python tem uma forma diferente de exibir matrizes), mas como não queremos trabalhar muito, usaremos o próximo script para modificar a matriz para um formato MQl5 que usaremos no EA. Este é o EA que podemos usar para a formatação da matriz:

import re
import os

def read_file(filename):
    if not os.path.exists(filename):
        print(f"Error: The file {filename} does not exist.")
        return None
    try:
        with open(filename, "r") as file:
            return file.read()
    except Exception as e:
        print(f"Error reading the file: {str(e)}")
        return None

def parse_matrix(file_content, matrix_name):
    pattern = rf"{matrix_name}\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, value = int(match[0]), int(match[1]), float(match[2])
        if i not in matrix:
            matrix[i] = {}
        matrix[i][j] = value
    return matrix

def parse_covariance_matrix(file_content):
    pattern = r"average_covariance_matrix\[(\d+)\]\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, k, value = int(match[0]), int(match[1]), int(match[2]), float(match[3])
        if i not in matrix:
            matrix[i] = {}
        if j not in matrix[i]:
            matrix[i][j] = {}
        matrix[i][j][k] = value
    return matrix

def format_matrix(matrix, is_3d=False):
    if not matrix:
        return "{     };"
    
    formatted = "{\n"
    for i in sorted(matrix.keys()):
        if is_3d:
            formatted += "        {  "
            for j in sorted(matrix[i].keys()):
                formatted += "{" + ", ".join(f"{matrix[i][j][k]:.8e}" for k in sorted(matrix[i][j].keys())) + "}"
                if j < max(matrix[i].keys()):
                    formatted += ",\n           "
            formatted += "}"
        else:
            formatted += "        {" + ", ".join(f"{matrix[i][j]:.8f}" for j in sorted(matrix[i].keys())) + "}"
        if i < max(matrix.keys()):
            formatted += ","
        formatted += "\n"
    formatted += "     };"
    return formatted

def main():
    input_filename = "USDJPY_output.txt"
    output_filename = "formatted_matrices.txt"
    content = read_file(input_filename)
    
    if content is None:
        return

    print(f"Input file size: {len(content)} bytes")
    print("First 200 characters of the file:")
    print(content[:200])

    transition_matrix = parse_matrix(content, "average_transition_matrix")
    means_matrix = parse_matrix(content, "average_means_matrix")
    covariance_matrix = parse_covariance_matrix(content)

    print(f"\nElements found in the transition matrix: {len(transition_matrix)}")
    print(f"Elements found in the means matrix: {len(means_matrix)}")
    print(f"Elements found in the covariance matrix: {len(covariance_matrix)}")

    output = "Transition Matrix:\n"
    output += format_matrix(transition_matrix)
    output += "\n\nMeans Matrix:\n"
    output += format_matrix(means_matrix)
    output += "\n\nCovariance Matrix:\n"
    output += format_matrix(covariance_matrix, is_3d=True)

    try:
        with open(output_filename, "w") as outfile:
            outfile.write(output)
        print(f"\nFormatted matrices saved in '{output_filename}'")
    except Exception as e:
        print(f"Error writing the output file: {str(e)}")

    print(f"\nFirst lines of the output file '{output_filename}':")
    output_content = read_file(output_filename)
    if output_content:
        print("\n".join(output_content.split("\n")[:20]))  # Display the first 20 lines

if __name__ == "__main__":
    main()

Também podemos usar sockets (sockets são uma boa forma de interagir com o MT5 usando dados externos) para importar as matrizes. Você pode fazer isso como é explicado neste artigo: Twitter Sentiment Analysis with Sockets - Artigos MQL5 e até adicionar análise de sentimento (como explicado nesse artigo) para obter melhores posições de tendência.

Este script nos dará um .txt que mostrará algo similar a isto:

Transition Matrix:
{
        {0.15741321, 0.07086962, 0.16785905, 0.08792403, 0.11101073, 0.05415263, 0.08019415, 0.12333382, 0.09794255, 0.04930020},
        {0.16646033, 0.11065086, 0.10447035, 0.13332935, 0.09136784, 0.08351764, 0.06722600, 0.09893912, 0.07936700, 0.06467150},
        {0.14182826, 0.15400641, 0.13617941, 0.08453877, 0.09214389, 0.04040276, 0.09065499, 0.11526167, 0.06725810, 0.07772574},
        {0.15037837, 0.09101998, 0.09552059, 0.10035540, 0.12851236, 0.05000596, 0.09542873, 0.12606514, 0.09394759, 0.06876588},
        {0.15552336, 0.08663776, 0.15694344, 0.09219379, 0.08785893, 0.08381830, 0.05572122, 0.10309824, 0.08512219, 0.09308276},
        {0.19806868, 0.11292565, 0.11482367, 0.08324432, 0.09808519, 0.06727817, 0.11549253, 0.10657752, 0.06889919, 0.03460507},
        {0.12257742, 0.11257625, 0.11910078, 0.07669820, 0.16660657, 0.04769350, 0.09667861, 0.12241177, 0.04856867, 0.08708823},
        {0.14716725, 0.12232022, 0.11135735, 0.08488571, 0.06274817, 0.07390905, 0.10742571, 0.12550373, 0.11431005, 0.05037277},
        {0.11766333, 0.11533807, 0.15497601, 0.14017237, 0.11214274, 0.04885795, 0.08394306, 0.12864406, 0.06945878, 0.02880364},
        {0.13559147, 0.07444276, 0.09785968, 0.13599698, 0.12947508, 0.06385211, 0.09042617, 0.16088280, 0.06588065, 0.04559230}
     };

Means Matrix:
{
        {0.06871601, 0.14572210, 0.05961646},
        {0.06903949, 1.05226034, -0.25687024},
        {-0.04607112, -0.00811718, 0.06488246},
        {-0.01769149, 0.63694700, 0.26965491},
        {-0.01874345, 0.58917438, -0.22484670},
        {-0.02026370, 1.09022869, 0.86790417},
        {-0.85455759, 0.48710677, 0.08980023},
        {-0.02589947, 0.84881170, 0.00453701},
        {-0.38270747, 0.86916742, -0.58792329},
        {-0.16057267, 1.17106076, 0.18531821}
     };

Covariance Matrix:
{
        {  {1.25299224e+00, -4.05453267e-02, 7.95036804e-02},
           {-4.05453267e-02, 1.63177290e-01, 1.58609858e-01},
           {7.95036804e-02, 1.58609858e-01, 8.09678270e-01}},
        {  {1.23040552e+00, 2.52108300e-02, 1.17595322e-01},
           {2.52108300e-02, 3.00175953e-01, -8.11027442e-02},
           {1.17595322e-01, -8.11027442e-02, 1.42259217e+00}},
        {  {1.76376507e+00, -7.82189996e-02, 1.89340073e-01},
           {-7.82189996e-02, 2.56222155e-01, -1.30202288e-01},
           {1.89340073e-01, -1.30202288e-01, 6.60591043e-01}},
        {  {9.08926052e-01, 3.02606081e-02, 1.03549625e-01},
           {3.02606081e-02, 2.30324420e-01, -5.46541678e-02},
           {1.03549625e-01, -5.46541678e-02, 7.40333449e-01}},
        {  {8.80590495e-01, 7.21102489e-02, 3.40982555e-02},
           {7.21102489e-02, 3.26639817e-01, -1.06663221e-01},
           {3.40982555e-02, -1.06663221e-01, 9.55477387e-01}},
        {  {3.19499555e+00, -8.63552078e-02, 5.03260281e-01},
           {-8.63552078e-02, 2.92184645e-01, 1.03141313e-01},
           {5.03260281e-01, 1.03141313e-01, 1.88060098e+00}},
        {  {3.22276957e+00, -6.37618091e-01, 3.80462477e-01},
           {-6.37618091e-01, 4.96770891e-01, -5.79521882e-02},
           {3.80462477e-01, -5.79521882e-02, 1.05061090e+00}},
        {  {2.16098355e+00, 4.02611831e-02, 3.01261346e-01},
           {4.02611831e-02, 4.83773367e-01, 7.20003108e-02},
           {3.01261346e-01, 7.20003108e-02, 1.32262495e+00}},
        {  {4.00745050e+00, -3.90316434e-01, 7.28032792e-01},
           {-3.90316434e-01, 6.01214190e-01, -2.91562862e-01},
           {7.28032792e-01, -2.91562862e-01, 1.30603500e+00}},
        {  {5.47457383e+00, -1.22088743e-02, 2.56784647e-01},
           {-1.22088743e-02, 4.65227101e-01, -2.88257686e-01},
           {2.56784647e-01, -2.88257686e-01, 1.44717234e+00}}
     };

Este é o formato para a matriz que usaremos no EA.

Agora temos dois símbolos que são negativamente correlacionados e cointegrados. Fizemos um HMM de um desses símbolos (precisamos de apenas um, porque sabemos que ambos os símbolos são correlacionados) e, como são negativamente correlacionados, quando supomos que um vai subir (com o HMM), aplicaremos Nash e, se tudo estiver correto, venderemos o outro símbolo.

Podemos fazer isso com mais símbolos (se forem correlacionados, compramos na mesma direção ou vendemos se forem negativamente correlacionados).

Mas primeiro, fiz um script em Python para mostrar quais seriam os resultados e brincar com os estados ocultos. Este é o script:

import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from hmmlearn import hmm
import matplotlib.pyplot as plt
from datetime import datetime

# Function to load matrices from the .txt file
def parse_matrix_block(lines, start_idx, matrix_type="normal"):
    matrix = []
    i = start_idx
    while i < len(lines) and not lines[i].strip().startswith("};"):
        line = lines[i].strip().replace("{", "").replace("}", "").replace(";", "")
        if line:  # Ensure the line is not empty
            if matrix_type == "covariance":
                # Split the line into elements
                elements = [float(x) for x in line.split(',') if x.strip()]
                matrix.append(elements)
            else:
                row = [float(x) for x in line.split(',') if x.strip()]  # Filter out empty values
                matrix.append(row)
        i += 1
    return np.array(matrix), i

def load_matrices(file_path):
    with open(file_path, 'r') as file:
        lines = file.readlines()
    
    transition_matrix = []
    means_matrix = []
    covariance_matrix = []
    
    i = 0
    while i < len(lines):
        line = lines[i].strip()
        
        if line.startswith("Transition Matrix:"):
            transition_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1  # Move forward to avoid repeating the same block

        elif line.startswith("Means Matrix:"):
            means_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1

        elif line.startswith("Covariance Matrix:"):
            covariance_matrix = []
            i += 1
            while i < len(lines) and not lines[i].strip().startswith("};"):
                block, i = parse_matrix_block(lines, i, matrix_type="covariance")
                covariance_matrix.append(block)
                i += 1
            covariance_matrix = np.array(covariance_matrix)
            covariance_matrix = covariance_matrix.reshape(-1, 3, 3)

        i += 1
    
    return transition_matrix, means_matrix, covariance_matrix

# Load the matrices from the .txt file
transition_matrix, means_matrix, covariance_matrix = load_matrices('formatted_matrices.txt')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed, error code =", mt5.last_error())
    quit()

# Set parameters to retrieve data
symbol = "USDJPY"  # You can change to your desired symbol
timeframe = mt5.TIMEFRAME_H4  # You can change the timeframe
start_date = datetime(2024, 1, 1)
end_date = datetime.now()

# Load data from MetaTrader 5
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
mt5.shutdown()

# Convert the data to a pandas DataFrame
data = pd.DataFrame(rates)
data['time'] = pd.to_datetime(data['time'], unit='s')
data.set_index('time', inplace=True)

# Use only the closing prices column
prices = data['close'].values.reshape(-1, 1)

# Create and configure the HMM model
n_components = len(transition_matrix)
model = hmm.GaussianHMM(n_components=n_components, covariance_type="full")
model.startprob_ = np.full(n_components, 1/n_components)  # Initial probabilities
model.transmat_ = transition_matrix
model.means_ = means_matrix
model.covars_ = covariance_matrix

# Fit the model using the loaded prices
model.fit(prices)

# Predict hidden states
hidden_states = model.predict(prices)

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3,7]  # States considered bearish
exclude_states = [0,9]  # States to exclude (neither buy nor sell)

# HMM strategy:
hmm_returns = np.zeros_like(prices)
for i in range(1, len(prices)):
    if hidden_states[i] in bullish_states:  # Buy if the state is bullish
        hmm_returns[i] = prices[i] - prices[i-1]
    elif hidden_states[i] in bearish_states:  # Sell if the state is bearish
        hmm_returns[i] = prices[i-1] - prices[i]
    # If the state is in exclude_states, do nothing

# Buy and hold strategy (holding)
holding_returns = prices[-1] - prices[0]

# Plot results
plt.figure(figsize=(7, 8))
plt.plot(data.index, prices, label='Price of '+str(symbol), color='black', linestyle='--')
plt.plot(data.index, np.cumsum(hmm_returns), label='HMM Strategy', color='green')
plt.axhline(holding_returns, color='blue', linestyle='--', label='Buy and Hold Strategy (Holding)')
plt.title('Backtesting Comparison: HMM vs Holding and Price')
plt.legend()
plt.savefig("playground.png")

# Print accumulated returns of both strategies
print(f"Accumulated returns of the HMM strategy: {np.sum(hmm_returns)}")
print(f"Accumulated returns of the Holding strategy: {holding_returns[0]}")

Vamos dar uma olhada nesse script. Ele abre o txt com as matrizes, baixa os dados do MetaTrader 5 para aquele símbolo e usa os dados da última data que usamos nos outros scripts, até hoje, para ver como o HMM funciona. Os resultados são mostrados em um .png, e podemos alterar os estados. Vamos ver quais são os resultados usando todos os estados, como o segundo script nos diz para usar:

A partir do segundo script:

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

Aqui está o que ele mostra:

Accumulated returns of the HMM strategy: -1.0609999999998365
Accumulated returns of the Holding strategy: 5.284999999999997

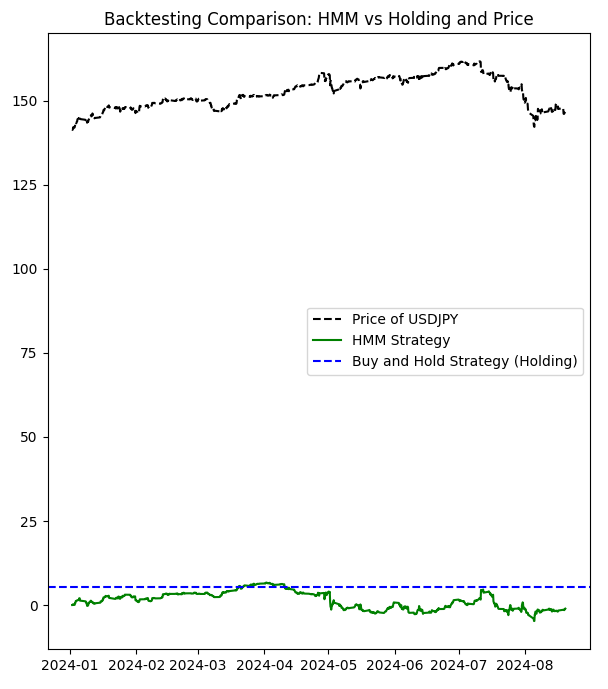
Como você pode ver, esta estratégia não é realmente boa. Então, vamos brincar com os estados ocultos (que escolheremos usando o gráfico de barras, vamos excluir o sétimo estado):

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3]  # States considered bearish
exclude_states = [0,7,9]  # States to exclude (neither buy nor sell)

Accumulated returns of the HMM strategy: 7.978000000000122
Accumulated returns of the Holding strategy: 5.284999999999997

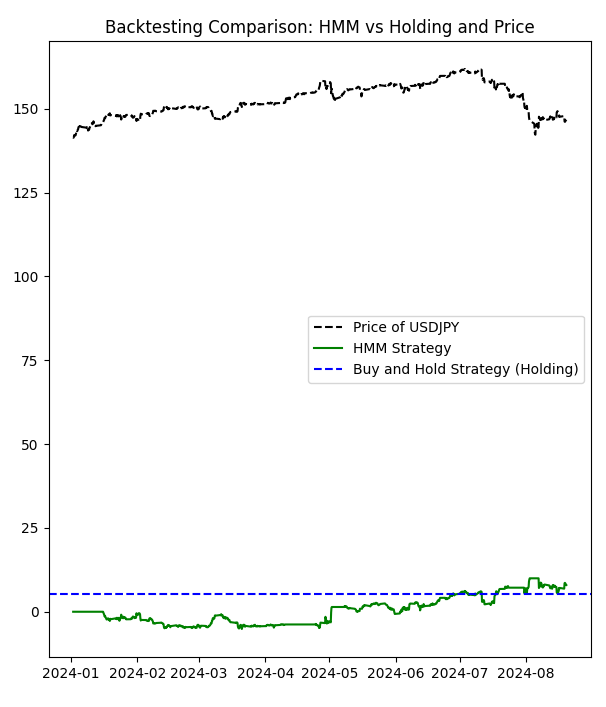
Aprendemos com isso que, ao não usar os piores estados ocultos, podemos ter uma estratégia mais lucrativa.

Mais uma vez, aplicar aprendizado profundo a isso poderia ajudar a detectar mais padrões do símbolo inicial (neste caso, USDJPY). Talvez, possamos experimentar com isso em outra oportunidade.

Implementação no MQL5

O Nash Expert Advisor (EA) é um sistema de negociação algorítmica sofisticado projetado para a plataforma MetaTrader 5. No seu núcleo, o EA adota uma abordagem multiestratégica, incorporando Modelos Ocultos de Markov (HMM), análise de Log-Likelihood, avaliação de Força de Tendência e conceitos do Equilíbrio de Nash para tomar decisões de negociação no mercado de câmbio.

O EA começa inicializando parâmetros e indicadores cruciais. Ele configura Médias Móveis Essenciais (EMAs), Índice de Força Relativa (RSI), Faixa de Preço Média Verdadeira (ATR) e Bandas de Bollinger. Esses indicadores técnicos formam a base para a análise de mercado do EA. O processo de inicialização também envolve configurar os parâmetros do Modelo Oculto de Markov, que são centrais para as capacidades preditivas do EA.

Uma das principais características do EA é o seu sistema de detecção de regimes de mercado. Este sistema utiliza tanto o HMM quanto os métodos de Log-Likelihood para classificar o estado atual do mercado em três categorias: Tendência de Alta, Tendência de Baixa ou Não Presente (neutro). O processo de detecção de regimes envolve cálculos complexos de probabilidades de emissão e transições de estado, proporcionando uma visão mais detalhada das condições do mercado.

O EA implementa quatro estratégias distintas de negociação: baseada em HMM, baseada em Log-Likelihood, Força de Tendência e Equilíbrio de Nash. Cada estratégia gera seu próprio sinal de negociação, que é então ponderado e combinado para formar uma decisão de negociação abrangente. A estratégia de Equilíbrio de Nash, em particular, visa encontrar um equilíbrio ótimo entre as outras estratégias, levando a decisões de negociação mais robustas.

A gestão de risco é um aspecto crítico do Nash EA. Ele incorpora funcionalidades como dimensionamento dinâmico de lotes baseado no saldo da conta e no desempenho da estratégia, níveis de stop-loss e take-profit e um mecanismo de trailing stop. Essas ferramentas de gestão de risco visam proteger o capital, permitindo ao mesmo tempo lucros potenciais em condições de mercado favoráveis.

O EA também inclui uma funcionalidade de backtesting, permitindo que os traders avaliem seu desempenho em dados históricos. Esta funcionalidade calcula várias métricas de desempenho para cada estratégia, incluindo lucro, total de negociações, negociações vencedoras e taxa de sucesso. Essas capacidades de teste abrangentes permitem que os traders ajustem os parâmetros do EA para um desempenho ótimo.

Em seu loop operacional principal, o Nash EA processa os dados do mercado a cada nova barra de preço. Ele recalcula os regimes de mercado, atualiza os sinais das estratégias e toma decisões de negociação com base na saída coletiva de todas as estratégias ativadas. O EA é projetado para abrir posições em pares, negociando potencialmente tanto o símbolo primário quanto o EURCHF simultaneamente, o que pode fazer parte de uma estratégia de hedge ou baseada em correlação.

Por fim, o EA inclui robustas funcionalidades de tratamento de erros e registros. Ele verifica continuamente os valores válidos dos indicadores, garante que a negociação é permitida pelas configurações do terminal e do expert, e fornece logs detalhados de suas operações e processo de tomada de decisões. Esse nível de transparência facilita a depuração e a análise de desempenho.

Agora, vamos olhar algumas funções importantes e os equilíbrios de Nash:

As principais funções usadas para implementar o conceito de Equilíbrio de Nash neste Expert Advisor (EA) são:

1. CalculateStrictNashEquilibrium()

Esta é a função principal para calcular o equilíbrio estrito de Nash. Aqui está sua implementação:

void CalculateStrictNashEquilibrium()
{
   double buySignal = 0;
   double sellSignal = 0;

   // Sum the weighted signals of the enabled strategies
   for(int i = 0; i < 3; i++) // Consider only the first 3 strategies for Nash equilibrium
   {
      if(strategies[i].enabled)
      {
         buySignal += strategies[i].weight * (strategies[i].signal > 0 ? 1 : 0);
         sellSignal += strategies[i].weight * (strategies[i].signal < 0 ? 1 : 0);
      }
   }

   // If there's a stronger buy signal than sell signal, set Nash Equilibrium signal to buy
   if(buySignal > sellSignal)
   {
      strategies[3].signal = 1; // Buy signal
   }
   else if(sellSignal > buySignal)
   {
      strategies[3].signal = -1; // Sell signal
   }
   else
   {
      // If there's no clear signal, force a decision based on an additional criterion
      double closePrice = iClose(_Symbol, PERIOD_CURRENT, 0);
      double openPrice = iOpen(_Symbol, PERIOD_CURRENT, 0);
      strategies[3].signal = (closePrice > openPrice) ? 1 : -1;
   }
}

Explicação:

• Esta função calcula sinais de compra e venda com base nos sinais ponderados das três primeiras estratégias.
• Ela compara os sinais de compra e venda para determinar a ação do equilíbrio de Nash.
• Se os sinais forem iguais, a decisão é tomada com base na direção do preço atual.

2. SimulateTrading()

Embora não seja exclusivamente para o equilíbrio de Nash, essa função implementa a lógica de negociação que inclui o equilíbrio de Nash:

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
   double buySignal = 0;
   double sellSignal = 0;

   for(int i = 0; i < ArraySize(strategies); i++)
   {
      if(strategies[i].enabled)
      {
         if(strategies[i].signal > 0)
            buySignal += strategies[i].weight * strategies[i].signal;
         else if(strategies[i].signal < 0)
            sellSignal -= strategies[i].weight * strategies[i].signal;
      }
   }

   // ... (code to simulate trades and calculate profits)
}

Explicação:

• Esta função simula a negociação com base nos sinais de todas as estratégias, incluindo a estratégia de equilíbrio de Nash.
• Ela calcula os sinais ponderados de compra e venda para todas as estratégias ativadas.

3. OnTick()

Na função OnTick(), a lógica para executar negociações com base no equilíbrio de Nash é implementada:

void OnTick()
{
   // ... (other code)

   // Check if the Nash Equilibrium strategy has generated a signal
   if(strategies[3].enabled && strategies[3].signal != 0)
   {
      if(strategies[3].signal > 0)
      {
         OpenBuyOrder(strategies[3].name);
      }
      else if(strategies[3].signal < 0)
      {
         OpenSellOrder(strategies[3].name);
      }
   }

   // ... (other code)
}

Explicação:

• Esta função verifica se a estratégia de equilíbrio de Nash (que é a 3ª estratégia no array de estratégias) está ativada e gerou um sinal.
• Se houver um sinal de compra (sinal > 0), abre-se uma ordem de compra.
• Se houver um sinal de venda (sinal < 0), abre-se uma ordem de venda.

Resumindo, o equilíbrio de Nash é implementado como uma das estratégias de negociação neste EA. A função CalculateStrictNashEquilibrium() determina o sinal de equilíbrio de Nash com base nos sinais das outras estratégias. Esse sinal é então usado na função OnTick() para tomar decisões de negociação. A implementação busca encontrar um equilíbrio entre as diferentes estratégias para tomar decisões de negociação mais robustas.

Essa abordagem para implementar o equilíbrio de Nash em uma estratégia de negociação é uma aplicação interessante da teoria dos jogos nos mercados financeiros. Ela tenta encontrar uma estratégia ótima, considerando as interações entre os diferentes sinais de negociação, o que é análogo a encontrar um equilíbrio em um jogo multiplayer, onde cada "jogador" é uma estratégia de negociação diferente.

Função DetectMarketRegime: Esta função é crucial para o processo de tomada de decisões do EA. Ela analisa as condições atuais do mercado usando indicadores técnicos e modelos estatísticos complexos para determinar o regime de mercado.

void DetectMarketRegime(MarketRegime &hmmRegime, MarketRegime &logLikelihoodRegime)
{
    // Calculate indicators
    double fastEMA = iMAGet(fastEMAHandle, 0);
    double slowEMA = iMAGet(slowEMAHandle, 0);
    double rsi = iRSIGet(rsiHandle, 0);
    double atr = iATRGet(atrHandle, 0);
    double price = SymbolInfoDouble(_Symbol, SYMBOL_BID);

    // Calculate trend strength and volatility ratio
    double trendStrength = (fastEMA - slowEMA) / slowEMA;
    double volatilityRatio = atr / price;

    // Normalize RSI
    double normalizedRSI = (rsi - 50) / 25;

    // Calculate features for HMM
    double features[3] = {trendStrength, volatilityRatio, normalizedRSI};

    // Calculate log-likelihood and HMM likelihoods
    double logLikelihood[10];
    double hmmLikelihoods[10];
    CalculateLogLikelihood(features, symbolParams.emissionMeans, symbolParams.emissionCovs);
    CalculateHMMLikelihoods(features, symbolParams.emissionMeans, symbolParams.emissionCovs, symbolParams.transitionProb, 10, hmmLikelihoods);

    // Determine regimes based on maximum likelihood
    int maxLogLikelihoodIndex = ArrayMaximum(logLikelihood);
    int maxHmmLikelihoodIndex = ArrayMaximum(hmmLikelihoods);

    logLikelihoodRegime = InterpretRegime(maxLogLikelihoodIndex);
    hmmRegime = InterpretRegime(maxHmmLikelihoodIndex);

    
    // ... (confidence calculation code)
}

Esta função combina indicadores técnicos com Modelos Ocultos de Markov e análise de Log-Likelihood para determinar o regime atual do mercado. É uma abordagem sofisticada para análise de mercado, proporcionando uma visão mais detalhada das condições do mercado.

Função CalculateStrategySignals: Esta função calcula os sinais de negociação para cada uma das estratégias do EA com base no regime de mercado atual e nos indicadores técnicos.

void CalculateStrategySignals(string symbol, datetime time, MarketRegime hmmRegime, MarketRegime logLikelihoodRegime)
{
    if(strategies[0].enabled) // HMM Strategy
    {
        CalculateHMMSignal();
    }
    
    if(strategies[1].enabled) // LogLikelihood Strategy
    {
        CalculateLogLikelihoodSignal();
    }
    
    if(strategies[2].enabled) // Trend Strength
    {
        double trendStrength = CalculateTrendStrength(PERIOD_CURRENT);
        strategies[2].signal = NormalizeTrendStrength(trendStrength);
    }
    
    if(strategies[3].enabled) // Nash Equilibrium
    {
        CalculateStrictNashEquilibrium();
    }
}

Esta função calcula os sinais para cada estratégia ativada, integrando diversos métodos analíticos para formar uma decisão abrangente de negociação.

Função SimulateTrading: Esta função simula a negociação com base nos sinais calculados e atualiza as métricas de desempenho de cada estratégia.

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
    double buySignal = 0;
    double sellSignal = 0;

    for(int i = 0; i < ArraySize(strategies); i++)
    {
        if(strategies[i].enabled)
        {
            if(strategies[i].signal > 0)
                buySignal += strategies[i].weight * strategies[i].signal;
            else if(strategies[i].signal < 0)
                sellSignal -= strategies[i].weight * strategies[i].signal;
        }
    }

    // Simulate trade execution and calculate profits
    // ... (trade simulation code)

    // Update strategy performance metrics
    // ... (performance update code)
}

Esta função é crucial para o backtesting e para avaliar o desempenho do EA. Ela simula negociações com base nos sinais calculados e atualiza as métricas de desempenho de cada estratégia.

Função CalculateHMMLikelihoods: Esta função calcula as probabilidades de diferentes estados do mercado usando o Modelo Oculto de Markov.

void CalculateHMMLikelihoods(const double &features[], const double &means[], const double &covs[], const double &transitionProb[], int numStates, double &hmmLikelihoods[])
{
    // Initialize and calculate initial likelihoods
    // ... (initialization code)

    // Forward algorithm to calculate HMM likelihoods
    for(int t = 1; t < ArraySize(features) / 3; t++)
    {
        // ... (HMM likelihood calculation code)
    }

    // Normalize and validate likelihoods
    // ... (normalization and validation code)
}

Esta função implementa o algoritmo forward dos Modelos Ocultos de Markov para calcular a probabilidade dos diferentes estados do mercado. É um método sofisticado para prever o comportamento do mercado com base em características observadas.

Essas funções formam o núcleo dos processos analíticos e de tomada de decisão do Nash Expert Advisor. A força do EA reside na combinação da análise técnica tradicional com métodos estatísticos avançados, como os Modelos Ocultos de Markov e os conceitos de Equilíbrio de Nash. Essa abordagem multiestratégica, combinada com robustas funcionalidades de backtesting e gestão de risco, torna-o uma ferramenta potencialmente poderosa para negociação algorítmica no mercado forex.

O aspecto mais importante deste EA é sua natureza adaptativa. Ao avaliar continuamente os regimes de mercado e ajustar os pesos das estratégias com base no desempenho, ele visa manter a eficácia em condições de mercado variáveis. No entanto, é crucial notar que, embora sofisticados, tais sistemas requerem monitoramento cuidadoso e recalibração periódica para garantir que permaneçam eficazes em ambientes de mercado em constante mudança.

Resultados

Com essas configurações

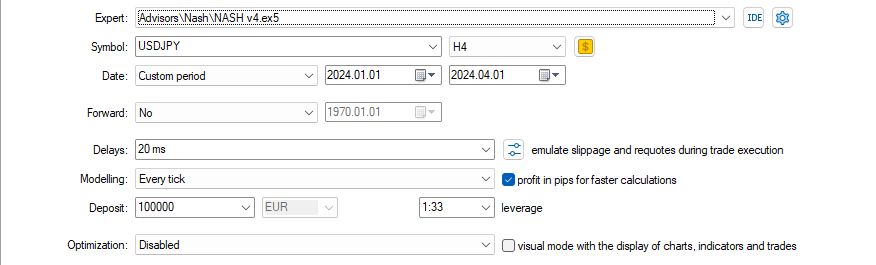
e essas Entradas

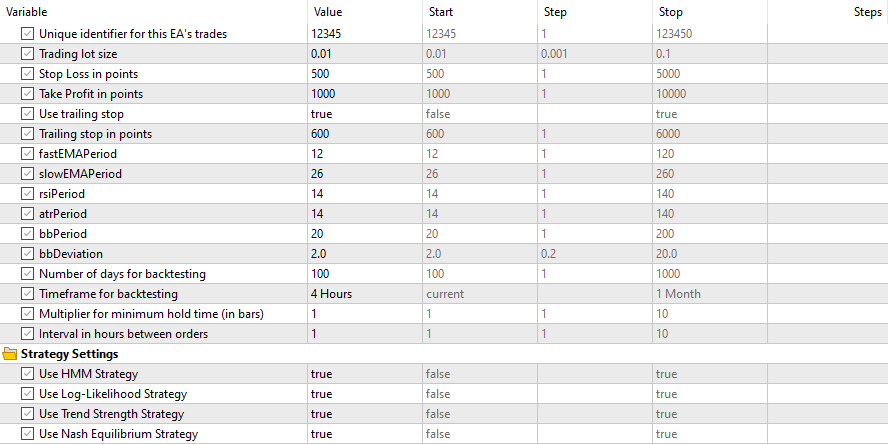
Os resultados para todas as estratégias foram os seguintes:

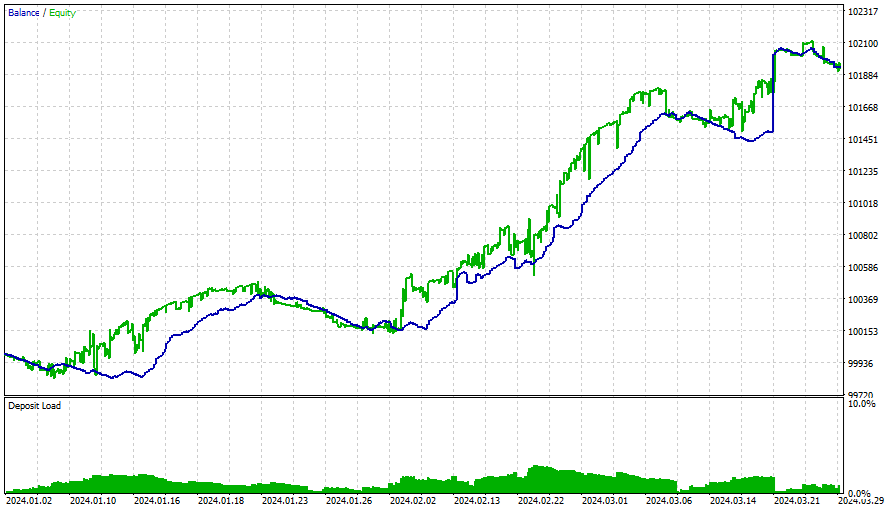
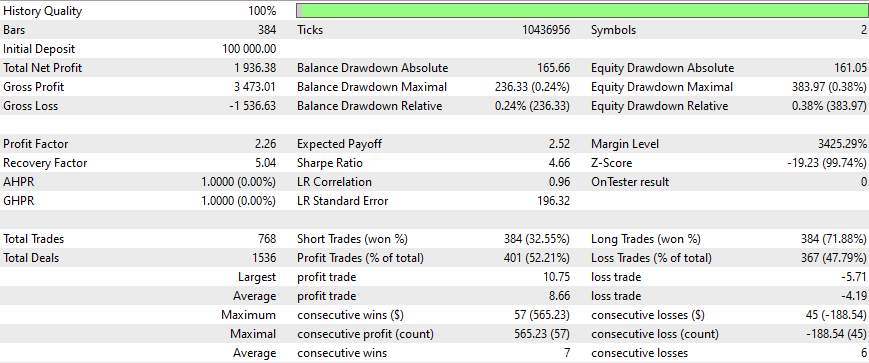
Após esse período, os ganhos diminuíram, e a otimização deveria ter sido feita a cada 3 meses (com todas essas condições iniciais). As estratégias são simples e utilizam um trailing stop (que é bem simples e fixo). Melhores resultados podem ser obtidos com mais otimizações, com matrizes mais recentes e com estratégias melhores e mais sofisticadas. Devemos também considerar adicionar análise de sentimento e aprendizado profundo a esse EA, sem esquecer o que foi dito antes.

Todas as estratégias precisam de Nash para funcionar.

Conclusão

A interseção da teoria dos jogos com o trading apresenta oportunidades empolgantes para aprimorar estratégias de mercado. Ao aplicar a teoria do equilíbrio de Nash, os traders podem tomar decisões mais calculadas, considerando as possíveis ações dos outros no mercado. Este artigo delineou como implementar esses conceitos usando Python e MetaTrader 5, oferecendo um conjunto de ferramentas poderosas para aqueles que buscam elevar sua abordagem de trading. À medida que os mercados continuam a evoluir, integrar teorias matemáticas como o Equilíbrio de Nash pode ser um diferencial importante para alcançar sucesso consistente no trading.

Espero que você tenha gostado de ler este artigo ou de revisá-lo, e espero que isso seja útil para o seu próprio EA. Este é um assunto interessante, e espero que tenha atendido às suas expectativas e que você tenha gostado tanto quanto eu gostei de produzi-lo.