Modificação do Grid-Hedge EA em MQL5 (Parte IV): Otimizando a Estratégia de Grid Simples (I)

Introdução

Neste episódio de nossa série sobre o Modified Grid-Hedge EA em MQL5, exploramos as complexidades do Grid EA. Com base em nossa experiência com o Simple Hedge EA, agora aplicamos técnicas semelhantes para melhorar o desempenho do Grid EA. Nossa jornada começa com um EA de Grid existente, que serve como nossa tela para a exploração matemática. O objetivo? Dissecar a estratégia subjacente, desvendar suas complexidades e descobrir as bases teóricas que impulsionam seu comportamento.

Mas vamos reconhecer o desafio assustador à frente. A análise que empreendemos é multifacetada, exigindo um mergulho profundo em conceitos matemáticos e cálculos rigorosos. Portanto, seria impraticável tentar cobrir tanto a otimização matemática quanto as melhorias subsequentes baseadas em código em um único artigo.

Assim, neste episódio, focaremos exclusivamente nos aspectos matemáticos. Prepare-se para um exame minucioso de teorias, fórmulas e complexidades numéricas. Não se preocupe, não deixaremos pedra sobre pedra em nossa busca para entender o processo de otimização em sua essência.

Em artigos futuros, voltaremos nossa atenção para o lado prático — a codificação real. Armados com nossa base teórica, traduziremos os insights matemáticos em técnicas de programação acionáveis. Fique atento enquanto conectamos teoria e prática para desbloquear todo o potencial do Grid EA.

Aqui está o plano para este artigo:

1. Recapitulação da Estratégia de Grid
2. Otimização Matemática
3. Simulação de Cálculos em Python
4. Conclusão

Recapitulação da Estratégia de Grid

Vamos recapitular a estratégia. Temos primeiro 2 opções:

No mundo do trading, enfrentamos duas escolhas básicas:

1. Comprar: Continuar comprando até que um determinado ponto seja alcançado.
   
2. Vender: Continuar vendendo até que uma condição específica seja atendida.
   

Primeiro, precisamos decidir se optamos por uma ordem de compra ou venda, dependendo de certas condições. Digamos que escolhemos uma ordem de compra. Colocamos a ordem e ficamos de olho no mercado. Se o preço do mercado subir, lucramos. Uma vez que o preço aumenta por uma certa quantidade que queremos como alvo (geralmente medido em pips), encerramos o ciclo de negociação. Mas se quisermos iniciar outro ciclo, também podemos fazer isso.

Agora, se o preço se mover contra nossas expectativas e cair pela mesma quantidade, digamos 'x' pips, respondemos colocando outra ordem de compra, mas desta vez com o dobro do tamanho do lote. Este movimento é estratégico porque dobrar o tamanho do lote reduz o preço médio ponderado para '2x/3' (pode ser facilmente calculado matematicamente) abaixo do preço da ordem inicial, que está a apenas 'x/3' de distância da segunda ordem, o que pode ser coberto facilmente pelo preço, que é exatamente o que queremos. Esse novo valor médio é nosso ponto de equilíbrio, onde nosso lucro líquido é zero, levando em consideração quaisquer perdas que tenhamos incorrido.

Nesse ponto de equilíbrio, temos duas maneiras de lucrar:

1. A primeira ordem, que agora é a ordem superior (referindo-se à ordem que foi aberta primeiro e tem um nível de preço mais alto), inicialmente mostra uma perda, pois o preço de mercado está abaixo do seu preço de abertura. Mas, à medida que o preço do mercado sobe de volta ao preço de abertura da primeira ordem, a perda dessa ordem diminui até atingir zero e continuar aumentando. Isso significa que nosso lucro líquido continua aumentando.
2. A segunda ordem, colocada com o dobro do tamanho do lote, já está gerando lucro. À medida que o preço do mercado continua subindo, o lucro dessa ordem também aumenta, e o principal ponto positivo é que o tamanho do lote foi multiplicado.
   

Essa abordagem é diferente das estratégias tradicionais de hedge, pois nos dá duas vias para lucrar, o que nos oferece mais flexibilidade na definição de metas. Se continuarmos aumentando o tamanho do lote de cada nova ordem por um determinado multiplicador (vamos supor dobrando), o efeito de reduzir as perdas e aumentar o lucro da última ordem torna-se progressivamente mais significativo. Isso ocorre porque a ordem mais recente e a anterior têm um tamanho de lote maior, e esse tamanho de lote continua aumentando à medida que abrimos mais ordens. Se acumulamos um bom número de ordens, o lucro que obtemos de cada pip pode ser muito maior em comparação com o hedge. Isso se torna especialmente importante quando combinamos o hedge com o grid trading posteriormente. Em uma estratégia híbrida como essa, o componente de grid tem o potencial de gerar lucros significativos.

O exemplo fornecido com duas ordens pode ser estendido para um número maior de ordens. À medida que a quantidade de ordens aumenta, especialmente quando colocadas em um intervalo consistente, o preço médio cumulativo tende a diminuir. Ao empregar um multiplicador de 2, o preço médio — que representa o ponto de equilíbrio para os lucros — converge em direção ao preço de abertura da terceira última ordem. Exploraremos esse conceito com prova matemática em discussões posteriores.

À medida que mergulhamos nas complexidades dessa estratégia de negociação, é crucial entender como o dimensionamento de lotes funciona e como os movimentos de preços afetam nossa posição. Ao gerenciar nossas ordens de forma estratégica e ajustar os tamanhos dos lotes, podemos navegar pelos mercados com precisão, aproveitando as tendências favoráveis e minimizando as possíveis perdas. A estratégia de lucro duplo que criaremos em um futuro próximo não só nos dará mais flexibilidade, mas também aumentará nossos ganhos potenciais, criando um sistema de negociação forte que prospera com a dinâmica do mercado.

Otimização Matemática

Primeiro, vamos dar uma olhada nos parâmetros que vamos otimizar, ou seja, os parâmetros da estratégia.

Parâmetros da Estratégia:

1. Posição Inicial (IP): A Posição Inicial é uma variável binária que define a direção da nossa estratégia de negociação. Um valor de 1 significa uma ação de compra, indicando que estamos entrando no mercado com a expectativa de que os preços subam. Por outro lado, um valor de 0 representa uma ação de venda, sugerindo que antecipamos uma queda nos preços. Essa escolha inicial pode ser um ponto crítico de decisão, pois determina o viés geral da nossa estratégia de negociação e define o tom para as ações subsequentes. Após a otimização, saberemos com certeza qual é a melhor opção: comprar ou vender.
2. Tamanho Inicial do Lote (IL): O Tamanho Inicial do Lote define a magnitude da nossa primeira ordem dentro de um ciclo de negociação. Ele estabelece a escala na qual participaremos no mercado e define a base para o tamanho de nossas transações subsequentes. Escolher um Tamanho Inicial do Lote adequado é crucial, pois impacta diretamente os potenciais lucros e perdas associados às nossas negociações. É essencial encontrar um equilíbrio entre maximizar nossos potenciais retornos e gerenciar nossa exposição ao risco. Isso depende fortemente do multiplicador de tamanho de lote que escolhermos, pois, se o multiplicador for alto, o lote inicial deve ser menor; caso contrário, o tamanho do lote das ordens subsequentes aumentaria rapidamente.
3. Distância (D): A Distância é um parâmetro espacial que determina o intervalo entre os níveis de preço de abertura de nossas ordens. Ela influencia os pontos de entrada em que executaremos nossas negociações e desempenha um papel significativo na definição da estrutura da nossa estratégia de negociação. Ajustando o parâmetro de Distância, podemos controlar o espaçamento entre nossas ordens e otimizar nossas entradas com base nas condições do mercado e na nossa tolerância ao risco.
4. Multiplicador do Tamanho do Lote (M): O Multiplicador do Tamanho do Lote é um fator dinâmico que nos permite aumentar o tamanho do lote de nossas ordens subsequentes com base na progressão do ciclo de negociação. Ele introduz um nível de adaptabilidade à nossa estratégia, permitindo-nos aumentar nossa exposição conforme o mercado se move a nosso favor ou reduzi-la quando enfrentamos condições adversas. Selecionando cuidadosamente o Multiplicador do Tamanho do Lote, podemos adaptar o dimensionamento das nossas posições para capitalizar as oportunidades lucrativas enquanto gerenciamos o risco.
5. Selecionando cuidadosamente o Multiplicador do Tamanho do Lote, podemos adaptar o dimensionamento das nossas posições para capitalizar as oportunidades lucrativas enquanto gerenciamos o risco. Isso não é exatamente um parâmetro da estratégia, mas sim um parâmetro que levaremos em conta ao otimizar os parâmetros reais da estratégia.

É crucial ter um bom entendimento dos parâmetros que serão o foco de nossos esforços de otimização. Esses parâmetros servem como a base sobre a qual construiremos nossa estratégia, e entender seus papéis e implicações é essencial para tomar decisões informadas e alcançar os resultados desejados.

Para simplificar, apresentamos esses parâmetros em suas formas básicas. No entanto, é importante notar que, em equações matemáticas, algumas dessas variáveis seriam denotadas usando notação de subscrito para distingui-las de outras variáveis.

Esses parâmetros servem como base para construir nossa função de lucro. A função de lucro é uma representação matemática de como nosso lucro (ou perda) é influenciado por mudanças nessas variáveis. Ela é um componente crucial de nosso processo de otimização, permitindo-nos avaliar quantitativamente os resultados de várias estratégias de negociação sob diferentes cenários.

Com esses parâmetros estabelecidos, agora podemos proceder à definição dos componentes da nossa função de lucro:

Vamos calcular a função de lucro para um cenário simplificado onde optamos por comprar e temos apenas duas ordens. Assumiremos que o multiplicador do tamanho do lote é 1, o que significa que ambas as ordens têm o mesmo tamanho de lote, 0,01.

Para encontrar a função de lucro, primeiro precisamos determinar o ponto de equilíbrio. Vamos assumir que temos duas ordens de compra, B1 e B2. B1 é colocada no preço 0, e B2 é colocada a uma distância D abaixo de B1, ou seja, no preço -D. (Observe que o preço negativo aqui é usado apenas para fins de análise e não afeta o resultado, pois a análise depende do parâmetro de distância D e não dos níveis exatos de preço.)

Agora, vamos supor que o ponto de equilíbrio está a uma distância x abaixo de B1. Nesse ponto, teremos uma perda de -x pips de B1 e um lucro de +x pips de B2.

Se os tamanhos dos lotes forem iguais (ou seja, o multiplicador do tamanho do lote é 1), o ponto de equilíbrio estaria exatamente no meio das duas ordens. No entanto, se os tamanhos dos lotes forem diferentes, precisamos considerar o multiplicador do tamanho do lote.

Por exemplo, se o multiplicador do tamanho do lote for 2 e o tamanho inicial do lote for 0,01, então B1 terá um tamanho de lote de 0,01 e B2 terá um tamanho de lote de 0,02.

Para encontrar o ponto de equilíbrio nesse caso, precisamos encontrar o valor de x resolvendo a seguinte equação:

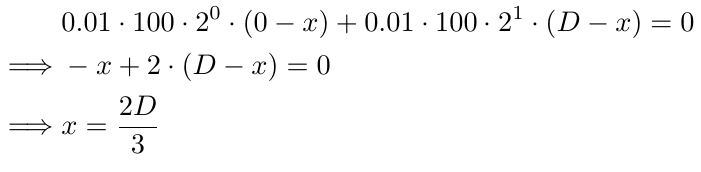
Vamos analisar os componentes da equação. O tamanho inicial do lote, 0,01, é repetido em cada parte da equação (a segunda parte refere-se à porção após o sinal de +). Multiplicamos isso por 100 para converter o tamanho do lote em um número inteiro e, como aplicamos essa conversão de forma consistente ao longo das equações, ela mantém seu significado. Em seguida, multiplicamos por 2^0 na primeira parte e 2^1 na segunda parte. Esses termos representam o multiplicador do tamanho do lote, com a potência começando em 0 para o tamanho inicial do lote e incrementando em 1 para cada ordem subsequente. Finalmente, usamos (0-x) na primeira parte, (D-x) na segunda parte, e ((i-1)D-x) na i-ésima parte, porque a i-ésima ordem é colocada (i-1) vezes D pips abaixo de B1. Resolver a equação para x resulta em 2D/3, o que significa que o ponto de equilíbrio fica 2D/3 pips abaixo de B1 (conforme definido por x em nossas equações). Se D for 10, o ponto de equilíbrio estaria 6,67 pips abaixo de B1 ou 3,34 pips acima de B2. Esse nível de preço tem mais chances de ser alcançado em comparação com o ponto de equilíbrio em B1 (se tivéssemos apenas uma ordem). Esse é o conceito principal por trás da Estratégia de Grade: apoiar ordens anteriores até que o lucro seja alcançado.

Agora, vamos considerar um caso com 3 ordens.

Para 3 ordens, seguimos a mesma abordagem. A explicação para a 1ª e 2ª partes permanece a mesma. Na 3ª parte, há duas mudanças: a potência de 2 é incrementada em 1, e D agora é multiplicado por 2. Todo o resto permanece inalterado.

Resolviendo para x ainda,

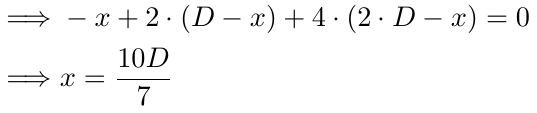
No caso de 3 ordens, descobrimos que o ponto de equilíbrio ocorre quando o preço atinge 10D/7 pips abaixo de B1. Se D for 10, o preço de equilíbrio seria 14,28 pips abaixo de B1, 4,28 pips abaixo de B2 e 5,72 pips acima de B3. Mais uma vez, o preço tem mais chances de atingir esse ponto em comparação com o ponto de equilíbrio em B1 (com 1 ordem) ou o ponto de equilíbrio anterior. O ponto de equilíbrio continua a se mover para baixo, aumentando a probabilidade de o preço alcançá-lo, apoiando efetivamente nossas ordens anteriores caso o preço se mova contra nós.

Vamos generalizar a fórmula para n ordens.

Nota: Assumimos que todas as posições são ordens de Compra. A análise para ordens de Venda é simétrica, então vamos mantê-la simples.

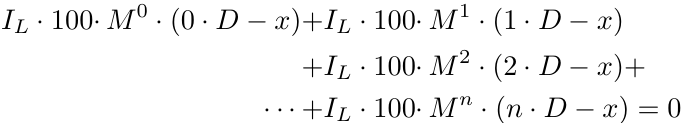
No entanto, descobrimos que essa generalização está incorreta.

A razão para isso pode ser explicada com um exemplo simples. Vamos supor que o tamanho inicial do lote seja 0,01 e o multiplicador seja 1,5. Primeiro, abrimos uma posição com um tamanho de lote de 0,01. Em seguida, abrimos uma segunda posição com um tamanho de lote de 0,01 * 1,5 = 0,015. No entanto, após o arredondamento, ele se torna 0,01, já que o tamanho do lote deve ser um múltiplo de 0,01. Há dois problemas aqui:

1. A equação calcula com base na abertura de uma posição com um tamanho de lote de 0,015, o que, na prática, não é possível. Em vez disso, abrimos uma posição com um tamanho de lote de 0,01.
2. Esse ponto não é exatamente um problema, mas algo que deve ser observado. Vamos considerar o mesmo exemplo. A primeira ordem foi 0,01, e a segunda ordem também foi 0,01 por razões de praticidade. Qual deve ser o tamanho do lote da terceira ordem? Multiplicamos o multiplicador do tamanho do lote pelo tamanho do último lote, mas devemos multiplicar 1,5 por 0,01 ou por 0,015? Se multiplicarmos por 0,01, ficamos presos em um ciclo que torna inútil o ponto de ter um multiplicador. Portanto, seguimos com 0,015 * 1,5 = 0,0225, que, na prática, se torna 0,02, e assim por diante.

Como mencionado acima, o segundo ponto não é exatamente um problema. Vamos corrigir o primeiro problema usando a Função do Maior Inteiro (GIF) ou a função "floor" na matemática, que diz que simplesmente removemos a parte decimal de qualquer número positivo (não entraremos em detalhes para números negativos, pois o tamanho do lote não pode ser negativo). Notação: floor(.) ou [.]. Exemplos: floor(1.5) = [1.5] = 1; floor(5.12334) = [5.12334] = 5; floor(2.25) = [2.25] = 2; floor(3.375) = [3.375] = 3.

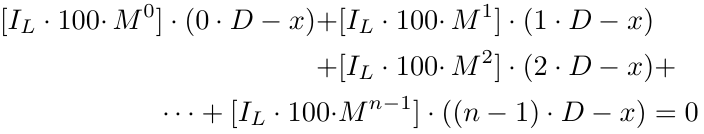
onde, [.] representa o GIF, ou seja, o Maior Fator Inteiro. Resolvido mais adiante, obtemos:

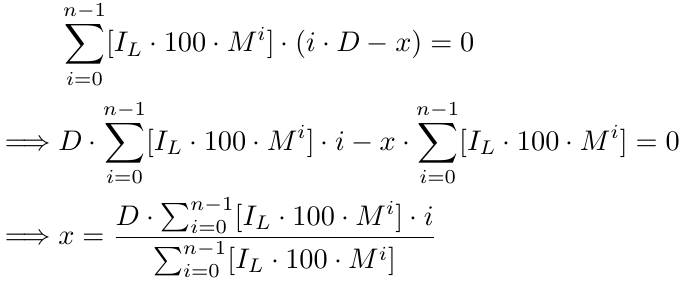
Mais formalmente, para x número de ordens, temos uma função de ponto de equilíbrio b(x),

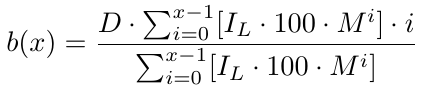
Agora, temos uma função de ponto de equilíbrio que nos dá o preço de equilíbrio. Ela retorna quantos pips abaixo de B1 está o preço de equilíbrio. Com o preço de equilíbrio, precisamos determinar o nível de Take Profit (TP), que é simplesmente TP pips acima de b(x). Como b(x) é o nível de preço de B1 menos o nível de preço de equilíbrio, para o nível de take profit, precisamos subtrair TP de b(x). Assim, temos nosso nível de take profit, que denotamos como t(x):

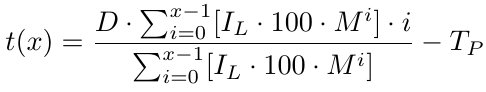
Dado x, ou seja, o número de ordens, temos nosso nível de take profit. Agora, precisamos calcular o lucro dado x. Vamos tentar encontrar a função de lucro.

Assumindo que o preço atinja t(x), ou seja, o nível de take profit, e o ciclo se feche, o lucro/prejuízo que recebemos de B1 é o nível de preço de B1 menos t(x), com pips como unidade. Um valor negativo significa que temos uma perda, enquanto um valor positivo indica que temos um lucro. Da mesma forma, o lucro/prejuízo que recebemos de B2 é o nível de preço de B2 menos t(x), com pips como unidade, e sabemos que o nível de preço de B2 está exatamente D pips abaixo do nível de preço de B1. Para B3, o lucro/prejuízo é o nível de preço de B3 menos t(x), com pips como unidade, e sabemos que o nível de preço de B3 está exatamente 2 vezes D pips abaixo do nível de preço de B1. Observe que também precisamos considerar o tamanho inicial do lote e o multiplicador do tamanho do lote.

Matematicamente, dado x (ou seja, o número de ordens é 3), temos:

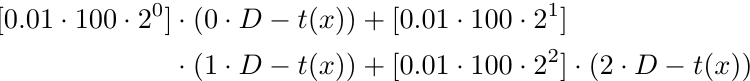
Mais formalmente, para x número de ordens, temos uma função de lucro p(x),

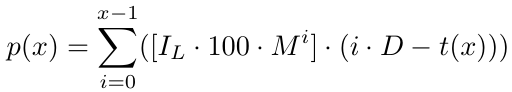
Vamos entender o que isso significa. Dado qualquer número de ordens, assumindo que o ciclo se feche em x ordens (onde "fechar" significa que atingimos o nível de take profit), teremos um lucro dado pela equação acima p(x). Agora que temos a função de lucro, vamos tentar calcular a função de custo, que se refere à perda que sofreremos se perdermos um ciclo de grade com x ordens (onde "perder" significa que não podemos abrir mais ordens para continuar o ciclo da grade devido a fundos insuficientes, já que a estratégia de grade requer muitos investimentos, ou por qualquer outro motivo).

A função de custo ficaria assim: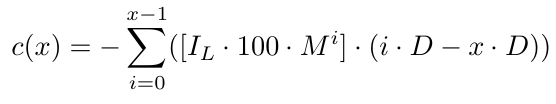

Nesta equação, a parte [.] leva em consideração o Tamanho Inicial do Lote e o Multiplicador do Tamanho do Lote. A outra parte (i.D-x.D) considera x.D, que é a distância entre o nível de preço B1 e D pips abaixo da ordem com o preço mais baixo. Usamos x.D porque é exatamente aí que abrimos uma nova ordem. Se, por algum motivo, mais provavelmente fundos insuficientes, não conseguirmos continuar o ciclo, esse é o ponto exato no qual podemos dizer com certeza que não poderíamos continuar o ciclo se não conseguirmos abrir a ordem nesse nível de preço (quando o preço chegar lá). Essencialmente, quando sabemos com certeza que falhamos em continuar o ciclo, o nível de preço estaria x.D pips abaixo do nível de preço B1. Como resultado, teremos uma perda de (0.D-x.D) na ordem B1, (1.D-x.D) na ordem B2 e assim por diante até a última ordem, que é a ordem Bx, da qual teremos uma perda de ((x-1).D-x.D)=-D. Isso faz sentido porque estamos D pips abaixo da última ordem (a ordem com o nível de preço mais baixo).

Mais formalmente, para x número de ordens, temos uma função de custo c(x),

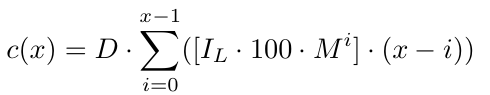
Também precisamos considerar o spread, que assumiremos como um spread constante para simplificar, pois considerar um spread dinâmico seria bastante complexo. Digamos que S seja o spread estático, que manteremos entre 1-1,5 para EURUSD. O spread pode mudar dependendo do par de moedas, mas essa estratégia funcionará melhor com moedas que tenham menor volatilidade, como EURUSD.

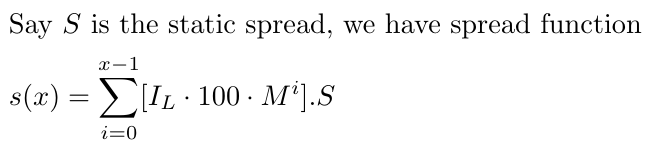
É importante notar que nosso ajuste leva em consideração todas as negociações, de zero a x-1, reconhecendo que o spread afeta todas as negociações, sejam lucrativas ou não. Para simplificar, estamos tratando o spread (denotado como S) como um valor constante. Essa decisão foi tomada para evitar complicar nossa análise matemática com a variabilidade adicional de um spread flutuante. Embora essa simplificação limite o realismo de nosso modelo, permite-nos focar nos aspectos principais de nossa estratégia sem nos perdermos em complexidades excessivas.

Agora que temos todas as funções necessárias, podemos plotá-las no Desmos.

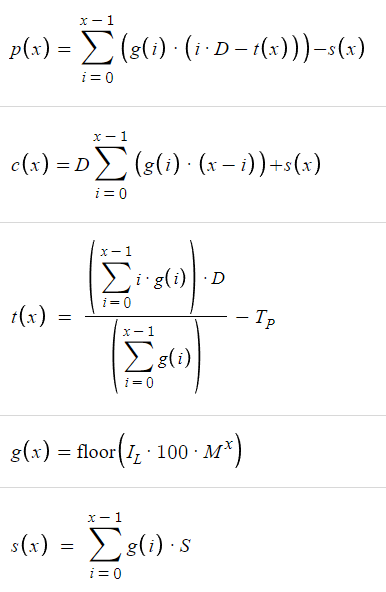
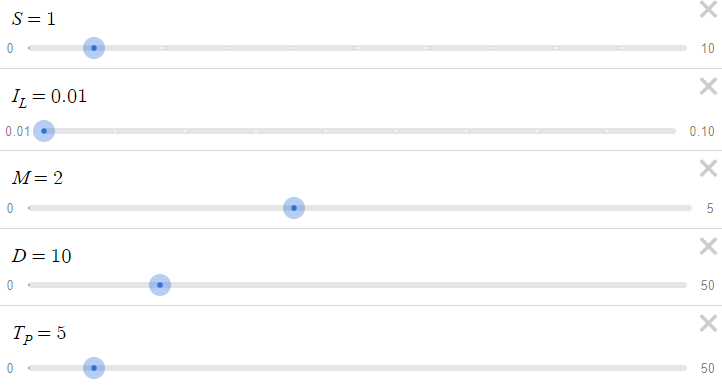
Dado os parâmetros acima, temos a seguinte tabela, onde alterar x gera diferentes valores de p(x) e c(x):

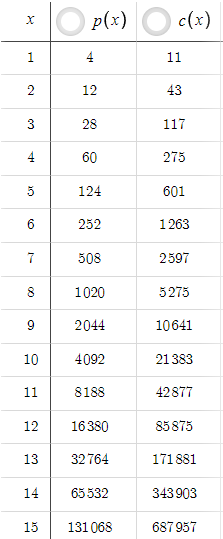
Neste cenário, p(x) é sempre menor que c(x), mas isso pode ser facilmente alterado aumentando o TP. Por exemplo, se aumentarmos o TP de 5 para 50:

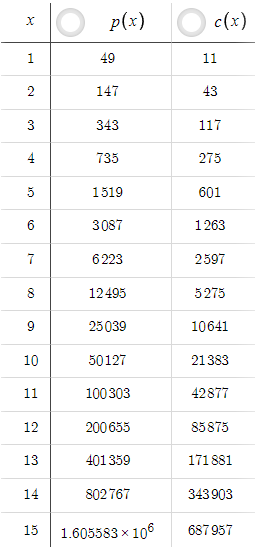
Agora, p(x) é sempre maior que c(x). Um trader iniciante pode pensar que, se podemos obter níveis tão altos de razão risco-recompensa com TP=50, por que manter TP=5? No entanto, devemos levar em consideração a probabilidade. O incremento do TP de 5 para 50 diminuiu drasticamente a probabilidade de o preço atingir o nível de take profit. Precisamos perceber que não adianta ter uma boa razão risco-recompensa se nunca ou raramente atingimos o take profit. Para levar em consideração as probabilidades, precisamos de dados de preços e otimização baseada em código, em vez de apenas equações, o que exploraremos nas próximas partes da série.

Você pode usar este Link do Gráfico Desmos para ver o gráfico dessas funções e brincar com os parâmetros para obter uma melhor compreensão dessa estratégia.

Com isso, concluímos a Parte Matemática da Otimização. Nas próximas seções, vamos nos aprofundar nos aspectos práticos de implementar essa estratégia, considerando as condições reais de mercado e os desafios que surgem com elas. Ao combinar a base matemática que estabelecemos aqui com análise baseada em dados e técnicas de otimização, podemos refinar a estratégia de negociação em grade para melhor atender às nossas necessidades e maximizar seu potencial de lucratividade.

Pensamentos Finais: Conforme mencionado anteriormente, inúmeros parâmetros indicam um alto potencial de lucro. No entanto, é crucial entender que esses números servem principalmente como ilustrações. O motivo disso é a ausência de um componente vital na otimização matemática: a probabilidade. Incorporar a probabilidade em nosso modelo matemático é uma tarefa complexa, mas é um fator indispensável que não pode ser ignorado. Para resolver isso, realizaremos simulações com dados de preços, o que nos permitirá considerar a probabilidade em nossos cálculos e melhorar a precisão de nosso modelo.

Simulação de Cálculos em Python

Nessa simulação, calcularemos e plotaremos p(x) e c(x) em relação a x, onde x representa o número de ordens. Os valores de p(x) e c(x) serão plotados no eixo y, enquanto x será no eixo x. Essa visualização fornecerá insights rápidos sobre as mudanças em p(x) e c(x), e ajudará a identificar qual função é maior em diferentes pontos. Além disso, geraremos uma tabela que exibe os valores exatos de p(x) e c(x) para cada x, pois esses valores podem não ser facilmente legíveis apenas a partir do gráfico. Essa combinação do gráfico e da tabela oferecerá uma compreensão abrangente do comportamento de p(x) e c(x).

Código Python:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

# Values of x to evaluate
x_values = range(1, 21)  # x from 1 to 20

def g(x, I_L, M):
    return np.floor(I_L * 100 * M ** x)

def s(x, I_L, M, S):
    return sum(g(i, I_L, M) * S for i in range(x))

def t(x, D, I_L, M, T_P):
    numerator = sum(i * g(i, I_L, M) for i in range(x)) * D
    denominator = sum(g(i, I_L, M) for i in range(x))
    return (numerator / denominator) - T_P

def p(x, D, I_L, M, S, T_P):
    return sum(g(i, I_L, M) * (i * D - t(x, D, I_L, M, T_P)) for i in range(x)) - s(x, I_L, M, S)

def c(x, D, I_L, M, S):
    return D * sum(g(i, I_L, M) * (x - i) for i in range(x)) + s(x, I_L, M, S)

# Calculate p(x) and c(x) for each x
p_values = [p(x, D, I_L, M, S, T_P) for x in x_values]
c_values = [c(x, D, I_L, M, S) for x in x_values]

# Formatter to avoid exponential notation
def format_func(value, tick_number):
    return f'{value:.2f}'

# Plotting
fig, axs = plt.subplots(2, 1, figsize=(12, 12))

# Combined plot for p(x) and c(x)
axs[0].plot(x_values, p_values, label='p(x)', marker='o')
axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange')
axs[0].set_title('p(x) and c(x) vs x')
axs[0].set_xlabel('x')
axs[0].set_ylabel('Values')
axs[0].set_xticks(x_values)
axs[0].grid(True)
axs[0].legend()
axs[0].yaxis.set_major_formatter(FuncFormatter(format_func))

# Create table data
table_data = [['x', 'p(x)', 'c(x)']] + [[x, f'{p_val:.2f}', f'{c_val:.2f}'] for x, p_val, c_val in zip(x_values, p_values, c_values)]

# Plot table
axs[1].axis('tight')
axs[1].axis('off')
table = axs[1].table(cellText=table_data, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.2, 1.2)

plt.tight_layout()
plt.show()

Explicação do Código:

1. Importar Bibliotecas:

   • numpy é importado como np para operações numéricas.
   • b0> matplotlib.pyplot é importado como plt para plotagem de gráficos.
   • FuncFormatter é importado de matplotlib.ticker para formatar os rótulos dos ticks dos eixos.

2. Definir Parâmetros:

   • Definir constantes D, I_L, M, S e T_P , que representam Distância, Tamanho Inicial do Lote, Multiplicador do Tamanho do Lote, Spread e Take Profit, respectivamente.

3. Definir Intervalo para x:

   • x_valuesé definido como um intervalo de inteiros de 1 a 20.

4. Definir Funções:

   • g(x, I_L, M): Calcula o valor de g com base na fórmula fornecida.
   • s(x, I_L, M, S): Calcula a soma de g(i, I_L, M) * S para i de 0 a x-1.
   • t(x, D, I_L, M, T_P): Calcula o valor de t com base na fórmula dada, usando um numerador e denominador.
   • p(x, D, I_L, M, S, T_P): Calcula p(x) usando a fórmula fornecida.
   • c(x, D, I_L, M, S): Calcula c(x) usando a fórmula fornecida.

5. Calcular Valores de p(x) e c(x):

   • p_valuesé uma lista de p(x) para cada x em x_values.
   • c_valuesé uma lista de c(x) para cada x em x_values.

6. Definir Formatador:

   • format_func(value, tick_number): Define uma função formatadora para formatar os rótulos dos ticks do eixo y com duas casas decimais.

7. Plotagem:

   • fig, axs = plt.subplots(2, 1, figsize=(12, 12)) : Cria uma figura e dois subplots organizados em uma única coluna.

   Primeiro Subplot (Gráfico Combinado de p(x) e c(x)):

   • axs[0].plot(x_values, p_values, label='p(x)', marker='o'): Plota p(x) em relação a x com marcadores.
   • axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange'): Plota c(x) em relação a x com marcadores na cor laranja.
   • axs[0].set_title('p(x) e c(x) vs x'): Define o título do primeiro subplot.
   • axs[0].set_xlabel('x'): Define o rótulo do eixo x.
   • axs[0].set_ylabel('Valores'): Define o rótulo do eixo y.
   • axs[0].set_xticks(x_values): Garante que os ticks do eixo x sejam exibidos para cada valor de x.
   • axs[0].grid(True): Adiciona uma grade ao gráfico.
   • axs[0].legend(): Exibe a legenda.
   • axs[0].yaxis.set_major_formatter(FuncFormatter(format_func)): Aplica o formatador ao eixo y para evitar notação exponencial.

   Segundo Subplot (Tabela):

   • table_data: Prepara os dados da tabela com colunas x, p(x), e c(x), e seus valores correspondentes.
   • axs[1].axis('tight'): Ajusta o eixo do subplot para se ajustar firmemente à tabela.
   • axs[1].axis('off'): Desativa o eixo para o subplot da tabela.
   • table = axs[1].table(cellText=table_data, cellLoc='center', loc='center'): Cria uma tabela no segundo subplot com texto centralizado.
   • table.auto_set_font_size(False): Desativa o ajuste automático do tamanho da fonte.
   • table.set_fontsize(10): Define o tamanho da fonte da tabela.
   • table.scale(1.2, 1.2): Escala o tamanho da tabela.

8. Layout e Exibição:

   • plt.tight_layout(): Ajusta o layout para evitar sobreposição.
   • plt.show(): Exibe os gráficos e a tabela.

Usamos os seguintes parâmetros padrão (podem ser facilmente alterados para ver resultados diferentes):

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

Resultado:

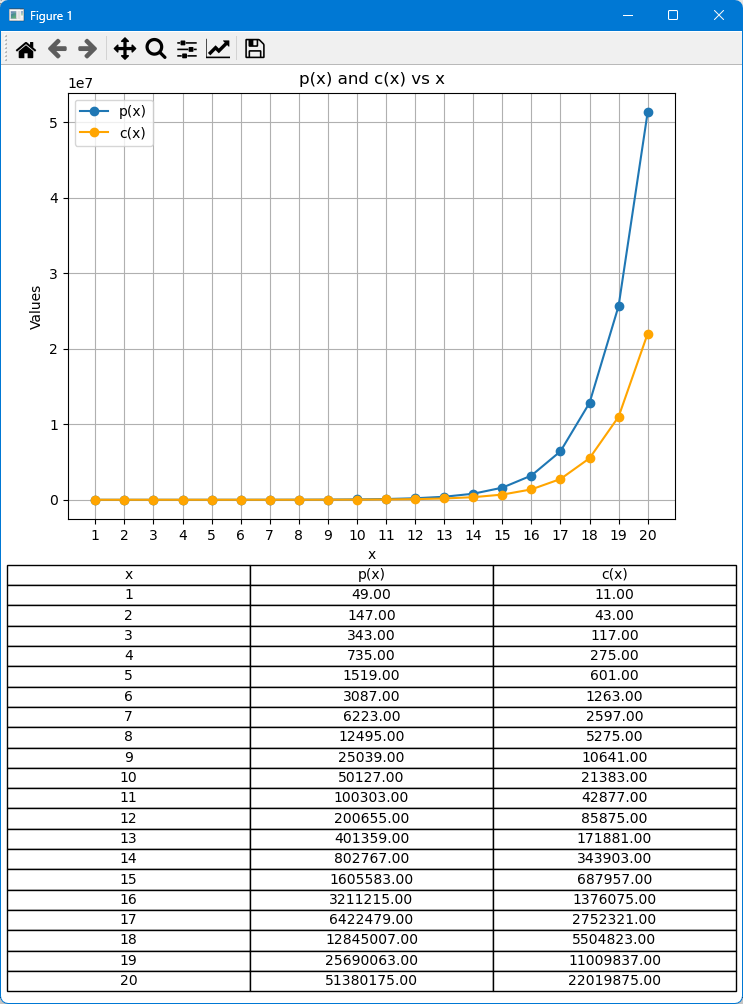
Nota: Um arquivo Python contendo o código discutido acima foi anexado ao final do artigo.

Conclusão

Na quarta parte de nossa série, focamos em otimizar a estratégia de Grid Simples por meio da análise matemática e do papel da probabilidade, muitas vezes negligenciado em estratégias de grid e hedge. Futuros artigos farão a transição da teoria para aplicações práticas baseadas em código, aplicando nossos insights em cenários reais de negociação para ajudar os traders a aumentar os retornos e gerenciar riscos de forma eficaz. Agradecemos seu feedback contínuo e incentivamos mais interação à medida que exploramos, refinamos e obtemos sucesso nas estratégias de negociação juntos.

Feliz Codificação! Feliz Negociação!