MQL5における修正グリッドヘッジEA（第4部）：シンプルなグリッド戦略の最適化（I）

はじめに

本連載「MQL5における修正グリッドヘッジEA」の第4部になる今回は、グリッドEAの複雑さについて掘り下げます。シンプルヘッジEAでの経験に基づき、同様のテクニックをグリッドEAのパフォーマンス向上に適用します。私たちの旅は、数学的探求のためのキャンバスとなる既存のグリッドEAから始まります。目標は、戦略の根底にあるものを解剖し、その複雑さを解き明かし、その行動の原動力となっている理論的裏付けを明らかにすることです。

前途多難な挑戦であることは白状します。私たちが手がける分析は多面的で、数学的概念に深く入り込み、厳密な計算を必要とします。したがって、数学的最適化とその後のコードに基づく改良の両方を1つの記事でカバーしようとするのは非現実的です。

そこで今回は、数学的な側面だけに焦点を当てます。理論、公式、数値の複雑さを徹底的に検証します。ご心配なく。最適化プロセスの核心をくまなく理解することになります。

今後の記事では、実践的な側面、つまり実際のコーディングに目を向けることにしましょう。理論的な基礎を身につけた上で、数学的な洞察を実用的なプログラミングテクニックに変換していきます。グリッドEAの可能性を最大限に引き出すために、理論と実践の橋渡しをするのでご期待ください。

次が、この記事の計画です。

1. グリッド戦略の総括
2. 数学的最適化
3. Pythonで計算をシミュレーションする
4. 結論

グリッド戦略の総括

まず、2つのオプションがあります。

取引の世界では、2つの基本的な選択を迫られます。

1. 買い：あるポイントに達するまで買い続ける
   
2. 売る：特定の条件が満たされるまで売り続ける
   

まず、ある条件によって買い注文にするか売り注文にするかを決める必要があります。買い注文で行くとしましょう。注文を出し、市場を監視します。市場価格が上がれば、利益を得ます。価格が目標とする一定量（通常はピップス単位）上昇したら、取引サイクルを終了し、その日を終了しますが、別のサイクルを始めたければ、それもできます。

さて、価格が予想に反して動き、同じ一定量、例えばxピップス下落したら、別の買い注文を出して対応しますが、今度はロットサイズを2倍にします。この動きは戦略的です。ロットサイズを 2 倍にすると、加重平均価格が最初の注文価格より「2x/3」(数学的に簡単に計算できる) 低くなります。最初の注文価格は、価格によって簡単に変換できる2番目の注文より「x/3」だけ高いため、これはまさに望まれていることです。この新たな平均が損益分岐点となり、発生した損失を考慮した純利益がゼロとなります。

この損益分岐点では、利益を上げる方法は2つあります。

1. 最初の注文は、現在上位の注文（最初に出され、価格レベルが高い注文を指す）であり、市場価格が開始価格を下回っているため、最初は損失を示しています。しかし、市場価格が最初の注文の始値まで上昇すると、その注文による損失はゼロになるまで減少し、さらにプラスになります。つまり、純利益は増え続けているのです。
2. ロットサイズを2倍にして発注した2番目の注文は、すでに利益を上げています。市場価格が上昇し続けるにつれて、その注文からの利益も上昇し、主なプラスポイントは、この注文には倍増したロットサイズがあることです。
   

このアプローチは従来のヘッジ戦略とは異なり、利益を上げるための2つの手段を提供するため、目標設定に柔軟性を持たせることができます。新規注文のロットサイズを一定の乗数（仮に2倍とする）で増やし続ければ、前回の注文から損失を減らし、利益を増やす効果が徐々に大きくなります。これは、直近の注文とその前の注文のロットサイズが大きく、注文が増えるにつれてこのロットサイズが増え続けるためです。多くの注文を積み重ねれば、1ピップから得られる利益はヘッジに比べてはるかに大きくなります。このことは、後にヘッジとグリッド取引を組み合わせる場合に特に重要になります。このようなハイブリッド戦略では、グリッドコンポーネントが大きな利益を生み出す可能性があります。

2つの注文で説明した例は、より多くの注文に拡張することができます。注文の数量が増えるにつれて、特に一定の間隔で発注される場合、累積平均価格は低下する傾向にあります。乗数を2にすると、利益の損益分岐点を示す平均価格は、最後の3番目の注文の始値に向かって変換されます。この概念については、後ほど数学的な証明を交えて説明します。

この取引戦略の複雑さをより深く理解するには、ロットサイジングの仕組みと、値動きがポジションに与える影響を理解することが重要です。注文を戦略的に管理し、ロットサイズを調整することで、市場を正確にナビゲートし、有利なトレンドを利用し、潜在的な損失を最小限に抑えることができます。近い将来におこなうであろう両建て戦略は、私たちに柔軟性を与えるだけでなく、潜在的な利益を増大させ、市場力学に繁栄する強力な取引システムを作り上げます。

数学的最適化

まず、最適化するパラメータ、つまり戦略のパラメータを見てみましょう。

戦略のパラメータ

1. 初期ポジション(IP)：初期ポジションは、取引戦略の方向性を決めるバイナリー変数です。値が1の場合は買い行動を意味し、価格の上昇を期待して市場に参入していることを示します。逆に、0の場合は売りで、価格の下落を予想しています。この最初の選択は、取引戦略の全体的なバイアスを決定し、その後の行動の基調を整えるため、重要な決定ポイントになるかもしれません。最適化の後、買うべきか売るべきかがはっきりわかるでしょう。
2. 初期ロットサイズ(IL)：初期ロットサイズは、取引サイクル内の最初の注文の大きさを定義します。市場に参加する規模を確立し、その後の取引規模の基礎を築くものです。適切な初期ロットサイズを選択することは、取引に関連する潜在的な利益と損失に直接影響するため、非常に重要です。潜在的リターンの最大化とリスクエクスポージャーの管理とのバランスを取ることが不可欠です。これは、どのロットサイズ乗数を選ぶかに大きく依存します。倍率が高ければ、これは低くするべきです。そうでなければ後続の注文のロットサイズはあっという間に爆発してしまうからです。
3. 距離(D)：距離は空間的なパラメータで、注文の始値レベルの間隔を決定します。取引を実行するエントリポイントに影響し、取引戦略の構造を定義する上で重要な役割を果たします。距離パラメータを調整することで、注文の間隔をコントロールし、市場の状況やリスク許容度に基づいてエントリを最適化することができます。
4. ロットサイズ乗数(M)：ロットサイズ乗数は、取引サイクルの進行に基づいて、後続の注文のロットサイズを増加させることができる動的な要因です。これは戦略に適応性のレベルを導入するもので、市場が有利に動けばエクスポージャーを増やし、不利な状況に直面すればエクスポージャーを減らすことができます。ロットサイズ乗数を慎重に選択することで、リスクを管理しながら、収益機会を生かすためにポジションサイジングを調整することができます。
5. 注文数(N)：注文数は、1取引サイクル/グリッドサイクル内で発注する注文の合計数を表します。これは正確には戦略のパラメータではなく、戦略の実際のパラメータを最適化する際に考慮するパラメータです。

最適化の焦点となるパラメータをしっかりと把握することが重要です。これらのパラメータは、戦略を構築するための基礎となるものであり、その役割と意味を理解することは、十分な情報に基づいた意思決定をおこない、望ましい結果を達成するために不可欠です。

分かりやすくするために、これらのパラメータを基本的な形で示します。しかし、数学の方程式では、これらの変数のいくつかは、他の変数と区別するために添え字表記で示されることに注意することが重要です。

これらのパラメータは、利益関数を構築するための基礎となります。利益関数とは、利益（または損失）がこれらの変数の変化によってどのように影響を受けるかを数学的に表したものです。これは最適化プロセスの重要な要素であり、さまざまなシナリオ下でさまざまな取引戦略の結果を定量的に評価できるようにします。

パラメータが確立されたので、次に利益関数の構成要素を定義します。

買いを選択し、注文が2つしかない単純化したシナリオで利益関数を計算してみましょう。ここでは、ロットサイズ乗数が1、つまり両方の注文が同じロットサイズ0.01であると仮定します。

利益関数を求めるには、まず損益分岐点を決定する必要があります。B1とB2の2つの買い注文があるとしましょう。B1は価格0に置かれ、B2はB1より距離D下、つまり価格-Dに置かれます。（ここでの負の価格は分析のために使用したものであり、分析が正確な価格レベルではなく距離パラメータDに依存するため、結果には影響しません)

ここで、損益分岐点がB1より距離xだけ下にあるとしましょう。この時点で、B1による損失は-xピップス、B2による利益は+xピップスとなります。

ロットサイズが等しい場合（すなわち、ロットサイズ乗数が1）、損益分岐点は2つの注文のちょうど真ん中になります。しかし、ロットサイズが異なる場合は、ロットサイズ乗数を考慮する必要があります。

例えば、ロットサイズ乗数が2で初期ロットサイズが0.01の場合、B1のロットサイズは0.01、B2のロットサイズは0.02となります。

この場合の損益分岐点を求めるには、以下の方程式を解いてxの値を求める必要があります。

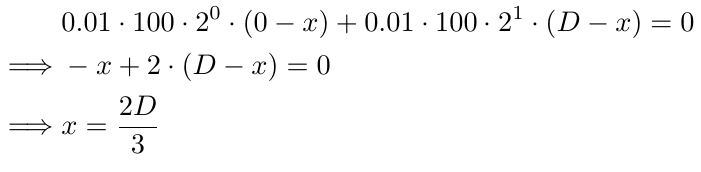
方程式の構成要素を分析してみましょう。初期ロットサイズである0.01は、式の各部分で繰り返されます（2番目の部分は+記号の後の部分を指す）。これを100倍してロットサイズを整数に変換するのですが、この変換は方程式全体を通して一貫して適用されるため、その意味が維持されます。次に、最初の部分に2^0を、2番目の部分に2^1を掛けます。これらの項はロットサイズ乗数を表し、最初のロットサイズに対して0から始まり、その後の注文ごとに1ずつ増加します。最後に、i番目の注文はB1より「(i-1)＊D」ピップス下に置かれるため、最初の部分では(0-x)、2番目の部分では(D-x)、i番目の部分では((i-1)D-x)を使用します。方程式をxについて解くと2D/3となり、損益分岐点はB1（方程式のxで定義される）より2D/3ピップス下にあることを意味します。Dが10の場合、損益分岐点はB1より6.67ピップス下、またはB2より3.34ピップス上となります。この価格レベルは、B1の損益分岐点（注文が1つだけの場合）に比べて到達する可能性が高いです。これがグライディング戦略の核となる概念です。利益が出るまで前の注文をバックアップするのです。

では、3つの注文がある場合を考えてみましょう。

3つの注文の場合は、同じアプローチに従います。1つ目と2つ目についての説明は変わりません。3つ目では、2つの変更があります。2の累乗が1ずつ増加し、Dが2倍されます。それ以外は何も変わりません。

さらにxについて解きます。

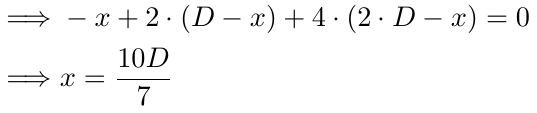
3つの注文の場合、損益分岐点は価格がB1より10D/7ピップス下に達したときに発生することがわかります。Dが10の場合、損益分岐価格はB1より14.28ピップス下、B2より4.28ピップス下、B3より5.72ピップス上となります。ここでも、B1（1つの注文）の損益分岐点や前回の損益分岐点と比べて、価格がこのポイントに到達する可能性が高いです。損益分岐点は下降を続け、価格が損益分岐点に到達する可能性が高まります。これは、価格が不利に動いた場合に、以前の注文を効果的にバックアップします。

この式をn個の注文について一般化してみましょう。

注：すべてのポジションを買い注文と仮定します。売り注文の分析は対称的なので、ここではシンプルにします。

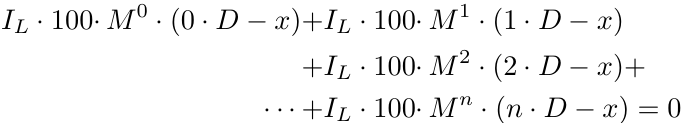
しかし、この一般論は正しくないことが判明しました。

その理由は簡単な例で説明できます。初期ロットサイズを0.01、乗数を1.5とします。まず、ロットサイズ0.01のポジションを建てます。次に、0.01 * 1.5 = 0.015のロットサイズで2つ目のポジションを建てます。しかし、四捨五入すると0.01となります。ロットサイズは0.01の倍数でなければならないからです。ここには2つの問題があります。

1. この計算式は、ロットサイズ0.015のポジションを建てることを前提に計算されているが、実際には不可能です。代わりに、ロットサイズ0.01のポジションを建てます。
2. この点は正確には問題ではなく、むしろ注意しなければならない点です。同じ例で考えてみましょう。1つ目の注文は0.01、2つ目の注文も実用上の理由から0.01としました。3つ目の注文のロットサイズはどうするべきでしょうか。ロットサイズ乗数に前回の注文のロットサイズを掛けますが、1.5に0.01を掛けるべきか、0.015を掛けるべきか。0.01を掛けるとループにはまり、乗数を持つ意味がなくなってしまいます。つまり、0.015 * 1.5 = 0.0225となり、実質的には0.02となります。

上記の通り、2点目は必ずしも問題ではありません。数学で言うところのGIF（Greatest Integer Factor）またはfloor関数を使用して最初の問題を解決してみましょう。これは、正の数の小数部を単純に削除することを意味します（ロットサイズは負にはできないため、負の数については詳しく説明しません）。表記: floor(.) または [.]。例： floor(1.5) = [1.5] = 1; floor(5.12334) = [5.12334] = 5; floor(2.25) = [2.25] = 2; floor(3.375) = [3.375] = 3。

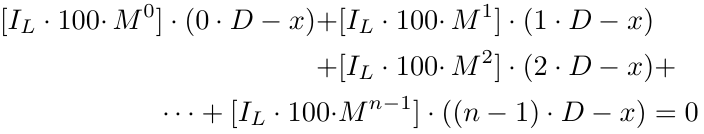
ここで、[.]はGIF、すなわちGreatest Integer Factorを表します。さらに解くとこうなります。

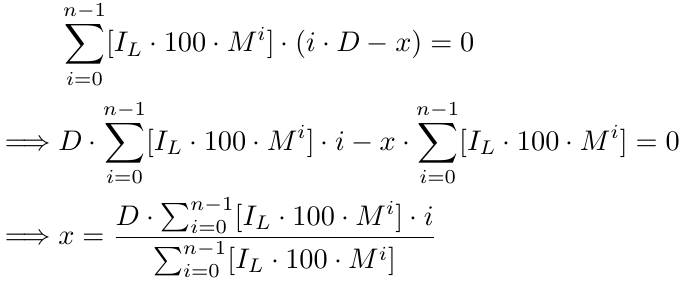
より正式には、注文数がxの場合、次の損益分岐点関数b(x)があります。

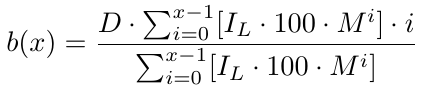
これで、損益分岐点価格がわかる損益分岐点関数ができました。損益分岐点がB1より何ピップス低いかを返します。損益分岐点価格を用いて、テイクプロフィット(TP)レベルを決定する必要があります。b(x)はB1価格レベルから損益分岐点価格レベルを引いたものなので、テイクプロフィットレベルについてはb(x)からTPを引く必要があります。こうして、t(x)と呼ぶテイクプロフィットレベルができました。

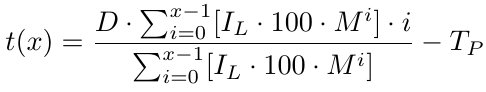
x、すなわち注文の数が与えられれば、テイクプロフィットレベルが決まります。では、xから利益を計算する必要があります。利益関数を求めてみましょう。

価格がt(x)、すなわちテイクプロフィットレベルに到達し、サイクルが閉じると仮定すると、B1から受け取る損益は、B1の価格レベルからt(x)を引いたもので、単位はピップスです。マイナスは損失、プラスは利益を意味します。同様に、B2から受け取る利益/損失は、B2の価格レベルからt(x)を引いたもので、単位はピップスです。そして、B2価格レベルはB1価格レベルより正確にDピップ低いことがわかります。B3の場合、利益/損失はB3の価格レベルからt(x)を引いたもので、単位はピップスであり、B3の価格レベルはB1の価格レベルよりちょうど2*Dピップス低いことが分かっています。初期ロットサイズとロットサイズ乗数も考慮する必要があります。

数学的には、x（つまり注文数は3）が与えられると、次のようになります。

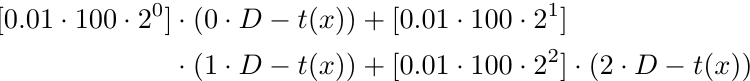
より正式には、注文数xに対して次の利益関数p(x)があります。

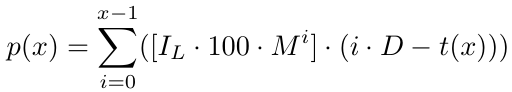
この意味を理解しましょう。任意の数の注文がある場合、サイクルがx回の注文でクローズすると仮定すると（ここで「クローズ」とは、利益確定レベルに達したことを意味する）、上式p(x)で与えられる利益が得られます。これは、x 個の注文でグリッドサイクルを失った場合に被る損失を意味します（ここで「失う」とは、資金不足のためにグリッドサイクルを継続するためにさらなる注文を建てることができない、またはその他の理由を意味します。グリッド戦略には多くの投資が必要です）。

コスト関数は次のようになります。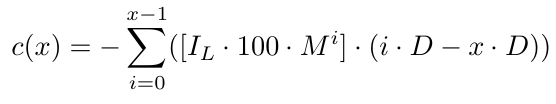

この式において、[.]の部分は初期ロットサイズとロットサイズ乗数を考慮したものです。もう1つの部分（i.D-x.D）はx.Dを考慮します。x.DはB1の価格レベルと最安値の注文からDピップス下の距離です。x.Dを使用するのは、それがまさに新しい注文を出す場所だからです。何らかの理由（資金不足の可能性が高い）で、サイクルを継続できなかった場合、その価格レベルで注文を出せなければ（価格がそこに到達すれば）、サイクルを継続できなかったと確実に言える正確な時点です。要するに、サイクルの継続に失敗したと確信した場合、価格レベルはB1価格レベルよりx.Dピップス下になります。その結果、B1注文からは(0.D-x.D)の損失、B2注文からは(1.D-x.D)の損失、そして最後の注文であるBx注文までは((x-1).D-x.D)=-Dの損失となります。これは、最後の注文（価格レベルが最も低い注文）よりDピップス下なので、理にかなっています。

より正式には、注文数xに対して、次のコスト関数c(x)があります。

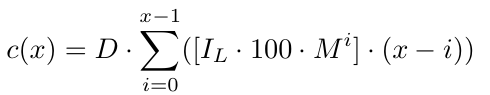
また、スプレッドを考慮する必要がありますが、動的スプレッドを考慮すると非常に複雑になるため、ここでは分かり居やすくするためにスプレッドが一定であると仮定します。Sを静的スプレッドとし、EURUSDでは1～1.5とします。スプレッドは通貨ペアによって変わる可能性がありますが、この戦略はEURUSDのようなボラティリティの低い通貨で最も効果的です。

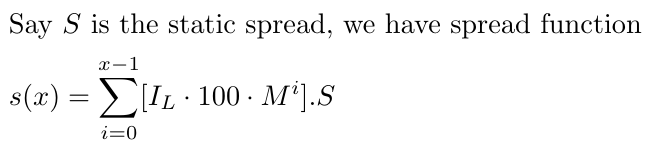
ここで重要なのは、調整がゼロからx-1までのすべての取引を考慮に入れていることです。スプレッドは利益が出ているかどうかにかかわらず、すべての取引に影響を与えるということを認識します。分かりやすくするために、現在はスプレッド（Sと表記）を一定値として扱っています。これは、スプレッドの変動という付加的な変動要因によって数学的分析が複雑になるのを避けるための決定です。このように単純化することで、モデルの現実性は制限されるものの、過剰な複雑さに悩まされることなく、戦略の核心部分に集中することができます。

必要な関数がすべて揃ったので、Desmosでプロットしてみましょう。

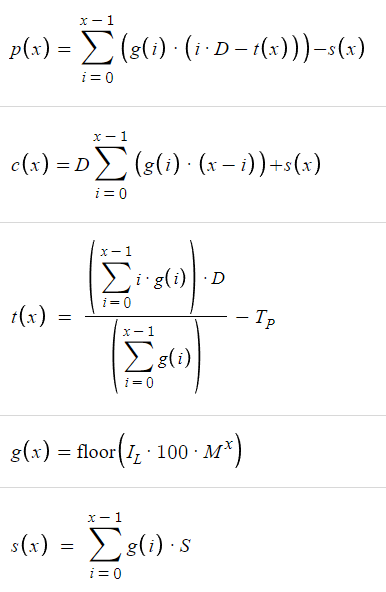
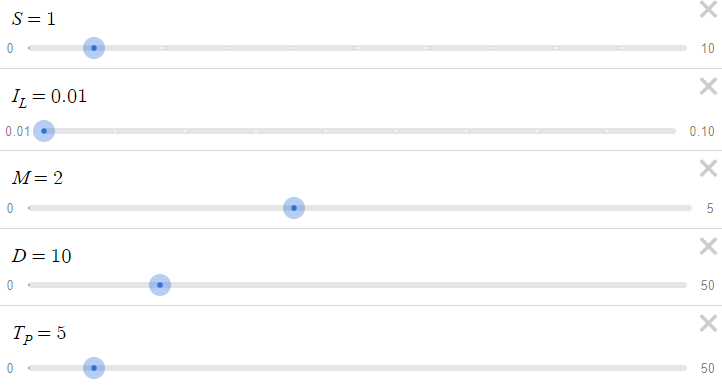
上記のパラメータを考慮すると、次の表が得られます。xを変えるとp(x)とc(x)の値が変わります。

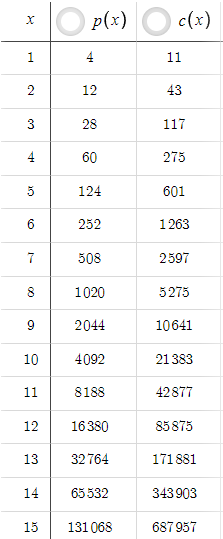
このシナリオでは、p(x)は常にc(x)よりも小さいですが、これはTPを増やすことで簡単に変更できます。例えば、TPを5から50に上げるとします。

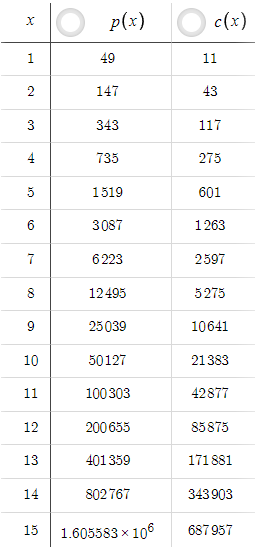
p(x)は常にc(x)より大きくなります。初心者のトレーダーは、TP=50でこれほど高いレベルのリスクリワード比が得られるのなら、なぜTP=5のままなのかと思うかもしれません。しかし、確率を考慮しなければなりません。TPを5から50に増やしたことで、価格がテイクプロフィットレベルに達する確率が大幅に減少しました。リスクとリターンの比率が良くても、テイクプロフィットに達することがない、あるいはごく稀にしか達っさないのであれば、意味がないことに気づかなければなりません。確率を考慮するためには、単なる方程式ではなく、価格データとコーディングに基づく最適化が必要です。これについては本連載で今後検討する予定です。

このDesmosグラフリンクを使用して、これらの関数のプロットを見たり、パラメータを弄って、この戦略の理解を深めることができます。

これで、最適化の数学的な部分は終了しました。次のセクションでは、現実の市場環境とそれに伴う課題を考慮しながら、この戦略を実行するための実践的な側面について掘り下げていきます。ここで確立した数学的基礎と、データ駆動型の分析および最適化技術を組み合わせることで、グリッド取引戦略をよりニーズに合ったものに改良し、収益性の可能性を最大化することができます。

結論として、前述したように、多くのパラメータが高い利益の可能性を示しています。しかし、これらの数字は主にイラストであることを理解することが重要です。この背景には、数学的最適化において不可欠な要素である「確率」が存在しないことがあります。確率を数学モデルに組み込むのは複雑な作業ですが、無視できない要素です。この問題に対処するため、価格データを使ったシミュレーションをおこない、確率を考慮した計算を可能にし、モデルの精度を向上させます。

Pythonで計算をシミュレーションする

このシミュレーションでは、p(x)とc(x)を計算し、x（注文数）に対してプロットします。p(x)とc(x)の値はy軸に、xはx軸にプロットされます。この視覚化によって、p(x)とc(x)の変化を素早く理解することができ、異なるポイントでどちらの関数が大きいかを識別するのに役立ちます。さらに、各xについてp(x)とc(x)の正確な値を表示する表を作成します。これらの値は、プロットだけでは容易に読み取れないかもしれないからです。プロットと表を組み合わせることで、p(x)とc(x)の挙動を包括的に理解することができます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

# Values of x to evaluate
x_values = range(1, 21)  # x from 1 to 20

def g(x, I_L, M):
    return np.floor(I_L * 100 * M ** x)

def s(x, I_L, M, S):
    return sum(g(i, I_L, M) * S for i in range(x))

def t(x, D, I_L, M, T_P):
    numerator = sum(i * g(i, I_L, M) for i in range(x)) * D
    denominator = sum(g(i, I_L, M) for i in range(x))
    return (numerator / denominator) - T_P

def p(x, D, I_L, M, S, T_P):
    return sum(g(i, I_L, M) * (i * D - t(x, D, I_L, M, T_P)) for i in range(x)) - s(x, I_L, M, S)

def c(x, D, I_L, M, S):
    return D * sum(g(i, I_L, M) * (x - i) for i in range(x)) + s(x, I_L, M, S)

# Calculate p(x) and c(x) for each x
p_values = [p(x, D, I_L, M, S, T_P) for x in x_values]
c_values = [c(x, D, I_L, M, S) for x in x_values]

# Formatter to avoid exponential notation
def format_func(value, tick_number):
    return f'{value:.2f}'

# Plotting
fig, axs = plt.subplots(2, 1, figsize=(12, 12))

# Combined plot for p(x) and c(x)
axs[0].plot(x_values, p_values, label='p(x)', marker='o')
axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange')
axs[0].set_title('p(x) and c(x) vs x')
axs[0].set_xlabel('x')
axs[0].set_ylabel('Values')
axs[0].set_xticks(x_values)
axs[0].grid(True)
axs[0].legend()
axs[0].yaxis.set_major_formatter(FuncFormatter(format_func))

# Create table data
table_data = [['x', 'p(x)', 'c(x)']] + [[x, f'{p_val:.2f}', f'{c_val:.2f}'] for x, p_val, c_val in zip(x_values, p_values, c_values)]

# Plot table
axs[1].axis('tight')
axs[1].axis('off')
table = axs[1].table(cellText=table_data, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.2, 1.2)

plt.tight_layout()
plt.show()

コードの説明

1. ライブラリをインポートする

   • numpy：数値演算のためにnpとしてインポート
   • matplotlib.pyplot：プロット用にpltとしてインポート
   • FuncFormatter：軸の目盛りラベルを形式するために matplotlib.tickerからインポート

2. パラメータを設定する

   • 定数D (Distance)、I_L (Initial Lot Size)、M (Lot Size Multiplier)、S (Spread)、 T_P (Take Profit)を定義

3. xの範囲を定義する

   • x_values：1から20までの整数の範囲に設定

4. 関数を定義する

   • g(x, I_L, M)：指定された式に基づいてgの値を計算
   • s(x, I_L, M, S)：0からx-1までのiについて、g(i, I_L, M) * Sの和を計算
   • t(x, D, I_L, M, T_P)：分子と分母を使用して、指定された式に基づいてtの値を計算
   • p(x, D, I_L, M, S, T_P)：指定された数式を使用して計算
   • c(x, D, I_L, M, S)：指定された数式を使用して計算

5. p(x)とc(x)の値を計算する

   • p_values：x_values内の各xに対するp(x)のリスト
   • c_values：x_values内の各xに対するc(x)のリスト

6. フォーマッターを定義する

   • format_func(value, tick_number)：Y軸の目盛ラベルを小数点以下2桁に書式設定するフォーマッター関数

7. プロッティング

   • fig, axs = plt.subplots(2, 1, figsize=(12, 12))：1つの列に配置された図と2つのサブプロットを作成

   最初のサブプロット（p(x)とc(x)の組み合わせプロット）

   • axs[0].plot(x_values, p_values, label='p(x)', marker='o')：p(x)をxに対してマーカーでプロット
   • axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange')：c(x)をxに対してオレンジ色のマーカーでプロット
   • axs[0].set_title('p(x) and c(x) vs x')：最初のサブプロットのタイトルを設定
   • axs[0].set_xlabel('x')：X軸ラベルを設定
   • axs[0].set_ylabel('Values')：Y軸ラベルを設定
   • axs[0].set_xticks(x_values)：各x値に対してx軸の目盛りが表示されるようにする
   • axs[0].grid(True)：プロットにグリッドを追加
   • axs[0].legend()：凡例を表示
   • axs[0].yaxis.set_major_formatter(FuncFormatter(format_func))：指数表記を避けるためにy軸にフォーマッターを適用

   第2のサブプロット（表）

   • table_data：列x、p(x)、c(x)と、それらに対応する値を持つテーブルデータを用意
   • axs[1].axis('tight')：表にぴったり合うようにサブプロットの軸を調整
   • axs[1].axis('off')：表サブプロットの軸をオフにする
   • table = axs[1].table(cellText=table_data, cellLoc='center', loc='center')：セルテキストが中央に配置された表を2番目のサブプロットに作成
   • table.auto_set_font_size(False)：フォントサイズの自動調整を無効にする
   • table.set_fontsize(10)：表のフォントサイズを設定
   • table.scale(1.2, 1.2)：テーブルのサイズを拡大縮小する

8. レイアウトと表示

   • plt.tight_layout()：重ならないようにレイアウトを調整
   • plt.show()：プロットと表を表示

以下のデフォルトパラメータを使用しました（異なる結果を見るために簡単に変更できます）。

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

結果

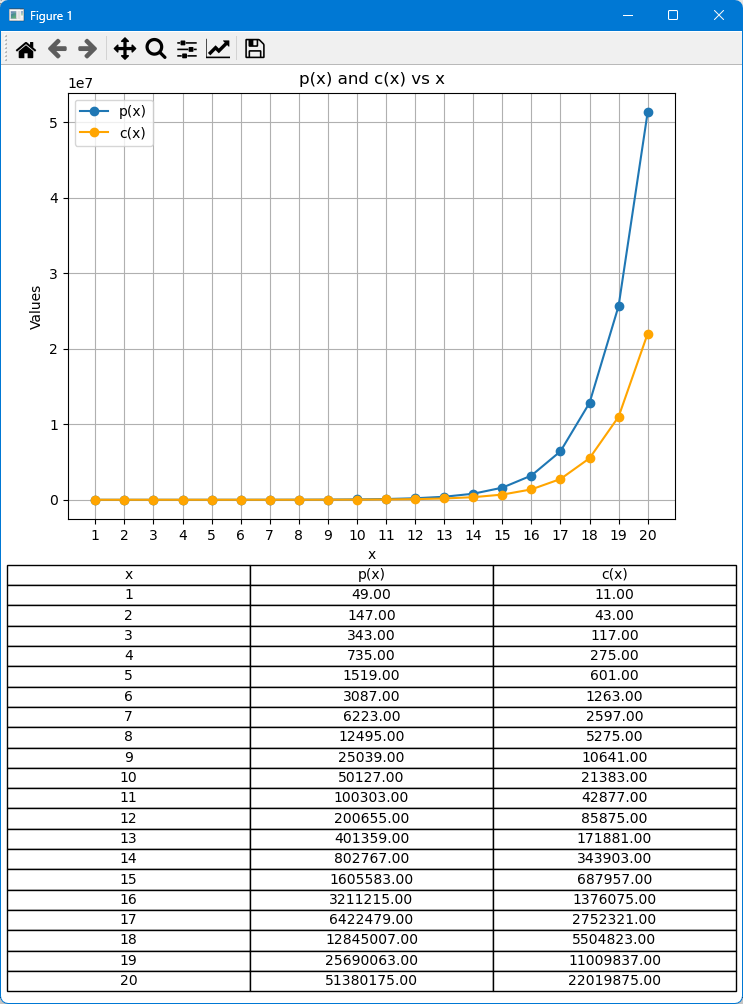
注意：上記のコードを含むPythonファイルが記事の下に添付されています。

結論

連載第4回では、グリッド戦略やヘッジ戦略で見落とされがちな確率の役割と数学的分析を通じて、シンプルグリッド戦略を最適化することに焦点を当てました。今後の記事では、理論から実践的なコードベースのアプリケーションへと移行し、トレーダーがリターンを高め、リスクを効果的に管理できるよう、洞察を実際の取引シナリオに適用していきます。皆様からの継続的なフィードバックに感謝し、共に取引戦略を探求し、洗練させ、成功させるために、さらなる交流を奨励しています。

ハッピーコーディング！ハッピー取引！