Modifizierter Grid-Hedge EA in MQL5 (Teil IV): Optimierung der einfachen Grid-Strategie (I)

Einführung

In diesem Teil unserer fortlaufenden Serie über den modifizierten Grid-Hedge EA in MQL5 befassen wir uns mit den Feinheiten des Grid EA. Aufbauend auf unseren Erfahrungen mit dem Simple Hedge EA wenden wir nun ähnliche Techniken an, um die Leistung des Grid EA zu verbessern. Unsere Reise beginnt mit einem bestehenden Grid EA, das uns als Hintergrund für die mathematische Erforschung dient. Das Ziel? Die zugrundeliegende Strategie zu sezieren, ihre Feinheiten zu entschlüsseln und die theoretischen Grundlagen aufzudecken, die ihr Verhalten bestimmen.

Aber wir sollten uns der gewaltigen Herausforderung stellen, die vor uns liegt. Die von uns durchgeführte Analyse ist vielschichtig und erfordert ein tiefes Eintauchen in mathematische Konzepte und strenge Berechnungen. Daher wäre es unpraktisch, in einem einzigen Artikel sowohl die mathematische Optimierung als auch die anschließenden codebasierten Verbesserungen zu behandeln.

Daher werden wir uns in dieser Ausgabe ausschließlich auf die mathematischen Aspekte konzentrieren. Bereiten Sie sich auf eine gründliche Untersuchung von Theorie, Formeln und numerischen Feinheiten vor. Keine Sorge, wir werden nichts unversucht lassen, um den Optimierungsprozess in seinem Kern zu verstehen.

In künftigen Artikeln werden wir uns der praktischen Seite zuwenden — der eigentlichen Codierung. Ausgestattet mit unseren theoretischen Grundlagen werden wir mathematische Erkenntnisse in praktikable Programmiertechniken umsetzen. Bleiben Sie dran, wenn wir eine Brücke zwischen Theorie und Praxis schlagen, um das volle Potenzial von Grid EA zu erschließen.

Hier ist der Plan für diesen Artikel:

1. Zusammenfassung der Grid-Strategie
2. Mathematische Optimierung
3. Simulationsberechnungen in Python
4. Schlussfolgerung

Zusammenfassung der Grid-Strategie

Lassen Sie uns die Strategie zusammenfassen. Zunächst haben wir also 2 Möglichkeiten:

In der Welt des Handels stehen wir vor zwei grundlegenden Entscheidungen:

1. Kaufen: Kaufen Sie weiter, bis ein bestimmter Punkt erreicht ist.
   
2. Verkaufen: Verkaufen Sie weiter, bis eine bestimmte Bedingung erfüllt ist.
   

Zunächst müssen wir entscheiden, ob wir einen Kauf- oder Verkaufsauftrag erteilen wollen, der von bestimmten Bedingungen abhängt. Nehmen wir an, wir entscheiden uns für einen Kaufauftrag. Wir geben den Auftrag und behalten den Markt im Auge. Wenn der Marktpreis steigt, machen wir einen Gewinn. Sobald der Kurs um einen bestimmten Betrag steigt, den wir als Ziel festlegen (in der Regel in Pips), schließen wir den Handelszyklus ab und machen Feierabend. Aber wenn wir einen neuen Zyklus beginnen wollen, können wir auch das tun.

Wenn sich nun der Kurs entgegen unseren Erwartungen bewegt und um denselben bestimmten Betrag, sagen wir „x“ Pips, fällt, reagieren wir mit einem weiteren Kaufauftrag, diesmal aber mit der doppelten Losgröße. Dieser Schritt ist strategisch, weil die Verdoppelung der Losgröße den gewichteten Durchschnittspreis auf „2x/3“ (kann leicht mathematisch berechnet werden) unter den Preis der ersten Bestellung bringt, der nur „x/3“ über der zweiten Bestellung liegt, die leicht durch den Preis konvertiert werden kann, was genau das ist, was wir wollen. Dieser neue Durchschnittswert ist unser Breakeven, an dem unser Nettogewinn gleich Null ist, wobei alle Verluste berücksichtigt werden, die wir erlitten haben.

An diesem Breakeven gibt es zwei Möglichkeiten, einen Gewinn zu erzielen:

1. Der erste Auftrag, der jetzt der obere Auftrag ist (d. h. der Auftrag, der zuerst eröffnet wurde und ein höheres Preisniveau hat), weist zunächst einen Verlust auf, da der Marktpreis unter seinem Eröffnungskurs liegt. Aber wenn der Marktpreis wieder auf den Eröffnungskurs des ersten Auftrags steigt, verringert sich der Verlust dieses Auftrags, bis er Null erreicht und weiter ins Positive geht. Das bedeutet, dass unser Nettogewinn ständig steigt.
2. Der zweite Auftrag, der mit der doppelten Losgröße erteilt wurde, wirft bereits Gewinn ab. Wenn der Marktpreis weiter steigt, steigt auch der Gewinn aus diesem Auftrag, und der Hauptvorteil ist, dass die Losgröße vervielfacht wird.
   

Dieser Ansatz unterscheidet sich von den traditionellen Hedging-Strategien, da er uns zwei Möglichkeiten zur Gewinnerzielung bietet, was uns mehr Flexibilität bei der Festlegung von Zielen ermöglicht. Wenn wir die Losgröße jeden neuen Auftrags um einen bestimmten Multiplikator erhöhen (z. B. verdoppeln), wird der Effekt der Verlustreduzierung und der Gewinnsteigerung aus dem letzten Auftrag immer deutlicher. Das liegt daran, dass der letzte Auftrag und der davor liegende Auftrag eine größere Losgröße hat, und diese Losgröße steigt weiter, wenn wir weitere Aufträge eröffnen. Wenn wir eine große Anzahl von Aufträgen ansammeln, kann der Gewinn, den wir mit jedem Pip erzielen, im Vergleich zum Hedging viel größer sein. Dies wird besonders wichtig, wenn wir später das Hedging mit dem Grid-Handel kombinieren. In einer solchen Hybridstrategie hat die Grid-Komponente das Potenzial, erhebliche Gewinne zu erzielen.

Das Beispiel mit zwei Aufträgen kann auf eine größere Anzahl von Aufträgen erweitert werden. Mit zunehmender Anzahl von Aufträgen, vor allem wenn sie in gleichmäßigen Abständen erteilt werden, sinkt der kumulierte Durchschnittspreis tendenziell. Bei Verwendung eines Multiplikators von 2 nähert sich der Durchschnittspreis, der die Gewinnschwelle darstellt, dem Eröffnungskurs des drittletzten Auftrags an. Wir werden dieses Konzept mit mathematischen Beweisen in einer späteren Diskussion untersuchen.

Wenn wir tiefer in die Komplexität dieser Handelsstrategie eintauchen, ist es wichtig zu verstehen, wie die Losgröße funktioniert und wie Kursbewegungen unsere Position beeinflussen. Indem wir unsere Aufträge strategisch verwalten und die Losgrößen anpassen, können wir die Märkte präzise steuern, von günstigen Trends profitieren und potenzielle Verluste minimieren. Die Dual-Profit-Strategie, die wir in naher Zukunft verfolgen werden, wird uns nicht nur mehr Flexibilität verschaffen, sondern auch unsere potenziellen Gewinne erhöhen und ein starkes Handelssystem schaffen, das von der Marktdynamik profitiert.

Mathematische Optimierung

Werfen wir zunächst einen Blick auf die Parameter, die wir optimieren werden, d.h. die Parameter der Strategie.

Parameter der Strategie:

1. Ausgangslage (Initial Position, IP): Die Ausgangsposition ist eine binäre Variable, die die Richtung unserer Handelsstrategie vorgibt. Ein Wert von 1 bedeutet eine Kaufaktion, d. h. wir steigen mit der Erwartung steigender Kurse in den Markt ein. Umgekehrt bedeutet ein Wert von 0 eine Verkaufsaktion, d. h. wir erwarten einen Preisrückgang. Diese erste Wahl kann ein kritischer Entscheidungspunkt sein, da sie die Gesamtausrichtung unserer Handelsstrategie bestimmt und den Ton für die nachfolgenden Aktionen angibt. Nach der Optimierung werden wir mit Sicherheit wissen, was besser zu kaufen oder zu verkaufen ist.
2. Anfangs-Losgröße (Initial Lot Size, IL): Die Anfangs-Losgröße definiert die Größe unseres ersten Auftrags innerhalb eines Handelszyklus. Sie legt die Größenordnung fest, in der wir am Markt teilnehmen werden, und schafft die Grundlage für den Umfang unserer nachfolgenden Transaktionen. Die Wahl einer angemessenen anfänglichen Losgröße ist entscheidend, da sie sich direkt auf die potenziellen Gewinne und Verluste auswirkt, die mit unseren Geschäften verbunden sind. Es ist wichtig, ein Gleichgewicht zwischen der Maximierung unseres Ertragspotenzials und der Steuerung unseres Risikos zu finden. Es hängt stark davon ab, welchen Losgrößenmultiplikator wir wählen, denn wenn der Multiplikator höher ist, sollte dieser niedriger sein, da sonst die Losgröße nachfolgender Aufträge recht schnell explodieren würde.
3. Distanz (D): Die Distanz ist ein räumlicher Parameter, der die Distanz zwischen den offenen Kursniveaus unserer Aufträge bestimmt. Sie beeinflusst die Einstiegspunkte, an denen wir unsere Trades ausführen, und spielt eine wichtige Rolle bei der Festlegung der Struktur unserer Handelsstrategie. Durch die Anpassung des Parameters Distanz können wir die Abstände zwischen unseren Aufträgen steuern und unsere Eingaben auf der Grundlage der Marktbedingungen und unserer Risikotoleranz optimieren.
4. Losgrößenmultiplikator (Lot Size Multiplier, M): Der Losgrößenmultiplikator ist ein dynamischer Faktor, der es uns ermöglicht, die Losgröße unserer Folgeaufträge in Abhängigkeit vom Verlauf des Handelszyklus zu erhöhen. Sie verleiht unserer Strategie ein gewisses Maß an Anpassungsfähigkeit und ermöglicht es uns, unser Engagement zu erhöhen, wenn sich der Markt zu unseren Gunsten entwickelt, oder es zu reduzieren, wenn wir mit ungünstigen Bedingungen konfrontiert werden. Durch die sorgfältige Auswahl des Losgrößenmultiplikators können wir unsere Positionsgröße so anpassen, dass wir gewinnbringende Gelegenheiten nutzen und gleichzeitig das Risiko kontrollieren können.
5. Anzahl der Aufträge (Number of Orders, N): Die Anzahl der Aufträge stellt die Gesamtzahl der Aufträge dar, die wir innerhalb eines einzelnen Handelszyklus/Rasterzyklus erteilen. Dabei handelt es sich nicht um einen eigentlichen Parameter der Strategie, sondern um einen Parameter, den wir bei der Optimierung der eigentlichen Parameter der Strategie berücksichtigen werden.

Es ist von entscheidender Bedeutung, die Parameter, die im Mittelpunkt unserer Optimierungsbemühungen stehen werden, genau zu kennen. Diese Parameter bilden die Grundlage, auf der wir unsere Strategie aufbauen werden, und das Verständnis ihrer Rolle und ihrer Auswirkungen ist von wesentlicher Bedeutung, um fundierte Entscheidungen zu treffen und die gewünschten Ergebnisse zu erzielen.

Der Einfachheit halber stellen wir diese Parameter in ihrer Grundform dar. Es ist jedoch wichtig zu wissen, dass einige dieser Variablen in mathematischen Gleichungen mit tiefgestellten Buchstaben bezeichnet werden, um sie von anderen Variablen zu unterscheiden.

Diese Parameter dienen als Grundlage für die Konstruktion unserer Gewinnfunktion. Die Gewinnfunktion ist eine mathematische Darstellung dessen, wie unser Gewinn (oder Verlust) durch Veränderungen dieser Variablen beeinflusst wird. Sie ist ein wesentlicher Bestandteil unseres Optimierungsprozesses, der es uns ermöglicht, die Ergebnisse verschiedener Handelsstrategien unter verschiedenen Szenarien quantitativ zu bewerten.

Mit diesen Parametern können wir nun die Komponenten unserer Gewinnfunktion definieren:

Berechnen wir die Gewinnfunktion für ein vereinfachtes Szenario, bei dem wir uns für den Kauf entscheiden und nur zwei Aufträge haben. Wir gehen davon aus, dass der Losgrößenmultiplikator 1 ist, d. h. beide Aufträge haben die gleiche Losgröße von 0,01.

Um die Gewinnfunktion zu ermitteln, müssen wir zunächst Breakeven bestimmen. Nehmen wir an, wir haben zwei Kaufaufträge, B1 und B2. B1 wird zum Preis 0 platziert, und B2 wird in einem Abstand D unter B1 platziert, d. h. zum Preis -D. (Beachten Sie, dass der negative Preis hier nur zu Analysezwecken verwendet wird und keinen Einfluss auf das Ergebnis hat, da die Analyse vom Abstandsparameter D und nicht vom genauen Preisniveau abhängt).

Nehmen wir nun an, Breakeven liegt in einem Abstand x unterhalb von B1. Zu diesem Zeitpunkt haben wir einen Verlust von -x Pips aus B1 und einen Gewinn von +x Pips aus B2.

Wenn die Losgrößen gleich sind (d. h. der Losgrößenmultiplikator ist 1), liegt Breakeven genau in der Mitte der beiden Aufträge. Wenn die Losgrößen jedoch unterschiedlich sind, müssen wir den Losgrößenmultiplikator berücksichtigen.

Wenn der Losgrößenmultiplikator beispielsweise 2 ist und die anfängliche Losgröße 0,01 beträgt, dann hat B1 eine Losgröße von 0,01 und B2 eine Losgröße von 0,02.

Um in diesem Fall Breakeven zu finden, müssen wir den Wert von x durch Lösen der folgenden Gleichung ermitteln:

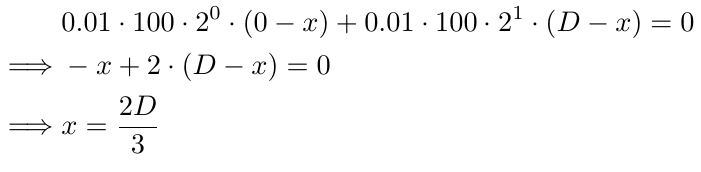
Analysieren wir die Bestandteile der Gleichung. Die anfängliche Losgröße, 0,01, wird in jedem Teil der Gleichung wiederholt (der zweite Teil bezieht sich auf den Teil nach dem + Zeichen). Wir multiplizieren dies mit 100, um die Losgröße in eine ganze Zahl umzuwandeln, und da wir diese Umwandlung in allen Gleichungen einheitlich anwenden, behält sie ihre Bedeutung. Anschließend multiplizieren wir sie mit 2^0 im ersten Teil und 2^1 im zweiten Teil. Diese Terme stellen den Multiplikator für die Losgröße dar, wobei die Potenz für die anfängliche Losgröße bei 0 beginnt und für jeden nachfolgenden Auftrag um 1 erhöht wird. Schließlich verwenden wir (0-x) im ersten Teil, (D-x) im zweiten Teil und ((i-1)D-x) im i-ten Teil, weil der i-te Auftrag (i-1) mal D Pips unter B1 platziert wird. Die Lösung der Gleichung für x ergibt 2D/3, was bedeutet, dass Breakeven 2D/3 Pips unter B1 liegt (wie durch x in unseren Gleichungen definiert). Wenn D 10 ist, wäre der Breakeven 6,67 Pips unter B1 oder 3,34 Pips über B2. Es ist wahrscheinlicher, dass dieses Preisniveau erreicht wird als der Breakeven bei B1 (wenn wir nur einen Auftrag hätten). Das ist das Kernkonzept der Griding-Strategie: frühere Aufträge aufstocken, bis ein Gewinn erzielt wird.

Betrachten wir nun einen Fall mit 3 Aufträgen.

Bei 3 Aufträgen verfolgen wir den gleichen Ansatz. Die Erklärung für den 1. und 2. Teil bleibt dieselbe. Im 3. Teil gibt es zwei Änderungen: Die Potenz von 2 wird um 1 erhöht, und D wird nun mit 2 multipliziert. Alles andere bleibt unverändert.

Auflösen nach x:

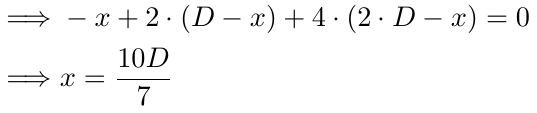
Im Fall des 3. Auftrags stellen wir fest, dass der Breakeven eintritt, wenn der Kurs 10D/7 Pips unter B1 liegt. Wenn D 10 ist, liegt der Breakeven 14,28 Punkte unter B1, 4,28 Punkte unter B2 und 5,72 Punkte über B3. Auch hier ist es wahrscheinlicher, dass der Preis diesen Punkt erreicht, als den Breakeven bei B1 (mit 1 Auftrag) oder den vorherigen Breakeven. Der Breakeven bewegt sich weiter nach unten, wodurch die Wahrscheinlichkeit steigt, dass der Preis ihn erreicht, und unsere vorherigen Aufträge werden effektiv unterstützt, wenn sich der Preis gegen uns entwickelt.

Verallgemeinern wir die Formel für n Aufträge.

Anmerkung: Wir gehen davon aus, dass alle Positionen Kaufaufträge sind. Die Analyse für Verkaufsaufträge ist symmetrisch, also können wir es einfach halten.

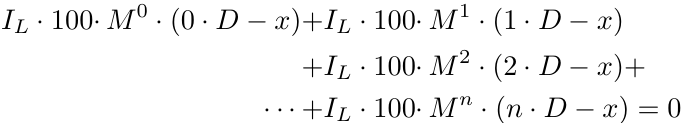
Es stellt sich jedoch heraus, dass diese Verallgemeinerung falsch ist.

Der Grund dafür lässt sich anhand eines einfachen Beispiels erklären. Nehmen wir an, die anfängliche Losgröße sei 0,01 und der Multiplikator 1,5. Zunächst eröffnen wir eine Position mit einer Losgröße von 0,01. Dann eröffnen wir eine zweite Position mit einer Losgröße von 0,01 * 1,5 = 0,015. Nach der Rundung ergibt sich jedoch 0,01, da die Losgröße ein Vielfaches von 0,01 sein muss. Hier gibt es zwei Probleme:

1. Die Gleichung geht von der Eröffnung einer Position mit einer Losgröße von 0,015 aus, was praktisch nicht möglich ist. Stattdessen eröffnen wir eine Position mit einer Losgröße von 0,01.
2. Dieser Punkt ist nicht wirklich ein Problem, sondern eher etwas, das beachtet werden muss. Betrachten wir das gleiche Beispiel. Der erste Auftrag war 0,01, und die zweite Auftrag war aus praktischen Gründen ebenfalls 0,01. Wie groß sollte die Losgröße für den dritten Auftrag sein? Wir multiplizieren den Losgrößenmultiplikator mit der Losgröße des letzten Auftrags, aber sollten wir 1,5 mit 0,01 oder 0,015 multiplizieren? Wenn wir mit 0,01 multiplizieren, bleiben wir in einer Schleife stecken, die den Sinn eines Multiplikators zunichte macht. Wir gehen also von 0,015 * 1,5 = 0,0225 aus, was praktisch zu 0,02 wird, und so weiter.

Wie bereits erwähnt, ist der zweite Punkt nicht wirklich ein Problem. Lösen wir das erste Problem mit Hilfe des größten, ganzen Faktors (Greatest Integer Factor, GIF) oder der Floor-Funktion in der Mathematik, die besagt, dass wir einfach den Dezimalteil von jeder positiven Zahl entfernen (wir gehen nicht ins Detail für negative Zahlen, da die Losgröße nicht negativ sein kann). Notation: floor(.) oder [.]. Beispiele: floor(1.5) = [1.5] = 1; floor(5.12334) = [5.12334] = 5; floor(2.25) = [2.25] = 2; floor(3.375) = [3.375] = 3.

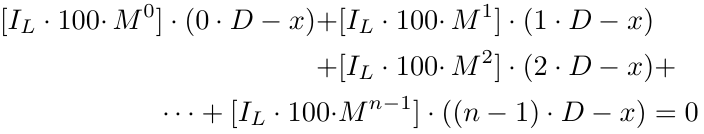
wobei [.] für GIF, d. h. Greatest Integer Factor (größter ganzer Faktor), steht. Wenn man weiter auflöst, erhält man:

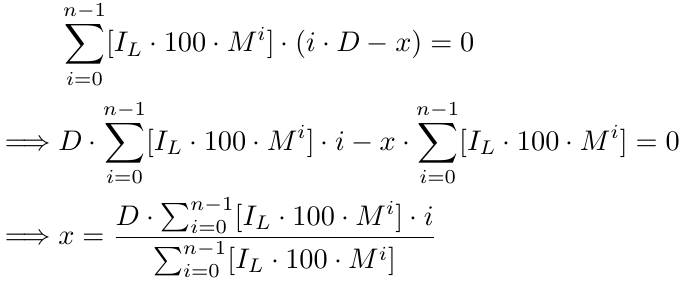
Formal ausgedrückt: Für eine Anzahl von x Aufträgen gibt es eine Breakeven-Funktion b(x),

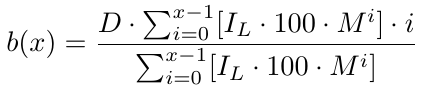
Jetzt haben wir eine Breakeven-Funktion, die uns den Breakeven-Preis liefert. Sie gibt an, wie viele Pips unter B1 der Breakeven-Preis liegt. Mit dem Breakeven-Preis müssen wir das Take-Profit-Niveau (TP) bestimmen, das einfach TP-Punkte über dem b(x) liegt. Da b(x) das B1-Preisniveau abzüglich des Breakeven-Preisniveaus ist, müssen wir, um das Take-Profit-Niveau zu ermitteln, TP von b(x) abziehen. Damit haben wir unser Take-Profit-Niveau, das wir als t(x) bezeichnen:

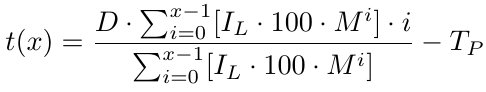
Bei x, d.h. der Anzahl der Aufträge, haben wir unser Take-Profit-Niveau. Nun müssen wir den Gewinn für x berechnen. Lassen Sie uns versuchen, die Gewinnfunktion zu finden.

Angenommen, der Kurs erreicht t(x), d. h. das Take-Profit-Niveau, und der Zyklus schließt sich, dann ist der Gewinn/Verlust, den wir von B1 erhalten, das Kursniveau von B1 minus t(x), wobei die Einheit Pips ist. Ein negativer Wert bedeutet, dass wir einen Verlust haben, während ein positiver Wert bedeutet, dass wir einen Gewinn haben. In ähnlicher Weise ist der Gewinn/Verlust, den wir von B2 erhalten, das Preisniveau von B2 minus t(x), mit Pips als Einheit, und wir wissen, dass das B2-Preisniveau genau D Pips unter dem B1-Preisniveau liegt. Für B3 ist der Gewinn/Verlust das Preisniveau von B3 minus t(x), mit Pips als Einheit, und wir wissen, dass das B3-Preisniveau genau 2 mal D Pips unter dem B1-Preisniveau liegt. Beachten Sie, dass wir auch die anfängliche Losgröße und den Losgrößenmultiplikator berücksichtigen müssen.

Mathematisch gesehen ergibt sich für x (d. h. die Anzahl der Aufträge ist 3) Folgendes:

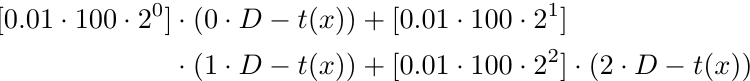
Formal ausgedrückt: Für eine Anzahl von x Aufträgen haben wir eine Gewinnfunktion p(x):

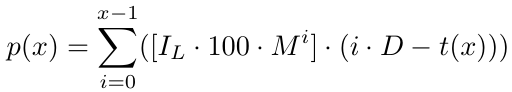
Wir wollen verstehen, was das bedeutet. Bei einer beliebigen Anzahl von Aufträgen und unter der Annahme, dass sich der Zyklus nach x Aufträgen schließt (wobei „schließt“ bedeutet, dass wir das Take-Profit-Niveau erreichen), erzielen wir einen Gewinn, der durch die obige Gleichung p(x) gegeben ist. Nachdem wir nun die Gewinnfunktion haben, wollen wir versuchen, die Kostenfunktion zu berechnen, die sich auf den Verlust bezieht, den wir erleiden, wenn wir einen Grid-Zyklus mit x Aufträgen verlieren (wobei „verlieren“ bedeutet, dass wir keine weiteren Aufträge eröffnen können, um den Grid-Zyklus fortzusetzen, da die Grid-Strategie eine Menge Investitionen erfordert oder aus einem anderen Grund).

Die Kostenfunktion würde wie folgt aussehen: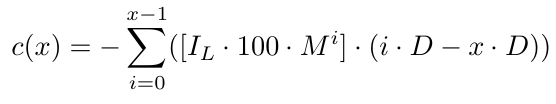

In dieser Gleichung berücksichtigt der [.]-Teil die anfängliche Losgröße und den Losgrößenmultiplikator. Der andere Teil (i.D-x.D) berücksichtigt x.D, d.h. den Abstand zwischen dem Preisniveau B1 und D Pips unter dem Auftrag mit dem niedrigsten Preis. Wir verwenden x.D, weil wir genau an dieser Stelle einen neuen Auftrag eröffnen. Wenn wir aus irgendeinem Grund, höchstwahrscheinlich wegen unzureichender Mittel, den Zyklus nicht fortsetzen können, ist das genau der Punkt, an dem wir mit Sicherheit sagen können, dass wir den Zyklus nicht fortsetzen konnten, wenn wir den Auftrag nicht zu diesem Preisniveau eröffnen können (wenn der Preis dieses Niveau erreicht). Wenn wir also mit Sicherheit wissen, dass wir den Zyklus nicht fortsetzen konnten, liegt das Kursniveau x.D Pips unter dem B1-Kursniveau. Daraus ergibt sich ein Verlust von (0.D-x.D) bei dem Auftrag B1, (1.D-x.D) bei dem Auftrag B2 und so weiter bis zum letzten Auftrag, des Auftrags Bx, bei der ein Verlust von ((x-1).D-x.D)=-D entsteht. Dies ist sinnvoll, da wir D Pips unter dem letzten Auftrag liegen (dem Auftrag mit dem niedrigsten Preisniveau).

Formal ausgedrückt: Für eine Anzahl von x Aufträgen gibt es eine Kostenfunktion c(x),

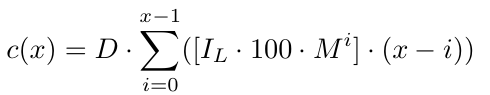
Wir müssen auch den Spread berücksichtigen, den wir der Einfachheit halber als konstanten Spread annehmen, da die Ermittlung eines dynamischen Spreads recht komplex wäre. Nehmen wir an, S ist der statische Spread, den wir für EURUSD bei 1-1,5 belassen. Der Spread kann sich je nach Währungspaar ändern, aber diese Strategie funktioniert am besten mit Währungen, die eine geringere Volatilität aufweisen, wie EURUSD.

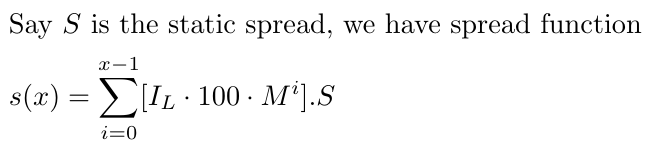
Es ist wichtig anzumerken, dass unsere Anpassung alle Handelsgeschäfte berücksichtigt, von Null bis x-1, da der Spread jedes Geschäft beeinflusst, ob profitabel oder nicht. Der Einfachheit halber behandeln wir den Spread (bezeichnet als S) derzeit als konstanten Wert. Diese Entscheidung wurde getroffen, um unsere mathematische Analyse nicht durch die zusätzliche Variabilität eines schwankenden Spreads zu erschweren. Diese Vereinfachung schränkt zwar die Realitätsnähe unseres Modells ein, ermöglicht es uns aber, uns auf die Kernaspekte unserer Strategie zu konzentrieren, ohne uns durch übermäßige Komplexität zu verzetteln.

Da wir nun alle notwendigen Funktionen haben, können wir sie in Desmos darstellen.

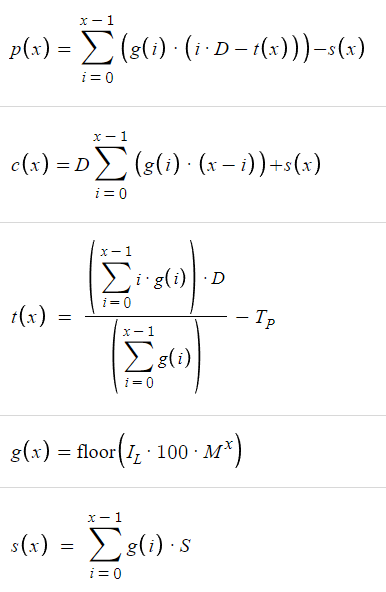
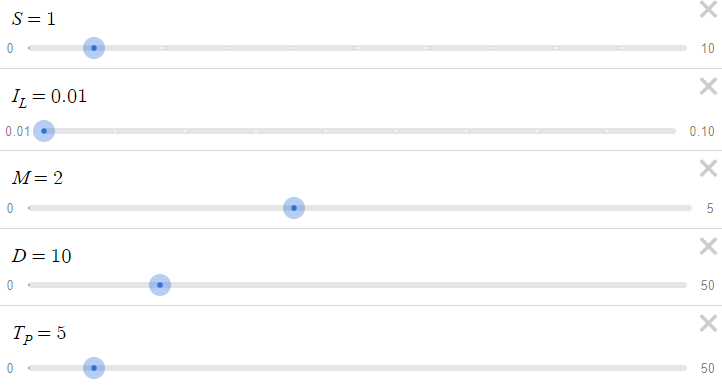
Ausgehend von den oben genannten Parametern ergibt sich die folgende Tabelle, in der eine Änderung von x unterschiedliche Werte für p(x) und c(x) ergibt:

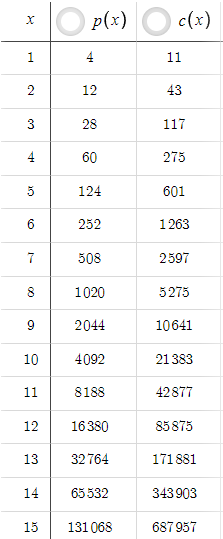
In diesem Szenario ist p(x) immer kleiner als c(x), aber das lässt sich leicht ändern, indem man den TP erhöht. Wenn wir zum Beispiel den TP von 5 auf 50 erhöhen:

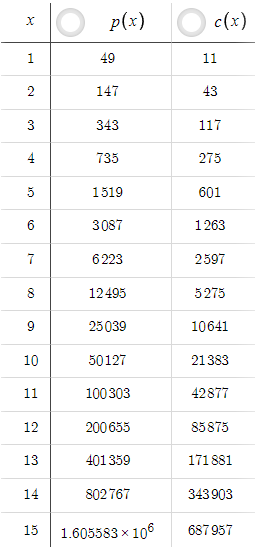
Nun ist p(x) immer größer als c(x). Ein unerfahrener Trader könnte denken, wenn wir mit TP=50 ein so hohes Risiko-Ertrags-Verhältnis erzielen können, warum dann TP=5 beibehalten? Wir müssen jedoch die Wahrscheinlichkeit berücksichtigen. Die Erhöhung des TP von 5 auf 50 hat die Wahrscheinlichkeit, dass der Kurs das Take-Profit-Niveau erreicht, drastisch verringert. Wir müssen uns darüber im Klaren sein, dass ein gutes Chance-Risiko-Verhältnis keinen Sinn macht, wenn wir den Take Profit nie oder nur sehr selten erreichen. Um Wahrscheinlichkeiten zu berücksichtigen, benötigen wir Preisdaten und eine auf Kodierung basierende Optimierung und nicht nur Gleichungen, die wir in weiteren Teilen der Serie untersuchen werden.

Sie können diesen Link zu Desmos Graph verwenden, um die Darstellung dieser Funktionen zu sehen und mit den Parametern zu spielen, um ein besseres Verständnis dieser Strategie zu erlangen.

Damit haben wir den mathematischen Teil der Optimierung abgeschlossen. In den nächsten Abschnitten werden wir uns eingehender mit den praktischen Aspekten der Umsetzung dieser Strategie befassen und dabei die realen Marktbedingungen und die damit verbundenen Herausforderungen berücksichtigen. Durch die Kombination der mathematischen Grundlage, die wir hier geschaffen haben, mit datengesteuerten Analyse- und Optimierungstechniken können wir die Grid-Handelsstrategie verfeinern, um sie besser an unsere Bedürfnisse anzupassen und ihr Rentabilitätspotenzial zu maximieren.

Abschließende Überlegungen: Wie bereits erwähnt, deuten zahlreiche Parameter auf ein hohes Gewinnpotenzial hin. Es ist jedoch wichtig zu verstehen, dass diese Zahlen in erster Linie zur Veranschaulichung dienen. Der Grund dafür ist das Fehlen einer wichtigen Komponente in der mathematischen Optimierung: die Wahrscheinlichkeit. Die Einbeziehung der Wahrscheinlichkeit in unser mathematisches Modell ist eine komplexe Aufgabe, aber sie ist ein unverzichtbarer Faktor, der nicht ignoriert werden darf. Um dieses Problem zu lösen, werden wir Simulationen mit Preisdaten durchführen, die es uns ermöglichen, Wahrscheinlichkeiten in unseren Berechnungen zu berücksichtigen und die Genauigkeit unseres Modells zu verbessern.

Simulationsberechnungen in Python

In dieser Simulation werden wir p(x) und c(x) in Abhängigkeit von x berechnen und aufzeichnen, wobei x die Anzahl der Aufträge darstellt. Die Werte von p(x) und c(x) werden auf der y-Achse aufgetragen, während x auf der x-Achse liegt. Diese Visualisierung ermöglicht einen schnellen Einblick in die Veränderungen von p(x) und c(x) und hilft dabei, zu erkennen, welche Funktion an verschiedenen Punkten größer ist. Zusätzlich werden wir eine Tabelle erstellen, die die genauen Werte von p(x) und c(x) für jedes x anzeigt, da diese Werte aus dem Diagramm allein möglicherweise nicht leicht ablesbar sind. Diese Kombination aus Diagramm und Tabelle ermöglicht ein umfassendes Verständnis des Verhaltens von p(x) und c(x).

Python-Code:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

# Values of x to evaluate
x_values = range(1, 21)  # x from 1 to 20

def g(x, I_L, M):
    return np.floor(I_L * 100 * M ** x)

def s(x, I_L, M, S):
    return sum(g(i, I_L, M) * S for i in range(x))

def t(x, D, I_L, M, T_P):
    numerator = sum(i * g(i, I_L, M) for i in range(x)) * D
    denominator = sum(g(i, I_L, M) for i in range(x))
    return (numerator / denominator) - T_P

def p(x, D, I_L, M, S, T_P):
    return sum(g(i, I_L, M) * (i * D - t(x, D, I_L, M, T_P)) for i in range(x)) - s(x, I_L, M, S)

def c(x, D, I_L, M, S):
    return D * sum(g(i, I_L, M) * (x - i) for i in range(x)) + s(x, I_L, M, S)

# Calculate p(x) and c(x) for each x
p_values = [p(x, D, I_L, M, S, T_P) for x in x_values]
c_values = [c(x, D, I_L, M, S) for x in x_values]

# Formatter to avoid exponential notation
def format_func(value, tick_number):
    return f'{value:.2f}'

# Plotting
fig, axs = plt.subplots(2, 1, figsize=(12, 12))

# Combined plot for p(x) and c(x)
axs[0].plot(x_values, p_values, label='p(x)', marker='o')
axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange')
axs[0].set_title('p(x) and c(x) vs x')
axs[0].set_xlabel('x')
axs[0].set_ylabel('Values')
axs[0].set_xticks(x_values)
axs[0].grid(True)
axs[0].legend()
axs[0].yaxis.set_major_formatter(FuncFormatter(format_func))

# Create table data
table_data = [['x', 'p(x)', 'c(x)']] + [[x, f'{p_val:.2f}', f'{c_val:.2f}'] for x, p_val, c_val in zip(x_values, p_values, c_values)]

# Plot table
axs[1].axis('tight')
axs[1].axis('off')
table = axs[1].table(cellText=table_data, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.2, 1.2)

plt.tight_layout()
plt.show()

Code-Erläuterung:

1. Bibliotheken importieren:

   • numpy wird als np für numerische Operationen importiert.
   • matplotlib.pyplot wird als plt zum Zeichnen importiert.
   • FuncFormatter wird aus matplotlib.ticker importiert, um Achsenbeschriftungen zu formatieren.

2. Parameter einstellen:

   • Wirt definieren die Konstanten D, I_L, M, S und T_P , die für den Distanz, die anfängliche Losgröße, den Losgrößenmultiplikator, den Spread bzw. den Take-Profit stehen.

3. Definieren des Bereichs für x:

   • x_values ist auf einen Bereich von ganzen Zahlen von 1 bis 20 festgelegt.

4. Definieren der Funktionen:

   • g(x, I_L, M): Berechnet den Wert von g auf der Grundlage der angegebenen Formel.
   • s(x, I_L, M, S): Berechnet die Summe von g(i, I_L, M) * S für i von 0 bis x-1.
   • t(x, D, I_L, M, T_P): Berechnet den Wert von t auf der Grundlage der angegebenen Formel unter Verwendung eines Zählers und eines Nenners.
   • p(x, D, I_L, M, S, T_P): Berechnet p(x) anhand der angegebenen Formel.
   • c(x, D, I_L, M, S): Berechnet c(x) anhand der angegebenen Formel.

5. Berechnen der Werte von p(x) und c(x):

   • p_values ist eine Liste von p(x)für jedes xin x_values.
   • c_valuesisteine Liste von c(x) für jedes xin x_values.

6. Definieren der Formatierung:

   • format_func(wert, tick_number): Definiert eine Formatierungsfunktion zum Formatieren von y-Achsenbeschriftungen mit zwei Dezimalstellen.

7. Zeichnen:

   • fig, axs = plt.subplots(2, 1, figsize=(12, 12)): Erzeugt eine Abbildung und zwei Teilflächen, die in einer einzigen Spalte angeordnet sind.

   Erster Subplot (Kombinierte Zeichnung von p(x) und c(x)):

   • axs[0].plot(x_values, p_values, label='p(x)', marker='o'): Stellt p(x) gegen x mit Markierungen dar.
   • axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange'): Zeichnet c(x) gegen x mit orangefarbenen Markierungen.
   • axs[0].set_title('p(x) and c(x) vs x'): Legt den Titel der ersten Teilhandlung fest.
   • axs[0].set_xlabel('x'): Legt die Beschriftung der x-Achse fest.
   • axs[0].set_ylabel('Values'): Legt die Beschriftung der y-Achse fest.
   • axs[0].set_xticks(x_values): Stellt sicher, dass für jeden x-Wert ein Häkchen auf der x-Achse angezeigt wird.
   • axs[0].grid(True): Fügt dem Diagramm ein Gitter hinzu.
   • axs[0].legend(): Zeigt die Legende an.
   • axs[0].yaxis.set_major_formatter(FuncFormatter(format_func)): Wendet das Formatierungsverfahren auf die y-Achse an, um eine exponentielle Schreibweise zu vermeiden.

   Zweite Teilfläche (Tabelle):

   • table_data: Bereitet Tabellendaten mit den Spalten x , p(x) und c(x) und ihren entsprechenden Werten vor.
   • axs[1].axis('tight'): Passt die Subplot-Achse so an, dass sie genau in die Tabelle passt.
   • axs[1].axis('off'): Schaltet die Achse für den Tabellen-Subplot aus.
   • table = axs[1].table(cellText=table_data, cellLoc='center', loc='center'): Erstellt eine Tabelle im zweiten Subplot mit zentriertem Zellentext.
   • table.auto_set_font_size(False): Deaktiviert die automatische Anpassung der Schriftgröße.
   • table.set_fontsize(10): Legt die Schriftgröße der Tabelle fest.
   • table.scale(1.2, 1.2): Skaliert die Größe der Tabelle.

8. Layout und Anzeige:

   • plt.tight_layout(): Passt das Layout an, um Überschneidungen zu vermeiden.
   • plt.show(): Zeigt die Diagramme und die Tabelle an.

Wir haben die folgenden Standardparameter verwendet (die leicht geändert werden können, um die verschiedenen Ergebnisse zu sehen):

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

Ergebnis:

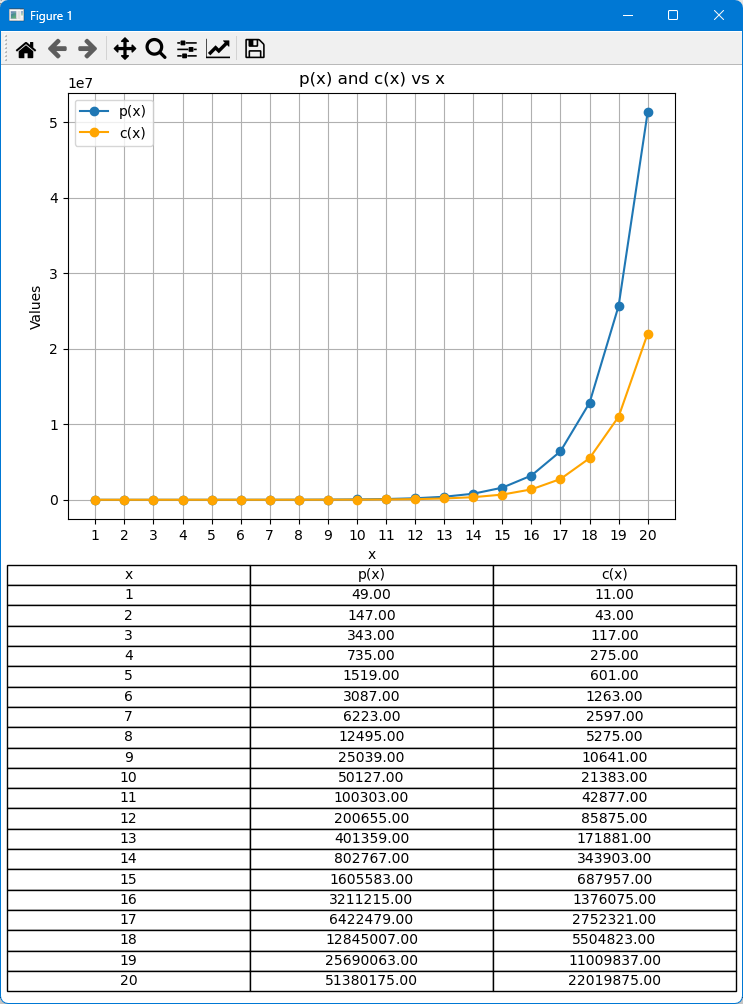
Hinweis: Eine Python-Datei, die den oben beschriebenen Code enthält, ist am Ende des Artikels angehängt.

Schlussfolgerung

Im vierten Teil unserer Serie haben wir uns auf die Optimierung der Simple-Grid-Strategie durch mathematische Analyse und die Rolle der Wahrscheinlichkeit konzentriert, die bei Grid- und Hedging-Strategien oft übersehen wird. Künftige Artikel werden von der Theorie zu praktischen, codebasierten Anwendungen übergehen und unsere Erkenntnisse auf reale Handelsszenarien anwenden, um Händlern zu helfen, ihre Rendite zu steigern und Risiken effektiv zu verwalten. Wir freuen uns über Ihr kontinuierliches Feedback und ermutigen Sie zur weiteren Interaktion, während wir gemeinsam Handelsstrategien erforschen, verfeinern und erfolgreich umsetzen.

Viel Spaß beim Coding! Viel Spaß beim Handeln!