Модифицированный советник Grid-Hedge в MQL5 (Часть IV): Оптимизация простой сеточной стратегии (I)

Введение

В новой статье из нашей серии, посвященной модифицированному советнику Grid-Hedge на MQL5, мы углубимся в тонкости работы советника Grid. Основываясь на опыте работы с экспертом Simple Hedge EA, в этот раз мы применим аналогичные методы для улучшения эффективности советника Grid EA. Начнем работу с уже существующего эксперта Grid EA, на основе которого и будем проводить математические исследования. Цель? Разобрать базовую стратегию, разобраться в ее тонкостях и раскрыть теоретические основы, определяющие ее поведение.

Однако надо признать, что нас ждет сложная задача. Мы будем проводить анализ с разных перспектив, при этом он требует глубокого погружения в математические концепции и строгих расчетов. И было бы нецелесообразно пытаться охватить в одной статье как математическую оптимизацию, так и последующие улучшения по коду.

Поэтому в этой части мы сосредоточимся исключительно на математических аспектах. Что вас ждет: теории, формулы и тонкости расчетов. Не переживайте, если это сейчас кажется сложным. Мы постараемся рассмотреть максимально подробно процесс оптимизации.

В будущих статьях мы перейдем к практической стороне — непосредственно к написанию кода. На основе полученной теоретической базы мы преобразуем математические идеи в практические методы программирования. Поэтому будьте внимательны и следите за статьями, чтобы объединить теорию и практику и раскрыть весь потенциал советника Grid EA.

План этой статьи:

1. Обзор стратегии Grid
2. Математическая оптимизация
3. Моделирование вычислений на Python
4. Заключение

Обзор стратегии Grid

Давайте кратко рассмотрим суть стратегии. Итак, для начала у нас есть 2 варианта:

В мире трейдинга мы имеем дела с двумя основными вариантами выбора:

1. Покупка — покупаем, пока не будет достигнута определенная точка.
   
2. Продажа — продаем, пока не будет выполнено определенное условие.
   

Прежде всего, нам необходимо решить, размещать ли ордер на покупку или продажу, в зависимости от определенных условий. Допустим, мы размещаем ордер на покупку. Мы устанавливаем ордер и следим за рынком. Если рыночная цена растет, мы получаем прибыль. Как только цена вырастет на определенную величину и достигнет нашей цели (обычно измеряемой в пунктах), мы завершаем торговый цикл и закрываем ордер. Если же нужно начать новый цикл, можно сделать и это.

Теперь, если цена движется против наших ожиданий и падает на ту же определенную величину, скажем, x пунктов, мы в ответ размещаем еще один ордер на покупку, но на этот раз с удвоенным размером лота. Этот шаг является стратегическим, поскольку удвоение размера лота снижает средневзвешенную цену до 2x/3 (что можно легко рассчитать математически) ниже первоначальной цены ордера, которая всего на x/3 выше второго ордера. Это можно легко преобразовать по цене, а это именно то, что нам нужно. Полученное новое среднее значение и есть наша точка безубытка, при которой наша чистая прибыль равна нулю, принимая во внимание все понесенные нами убытки.

В этой точке безубытка у нас есть два способа получить прибыль:

1. Первый ордер, который теперь является верхним (имеется в виду ордер, который был открыт первым и имеет более высокий уровень цены), изначально показывает убыток, поскольку рыночная цена ниже цены его открытия. Но по мере того, как рыночная цена снова поднимается до цены открытия первого ордера, убыток по этому ордеру уменьшается, пока не достигнет нуля, и далее становится положительным. Это означает, что наша чистая прибыль продолжает расти.
2. Второй ордер, размещенный с удвоенным размером лота, уже приносит прибыль. Поскольку рыночная цена продолжает расти, прибыль от этого ордера также увеличивается, и главным плюсом является то, что размер лота здесь увеличен.
   

Этот подход отличается от традиционных стратегий хеджирования, поскольку он дает нам два пути получения прибыли, что обеспечивает большую гибкость в постановке целей. Если продолжать увеличивать размер лота каждого нового ордера на определенный множитель (скажем, удваивать его), эффект снижения убытков и увеличения прибыли от последнего ордера станет все более значимым. Это связано с тем, что последний и предпоследний ордера имеют больший размер лота, и этот размер лота продолжает увеличиваться по мере того, как мы открываем больше ордеров. Если накопить достаточное количество ордеров, прибыль, которую можно получить с каждого пункта, может быть намного больше по сравнению с хеджированием. Обратите на это внимание — это важно, когда мы объединяем хеджирование с сеточной торговлей. В такой гибридной стратегии сеточный компонент имеет потенциал для получения значительной прибыли.

Приведенный пример с двумя ордерами можно распространить на большее количество ордеров. По мере увеличения количества ордеров, особенно если они размещаются через равные промежутки времени, совокупная средняя цена имеет тенденцию к снижению. При использовании множителя 2 средняя цена, представляющая собой точку безубытка, стремится к цене открытия пред-предпоследнего ордера. Далее в обсуждении мы рассмотрим эту концепцию с помощью математических доказательств.

По мере того, как мы глубже погружаемся в сложности этой торговой стратегии, крайне важно понимать, как в ней работает размер лота и как движение цены влияет на нашу позицию. Цель стратегии — стратегически управлять ордерами и размером лота, использовать благоприятные тренды и минимизировать потенциальные убытки. Стратегия двойной прибыли, которую мы реализуем в ближайшем будущем, не только даст больше гибкости, но и увеличит потенциальную прибыль, создав надежную торговую систему, которая работает за счет динамики рынка.

Математическая оптимизация

Для начала рассмотрим параметры, которые мы будем оптимизировать, т.е. параметры стратегии.

Параметры стратегии:

1. Initial Position (IP) — стартовая позиция, бинарная переменная, которая задает направление торговой стратегии. Значение 1 означает покупку, то есть мы выходим в рынок в ожидании роста цен. Значение 0 означает продажу, предполагается, что мы ожидаем снижения цен. Этот первый выбор может оказаться решающим моментом, поскольку он определяет общую направленность торговой стратегии и задает тон для последующих действий. Оптимизация должна помочь определить точно, что лучше купить или продать.
2. Initial Lot Size (IL) — начальный лот, размер первого ордера в торговом цикле. Он устанавливает масштаб нашего участия в рынке и закладывает основу для размера наших последующих сделок. Выбор правильного размера начального лота имеет решающее значение, поскольку он напрямую влияет на потенциальную прибыли и убытки от наших сделок. Крайне важно найти баланс между максимизацией потенциальной прибыли и управлением рисками. Это во многом зависит от того, какой множитель размера лота мы выберем: если множитель выше, то этот показатель должен быть ниже, иначе размер лота последующих ордеров довольно быстро увеличится.
3. Distance (D) — расстояние между уровнями цен открытия ордеров. Он определяет точки входа, в которых мы будем совершать сделки, и тем самым по сути определяет всю структуру нашей торговой стратегии. Регулируя параметр Distance, мы можем контролировать расстояние между ордерами и оптимизировать входы в зависимости от рыночных условий и допустимого риска.
4. Lot Size Multiplier (M) — множитель лота, динамический коэффициент, который увеличивает размер лота для последующих ордеров в зависимости от хода торгового цикла. Он вводит определенную степень адаптивности нашей стратегии, позволяя увеличивать объем инвестиций по мере того, как рынок движется в благоприятном направлении, или уменьшать его при возникновении неблагоприятных условий. Тщательно выбирая множитель размера лота, можно адаптировать размер позиции для извлечения выгоды из прибыльных возможностей и управления рисками.
5. Number of Orders (N) — общее количество ордеров, размещаемых в одном торговом цикле, т.е. в одном цикле сетки. Это не совсем параметр стратегии, а скорее параметр, который мы будем учитывать при оптимизации реальных параметров стратегии.

Дальнейшая работа по оптимизации будет направлена именно на эти параметры, поэтому важно в них разобраться. Вообще эти параметры служат основой, на которой мы будем строить стратегию, искать оптимальные варианты торговых решений для получения желаемых результатов.

Для простоты представим эти параметры в основных формах. Однако важно отметить, что в математических уравнениях некоторые из этих переменных обозначаются с помощью нижних индексов, чтобы отличать их от других переменных.

Функция прибыли будет строиться на основе этих параметров. Функция прибыли — это математическое представление того, как изменения переменных влияют на нашу прибыль (или убыток). Это важнейший компонент процесса оптимизации, позволяющий количественно оценивать результаты различных торговых стратегий при разных сценариях.

Теперь давайте перейдем к определению компонентов нашей функции прибыли:

Рассчитаем функцию прибыли для упрощенного сценария, когда мы решаем войти с покупкой и только двумя ордерами. Предположим, что множитель размера лота равен 1, то есть оба ордера имеют одинаковый размер лота — 0,01.

Чтобы найти функцию прибыли, сначала нужно определить точку безубытка. Допустим, у нас есть два ордера на покупку: B1 и B2. B1 размещается по цене 0, а B2 размещается на расстоянии D ниже B1, т.е. по цене -D. (Обратите внимание, что отрицательная цена здесь используется в целях анализа и не влияет на результат, поскольку анализ зависит от параметра расстояния D, а не от конкретных уровней цены.)

Теперь предположим, что точка безубытка находится на расстоянии x ниже B1. В этой точке мы получим убыток в размере -x пунктов от B1 и прибыль в размере +x пунктов от B2.

Если размеры лотов равны (т.е. множитель размера лота равен 1), точка безубытка будет находиться ровно посередине между двумя ордерами. Но если размеры лотов различаются, необходимо учитывать множитель размера лота.

Например, если множитель размера лота равен 2, а начальный размер лота равен 0,01, то B1 будет иметь размер лота 0,01, а B2 — размер лота 0,02.

Чтобы найти точку безубытка в этом случае, нужно найти значение x с помощью следующего уравнение:

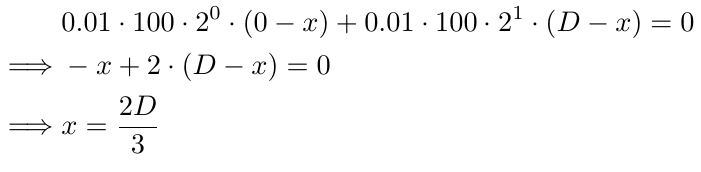
Давайте посмотрим на компоненты уравнения. Первоначальный размер лота 0,01 повторяется в каждой части уравнения (вторая часть относится к части после знака +). Мы умножаем его на 100, чтобы преобразовать размер лота в целое число, и поскольку мы последовательно применяем это преобразование во всех уравнениях, оно сохраняет свою значимость. Далее умножаем на 2^0 в первой части и на 2^1 во второй части. Эти члены уравнения представляют собой множитель размера лота, при этом степень начинается с 0 для начального размера лота и увеличивается на 1 для каждого последующего ордера. Наконец, мы используем (0-x) в первой части, (Dx) во второй и ((i-1)Dx) в i-й части, поскольку i-й ордер размещен на (i-1) пунктов D ниже B1. Решение уравнения относительно x дает 2D/3, что означает, что точка безубытка находится на 2D/3 пункта ниже B1 (как определено x в наших уравнениях). Если D равен 10, то точка безубытка будет на 6,67 пункта ниже B1 или на 3,34 пункта выше B2. Этот уровень цен будет достигнут с большей вероятностью по сравнению с точкой безубытка в точке B1 (если бы у нас был только один ордер). Это основная концепция сеточной стратегии — поддержание предыдущих ордеров до тех пор, пока не будет получена прибыль.

Теперь рассмотрим случай с 3 ордерами.

Для трех ордеров используем тот же подход. Объяснение для 1-й и 2-й частей остается прежним. В 3-й части есть два изменения: степень числа 2 увеличивается на 1, а D теперь умножается на 2. Все остальное остается без изменений.

Находим значение x:

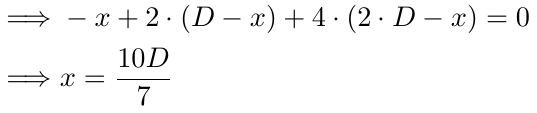
В случае с тремя ордерами точка безубытка наступает, когда цена достигает 10D/7 пунктов ниже B1. Так, если D равен 10, цена безубытка будет на 14,28 пункта ниже B1, на 4,28 пункта ниже B2 и на 5,72 пункта выше B3. Опять же, цена с большей вероятностью достигнет этой точки по сравнению с точкой безубытка в точке B1 (с одним ордером) или предыдущей точкой безубытка (с двумя). Уровень безубытка продолжает снижаться, увеличивая вероятность того, что цена его достигнет, что фактически поддерживает наши предыдущие ордера, если цена пойдет против нас.

Теперь обобщим формулу для n ордеров.

Примечание: здесь предполагается, что мы имеем дело только с ордерами на покупку. Анализ ордеров на продажу симметричен, поэтому мы его упростим.

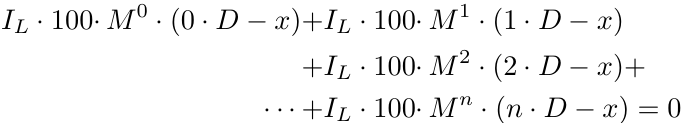
Но получается , что это обобщение неверно.

Причину можно объяснить на простом примере. Возьмем начальный размер лота 0,01, а множитель 1,5. Сначала мы открываем позицию с размером лота 0,01. Затем открываем вторую позицию с размером лота 0,01 * 1,5 = 0,015. Однако после округления он становится равным 0,01, поскольку размер лота должен быть кратен 0,01. Здесь есть две проблемы:

1. Уравнение рассчитывается исходя из открытия позиции с размером лота 0,015, что практически невозможно. Но на деле открывается позиция размером лота 0,01.
2. Этот момент не является проблемой, но на него следует обратить внимание. Давайте рассмотрим тот же пример. Первый порядок был 0,01, и второй ордер также был 0,01 из практических соображений. Каким должен быть размер лота третьего ордера? Умножаем множитель размера лота на размер лота последнего ордера, но на что умножать 1,5: на 0,01 или 0,015? Если умножаем на 0,01, мы попадаем в замкнутый круг, который делает смысл использования множителя бесполезным. Итак, мы получаем 0,015 * 1,5 = 0,0225, что фактически становится 0,02, и так далее.

Как было сказано выше, второй момент не является проблемой. Давайте решим первую проблему, используя наибольший целый множитель (GIF — Greatest Integer Factor) или функцию пола (целая часть вещественного числа)в математике, которая гласит, что мы просто удаляем десятичную часть любого положительного числа (не будем вдаваться в подробности для отрицательных чисел, поскольку размер лота не может быть отрицательным). Запись: floor(.) или [.]. Примеры: floor(1.5) = [1.5] = 1; floor(5.12334) = [5.12334] = 5; floor(2.25) = [2.25] = 2; floor(3.375) = [3.375] = 3.

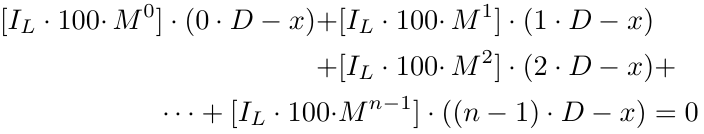
где [.] представляет GIF, т.е. наибольший целый множитель. Решая далее, получаем:

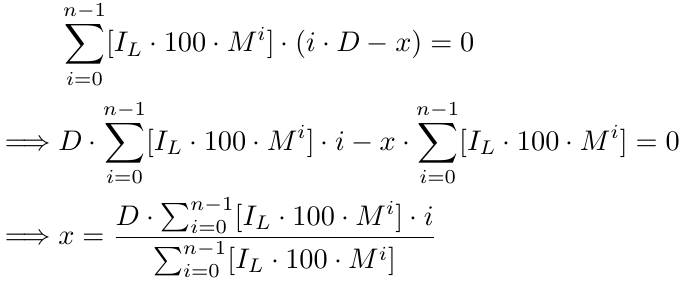
Формально, для x количества ордеров мы имеем функцию безубытка b(x),

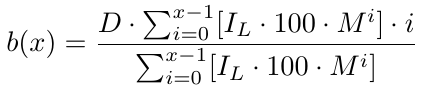
Теперь у нас есть функция безубытка, которая позволяет определить цену уровня безубытка. Она возвращает, на сколько пунктов ниже B1 находится цена безубытка. Зная цену безубытка, нам необходимо определить уровень тейк-профита (TP), который представляет собой просто количество пунктов TP выше b(x). Поскольку b(x) — это уровень цены B1 за вычетом уровня цены безубыточности, для уровня тейк-профита нам необходимо вычесть TP из b(x). Таким образом, у нас есть уровень тейк-профита, который мы обозначим как t(x):

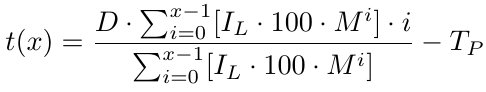
Учитывая x, т.е. количество ордеров, мы получаем уровень тейк-профита. Теперь нам нужно рассчитать прибыль при заданном x. Попробуем найти функцию прибыли.

Предположим, что цена достигает t(x), т.е. уровня тейк-профита, и цикл закрывается, тогда прибыль/убыток, который мы получаем от B1, равен уровню цены B1 минус t(x), где единицей измерения являются пункты. Отрицательное значение означает, что у нас убыток, а положительное — прибыль. Аналогично, прибыль/убыток, который мы получаем от B2, равен уровню цены B2 минус t(x), где единицей измерения являются пункты, и мы знаем, что уровень цены B2 ровно на D пунктов ниже уровня цены B1. Для B3 прибыль/убыток равен уровню цены B3 минус t(x), где единицей измерения являются пункты, и мы знаем, что уровень цены B3 ровно на 2*D пунктов ниже уровня цены B1. Обратите внимание, что нам необходимо также учитывать начальный размер лота и множитель размера лота.

Математически, при x (т.е. количество ордеров равно 3), мы имеем:

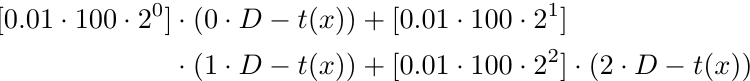
Получается, для количества ордеров x мы имеем функцию прибыли p(x),

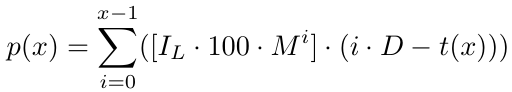
Давайте разберемся, что это значит. При любом количестве ордеров, предполагая, что цикл закроется через x ордеров (где «закроется» означает, что мы достигнем уровня тейк-профита), мы получим прибыль, которую можно вычислить по уравнению p(x) выше. Итак, у нас есть функция прибыли. Теперь давайте попробуем вычислить функцию убытков, которые мы понесем, если цикл сетки с x количеством ордеров будет закрыт с убытком («закрыт с убытком» означает, что мы не можем открыть дополнительные ордера для продолжения цикла сетки из-за недостатка средств, поскольку стратегия сетки требует больших инвестиций, или по любой другой причине).

Тогда функция убытка будет выглядеть так: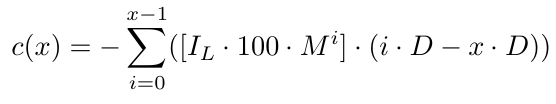

В этом уравнении часть [.] учитывает начальный размер лота и множитель размера лота. Другая часть (iD-xD) учитывает xD, то есть расстояние между уровнем цены B1 и на D пипсов ниже ордера с самой низкой ценой. Мы используем xD, потому что именно там открывается новый ордер. Если по какой-то причине, скорее всего это из-за недостатка средств, нам не удастся продолжить цикл, то это как раз тот момент, когда мы можем с уверенностью сказать, что без открытия ордера на этом уровне цены (когда цена достигнет этого уровня) мы не сможем продолжить цикл. По сути, когда мы точно знаем, что нам не удалось продолжить цикл, уровень цены будет на xD пунктов ниже уровня цены B1. В результате мы получим убыток (0.Dx.D) от ордера B1, (1.Dx.D) от ордера B2 и так далее до последнего ордера Bx, от которого мы получим убыток ((x-1).Dx.D)=-D. В этот момент мы находимся на D пунктов ниже последнего ордера (ордера с самым низким уровнем цены).

Итак, для количества ордеров x мы имеем функцию убытка c(x),

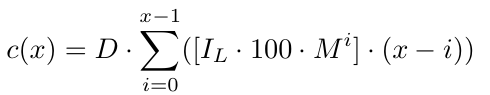
Нам также необходимо учесть спред, который для простоты мы будем считать постоянным, поскольку расчет динамического спреда будет довольно сложным. Допустим, S — статический спред, который у нас будет равным 1–1,5 для EURUSD. Спред может меняться в зависимости от валютной пары, но эта стратегия лучше всего работает с валютами с меньшей волатильностью, такими как EURUSD.

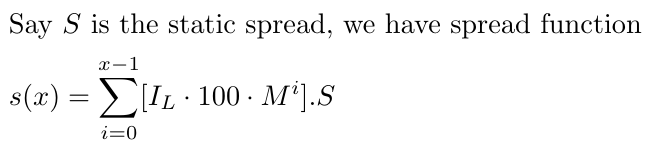
Важно отметить, что наша корректировка учитывает все сделки от нуля до x-1 — спред влияет на каждую сделку, независимо от того, прибыльна она или нет. Для простоты в настоящее время мы рассматриваем спред (обозначенный как S) как постоянное значение. Это решение принято, чтобы не усложнять математический анализ дополнительной изменчивой величиной. Хотя это упрощение ограничивает реалистичность модели, оно позволяет сосредоточиться на основных аспектах стратегии, не увязая в чрезмерной сложности.

Теперь, когда у нас есть все необходимые функции, мы можем построить их график в Desmos.

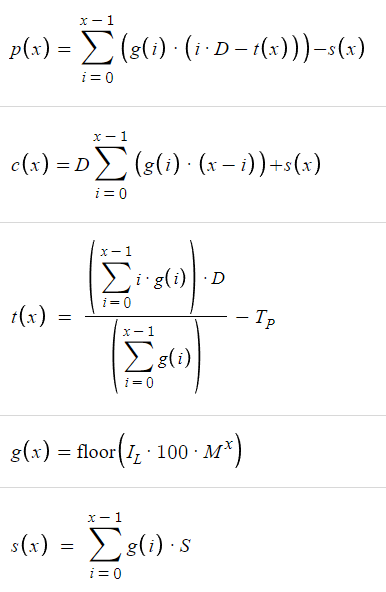
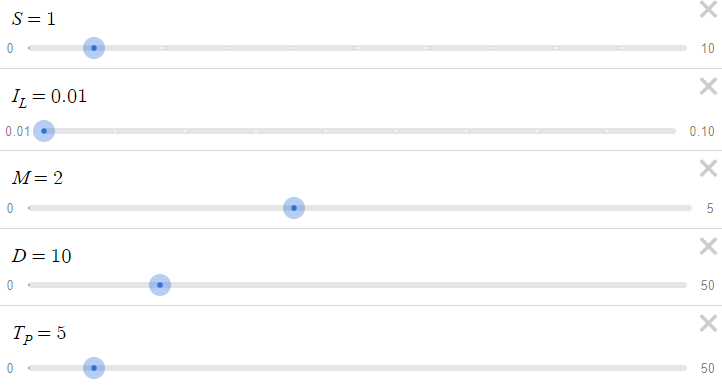
Учитывая приведенные выше параметры, мы имеем следующую таблицу, где изменение x дает различные значения прибыли p(x) и убытка c(x):

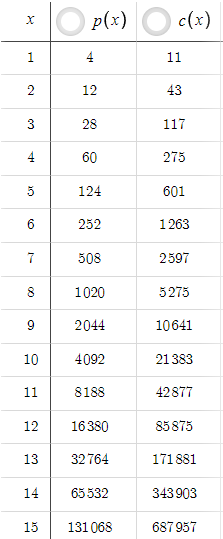
В этом сценарии p(x) всегда меньше c(x), но это можно легко изменить, увеличив тейк-профит TP. Например, если мы увеличим TP с 5 до 50:

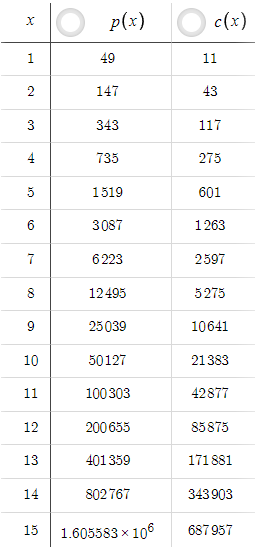
Теперь прибыль p(x) всегда больше убытка c(x). Начинающий трейдер может подумать, что если мы можем получить такой высокий уровень соотношения риска и прибыли при TP=50, зачем оставлять TP=5? Нужно учитывать вероятность. Увеличение тейк-профита с 5 до 50 резко снизило вероятность достижения ценой уровня тейк-профита. Мы должны понимать, что нет смысла иметь хорошее соотношение риска и прибыли, если мы никогда или очень редко достигаем тейк-профита. Для учета вероятностей нам нужны данные о ценах и оптимизация на основе кода, а не просто уравнения. Мы рассмотрим это в следующих частях серии.

По этой ссылке на график Desmos вы можете увидеть график этих функций и поиграть с параметрами, чтобы лучше понять стратегию.

На этом завершим математическую часть оптимизации. В следующих разделах мы более подробно рассмотрим практические аспекты реализации этой стратегии, принимая во внимание реальные рыночные условия и связанные с ними проблемы. Объединив созданную нами математическую основу с методами анализа и оптимизации на основе данных, мы сможем улучшить стратегию сеточной торговли, чтобы она лучше соответствовала нашим потребностям и максимально увеличила ее потенциальную прибыльность.

Небольшой вывод: как упоминалось ранее, многочисленные параметры указывают на высокий потенциал прибыли. Однако важно понимать, что эти цифры служат в первую очередь для демонстрации. Причиной этого является отсутствие важнейшего компонента математической оптимизации: вероятности. Включение вероятности в нашу математическую модель — сложная задача, но это незаменимый фактор, который нельзя игнорировать. Для решения этой проблемы мы проведем моделирование на основе данных о ценах. Это позволит учесть вероятность в наших расчетах и повысить точность нашей модели.

Моделирование вычислений на Python

В этом моделировании мы вычислим и построим графики функции прибыли p(x) и убытка c(x) в зависимости от x, где x — это количество ордеров. Значения p(x) и c(x) будут отложены на оси Y, а x — на оси X. Эта визуализация позволит быстро оценить изменения функции прибыли p(x) и убытка c(x) и определить, какая из них больше в разных точках. Кроме того, мы создадим таблицу, которая отобразит точные значения p(x) и c(x) для каждого x, поскольку эти значения может быть сложно прочитать только из графика. Такое сочетание графика и таблицы даст полное представление о поведении функций прибыли p(x) и убытка c(x).

Код на Python:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

# Values of x to evaluate
x_values = range(1, 21)  # x from 1 to 20

def g(x, I_L, M):
    return np.floor(I_L * 100 * M ** x)

def s(x, I_L, M, S):
    return sum(g(i, I_L, M) * S for i in range(x))

def t(x, D, I_L, M, T_P):
    numerator = sum(i * g(i, I_L, M) for i in range(x)) * D
    denominator = sum(g(i, I_L, M) for i in range(x))
    return (numerator / denominator) - T_P

def p(x, D, I_L, M, S, T_P):
    return sum(g(i, I_L, M) * (i * D - t(x, D, I_L, M, T_P)) for i in range(x)) - s(x, I_L, M, S)

def c(x, D, I_L, M, S):
    return D * sum(g(i, I_L, M) * (x - i) for i in range(x)) + s(x, I_L, M, S)

# Calculate p(x) and c(x) for each x
p_values = [p(x, D, I_L, M, S, T_P) for x in x_values]
c_values = [c(x, D, I_L, M, S) for x in x_values]

# Formatter to avoid exponential notation
def format_func(value, tick_number):
    return f'{value:.2f}'

# Plotting
fig, axs = plt.subplots(2, 1, figsize=(12, 12))

# Combined plot for p(x) and c(x)
axs[0].plot(x_values, p_values, label='p(x)', marker='o')
axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange')
axs[0].set_title('p(x) and c(x) vs x')
axs[0].set_xlabel('x')
axs[0].set_ylabel('Values')
axs[0].set_xticks(x_values)
axs[0].grid(True)
axs[0].legend()
axs[0].yaxis.set_major_formatter(FuncFormatter(format_func))

# Create table data
table_data = [['x', 'p(x)', 'c(x)']] + [[x, f'{p_val:.2f}', f'{c_val:.2f}'] for x, p_val, c_val in zip(x_values, p_values, c_values)]

# Plot table
axs[1].axis('tight')
axs[1].axis('off')
table = axs[1].table(cellText=table_data, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.2, 1.2)

plt.tight_layout()
plt.show()

Объяснение кода:

1. Импорт библиотек:

   • numpy импортируется как np, используется для числовых операций.
   • matplotlib.pyplot импортируется как plt, используется для построения графиков.
   • FuncFormatter импортируем из matplotlib.ticker , используется для форматирования меток делений осей.

2. Настройка параметров:

   • Определяем константы D, I_L, M, S, и T_P которые представляют собой расстояние, начальный размер лота, множитель размера лота, спред и тейк-профит соответственно.

3. Определение диапазона для параметра x:

   • x_values установим в диапазоне целых чисел от 1 до 20.

4. Определение функций:

   • g(x, I_L, M) — вычисляет значение g на основе заданной формулы.
   • s(x, I_L, M, S) — вычисляет сумму g(i, I_L, M) * S для значений i от 0 до x-1 .
   • t(x, D, I_L, M, T_P) — вычисляет значение t на основе заданной формулы, используя числитель и знаменатель.
   • p(x, D, I_L, M, S, T_P) — вычисляет p(x) по заданной формуле.
   • c(x, D, I_L, M, S) — вычисляет c(x) по заданной формуле.

5. Расчет значений p(x) и c(x):

   • p_values — это список значений p(x) для каждого x в x_values.
   • c_values — это список значений c(x) для каждого x в x_values.

6. Определение форматера:

   • format_func(value, tick_number) — определяет функцию для форматирования меток делений оси Y до двух десятичных знаков.

7. Построение:

   • fig, axs = plt.subplots(2, 1, figsize=(12, 12)) — создает изображение и два построения, расположенных в одном столбце.

   Первое построение — комбинированная диаграмма p(x) и c(x):

   • axs[0].plot(x_values, p_values, label='p(x)', marker='o') — строит значения прибыли p(x) от x с метками.
   • axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange') — строит значения убытка c(x) от x с метками оранжевого цвета.
   • axs[0].set_title('p(x) and c(x) vs x') — устанавливает заголовок первого построения.
   • axs[0].set_xlabel('x') — устанавливает метку оси x.
   • axs[0].set_ylabel('Values') — устанавливает метку оси y.
   • axs[0].set_xticks(x_values) — Обеспечивает отображение делений оси x для каждого значения x.
   • axs[0].grid(True) — добавляет сетку на график.
   • axs[0].legend() — отображает легенду графика.
   • axs[0].yaxis.set_major_formatter(FuncFormatter(format_func)) — применяет форматирование для оси y, чтобы избежать экспоненциальной записи.

   Второе построение (таблица):

   • table_data — подготавливает данные таблицы для столбцов x , p(x) и c(x), а также соответствующие значения для них.
   • axs[1].axis('tight') — строит ось построения, чтобы точно вместить таблицу.
   • axs[1].axis('off') — отключает ось в построении таблицы.
   • table = axs[1].table(cellText=table_data, cellLoc='center', loc='center') — создает таблицу во втором построении с центрированным текстом ячеек.
   • table.auto_set_font_size(False) — отключает автоматическую настройку размера шрифта.
   • table.set_fontsize(10) — устанавливает размер шрифта таблицы.
   • table.scale(1.2, 1.2) — масштабирует размер таблицы.

8. Разметка и отображение:

   • plt.tight_layout() — настраивает разметку, чтобы не было наложения элементов.
   • plt.show() — отображает построения и таблицу.

Мы использовали следующие параметры по умолчанию (их можно легко изменить, чтобы получить другие результаты):

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

Результат:

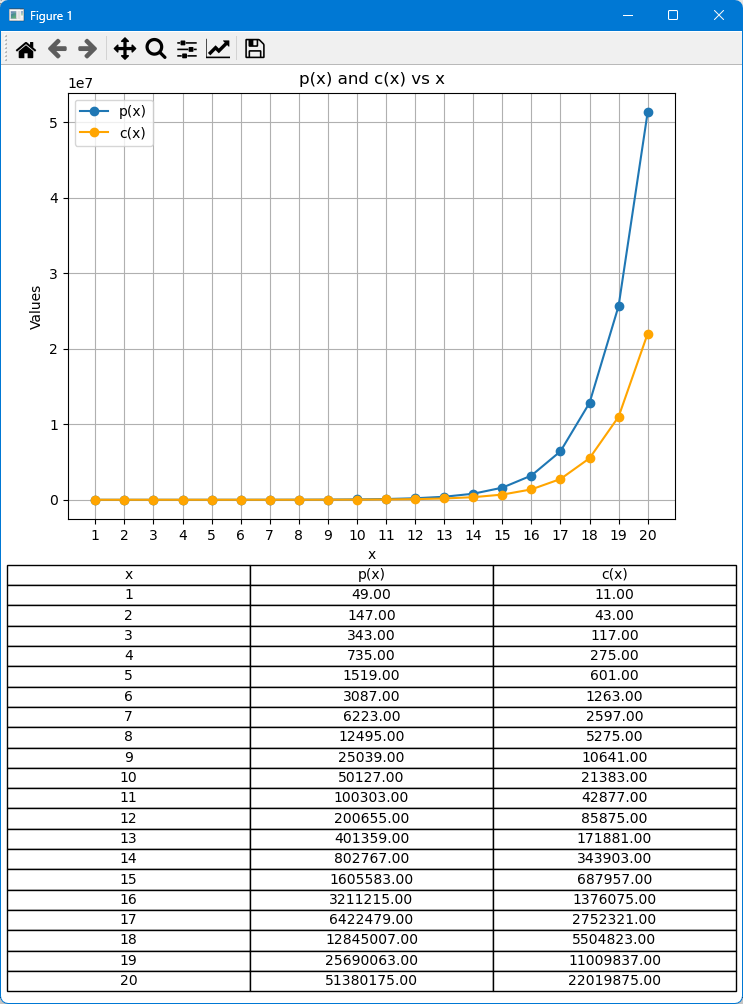
Примечание: файл Python с кодом, показанным выше, прикреплен в конце статьи.

Заключение

В четвертой части нашей серии мы занимались оптимизацией простой сеточной стратегии Simple Grid с помощью математического анализа и роли вероятности, которую часто упускают из виду в стратегиях с использованием сеток и хеджирования. В следующих статьях мы перейдем от теории к практическим приложениям и применим эти идеи к реальным торговым сценариям. Разработаем приложения и попытаемся получить прибыль, при этом эффективно управляя рисками. Ваши отзывы и комментарии приветствуются. Призываю всех активно участвовать, чтобы вместе узнавать новое, совершенствоваться и добиваться успехов в торговых стратегиях.

Удачного программирования! Удачной торговли!