Data Science e Machine Learning (Parte 22): Aproveitando Redes Neurais Autoencoders para Operações Mais Inteligentes, Movendo-se do Ruído para o Sinal

O que são Autoencoders?

Autoencoders são redes neurais artificiais não supervisionadas. Na sua forma mais simples, um autoencoder é uma rede neural que tenta fazer duas coisas. Ele comprime seus dados de entrada em uma dimensão mais baixa e, em seguida, tenta usar essa representação de dimensão inferior dos dados para recriar a entrada original.

Suponha que você tenha uma imagem desfocada de um gato passada para o autoencoder; essa imagem será comprimida e descomprimida de volta ao seu estado original, perdendo alguns dos seus pixels ruidosos/desfocados ao longo do processo, resultando em uma imagem nítida de um gato.

Neste artigo, veremos como podemos usar uma rede neural autoencoder no espaço financeiro para nos ajudar a remover o ruído no mercado, permitindo que descubramos oportunidades de trading.

Este artigo é uma leitura fácil se você tiver uma compreensão básica de ONNX, PCA e Redes Neurais em geral.

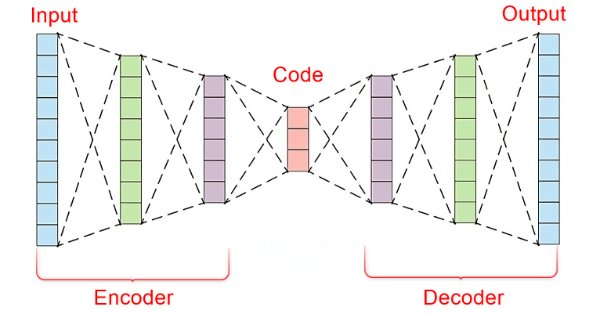
Um Autoencoder consiste em duas partes:

1. Um Encoder recebe os dados de entrada e os comprime em uma representação latente de dimensão inferior, capturando as características essenciais.
2. Um Decoder recebe a representação latente e tenta reconstruir os dados de entrada originais com a maior precisão possível.

Vantagens dos Autoencoders:

• Eles podem ser úteis para tarefas de redução de dimensionalidade, pois podem aprender uma representação compacta dos dados de trading forex, o que é útil para tarefas como extração de características, compressão de dados e visualização em conjuntos de dados de alta dimensão.
• Ao tentar reconstruir os dados de entrada, o autoencoder aprende características essenciais e remove ruído ou informações irrelevantes. Essas características aprendidas podem ser benéficas para outras tarefas de machine learning, como classificação ou detecção de anomalias.
• Como são não supervisionados, eles podem descobrir padrões ocultos nos dados de trading sem interação humana.
• A representação latente aprendida de um autoencoder pode ser usada como características pré-treinadas para outros modelos, potencialmente melhorando seu desempenho.

Do que eles são feitos?

Vamos dissecar os autoencoders e observar do que eles são feitos e o que os torna especiais.

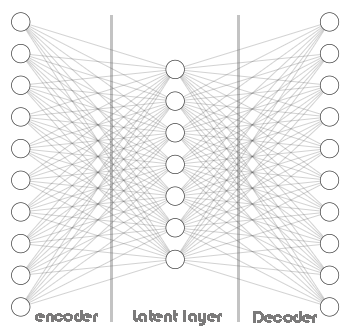
No núcleo de um autoencoder, há uma rede neural artificial composta por três partes.

1. O Encoder
2. A camada de vetor de Embedding/latente
3. O Decoder

A parte esquerda da rede neural é chamada de encoder. Sua função é transformar os dados de entrada originais em uma representação de dimensão inferior.

A parte do meio da rede neural é chamada de camada latente ou vetor de Embedding, e sua função é comprimir os dados de entrada em dados de dimensão inferior. Espera-se que essa camada tenha menos neurônios do que tanto o encoder quanto o decoder.

A parte direita dessa rede neural é chamada de decoder. Sua função é recriar a entrada original usando a saída do encoder. Em outras palavras, ele tenta reverter o processo de codificação.

Isso é fascinante porque o decoder tenta recriar dados de alta dimensão a partir de dados de dimensão inferior retornados pelo encoder. Algo como tentar construir uma casa apenas olhando uma foto dela.

Isso força a perda de informação, o que é fundamental para o funcionamento de todo esse processo. Ao fazer com que o decoder tenha informações imperfeitas e treinar toda a rede para minimizar o erro de reconstrução. Durante o treinamento, o encoder e o decoder são forçados a trabalhar juntos para minimizar o erro de construção.

Erro de construção é a diferença entre a recriação tentada e os dados de entrada originais.

Se não tivermos perda de informação entre o encoder e o decoder, a rede aprenderia simplesmente a multiplicar a entrada por um e obter uma reconstrução perfeita, tornando o autoencoder inútil. Ter um encoder com algum grau de erros é crucial para essa técnica de machine learning, certifique-se de não sobrecarregar seu modelo.

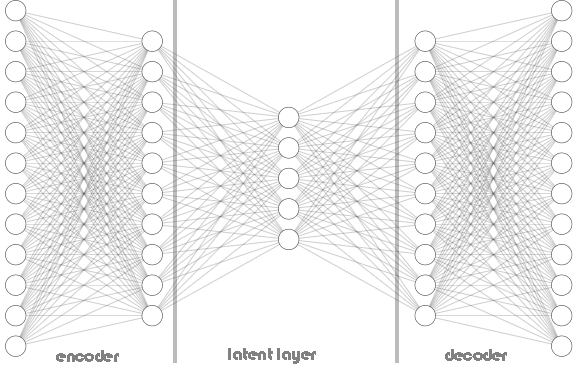
Tanto encoders quanto decoders não estão limitados a uma única camada, como pode ser visto na imagem da arquitetura do Autoencoder acima. Ele pode conter várias camadas, como visto no código Python abaixo, onde temos uma lista chamada hidden_dims para armazenar os neurônios das camadas do encoder e do decoder.

Python:

class Autoencoder(Model):
  def __init__(self, input_dim, latent_dim, hidden_dims=[]):
    super(Autoencoder, self).__init__()

    self.encoder = tf.keras.Sequential()
    # Add hidden layers to the encoder (if any)
    for dim in hidden_dims:
      self.encoder.add(layers.Dense(dim, activation='relu'))
      self.encoder.add(layers.Dropout(0.5))

    # Define the latent layer
    self.encoder.add(layers.Dense(latent_dim, activation='relu'))

    # Decoder ( mirrored structure )
    self.decoder = tf.keras.Sequential()
    # Add hidden layers to the decoder (in reverse order)
    for dim in hidden_dims[::-1]:
      self.decoder.add(layers.Dense(dim, activation='relu'))
      self.decoder.add(layers.Dropout(0.5))

    # Define the output layer
    self.decoder.add(layers.Dense(input_dim, activation='sigmoid'))  #the output layer with dimensions matching the original input data

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

Chamando a classe Autoencoder:

Python:

input_dim = dataset.shape[1]  # number of columns in the data
latent_dim = 5  # Dimension of latent layer
hidden_dims = [12, 10]

autoencoder = Autoencoder(input_dim, latent_dim, hidden_dims)

Abaixo está como a arquitetura do Autoencoder se parece:

Na classe Autoencoder, você viu o uso de RELU (Rectified Linear Unit) tanto no encoder quanto no decoder. Essa função de ativação é amplamente utilizada na maioria dos Autoencoders, e há uma razão importante para isso.

RELU é computacionalmente eficiente, evita gradientes que desaparecem e pode aprender representações esparsas, que geralmente são encontradas nos dados de trading. Outras variantes do RELU, como GELU e Leaky RELU, podem ser úteis ao trabalhar com dados financeiros.

Quando o sigmoid foi aplicado ao Autoencoder, a rede não convergiu, pois continuava oscilando em direção a mínimos locais:

Sigmoid:

• Prós: Frequentemente usada para reconstrução de imagens, onde a saída precisa estar entre 0 e 1 (representando a intensidade dos pixels).
• Contras: Pode não ser ideal para dados financeiros, pois pode introduzir gradientes que desaparecem durante a retropropagação, especialmente em arquiteturas profundas.
  Quando o sigmoid foi aplicado ao Autoencoder, a rede não convergiu, pois continuava oscilando em direção a mínimos locais:
  

  Epoch 1/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 3s 5ms/step - loss: 0.4001 - val_loss: 0.3753
  Epoch 2/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3733 - val_loss: 0.3745
  Epoch 3/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3724 - val_loss: 0.3746
  Epoch 4/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3758 - val_loss: 0.3746
  Epoch 5/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3692 - val_loss: 0.3745
  Epoch 6/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3747 - val_loss: 0.3746
  Epoch 7/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3716 - val_loss: 0.3746
  Epoch 8/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3740 - val_loss: 0.3745
  Epoch 9/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3698 - val_loss: 0.3745
  Epoch 10/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3713 - val_loss: 0.3745
  Epoch 11/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3726 - val_loss: 0.3745
  Epoch 12/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3739 - val_loss: 0.3745
  Epoch 13/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3725 - val_loss: 0.3746
  Epoch 14/50
  110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3749 - val_loss: 0.3746

Tanh (Tangente Hiperbólica):

• Prós: As saídas variam entre -1 e 1, semelhante ao sigmoid, mas com gradientes mais íngremes, o que pode levar a uma convergência mais rápida.
• Contras: Ainda pode sofrer de gradientes que desaparecem em redes muito profundas.

Essas funções de ativação Sigmoid e TANH e outras de seu tipo funcionam melhor quando usadas na camada de saída do decoder, com o objetivo de reconstruir os dados de entrada da maneira mais precisa possível. Nesse contexto, a saída do autoencoder deve se assemelhar à entrada original. Como os dados de entrada geralmente são normalizados para o intervalo [0, 1] ou [-1, 1], dependendo do pré-processamento, a função de ativação sigmoid é comumente usada para escalar os valores de saída para esse intervalo.

Python:

#Definir a camada de saída
self.decoder.add(layers.Dense(input_dim, activation='sigmoid')) # a camada de saída do decoder com dimensões que correspondem aos dados de entrada originais

Min-Max Scaler é seu Amigo

Autoencoders são simples de codificar e implementar, no entanto, precisam receber as informações e ferramentas corretas para funcionarem bem. Como acabamos de ver, a escolha de uma função de ativação é crucial para esse tipo de rede neural, assim como a técnica de escala.

Como estamos usando a função de ativação RELU, que retorna o valor zero quando um valor menor ou igual a zero é dado a ela, caso contrário, retorna o valor dado, ou seja: (x = 0 quando x<=0, caso contrário, x = x).

Quando você usa o Standard-Scaler, ele centraliza os dados subtraindo a média e escala para variância unitária. Isso pode empurrar valores discrepantes com grandes valores positivos para valores muito negativos (potencialmente -1) durante a padronização. Se um valor padronizado de um outlier se tornar -1, quando esse valor negativo passar pela ativação RELU no encoder, sempre produzirá 0 para essa característica específica.

Isso pode levar a um fenômeno chamado neurônios RELU mortos, onde alguns neurônios no encoder nunca são ativados devido a esses valores de entrada negativos. Esses neurônios RELU mortos podem prejudicar o aprendizado no encoder, pois essencialmente se tornam inativos e não contribuem para o processo de codificação. A maioria dos outliers ou picos nos dados de trading será prevista como plana na maioria das vezes: veja a imagem abaixo onde o Standard-Scaler foi usado.

 

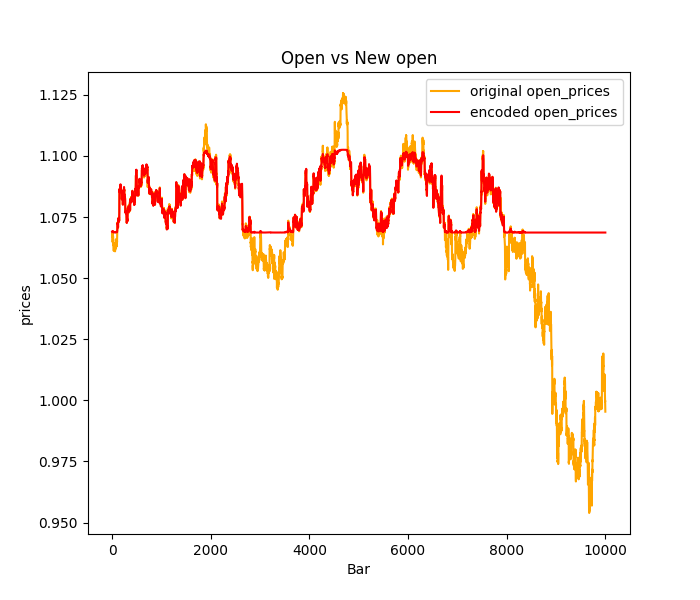
Para resolver esse problema:

Experimente outras técnicas de normalização, como o Min-Max Scaler, que escala os dados para um intervalo específico entre 0 e 1, evitando potencialmente a criação de valores -1 que causam problemas com RELU. No entanto, considerando as limitações do Min-Max Scaler, você também pode explorar o Robust Scaler, que é menos sensível a outliers do que o Standard Scaler e pode oferecer melhor escalonamento para ativações RELU.

Além disso, você pode considerar usar o Leaky RELU (leaky_relu = 0.01x para x <= 0, relu = x para x > 0) em vez do RELU padrão. Leaky RELU permite um pequeno gradiente não nulo, mesmo para entradas negativas, mitigando o problema dos neurônios RELU mortos.

Treinando o Autoencoder

Agora que discutimos brevemente os fundamentos de um Autoencoder, vamos treinar um e ver como podemos usá-lo para nos ajudar no trading.

Python:

import sklearn
from sklearn.model_selection import train_test_split
from keras import optimizers
from keras.callbacks import EarlyStopping

x_train, x_test = train_test_split(dataset, test_size=0.3, random_state=42) #train test the data

# Normalizing the input data 

scaler = sklearn.preprocessing.MinMaxScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

print(f"x_train {x_train.shape}.dtype({x_train.dtype}) x_test {x_test.shape}.dtype({x_test.dtype})")

# compile the autoencoder

input_dim = dataset.shape[1]
latent_dim = 32  # Dimension of latent space
hidden_dims = [256, 128, 64]

autoencoder = Autoencoder(input_dim, latent_dim, hidden_dims)

optimizer = optimizers.Adam(learning_rate=1e-5)
autoencoder.compile(optimizer=optimizer, loss=losses.MeanSquaredError())

early_stopping = EarlyStopping(monitor='val_loss', patience = 5, restore_best_weights=True) //stop the training process if 5 epochs have no change in loss
history = autoencoder.fit(x_train, x_train, epochs=50, shuffle=True, callbacks=[early_stopping], validation_data=(x_test, x_test), batch_size=64, verbose=1)

Escolhi uma arquitetura complexa de rede neural [256, 128, 64] para o encoder e uma disposição inversa de [64, 128, 256] será aplicada ao decoder, com 32 neurônios na camada latente.

Uma rede neural tão complexa tem maior chance de overfitting nos dados de treinamento, sinta-se à vontade para começar com arquiteturas mais simples, este é apenas um exemplo. 

Saídas:

x_train (7000, 4).dtype(float64) x_test (3000, 4).dtype(float64)
Epoch 1/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 3s 5ms/step - loss: 0.0669 - val_loss: 0.0636
Epoch 2/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0648 - val_loss: 0.0608
Epoch 3/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0624 - val_loss: 0.0550

....
....
....

Epoch 46/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.2096e-04 - val_loss: 1.0195e-04
Epoch 47/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.0758e-04 - val_loss: 9.7759e-05
Epoch 48/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.0923e-04 - val_loss: 9.4798e-05
Epoch 49/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - loss: 1.0243e-04 - val_loss: 9.0442e-05
Epoch 50/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - loss: 1.0222e-04 - val_loss: 8.7384e-05

Loss vs Iteration graph:

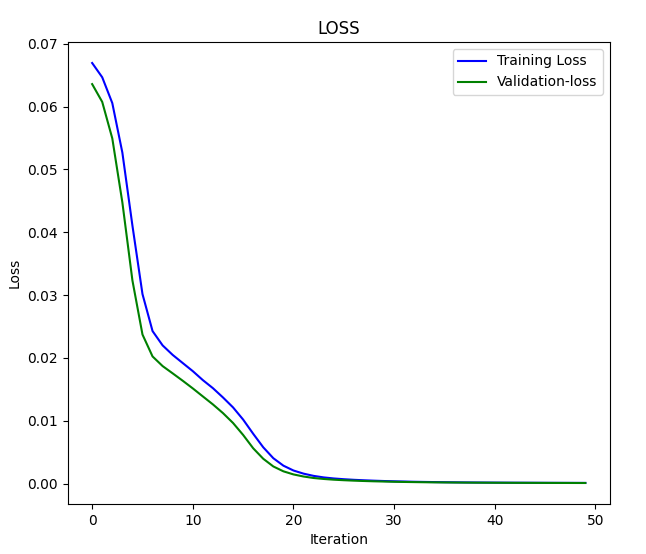
Vamos passar os dados para o Autoencoder e observar o resultado:

Python:

original_norm_data = scaler.transform(dataset)

new_data = autoencoder.call(original_norm_data)

new_data = scaler.inverse_transform(new_data) #return data to the original form 

print("original data\n",dataset,"\nnew data\n",new_data)

Saídas:

dados originais
 [[1.06507 1.06633 1.06497 1.06538]
 [1.06628 1.06685 1.06463 1.06508]
 [1.06771 1.06797 1.06599 1.06627]
 ...
 [0.99941 0.99996 0.9991  0.99916]
 [0.99687 0.99999 0.99646 0.99941]
 [0.99536 0.99724 0.99444 0.99687]] 
new data
 [[1.06612682 1.06676685 1.06537819 1.06605109]
 [1.06617137 1.06679912 1.06541834 1.06609218]
 [1.06742607 1.06804771 1.06668032 1.06736937]
 ...
 [0.99906356 1.00121275 0.9980908  0.99980352]
 [0.998204   1.00034005 0.9972261  0.99893805]
 [0.99581326 0.99789913 0.99494114 0.99651365]]

Decidi visualizar os preços de fechamento:

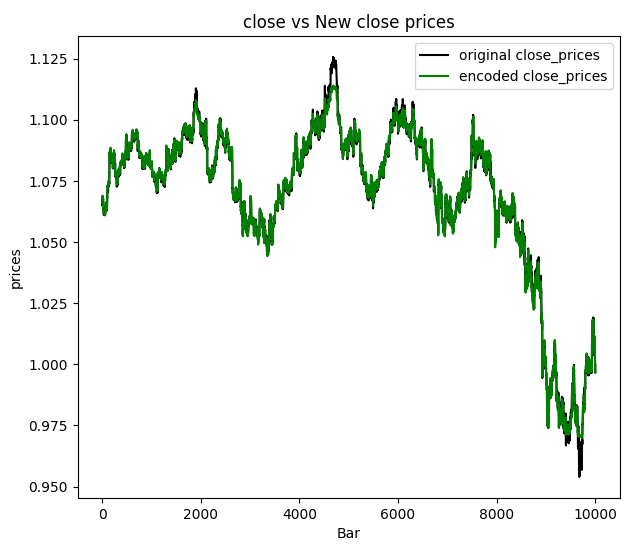
Podemos concluir que os novos dados passados pelo autoencoder tiveram algum ruído filtrado e é fácil detectar os outliers apenas observando o gráfico. Agora que temos certeza de que funciona, vamos discutir as aplicações dos autoencoders e como finalmente podemos usá-los em nossos programas baseados em MQL5.

Aplicações de Autoencoders

Autoencoders têm sido usados em vários campos e indústrias, como engenharia, medicina, entretenimento e muito mais, para redução de dimensionalidade, aprendizado de características, detecção de anomalias, em sistemas de recomendação e remoção de ruído em imagens.

Redução de Dimensionalidade

Autoencoders se destacam ao comprimir dados de alta dimensão em um espaço latente de dimensão inferior. Isso é particularmente valioso ao lidar com conjuntos de dados que contêm um grande número de características, eles capturam as características essenciais em uma representação mais compacta que pode:

• Melhorar a eficiência computacional em tarefas subsequentes de machine learning, reduzindo o número de características a serem processadas. 
• Aprimorar a visualização de dados de alta dimensão, permitindo a aplicação de técnicas de redução de dimensionalidade, como Análise de Componentes Principais (PCA), no espaço latente aprendido.

Para realizar essa tarefa, precisamos usar apenas a parte do encoder de nossa rede neural 

Precisamos modificar a classe Autoencoder adicionando a função build, que deve ser chamada logo após a classe Autoencoder ser iniciada. Esse método é útil para criar dinamicamente camadas com base na forma dos dados de entrada, permitindo que você adie a construção das camadas até que suas formas sejam conhecidas.

Python:

class Autoencoder(Model):
  def __init__(self, input_dim, latent_dim, hidden_dims=[]):
    super(Autoencoder, self).__init__()
    self.hidden_dims = hidden_dims
    self.input_dim = input_dim
    
    # Encoder
    self.encoder = tf.keras.Sequential(name='encoder') #give the encoder Sequential layer name=encoder
    # Decoder ( mirrored structure )
    self.decoder = tf.keras.Sequential(name='decoder') #give the decoder Sequential layer name=decoder
    
  def build(self):

    # Add hidden layers to the encoder (if any)
    for dim in hidden_dims:
      self.encoder.add(layers.Dense(dim, activation='relu'))
      self.encoder.add(layers.Dropout(0.5))

    # Define the latent layer
    self.encoder.add(layers.Dense(latent_dim, activation='relu'))
        
    # Add hidden layers to the decoder (in reverse order)
    for dim in hidden_dims[::-1]:
      self.decoder.add(layers.Dense(dim, activation='relu'))
      self.decoder.add(layers.Dropout(0.5))

    # Define the output layer
    self.decoder.add(layers.Dense(self.input_dim, activation='sigmoid'))  #the output layer with dimensions matching the original input data

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

Também precisamos mudar um pouco a forma como chamamos as funções da nossa classe, como mencionado anteriormente, devemos chamar a função build antes de compilar e treinar nosso modelo de rede neural. Aordem de chamada dos métodos da classe é importante!

Python:

# Instantiate the autoencoder and build the model
autoencoder = Autoencoder(input_dim, latent_dim, hidden_dims)
autoencoder.build()

optimizer = optimizers.Adam(learning_rate=1e-5)
autoencoder.compile(optimizer=optimizer, loss=losses.MeanSquaredError())

Agora que temos a função build implementada, finalmente podemos extrair ambas as redes neurais, tanto o codificador quanto o decodificador, separadamente após o Autoencoder ter sido treinado com sucesso sem erros.

Python:

# Extract Encoder
encoder_input = autoencoder.encoder.layers[0].input
encoder_output = autoencoder.encoder.get_layer(index=-1).output # the layer at index -1 is the last layer

# Define the encoder model
encoder_model = tf.keras.Model(inputs=encoder_input, outputs=encoder_output)

# Extract Decoder
decoder_input = autoencoder.decoder.layers[0].input
decoder_output = autoencoder.decoder.get_layer(index=-1).output # the layer at index -1 is the last layer

# Define the decoder model
decoder_model = tf.keras.Model(inputs=decoder_input, outputs=decoder_output)

Uma vez que temos o codificador, podemos passar a informação e obter a matriz de resultados passada pela camada latente (espaço).

Python:

from sklearn.decomposition import PCA

# Fit & transform the encoded data 
encoded_data = encoder_model.predict(original_norm_data)
print("decoded data.shape: ",encoded_data.shape)

# Create PCA object
pca = PCA(n_components=encoded_data.shape[1])

reduced_data = pca.fit_transform(encoded_data)
print("pca reduced data.shape: ",reduced_data.shape)

print("explained var:\n",np.cumsum(pca.explained_variance_ratio_))

# Plotting the scree plot
plt.figure(figsize=(10, 6))
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Scree Plot')
plt.grid(True)
plt.show()

Ao atribuir o número de colunas encoded_data.shape[1] aos componentes do PCA, podemos medir a variância explicada de cada característica e desenhar um gráfico de scree que pode nos ajudar a entender o melhor número de componentes a aplicar no PCA para reduzir a dimensão dos dados.

313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
decoded data.shape:  (10000, 32)
pca reduced data.shape:  (10000, 32)
explained var:
 [0.99623495 0.9989214  0.99982804 0.9999363  0.99996614 0.9999872
 0.99999297 0.9999953  0.9999972  0.9999982  0.9999987  0.9999991
 0.9999994  0.9999996  0.9999997  0.9999998  0.99999994 1.
 1.         1.         1.         1.         1.         1.
 1.         1.         1.         1.         1.         1.
 1.         1.        ]

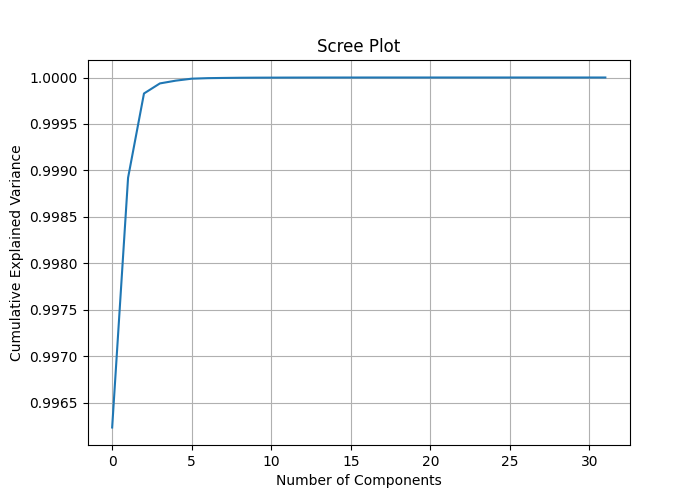
Ao observar a Variância Explicada Cumulativa, podemos ver que as proporções de variância explicada são próximas de 1 para a maioria dos componentes e 1 para alguns componentes. Isso implica que você pode conseguir uma redução significativa da dimensionalidade sem perder muita informação.
O gráfico scree mostra o ponto de cotovelo em quase 2 componentes, o que explica cerca de 0,9989 da variância total, sendo esse o melhor número de componentes para reduzir nossos dados. Mesmo 1 componente deve funcionar bem, pois não consegui ver uma distinção significativa entre os componentes quando os plotei em um eixo.

Na próxima vez que a classe PCA for chamada, ela deve ser chamada com o valor 2 aplicado para obter 2 componentes.

# Create PCA object
pca = PCA(n_components=2)

reduced_data = pca.fit_transform(encoded_data)
print("pca reduced data.shape: ",reduced_data.shape)

Resultado:

pca reduced data.shape:  (10000, 2)

Decidi plotar todos os 32 componentes da camada latente em um eixo. Apenas uma característica foi muito distinta das outras, que pareciam quase iguais no gráfico, isso serve para esclarecer que poucos componentes neste dado reduzido fazem sentido.

bar = [count+1 for count in range(reduced_data.shape[0])]

plt.figure(figsize = (7,10))
for col in range(reduced_data.shape[1]):
    plt.plot(bar,  reduced_data[:, col],label=f'feature {col}')
    
plt.xlabel("index")
plt.ylabel("feature")
plt.title("PCA encoded features")
plt.legend()
plt.savefig("pca-encoded features")

Gráfico de Componentes vs Índice:

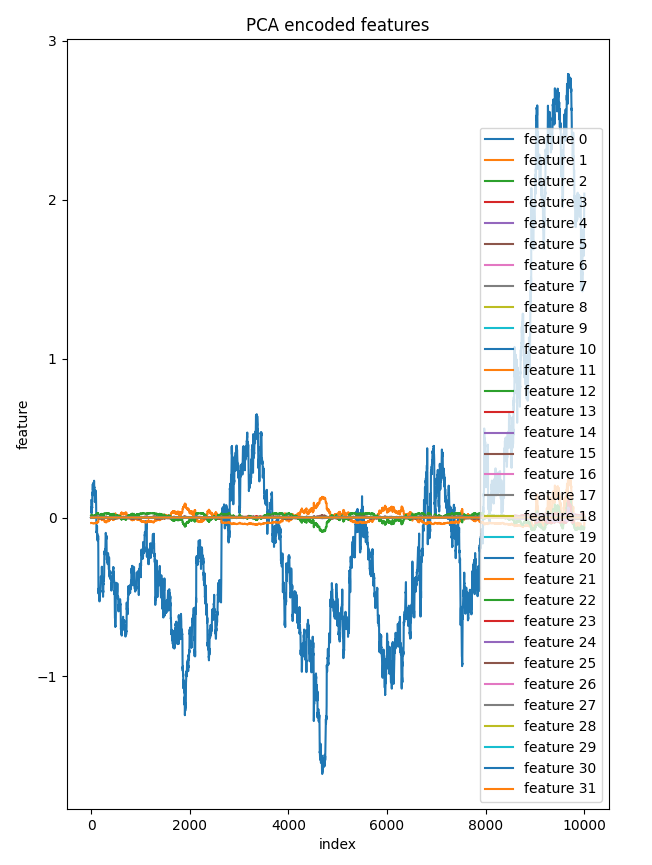
Aplicar PCA ao espaço latente do autoencoder oferece mais controle sobre o processo de redução em comparação com aplicar diretamente o PCA aos dados originais de alta dimensionalidade, sem mencionar que ajuda a reduzir o ruído desnecessário nos dados ao longo do processo.

Um Elefante na sala:

No exemplo discutido, reduzimos a dimensão de todos os dados de entrada, o que pode não ser ideal quando você deseja aplicar os dados reduzidos após o PCA em modelos preditivos. Nesse caso, pode ser necessário aplicar o PCA apenas às variáveis independentes.

Mas antes de podermos usar esse autoencoder que criamos para reduzir o ruído dos dados de negociação no MetaTrader 5, como outra aplicação do Autoencoder, precisamos salvá-lo no formato ONNX.

Salvando o Modelo Autoencoder no formato ONNX

Já extraímos tanto o codificador quanto o decodificador antes de aplicá-los para redução de dimensão. Converter e salvar no formato ONNX deve ser fácil. Vamos começar com o modelo do codificador, pois salvaremos ambos separadamente.

Python:

import tf2onnx
import onnx
import os

output_path = os.path.join('/kaggle/working/',"encoder.eurusd.h1.onnx")

# saving the encoder for MetaTrader 5

input_signature = [tf.TensorSpec(encoder_input.shape, tf.float16, name='x_inputs')] #onnx input signature
# Use from_function for tf functions
onnx_model, _ = tf2onnx.convert.from_keras(encoder_model, input_signature, opset=13)
onnx.save(onnx_model, output_path)

A input_signature para ONNX ajuda a evitar erros com as versões mais recentes do TensorFlow e ONNX, pois ajuda a esclarecer os nomes de entrada para o nosso arquivo .onnx ao carregar um modelo deste formato no MetaTrader 5.

Salvando o modelo decodificador:

Python:

# saving the decoder

output_path = os.path.join('/kaggle/working/',"decoder.eurusd.h1.onnx")

input_signature = [tf.TensorSpec(decoder_input.shape, tf.float16, name='decoder_inputs')] #onnx input signature

onnx_model, _ = tf2onnx.convert.from_keras(decoder_model, input_signature, opset=13) #conver keras model to onnx
onnx.save(onnx_model, output_path)

No artigo Superando os Desafios de Integração com ONNX, abordei o problema de integrar as mesmas técnicas de redução de dimensão e escalonamento disponíveis tanto para Python quanto para a linguagem de programação mql5 com precisão, mas encontrei uma solução fácil para mitigar o problema de escalonamento.

Salvando o Scaler:

Usar o mesmo scaler em Python e mql5 é crucial. Não posso enfatizar o quão importante isso é.

Python:

scaler.data_min_.tofile("minmax_min.bin")
scaler.data_max_.tofile("minmax_max.bin")

Salvamos os arrays de informações do Min-Max scaler em arquivos binários simples que podemos incluir em nosso indicador MetaTrader 5. Após salvá-los na pasta MQL5\Files.

MQL5 (AutoEncoder Indicator.mq5):

//Load both the encoder_model and the decoder_model
#resource "\\Files\\encoder.eurusd.h1.onnx" as uchar encoder_onnx[];
#resource "\\Files\\decoder.eurusd.h1.onnx" as uchar decoder_onnx[];

// Load the MinMax scaler also
#resource "\\Files\\minmax_min.bin" as double min_values[];
#resource "\\Files\\minmax_max.bin" as double max_values[];

Reduzindo o Ruído dos Dados de Negociação

O Autoencoder pode remover ruído dos dados, como visto em vários aspectos diferentes, como a remoção de ruído de imagens. Ainda precisamos provar isso nos dados financeiros. Observando a imagem dos preços de fechamento e os novos preços de fechamento, fica claro que os valores de preço de fechamento Auto-encodados são menos ruidosos. Vamos criar um indicador para nos ajudar a desenhar os candles para o novo OHLC fornecido pelo Autoencoder.

MQL5 (AutoEncoder Indicator.mq5):

#property indicator_chart_window
#property indicator_plots 1
#property indicator_buffers 5

input bool show_bars = true;
input bool show_bullish_bearish = false;

//--- plot Candle
#property indicator_label1  "autoencoded open; high; low; close"
#property indicator_type1   DRAW_COLOR_CANDLES
#property indicator_color1  clrRed, clrGray
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

Precisamos criar uma classe Autoencoder para facilitar o uso dos modelos ONNX carregados em MQL5, como se estivéssemos usando-os em Python.

MQL5(Autoencoder-onnx.mqh):

class CAutoEncoderONNX
  {
protected:

   bool initialized;
   long onnx_handle;
   void PrintTypeInfo(const long num,const string layer,const OnnxTypeInfo& type_info);
   long inputs[], outputs[];
   
   void replace(long &arr[]) { for (uint i=0; i<arr.Size(); i++) if (arr[i] <= -1) arr[i] = UNDEFINED_REPLACE; }
   
public:
                     CAutoEncoderONNX(void);
                    ~CAutoEncoderONNX(void);
                     
                     bool Init(const uchar &onnx_buff[], ulong flags=ONNX_DEFAULT); //load the onnx model from a resource uchar array
                     bool Init(string onnx_filename, uint flags=ONNX_DEFAULT); //load the onnx model from a .onnx file 
                     
                     matrix predict(const matrix &x); //passing inputs for either the encoder or the decoder to the outputs in matrix form
                     vector predict(const vector &x); //passing inputs for either the encoder or the decoder to the outputs in matrix form
  };

Instanciando a classe CAutoEncoderONNX para cada modelo separadamente, como estão:

MQL5 (AutoEncoder Indicator.mq5):

#include <Autoencoder-onnx.mqh>
#include <MALE5\preprocessing.mqh>

CAutoEncoderONNX encoder_model; //for the encoder model
CAutoEncoderONNX decoder_model; //for the decoder model
MinMaxScaler *scaler; //Python-like MinMax scaler

Inicializando os modelos:

MQL5 (AutoEncoder Indicator.mq5):

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   if (!encoder_model.Init(encoder_onnx)) //initializing the encoder
     return INIT_FAILED;
   
   if (!decoder_model.Init(decoder_onnx)) //initializing the decoder
     return INIT_FAILED;
   
   scaler = new MinMaxScaler(min_values, max_values); //Load the Minmax scaler saved in python
     
//---
   return(INIT_SUCCEEDED);
  }

Para obter as previsões do modelo, vamos passar os dados brutos para o codificador e, em seguida, passar o resultado para o decodificador para a saída final. Lembre-se! Em Python, tínhamos dois modelos separados passados um após o outro na função call.

Python:

class Autoencoder(Model):
...
...

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

Vamos ver isso em ação no mql5:

MQL5 (AutoEncoder Indicator.mq5):

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime& time[],
                const double& open[],
                const double& high[],
                const double& low[],
                const double& close[],
                const long& tick_volume[],
                const long& volume[],
                const int& spread[])
  {
//---
   
   int start = prev_calculated;
   if(start>=rates_total)
      start = rates_total-1;
   
   
   vector encoded_data = {}, decoded_data = {};
   for(int i = start; i<rates_total; i++)
     {
        vector x_inputs = {open[i], high[i], low[i], close[i]};
        
        x_inputs = scaler.transform(x_inputs); //Normalize the input data, important!
        encoded_data = encoder_model.predict(x_inputs); //encode the data
        decoded_data = decoder_model.predict(encoded_data); //decode the data
        
        decoded_data = scaler.inverse_transform(decoded_data); //return data to its original state  
          
        open_candle[i]= decoded_data[0];
        high_candle[i]= decoded_data[1];
        low_candle[i]=  decoded_data[2];
        close_candle[i]=decoded_data[3];
        
        // Set upper and lower body colors based on the gradient
        
        if (close_candle[i]>open_candle[i])
         {
           color_buffer[i] = 1.0; //Draw gray for bullish candle
         }
        else
         {
          color_buffer[i] = 0.0; //draw red when there was a bearish candle
         }
                         
        if (MQLInfoInteger(MQL_DEBUG))
         Comment(StringFormat("plotting [%d/%d] OPEN[%.5f] HIGH[%.5f] LOW[%.5f] CLOSE[%.5f]",i,rates_total,open_candle[i],high_candle[i],low_candle[i],close_candle[i]));
     }
     
//--- return value of prev_calculated for next call
   return(rates_total);
  }

Plot do Indicador:

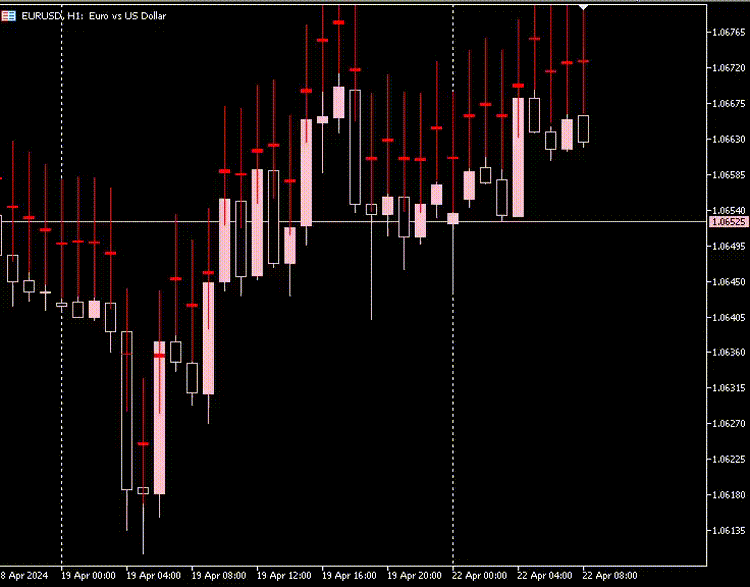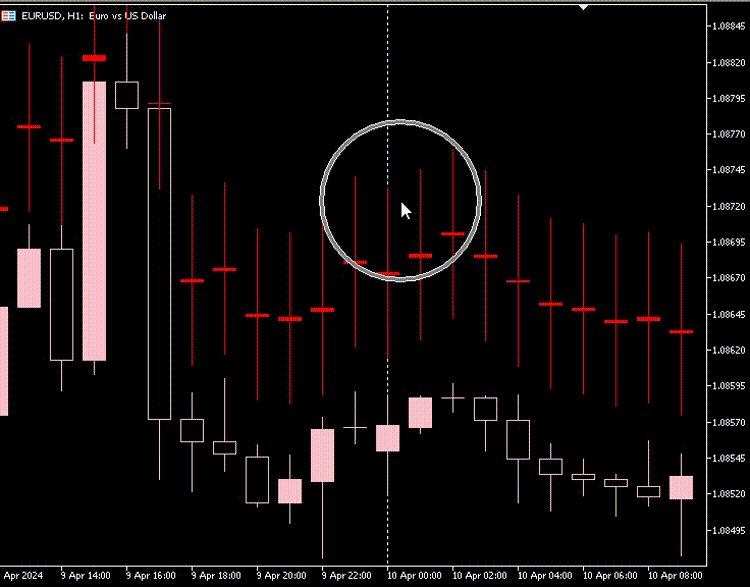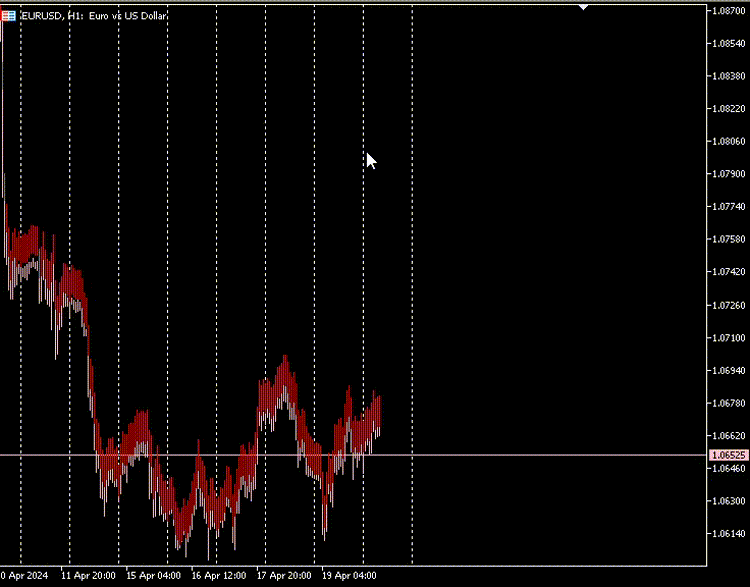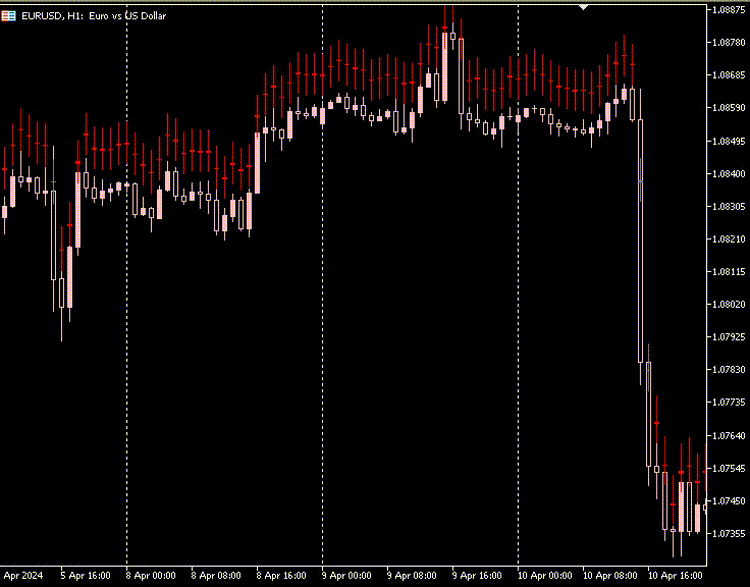
Da minha observação, os candlesticks feitos pelo Autoencoder têm quase o mesmo tamanho de corpo, e a diferença entre os preços mais baixos e mais altos é alta e quase a mesma para todas as velas.

A maioria das velas está em um mercado de baixa em vermelho, e poucas velas são de alta em cinza.

Para que este indicador apareça bem no gráfico, podemos preencher o espaço entre o preço mais baixo e o mais alto do candle. Para ambos os candles de alta e baixa.

MQL5 (AutoEncoder Indicator.mq5):

  if (close_candle[i]>open_candle[i])
   {
     color_buffer[i] = 1.0; //Draw gray for bullish candle

     close_candle[i] = high_candle[i];
     open_candle[i] = low_candle[i];
   }
  else
   {
     color_buffer[i] = 0.0; //draw red when there was a bearish candle
    
     close_candle[i] = low_candle[i];
     open_candle[i] = high_candle[i];
   }

Plot do Indicador:

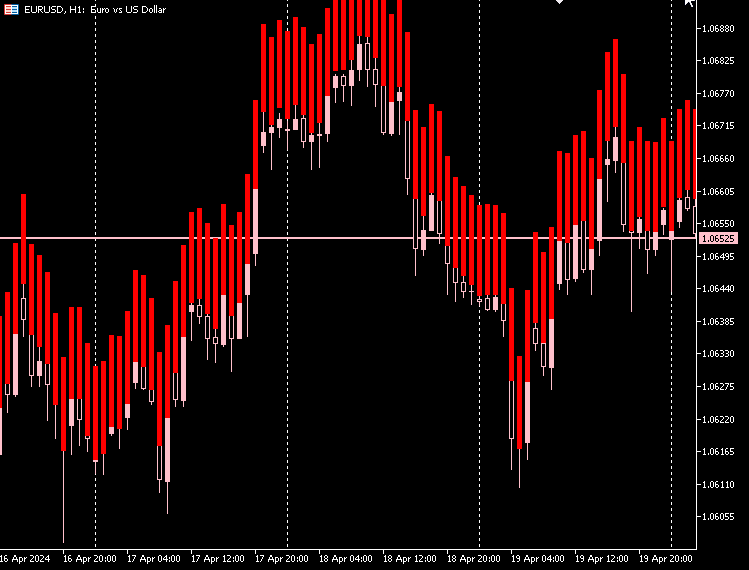
Podemos dar ao nosso indicador uma opção para distinguir entre candles de alta e baixa com base nos preços reais de abertura e fechamento do mercado.

MQL5 (AutoEncoder Indicator.mq5):

if (show_bullish_bearish)
 {
  if (close[i]>open[i])
   color_buffer[i] = 1.0;
  else
    color_buffer[i] = 0.0;
 }

Plot do Indicador:

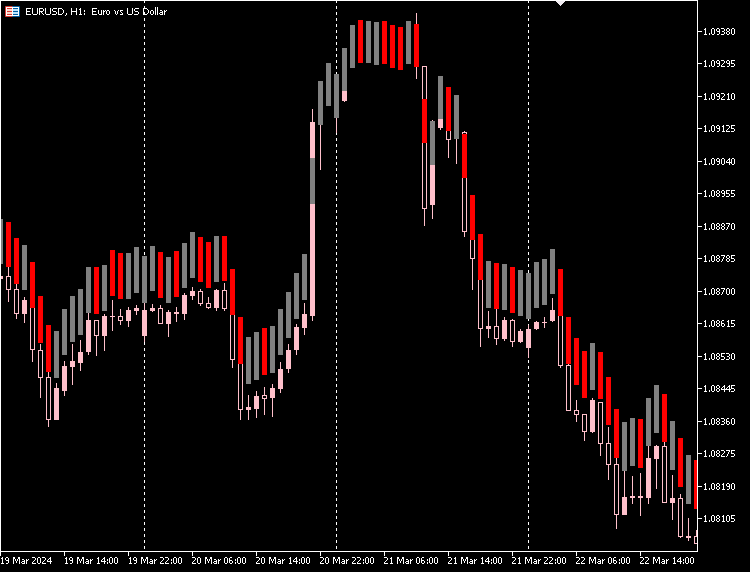
Também temos a opção de ocultar os candles originais e ficar apenas com os novos candles feitos com o autoencoder.

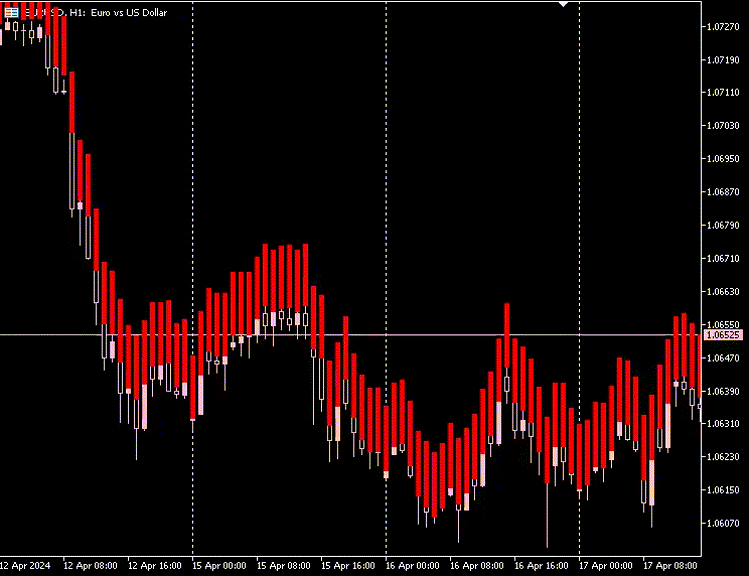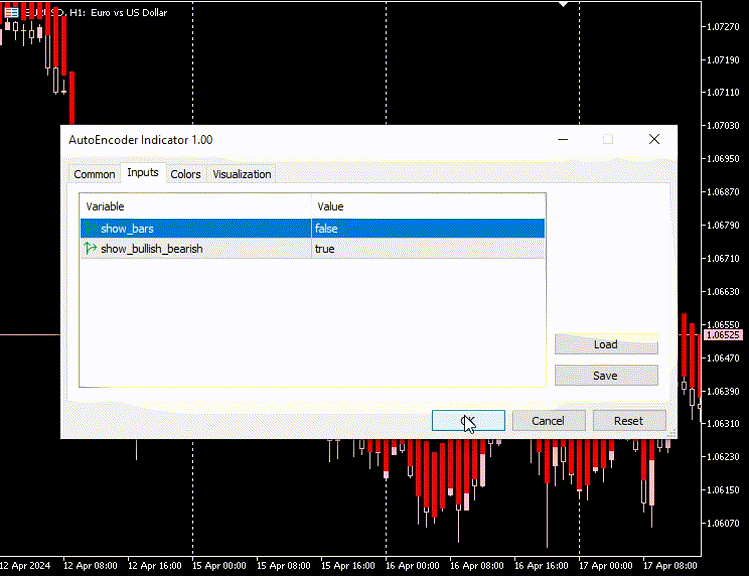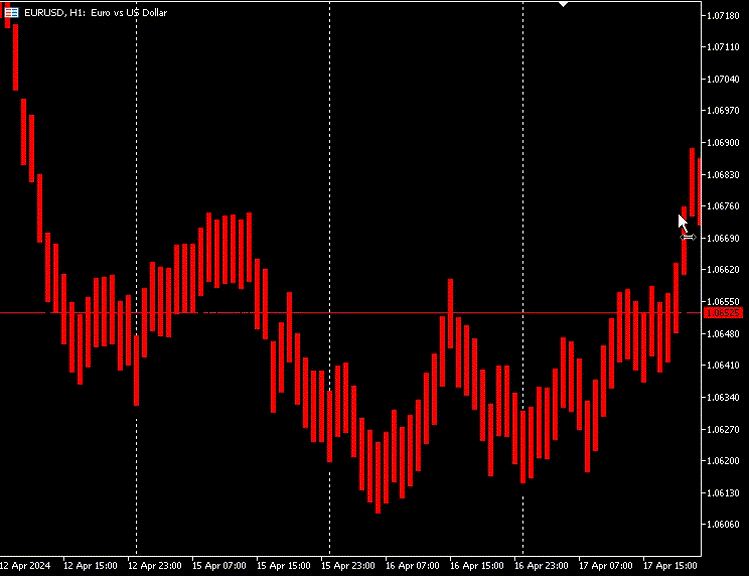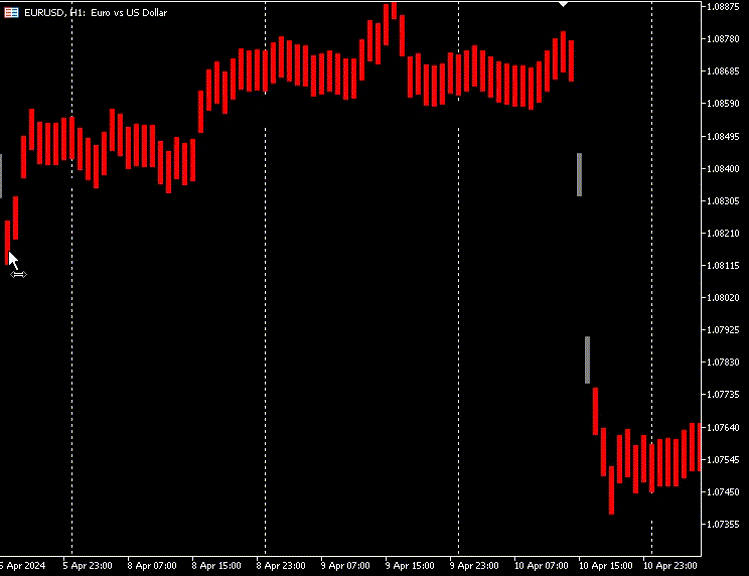
Desvantagens dos Autoencoders

Autoencoders, como todos os modelos de machine learning, têm seus próprios desafios:

1. Reconstrução Imperfeita dos Dados
   Os Autoencoders tentam recriar os dados após compactá-los. Às vezes, eles não fazem um bom trabalho, levando a erros na reconstrução dos dados originais. Isso é um problema se você precisa de uma recriação muito precisa dos dados originais.

2. Difícil de Entender
   Os formatos de dados compactados que os autoencoders produzem podem ser difíceis de interpretar. Frequentemente, não é claro quais características dos dados o autoencoder conseguiu capturar, o que dificulta a explicação de como o modelo funciona.

3. Sensível ao Ruído
   Os Autoencoders visam destacar os principais padrões nos dados, mas podem ter dificuldade com ruídos e outliers. Isso pode resultar em uma reconstrução ruim e em características tendenciosas, o que não é ideal.

4. Gargalo de Dimensionalidade
   A camada intermediária de um autoencoder, onde os dados são compactados, às vezes pode ser muito pequena. Se não tiver dimensões suficientes, pode não capturar todas as informações importantes para o que você precisa fazer. Escolher o tamanho certo para essa camada é fundamental e depende do que você está tentando alcançar.

5. Caro para Treinar
   Treinar autoencoders profundos, especialmente em grandes conjuntos de dados, pode consumir muito poder computacional. Isso é importante de lembrar se você tiver recursos ou tempo limitados.

6. Não é Bom para Todas as Tarefas
   Os Autoencoders podem não ser a melhor escolha para tarefas como classificação ou regressão, onde trabalhar diretamente com os dados de entrada pode ser mais eficaz.

7. Risco de Overfitting
   Usar modelos complexos para problemas simples pode levar ao overfitting, onde o modelo aprende muito bem os dados de treinamento, mas apresenta um desempenho ruim em novos dados não vistos.

Considerações Finais

Os Autoencoders podem ser uma ótima ferramenta para reduzir o ruído no mercado de forex, como visto no indicador em que acabamos com candles menos ruidosos que ainda refletem o mercado. Eles podem ser melhores ou piores que os candles originais. Esses novos candles nos dão uma perspectiva diferente do mercado.

Sinta-se à vontade para explorar os novos candles extraindo sinais de padrões e construindo estratégias de negociação sobre eles.

Até mais.

Tabela de Anexos: 

Arquivo	Descrição|Uso
Include\MatrixExtend.mqh	Contém funções adicionais para manipulação de matrizes.
Include\ preprocessing.mqh	A biblioteca para pré-processamento de dados brutos de entrada para torná-los adequados para uso em modelos de machine-learning.
Indicators\ AutoEncoder Indicator.mq5	O arquivo principal do indicador. Ele implementa o autoencoder discutido e desenha candles nas previsões resultantes.
Include\ Autoencoder-onnx.mqh	Uma biblioteca para carregar um modelo de machine-learning no formato ONNX e interpretar os resultados.
Arquivo\...	Salve esses arquivos na pasta MQL5\Files
autoencoders.ipynb	Python Jupyter notebook para rodar todo o código Python discutido.