Filtragem e extração de características no domínio da frequência

Introdução

No mercado financeiro, há uma demanda especial por modelos de previsão precisos. Assim, modelos preditivos confiáveis precisam de informações significativas e atuais. Neste artigo, vamos examinar o uso de vários filtros digitais, aplicados no domínio da frequência, como ferramentas para a extração de características. Vamos analisar algumas vantagens e desvantagens da análise de séries temporais transformadas no domínio da frequência usando Transformada Discreta de Fourier (TDF). Em particular, vamos abordar três tipos de filtros digitais: síncronos, em quadratura e em quadratura espelhados. Discutiremos sua utilidade de cada tipo na análise de séries temporais. E, por fim, apresentaremos o código que implementa exemplos de cada tipo.

Filtragem no domínio da frequência

No artigo "Implementação prática de filtros digitais no MQL5 para iniciantes", o autor apresentou filtros digitais aplicados ao domínio temporal. No artigo, a série é multiplicada por um conjunto único de pesos de diferentes comprimentos, dependendo do tipo de filtro e seus parâmetros. A quantidade de pesos determina a janela deslizante, que é convolvida com os valores correspondentes da série de dados ao aplicar o filtro em todo o conjunto de dados. As médias móveis funcionam de maneira semelhante.

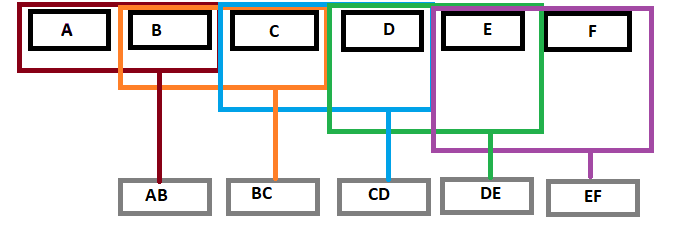
Neste artigo, aplicaremos filtros no domínio da frequência. Os principais passos ao aplicar filtros são:

1.  Primeiro, a série é pré-processada para a operação da TDF.
2.  A TDF é aplicada à série usando o algoritmo de Transformada Rápida de Fourier (TRF, FFT).
3.  Em seguida, alteramos a forma de onda da série de dados de qualquer maneira que consideremos necessária. Em outras palavras, o filtro é aplicado, alterando assim a forma original do sinal da série.
4.  A forma de onda alterada é então transformada de volta ao domínio temporal pela operação inversa da TDF.
5. Por fim, desfazemos quaisquer efeitos causados pelas operações realizadas na fase inicial de pré-processamento.

Semelhante à convolução no domínio temporal, os membros da TDF são multiplicados por coeficientes que determinam o filtro específico. Devido ao grande número de etapas, pode parecer que a filtragem no domínio da frequência exige muito mais esforço computacional. Mas isso nem sempre é verdade.

Ao trabalhar com grandes conjuntos de dados, o uso do algoritmo da transformada rápida de Fourier (TRF) pode, na verdade, ser muito mais rápido do que a convolução da série no domínio temporal. Especialmente quando se aplicam métodos avançados e "melhores práticas", que discutiremos mais adiante.

Filtragem de formas e funções

Um filtro é definido por uma função, cujos dados de saída podem ser alterados de acordo com a especificação do filtro. Modificar a saída da função muda a forma do filtro. A forma do filtro representa a curva de resposta do filtro. Ela determina o comportamento do filtro no domínio da frequência. Existem muitas formas de filtros usadas no processamento de sinais em várias áreas de pesquisa. Na análise de séries temporais, são preferidos filtros com cantos arredondados.

Os filtros de cantos arredondados possuem características únicas que são muito importantes para a análise de séries temporais. Primeiro, os cantos arredondados proporcionam características de frequência mais suaves. Isso ajuda a minimizar distorções que ocorrem nas transições entre componentes de frequência. Além disso, os cantos arredondados dos filtros facilitam sua implementação prática no mundo real. Como suas construções são baseadas em aproximações matemáticas, frequentemente oferecem desempenho superior. Assim, alcança-se um bom equilíbrio entre a capacidade de distinguir componentes de frequência úteis e indesejáveis e a minimização de distorções.

Neste caso, a função de filtragem utilizada é a função de filtragem de Gauss. De acordo com sua forma, o filtro é concentrado no domínio temporal. Ou seja, dura um tempo relativamente curto em comparação com outras funções de filtro. Existem muitos fatores a serem considerados ao escolher uma função para filtragem. Os requisitos da área de aplicação específica são prioritárias.

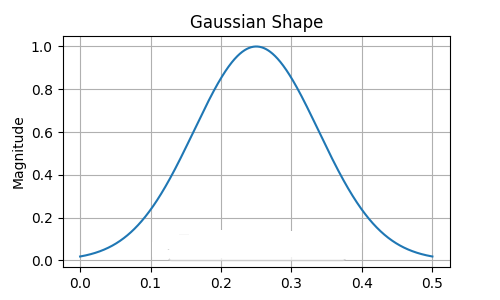
Especificação do filtro

Todos os filtros discutidos neste artigo são definidos por dois parâmetros. A frequência central e o parâmetro de largura, às vezes chamado de escala. Ambos os valores devem ser expressos em número de ciclos de frequência por amostra. A frequência central pode variar de 0 a 0,5. O parâmetro de largura define a faixa de frequências acima e abaixo da frequência central na banda de passagem que será permitida através da função do filtro sem distorção significativa da sua forma. A largura deve ter valores a partir de 0,01.

Filtros síncronos

Vamos começar a análise dos tipos com os filtros síncronos. A posição do sinal no tempo é chamada de sua fase. Os filtros síncronos mantêm a relação de fase do sinal de entrada com o sinal de saída. Isso significa que, quando o sinal de entrada passa por um filtro síncrono, o sinal de saída filtrado manterá as mesmas relações temporais que o sinal de entrada, dentro da faixa de frequências permitida.

Um filtro passa-faixa é o tipo básico de filtro síncrono, um bloco do qual podem ser construídos vários outros filtros. O filtro permite a passagem de uma determinada faixa de frequências, atenuando ou suprimindo frequências fora dessa faixa. Ele reduz os sinais com frequências abaixo ou acima da banda de passagem.

Filtros passa-baixa e passa-alta são implementados modificando o filtro passa-faixa. O filtro passa-baixa prioriza as baixas frequências no sinal. Geralmente é usado para detectar a tendência geral de um processo. Quanto mais baixa for a frequência central, mais suavizado será o sinal de saída filtrado. Usando a função de filtro passa-faixa, multiplicamos todas as frequências menores ou iguais à frequência central por uma constante de 1,0 e atenuamos todas as outras frequências que estão acima. 

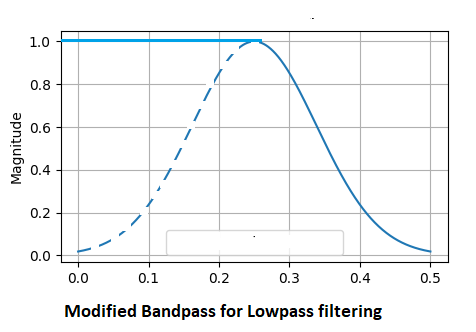
O filtro passa-alta remove todas as mudanças lentas do sinal, deixando apenas informações sobre mudanças rápidas. Neste caso, todas as frequências abaixo da banda de passagem da frequência central são atenuadas. Apenas as frequências nos intervalos mais altos passam.

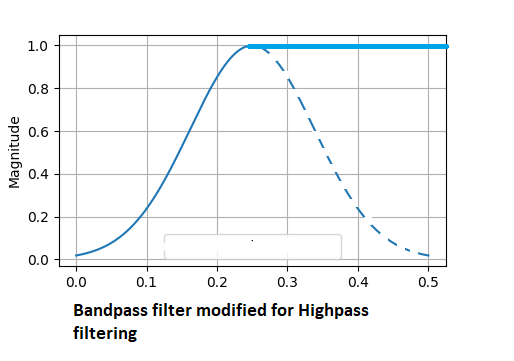
Existem muitas variantes de filtros síncronos,e alguns provavelmente funcionam melhor do que os que mencionamos. Todos os filtros discutidos aqui têm uma característica comum essencial: uma forma suficientemente arredondada, o que é uma qualidade importante.  

Filtros em quadratura

Esses filtros (também chamados de filtros analíticos) são projetados para processar sinais aplicando um deslocamento de fase de 90 graus (Pi/2 radianos) em relação ao sinal de entrada. Eles são frequentemente usados em conjunto com filtros síncronos, raramente usados isoladamente. Em determinadas situações, permitem detectar relações de fase em séries temporais.

Para entender as vantagens do filtro em quadratura, vamos considerar um exemplo. Abaixo está uma série representada por um componente periódico curto.

O gráfico a seguir mostra o sinal de saída da série com o filtro passa-faixa mostrado acima. Ele mostra a sincronia do filtro passa-faixa. Os movimentos do sinal filtrado coincidem com os movimentos da série original.

O próximo gráfico mostra o sinal de saída filtrado da versão quadratura do filtro passa-faixa. Ao observar atentamente, pode-se ver que os picos do sinal filtrado correspondem às transições pelo zero no sinal original. Essencialmente, o sinal de saída na filtragem em quadratura está alinhado com o deslocamento aplicado ao sinal de saída da faixa de passagem síncrona.

Os picos do sinal de saída em quadratura indicam mudanças significativas na série de entrada. Os picos e vales do filtro em quadratura indicam mudanças rápidas que ocorrem no sinal de entrada. E quando o sinal de entrada é estável, o sinal de saída será igual ou próximo de zero. Isso significa que os filtros em quadratura são sensíveis a mudanças que ocorrem em uma determinada velocidade.

Vamos considerar outro exemplo. A série abaixo é caracterizada por um movimento brusco para cima.

A seguir, apresentamos os resultados filtrados síncrona e em quadratura. Novamente, observe a posição dos picos e vales em relação ao movimento brusco para cima. Se identificar o movimento pelo sinal de saída síncrono é difícil, a série com filtragem em quadratura revela claramente o movimento explosivo.

Então, pode ser vantajoso usar esses dois tipos de filtros juntos. O uso conjunto do filtro síncrono e do filtro em quadratura com os mesmos parâmetros é chamado de filtro quadratura-espelho (filtro QM).

Filtros quadratura-espelho

Os filtros QM permitem detectar instâncias localizadas de componentes periódicos. Ao usar esse filtro, analisamos o sinal de saída síncrono em relação ao sinal de saída em quadratura. Ambos os sinais serão zero quando um determinado evento periódico estiver ausente. Os sinais de saída de ambos podem ser combinados, considerando o sinal de saída síncrono como a parte real e o de quadratura como a parte imaginária. Incluindo o cálculo da amplitude e fase do sinal filtrado.

Antes de passarmos para a implementação do código, precisamos lidar com um dos aspectos mais importantes de qualquer procedimento de análise de séries temporais.

Pré-processamento da série antes da transformação

O fato de as séries temporais terem comprimento finito cria problemas ao transformá-las para o domínio da frequência usando a TDF. A TDF assume que a série não processada é periódica e, portanto, se repete infinitamente. Aplicar a TDF a um sinal não periódico pode causar distorções na forma do sinal de saída.

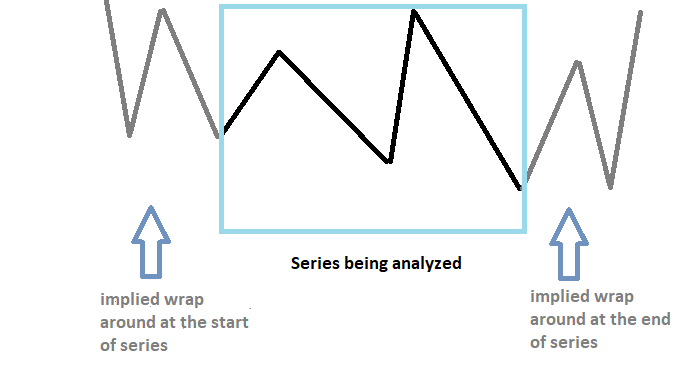
Para reduzir esse efeito de vazamento, precisamos ajustar o final da série com valores constantes adicionais. O aumento artificial do número de amostras na série pode fornecer uma resolução de frequência mais precisa e reduzir o vazamento espectral. Essa operação é chamada de complementação. A série complementada é transformada usando a TDF. Os valores adicionais incluídos na série ajudam a reduzir distorções no espectro da série, mas esses não são os únicos benefícios.

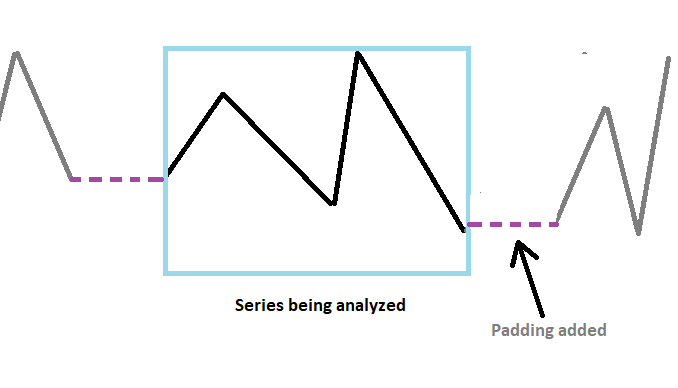
Aumentar o comprimento da série para que o número total de amostras seja uma potência de 2 melhora significativamente a eficiência computacional do algoritmo FFT. À primeira vista, parece estranho que aumentar intencionalmente o comprimento melhore o desempenho, mas é realmente assim. Por isso, essa operação não deve ser negligenciada. Além do uso de zeros, uma série pode ser completada com a média calculada da própria série.

Séries temporais financeiras geralmente apresentam uma característica indesejada: são não estacionárias. Quando a série é completada e contém um componente de variação lenta, o contraste acentuado entre os valores nas extremidades da série original e os valores usados para preenchimento pode se manifestar como um componente frequente notável na área de frequência. Isso causa a chamada contaminação.

Para se proteger dessa forma de distorção, é necessário excluir a tendência dos valores originais da série. Assim, os valores originais da série são substituídos por valores sem tendência. Quando for necessário retornar ao intervalo de tempo original da série, basta restaurar a tendência. Abordaremos isso ao discutir a implementação do código na próxima seção.

Classe CFilter

A classe CFilter encapsula os principais exemplos dos três tipos de filtros discutidos. O código está no arquivo Filter.mqh, que começa incluindo o arquivo fasttransforms.mqh da biblioteca ALGLIB.

//+------------------------------------------------------------------+
//|  CFilter - class implementing select filters in the freq domain  |
//+------------------------------------------------------------------+
class CFilter
  {
   int               m_length;                   //length of original series
   int               m_padded_len;                //modified length of series
   int               m_half_padded_len;           //half of modded series
   double            m_slope, m_intercept;     //slope and intercept of trend in series
   double            m_buffer[];               //general internal buffer
   bool              m_initialized;              //initialization flag
   complex           m_dft[];                 //general complex buffer

public:
                     CFilter(double &series[],uint min_padding=0, bool detrend=true);
                    ~CFilter(void);

   void              Lowpass(double freq,double width,double &out[],bool add_trend);
   void              Highpass(double freq,double width, double &out[]);
   void              Bandpass(double freq,double width, double &out[]);
   void              Qmf(double freq,double width, complex &out[]);
   bool              IsInitialized(void) { return m_initialized; }
  };

A classe CFilter possui um construtor paramétrico, ao qual o usuário deve passar a série bruta para filtragem, além de dois outros parâmetros que determinam a magnitude do preenchimento aplicado e a necessidade de uma operação de remoção de tendência antes de aplicar a transformação FFT. Se min_padding for definido como 0, a magnitude real do preenchimento será determinada apenas pelo número de amostras. O parâmetro min_padding define o número mínimo de valores que serão adicionados à série, excluindo quaisquer valores adicionais incluídos para estender a série ao próximo número potência de dois.

Dentro do construtor, após verificar todos os argumentos, calcula-se o comprimento final da série completada e, se necessário, realiza-se a operação de remoção de tendência. A série completada é armazenada no array m_buffer. Em seguida, a FFT é aplicada à forma de onda definida no array de números complexos m_dft. Se ocorrer um erro no construtor, o parâmetro m_initialized será definido como false.

//+------------------------------------------------------------------+
//|constructor                                                       |
//+------------------------------------------------------------------+
CFilter::CFilter(double &series[],uint min_padding=0,bool detrend=true)
  {
//---local variables
   m_initialized=false;
   int i;
   int npts = ArraySize(series);
   int pad = (int)MathAbs(min_padding);
//--- check size of series
   if(npts<=0)
     {
      Print("Input array is empty");
      return ;
     }
//---
   m_length = npts ;
   for(m_padded_len=2 ; m_padded_len<INT_MAX ; m_padded_len*=2)
     {
      if(m_padded_len >= npts+pad)
         break ;
     }
//---
   if(m_padded_len<npts+pad)
     {
      Print("Warning, calculated length of modified series is too long");
      return;
     }
//---
   m_half_padded_len = m_padded_len / 2;
//---
   ArrayResize(m_buffer,m_padded_len);
//---
   if(m_padded_len > npts)            // Any padding needed?
     {

      if(detrend)
        {
         m_intercept = series[0] ;
         m_slope = (series[npts-1] - series[0]) / (npts-1) ;
        }
      else
        {
         m_intercept = m_slope = 0.0 ;
         for(i=0 ; i<npts ; i++)
            m_intercept += series[i] ;
         m_intercept /= npts ;
        }

      for(i=0 ; i<npts ; i++)
        {
         m_buffer[i]=series[i] - m_intercept - m_slope * i ;
        }
      for(i=npts ; i<m_padded_len ; i++)
        {
         m_buffer[i]=0.0;
        }
     }

   else
     {
      ArrayCopy(m_buffer,series);
      m_intercept = m_slope = 0.0 ;
     }
//---Compute the Fourier transform of the padded series
   CFastFourierTransform::FFTR1D(m_buffer,int(m_padded_len),m_dft);
//---
   m_initialized = true;

  }

O usuário deve verificar se a instância foi criada corretamente. Para isso, chama-se IsInitialized(). Em caso de sucesso, a função deve retornar true.

Após a criação bem-sucedida da instância, o usuário pode chamar qualquer um dos métodos públicos que aplica o filtro especificado ao sinal armazenado em m_dft. A maioria deles tem requisitos de entrada semelhantes. Primeiro, as características do filtro são determinadas pelos parâmetros de frequência freq e largura width. Eles correspondem à frequência central e à largura da banda passante aplicada. Quase todos os métodos esperam pelo menos um último array de entrada, no qual os resultados da operação de filtragem serão armazenados.

Lowpass() é o único método que aceita um quarto parâmetro de entrada, que determina se a operação de remoção de tendência inicialmente aplicada ao sinal original deve ser desfeita na saída do filtro.

//+--------------------------------------------------------------------+
//|Filters series in frequency domain and returns output in time domain|
//+--------------------------------------------------------------------+
void CFilter::Lowpass(double freq,double width,double &out[],bool add_trend)
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=0 ; i<=m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;  // This frequency
      if(f <= freq)                  // Flat to here
         wt = 1.0 ;
      else
        {
         dist = (f - freq) / width ;
         wt = exp(-dist * dist) ;
        }
      dft_temp[i].real*=wt;
      dft_temp[i].imag*=wt;
     }
//---
   double temp[];
//---
   CFastFourierTransform::FFTR1DInv(dft_temp,m_padded_len,temp);
//---
   ArrayResize(out, m_length);
//---
   for(int i = 0; i<m_length; i++)
      out[i]=(add_trend)?temp[i] + m_intercept + m_slope*i:temp[i];

  }

 A implementação dos filtros síncronos consiste em duas etapas: primeiro, a forma do sinal colocada em m_dft é multiplicada por uma função de filtro modificada. Nesta implementação, é usada a função Gaussiana. Depois, realiza-se a operação inversa da FFT, que retorna a série para o domínio do tempo.  

Para calcular os parâmetros de saída do filtro QM, multiplicamos os componentes da FFT do sinal pela versão em quadratura da função do filtro. A função do filtro de quadratura é a função do filtro síncrono com um deslocamento de fase de 90 graus aplicado. Para obter esse deslocamento de fase, a função do filtro síncrono é multiplicada por i, o que a torna puramente imaginária. O resultado é uma função cujos dados de saída são simétricos em relação à frequência de Nyquist. Os componentes de saída de ambos os lados da frequência 0,5 serão iguais em valor absoluto, mas opostos em sinal.

Com base nesse fato, o método Qmf() multiplica os componentes da FFT da forma de onda pelo somatório das funções do filtro síncrono e do filtro de quadratura. Para isso, a função do filtro de quadratura é tornada real (lembrando que a função do filtro de quadratura é imaginária) – para isso, multiplicamos por i. Quando as funções de filtro são somadas, os dados de saída além da frequência de Nyquist se anulam. No código, os componentes filtrados da FFT acima de 0,5 são definidos como 0. É necessário calcular apenas os dados de saída filtrados que estão abaixo ou iguais à frequência de Nyquist. Depois que o sinal é filtrado, realiza-se a operação inversa da FFT complexa para retornar ao domínio do tempo.

//+------------------------------------------------------------------+
//| Implements Quadrature Mirror Filter, output is complex           |
//+------------------------------------------------------------------+
void CFilter::Qmf(double freq,double width,complex &out[])
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=1 ; i<m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;    // This frequency
      dist = (f - freq) / width ;
      wt = exp(-dist * dist) ;
      dft_temp[i].real *= wt ;
      dft_temp[i].imag *= wt ;
      dft_temp[m_padded_len-i].real = dft_temp[m_padded_len-i].imag = 0.0 ;  // Causes QMF outputs
     }

//---
   dft_temp[0].real = 0.0 ;
   dist = (0.5 - freq) / width ;
   dft_temp[m_half_padded_len].real = 0.5 * dft_temp[m_half_padded_len].imag * exp(-dist * dist) ;
//---
   dft_temp[0].imag = dft_temp[m_half_padded_len].imag = 0.0 ;     // By definition of real transform
//---
   CFastFourierTransform::FFTC1DInv(dft_temp,m_padded_len);
   ArrayResize(out,m_length);
//---
   for(i=0 ; i<m_length ; i++)
     {
      out[i].real = dft_temp[i].real/double(m_half_padded_len) ;
      out[i].imag = dft_temp[i].imag/double(m_half_padded_len) ;
     }
  }
//+------------------------------------------------------------------+

Programa AFD.mq5

Vamos analisar o uso da função CFilter com o exemplo do aplicativo AFD.mq5. O aplicativo é implementado como um EA. O EA permite aos usuários gerar sequências aleatórias de um comprimento específico. Os usuários podem definir o comprimento da série gerada, bem como configurar o valor inicial dos números aleatórios. A série é representada em azul no gráfico superior. No segundo gráfico, é possível observar o resultado da aplicação do filtro selecionado à série gerada. Todos os parâmetros do filtro podem ser configurados na interface gráfica do programa. É assim que o aplicativo se apresenta.

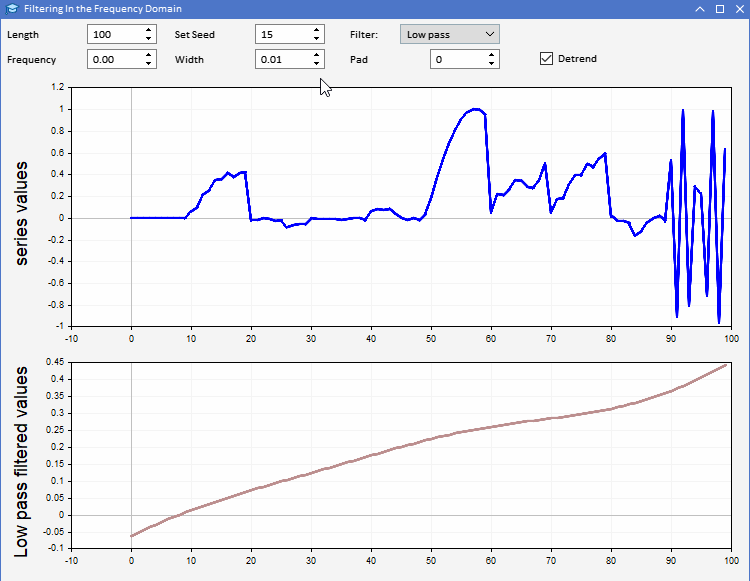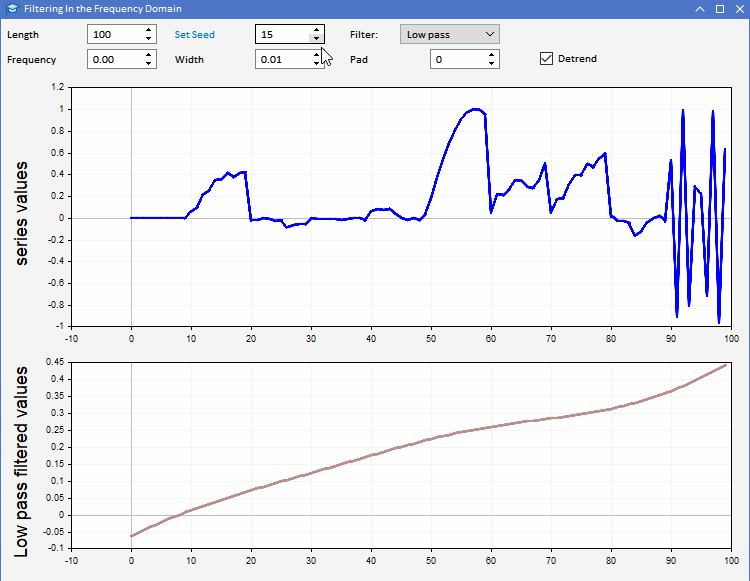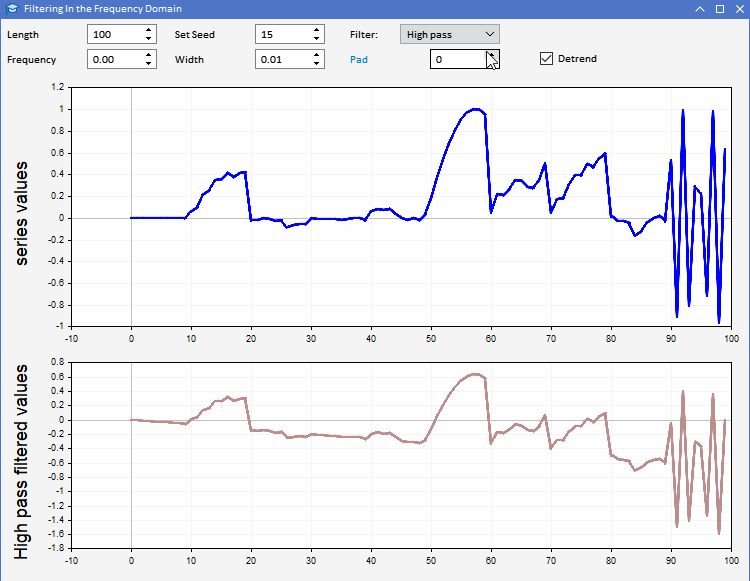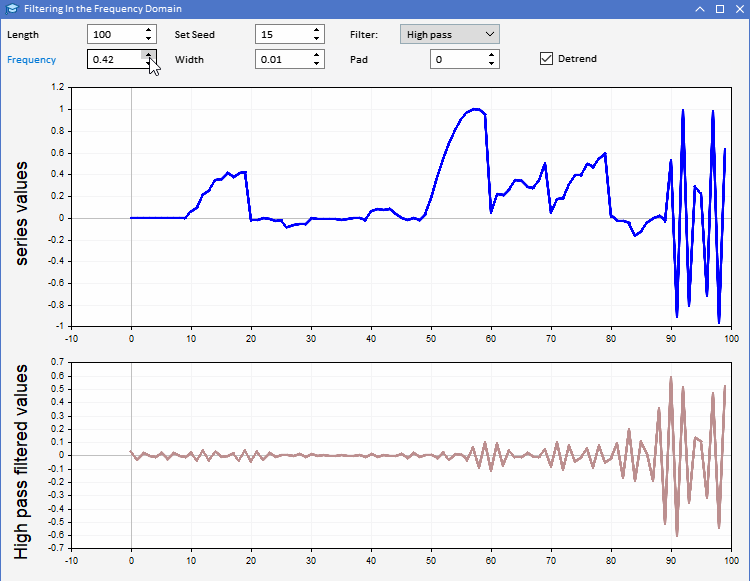
Usando o aplicativo AFD, podemos entender melhor os diferentes tipos de informações obtidas com os filtros. Existem duas maneiras de usar o sinal dos filtros síncronos. O sinal de saída do filtro passa-baixa pode ser usado para fornecer informações sobre o valor médio da série de entrada em qualquer momento. O sinal de saída do filtro passa-alta revela máximos e mínimos aleatórios observados na série original. Esses dados de saída fornecem uma visão sobre o estado da série de entrada a cada momento.

Os dados de saída do filtro passa-banda são menos óbvios em termos de sua significância. Provavelmente, ninguém será capaz de entender o significado do sinal de saída do filtro apenas observando-o. No entanto, é possível que esses dados possam ser úteis para um modelo de previsão. Talvez, encontrar o sinal de saída de uma determinada banda de frequência em um pico ou mínimo indique algo na série original.

Vamos analisar o sinal de saída do filtro passa-banda de uma série aleatória em diferentes frequências.

Os resultados mostram um tipo diferente de informação. Os picos dos sinais de saída do filtro passa-banda exibem a magnitude das mudanças periódicas em um determinado intervalo de tempo. Mais precisamente, eles mostram a amplitude da variação, indicando a presença de uma mudança periódica. Picos mais baixos sinalizam uma menor variação.

A amplitude é determinada pela amostragem do sinal de saída do filtro QM. Os cálculos de amplitude e fase usando os valores do filtro QM são mostrados no trecho de código abaixo do AFD.mq5.

 case ENUM_QMF_AMPLITUDE:
        {
         y_name = "Amplitude";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=MathSqrt(comp[i].real*comp[i].real + comp[i].imag*comp[i].imag);
        }
      break;
      case ENUM_QMF_PHASE:
        {
         y_name = "Phase";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=(comp[i].real>=1.e-40 || comp[i].imag>=1.e-40)?atan2(comp[i].imag, comp[i].real):0.0;
        }
      break;

A diferença no sinal de saída do filtro passa-banda em diferentes frequências mostra que uma variedade de informações está disponível. Assim, é possível criar funções únicas para uso em algoritmos de aprendizado de máquina. Para construir conjuntos de dados adequados, o praticante precisa entender claramente os parâmetros que definem um filtro específico.

Parâmetro de largura

Como mencionado anteriormente, os parâmetros de todos os filtros implementados são expressos em ciclos de frequência por unidade de tempo. Uma das desvantagens da análise no domínio da frequência é a dificuldade de relacionar componentes de frequência com sua extensão no domínio do tempo. Usando o exemplo da série aleatória que discutimos na seção anterior, os sinais de saída do filtro passa-banda foram discretizados nas frequências 0,15, 0,3 e 0,45 com a mesma largura de 0,03. É importante entender o que esses valores significam, especialmente em relação ao domínio do tempo da série.

A frequência 0,15 tem um período de 1/0,15 = 6,67 amostras por ciclo. A largura define a resolução no domínio da frequência. Se quisermos isolar uma faixa estreita de frequências, aplicamos uma largura pequena, geralmente 0,01 — isso é o mínimo, embora possa ser ainda menor. Voltando ao nosso exemplo. A largura foi definida como 0,03, então a faixa passante se estende de 0,15-0,03 a 0,15+0,03, ou seja, de 0,12 a 0,18. As frequências dentro desse intervalo passarão, enquanto as frequências acima e abaixo serão quase totalmente filtradas.

A largura também indica a resolução no domínio do tempo. A relação entre a resolução no domínio da frequência e a resolução no domínio do tempo é inversa. Uma resolução mais alta em um domínio leva à perda de resolução no outro. Para estimar a extensão no domínio do tempo em relação à largura, usamos a fórmula 0,8/largura.

Com ela, podemos estimar o número de amostras no domínio do tempo que serão influenciadas pela faixa passante da frequência em relação à posição atual. Em outras palavras, estimamos o número de amostras antes e depois da posição atual que afetarão o resultado observado. Voltando ao exemplo, uma largura de 0,03 implica um tamanho temporal de 0,8/0,03 = 27 amostras. Isso significa que o valor de cada sinal de saída é determinado ou depende de 27 observações anteriores e de 27 observações seguintes.

Em geral, a largura do filtro deve ser proporcional à frequência central da faixa passante que queremos estudar. Isso está relacionado ao período da frequência. Frequências mais baixas têm períodos mais longos, enquanto frequências mais altas têm períodos mais curtos. Portanto, para frequências mais baixas, podemos sacrificar a resolução no domínio do tempo e escolher uma largura estreita. Por outro lado, frequências mais altas se beneficiam de parâmetros de largura mais amplos, o que se traduz menos no domínio do tempo.

Finalmente, o parâmetro de largura também influencia os valores passados para o modelo de previsão. Voltando ao exemplo anterior, o intervalo de tempo implícito, pelos nossos cálculos, é de cerca de 27 observações. Suponha que precisamos prever o próximo valor da série em um intervalo de tempo de 201. Forneceremos o valor da saída filtrada, calculado com base em 200 valores conhecidos, ou seja, 27 slots antes do fim da série. Não podemos usar conscientemente qualquer dado de saída filtrado além desse ponto, pois sabemos que eles estarão sujeitos aos efeitos causados pela FFT, de acordo com as limitações dos parâmetros do filtro.

No último exemplo, filtramos os dados de saída em diferentes frequências, mas com a mesma largura. Na prática, seria mais útil amostrar os dados de saída filtrados em frequências e larguras estrategicamente escolhidas para obter o máximo de informações úteis.

Considerações finais

Bem, examinamos três tipos de filtros:

• Os filtros síncronos ajudam a decompor uma série ruidosa em diferentes componentes, destacando informações importantes e removendo características distrativas. Passando informações relevantes para os algoritmos de aprendizado, podemos construir modelos de previsão mais eficazes.

• Os filtros de quadratura podem ser usados para identificar áreas de rápida mudança de nível na série. Embora identificar movimentos importantes na série possa ser fácil, transmitir esses fenômenos para um algoritmo de aprendizado pode ser difícil. Aqui reside o valor dos filtros de quadratura.

• A combinação de filtros síncronos e de quadratura permite identificar a presença de características periódicas. Essas ferramentas podem ser eficazes na identificação e estudo de características que parecem se manifestar de forma aleatória em séries temporais.

A filtragem no domínio da frequência melhora a eficiência computacional, proporcionada pelo algoritmo FFT. Em comparação com o método de convolução no domínio do tempo, é um nível completamente diferente. Mas nem tudo é perfeito. A transformação das séries para o domínio da frequência traz armadilhas que podem levar a conclusões completamente errôneas devido a distorções causadas pelo manuseio descuidado dos dados. Sendo assim, é necessário ter extrema cautela ao aplicar essas técnicas.

O código de todas as ferramentas e programas discutidos está anexado. O arquivo AFD.mq5 usa a notável biblioteca de interface gráfica Easy and Fast (EAF). Ela está disponível na biblioteca de códigos no mql5.com. Nota: ao usar a biblioteca EAF junto com a ALGLIB, sempre inclua a EAF por último em seu aplicativo, pois há alguns conflitos de nomes entre essas bibliotecas que causam erros de compilação.  

Nome do arquivo	Descrição
Mql5\Include\Filter.mqh	Contém a definição da classe CFilter, que implementa filtros digitais básicos no domínio da frequência.
Mql5\Include\RandomStationarySeries.mqh	Contém sub-rotinas (funções) para gerar séries aleatórias com várias características. Usado no aplicativo AFD.ex5.
Mql5\Experts\AFD.mq5	Este é o código-fonte do aplicativo AFD, que usa a biblioteca de GUI Easy and Fast, publicada na Code Base do mql5.com.
Mql5\Experts\AFD.ex5	Aplicativo AFD compilado, implementado como um EA.