조건에 따라 현재 예금 금액의 일정한 비율 q 가 매월 발생하는 사용 중인 시간 t 에 대한 예금이 있고 고정 비율 k 를 q 이하로 인출해야 함을 상기시켜 드리겠습니다. 매월 0% 이상. 모든 것.
예금의 자금을 고려하지 않고 기간 t 동안 인출된 자금을 최대화하는 kOpt 를 찾아야 합니다. 이 솔루션은 두 매개변수 q 및 t 의 함수로 분석 형식으로 표현되어야 합니다(수치 솔루션, 다양한 그래프 및 종속성 형태의 특정 솔루션은 이미 얻어졌기 때문에 관심이 없습니다). 분석 솔루션이 근사적이면 문제 솔루션의 선언된 정확도가 달성되는 q 및 t 에 대한 한계를 표시해야 합니다.
추신 모든 종류의 종소리와 휘파람 - 인플레이션에 대한 설명, 발생한이자 q 의 불변성, 매개 변수 k 의 변화 등 가장 단순한 경우에 대한 솔루션을 얻기 전에 고려하는 것은 의미가 없다고 생각합니다.
Oleg , Forex와 관련하여 t 는 50으로 설정할 수 있습니다. 덜 의미가 없기 때문에 일반적인 예금 수명 이 5년 미만인 경우 전체 이익을 인출하는 것이 옳고 초기 예금의 규모는 이자 측면에서 "평생"을 제공해야 합니다. 수명이 5년 이상인 경우 초기 보증금은 작업에 포함되지 않으며 1000루블부터 시작할 수 있습니다. 그러나 자금 인출의 최적 비율이 있습니다. 또한 특성 수명이 필수 값이 아니라는 점을 고려하면(통계에 대해 이야기하고 있음) 상수 = 50으로 설정하여 이 매개변수를 공식에서 제외할 수 있습니다. 따라서 kOpt에 대해 (이상적으로는) 단 하나의 매개변수(TS - q 의 평균 수익성)의 분석적 근사값이 있습니다.
나는 공식을 간단하게 만드는 방법을 아직 모른다. Newton의 방법 은 적어도 세 번째 또는 네 번째 반복에서 다소 정확한 솔루션을 제공합니다. 그것은 매우 번거롭고 다층적인 공식이 될 것입니다.
q 에 대한 설명은 이제 이항 확장이 여기서 쓸모가 없다는 것을 추가로 확인합니다. q = 0.1 및 t = 10일지라도 너무 많은 이항 항이 유지되어야 합니다. 그리고 t 와 q 가 많을수록 더 나빠집니다. 즉, 합리적인 t (아마도 20 이상)에 대해 거의 항상
(1+ qk )^ t ~ exp(( qk ) t )
관찰에 따르면 큰 q 와 작은 t (각각 0.3과 10) 의 경우 월 수입의 대부분(70%)을 인출하는 것이 최적입니다.
그리고 작은 q 와 작은 t 의 경우 합리적인 범위 내에 극한값이 없습니다. 얻은 모든 것을 인출해야 합니다.
동시에 평균 q 와 평균 t (0.2 및 20)로 수입의 상당 부분, 즉 절반(44%)을 인출하는 것이 합리적입니다.
또한 중형 q 및 대형 t (0.2 및 30)의 경우 수입의 더 작은 부분(26%)을 인출하는 것이 합리적입니다.
등. 등. 태스크는 매개변수에 따라 질적으로 다르게 작동합니다. 낙관적이고 단 하나의 답은 없는 것 같습니다. q 와 t 에 따라 k 를 추정해 볼까요?
추신 Sergey , 귀하의 의견을 참조하십시오. 자, t = 50을 수정합니다. 작업이 더 쉬워졌습니다. 번 돈의 더 작은 부분을 인출하는 것으로 충분합니다( q = 0.1, t = 50 -> k / q = 0.3, 즉 30%). 이것은 가능한 최대 k / q 입니다.
Sorento :
다른 무엇? 결국 더 많은 것이 필요합니다. :)
글쎄요, 그를 위한 신은 엄격하게 엄격합니다! 동의한다.
방법에 따라 평가하고 결과를 제시하십시오.
{ N =120, q (month)=60.91%/12 Initial Capital=100 } 조건에서 차트에 표시했습니다. 그리고 K와 샤먼화 하는 것 - 할 수 없다. .
누군가가 이러한 조건에 대해 kOpt 를 제공하면 사후 숫자를 표로 작성하고 반올림을 고려합니다 ...
;)
자, 이제 수학자 와 쏘렌토 를 위한 질문입니다. 위에서 두 분 모두 고유한 Mikhail Andreevich 의 솔루션을 의미에서 언급했습니다. 이제 어떻게 될까요? 모든 것이 명확합니다 ... 다음은 무엇입니까?
존경받는 Mikhail Andreevich는 계정의 두 배 시간에 대한 신성한 공식 외에는 아무것도 없다는 것이 밝혀졌습니다. :-) 일반적으로 우리는 Alesei 의 kOpt 에 대한 대략적인 솔루션을 기다리고 있다고 가정합니다.
자, 이제 수학자와 쏘렌토를 위한 질문입니다. 위에서 두 분 모두 고유한 Mikhail Andreevich 의 솔루션을 다음과 같은 의미에서 언급했습니다. 이제 어떻게 될까요? 모든 것이 명확합니다 ... 다음은 무엇입니까?
존경받는 Mikhail Andreevich는 계정의 두 배 시간에 대한 신성한 공식 외에는 아무것도 없다는 것이 밝혀졌습니다. :-) 일반적으로 우리는 Alesei 의 kOpt 에 대한 대략적인 솔루션을 기다리고 있다고 가정합니다.
궁금한 결론.
Topt 기간 전에 (비례 포함) 철수를 포함하는 전략은 최적이 아닙니다. 단, 디포 기간이 TT 이상인 경우 - 당연히.
사진(숫자)을 봐주세요...
;)
약간 다른 문제(더 복잡한)를 해결하기 시작한 것 같습니다.
조건에 따라 현재 예금 금액의 일정한 비율 q 가 매월 발생하는 사용 중인 시간 t 에 대한 예금이 있고 고정 비율 k 를 q 이하로 인출해야 함을 상기시켜 드리겠습니다. 매월 0% 이상. 모든 것.
예금의 자금을 고려하지 않고 기간 t 동안 인출된 자금을 최대화하는 kOpt 를 찾아야 합니다. 이 솔루션은 두 매개변수 q 및 t 의 함수로 분석 형식으로 표현되어야 합니다(수치 솔루션, 다양한 그래프 및 종속성 형태의 특정 솔루션은 이미 얻어졌기 때문에 관심이 없습니다). 분석 솔루션이 근사적이면 문제 솔루션의 선언된 정확도가 달성되는 q 및 t 에 대한 한계를 표시해야 합니다.
추신 모든 종류의 종소리와 휘파람 - 인플레이션에 대한 설명, 발생한이자 q 의 불변성, 매개 변수 k 의 변화 등 가장 단순한 경우에 대한 솔루션을 얻기 전에 고려하는 것은 의미가 없다고 생각합니다.
"조건에 따라 저는 현재 예금 금액의 일정 비율 q 가 매월 청구되고 q 이하의 고정 비율 k 를 인출해야 하는 시간 t 에 대한 예금을 사용하고 있음을 상기시켜 드리겠습니다. 매달 0% 이상."
.
Sergey,하지만 공식이 너무 간단하지는 않지만 꽤 볼 수 있지만 이미 질문에 대한 답변이 있습니다. 이러한 경우에 대한 답은 일반적으로 노모그램 형식의 참고서에 나와 있습니다.
문제의 설명에서 " q 는 0.1< q <0.3 내에 있음"이 분명합니다.
더 많은 범위 지정 "시간 t "
Oleg , Forex와 관련하여 t 는 50으로 설정할 수 있습니다. 덜 의미가 없기 때문에 일반적인 예금 수명 이 5년 미만인 경우 전체 이익을 인출하는 것이 옳고 초기 예금의 규모는 이자 측면에서 "평생"을 제공해야 합니다. 수명이 5년 이상인 경우 초기 보증금은 작업에 포함되지 않으며 1000루블부터 시작할 수 있습니다. 그러나 자금 인출의 최적 비율이 있습니다. 또한 특성 수명이 필수 값이 아니라는 점을 고려하면(통계에 대해 이야기하고 있음) 상수 = 50으로 설정하여 이 매개변수를 공식에서 제외할 수 있습니다. 따라서 kOpt에 대해 (이상적으로는) 단 하나의 매개변수(TS - q 의 평균 수익성)의 분석적 근사값이 있습니다.
kOpt=q t<50
kOpt=F(q) for t>50
특정 조건에서 분석적 의존성 F(q) 의 대략적인 형태를 찾고자 합니다.
나는 공식을 간단하게 만드는 방법을 아직 모른다. Newton의 방법 은 적어도 세 번째 또는 네 번째 반복에서 다소 정확한 솔루션을 제공합니다. 그것은 매우 번거롭고 다층적인 공식이 될 것입니다.
q 에 대한 설명은 이제 이항 확장이 여기서 쓸모가 없다는 것을 추가로 확인합니다. q = 0.1 및 t = 10일지라도 너무 많은 이항 항이 유지되어야 합니다. 그리고 t 와 q 가 많을수록 더 나빠집니다. 즉, 합리적인 t (아마도 20 이상)에 대해 거의 항상
(1+ qk )^ t ~ exp(( qk ) t )
관찰에 따르면 큰 q 와 작은 t (각각 0.3과 10) 의 경우 월 수입의 대부분(70%)을 인출하는 것이 최적입니다.
그리고 작은 q 와 작은 t 의 경우 합리적인 범위 내에 극한값이 없습니다. 얻은 모든 것을 인출해야 합니다.
동시에 평균 q 와 평균 t (0.2 및 20)로 수입의 상당 부분, 즉 절반(44%)을 인출하는 것이 합리적입니다.
또한 중형 q 및 대형 t (0.2 및 30)의 경우 수입의 더 작은 부분(26%)을 인출하는 것이 합리적입니다.
등. 등. 태스크는 매개변수에 따라 질적으로 다르게 작동합니다. 낙관적이고 단 하나의 답은 없는 것 같습니다. q 와 t 에 따라 k 를 추정해 볼까요?
추신 Sergey , 귀하의 의견을 참조하십시오. 자, t = 50을 수정합니다. 작업이 더 쉬워졌습니다. 번 돈의 더 작은 부분을 인출하는 것으로 충분합니다( q = 0.1, t = 50 -> k / q = 0.3, 즉 30%). 이것은 가능한 최대 k / q 입니다.
..................
..................
.......................
알파의 최적 값은 양수 영역에서 음수 영역으로의 전환에 해당합니다.
.
공식은 위에 주어졌습니다. 여기서 반복하겠습니다.
Matkad에서 재현하는 것은 어렵지 않습니다 --- 매개변수를 빠르게 선택할 수 있습니다.
(역할을 하지 않음)
q 와 t 에 따라 k 를 추정해 볼까요?
그러면 분석 솔루션의 우아함이 사라집니다. 이 경우 수치해를 사용하는 것이 더 정확합니다. 간단한 표현으로는 문제가 너무 어려운 것 같습니다...
출금 금액에 대한 원래 표현을 단순화하려고했습니다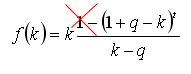 .
.
이 경우 매개변수 k 에 대한 1차 도함수의 일반 형식은 다음과 같이 간단한 2차 방정식으로 크게 단순화됩니다.
를 풀면 대략적인 식을 얻을 수 있습니다.
범위 t >50, q >0.1에서 허용 가능한 정확도
더 원함...