아니 아니. 나는 틀렸어. 다음은 반복 공식(빨간색)과 분석 의존성(파란색)에 따라 인출된 금액의 종속성입니다.
그것들이 일치하고 k 에 최대값이 있음을 알 수 있습니다(토픽의 이전 페이지에서).
분명히, 당신은 별개의 인출이 아니라 동일한 몫의 지속적인 인출이 있습니다. 따라서 다른 기간에 다른 방식으로 촬영할 결정이 없습니다. 따라서 이전에 제거하지 않고 마지막에 모두 제거하는 솔루션은 없습니다. 이것은 문제의 조건이 아니라 사용하는 공식에서 따릅니다(k는 고정되어 있으며 변수 ki, i=0...T가 아님)
이제 나는 k의 거듭제곱으로 도함수에 대한 표현을 확장하려고 노력하고 있지만 좋은 결과가 나오지 않습니다. 최대 6개의 차수를 유지해야 합니다. 이것은 분석적으로 해결할 수 없다는 것이 분명합니다. 더 많은 아이디어가 있지 않을까요? 누군가가 difurki를 언급했습니다 ...
이제 나는 k의 거듭제곱으로 도함수에 대한 표현을 확장하려고 노력하고 있지만 좋은 결과가 나오지 않습니다. 최대 6개의 차수를 유지해야 합니다. 이것은 분석적으로 해결할 수 없다는 것이 분명합니다. 더 많은 아이디어가 있지 않을까요? 누군가가 difurki를 언급했습니다 ...
분석적으로 어렵다. q와 t에서. 그것은 어떻게 든 까다 롭습니다 :) t와 마찬가지로 q가 증가함에 따라 최적의 철수 비율이 지속적으로 감소합니다
이제 나는 k의 거듭제곱으로 도함수에 대한 표현을 확장하려고 노력하고 있지만 좋은 결과가 나오지 않습니다. 최대 6개의 차수를 유지해야 합니다. 이것은 분석적으로 해결할 수 없다는 것이 분명합니다. 더 많은 아이디어가 있지 않을까요? 누군가가 difurki를 언급했습니다 ...
Difurki는 그렇게 쉽게 해결되지 않을 것입니다. 차이를 도함수로 간단히 다시 작성하는 것은 올바르지 않으며 결과가 왜곡되며 정확한 변환은 여전히 머리카락이 훨씬 더 높게 서있는 방정식으로 이어집니다. . IMHO, 걱정할 필요 없음
당신은 특정에서 일반으로 갈 수 있습니다. 예를 들어 t = 1이면 한 번만 돈을 인출할 수 있으므로 q만큼 인출해야 합니다. 다음으로 t = 2, t = 3 등의 경우를 고려합니다.
극한값에 의해 인출 금액을 f(t)와 같이 구할 수 있습니다.
아마도 당신이 옳습니다. 이제 t = 3에 대해서만 방정식에 따라 가집니다. 차수 k 는 1차 도함수 df(k)/dk=0 에서 삼중이고 모든 결과와 함께 3차 방정식의 근을 찾아야 합니다... 즉. t = 3을 넘어서면 이 시나리오를 통과할 수 없습니다. 내가 당신에게 그것을 상기시켜 드리겠습니다 , 그리고 t=1의 경우 최적의 크기는 k=q, t=2의 경우 k=q, t=3의 경우 k=q입니다. 그러나 t 를 더 늘리고 분석적으로 푸는 것은 효과가 없습니다. 이를 수치적으로 풀면 월 10% 이내의 예금 증가율 q 에 대해 t > 30개월에서 최적의 계좌 출금 비율이 q 보다 작아지는 것을 알 수 있다.
이에 대한 결론은 다음과 같습니다. TS의 신뢰성이 예금의 평균 수명이 3년을 초과하지 않는 정도라면 모든 이익의 월별 인출이 최적의 행동(예금이 증가하지 않음)이 될 것입니다. 그렇지 않으면 최적의 출력 백분율 k 에 대한 분석 솔루션을 찾고 공식에 따라 행동해야 합니다. 이 시나리오는 예금의 예상 수명 동안 주머니에 넣을 수 있는 최대 금액을 보장합니다.
자동 :
PS를 작성하기 위해 연결된 혈관의 다이어그램을 고려할 수 있습니다.첫 번째 혈관의 초기 부피는 B0
용기(액체 흐름)가 동적 평형 상태에 있는 경우(즉, 단위 시간당 얼마나 많은 유체가 첫 번째 용기로 흘러들어가는 것과 동일한 양이 후자의 용기 밖으로 흐릅니다), 각 용기의 수위 문제는 기본적으로 해결되고 다음을 수행합니다. 예금의 정해진 문제로 줄이지 마십시오. 채우는 과정에서 용기를 고려하면 예금과의 비유가 완전히 명확하지 않습니다. avtomat ,설명 , 제발, 그런 해석을 제공한다는 것은 무엇을 의미했습니까?
추신 : 방정식 df/dk=0의 근사적인 해석적 해를 얻기 위한 요구는 여전히 유효합니다. 모든 아이디어가 허용됩니다.
아니 아니. 나는 틀렸어. 다음은 반복 공식(빨간색)과 분석 의존성(파란색)에 따라 인출된 금액의 종속성입니다.
그것들이 일치하고 k 에 최대값이 있음을 알 수 있습니다(토픽의 이전 페이지에서).
분명히, 당신은 별개의 인출이 아니라 동일한 몫의 지속적인 인출이 있습니다. 따라서 다른 기간에 다른 방식으로 촬영할 결정이 없습니다. 따라서 이전에 제거하지 않고 마지막에 모두 제거하는 솔루션은 없습니다. 이것은 문제의 조건이 아니라 사용하는 공식에서 따릅니다(k는 고정되어 있으며 변수 ki, i=0...T가 아님)
인출된 총 자금
충분히 큰 성장 인자에서 효과가 두드러집니다.
비슷한 종속성이 있습니다.
이제 나는 k의 거듭제곱으로 도함수에 대한 표현을 확장하려고 노력하고 있지만 좋은 결과가 나오지 않습니다. 최대 6개의 차수를 유지해야 합니다. 이것은 분석적으로 해결할 수 없다는 것이 분명합니다. 더 많은 아이디어가 있지 않을까요? 누군가가 difurki를 언급했습니다 ...
비슷한 종속성이 있습니다.
이제 나는 k의 거듭제곱으로 도함수에 대한 표현을 확장하려고 노력하고 있지만 좋은 결과가 나오지 않습니다. 최대 6개의 차수를 유지해야 합니다. 이것은 분석적으로 해결할 수 없다는 것이 분명합니다. 더 많은 아이디어가 있지 않을까요? 누군가가 difurki를 언급했습니다 ...
분석적으로 어렵다. q와 t에서. 그것은 어떻게 든 까다 롭습니다 :) t와 마찬가지로 q가 증가함에 따라 최적의 철수 비율이 지속적으로 감소합니다
비슷한 종속성이 있습니다.
이제 나는 k의 거듭제곱으로 도함수에 대한 표현을 확장하려고 노력하고 있지만 좋은 결과가 나오지 않습니다. 최대 6개의 차수를 유지해야 합니다. 이것은 분석적으로 해결할 수 없다는 것이 분명합니다. 더 많은 아이디어가 있지 않을까요? 누군가가 difurki를 언급했습니다 ...
당신은 특정에서 일반으로 갈 수 있습니다. 예를 들어 t = 1이면 한 번만 돈을 인출할 수 있으므로 q만큼 인출해야 합니다. 다음으로 t = 2, t = 3 등의 경우를 고려합니다.
저것들. t = 2에서 한 번에 q보다 작게 출력하는 것이 최적이면 t = 2에서 극한값을 찾고 모든 q에 대해 일반화합니다.
유사하게 t = 3, t = 4 등입니다.
극한값에 의해 인출 금액을 f(t)와 같이 구할 수 있습니다.
컨트롤을 작성하기 위해 연결된 선박의 다이어그램을 고려할 수 있습니다.
첫 번째 용기의 초기 부피 B0
당신은 특정에서 일반으로 갈 수 있습니다. 예를 들어 t = 1이면 한 번만 돈을 인출할 수 있으므로 q만큼 인출해야 합니다. 다음으로 t = 2, t = 3 등의 경우를 고려합니다.
극한값에 의해 인출 금액을 f(t)와 같이 구할 수 있습니다.
아마도 당신이 옳습니다. 이제 t = 3에 대해서만 방정식에 따라 가집니다.
차수 k 는 1차 도함수 df(k)/dk=0 에서 삼중이고 모든 결과와 함께 3차 방정식의 근을 찾아야 합니다... 즉. t = 3을 넘어서면 이 시나리오를 통과할 수 없습니다. 내가 당신에게 그것을 상기시켜 드리겠습니다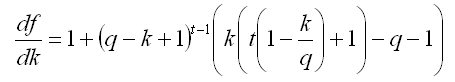 
, 그리고 t=1의 경우 최적의 크기는 k=q, t=2의 경우 k=q, t=3의 경우 k=q입니다. 그러나 t 를 더 늘리고 분석적으로 푸는 것은 효과가 없습니다. 이를 수치적으로 풀면 월 10% 이내의 예금 증가율 q 에 대해 t > 30개월에서 최적의 계좌 출금 비율이 q 보다 작아지는 것을 알 수 있다.
이에 대한 결론은 다음과 같습니다. TS의 신뢰성이 예금의 평균 수명이 3년을 초과하지 않는 정도라면 모든 이익의 월별 인출이 최적의 행동(예금이 증가하지 않음)이 될 것입니다. 그렇지 않으면 최적의 출력 백분율 k 에 대한 분석 솔루션을 찾고 공식에 따라 행동해야 합니다. 이 시나리오는 예금의 예상 수명 동안 주머니에 넣을 수 있는 최대 금액을 보장합니다.
자동 :
PS를 작성하기 위해 연결된 혈관의 다이어그램을 고려할 수 있습니다.첫 번째 혈관의 초기 부피는 B0
용기(액체 흐름)가 동적 평형 상태에 있는 경우(즉, 단위 시간당 얼마나 많은 유체가 첫 번째 용기로 흘러들어가는 것과 동일한 양이 후자의 용기 밖으로 흐릅니다), 각 용기의 수위 문제는 기본적으로 해결되고 다음을 수행합니다. 예금의 정해진 문제로 줄이지 마십시오. 채우는 과정에서 용기를 고려하면 예금과의 비유가 완전히 명확하지 않습니다. avtomat , 설명 , 제발, 그런 해석을 제공한다는 것은 무엇을 의미했습니까?
추신 : 방정식 df/dk=0의 근사적인 해석적 해를 얻기 위한 요구는 여전히 유효합니다. 모든 아이디어가 허용됩니다.