내 차량에서는 항상 최적의 창 너비를 찾으려고 노력합니다. 30-70 관측치 내에서 변동합니다(H1의 경우).
정확히 어떤 창인가요? 예를 들어, 가우스는 일반적인 직사각형과 비교 하여 경계 효과 를 매우 크게 억제합니다(주파수 영역에서도 가우시안이 됩니다. 즉, 측면 최대값 없이 옥타브당 -40dB를 제공합니다). 그런 다음 더 많은 신호 값을 고려하여 동일한 반응성을 얻을 수 있습니다.
" H는 외부 환경을 더 많이 특징짓는다"를 보면 Hirst와 관련하여 사용되는 영어 용어에주의를 기울여야합니다. 다음은 VR의 논문에서 복사하여 붙여넣기한 것입니다.
일부 시계열 은 높은 시차에서 현저한 상관 관계를 나타내며 참조됩니다.
장기 메모리 프로세스 로 . 장기 기억은 많은 지구 물리학의 특징입니다.
시계열. 나일 강의 흐름은 높은 시차에서 상관 관계가 있습니다.
그리고 Hurst(1951)는 이것이 최적의 설계 능력에 영향을 미친다는 것을 보여주었습니다.
여자의. Mudelsee(2007)는 장기 기억이 수문학적 속성임을 보여줍니다.
극심한 가뭄이나 일시적인 클러스터링으로 이어질 수 있습니다.
홍수. 다소 다른 규모에서 Leland et al. (1993) 이더넷이
근거리 통신망(LAN) 트래픽은 통계적으로 자기 유사하고
장기 기억 프로세스. 그들은 에 의해 생성되는 혼잡의 성질을 보여주었다.
자기 유사 트래픽은 트래픽 모델에서 예측한 것과 크게 다릅니다.
당시 사용. Mandelbrot와 동료들은 관계를 조사합니다.
자기 유사성과 장기기억 사이에서 주도적인 역할을 하였다.
프랙탈 기하학을 연구 주제로 설정합니다.
이 단어들을 주목하십시오.
일부 시계열은 높은 지연 시간에서 현저한 상관 관계를 나타냅니다.
그리고
그 긴 기억을 보여줍니다
나는 알아내려고 노력했다: 긴 기억이란 무엇인가? 이것은 40개 이상의 관측치의 자기상관으로 밝혀졌습니다! 그러나 인용문에서 한 기호의 그러한 장기적인 상관 관계는 극히 드뭅니다. 어쨌든 한 시간을 보낸 후에도 찾지 못했습니다.
많은 사람들이 허스트 지수를 사용하려고 합니다. 긍정적인 결과를 본 적이 없습니다. 따옴표를 먼저 찾아야 할 수도 있습니다. 어느 긴 기억 속에?
어떤 인용문에서도 이 가장 긴 메모리를 식별할 수 있습니다. 그러나 ACF는 여기에 적합하지 않습니다. Peters는 장기 기억에 대한 흥미로운 정의를 제공합니다. 읽다. 이 주제에 관한 그의 책에는 흥미로운 것들이 많이 있습니다. 그것에 따르면 그러한 과정은 평범한 ACF로 측정 할 수 없다는 것이 밝혀졌습니다. ACF는 5-6 시차의 규모로 작동하며 그게 전부입니다. H가 거리의 제곱근과 같은 발산을 갖는 입자의 도보로 표현되면 정규 분포 StdDev = Sqrt(T) = T^(0.5)의 특별한 경우를 얻습니다. 따라서 입자의 분산이 0.5보다 약간 높거나 낮으면 한 가지 경우에만 가능합니다. 입자는 과거 상태를 기억해야 합니다. 즉, 이러한 프로세스에 메모리가 있습니다. 저것들. H, 이것은 여전히 외부 영향의 특성이 아니라 프로세스의 이전 상태에 대한 종속성입니다. 그리고 탈출 궤적을 유지하면 이전 값에 따라 달라지며 메모리 기간을 계산할 수 있습니다. 그리고 모든 계산 규모에서 경사각이 변하지 않고 동시에 0.5와 같지 않은 경우가 종종 있습니다. 이러한 경우 프로세스는 무한 메모리를 갖는 진정한 Hurst 프로세스 라고 합니다. 여기에서만 ACF는 그런 것을 보여주지 않을 것입니다.
C-4 : 어떤 인용문에서도 이 가장 긴 메모리를 식별할 수 있습니다. 그러나 ACF는 여기에 적합하지 않습니다. Peters는 장기 기억에 대한 흥미로운 정의를 제공합니다. 읽다. 이 주제에 관한 그의 책에는 흥미로운 것들이 많이 있습니다. 그것에 따르면 그러한 과정은 평범한 ACF로 측정 할 수 없다는 것이 밝혀졌습니다. ACF는 5-6 시차의 규모로 작동하며 그게 전부입니다. H가 거리의 제곱근과 같은 발산을 갖는 입자의 도보로 표현되면 정규 분포 StdDev = Sqrt(T) = T^(0.5)의 특별한 경우를 얻습니다. 따라서 입자의 분산이 0.5보다 약간 높거나 낮으면 한 가지 경우에만 가능합니다. 입자는 과거 상태를 기억해야 합니다. 즉, 이러한 프로세스에 메모리가 있습니다. 저것들. H, 이것은 여전히 외부 영향의 특성이 아니라 프로세스의 이전 상태에 대한 종속성입니다. 그리고 탈출 궤적을 유지하면 이전 값에 따라 달라지며 메모리 기간을 계산할 수 있습니다. 그리고 모든 계산 규모에서 경사각이 변하지 않고 동시에 0.5와 같지 않은 경우가 종종 있습니다. 이러한 경우 프로세스는 무한 메모리를 갖는 진정한 Hurst 프로세스 라고 합니다. 여기에서만 ACF는 그런 것을 보여주지 않을 것입니다.
왜 그렇게 멀리 가니?
여기서 우리는 평범한 칠면조를 다룰 것입니다 ...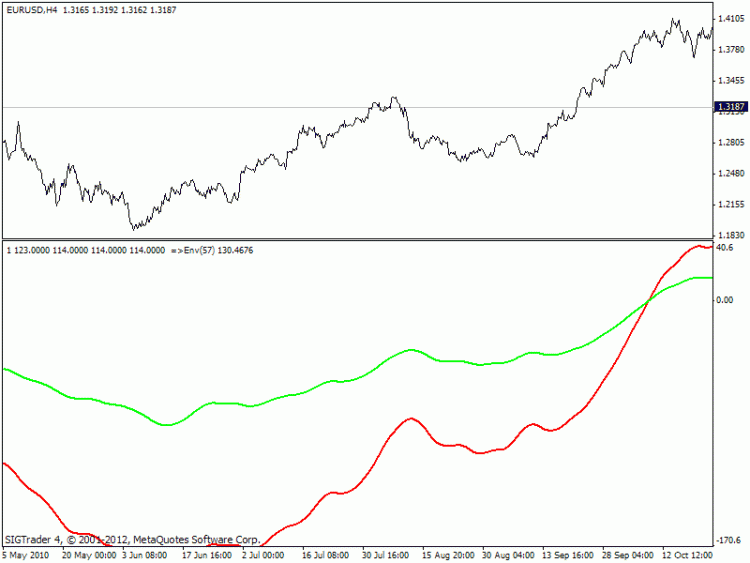
내 차량에서는 항상 최적의 창 너비를 찾으려고 노력합니다. 30-70 관측치 내에서 변동합니다(H1의 경우).
정확히 어떤 창인가요? 예를 들어, 가우스는 일반적인 직사각형과 비교 하여 경계 효과 를 매우 크게 억제합니다(주파수 영역에서도 가우시안이 됩니다. 즉, 측면 최대값 없이 옥타브당 -40dB를 제공합니다). 그런 다음 더 많은 신호 값을 고려하여 동일한 반응성을 얻을 수 있습니다.
왜 그렇게 멀리 가니?
여기서 우리는 평범한 칠면조를 다룰 것입니다 ...
누구세요?))
프라이빗 데르수!
마음 편하게! 빨강 및 녹색과 같은 봉투용 Che?
봉투 같은 봉투.
내장.
토요일 휴무...
주제에서 벗어나?
" H는 외부 환경을 더 많이 특징짓는다"를 보면 Hirst와 관련하여 사용되는 영어 용어에주의를 기울여야합니다. 다음은 VR의 논문에서 복사하여 붙여넣기한 것입니다.
프랙탈 기하학을 연구 주제로 설정합니다.
이 단어들을 주목하십시오.
일부 시계열은 높은 지연 시간에서 현저한 상관 관계를 나타냅니다.
그리고
그 긴 기억을 보여줍니다
나는 알아내려고 노력했다: 긴 기억이란 무엇인가? 이것은 40개 이상의 관측치의 자기상관으로 밝혀졌습니다! 그러나 인용문에서 한 기호의 그러한 장기적인 상관 관계는 극히 드뭅니다. 어쨌든 한 시간을 보낸 후에도 찾지 못했습니다.
많은 사람들이 허스트 지수를 사용하려고 합니다. 긍정적인 결과를 본 적이 없습니다. 따옴표를 먼저 찾아야 할 수도 있습니다. 어느 긴 기억 속에?
Peters는 장기 기억에 대한 흥미로운 정의를 제공합니다. 읽다. 이 주제에 관한 그의 책에는 흥미로운 것들이 많이 있습니다. 그것에 따르면 그러한 과정은 평범한 ACF로 측정 할 수 없다는 것이 밝혀졌습니다. ACF는 5-6 시차의 규모로 작동하며 그게 전부입니다. H가 거리의 제곱근과 같은 발산을 갖는 입자의 도보로 표현되면 정규 분포 StdDev = Sqrt(T) = T^(0.5)의 특별한 경우를 얻습니다. 따라서 입자의 분산이 0.5보다 약간 높거나 낮으면 한 가지 경우에만 가능합니다. 입자는 과거 상태를 기억해야 합니다. 즉, 이러한 프로세스에 메모리가 있습니다. 저것들. H, 이것은 여전히 외부 영향의 특성이 아니라 프로세스의 이전 상태에 대한 종속성입니다. 그리고 탈출 궤적을 유지하면 이전 값에 따라 달라지며 메모리 기간을 계산할 수 있습니다. 그리고 모든 계산 규모에서 경사각이 변하지 않고 동시에 0.5와 같지 않은 경우가 종종 있습니다. 이러한 경우 프로세스는 무한 메모리를 갖는 진정한 Hurst 프로세스 라고 합니다. 여기에서만 ACF는 그런 것을 보여주지 않을 것입니다.
어떤 인용문에서도 이 가장 긴 메모리를 식별할 수 있습니다. 그러나 ACF는 여기에 적합하지 않습니다.
Peters는 장기 기억에 대한 흥미로운 정의를 제공합니다. 읽다. 이 주제에 관한 그의 책에는 흥미로운 것들이 많이 있습니다. 그것에 따르면 그러한 과정은 평범한 ACF로 측정 할 수 없다는 것이 밝혀졌습니다. ACF는 5-6 시차의 규모로 작동하며 그게 전부입니다. H가 거리의 제곱근과 같은 발산을 갖는 입자의 도보로 표현되면 정규 분포 StdDev = Sqrt(T) = T^(0.5)의 특별한 경우를 얻습니다. 따라서 입자의 분산이 0.5보다 약간 높거나 낮으면 한 가지 경우에만 가능합니다. 입자는 과거 상태를 기억해야 합니다. 즉, 이러한 프로세스에 메모리가 있습니다. 저것들. H, 이것은 여전히 외부 영향의 특성이 아니라 프로세스의 이전 상태에 대한 종속성입니다. 그리고 탈출 궤적을 유지하면 이전 값에 따라 달라지며 메모리 기간을 계산할 수 있습니다. 그리고 모든 계산 규모에서 경사각이 변하지 않고 동시에 0.5와 같지 않은 경우가 종종 있습니다. 이러한 경우 프로세스는 무한 메모리를 갖는 진정한 Hurst 프로세스 라고 합니다. 여기에서만 ACF는 그런 것을 보여주지 않을 것입니다.
불행히도 저는 이 문제에 대해 의견이 없습니다.
하지만 나는 책을 참조할 수 있다
Cowpertwait 및 A.V. Metcalfe, R을 사용한 입문 시계열, 159
R 사용, DOI 10.1007/978-0-387-88698-5 8,
© Springer Science+Business Media, LLC 2009
8장에서는 FARIMA 피팅 프로세스를 설명합니다. 이 프로세스는 ACF를 사용합니다.
본문을 첨부했습니다. 불행히도 공식과 이론적인 부분이 제대로 작동하지 않았습니다.
그러나 FARIMA 피팅 프로세스는 구체적으로 설명되어 있습니다.