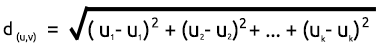
データサイエンスと機械学習(第08回)::簡単なMQL5でのK平均法
データはゴミのようなものです。収集する前に、それでどうするのかを知っておくべきです。
マーク・トウェイン
教師なし学習
使用可能なデータがラベル付けされていない例で構成されている問題の機械学習パラダイムです。回帰法、SVM、決定木、ニューラルネットワーク、およびこの連載で説明した他の多くの教師あり学習手法ではモデルを適合させるデータセットに常にラベルを付けますが、それとは異なります。教師なし学習では、データにラベルが付けられていないため、関係とそれ以外のすべてを把握するのはアルゴリズム次第です。
教師なし学習タスクの例としては、クラスタリング、次元削減、密度推定があります。
クラスタリング分析
クラスタリング分析は、同じ属性を持つオブジェクトが同じグループ(クラスター)内に配置されるように、一連のオブジェクトをグループ化するタスクです。
ショッピングモールに行けば、似たような商品は一緒に並んでいます。誰かがそれらをグループ化するプロセスをおこなったわけです。データセットがグループ化されていない場合、クラスタリング分析はそのようにおこなわれ、他のグループ(クラスター)よりも(ある意味で)互いに類似しているデータ値がグループ化されます。
クラスタリング分析自体は特定のアルゴリズムではありません。一般的なタスクは、クラスターを構成するものを理解するという点で大きく異なるさまざまなアルゴリズムによって解決できます。
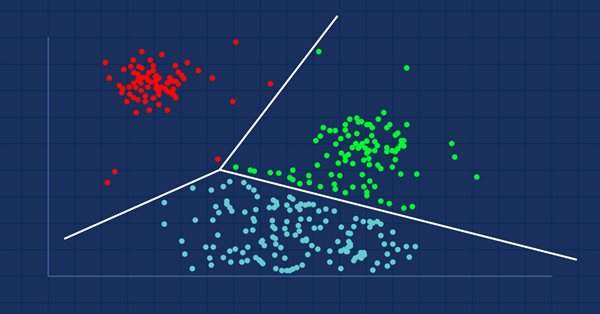
画像出典:ウィキペディア
広く知られているクラスタリングには、次の3つのタイプがあります。- 排他的クラスタリング
- 重複クラスタリング
- 階層クラスタリング
排他的クラスタリング
これは、k平均など、データポイント/アイテムが互いに排他的に属するハードクラスタリングです。
重複クラスタリング
データポイント/アイテムが複数のクラスターに属するタイプのクラスタリングです。例は、ファジィc-meansアルゴリズムです。
階層クラスタリング
このタイプのクラスタリングは、クラスターの階層を構築しようとします。
クラスタリングアルゴリズムはどこで使用されるのでしょうか。
クラスタリング手法は、アマゾンや多くのeコマースサイトで、以前にまとめられた類似商品を推奨するために使用されています。Netflixは、興味に基づいて一緒にみられた映画を推奨することで、同じことをおこないます。
基本的に、それらは、マーケティング、生物医学、地理空間などの分野から収集された多変量データセットで、類似したオブジェクトまたは関心のグループを識別するために使用されます。
K平均
k近傍法と混同しないでださい。これについては、次の記事で説明します。
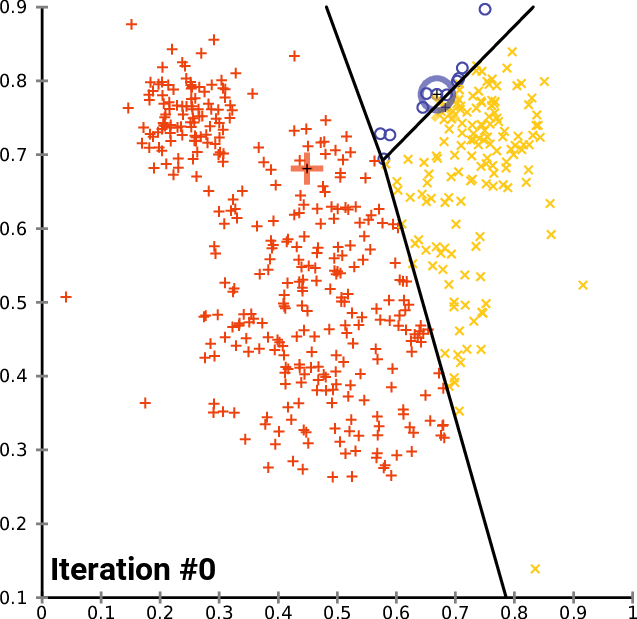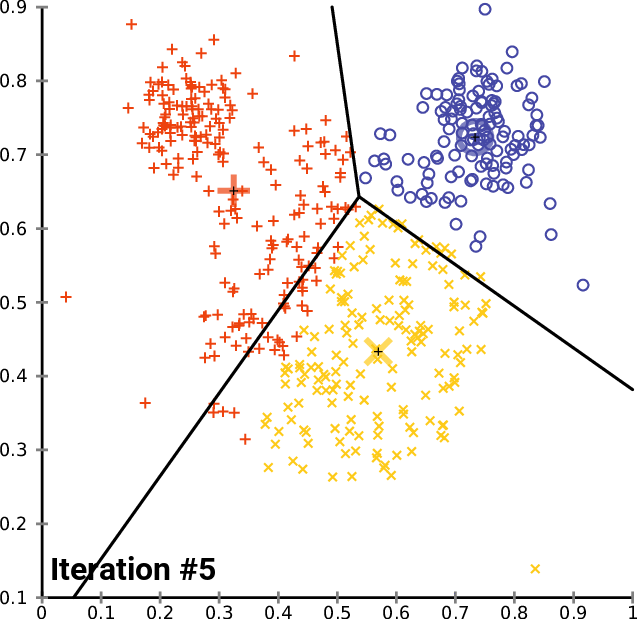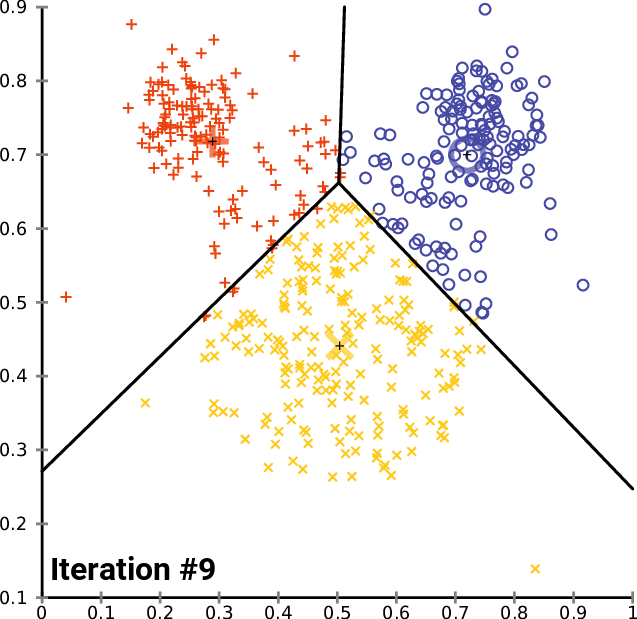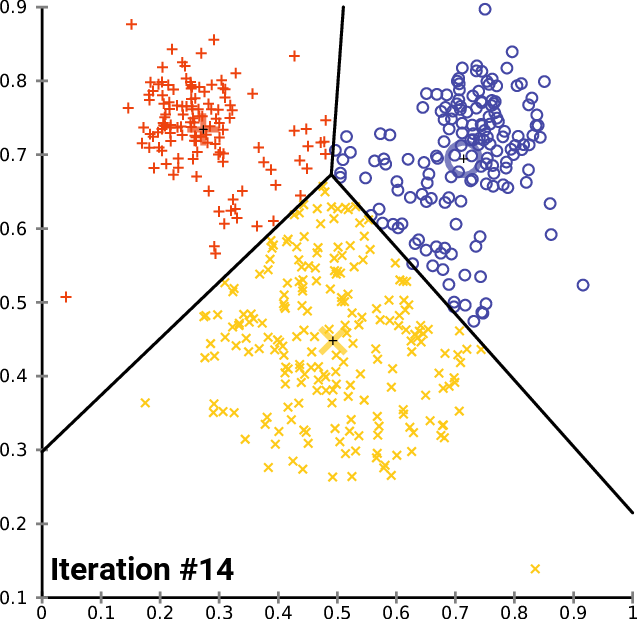
k平均法アルゴリズムはベクトル量子化の方法であり、n個の観測値をk個のクラスターに分割することを目的としています。各観測値は、k < nである最も近い平均/最も近い重心を持つクラスターに属します。これは、最も広く知られ、最も使用されているクラスタリングアルゴリズムです。アルゴリズムの背後にある計算は簡単です。以下は、アルゴリズムに含まれるプロセスの図です。 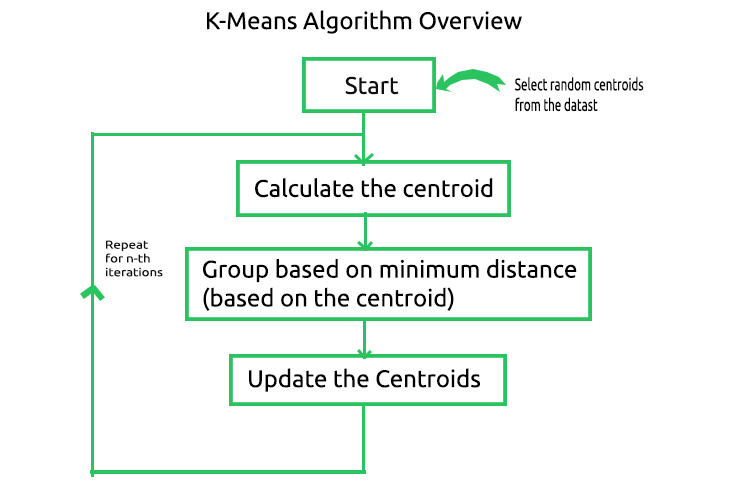
ここで、このプロセスがどのように機能するかを理解するために、メタエディターでコーディングしてプロセスを自動化しながら、手動で操作をおこないましょう。CKMeansライブラリのprivateセクションで、サンプルデータセットの重心を格納するための行列を作成します。
class CKMeans { private: ulong n; uint m_clusters; ulong m_cols; matrix InitialCentroids; //Intitial Centroids matrix vector cluster_assign; }
いつものように、ライブラリを構築するために単純なデータセットを使用します。実際のデータセットの状況でアルゴリズムをどのように使用できるかを見ていきます。
matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} };
01:アルゴリズムの開始& 02:重心の計算
アルゴリズムを開始するには、探している各クラスターの初期中心を取得する必要があるため、ランダムな重心を選択して、それらをInitialCentroid行列に格納します。
m_cols = Matrix.Cols(); n = Matrix.Rows(); //number of elements | Matrix Rows InitialCentroids.Resize(m_clusters,m_cols); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids);
初期の重心は次のとおりです。
CS 0 06:44:02.152 K-means test (EURUSD,M1) Initial Centroids matrix CS 0 06:44:02.152 K-means test (EURUSD,M1) [[2,10] CS 0 06:44:02.152 K-means test (EURUSD,M1) [5,8] CS 0 06:44:02.152 K-means test (EURUSD,M1) [1,2]]
最初のまだ非常に重要なステップが完了しました。図によると、次のステップは重心の計算です。ちょっと待ってください。重心は上で計算したのではないでしょうか。その通りです。初期の重心は計算したので計算する必要はありません。重心は最後に更新されます。
03:最小距離に基づくグループ化
次に、取得した重心からデータセット内のすべてのポイントとの間の距離を調べます。すべての重心よりも特定の重心に最も近いデータポイントがそのクラスターに割り当てられます。
距離を求めるには、ユークリッド距離または直線距離の2つの数式を使用できます。
ユークリッド距離
これはピタゴラスの定理に基づいて2点間の距離を測定する方法です。式は次のとおりです。
直線距離
直線距離は、単に2点間のx座標とy座標の差の合計です。式は次のとおりです。
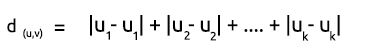
簡単にするために、私は直線法を使用して重心と点の間の距離を見つけることを好みます。Excelで行列をプロットしてみましょう。
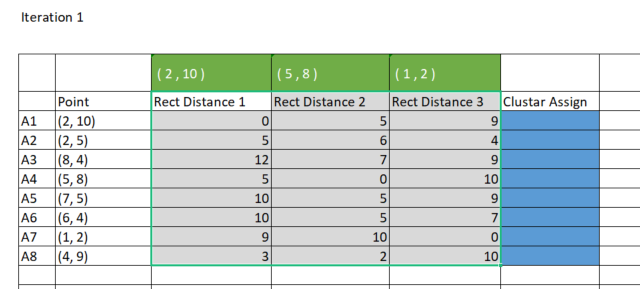
MetaEditorで同じ結果を得るには、クラスターに割り当てるために使用する直線距離を格納するために、8行x3クラスターの行列を作成する必要があります。なぜ3つのクラスターなのでしょうか。 ライブラリの初期化中に3つのクラスターを選択しました。達成したいことに基づいて、クラスターの初期数を選択できます。これについては後で詳しく説明します。以下はライブラリコンストラクタです。
CKMeans::CKMeans(int clusters=3) { m_clusters = clusters; }以下は、直線距離を格納するための行列を作成する方法です。
matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters);
次に、直線距離を計算し、作成したばかりのrect_distance行列に結果を格納しましょう。
vector v_matrix = {}, v_centroid = {}; double output = 0; for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Rectilinear distance rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance);
出力
CS 0 15:17:52.136 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[0,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,6,4] CS 0 15:17:52.136 K-means test (EURUSD,M1) [12,7,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,0,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,7] CS 0 15:17:52.136 K-means test (EURUSD,M1) [9,10,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [3,2,10]]
前述のように、k平均法では、特定のクラスターからの距離が最小のデータポイントがそのクラスターに属するようにすることで、データポイントをグループ化します。rect_distance行列から、各列はクラスターを表すため、行の最小値、つまり最小数の列がそのクラスターに割り当てられていることを確認します。下の画像を参照してください。
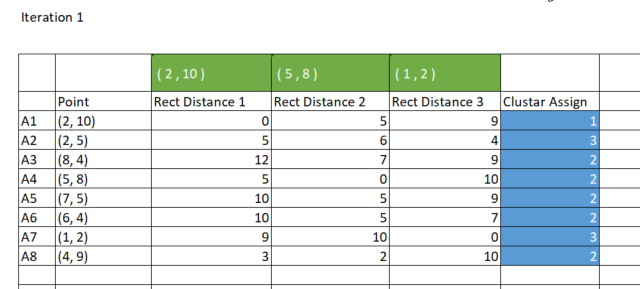
次は、クラスターを割り当てるためのコードです。
//--- Assigning the Clusters matrix cluster_cent = {}; //cluster centroids ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign);
出力
CS 0 15:17:52.136 K-means test (EURUSD,M1) Assigned clusters CS 0 15:17:52.136 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1]
ポイントをそれぞれのクラスターに割り当てたので、今度は新しく見つかったクラスターに基づいてデータポイントをグループ化します。Excelでプロセスを実行すると、クラスターは以下の図のようになります。
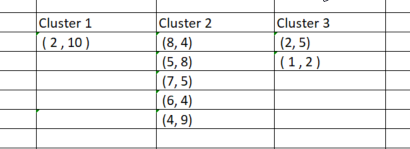
データポイントを手動でグループ化するプロセスは単純でしたが、クラスターのサイズは常に異なるため、コードを作成しようとするとそれほど単純ではありません。したがって、行列を使用してクラスターを格納しようとすると、列の行数に違いが生じます。配列手法は不便で読みにくいです。CSVファイルを使用して値を保存しようとすると、各クラスターの列を動的に書き込むことになっているため、プロセスが失敗します。
3 x n clusters_matrixを使用してクラスターを格納するというアイデアを思いつきました。これは、行数がクラスター数と等しくなり、列数がクラスターの最大数になるように最初にサイズ変更されたゼロ値の行列です。
最終的に、各クラスターは行列の行に水平に格納されます。
以下は出力です。
CS 0 15:17:52.136 K-means test (EURUSD,M1) clustered Matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [2,5,1,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [8,4,5,8,7,5,6,4,4,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0]]この行列は、これらすべての操作がおこなわれるKMeansClustering関数で参照として渡されるため、抽出して、最後の非負のゼロ値の後のゼロ値を無視するように値をフィルタリングできます。
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix)
04:重心の更新
各クラスターの新しい重心は、クラスター内のすべての個々の要素の平均を見つけることによって取得されます。そのコードは次のとおりです。
vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids,"\nclustered Matrix\n",clustered_matrix);
以下は出力です。
CS 0 15:17:52.136 K-means test (EURUSD,M1) New Centroids CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [1.5,3.5] CS 0 15:17:52.136 K-means test (EURUSD,M1) [6,6]]
プロセス全体がどのように機能するかを確認したので、データがそれぞれのクラスターに適切に配置されるまで、2番目のステップから最後のステップまで繰り返す必要があります。これは2つの方法で実現できます。クラスターの新しい重心が変化しなくなるたびに、すべてのクラスターの最適値が既に見つかっているような方法でロジックを配置する人と、このアルゴリズムの反復回数を制限しする人がいます。最初の方法の問題は、breakステートメントをプルするためにifステートメントによって制御される無限ループを配置する必要があることだと思います。アルゴリズムで反復回数を制限するのは賢いことだと思います。
以下は、反復が追加された完全なk平均法アルゴリズム関数です。
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix,int iterations = 10) { m_cols = Matrix.Cols(); n = Matrix.Rows(); //number of elements | Matrix Rows InitialCentroids.Resize(m_clusters,m_cols); cluster_assign.Resize(n); clustered_matrix.Resize(m_clusters, m_clusters*n); clustered_matrix.Fill(NULL); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids); //--- vector v_row; vector n_each_cluster; //Each cluster content matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters); vector v_matrix = {}, v_centroid = {}; double output = 0; //--- for (int iter=0; iter<iterations; iter++) { printf("\n<<<<< %d >>>>>\n",iter ); for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Rectilinear distance rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance); //--- Assigning the Clusters matrix cluster_cent = {}; //cluster centroids ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign); //--- Combining the clusters n_each_cluster.Resize(m_clusters); for (ulong i=0, index =0, sum_count = 0; i<cluster_assign.Size(); i++) { for (ulong j=0, count = 0; j<cluster_assign.Size(); j++) { //printf("cluster_assign[%d] cluster_assign[%d]",i,j); if (cluster_assign[i] == cluster_assign[j]) { count++; n_each_cluster[index] = (uint)count; cluster_comb_m.Resize(count, m_cols); cluster_comb_m.Row(Matrix.Row(j) , count-1); cluster_cent.Resize(count, m_cols); // New centroids cluster_cent.Row(Matrix.Row(j),count-1); sum_count++; } else continue; } //--- MatrixToVector(cluster_comb_m, cluster_comb_v); // solving for new cluster and updtating the old ones if (iter == iterations-1) clustered_matrix.Row(cluster_comb_v, index); //--- index++; //--- vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids);//,"\nclustered Matrix\n",clustered_matrix); } //end of iterations } //+------------------------------------------------------------------+
10回の反復の後、アルゴリズムのログは次のようになります。
CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 0 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,6,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,0,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,7] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,10,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,2,10]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6,6]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 1 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,7,8] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,2,5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,8,3] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,7,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,2,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,8,5]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,2,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3,9.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6.5,5.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 2 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[1.5,7,9.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.5,2,4.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10.5,7,2.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3.5,8,4.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,7,0.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,5,1.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.5,2,8.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,8,6.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 3 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) ..... ..... ..... ..... CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 9 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]]
2回の反復の後、アルゴリズムはすでに収束しており、重心に最適な値を提供しています。これで、この種のアルゴリズムに最適な反復回数がわかります。勾配降下法やその他のアルゴリズムとは異なり、k平均法クラスタリングでは、最適な値に到達するために多くの反復を必要としません。単純なデータセットを完全にクラスター化するのに必要は反復は、多くの場合5~10回です。
k平均法テストスクリプトの内部
テストスクリプトのメイン関数では、ライブラリを初期化し、k-MeansClustering関数を呼び出し、クラスターを同じ軸にプロットし、最後にライブラリのオブジェクトを削除します。 void OnStart() { //--- matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} }; int clusters =3; matrix clusterd_mat; clustering = new CKMeans(clusters); clustering.KMeansClustering(DMatrix,clusterd_mat); ObjectsDeleteAll(0,0); ScatterPlotsMatrix("graph",clusterd_mat,"cluster 1"); delete(clustering); }
以下は、クラスターのプロットです。
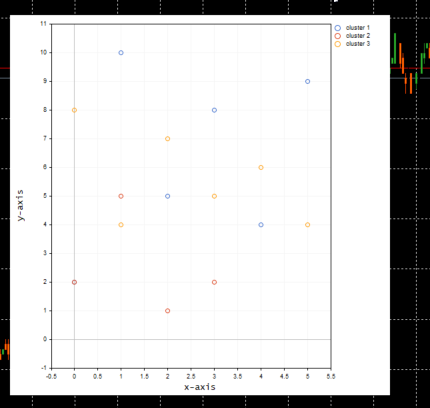
すばらしいです。ScatterPlotsMatrix()関数内で、値がグラフにプロットされる前にゼロ値をフィルタリングする関数が呼び出されました。プロットのxまたはy軸の線上に正確にあるすべての値は無視する必要があります。
vectortoArray(x,x_arr); FilterZeros(x_arr); graph.CurveAdd(x_arr,CURVE_POINTS," cluster "+string(i+1));
kクラスターの正しい数は何でしょうか。
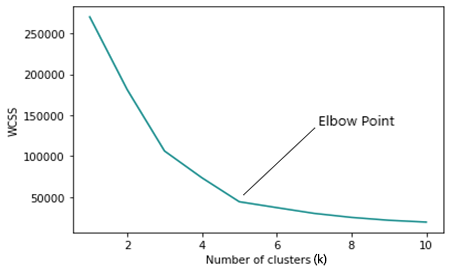
アルゴリズムがどのように機能するかは理解できました。k平均法のメイン関数を呼び出して、クラスターの数を設定するだけです。このアルゴリズムは初期化子の影響を受けるため、選択したクラスターの数が最適なものであることはどのようにわかるのでしょうか。これを理解するために、エルボー法と呼ばれるものを見てみましょう。
エルボー法
エルボー法は、k平均法で最適なクラスター数を見つけるために使用され、クラスター(k)のさまざまな値によって生成されたコスト関数のグラフがプロットされます。
kの数が増加すると、コスト関数が減少します。これは過学習として識別できます。
エルボーグラフを分析すると、グラフの方向が急速に変化して、その後、プロットはx軸に平行に移動し始めるポイントが見られます。
WCSS
クラスタ内平方和(Within Cluster Sum of Squared、WCSS)残差は、クラスター内の各ポイントと重心との間の二乗距離の合計です。
式は次のとおりです。
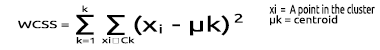
エルボー法はk平均法の最適化方法であるため、反復ごとにK平均法関数を呼び出す必要があります。
ここで、エルボー法を実行して結果を取得できるようにするには、k平均法のメイン関数でいつかの変更が必要です。最初に変更する必要があるのは、重心を取得するときです。これは、選択したクラスターが行列の行数と等しくなるか、それに近い数になると、初期の重心をランダムに選択する方法が不十分になるためです。
for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i); InitialCentroids.Row(rand_v,i); }
また、初期クラスターの最大数がデータセット内のnサンプルの数を超えないようにロジックを変更する必要があります。k平均法の定義から、k < nであることを思い出してください。
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //>>k should always be less than n
以下はエルボー法の完全なコードです。
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //k should always be less than n vector centroid_v={}, x_y_z={}; vector short_v = {}; //vector for each point vector minus_v = {}; //vector to store the minus operation output double wcss = 0; double WCSS[]; ArrayResize(WCSS,total_k); double kArray[]; ArrayResize(kArray,total_k); for (int k=initial_k, count_k=0; k<ArraySize(WCSS)+initial_k; k++, count_k++) { wcss = 0; m_clusters = k; KMeansClustering(clustered_mat,_centroids,1); for (ulong i=0; i<_centroids.Rows(); i++) { centroid_v = _centroids.Row(i); x_y_z = clustered_mat.Row(i); FilterZero(x_y_z); for (ulong j=0; j<x_y_z.Size()/m_cols; j++) { VectorCopy(x_y_z,short_v,uint(j*m_cols),(uint)m_cols); //--- WCSS ( within cluster sum of squared residuals ) minus_v = (short_v - centroid_v); minus_v = MathPow(minus_v,2); wcss += minus_v.Sum(); } } WCSS[count_k] = wcss; kArray[count_k] = k; } Print("WCSS"); ArrayPrint(WCSS); Print("kArray"); ArrayPrint(kArray); //--- Plotting the Elbow on the graph if (showPlot) { ObjectDelete(0,"elbow"); ScatterCurvePlots("elbow",kArray,WCSS,WCSS,"Elbow line","k","WCSS"); } }
以下は、上記のコードブロックの出力です。
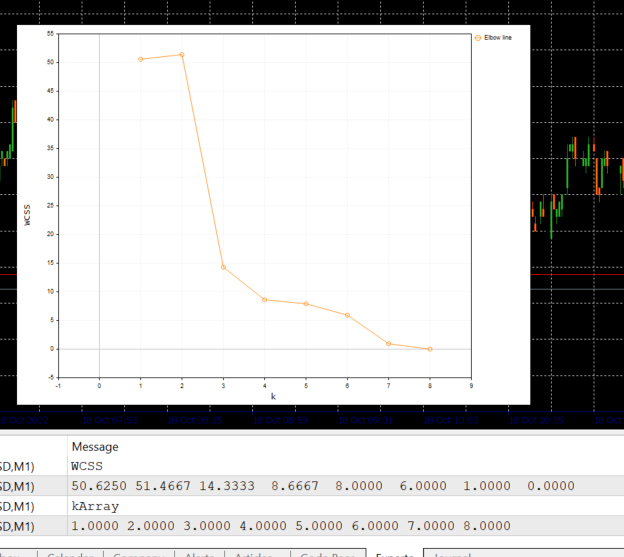
エルボープロットを見ると、最適なクラスター数が3であることが非常に明確です。この時点で、WCSSの値は、51.4667から14.333まで、他のすべての値よりも大幅に低下しています。
以上で、MQL5でk平均法アルゴリズムを実装するために必要なものがすべて揃ったので、取引環境でアルゴリズムを実装する方法を見てみましょう。
同じ市場価格データを複数のクラスターにグループ化する方法を見てみましょう。
matrix DMatrix = {}; DMatrix.Resize(bars, 1); //columns determines the dimension of the dataset 1D won't be visualized properly vector column_v = {}; column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,1,bars); DMatrix.Col(column_v,0);
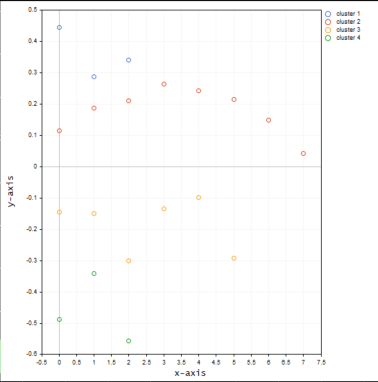
行列を市場価格値のnx1行列に置き換えました。今回は1次元行列を使用しました。クラスタリングアルゴリズムをコーディングした方法によると、1次元行列は適切に視覚化およびクラスタ化されません。たとえば、次のようになります。20本のバーのNASDAQ銘柄のクラスタリング操作全体の結果を下のグラフ画像で参照してください。
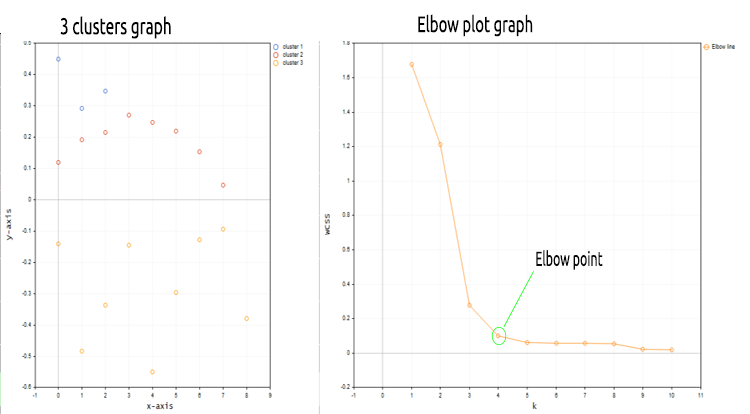
上のグラフでエルボー法に従って適合された4つのクラスターは、グラフにプロットすると、はるかによく見えます。
次に、同じ銘柄の値を3D行列に入れ、クラスターに何が起こるかを見てみましょう。
matrix DMatrix = {}; DMatrix.Resize(bars, 3); //columns determines the dimension of the dataset 1D won't be visualized properly vector column_v = {}; ulong start = 0; for (ulong i=0; i<2; i++) { column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,start,bars); DMatrix.Col(column_v,i); start += bars; }
以下は、プロット上のクラスターがです。
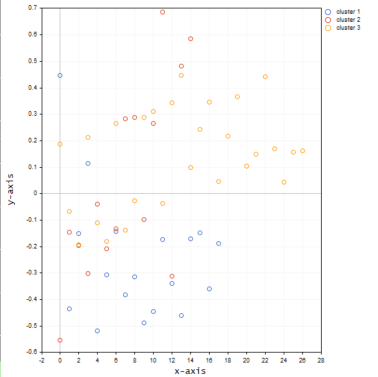
同じ軸上にクラスター化すると、3次元行列がクラスター内に多くの外れ値を提供するように見えます。
たとえば、値が異なるレベル/スケールにあるさまざまなサンプルをクラスター化しようとするときに、複数次元の行列を使用することを考えることができます。RSI指標値と移動平均指標値を試してみてください。ただし、これらの値を常に1次元の行列にまとめて、行列の1つの列を意味するようにするのが理想的です。自由に探索して、ディスカッションセクションでみんなと共有してください。
プロットの画像を表示する前に言い忘れましたが、NASDAQ価格値は平均正規化手法を使用して正規化しています。
MeanNormalization(DMatrix);
これは、プロット上でデータを適切に分散させるためです。以下は完全なコードです。
void MeanNormalization(matrix &mat) { vector v = {}; for (ulong i=0; i<mat.Cols(); i++) { v = mat.Col(i); MeanNormalization(v); mat.Col(v,i); } } //+------------------------------------------------------------------+ void MeanNormalization(vector &v) { double mean = v.Mean(), max = v.Max(), min = v.Min(); for (ulong i=0; i<v.Size(); i++) v[i] = (v[i] - mean) / (max - min); }
最後に
k平均法は、すべてのトレーダーとデータサイエンティストのツールボックスに必要な、非常に便利なアルゴリズムです。覚えておくべきことの1つは、このアルゴリズムは初期化子の影響を大きく受けるということです。エルボー法を使用して最適なアルゴリズムの検索を2つのクラスターから開始した場合、4つのクラスターを選択した場合とは異なる最適なクラスター数に到達する可能性があります。また、初期の重心は非常に重要です。初期の重心をランダムに選択するか、代わりに行列の最初の3行を選択するかを選べるように、メインのクラスタリング関数に入力できるようにしたのはそのためです。void CKMeans::KMeansClustering(matrix &clustered_matrix,matrix ¢roids,int iterations = 1,bool rand_cluster =false)
重心をランダムに選択するための関数引数rand_clusterは、デフォルトでfalseに設定されています。これは、k平均法関数がエルボー法関数で呼び出されるときに役立ちます。最適なクラスターを探しながらランダムな重心を選択のはうまくいかないためです。これは、クラスターの数がわかっている場合はうまく機能します。
ご精読ありがとうございました。
この記事で使用されているMQL5コードファイルは以下に添付されています。zipファイルにあるコードは、上記のコードからわずかに変更されています。一部の行はパフォーマンスのために削除されていますが、他の行はプロセス全体を理解しやすくするために追加されています。
GITHUBレポジトリ >> https://github.com/MegaJoctan/Data-Mining-MQL5
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/11615
 フラクタルによる取引システムの設計方法を学ぶ
フラクタルによる取引システムの設計方法を学ぶ
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索