適応型インジケーター

はじめに

おそらく、現在の市場状況に適応してレンジセグメントとトレンドセグメントを定義し、関連する価格の変化を考慮することができるインジケーターはすべてのトレーダーの夢でしょう。従来のテクニカル指標は、入力信号を処理する際に一定の比率を使用します。これらの比率は、入力信号の特性とその経時変化にはまったく依存しません。

適応型インジケーターは、入力信号と出力信号の値の間のフィードバックの存在によって特徴付けられます。このフィードバックにより、インジケーターは金融時系列値の最適な処理に個別に適応できるようになります。さらに簡単に言えば、適応型インジケーターは、現在の市場状況に応じて時間の経過とともに比率が変化する、通常の線形指標です。

適応アルゴリズムは非常に多様です。特定のアルゴリズムの選択は、インジケーターの目的によって異なります。ただし、ほとんどの場合、これらのアルゴリズムはさまざまな最小二乗法に基づいています。適応型インジケーターの開発例をいくつか見てみましょう。

初めの試み

適応型インジケーターを作成してみましょう。インジケーターを適応させる最も明白な方法は、最新のエラーを何らかの方法で考慮することです。その方法を見てみましょう。

Indicator[i]をi番目のバーのインジケーター値とします。エラーはError[i] = price[i] - Indicator[i]です。

このエラーは、次のカウント中にインジケーター値を修正するために使用できます。さらに、さまざまな方法でエラーを処理できます。例は、最近のいくつかのエラーの平均を取得することや、それらに指数平滑法を適用することです。

この方法がチャートでどのように見えるか見てみましょう。テクニカル指標に関する記事のテンプレートを基礎として使用します。ただし、いくつかの変更を加えます。まず、エラーの数を設定します。

      double sum=0;
      for(int j=0; j<size; j++)
         sum=sum+coeff[j]*price[i+j];//Calculate the indicator value

      if(i>0)
        {
        double cur_error=price[i]-sum;//Current error
         if(NumErrors==0)
            cur_error=(error+cur_error)/2;
         if(NumErrors==1)
            error=cur_error/2;
         if(NumErrors>1)
           {
            for(int j=NumErrors-1; j>0; j--)
               errors[j]=errors[j-1];
            errors[0]=cur_error;

            cur_error=0;
            for(int j=0; j<NumErrors; j++)
               cur_error=cur_error+errors[j];
            error=cur_error/NumErrors;
           }
        }

      buffer[i]=sum+error;//Indicator value considering the error

単純な移動平均（赤い線）と比較して、新しいインジケーターは次のように見えます。

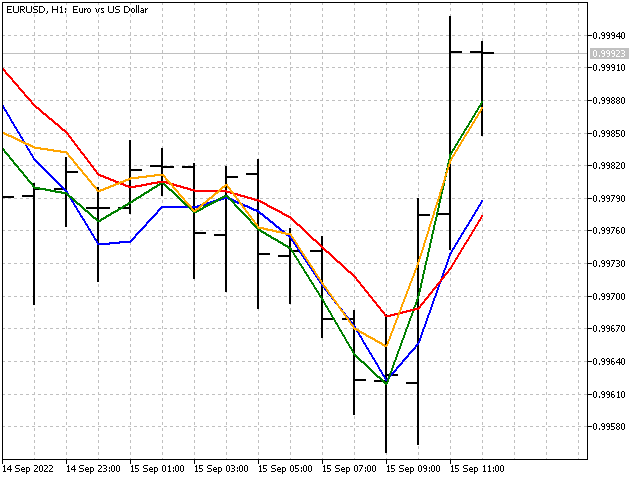
図はきれいに見えますが、インジケーターは適応しているでしょうか。残念ながら、していません。実際、重み係数は暗黙的に設定されていますが、これは通常の線形指標です。

最後の3つのエラーの平均を特徴とする3の期間で単純な移動平均を取りましょう。最初にエラーを計算しましょう。

Error[1] = price[1] - (price[1] + price[2] + price[3])/3

Error[2] = price[2] - (price[2] + price[3] + price[4])/3

Error[3] = price[3] - (price[3] + price[4] + price[5])/3

インジケーターの方程式は次のようになります。

Indicator[0] = (price[0] + price[1] + price[2])/3+(Error[1] + Error[2] + Error[3])/3 =>

Indicator[0] = (3*price[0] + 5*price[1] + 4*price[2] + 0*price[3] - 2*price[4] - 1*price[5])/9

その結果、通常の線形インジケーターが得られます。これには単純な結論が伴います。エラー処理だけではインジケーターは適応しないということです。

日の出

ピエール=シモン・ラプラスはかつて、「日の出問題」として知られるようになった問題を定式化しました。この問題の本質は、「日の出を1000日間見た場合、1001日目に太陽が昇るという確信はどうなるか」ということです。この問題は興味深いです。取引の観点から見てみましょう。9回の取引をおこない、そのうち6回が利益を上げたとします。この情報に基づいて、利益を生んだ取引の確率は何かという質問に答えてみてください。

原則として、確率は、利益を生んだ取引の総数に対する比率として定義されます。

この例では、確率は6/9になります。しかし、さらに一歩進んでみましょう。将来の取引で勝つ確率は何でしょうか。分数の分母は、どの結果でも1ずつ増加します。しかし、分子については2つのオプションが可能になります。将来の取引は、利益を生むか生まないかのいずれかになる可能性があります。つまり、次の2つのオプションがあります。

これらの値の平均をとってみましょう。この場合、勝つ確率の推定は次のようになります。

これは、元の値である6/9よりわずかに小さくなっています。この手法は、ラプラススムージングと呼ばれ、変数が複数の定義された値（この例では「成功または失敗」）を取ることができるカテゴリデータに使用できます。

この平滑化をインジケーターに適用してみましょう。これをおこなうために、1つの小さな仮定を立てます。価格フローに別の隠れた「架空」の価格があると仮定します。これも指標の読み取りに影響します。

この場合、インジケーターの方程式がどのように変化するかを見てみましょう。単純移動平均方程式は次のようになります。

架空の価格があると、同じ平均は次のようになります。

一見すると、すべてが素晴らしく見えますが、ここにはいくつか不快なことがあります。まず、架空の価格自体が不安定になります。

次に、架空の価格を時系列の次のポイントに移動すると、インジケーターが単純化されます。

この単純化は、インジケーターを安定させる役には立ちませんでした（price[1]比率は1に等しい）。ただし、この失敗は、別のインジケーターの基礎として役立つ可能性があります。

まず、インジケーターの期間(iPeriod)を設定します。次に、1からiPeriodまでの値を持つすべてのNのSL値を見つけます。次のステップは、すべてのSL値の合計の平均を計算することです。その結果、安定した価格値を示すインジケーターが得られます。このインジケーターは、単純な予測（過去=未来）とわずかに弱い線形トレンドとして説明できます。

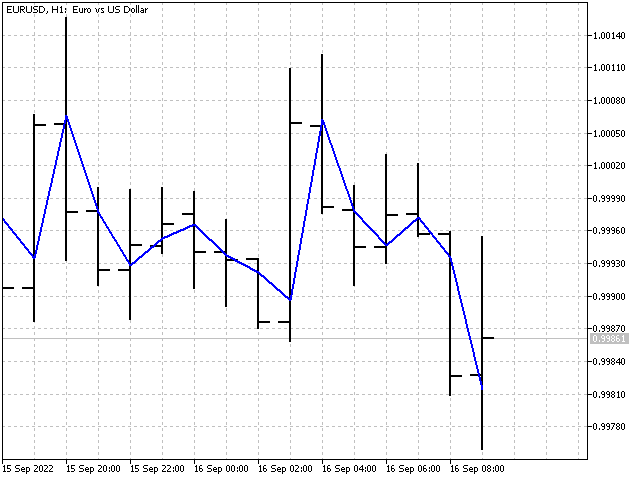
これでインジケーターができました。ただし、適応は達成されていません。また試みてまた失敗です。少し休憩してから、適応型インジケーターを作成してみましょう。さもないと、この記事のタイトルを変更する必要があります。

月の入り

ロシア人のフィクション作家Kozma Prutkovはかつて、非常に賢明に次のように述べました。「太陽と月のどちらがもっと役に立つかを尋ねられたら、月と答えます。太陽はすでに明るい昼間にのみ輝くが、月は夜に輝くからです。」このことわざを取引の世界にどのように置き換えできるか見てみましょう。

ラプラススムージングでは、同じ重みの比率で価格値を使用しましたが、価格に一定の重みを与えるとどうなるでしょうか。ウィンドウ関数では、重みの比率は、指定された読み取り値がインジケーターの重心からどれだけ離れているかによって異なります。次にこれを別の方法でおこなうことにします。まず、特定の価格値を中心値として選択します。この重みが一番大きくなります。残りの価格の重みの比率は、価格がこの値からどれだけ離れているかによって異なります。距離が離れているほど、その重みは小さくなります。つまり、時間領域ではなく、価格領域でウィンドウ関数を作成します。このようなアルゴリズムが実際にどのように見えるか見てみましょう。

      double value=price[i+center],//Price value at the center
             max=_Point;           //Maximum deviation
      for(int j=0; j<period; j++)//Calculate price deviations from the central one and the max deviation
        {
         weight[j]=MathAbs(value-price[i+j]);
         max=MathMax(max,weight[j]);
        }

      double width=(period+1)*max/period,//correct the maximum deviation from the center so that there are no zeros at the ends
             sum=0,
             denom=0;
      for(int j=0; j<period; j++)//calculate weight ratios for each price
        {
         if(Smoothing==Linear)//linear smoothing
            weight[j]=1-weight[j]/width;
         if(Smoothing==Quadratic)//quadratic smoothing
            weight[j]=1-MathPow(weight[j]/width,2);
         if(Smoothing==Exponential)//exponential smoothing
            weight[j]=MathExp(-weight[j]/width);

         sum=sum+weight[j]*price[i+j];
         denom=denom+weight[j];
        }

      buffer[i]=sum/denom;//indicator value

次は、チャート上でのインジケーターの様子です。

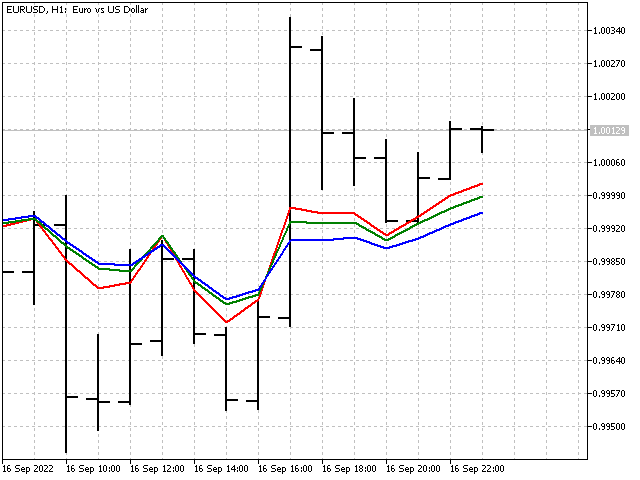
インジケーターの重み比率は変わっていますが、これは適応とは言えません。このインジケーターは現在の市場状況に適応すると言ったほうが正しいでしょう。適応型インジケーターは機能しませんでしたが、少なくとも最初の一歩を踏み出しました。

2回目の試み

長方形のウィンドウ関数を基礎として使用しましょう。ただし、小さな変更を加えて、ウィンドウの最初と最後で比率が変わる可能性があるとします。インジケーターの式は次のようになります。

ここで、Nはインジケーターの期間、C1とC2は適応比率です。

これらの比率の値が既にあるとします。新しい価格値が表示されます。これに伴い、インジケーターの誤差が変化する場合があります。

エラーを減らすには、特定のR補正係数で各比率を補正する必要があります。

言うまでもなく、比率の変化によってインジケーターの誤差がゼロになるように努力しますが、これが唯一の条件ではありません。さらに、R補正も小さいことを要求しましょう。両方の条件が満たされている場合、適応比率の値がいくつかの最適値（存在する場合）の周りで変動することを期待できます。

したがって、次の問題の解を見つける必要があります。

最小二乗法を使用してR補正を見つけてみましょう。この場合、計算はいくつかのステップで実行できます。まず、収束係数を計算します。

補正値はR = price*Error*Mに等しくなります。

したがって、比率を更新する式は次のようになります。

単純移動平均（赤い線）と比較して、インジケーターは次のように見えます。

適応

2つの比率に対処することができました。すべての比率が適応するインジケーターを作成することはできるでしょうか。できます。そのような指標の比率の計算は、前のケースで考慮されたものと似ています。唯一の違いは、収束係数の計算です。

Pパラメータを使用すると、各ステップでの比率の変化率を調整できます。その値は1以上である必要があります。Pが小さい場合、指標比率は非常に迅速に最適値に達します。ただし、指標比率の変化は過度であることが判明する可能性があります。Pが大きい場合、指標の比率はゆっくりと変化します。P値が高いほど、インジケーターはより滑らかになります。たとえば、P=1およびP=1000の場合、インジケーターは次のようになります。

一般的な推奨事項：:最初にパラメータ値を指標期間と等しく設定し、次に希望する結果が得られるまで、いずれかの方向に変更します。

適応型インジケーターの重要な特徴は、潜在的な不安定性です。このようなインジケーターの比率の合計は1に等しくなく、入力データによって異なる場合があります。指数平均を例に取りましょう。従来の方程式は次のようになります。.

適応型EMAの方程式は次のようになります。.

C1とC2は相互に依存しません。比率は、前のインジケーターと同じ方法で更新されます。違いは、インジケーター自体の以前の値が価格とは別に使用されるという事実にあります。

次に、更新された比率は次のようになります。

P値の異なる適応型EMA自体は次のようになります。

適応アルゴリズムはウィンドウ関数にも適用できます。ただし、正規化比率の変更により適応が発生するため、結果はそれほど印象的ではありません。

期間が5のLWMAインジケーターを基準として考えてみましょう。その方程式は次のように書くことができます。.

ここで、Cは正規化比率です。通常、この比率の値は一定であり、事前に計算できます。ここで、ある方向または別の方向に変化する可能性を許可します。

まず、加重合計を計算する必要があります。.

この場合、正規化比率の調整値は、次の式を使用して求めることができます。

この方法は、短期間のインジケーターに役立ちます。長期的には、適応とPパラメータの影響はほとんど見えません。

適応型インジケーターに基づいて、さまざまなオシレーターを作成できます。たとえば、CCI適応型インジケーターは次のようになります。

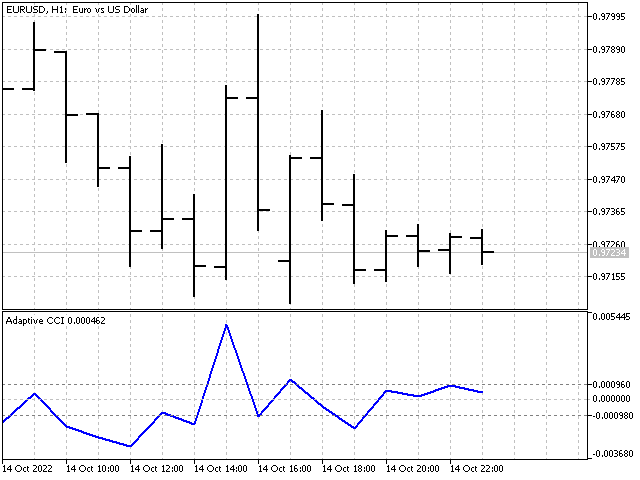
線形予測

適応型インジケーターの構築は、多くの点で線形予測問題の解決に似ています。実際、インジケーター値と将来の（インジケーター自体に関連する）価格の差をエラーとして使用すると、適応型インジケーターは予測型インジケーターに変わります。

たとえば、始値を見てみましょう。インジケーターの式とエラー値は次のようになります。

他のすべての計算は、すでにおなじみの方程式に従って実行されます。このインジケーターに追加する唯一のものは、平均予測誤差の計算です。その結果、インデックスが-1のバーの始値の予測値を取得します。

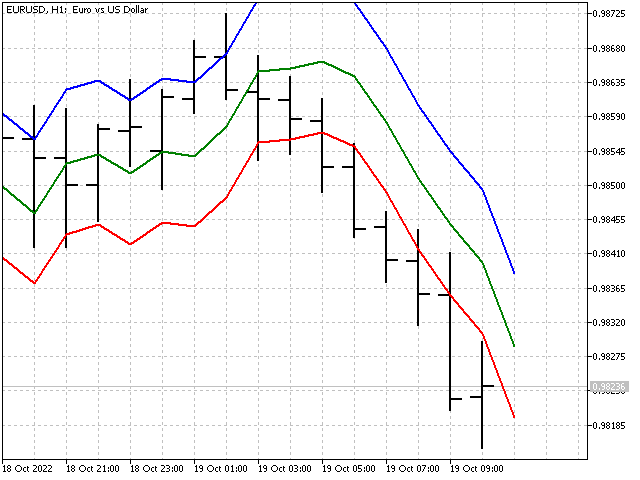
線形確率予測

線形予測のタスクは、価格変動方程式で表すこともできます。物理的な世界では、すべてが非常に単純に見えます。点の現在の位置、速度、および加速度がわかっている場合、次の瞬間の位置を予測することは難しくありません。値動きの場合、すべてがより複雑になります。

価格値はわかっています。数学の言葉では、速度と加速度は一次導関数と二次導関数です。それらを個別のアナログに置き換え、対応する次数の違いを分割します。分割された差の比率は、パスカルの三角形の対応する行から取得できます。各比率の前の記号を交互に変更するだけです。次のようになります。

1*open[0] -1*open[1] – 速度の離散アナログ

1*open[0] -2*open[1] +1*open[2] – 加速度の離散アナログ

次に、価格変動方程式は次のように表すことができます。

open[0] + (open[0] – open[1]) + (open[0] – 2*open[1] + open[2]).

この方程式に適応比率を追加すると、次の結果が得られます。

open[-1] = open[0] + c1*(open[0] – open[1]) + c2*(open[0] – 2*open[1] + open[2]).

括弧を開いて比率を整理すると、方程式は次のようになります。

open[-1] = (1 + с1 + с2)*open[0] + (-c1 – 2*с2)*open[1] + c2*open[2].

覚えていらっしゃるかもしれませんが、安定したインジケーターの比率は-1から+1の範囲にあるべきです。次に、次の一連の不等式を解く必要があります。

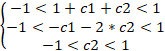
その結果、次の3つのオプションが得られます。

これで、比率の値を選択してインジケーターで使用できるようになりました。

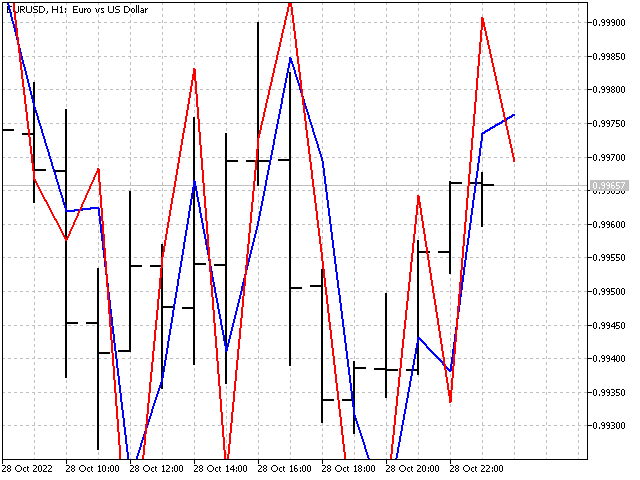
もちろん、高次の差を使用すると、より多くのオプションが提供され、インジケーターの外観に好影響を与えます。

結論

適応アルゴリズムを使用すると、非常に珍しいインジケーターを取得できます。それらの主な利点は、現在の市場状況に自己適応できることです。欠点には、制御パラメータの数が増えることが含まれ、その選択には時間がかかる場合があります。一方、適応型インジケーターは非常に広い範囲で変化する可能性があり、テクニカル分析への新しいアプローチを生み出す可能性があります。