ニューラルネットワークが簡単に（第17部）：次元削減

MetaTrader 5 — トレーディングシステム | 14 9月 2022, 09:31

620

Dmitriy Gizlyk

内容

はじめに

モデルと教師なし学習アルゴリズムの研究を続けます。データクラスタリングアルゴリズムについては既に説明しました。この記事では、次元削減に関連する問題の解決策を探ります。基本的に、これらは実際に広く使用されている特定のデータ圧縮アルゴリズムです。これらのアルゴリズムの1つの実装を調べて、取引モデルの構築にどのように使用できるかを見てみましょう。

1.次元削減問題について

新しい日、新しい時間、新しい瞬間は、人間の生活のあらゆる分野で膨大な量の情報を提供します。今日の世界で絶え間なく広がる情報技術により、人々はできるだけ多くの情報を保存して処理しようとします。ただし、大量の情報を保存するには、大容量のデータストレージが必要です。さらに、この情報を処理するには大規模なコンピューティングリソースが必要です。この問題の可能な解決策の1つは、利用可能な情報をより簡潔な形式で記録することです。さらに、完全なデータコンテキストを圧縮形式で保持すれば、その処理に必要なリソースは少なくなります。

たとえば、200*200ピクセルの画像でパターン認識を行う場合、各ピクセルはメモリ内で4バイトを占有する色形式で書き込まれます。各ピクセルを1650万色のいずれかで表現する能力は、この問題には過剰です。ほとんどの場合、グラデーションを16色または32色に減らしても、モデルのパフォーマンスは影響を受けません。この場合、各ピクセルの色番号を書き込むための1バイトのみを使用します。もちろん、色行列を書き込むには、16色で64バイト、32色で128バイトの1回限りのコストが必要です。すべての画像のサイズを4分の1に縮小するために支払う代償としては、これは大きくありません。実は、このような問題は、すでに知っているデータクラスタリング手法を使用して解決できます。ただし、これは最も効率的な方法ではない可能性があります。

次元削減手法を使うもう1つの分野は、データの視覚化です。たとえば、10個のパラメータで表される特定のシステム状態を表すデータがあって、このデータを視覚化する方法を見つける必要があるとします。人間の知覚には、2Dおよび3D画像が最も適しています。2、3個のパラメータのさまざまなバリエーションを使用して、複数のスライドを作成できますが、システム状態の全体像は提供されません。ほとんどの場合、異なるスライドの異なる状態は1つのポイントにマージされますが、これらは異なる状態である可能性があります。

したがって、すべてのシステム状態を10個のパラメータから2次元または3次元空間に変換するのに役立つようなアルゴリズムを見つける必要があります。また、このアルゴリズムは、相対的な位置を維持しながらシステムの状態を分割する必要があります。もちろん、失われる情報はできるだけ少なくする必要があります。

「どれもこれも面白いけど、取引で何の役に立つのか」と思われるかもしれません。ターミナルを見てみましょう。いくつの指標がありますか。それらの多くは特定のデータ相関を持っているかもしれませんが、それぞれが、市場の状況を説明する少なくとも1つの値を提供します。これに取引商品の数を掛けるとどうなるでしょうか。さらに、指標のさまざまなバリエーションと分析された時間枠により、現在の市場状態を表すパラメータの数が無限に増加する可能性があります。

もちろん、1つのモデルですべてのツールとすべての可能な指標を検討するわけではありませんが、最適な組み合わせを探す際には、それらの多くを組み合わせて使用することができいるので、モデルが複雑になり、訓練時間が長くなります。したがって、最大の情報を維持しながら初期データの次元を減らすことで、モデルの訓練コストを削減し、意思決定の時間を短縮します。市場の挙動への反応は非常に速くなる可能性があります。取引は非常に良い価格で実行されます。

次元削減アルゴリズムは、常にデータの前処理にのみ使用されます。これは、圧縮された形式のソースデータのみが返されるためです。その後、データは保存されるか、さらに処理するために使用されます。これには、データの視覚化や他のモデルによる処理が含まれる場合があります。

したがって、取引システムを構築するために、必要最小限の情報を使用して現在の市場状態を記述し、次元削減アルゴリズムの1つを使用して圧縮することができます。縮小プロセスにより、ノイズと相関データが除去されることを期待する必要があります。次に、削減されたデータを取引意思決定モデルに入力します。

アイデアが明確であることを願っています。次元削減アルゴリズムを実装するには、最も一般的な主成分分析法の1つを使用することをお勧めします。このアルゴリズムは、さまざまな問題を解決することが証明されており、新しいデータで複製できます。これにより、受信データを削減し、意思決定モデルに転送して、リアルタイムの取引決定を生成できます。

2.主成分分析(PCA)法

主成分分析は、1901年にイギリスの数学者カール・ピアソンによって発明され、それ以来、多くの科学分野で成功裏に使用されてきました。

この手法の本質を理解するために、2次元データ配列の次元をベクトルに縮小することに関連する単純化されたタスクを使用することを提案します。幾何学的な観点から、これは平面の点の直線への投影として表すことができます。

下の図では、初期データは青い点で表されています。橙色と灰色の線上に2つの投影があり、対応する色の点があります。ご覧のとおり、最初の点から橙色の投影までの平均距離は、灰色の投影までの同様の距離よりも短くなっています。灰色の投影には、点の投影が重なっています。したがって、橙色の投影法は、すべての個々のポイントを分離し、次元（ポイントから投影までの距離）を縮小するときに失われるデータが少ないため、より好ましくなります。

このような線は主成分と呼ばれます。そのため、この方法は主成分分析と呼ばれます。

数学的な観点からは、各主成分は、サイズが元のデータの次元に等しい数値ベクトルです。1つのシステム状態を表す元のデータのベクトルと対応する主成分のベクトルの積は、分析された状態の投影点を直線上に生成します。

元のデータ次元と次元削減の要件によっては、複数の主成分が存在する場合がありますが、元のデータ次元を超えるものは存在しません。ボリュームの投影をレンダリングする場合、それらは3つになります。データを圧縮する場合、許容誤差は通常、データの最大1%の損失です。

主成分法

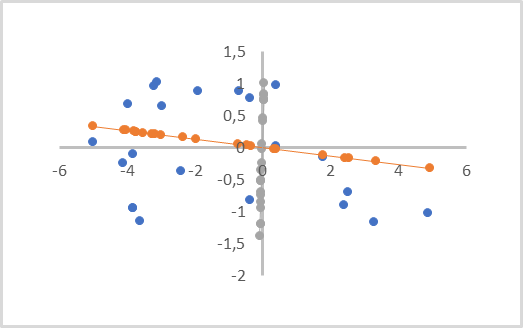
これは視覚的には線形回帰に似ていますが、これらはまったく異なる方法であり、異なる結果をもたらします。

線形回帰は、ある変数の別の変数への線形依存を表し、距離は座標軸に対して垂直に最小化されます。このような線は、平面のどの部分も通過できます。

主成分分析では、すべての軸に沿った値は完全に独立しており、同等です。軸ではなく線に垂直な距離は最小化されます。主成分線は必ず原点を通ります。したがって、この手法を適用する前に、すべての初期データを正規化する必要があります。少なくとも、原点を中心に配置する必要があります。つまり、各次元で0を基準にしてデータを中央に配置する必要があります。

主成分分析法のもう1つの重要な特徴は、その適用によって主成分の直交ベクトルの行列が得られるということです。つまり、すべての主成分ベクトル間には相関関係がまったくありません。この事実は、削減されたデータを入力として受け取る将来の意思決定モデルの学習プロセス全体にプラスの影響を与えます。

数学的な観点から、主成分分析法は、初期データの共分散行列のスペクトル分解として表すことができます。共分散行列は次の式で求めることができます。

共分散行列式

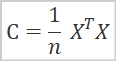
ここで

Cは共分散行列、
Xは元のデータ行列、
nはソースデータの要素数です。

この操作の結果、正方共分散行列が得られます。そのサイズは、システム状態を記述する特徴の数と同じです。特徴の分散は、行列の主対角線に沿って配置されます。行列の他の要素は、対応する特徴ペアの共分散度を表します。

次の段階では、結果の共分散行列の特異値分解を実行する必要があります。行列の特異値分解は、かなり複雑な数学的作業です。しかし、MQL5での行列と行列演算の導入により、この演算は行列に対して既に実装されているため、この作業は大幅に簡素化されています。したがって、すぐに特異値分解の結果に進みましょう。

行列の特異値分解の結果として、3つの行列が得られ、その積は元の行列に等しくなります。2番目の行列∑は、元の行列と同じサイズの対角行列です。特異ベクトルの軸に沿った値の分散を表す特異数はこの行列の主対角線に沿ってあります。特異数は負ではなく、降順に並べられます。行列の他のすべての要素は0に等しくなります。そのため、ベクトルとして表されることがよくあります。

UとVは、それぞれ左と右の特異ベクトルを含むユニタリ正方行列です。行列Uは元の行列と同じ行数を持ち、行列Vは元の行列と同じ列数を持ちます。

この場合、正方共分散行列の特異値分解を実行すると、行列UとVは同じサイズになります。

次元削減のために、行列Uを使用します。特異数は降順で配置されるため、行列Uの最初の列の必要な数を単純に取得できます。新しい行列を行列URとします。次元を減らすには、元のデータ行列に新しく作成した行列URを乗算するだけです。

ここで疑問が生じます。どの値まで削減するのが最適でしょうか。タスクがデータの可視化であれば、そのような疑問は生じません。1から3の間の最終次元の選択は、目的の投影によって異なります。ここでのタスクは、情報の損失を最小限に抑えてデータを削減し、それを別の意思決定モデルに渡すことです。したがって、主な基準は失われる情報の量です。

保持されるデータ量を決定するための最良のオプションは、使用される特異ベクトルに対応する特異値の比率を計算することです。

情報発信率

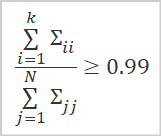
ここで

kは使用されるベクトルの数
Nは特異値の総数

です。実際には、この列数kは通常、上記の比率の値が少なくとも0.99になるように選択されます。これは、情報の99%を保持することに相当します。

一般的な理論的側面を検討したので、メソッドの実装に進みます。

3.MQL5を使用したPCAの実装

主成分分析アルゴリズムを実装するために、CObject基本クラスから継承された新しいクラスCPCAを作成します。新しいクラスのコードはpca.mqhファイルに保存されます。

このクラスを実装するには行列演算を使用します。したがって、モデルの訓練結果（行列UR）は行列m_Ureduceに保存されます。

さらに、3つのローカル変数を宣言しましょう。モデル訓練ステータスb_Studiedと2つのベクトルv_Meansとv_STDsです。ここには、さらにデータを正規化するために算術平均と標準偏差の値を保存します。

class CPCA : public CObject
  {
private:
   bool              b_Studied;
   matrix            m_Ureduce;
   vector            v_Means;
   vector            v_STDs;

クラスコンストラクタで、モデル訓練状態フラグb_Studiedにfalse値を指定し、行列m_Ureduceをサイズ0で初期化します。クラス内でネストされたオブジェクトを作成しないため、クラスのデストラクタを空のままにします。

CPCA::CPCA()   :  b_Studied(false)
  {
   m_Ureduce.Init(0, 0);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPCA::~CPCA()
  {
  }

次に、モデルの訓練メソッドStudyを再作成します。このメソッドは、パラメータで元のデータ行列を受け取り、演算の論理結果を返します。

前述のように、主成分分析を実行するには正規化されたデータを使用する必要があります。したがって、メインメソッドアルゴリズムの実装に進む前に、以下の式を使用して初期データを正規化します。

データの正規化

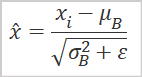
行列演算を使用するとこのタスクが簡素化されます。ループシステムを作成する必要がなくなります。すべての特徴の算術平均値を見つけるには、Mean行列演算メソッドを使用できます。その中で、値をカウントする次元を指定します。操作の結果、すべての特徴の算術平均値を含むベクトルがすぐに得られます。

データの正規化式の分母には分散の平方根が含まれます。これは標準偏差に対応します。ここでも行列演算を使用できます。STDメソッドは、指定された次元の標準偏差のベクトルを返します。ゼロ除算エラーをなくすために小さな定数を追加するだけです。

結果のベクトルを対応する変数v_Meansおよびv_STDsに保存します。このような初期データの正規化は、モデルの訓練段階と運用段階の両方で実行する必要があります。

次に、データを正規化します。このために、元のデータサイズと同じサイズの行列Xを用意します。ソースデータ行列の行数と等しい反復回数でループを実装します。

ループ本体で、初期データを正規化して演算結果を以前に作成した行列Xに保存します。ベクトル演算を使用すると、ネストされたループを作成する必要がなくなります。

bool CPCA::Study(matrix &data)
  {
   matrix X;
   ulong total = data.Rows();
   if(!X.Init(total,data.Cols())
      return false;
   v_Means = data.Mean(0);
   v_STDs = data.STD(0) + 1e-8;
   for(ulong i = 0; i < total; i++)
     {
      vector temp = data.Row(i) - v_Means;
      temp /= v_STDs;
      X = X.Row(temp, i);
     }

元のデータを正規化した後は、主成分分析アルゴリズムの実装に直接進みます。前述のように、まず共分散行列を計算する必要があります。行列演算のおかげで、これは1行のコードに簡単に収まります。不要なオブジェクトを作成しないために、演算結果を行列Xに上書きします。

   X = X.Transpose().MatMul(X / total);

上記のアルゴリズムによると、次の操作は共分散行列の特異値分解です。この操作の結果、左特異ベクトル、特異値、右特異ベクトルの3つの行列が得られると予想されます。すでに説明したように、主対角に沿った特異値行列の要素のみが0以外の値を持つことができます。したがって、リソースを節約するために、MQL5実装では行列の代わりに特異値のベクトルが返されます。

関数を呼び出す前に、結果を受け取るための2つの行列とベクトルを宣言します。その後、特異値分解のためにSVD行列ベクトルを呼び出すことができます。パラメータでは、操作結果を記録するための行列とベクトルをメソッドに渡します。

   matrix U, V;
   vector S;
   if(!X.SVD(U, V, S))
      return false;

特異ベクトルの直交行列を取得したので、元のデータの次元をどこまで下げるかを決定する必要があります。一般的な慣行として、元のデータに含まれる情報の少なくとも99%を保持します。

上記のロジックに従って、最初に特異値ベクトルのすべての要素の総和を決定し、結果値が0より大きいことを確認します。特異値は負ではないため、結果値が負になることはありません。さらに、ゼロ除算エラーを除外する必要があります。

その後、特異値ベクトルの値の累積和を計算し、結果のベクトルを特異値の総和で除算します。

その結果、最大値が1に等しい増加する値のベクトルが得られます。

次に、必要な列の数を決定するには、ベクトル内でしきい値情報保持値以上の最初の要素の位置を見つける必要があります。上記の例では0.99です。これは、情報の99%を保持することに相当します。

   double sum_total = S.Sum();
   if(sum_total<=0)
      return false;
   S = S.CumSum() / sum_total;
   int k = 0;
   while(S[k] < 0.99)
      k++;

行列サイズを変更して、その内容をクラス行列に転送するだけです。その後、モデル訓練フラグを切り替えて、メソッドを終了します。

   if(!U.Resize(U.Rows(), k + 1))
      return false;
//---
   m_Ureduce = U;
   b_Studied = true;
   return true;
  }

モデル訓練メソッドを作成した後、つまり、元のデータの次元削減行列を決定したら、ReduceMメソッドを作成して入力データを削減することもできます。パラメータで元のデータを受け取り、縮小された次元の行列を返します。

もちろん、入力データは、モデルの訓練段階で使用されるデータと比較できる必要があります。ここでは、観察の数ではなく、特徴を記述するシステム状態の量と質について話しています。

メソッドの初めに、コントロールのブロックを作成してモデル訓練フラグを確認します。ここでは、初期データ行列の列数（特徴の数）が縮小行列m_Ureduceの行数と等しいかどうかも確認します。いずれかの条件が満たされない場合は、メソッドを終了してサイズが0の行列を返します。

matrix CPCA::ReduceM(matrix &data)
  {
   matrix result;
   if(!b_Studied || data.Cols() != m_Ureduce.Rows())
      return result.Init(0, 0);

コントロールのブロックを正常に通過したら、次元削減を実行する前に元のデータを正規化します。正規化アルゴリズムはモデル訓練時に説明したものと似ています。唯一の違いは、今回は算術平均と標準偏差を計算しないということです。代わりに、訓練中に保存された対応するベクトルを使用します。したがって、新しい結果と訓練中に得られた結果の比較可能性を保証します。

   ulong total = data.Rows();
   if(!X.Init(total,data.Cols()))
      return false;
   for(ulong r = 0; r < total; r++)
     {
      vector temp = data.Row(r) - v_Means;
      temp /= v_STDs;
      result = result.Row(temp, r);
     }

メソッドアルゴリズムを完了する前に、正規化された値の行列を縮小行列に乗算し、演算結果を呼び出し元に返す必要があります。

   return result.MatMul(m_Ureduce);
  }

元のデータの次元を削減するモデルを訓練するメソッドを構築しました。行列演算を使用したおかげで、結果のコードは非常に簡潔になり、数学に深く入り込む必要がありませんでした。ただし、これは行列演算を使用して記述されたライブラリの最初のコードです。以前は、CBufferDoubleオブジェクトで動的配列を使用していました。したがって、オブジェクトの互換性を提供するには、動的バッファから行列へ、またはその逆にデータを転送するためのインターフェイスを作成する必要があります。

このプロセスを整理するために、 FromBufferおよびFromMatrixの2つのメソッドを作成します。最初のメソッドは、動的データバッファと1つのシステム状態を表すベクトルのサイズを含むパラメータを受け取り、バッファの内容の転送先となる行列を返します。

メソッド本体では、最初にコントロールのブロックを編成し、初期データバッファオブジェクトへのポインタの有効性をチェックします。次に、バッファサイズが、解析されたシステムの1つの状態を表すベクトルの倍数であるかどうかを確認します。

matrix CPCA::FromBuffer(CBufferDouble *data, ulong vector_size)
  {
   matrix result;
   if(CheckPointer(data) == POINTER_INVALID)
     {
      result.Init(0, 0);
      return result;
     }
//---
   if((data.Total() % vector_size) != 0)
     {
      result.Init(0, 0);
      return result;
     }

すべてのチェックに合格した場合、行列の行数を決定し、結果の行列を初期化します。

   ulong rows = data.Total() / vector_size;
   if(!result.Init(rows, vector_size))
     {
      result.Init(0, 0);
      return result;
     }

次に、動的バッファのすべての内容を行列に移動するネストされたループのシステムを編成します。

   for(ulong r = 0; r < rows; r++)
     {
      ulong shift = r * vector_size;
      for(ulong c = 0; c < vector_size; c++)
         result[r, c] = data[(int)(shift + c)];
     }
//---
   return result;
  }

ループシステムが完了したら、メソッドを終了し、作成された行列を呼び出し元に返します。

2番目のメソッドFromMatrixは逆の操作を実行します。パラメータでは、データを含む行列をメソッドに入力し、出力で動的データバッファを受け取ります。

メソッド本体では、まず動的配列のオブジェクトを新規作成してから、操作結果を確認します。

CBufferDouble *CPCA::FromMatrix(matrix &data)
  {
   CBufferDouble *result = new CBufferDouble();
   if(CheckPointer(result) == POINTER_INVALID)
      return result;

そして、行列の内容全体を格納するのに十分な大きさの動的配列のサイズを予約します。

   ulong rows = data.Rows();
   ulong cols = data.Cols();
   if(!result.Reserve((int)(rows * cols)))
     {
      delete result;
      return result;
     }

次に、行列の内容を動的配列に転送する必要があります。この操作は、2つのネストされたループのシステム内で実行されます。

   for(ulong r = 0; r < rows; r++)
      for(ulong c = 0; c < cols; c++)
         if(!result.Add(data[r, c]))
           {
            delete result;
            return result;
           }
//---
   return result;
  }

すべてのループ操作が正常に完了したら、メソッドを終了し、作成されたデータバッファオブジェクトを呼び出し元に返します。

ここで、作成されたオブジェクトへのポインタを保存しないことに注意してください。したがって、その状態の監視に関連する操作と、操作の完了後にメモリから削除する操作は、呼び出し元のプログラム側で編成する必要があります。

ベクトルを操作する同様のメソッドを作成しましょう。バッファからベクトルへのデータは、オーバーロードされたメソッドFromBufferを使用して移動されます。FromVectorメソッドでは逆の操作が行われます。メソッドを構築するためのアルゴリズムは上記と似ています。メソッドの完全なコードは、以下の添付ファイルに記載されています。

データ転送メソッドを作成した後、モデル訓練メソッドのオーバーロードを作成できます。このオーバーロードは、パラメータで動的データバッファと1つのシステム状態記述ベクトルのサイズを受け取ります。メソッド構築アルゴリズムは非常に単純です。まず、前述のメソッドFromBufferを使用して、動的バッファから行列にデータを転送します。次に、結果の行列を渡して、前に検討したモデル訓練メソッドを呼び出します。

bool CPCA::Study(CBufferDouble *data, int vector_size)
  {
   matrix d = FromBuffer(data, vector_size);
   return Study(d);
  }

次元削減メソッドReduceMに同様のオーバーロードを作成してみましょう。訓練メソッドのオーバーロードとの唯一の違いは、メソッドパラメータでは1つのシステム状態を表すベクトルのサイズを指定せずに初期データバッファのみを渡すことです。これは、この時点までにモデルが既に訓練されており、状態記述ベクトルのサイズがリダクション行列の行数と等しくなければならないという事実に関連しています。

このメソッドのもう1つの違いは、過剰なデータ転送を防ぐために、まずモデルが訓練されているかどうか、およびバッファサイズが状態記述ベクトルのサイズの倍数であるかどうかを確認することです。すべてのチェックに合格したしたら初めて、データ転送メソッドを呼び出します。

matrix CPCA::ReduceM(CBufferDouble *data)
  {
   matrix result;
   result.Init(0, 0);
   if(!b_Studied || (data.Total() % m_Ureduce.Rows()) != 0)
      return result;
   result = FromBuffer(data, m_Ureduce.Rows());
//---
   return ReduceM(result);
  }

動的データバッファの形式で縮小された次元の行列を取得するには、さらに2つのオーバーロードされたメソッドReduceを作成します。そのうちの1つは、パラメータに初期データを含む動的データバッファを受け取ります。2つ目は行列を受け取ります。以下がそのコードです。

CBufferDouble *CPCA::Reduce(CBufferDouble *data)
  {
   matrix result = ReduceM(data);
//---
   return FromMatrix(result);
  }

CBufferDouble *CPCA::Reduce(matrix &data)
  {
   matrix result = ReduceM(data);
//---
   return FromMatrix(result);
  }

奇妙に思えるかもしれませんが、メソッドのパラメータが異なるにもかかわらず、それらの内容はまったく同じです。しかし、これはReduceMメソッドのオーバーロードを使用することで簡単に説明できます。

クラスの機能を考慮しました。次に、ファイルを操作するためのメソッドを作成する必要があります。覚えているように、一度訓練されたモデルは、後で使用するためにその操作をすばやく復元できる必要があります。いつものように、データ保存メソッドSaveから始めます。

しかし、データ保存メソッドのアルゴリズムの構築に進む前に、クラスの構造を見て、何をファイルに保存する必要があるかを考えてみましょう。

Privvateクラス変数には、1つのモデル訓練フラグb_Studied、次元削減行列m_Ureduce、算術平均v_Meansと標準偏差v_STDsの2つのベクトルがあります。モデルのパフォーマンスを完全に復元できるようにするには、これらすべての要素を保存する必要があります。

class CPCA : public CObject
  {
private:
   bool              b_Studied;
   matrix            m_Ureduce;
   vector            v_Means;
   vector            v_STDs;
   //---
   CBufferDouble     *FromMatrix(matrix &data);
   CBufferDouble     *FromVector(vector &data);
   matrix            FromBuffer(CBufferDouble *data, ulong vector_size);
   vector            FromBuffer(CBufferDouble *data);

public:
                     CPCA();
                    ~CPCA();
   //---
   bool              Study(CBufferDouble *data, int vector_size);
   bool              Study(matrix &data);
   CBufferDouble     *Reduce(CBufferDouble *data);
   CBufferDouble     *Reduce(matrix &data);
   matrix            ReduceM(CBufferDouble *data);
   matrix            ReduceM(matrix &data);
   //---
   bool              Studied(void)  {  return b_Studied; }
   ulong             VectorSize(void)  {  return m_Ureduce.Cols();}
   ulong             Inputs(void)   {  return m_Ureduce.Rows();   }
   //---
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)  { return defUnsupervisedPCA; }
  };

さまざまなモデルを構築するとき、データを保存するためにこれまで考えられていたすべてのメソッドは、データを書き込むためのファイルハンドルをパラメータで受け取ります。このクラスの同様のメソッドも例外ではありません。メソッド本体では、受け取ったハンドルの有効性をすぐに確認します。

bool CPCA::Save(const int file_handle)
  {
   if(file_handle == INVALID_HANDLE)
      return false;

次に、モデル訓練フラグの値を保存します。その状態によって、他のデータを保存する必要性が決まるためです。モデルがまだ訓練されていない場合、空のベクトルと行列を保存する必要はありません。この場合、メソッドを完了します。

   if(FileWriteInteger(file_handle, (int)b_Studied) < INT_VALUE)
      return false;
   if(!b_Studied)
      return true;

モデルが訓練されている場合は、残りの要素の保存に進みます。まず、縮小行列を保存します。MQL5言語では、行列のデータ保存機能はまだ実装されていません。しかし、データバッファファイルに書き込むメソッドがあるので、このメソッドを利用していきます。

まず、行列から動的データバッファにデータを移動してから、行列の列数を保存します。次に、関連するメソッドを呼び出して、データバッファを保存します。行列からバッファにデータを移動するメソッドでは、オブジェクトポインタを保存しなかったことに注意してください。また、このようなオブジェクトメモリのクリアに関連する操作は、呼び出し元が実行する必要があることは既に述べました。そのため、データの保存に関する操作が完了したら、作成したオブジェクトを削除します。

   CBufferDouble *temp = FromMatrix(m_Ureduce);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(FileWriteLong(file_handle, (long)m_Ureduce.Cols()) <= 0)
     {
      delete temp;
      return false;
     }
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;

同様のアルゴリズムを使用してベクトルデータを保存してみましょう。

   temp = FromVector(v_Means);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;

   temp = FromVector(v_STDs);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;
//---
   return true;
  }

操作が正常に完了したら、メソッドをtrueの結果で終了します。

データは、Loadメソッドで同じ順序でファイルから復元されます。まず、データをロードするためにファイルハンドルの有効性を確認します。

bool CPCA::Load(const int file_handle)
  {
   if(file_handle == INVALID_HANDLE)
      return false;

次に、モデルの訓練フラグの状態を読み取ります。モデルがまだ訓練されていない場合は、正の結果でメソッドを終了します。モデルの訓練中に上書きされるため、行列とベクトルの削減に関連する作業を実行する必要はありません。訓練の前にデータの次元削減を実行しようとすると、メソッドは訓練フラグの状態を確認し、負の結果で終了します。

   b_Studied = (bool)FileReadInteger(file_handle);
   if(!b_Studied)
      return true;

訓練済みモデルの場合、まず動的バッファオブジェクトを作成します。次に、縮少行列の列数を数えます。縮少行列の内容をデータバッファに読み込みます。

データの読み込みが成功したら、動的バッファのコンテキストを行列に転送するだけです。

   CBufferDouble *temp = new CBufferDouble();
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   long cols = FileReadLong(file_handle);
   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   m_Ureduce = FromBuffer(temp, cols);

同様のアルゴリズムを使用して、ベクトルの内容を読み込みます。

   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   v_Means = FromBuffer(temp);

   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   v_STDs = FromBuffer(temp);

すべてのデータを正常に読み込んだら、動的データバッファオブジェクトを削除し、正の結果でメソッドを終了します。

   delete temp;
//---
   return true;
  }

これで、主成分メソッドクラスが完成しました。すべてのメソッドと関数の完全なコードは、添付ファイルにあります。

4.テスト

主成分分析法のクラスの操作は、2段階で実行されました。最初のテストでは、モデルを訓練しました。この目的のために、前回の記事で検討したkmeans.mq5エキスパートアドバイザー(EA)に基づいてpca.mq5 EAを作成しました。変更が影響を与えたのは使用されているモデルのオブジェクトとモデルの訓練関数だけです。

繰り返しますが、手順の最初に、訓練期間の開始日を決定します。

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

次に、クオートと使用される指標の値をダウンロードします。

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
      return;
   if(!ArraySetAsSeries(Rates, true))
      return;
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

その後、受け取ったデータを1つの行列にグループ化します。

   int total = bars - (int)HistoryBars;
   matrix data;
   if(!data.Init(total, 8 * HistoryBars))
     {
      ExpertRemove();
      return;
     }
//---
   for(int i = 0; i < total; i++)
     {
      Comment(StringFormat("Create data: %d of %d", i, total));
      for(int b = 0; b < (int)HistoryBars; b++)
        {
         int bar = i + b;
         int shift = b * 8;
         double open = Rates[bar]
                       .open;
         data[i, shift] = open - Rates[bar].low;
         data[i, shift + 1] = Rates[bar].high - open;
         data[i, shift + 2] = Rates[bar].close - open;
         data[i, shift + 3] = RSI.GetData(MAIN_LINE, bar);
         data[i, shift + 4] = CCI.GetData(MAIN_LINE, bar);
         data[i, shift + 5] = ATR.GetData(MAIN_LINE, bar);
         data[i, shift + 6] = MACD.GetData(MAIN_LINE, bar);
         data[i, shift + 7] = MACD.GetData(SIGNAL_LINE, bar);
        }
     }

モデルの訓練メソッドを呼び出します。

   ResetLastError();
   if(!PCA.Study(data))
     {
      printf("Runtime error %d", GetLastError());
      return;
     }

訓練が成功したら、モデルをファイルに保存し、EAを呼び出して作業を完了します。

   int handl = FileOpen("pca.net", FILE_WRITE | FILE_BIN);
   if(handl != INVALID_HANDLE)
     {
      PCA.Save(handl);
      FileClose(handl);
     }
//---
   Comment("");
   ExpertRemove();
  }

完全なEAコードは添付ファイルにあります。

過去15年間の履歴データに対するEAのパフォーマンスの結果、初期データの次元は160要素から68要素に減少しました。つまり、ソースデータのサイズがほぼ2.4倍縮小され、情報の1%のみが失われるリスクがあります。

次のテスト段階では、事前に訓練された主成分分析モデルを使用しました。ソースデータのサイズを縮小した後、クラス操作の結果を全結合パーセプトロンに入力します。このテストのために、以前の記事のkmeans_net.mq5と同様のEAに基づいてEA pca_net.mq5を作成しました。パーセプトロンは、過去2年間の履歴データを使用して訓練されました。

削減されたデータでのパーセプトロンの訓練結果

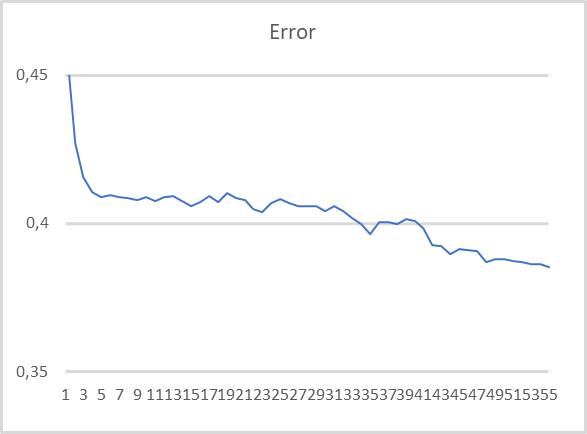
グラフからわかるように、圧縮データでモデルを訓練すると、かなり安定してエラーが減少する傾向があります。55回の訓練エポックの後、エラーサイズはまだ安定していません。訓練を続ければ、さらにエラーを減らすことができるということです。

結論

この記事では、教師なし学習アルゴリズムを使用して別の種類の問題の解決策を検討しました。次元削減です。このような問題を解決するためにCPCAクラスを作成し、主成分分析法アルゴリズムを実装しました。これは非常に効率的なデータ圧縮方法で、予測可能な情報損失しきい値を提供します。

作成したクラスをテストするとき、元のデータをほぼ2.4倍に圧縮しますが、情報が1%しか失われないリスクがあります。結果は非常に良好で、圧縮データで訓練されたモデルの効率を向上させることができます。

さらに、次元削減に直交行列を使用することも主成分法の大きな特徴の1つです。これにより、圧縮データ内の特徴間の相関がほぼ0になります。この特性によって、圧縮データを使用した後続のモデル訓練の効率も向上します。これは、2回目のテストの結果によって確認されています。

同時に、モデルの過剰適合に対抗するために主成分法を使用することは避けるようにしてください。このような実践はかなり望ましくありません。そのような場合には正則化メソッドを使用することをお勧めします。

そして、ここで一般的な実践から観察したことがもう1つあります。データ圧縮の過程でかなりの量の情報が失われますが、これはいずれにしても発生するということです。よって、次元削減方法の使用は、それを使用せずにモデルを訓練しても期待される結果が得られなかった場合にのみ推奨されます。

また、新しい行列演算についても学びました。MQL5言語でこのような操作を実装したMetaQuotesに感謝します。人工知能の問題の解決に関連するモデルやモデルを作成する際のコード記述は、行列演算を使用することによって大幅に簡素化されます。

参考文献リスト

記事で使用されているプログラム

#	ファイル名	タイプ	詳細
1	pca.mq5	EA	モデルを訓練するEA
2	pca_net.mq5	EA	2つ目のモデルにデータを渡すテストをおこなうEA
3	pсa.mqh	クラスライブラリ	主成分分析法を実装するためのライブラリ
4	kmeans.mqh	クラスライブラリ	k-means法を実装するためのライブラリ
5	unsupervised.cl	コードベース	k-means法を実装するためのOpenCLプログラムコードライブラリ
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11032

添付されたファイル |

ZIPをダウンロード

MQL5.zip (70.9 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

MFIによる取引システムの設計方法を学ぶ

最も人気のあるテクニカル指標に基づいて取引システムを設計する連載のこの新しい記事では、新しくマネーフローインデックス（Money Flow Index、MFI）テクニカル指標を考察します。その詳細を学び、MQL5によって簡単な取引システムを開発し、MetaTrader 5で実行します。

価格変動モデルとその主な規定（第1回）。最もシンプルなモデルバージョンとその応用

この記事は、数学的に厳密な値動きと市場機能の理論の基礎を提供するものです。現在に至るまで、数学的に厳密な値動き理論は存在しません。その代わりに、「あるパターンの後に、ある方向に価格が動く」という経験則に基づいた仮定で対処する必要がありました。もちろん、これらの仮定は統計にも理論にも裏付けられていません。

Volumesによる取引システムの設計方法を学ぶ

最も人気のあるテクニカル指標に基づいて取引システムを設計する方法を学ぶための連載の新しい記事です。今回は、Volumes指標について紹介します。出来高という概念は、金融市場の取引において非常に重要な要素の1つであり、注意を払う必要があります。この記事では、Volumes指標を使用した簡単な取引システムの設計方法について説明します。

モスクワ取引所(MOEX)の指値注文を使用した自動グリッド取引

この記事では、MOEXでの作業を目的としたMetaTrader 5用のMQL5エキスパートアドバイザー(EA)の開発について考察します。EAは、MetaTrader 5ターミナルを使用して、グリッド戦略に従いながらMOEXで取引することになります。EAには、ストップロスとテイクプロフィットによるポジションの決済、および特定の市況での未決注文の削除が含まれます。