ニューラルネットワークが簡単に（第20部）：オートエンコーダ

MetaTrader 5 — トレーディングシステム | 27 10月 2022, 07:44

228

Dmitriy Gizlyk

内容

はじめに

教師なし学習法の研究を続けます。これまでの記事で、クラスタリング、データ圧縮、アソシエーションルールマイニングのアルゴリズムについてすでに分析しています。しかし、これまで考えられてきた教師なしアルゴリズムは、ニューラルネットワークを使用していません。今回は、ニューラルネットワークの研究に戻り、「オートエンコーダ」を取り上げます。

1.オートエンコーダアーキテクチャ

オートエンコーダアーキテクチャの説明に進む前に、教師あり学習アルゴリズムによるニューラルネットワークの学習方法について振り返っておきましょう。アルゴリズムを検討する際には、パターンと対象結果からなるラベル付きデータのペアを使用しました。ニューラルネットワークの演算結果と目標値との誤差が最小になるように、重みを最適化していました。

この場合、ニューラルネットワークは何を学習できるのでしょうか。私達が期待していることを正確に学習します。つまり、目標とする結果に影響を与える特徴を見つけることができます。ただし、目標結果に影響を与えない、あるいはその影響が軽微な特徴については、ネットワークの重みをゼロにします。つまり、このモデルはかなり狭く定義された方向で訓練するわけですが、一切問題はありません。このモデルは、私たちが求めることを完璧におこないます。

ただし、もう1つの側面があります。新しい問題を解決するために事前に訓練されたモデルを使用することを意味する「転移学習」の概念には既に遭遇しています。この場合、以前の目標値と新しい目標値が同じ特徴に依存する場合にのみ、良い結果が得られます。そうでなければ、前の訓練段階でゼロにされた欠落特徴によって、モデル性能が影響を受ける可能性があります。

タスクソリューションにどのような影響があるのでしょうか。私たちの世界は静止しているわけではなく、常に変化しています。今日の市場のリーダーは、明日にはその影響力を失う可能性があるのです。市場は他の力によって動かされていきます。このため、モデルの使用期間が制限されます。これはごく当たり前のことです。例えば、トレーダーは時々自分の戦略を見直します。このことは、古典的な戦略記述法を用いて構築されたアルゴリズム取引ロボットの収益性からも確認できます。

ニューラルネットワークの研究を始めたとき、人工知能を使うことでモデルの寿命が延びることを期待しました。さらに、随時追加訓練をおこなうことで、非常に長い期間、利益を出すことができるようになるでしょう。

上記の性質に伴うリスクを最小化するために、教師なし学習の分野の1つである表現学習や特徴学習を利用します。表現学習は、生の入力データから自動的に特徴を抽出する一連のアルゴリズムを組み合わせたものです。先に考察したクラスタリングや次元削減のアルゴリズムも表現学習のことを指しています。それらのアルゴリズムには線形変換を使用しました。オートエンコーダは、より複雑な形の学習を可能にします。

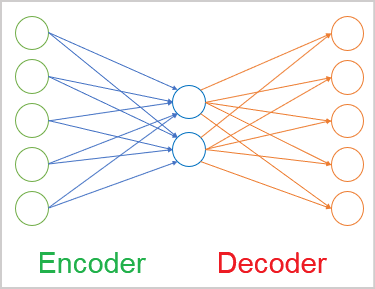
一般的な場合、オートエンコーダは2つのエンコーダとデコーダのブロックからなるニューラルネットワークです。エンコーダの元データ層とデコーダの結果層は同じ数の要素を含んでいます。その間に、通常、元データより小さい隠れ層があります。学習過程で、この層のニューロンは、元データを圧縮した形で記述できる潜在的な（隠れた）状態を形成します。

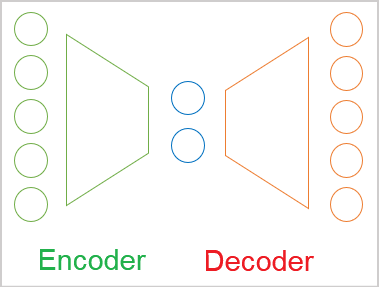
これは、「主成分分析」手法で解決したデータ圧縮の問題と似ていますが、後述するように、これらのアプローチには違いがあります。

前述したように、オートエンコーダはニューラルネットワークで、バックプロパゲーション方式で訓練されます。ラベルのないデータを使うので、コツは、まずエンコーダを使ってデータを潜在状態のサイズに圧縮するようにモデルを訓練することです。そして、復号器では、このモデルによって、情報の損失を最小限に抑えながら、データを元の状態に復元します。

そこで、すでに知られているバックプロパゲーション法を用いてオートエンコーダを訓練します。訓練標本そのものを対象結果とします。

ニューラルレイヤーのアーキテクチャは異なることがあります。最も単純なバージョンでは、これらは完全に接続された層とすることができます。画像からの特徴抽出には、畳み込みモデルが広く用いられています。

シーケンスを扱うためには、反復モデルと注意のアルゴリズムを使用できます。詳細については、今後の記事で検討していきます。

2.オートエンコーダが解決する古典的な問題

オートエンコーダのj訓練方法はやや非標準的ですが、非常に多様な問題解決に適用できます。まず、データ圧縮や前処理などの作業です。

データ圧縮のアルゴリズムは、2種類に分けられます。

非可逆圧縮
可逆圧縮

非可逆圧縮の例として、前回紹介した主成分分析(PCA)があります。コンポーネントの選定にあたっては、最大情報損失に留意しました。

可逆データ圧縮の例として、各種のアーカイバやジッパーが考えられます。解凍後にデータを失わってはいけません。

理論的には、オートエンコーダはどのようなデータででも訓練できます。エンコーダでデータを圧縮し、デコーダで元のデータを復元することができますが、これは渡された潜伏状態に基づいておこなわれます。オートエンコーダモデルの複雑さのレベルに応じて、非可逆圧縮と可逆圧縮があります。もちろん、可逆的なデータ圧縮には、より複雑なモデルが必要になります。これは、通信において、使用するトラフィックを減らしながらデータ伝送品質を向上させるために広く利用されており、最終的には使用するネットワークのスループットを向上させることができます。

圧縮の次は、元データの前処理です。例えば、いわゆる次元の呪いを解決するために、オートエンコーダによるデータ圧縮が利用されています。多くの機械学習は、低次元のデータに対してより効果的かつ高速に動作します。したがって、入力データの次元が小さいニューラルネットワークは、学習可能な重みの数が少なくなります。過剰適合のリスクを抑えながら、より速く学習/作業できるということです。

オートエンコーダが解決するもう1つの課題は、元データのノイズを除去することです。この問題を解決するためには、2つのアプローチがあります。1つ目は、PCAと同様、非可逆的なデータ圧縮です。ただし、圧縮で失われるのはノイズであると予想します。

2つ目の方法は、画像処理で広く使われています。良質な（ノイズのない）ソース画像を撮影し、様々な歪み（アーチファクト、ノイズなど）を加えます。歪んだ画像は、オートエンコーダに供給されます。このモデルは、元の高画質画像との類似度が最大になるように学習されます。ただし、歪みを選択する際には特に注意が必要です。自然なノイズに匹敵するものでなければなりません。そうでなければ、実際の条件下でモデルが正しく動作しない可能性が高くなります。

オートエンコーダは、画像からノイズを除去するだけでなく、画像にオブジェクトを削除したり、追加したりするのにも使用できます。例えば、1つだけオブジェクトが異なる2枚の画像をエンコーダに入力すると、2枚の画像の潜在状態の差分ベクトルは、1枚の画像にしか存在しないオブジェクトに対応します。このように、得られたベクトルを他の画像の潜像状態に加えることで、画像にオブジェクトを追加することができるのです。同様に、潜像状態からベクトルを減算することで、画像からオブジェクトを取り除くことができます。

オートエンコーダの分離学習技術により、潜在的な状態をコンテンツと画像スタイルに分離することができます。スタイルを維持したコンテンツ置換により、デコーダ出力で新しい画像を得ることができます。この画像は、ある画像のコンテンツと別の画像のスタイルを組み合わせたものです。このような実験の展開により、訓練済みのオートエンコーダを画像生成に利用することができます。

一般に、オートエンコーダで解くことのできる課題は非常に幅広くなりますが、そのすべてを取引に応用できるわけではありません。少なくとも、生成する能力の使い方が今ひとつわかりません。もしかしたら、規格外のアイデアを思いつく人がいるかもしれないし、それを実現できるかもしれません。

3.PCAとオートエンコーダの比較

前述したように、オートエンコーダが解決する課題は、先に検討したアルゴリズムと一部重複しています。特に、オートエンコーダや主成分分析法は、データの圧縮（次元の減少）や元データからノイズを除去することができます。では、なぜ同じ問題を解決するために、別の道具が必要なのでしょうか。それぞれのアプローチの違いと性能について見ていきましょう。

まず、主成分分析法のアルゴリズムの詳細を思い出してみましょう。これは、厳密な数式に基づいた純粋な数学的手法で、主成分の抽出に使用されます。同じ元データに対してこの方法を用いると、常に同じ結果が得られます。オートエンコーダではこうはいきません。

オートエンコーダはニューラルネットワークです。ランダムな重みで初期化され、勾配降下法を用いて繰り返し訓練されます。訓練は同じ数式を使います。しかし、何らかの理由により、同じモデルを同じ元データで学習させると、全く異なる結果が得られる可能性が高いです。精度は同等でも、やはり違います。

第二の側面は、変換の種類に関連するものです。PCAでは、行列の乗算という形で線形変換をおこないますが、その一方、ニューラルネットワークでは、通常、非線形の活性化関数を使用します。つまり、オートエンコーダの変換がより複雑になります。

さて、主成分分析法と活性化関数のない3層オートエンコーダを比較することができます。しかし、この場合でさえ、隠れ層の要素数が主成分の数と同じであっても、同じ結果が保証されるわけではありません。逆に、この場合、PCAの方が良い結果を生むことが保証されています。

また、主成分の計算は、オートエンコーダモデルの学習よりもはるかに高速におこなえるでしょう。したがって、データに線形関係がある場合は、主成分分析の手法で圧縮するのがよいです。オートエンコーダは、より複雑なタスクに適しています。

4.取引におけるオートエンコーダ活用の可能性

ここまでオートエンコーダアルゴリズムの理論的な部分を考えてきましたが、次にその能力を取引戦略にどのように利用できるかを見てみましょう。まず考えられるのは、データの圧縮やノイズ除去といった前処理です。先に、主成分分析法を用いて同様の実験をおこなったので、比較分析が可能です。

オートエンコーダの生成能力をどう使うか、今の私にはなかなか想像がつきません。また、フェイクチャートの価値にも疑問があります。もちろん、オートエンコーダを訓練して、少し先の時間をずらしたデコーダの結果を得るようにすることも可能ですが、これは先に述べた教師あり学習の方法とあまり変わらないでしょう。いずれにせよ、このようなアプローチの価値は、実験的にしか評価できません。

また、市場状況の変化のダイナミクスを評価しようとすることも可能です。なぜなら、取引は一般的に市場の状況の変化を監視し、将来の動きを予測しようとすることに基づいているからです。潜在的な状態を利用して、画像からオブジェクトを追加したり削除したりするアプローチについては、すでに説明しました。この特性を生かさない手はないでしょう。しかし、デコーダの出力で市場の状況を歪めることはしません。連続する2つの潜在状態の差のベクトルに基づき、市場のダイナミクスを評価することを試みます。

また、転移学習も利用します。ここからが本番です。オートエンコーダ訓練技術により、元データから特徴を抽出するモデルを訓練することができます。そして、エンコーダだけを使い、そこにいくつかの決定層を追加し、教師あり学習を使って、課題を解決するためのモデルを訓練します。オートエンコーダを訓練するとき、その潜在的な状態には元データからのすべての特徴が含まれます。そのため、一度エンコーダを訓練すれば、様々な問題解決に利用することができるのです。もちろん、同じ元データを使っていることが条件になります。

実験に必要な作業の概要を説明しました。なお、その全容は1つの記事の範囲を超えていますが、挑戦を恐れてはいません。実践編を始めましょう。

5.実践的な実験

いよいよ実践的な実験です。まず、完全連結層を用いた簡単なオートエンコーダを作成して訓練します。オートエンコーダモデルの構築には、教師あり学習法の学習時に作成したニューラルレイヤーライブラリを使用します。

直接コードを作成する前に、何をどのようにオートエンコーダを訓練するかについて考えてみましょう。先にエンコーダについて説明し、エンコーダが元データを返すことを理解しました。では、なぜこのような疑問があるのでしょうか。実は、均質なデータを扱えば、すべてが明確になります。この場合、単純に元データを返すようにモデルを訓練しますが、元データは均質ではありません。モデルには、価格データだけでなく、指標値も入力することができます。また、さまざまな指標を読み解くことで、異なるデータを得ることができます。このことは、教師あり学習アルゴリズムについて考えたときに既に述べました。以前の記事で、異なる振幅のデータがモデル結果に異なる影響を与えることに注目しました。ただし、デコーダの結果層で活性化関数を指定しなければならないので、問題はさらに複雑になります。この活性化関数は、異なる初期値の全範囲を返すことができるものでなければなりません。

私の解決策は、教師あり学習法と同じく、元データを正規化することでした。これは、別のプロセスとして実装するか、バッチ正規化層を使用することができます。

オートエンコーダの最初の隠れ層は、バッチ正規化層とします。デコーダが正規化されたデータを返すように、オートエンコーダを訓練します。デコーダ結果層には、活性化関数として双曲線正接を使用することにします。これにより、-1～1の範囲で結果を正規化することができます。

これが理論的な解決策です。実際に実装するためには、モデルの訓練を繰り返すたびに、モデルの第1隠れ層の結果にアクセスする必要があります。モデルの中を見たことはまだありません。ニューラルネットワークの隠し状態は、常に「ブラックボックス」でした。今回は、学習プロセスを整理するために開く必要があります。そのために、ニューラルネットワークの演算を整理するCNetクラスに、任意の隠れ層の結果バッファの値を取得するGetLayerOutputメソッドを追加してみましょう。

この新しいメソッドのパラメータには、必要な層の序数、および結果を書き込むためのバッファへのポインタを渡します。

メソッド本体に結果確認ブロックを追加することを忘れないでください。この場合、有効なモデル層バッファの存在を確認します。また、指定されたニューラルレイヤーの序数が、モデルのニューラルレイヤーの範囲内であることを確認します。誤って指定された負の序数に対しての確認ではありません。その代わり、符号なし整数型変数を使ってこのパラメータを取得するため、その値は常に0以上となります。そこで、制御ブロックでは、単純にモデルのニューラルレイヤー数の上限を確認します。

制御ブロックをうまく通過したら、指定したニューラルレイヤーへのポインタをローカル変数に取得します。受信したポインタの有効性を即座に確認します。

メソッドの次の手順は、パラメータで受け取った結果バッファへのポインタの有効性を確認することです。必要であれば、新しいデータバッファの作成を開始します。

その後、対応するニューラルレイヤーに結果バッファの値を要求します。各手順で結果を確認することを忘れないでください。

bool CNet::GetLayerOutput(uint layer, CBufferDouble *&result)
  {
   if(!layers || layers.Total() <= (int)layer)
      return false;
   CLayer *Layer = layers.At(layer);
   if(!Layer)
      return false;
//---
   if(!result)
     {
      result = new CBufferDouble();
      if(!result)
         return false;
     }
//---
   CNeuronBaseOCL *temp = Layer.At(0);
   if(!temp || temp.getOutputVal(result) <= 0)
      return false;
//---
   return true;
  }

これで準備作業は終了です。次に、最初のオートエンコーダを作り始めることができます。それを実装するために、エキスパートアドバイザー(EA)を作成し、ae.mq5という名前をつけます。教師あり学習モデルEAが基盤になります。

元データは、価格相場とRSI、CCI、ATR、MACDの4つの指標の読み取り値です。過去のすべてのモデルのテストに同じデータが使用されました。指標のパラメータは全てEAの外部パラメータで指定します。OnInit関数では、指標を操作するためのオブジェクトのインスタンスを初期化しています。

int OnInit()
  {
//---
   Symb = new CSymbolInfo();
   if(CheckPointer(Symb) == POINTER_INVALID || !Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();
//---
   RSI = new CiRSI();
   if(CheckPointer(RSI) == POINTER_INVALID || !RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice))
      return INIT_FAILED;
//---
   CCI = new CiCCI();
   if(CheckPointer(CCI) == POINTER_INVALID || !CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice))
      return INIT_FAILED;
//---
   ATR = new CiATR();
   if(CheckPointer(ATR) == POINTER_INVALID || !ATR.Create(Symb.Name(), TimeFrame, ATRPeriod))
      return INIT_FAILED;
//---
   MACD = new CiMACD();
   if(CheckPointer(MACD) == POINTER_INVALID || !MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice))
      return INIT_FAILED;

次に、エンコーダのアーキテクチャを指定する必要があります。ニューラルネットワーク構築のアルゴリズムと原理は、教師あり学習モデル構築に用いたものと完全に一致しています。唯一の違いは、ニューラルネットワークのアーキテクチャにあります。

ニューラルネットワークのアーキテクチャをモデル初期化モデルに渡すために、オブジェクトの動的配列CArrayObjを作成します。この配列の各オブジェクトは、1つのニューラルレイヤーを記述します。その配列の順番は、モデルのニューラルレイヤーの順番に対応します。ニューラルレイヤーアーキテクチャを記述するために、特別に作成したCLayerDescriptionオブジェクトを使用します。

class CLayerDescription    :  public CObject
  {
public:
   /** Constructor */
                     CLayerDescription(void);
   /** Destructor */~CLayerDescription(void) {};
   //---
   int               type;          ///< Type of neurons in layer (\ref ObjectTypes)
   int               count;         ///< Number of neurons
   int               window;        ///< Size of input window
   int               window_out;    ///< Size of output window
   int               step;          ///< Step size
   int               layers;        ///< Layers count
   int               batch;         ///< Batch Size
   ENUM_ACTIVATION   activation;    ///< Type of activation function (#ENUM_ACTIVATION)
   ENUM_OPTIMIZATION optimization;  ///< Type of optimization method (#ENUM_OPTIMIZATION)
   double            probability;   ///< Probability of neurons shutdown, only Dropout used
  };

最初の層は元データ層で、全結合層として宣言されています。ローソク足1本を表現するために12個の要素が必要です。したがって、層のサイズは1パターンの歴史的深さの12倍となります。元データ層には活性化関数を使用しません。

   Net = new CNet(NULL);
   ResetLastError();
   double temp1, temp2;
   if(CheckPointer(Net) == POINTER_INVALID || !Net.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
     {
      printf("%s - %d -> Error of read %s prev Net %d", __FUNCTION__, __LINE__, FileName + ".nnw", GetLastError());
      CArrayObj *Topology = new CArrayObj();
      if(CheckPointer(Topology) == POINTER_INVALID)
         return INIT_FAILED;
      //--- 0
      CLayerDescription *desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      int prev = desc.count = (int)HistoryBars * 12;
      desc.type = defNeuronBaseOCL;
      desc.activation = None;
      if(!Topology.Add(desc))
         return INIT_FAILED;

ニューラルレイヤーのアーキテクチャを記述したら、それをモデルアーキテクチャ記述の動的配列に追加します。

次の層は、バッチ正規化層です。少し前に作成する必要があると話し合いました。バッチ正規化層の要素数は、前の層のニューロン数と同じです。ここでは活性化関数も使わないことにします。ここでは、正規化バッチのサイズを1000要素とし、学習パラメータの最適化方法を示します。また、モデルアーキテクチャの動的配列に、もう1つのニューラルレイヤーの記述を追加してみましょう。

      //--- 1
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = prev;
      desc.batch = 1000;
      desc.type = defNeuronBatchNormOCL;
      desc.activation = None;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

オートエンコーダのアーキテクチャにおける正規化層のインデックスについて思い出してください。

次に、オートエンコーダのエンコーダの構築を始めます。エンコーダでは、潜在状態の2要素までニューラルレイヤーのサイズを徐々に小さくしていきます。その構造は、漏斗に似ています。

エンコーダのすべてのニューラルレイヤーは、活性化関数として双曲線正接を使用しています。潜伏状態を活性化させるために、シグモイドを使いました。

オートエンコーダを構築する際、ニューラル層の数や使用する活性化関数に特別な条件はありません。どんなニューラルネットワークのモデルでも構築するときに使われるのと同じ原則を適用します。オートエンコーダモデルを構築する際には、様々なアーキテクチャを試してみることをお勧めします。

      //--- 2
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      prev = desc.count = (int)HistoryBars;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      //--- 3
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      prev = desc.count = prev / 2;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      //--- 4
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      prev = desc.count = prev / 2;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      //--- 5
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = 2;
      desc.type = defNeuronBaseOCL;
      desc.activation = SIGMOID;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

次に、デコーダのアーキテクチャを規定します。今回は、ニューラル層の要素数を徐々に増やしていきます。デコーダのアーキテクチャは、エンコーダの鏡像であることが多いのですが、ニューラルネットワークの数や含まれるニューロンを変えてみることにしました。ただし、バッチ正規化層のニューロン数がデコーダ結果層のニューロン数と等しいことを確認する必要があります。

      //--- 6
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      //--- 7
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars * 4;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      //--- 8
      desc = new CLayerDescription();
      if(CheckPointer(desc) == POINTER_INVALID)
         return INIT_FAILED;
      desc.count = (int) HistoryBars * 12;
      desc.type = defNeuronBaseOCL;
      desc.activation = TANH;
      desc.optimization = ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

モデルアーキテクチャの記述を作成した後は、オートエンコーダのニューラルネットワークの作成に移ります。ニューラルネットワークオブジェクトの新しいインスタンスを作成し、そのコンストラクタにオートエンコーダの記述を渡します。

      delete Net;
      Net = new CNet(Topology);
      delete Topology;
      if(CheckPointer(Net) == POINTER_INVALID)
         return INIT_FAILED;
      dError = DBL_MAX;
     }

EA初期化関数を完成させる前に、一時的なデータのバッファと、モデルの訓練を開始するためのイベントを作成しましょう。

   TempData = new CBufferDouble();
   if(CheckPointer(TempData) == POINTER_INVALID)
      return INIT_FAILED;
//---
   bEventStudy = EventChartCustom(ChartID(), 1, (long)MathMax(0, MathMin(iTime(Symb.Name(), 
                                  PERIOD_CURRENT, (int)(100 * Net.recentAverageSmoothingFactor * 10)),
                                  dtStudied)), 0, "Init");
//---
   return(INIT_SUCCEEDED);
  }

すべてのメソッドと関数の完全なコードは、添付ファイルにあります。

作成したオートエンコーダを学習させる必要があります。EAテンプレートでは、モデルの学習にTrain関数を使用しています。この関数は、パラメータで訓練開始日を受け取ります。関数本体では、ローカル変数を作成して学習期間を定義しています。

void Train(datetime StartTrainBar = 0)
  {
   int count = 0;
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);
   dtStudied = MathMax(StartTrainBar, st_time);
   ulong last_tick = 0;

   double prev_er = DBL_MAX;
   datetime bar_time = 0;
   bool stop = IsStopped();
   CArrayDouble *loss = new CArrayDouble();
   MqlDateTime sTime;

その後、モデルを訓練するために過去のデータを読み込みます。

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   prev_er = dError;
//---
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
   RSI.Refresh(OBJ_ALL_PERIODS);
   CCI.Refresh(OBJ_ALL_PERIODS);
   ATR.Refresh(OBJ_ALL_PERIODS);
   MACD.Refresh(OBJ_ALL_PERIODS);

モデルの訓練は、入れ子ループのシステムでおこなわれます。外側のループは、訓練エポックをカウントします。内側のループは、学習エポック内の履歴データを繰り返し処理します。

外側のループ本体には、前回の訓練エポックのエラー値を格納します。これは、学習ダイナミクスを制御するために使用されます。次の学習エポック終了後の誤差変化ダイナミクスが有意でない場合は、学習プロセスを中断します。また、ユーザーがプログラムを停止したことを示すフラグを確認する必要があります。この後、入れ子ループが続きます。

   int total = (int)(bars - MathMax(HistoryBars, 0));
   do
     {
      //---
      stop = IsStopped();
      prev_er = dError;
      for(int it = total - 1; it >= 0 && !stop; it--)
        {
         int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (total));
         if((GetTickCount64() - last_tick) >= 250)
           {
            com = StringFormat("Study -> Era %d -> %.6f\n %d of %d -> %.2f%% \nError %.5f",
                               count, prev_er, bars - it + 1, bars,
                               (double)(bars - it + 1.0) / bars * 100, Net.getRecentAverageError());
            Comment(com);
            last_tick = GetTickCount64();
           }

入れ子ループの本体では、学習プロセスに関する情報を表示します。この情報は、チャート上にコメントとして表示されます。そして、次のパターンをランダムに決定し、モデルを訓練します。その後、一時バッファに履歴データを入力します。

         TempData.Clear();
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;
         //---
         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            double open = Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            double rsi = RSI.Main(bar_t);
            double cci = CCI.Main(bar_t);
            double atr = ATR.Main(bar_t);
            double macd = MACD.Main(bar_t);
            double sign = MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE ||
               macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!TempData.Add(Rates[bar_t].close - open) || !TempData.Add(Rates[bar_t].high - open) ||
               !TempData.Add(Rates[bar_t].low - open) || !TempData.Add((double)Rates[bar_t].tick_volume / 1000.0) ||
               !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) || !TempData.Add(sTime.mon) ||
               !TempData.Add(rsi) || !TempData.Add(cci) || !TempData.Add(atr) || !TempData.Add(macd) || !TempData.Add(sign))
               break;
           }
         if(TempData.Total() < (int)HistoryBars * 12)
            continue;

履歴データを収集した後、オートエンコーダのFeedForwardメソッドを呼び出します。収集された履歴データは、メソッドのパラメータとして渡されます。

         Net.feedForward(TempData, 12, true);
         TempData.Clear();

次の手順では、モデルのバックプロパゲーションメソッドを呼び出す必要があります。以前は、メソッドのパラメータに目標結果のバッファを渡していました。次に、エンコーダが目標とする結果は、正規化された元データです。そのためには、まずバッチ正規化層の結果を取得し、それをモデルのバックプロパゲーションに渡す必要があります。すでにご存知のように、このモデルのバッチ正規化層のインデックスは1です。

         if(!Net.GetLayerOutput(1, TempData))
            break;
         Net.backProp(TempData);
         stop = IsStopped();
        }

バックプロパゲーションが終了したら、プログラムの実行がユーザーによって中断されたかどうかのフラグを確認し、入れ子ループの次の反復に移ります。

訓練エポック終了後、現在のモデル訓練結果を保存します。現在のモデル誤差の値は、ユーザーに通知するためにログに記録され、訓練ダイナミクスバッファに保存されます。

新しい学習エポックを開始する前に、さらなる訓練の実行可能性を確認します。

      if(!stop)
        {
         dError = Net.getRecentAverageError();
         Net.Save(FileName + ".nnw", dError, 0, 0, dtStudied, false);
         printf("Era %d -> error %.5f %%", count, dError);
         loss.Add(dError);
         count++;
        }
     }
   while(!(dError < 0.01 && (prev_er - dError) < 0.01) && !stop);

訓練終了後、モデルの訓練プロセス全体のエラーダイナミクスをファイルに保存し、EAを強制終了させる関数を呼び出します。

   Comment("Write dynamic of error");
   int handle = FileOpen("ae_loss.csv", FILE_WRITE | FILE_CSV | FILE_ANSI, ",", CP_UTF8);
   if(handle == INVALID_HANDLE)
     {
      PrintFormat("Error of open loss file: %d", GetLastError());
      delete loss;
      return;
     }
   for(int i = 0; i < loss.Total(); i++)
      if(FileWrite(handle, loss.At(i)) <= 0)
         break;
   FileClose(handle);
   PrintFormat("The dynamics of the error change is saved to a file %s\\%s",
               TerminalInfoString(TERMINAL_DATA_PATH), "ae_loss.csv");
   delete loss;
   Comment("");
   ExpertRemove();
  }

上記のバージョンでは、EAの目的はモデルの訓練なので、ExpertRemove関数を使ってEA作業を完了させています。EAに他の目的がある場合は、この関数をコードから削除してください。オプションで、EAが割り当てられたタスクをすべて実行した後に実行するよう、この関数を最後に移動させることができます。

添付ファイルには、EAの全コードと全クラスのコードがあります。

次に、作成したEAを実際のデータでテストします。オートエンコーダは、過去15年間のデータを使用して、H1タイムフレームのEURUSDについて学習されました。そこで、40本のキャンドルの92,000以上のパターンからなる学習セットでオートエンコーダを訓練しました。学習誤差のダイナミクスを下図に示します。

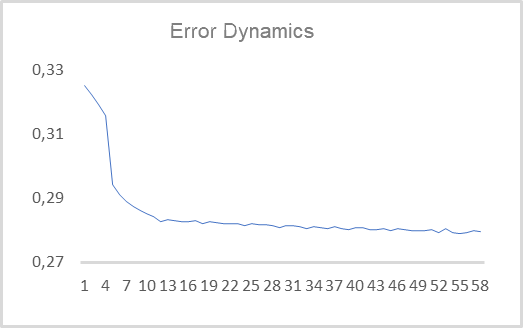
ご覧のように、10エポックで二乗平均平方根誤差の値は0.28に減少し、その後も緩やかに減少しています。つまり、480の特徴（40ローソク足×1ローソク足あたり12の特徴）から2要素の潜在状態までの情報を78%保存したまま圧縮することができるのです。思い起こせば、PCAでは、最初の2成分で保存される類似データは25%以下です。

潜在的な状態のサイズは、わざと2要素に等しくしています。これにより、主成分分析の手法で得られた類似のプレゼンテーションと比較し、可視化することが可能となります。このようなデータを用意するために、上記のEAを少し改造してみましょう。主な変更点は、モデル訓練関数「Train」に影響します。関数の始まりは変わりません。訓練標本の作成プロセスも含まれます。

訓練標本を作成した直後に、主成分分析法による学習を追加してみましょう。

void Train(datetime StartTrainBar = 0)
  {
//---
    The process of creating a training sample has not changed
//---
   if(!PCA.Study(data))
     {
      printf("Runtime error %d", GetLastError());
      return;
     }

上記のEAでは、2つのループを入れ子にしてモデルを訓練するシステムを作りました。ここでは、オートエンコーダを再訓練せず、以前に訓練したモデルを使用します。したがって、入れ子ループの仕組みは必要ありません。訓練標本の要素を通過するループは1回だけで大丈夫です。また、92,000パターンすべてについて潜在的な状態を可視化するわけではありません。これでは、情報がわかりにくくなってしまうので、1000パターンだけを可視化することにします。私の実験は、好きな数のパターンで可視化して繰り返すことができます。

今回は標本全体を可視化しないことにしたので、訓練標本からランダムに可視化用のパターンを選択します。そこで、選択されたパターンの特徴量を一時バッファに詰め込みます。

     {
      //---
      stop = IsStopped();
      bool add_loop = false;
      for(int it = 0; i < 1000 && !stop; i++)
        {
         if((GetTickCount64() - last_tick) >= 250)
           {
            com = StringFormat("Calculation -> %d of %d -> %.2f%%", it + 1, 1000, (double)(it + 1.0) / 1000 * 100);
            Comment(com);
            last_tick = GetTickCount64();
           }
         int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (total));
         TempData.Clear();
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;
         //---
         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            double open = Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            double rsi = RSI.Main(bar_t);
            double cci = CCI.Main(bar_t);
            double atr = ATR.Main(bar_t);
            double macd = MACD.Main(bar_t);
            double sign = MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!TempData.Add(Rates[bar_t].close - open) || !TempData.Add(Rates[bar_t].high - open) ||
               !TempData.Add(Rates[bar_t].low - open) || !TempData.Add((double)Rates[bar_t].tick_volume / 1000.0) ||
               !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) || !TempData.Add(sTime.mon) ||
               !TempData.Add(rsi) || !TempData.Add(cci) || !TempData.Add(atr) || !TempData.Add(macd) || !TempData.Add(sign))
               break;
           }
         if(TempData.Total() < (int)HistoryBars * 12)
            continue;

パターンの情報を受け取った後、オートエンコーダのフィードフォワード方式を呼び出し、主成分分析方式でデータを圧縮します。そして、オートエンコーダの潜在状態の結果バッファの値を取得します。

         Net.feedForward(TempData, 12, true);
         data = PCA.ReduceM(TempData);
         TempData.Clear();
         if(!Net.GetLayerOutput(5, TempData))
            break;

前回、モデルをテストする際に、フラクタル形成の予測能力を確認しました。今回は、視覚的にパターンを分けるために、チャート上のパターンを色分けして表示します。したがって、レンダリングされたパターンがどのタイプに属するかを指定する必要があります。これを理解するためには、パターンの後にフラクタルが形成されることを確認する必要があります。

         bool sell = (Rates[i - 1].high <= Rates[i].high && Rates[i + 1].high < Rates[i].high);
         bool buy = (Rates[i - 1].low >= Rates[i].low && Rates[i + 1].low > Rates[i].low);
         if(buy && sell)
            buy = sell = false;

受信したデータはファイルに保存され、さらに可視化することができます。そして、次のパターンに移ります。

         FileWrite(handle, (buy ? DoubleToString(TempData.At(0)) : " "), (buy ? DoubleToString(TempData.At(1)) : " "),
                   (sell ? DoubleToString(TempData.At(0)) : " "), (sell ? DoubleToString(TempData.At(1)) : " "),
                   (!(buy || sell) ? DoubleToString(TempData.At(0)) : " "),
                   (!(buy || sell) ? DoubleToString(TempData.At(1)) : " "),
                   (buy ? DoubleToString(data[0, 0]) : " "), (buy ? DoubleToString(data[0, 1]) : " "),
                   (sell ? DoubleToString(data[0, 0]) : " "), (sell ? DoubleToString(data[0, 1]) : " "),
                   (!(buy || sell) ? DoubleToString(data[0, 0]) : " "),
                   (!(buy || sell) ? DoubleToString(data[0, 1]) : " "));
         stop = IsStopped();
        }
     }

ループのすべての繰り返しが終わったら、チャートのコメント欄をクリアし、EAを閉じます。

   Comment("");
   ExpertRemove();
  }

完全なEAコードは添付ファイルにあります。

EAの操作の結果、オートエンコーダの潜在状態のデータと、対応するパターンに対する最初の2つの主成分を含むAE_latent.csvファイルが得られます。ファイルのデータを使って、2つのグラフを作成しました。

オートエンコーダの潜在的な状態の可視化 2つの第1主成分の可視化

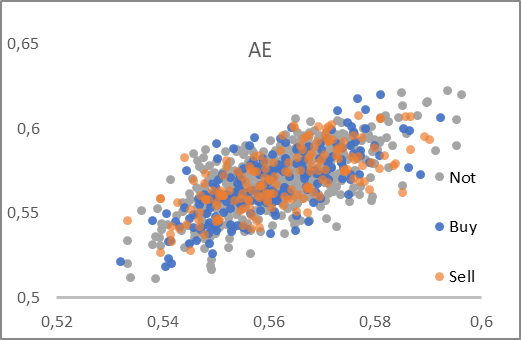
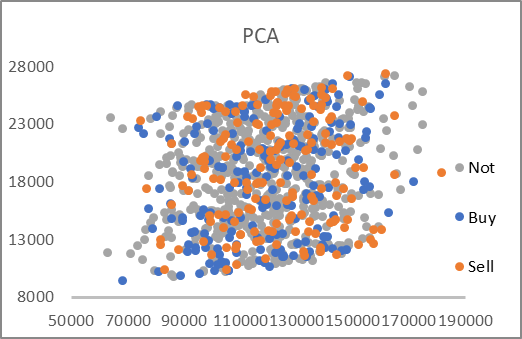
このように、どちらのグラフも、目的のグループにパターンを明確に分けることができません。しかし、オートエンコーダ遅延データは、両軸とも0.5に近い値になっています。今回は潜在状態のニューラルレイヤーの活性化関数としてシグモイドを使用しました。そして、この関数は常に0から1の範囲の値を返します。したがって、得られた分布の中心は、関数値の範囲の中心に近くなります。

主成分分析法によるデータ圧縮では、かなり大きな値が得られます。軸に沿った数値には6〜7倍の差があります。分布の中心はおよそ[18000,130000]にあります。また、レンジの上限と下限が直線的であることも顕著です。

提示されたグラフの分析に基づき、オートエンコーダを意思決定ニューラルネットワークにデータを投入する前のデータ前処理に選択すると思います。

結論

今回は、様々な問題を解決するために広く使われているオートエンコーダについて知ることができました。完全連結層を用いた最初のオートエンコーダを構築し、その性能を主成分分析で比較しました。テストの結果、非線形問題を解く際にオートエンコーダを使用する利点があることがわかりました。しかし、オートエンコーダに関する話題は非常に広範で、1つの記事で収まるものではありません。次回は、オートエンコーダの効率を上げるための様々なヒューリスティックを検討することを提案します。

記事のフォーラムスレッドでご質問いただければお答えします。

参考文献リスト

記事で使用されているプログラム

#	ファイル名	タイプ	詳細
1	ae.mq5	EA	オートエンコーダ学習EA
2	ae2.mq5	EA	ビジュアライゼーションのためのデータ準備のためのEA
2	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
3	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11172

添付されたファイル |

ZIPをダウンロード

MQL5.zip (67.49 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

DoEasy-コントロール（第10部）：WinFormsオブジェクト - インターフェイスのアニメーション化

ユーザーやオブジェクトとのオブジェクト対話機能を実装して、グラフィカルインターフェイスをアニメーション化するときが来ました。より複雑なオブジェクトを正しく動作させるためにも、新しい機能が必要になります。

知っておくべきMQL5ウィザードのテクニック（第02回）：コホネンマップ

この連載では、MQL5ウィザードがトレーダーの主力であるべきことを示します。なぜでしょうか。MQL5ウィザードを使用すれば、新しいアイデアを組み立てることで時間を節約できるだけでなく、コーディングの重複によるミスを大幅に減らすことができるため、最終的に、取引の哲学のいくつかの重要な分野にエネルギーを注ぐことができるからです。

一からの取引エキスパートアドバイザーの開発（第23部）：新規受注システム(IV)

受注システムをより柔軟にします。ここでは、コードをより柔軟にする変更を検討して、ポジションストップレベルをより迅速に変更できるようにします。

一からの取引エキスパートアドバイザーの開発（第22部）：新規受注システム(V)

今日は、新しい受注システムの開発を進めていきます。新しいシステムを導入するのはそう簡単なことではありません。プロセスが非常に複雑になるような問題がしばしば発生します。このような問題が発生したときは、一度立ち止まって、自分たちの進むべき方向を再分析しなければなりません。