ニューラルネットワークが簡単に（第15部）：MQL5によるデータクラスタリング

目次

• はじめに
• 1.モデル構築の原則
• 2.OpenCLのプログラムを作成する
• 3.メインプログラム側の準備作業
• 4.k-meansアルゴリズムのための組織クラスの構築
• 5.テスト
• 終わりに
• 参照文献
• 記事で使用されているプログラム

はじめに

前回は、k-meansクラスタリング手法を考察し、Python言語による実装を検討しました。ただし、統合の利用には一定の制約や追加コストが発生することが多いです。特に、現在の統合状態では、指標やターミナルのイベント処理など、内蔵アプリケーションのデータを利用することができません。古典的な指標の多くは様々なライブラリで実装されていますが、カスタム指標の話になると、そのアルゴリズムをスクリプトで再現する必要があります。指標のソースコードがなく、動作のアルゴリズムがわからない場合はどうすればよいのでしょうか。あるいは、クラスタリングの結果を他のMQL5プログラムで使用する場合は？そのような場合、MQL5のツールを使ったクラスタリング手法の実装が有効です。

1.モデル構築の原則

k-meansクラスタリング法はすでに検討しており、以下のように実装されています。

1. 訓練サンプルからk個のランダムな点をクラスタの中心として決定する
2. 操作のループを作成する
   • 各点から各中心までの距離を決定する
   • 最も近い中心を見つけてこのクラスタに点を割り当てる
   • 算術平均を使用して各クラスタの新しい中心を決定する
3. クラスタの中心が「動かなくなる」まで反復処理で操作を繰り返す

メソッドのコードを書く前に、今回の実装の要点を簡単に説明します。

先に検討したアルゴリズムの主な動作はループとして実装されています。ループ本体の冒頭で、訓練サンプルの各要素から各クラスタの中心までの距離を求める必要があります。訓練サンプルの各要素に対するこの操作は、他の要素から絶対に独立したものです。そこで、OpenCLの技術を利用して、並列計算を実現することができます。さらに、異なるクラスタの中心までの距離を計算する演算も独立しています。そのため、2次元のタスク空間で演算を並列化することができます。

次の手順では、配列のある要素が特定のクラスタに属するかどうかを判断する必要があります。この操作は、シーケンスの各要素の計算が独立であることも意味します。ここでは、訓練セットの個々の要素に適用される並列計算のためのOpenCLの技術を使用することができます。

ループ体の最後には、新しいクラスタの中心を定義しています。そのためには、訓練サンプルの全要素をループし、システムの状態を記述するベクトルの各要素と各クラスタの文脈における算術平均値を計算する必要があります。クラスタ中心の算出には、このクラスタに属する要素のみが使用されます。その他の要素は無視されます。そのため、各要素の値は一度しか使用されません。この場合、2次元空間での並列計算技術を利用することも可能です。1つの軸にはシステムの状態を表すベクトル要素があり、2つ目の軸には分析されたクラスタがあります。

データクラスタリングをおこなった後、モデルの性能を評価するために、損失関数を計算する必要があります。前述のように、これは、対応するクラスタの中心からのシステム状態の算術平均偏差を計算することによっておこなうことができます。もちろん、算術平均の計算を明示的にスレッドに分割することはできませんが、このタスクは2つのサブタスクに分けることができます。まず、それぞれの中心までの距離を計算します。このタスクは、システムの単一の状態のコンテキストで簡単に並列化することができます。そして、その後、得られた距離ベクトルの算術平均を計算すればよいのです。

2.OpenCLプログラムの作成

このように、並列計算を整理するためのサブタスクは4つに分かれています。以前の記事で説明したように、OpenCLを使った並列計算を実装するためには、OpenCLのコンテキスト側でこの操作をダウンロードして実行するプログラムを別に作成する必要があります。実行プログラムカーネルは、上記の作業の順に、unsupervised.clという別ファイルに作成されます。

この作業をカーネルKmeansCulcDistanceを書くことから始めましょう。このカーネルでは、システムの状態から全クラスタの現在の中心までの距離の計算に関連する操作を実装します。このカーネルは、2次元のタスク空間で実行されます。1次元は、訓練サンプルからシステムの状態を分離するために使用されます。2次元目は、モデルのクラスタのためです。

カーネルの入力パラメータには、3つのデータバッファへのポインタと、解析システムの1つの状態を記述するベクトルのサイズが示されています。指定されたバッファのうち2つがソースデータを含むことになります。これが訓練サンプルであり、クラスタ中心ベクトルの行列です。3つ目のデータバッファは結果テンソルです。

カーネル本体では、両次元で現在の演算スレッドの識別子を取得し、2次元で演算スレッド数によるクラスタ総数を取得します。これらのデータは、前述のすべてのテンソルにおいて、目的の要素へのオフセットを決定するために必要です。ここでは、ソースデータのテンソルにおけるオフセットも決定し、変数を0に初期化してクラスタ中心までの距離を計算します。

次に、システムの1つの状態を記述するベクトルのサイズに等しい反復回数のループを実装します。このループの本文では、システム状態ベクトルの対応する要素の値とクラスタ中心との二乗距離をまとめています。

すべてのループ反復の後、受信した値を結果バッファの対応する要素に保存するだけです。数学的な観点から、空間上の2点間の距離を求めるには、得られた値の平方根を抽出することが必要ですが、この場合、2点間の正確な距離には興味がありません。最小の距離を求めればいいのです。したがって、資源節約のため、平方根はとらないことにします。

__kernel void KmeansCulcDistance(__global double *data,
                                 __global double *means,
                                 __global double *distance,
                                 int vector_size
                                )
  {
   int m = get_global_id(0);
   int k = get_global_id(1);
   int total_k = get_global_size(1);
   double sum = 0.0;
   int shift_m = m * vector_size;
   int shift_k = k * vector_size;
   for(int i = 0; i < vector_size; i++)
      sum += pow(data[shift_m + i] - means[shift_k + i], 2);
   distance[m * total_k + k] = sum;
  }

最初のカーネルのコードができたので、次のサブプロセスの作業に移ります。本手法のアルゴリズムによれば、次の手順で、訓練サンプルの各状態がどのクラスタに属するかを決定する必要があります。そのために、どちらのクラスタ中心が分析状態に近いかを判断します。距離は前のカーネルですでに計算しています。あとは、一番小さい値の数字を決めればいいだけです。すべての操作は、システムの単一の状態のコンテキストで実行されます。

この処理を実現するために、カーネルKmeansClusteringを作成しましょう。前のカーネルと同様、このカーネルはパラメータを介して3つのデータバッファとクラスタの総数へのポインタを受け取ります。奇妙に思えるかもしれませんが、3つあるバッファのうち、1つのバッファ（距離 ）だけが元のデータを含んでいることになります。残りの2つのバッファには、演算結果が格納されます。クラスタバッファに、分析したシステム状態が属するクラスタのインデックスを書き込みます。

3番目のバッファ(flags)は、以前の状態と比較したクラスタ変更フラグを書き込むために使用されます。これらのフラグを分析することで、モデル訓練プロセスのブレークポイントを定義することができます。この処理のロジックは非常にシンプルです。もし、システムのどの状態もそのクラスタを変更しないなら、結果として、クラスタの中心も変更されません。つまり、これ以上操作のループを続けても意味がないのです。そこでモデルの訓練が停止します。

さて、カーネルアルゴリズムに話を戻しましょう。解析したシステムの状態に合わせて、1次元のタスク空間で立ち上げることになります。カーネル本体では、解析状態の序数とデータバッファの関連シフトを定義しています。2つの結果バッファには、それぞれの状態に対して1つの値が格納されます。したがって、指定されたバッファのシフト量は、スレッドIDと等しくなります。したがって、クラスタ中心までの計算された距離を含むソースデータバッファのシフトを決定するだけですみます。

ここでは、2つのprivate変数を用意します。valueに中心までの距離を書き込みます。クラスタ番号は2番目のresultに書き込みます。.初期段階では、インデックス「0」のクラスタの値を格納します。

そして、すべてのクラスタ中心までの距離をループさせます。すでに「0」クラスタの値を変数に保存しているので、次のクラスタから始めましょう。

ループ本体では、次の中心までの距離を確認します。そして、すでに変数に格納されているものを上回っていれば、次のクラスタの確認に進みます。

より近い中心が見つかれば、private変数の値を上書きしていきます。その中に短い距離と対応するクラスタのシリアル番号を保存しておきます。

すべてのループの反復が完了すると、result変数に分析状態に最も近いクラスタの識別子が格納されます。現在の状態が参照されることになります。しかし、受け取った値を結果バッファの対応する要素に保存する前に、クラスタ番号が前の反復と比較して変化しているかどうかを確認する必要があります。比較結果はフラグバッファに保存されます。

__kernel void KmeansClustering(__global double *distance,
                               __global double *clusters,
                               __global double *flags,
                               int total_k
                              )
  {
   int i = get_global_id(0);
   int shift = i * total_k;
   double value = distance[shift];
   int result = 0;
   for(int k = 1; k < total_k; k++)
     {
      if(value <= distance[shift + k])
         continue;
      value =  distance[shift + k];
      result = k;
     }
   flags[i] = (double)(clusters[i] != (double)result);
   clusters[i] = (double)result;
  }

クラスタリングアルゴリズムの最後には，平均行列に集められたすべてのクラスタの中心ベクトルの値を更新する必要があります．このタスクを実行するために、別のカーネルKmeansUpdatingを作成します。上で説明したカーネルと同様に、パラメータで考慮されるものは、3つのデータバッファと1つの定数へのポインタを受け取ることになります。2つのバッファには元データが、1つのバッファには結果が格納されます。前述のように、このカーネルは2次元のタスク空間で実行することになります。KmeansCulcDistanceカーネルと異なり，タスク空間の1次元目では，1つのシステム状態を記述するベクトルの要素に対して反復処理をおこない，total_m定数では，訓練セットの要素数を表します．

カーネル本体では、まずスレッドIDを両次元で定義して、前回と同様に、解析された要素とデータバッファのオフセットを決定するために使用します。ここでは、1つのシステム状態を記述するベクトルの長さを決定します。これは、1次元目の実行スレッド数の合計に等しくなります。さらに、システム状態記述の関連要素の値とそのカウントを合計する2つのprivate変数を初期化します。

総和演算はこれから作成するループの中で実装され、その反復回数は訓練サンプルの要素数に等しくなります。要約するのは分析したクラスタに属する要素のみです。ループ本体では、まず、現在の要素がどのクラスタに属するかを確認します。解析したものと一致しない場合は、次の要素に進みます。

その要素が検証に合格した場合、すなわち分析されたクラスタに属する場合、システム状態記述ベクトルの該当する要素の値を加算し、カウンタを1増加させます。

ループを抜けた後は、累積和を和の要素数で割るだけです。しかし、ここで忘れてはならないのは、ゼロによる除算という重大なエラーが発生する可能性があることです。もちろん、アルゴリズムの構成を考えれば、そのような事態は考えにくいですが、プログラムの信頼性を確保するために、このチェックを追加することにします。なお、クラスタに属する要素が見つからない場合は、値を戻さずにそのままにしておきます。

__kernel void KmeansUpdating(__global double *data,
                             __global double *clusters,
                             __global double *means,
                             int total_m
                            )
  {
   int i = get_global_id(0);
   int vector_size = get_global_size(0);
   int k = get_global_id(1);
   double sum = 0;
   int count = 0;
   for(int m = 0; m < total_m; m++)
     {
      if(clusters[m] != k)
         continue;
      sum += data[m * vector_size + i];
      count++;
     }
   if(count > 0)
      means[k * vector_size + i] = sum / count;
  }

この段階までで、k-meansデータクラスタリングアルゴリズムを実装するための3つのカーネルを作成しました。しかし、メインプログラムのオブジェクトの作成に進む前に、損失関数を計算するための別のカーネルを作成する必要があります。

損失関数の値は、2段階で決定されます。まず、訓練サンプルの個々の要素について、対応するクラスタの中心からの偏差を求めます。そして、サンプル全体の算術平均偏差値を算出します。前段の演算をスレッドに分割し、OpenCLツールで並列計算をおこなうことができます。この機能を実装するために、4つのバッファと1つの定数へのポインタをパラメータとして受け取るKmeansLossカーネルを作成しましょう。3つのバッファには元データを格納し、1つのバッファには結果を格納します。

訓練セットの要素数と同じ数のスレッドを持つ1次元タスク空間でカーネルを起動します。カーネル本体では、まず訓練セットから分析パターンの序数を決定してから、どのクラスタに属するかを判断します。今回は、全クラスタの中心までの距離の再計算はおこなわず、代わりに、要素の序数に従ってクラスタバッファから該当する値を取得するだけです。KmeansClusteringカーネルでは、クラスタの序数がこのバッファに保存されました。

これで、訓練サンプルのテンソルとクラスタ中心の行列において、必要なベクトルの先頭へのオフセットを決定することができます。

次に、2つのベクトル間の距離を計算するだけです。そのために、偏差の総和を蓄積するprivate変数を初期化し、1つのシステム状態を記述するベクトルの全要素を通過するループを作成します。ループ本体では、ベクトルの対応する要素の偏差の二乗を合計することになります。

すべてのループ反復の後、累積和をの損失結果バッファの対応する要素に移動させます。

__kernel void KmeansLoss(__global double *data,
                         __global double *clusters,
                         __global double *means,
                         __global double *loss,
                         int vector_size
                        )
  {
   int m = get_global_id(0);
   int c = clusters[m];
   int shift_c = c * vector_size;
   int shift_m = m * vector_size;
   double sum = 0;
   for(int i = 0; i < vector_size; i++)
      sum += pow(data[shift_m + i] - means[shift_c + i], 2);
   loss[m] = sum;
  }

OpenCLのコンテキスト側で全プロセスを構築するアルゴリズムについて検討しました。次に、メインプログラムの側での処理の整理に移ることができます。

3.メインプログラム側の準備作業

メインプログラム側では、新しいクラスCKmeansを作成します。クラスコードは、kmeans.mqhファイルに保存されます。ただし、新しいクラスに直接進む前に、いくつかの準備作業を実施する必要があります。まず、OpenCLのコンテキストにデータを転送するために、本連載ですでに説明したクラスオブジェクトを使用します。CBufferDoubleです。指定されたクラスのコードは書き直さず、先に作成されたライブラリをインクルードするだけです。

#include "..\NeuroNet_DNG\NeuroNet.mqh"

そして、上記で作成したOpenCLプログラムのコードをリソースとして接続します。

#resource "unsupervised.cl" as string cl_unsupervised

次に、名前付き定数を作成します。今回は、そのような定数がいくつも必要です。将来的に互換性を持たせ、以前に作成したライブラリと併用するために、作成した定数は一意であることを確認する必要があります。

まず、新しいクラスを識別するための定数が必要です。

#define defUnsupervisedKmeans    0x7901

第二に、カーネルとそのパラメータを識別するための定数が必要です。カーネルは、1つのOpenCLプログラム内で連続した番号で識別されます。ただし、パラメータは1つのカーネル内で番号付けされています。コードの可読性を高めるために、定数を所属するカーネルごとにグループ化することにしました。

#define def_k_kmeans_distance    0
#define def_k_kmd_data           0
#define def_k_kmd_means          1
#define def_k_kmd_distance       2
#define def_k_kmd_vector_size    3

#define def_k_kmeans_clustering  1
#define def_k_kmc_distance       0
#define def_k_kmc_clusters       1
#define def_k_kmc_flags          2
#define def_k_kmc_total_k        3

#define def_k_kmeans_updates     2
#define def_k_kmu_data           0
#define def_k_kmu_clusters       1
#define def_k_kmu_means          2
#define def_k_kmu_total_m        3

#define def_k_kmeans_loss        3
#define def_k_kml_data           0
#define def_k_kml_clusters       1
#define def_k_kml_means          2
#define def_k_kml_loss           3
#define def_k_kml_vector_size    4

名前付きの定数を作成したら、次の準備作業に移りましょう。教師あり学習モデルにおける マルチスレッド計算の実装を説明した際に、ニューラルネットワークのディスパッチクラスのコンストラクタでOpenCLコンテキストを扱うためのオブジェクトを初期化しました。今回は、他のモデルを使わず、CKmeans クラスタリングクラスを使用します。さて、COpenCLMyオブジェクトインスタンスの初期化関数を新しいクラスCKmeans 内に移動することができました。しかし、クラスタリングはいつの日か、他のより複雑なモデルの一部として使われるようになるかもしれません。これは今回の記事の範囲を超えていますが、この連載中にさらに詳しく説明します。とにかく、この可能性に備えるべきでしょう。そこで、COpenCLMyオブジェクトクラスのインスタンスを初期化する関数を別途作成することにしました。

OpenCLCreate関数のアルゴリズムを見てみましょう。OpenCLプログラムのテストをパラメータとして受け取り、初期化されたオブジェクトのインスタンスへのポインタを返すように構成されています。関数本体では、まずCOpenCLMyクラスのインスタンスを新規作成して、新規オブジェクト作成操作の結果を直ちに確認します。

COpenCLMy *OpenCLCreate(string programm)
  {
   COpenCL *result = new COpenCLMy();
   if(CheckPointer(result) == POINTER_INVALID)
      return NULL;

次に、新しいオブジェクトの初期化メソッドを呼び出し、パラメータにOpenCLプログラムテキストを含む文字列変数を渡します。再度、動作結果を確認します。操作の結果、エラーが発生した場合は、上記で作成したオブジェクトを削除してメソッドを終了し、空のポインタを返します。

   if(!result.Initialize(programm, true))
     {
      delete result;
      return NULL;
     }

プログラムの初期化に成功したら、OpenCLのコンテキストでカーネルの作成に進みます。まず、作成するカーネルの数を指定し、先に説明したすべてのカーネルを1つずつ作成します。各操作の結果を確認しながら、プロセスを制御することを忘れないでください。

以下のコードは、カーネルを1つだけ初期化する例です。残りも同じように初期化されます。すべてのメソッドと関数の完全なコードは、添付ファイルにあります。

   if(!result.SetKernelsCount(4))
     {
      delete result;
      return NULL;
     }
//---
   if(!result.KernelCreate(def_k_kmeans_distance, "KmeansCulcDistance"))
     {
      delete result;
      return NULL;
     }
//---
...........
//---
   return result;
  }

すべてのカーネルの作成に成功したら、作成したオブジェクトのインスタンスへのポインタを返して、このメソッドを終了します。

これで準備作業は終了し、そのまま新しいデータクラスタリングクラスの作業に入ることができます。

4.k-meansアルゴリズムのための組織クラスの構築

新しいデータクラスタリングクラスCKmeansの作業を開始し、その内容を説明します。どんな機能を持たせるべきでしょうか。この機能を実現するために、どのメソッドと変数が必要でしょうか。すべての変数はprotectedブロックに実装されます。

作成するクラスタ数(m_iClusters)と個々のシステム状態の記述ベクトルのサイズ(m_iVectorSize)という、モデルのハイパーパラメータを格納するための別の変数が必要です。

訓練済みモデルの品質を評価するために、損失関数を計算し、その値を変数m_dLossに格納します。

また、モデルの状態（訓練済みか否か）を把握するために、m_bTrainedフラグが必要です。

このリストだけで、必要な機能を実装することができると思います。次に、使用するオブジェクトの宣言に移ります。ここでは、OpenCLコンテキスト(c_OpenCL)で動作するクラスのインスタンスを1つ宣言しています。また、情報を保存し、OpenCLのコンテキストと情報を交換するためのデータバッファも必要です。OpenCLのプログラムを開発する際に、先に使用したものと同じ名前にします。

• c_aDistance
• c_aMeans
• c_aClasters
• c_aFlags
• c_aLoss

変数の宣言が終わったら、クラスメソッドに進みましょう。ここでは何も隠さないので、すべてのメソッドがpublicになります。

当然ながら、クラスのコンストラクタとデストラクタから始めます。コンストラクタでは、使用するオブジェクトのインスタンスを作成し、変数の初期値を設定します。

void CKmeans::CKmeans(void)   :  m_iClusters(2),
                                 m_iVectorSize(1),
                                 m_dLoss(-1),
                                 m_bTrained(false)
  {
   c_aMeans = new CBufferDouble();
   if(CheckPointer(c_aMeans) != POINTER_INVALID)
      c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0);
   c_OpenCL = NULL;
  }

クラスのデストラクタでは、メモリの後始末と、クラス内で生成されたすべてのオブジェクトの削除をおこないいます。

void CKmeans::~CKmeans(void)
  {
   if(CheckPointer(c_aMeans) == POINTER_DYNAMIC)
      delete c_aMeans;
   if(CheckPointer(c_aDistance) == POINTER_DYNAMIC)
      delete c_aDistance;
   if(CheckPointer(c_aClasters) == POINTER_DYNAMIC)
      delete c_aClasters;
   if(CheckPointer(c_aFlags) == POINTER_DYNAMIC)
      delete c_aFlags;
   if(CheckPointer(c_aLoss) == POINTER_DYNAMIC)
      delete c_aLoss;
  }

次に、クラスの初期化メソッドを作成します。このメソッドには、パラメータとして、OpenCLコンテキストとモデルのハイパーパラメータを持つ演算オブジェクトのポインタを渡します。メソッド本体では、まず、パラメータで受け取ったデータを確認するための小さなコントロールのブロックを作成します。

その後，得られたハイパーパラメータを対応する変数に保存し，平均クラスタベクトルの行列のバッファをゼロ値で初期化します。バッファの初期化操作の結果を確認することを忘れないでください。

bool CKmeans::Init(COpenCLMy *context, int clusters, int vector_size)
  {
   if(CheckPointer(context) == POINTER_INVALID || clusters < 2 || vector_size < 1)
      return false;
//---
   c_OpenCL = context;
   m_iClusters = clusters;
   m_iVectorSize = vector_size;
   if(CheckPointer(c_aMeans) == POINTER_INVALID)
     {
      c_aMeans = new CBufferDouble();
      if(CheckPointer(c_aMeans) == POINTER_INVALID)
         return false;
     }
   c_aMeans.BufferFree();
   if(!c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0))
      return false;
   m_bTrained = false;
   m_dLoss = -1;
//---
   return true;
  }

初期化の後は、モデルの訓練が必要です。この機能はStudyメソッドで実装しています。メソッドのパラメータには、訓練サンプルと、クラスタ中心の行列の初期化フラグを渡します。フラグを使用することで，ファイルから読み込まれた完全または部分的な事前訓練済みモデルの訓練を継続する際に，行列の初期化を無効にすることが可能です。

コントロールのブロックは、メソッド本体に実装されています。まず、訓練サンプルとOpenCLコンテキストのパラメータで受け取ったオブジェクトポインタの妥当性を確認します。

次に、訓練サンプルのデータの有無を確認します。また、その数は初期化時に指定された一つのシステム状態の記述ベクトルの大きさの倍数であることを確認します。

さらに、訓練サンプルの要素数がクラスタ数の10倍以上であることを確認します。

bool CKmeans::Study(CBufferDouble *data, bool init_means = true)
  {
   if(CheckPointer(data) == POINTER_INVALID || CheckPointer(c_OpenCL) == POINTER_INVALID)
      return false;
//---
   int total = data.Total();
   if(total <= 0 || m_iClusters < 2 || (total % m_iVectorSize) != 0)
      return false;
//---
   int rows = total / m_iVectorSize;
   if(rows <= (10 * m_iClusters))
      return false;

次の手順は、クラスタ中心の行列を初期化することです。もちろん、行列を初期化する前に、メソッドのパラメータで受け取った初期化フラグの状態を確認します。

この行列は、訓練サンプルからランダムに選択されたベクトルで初期化されます。ここでは、複数のクラスタが同じシステム状態で初期化されないようなアルゴリズムを作成する必要があります。そのために、訓練セットのシステム状態の数に等しい要素数のフラグの配列を作成します。初期段階では、この配列をfalse値で初期化します。次に、モデルのクラスタ数に等しい反復回数のループを実装します。ループ本体では、訓練サンプルの大きさの範囲内でランダムに数字を生成し、得られたインデックスのフラグを確認します。このシステム状態がすでにいずれかのクラスタを初期化している場合は、反復カウンタの状態をデクリメントし、ループの次の反復に移ります。

選択された要素がまだクラスタ初期化に参加していない場合、訓練サンプルにおける与えられたシステム状態の始まりへのオフセットを決定し、中心ベクトルの行列を決定します。その後、データをコピーするためのネストループを実装します。ループの次の繰り返しに移る前に、処理したインデックスを持つフラグを変更します。

   bool flags[];
   if(ArrayResize(flags, rows) <= 0 || !ArrayInitialize(flags, false))
      return false;
//---
   for(int i = 0; (i < m_iClusters && init_means); i++)
     {
      Comment(StringFormat("Cluster initialization %d of %d", i, m_iClusters));
      int row = (int)((double)MathRand() * MathRand() / MathPow(32767, 2) * (rows - 1));
      if(flags[row])
        {
         i--;
         continue;
        }
      int start = row * m_iVectorSize;
      int start_c = i * m_iVectorSize;
      for(int c = 0; c < m_iVectorSize; c++)
        {
         if(!c_aMeans.Update(start_c + c, data.At(start + c)))
            return false;
        }
      flags[row] = true;
     }

中心の行列を初期化した後、ポインタの検証を行い、必要に応じて、距離行列(c_aDistance)、システムの各状態のクラスタ識別ベクトル(c_aClusters)、個々のシステムの状態のクラスタ変更フラグのベクトル(c_aFlags)を書き込むためのバッファオブジェクトのインスタンスを新たに作成することに進みます。操作の実行を制御することを忘れないでください。

   if(CheckPointer(c_aDistance) == POINTER_INVALID)
     {
      c_aDistance = new CBufferDouble();
      if(CheckPointer(c_aDistance) == POINTER_INVALID)
         return false;
     }
   c_aDistance.BufferFree();
   if(!c_aDistance.BufferInit(rows * m_iClusters, 0))
      return false;

   if(CheckPointer(c_aClasters) == POINTER_INVALID)
     {
      c_aClasters = new CBufferDouble();
      if(CheckPointer(c_aClasters) == POINTER_INVALID)
         return false;
     }
   c_aClasters.BufferFree();
   if(!c_aClasters.BufferInit(rows, 0))
      return false;

   if(CheckPointer(c_aFlags) == POINTER_INVALID)
     {
      c_aFlags = new CBufferDouble();
      if(CheckPointer(c_aFlags) == POINTER_INVALID)
         return false;
     }
   c_aFlags.BufferFree();
   if(!c_aFlags.BufferInit(rows, 0))
      return false;

最後に、OpenCL コンテキストでバッファを作成します。

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aMeans.BufferCreate(c_OpenCL) ||
      !c_aDistance.BufferCreate(c_OpenCL) ||
      !c_aClasters.BufferCreate(c_OpenCL) ||
      !c_aFlags.BufferCreate(c_OpenCL))
      return false;

準備段階は完了です。あとは、モデルの訓練処理に直接関係するループ操作の実装に進みます。そこで、先に検討したように、アルゴリズムの主なマイルストーンは次のようになります。

• 訓練サンプルの各要素から各クラスタ中心までの距離の決定
• クラスタによるシステム状態の分散（最小距離による）
• クラスタセンターの更新

このアルゴリズムの段階を見てください。各段階を実行するためのカーネルはOpenCLプログラムで作成済みです。したがって、今度は対応するカーネルのループコールを実装する必要があります。

訓練ループを実装し、ループ本体でまずクラスタ中心への距離を計算するためのカーネルを呼び出します。必要なバッファはOpenCL コンテキストのメモリにすべてロード済みです。したがって、すぐにカーネルパラメータの指定に移ることができます。ここでは、使用するデータバッファへのポインタと、1つのシステム状態を記述するベクトルの大きさを示しています。なお、特定のパラメータを指定するには「カーネル識別子 - パラメータ識別子」という定数のペアを使用します。

   int count = 0;
   do
     {
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_data, data.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_means, c_aMeans.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_distance, c_aDistance.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_distance, def_k_kmd_vector_size, m_iVectorSize))
         return false;

次に、タスク空間の次元と、それぞれにおけるオフセットを指定します。このカーネルを2次元のタスク空間で実行することになったのです。タスク空間と同じ要素数の静的配列を2つ作成しましょう。

• global_work_size - タスク空間の次元を指定します。
• global_work_offset - 各ディメンジョンのオフセットを指定します。

その中で、両次元でのゼロオフセットを示すことにします。1次元目のサイズは、訓練セットに含まれるシステムの個々の状態の数に等しくなります。2次元目のサイズは、我々のモデルにおけるクラスタ数と同じになります。

      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2];
      global_work_size[0] = rows;
      global_work_size[1] = m_iClusters;

後は、カーネルを実行して演算結果を読み出すだけです。

      if(!c_OpenCL.Execute(def_k_kmeans_distance, 2, global_work_offset, global_work_size))
         return false;
      if(!c_aDistance.BufferRead())
         return false;

同様に、2番目のカーネルを呼び出して、システム状態が特定のクラスタに属しているかどうかを判断します。なお、このカーネルは1次元のタスク空間で起動されます。従って、次元とオフセットを示す別の配列が必要です。

      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_flags, c_aFlags.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_clusters, c_aClasters.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_distance, c_aDistance.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_clustering, def_k_kmc_total_k, m_iClusters))
         return false;
      uint global_work_offset1[1] = {0};
      uint global_work_size1[1];
      global_work_size1[0] = rows;
      if(!c_OpenCL.Execute(def_k_kmeans_clustering, 1, global_work_offset1, global_work_size1))
         return false;
      if(!c_aFlags.BufferRead())
         return false;

カーネルが実行キューに入った後は、フラグバッファのデータを読むだけです。この時点で、このデータだけでモデルの訓練終了を判断することができます。クラスタインデックスの中間データをロードすることに意味はなく、追加コストがかかります。そのため、現段階では使用しません。 

訓練サンプルの全要素がクラスタごとに分配された後、クラスタごとに要素の再分配が行われたかどうかを確認します。そのために、フラグデータバッファの最大値を確認します。覚えていらっしゃるように、関連するカーネル コードでは、前回の反復からのクラスタIDと新しく割り当てられたクラスタIDを比較したブール値の結果をフラグ バッファーに入力しました。等しい場合、0がバッファに書き込まれたことになります。クラスタが変更された場合は、1を書きました。クラスタを変更した要素の正確な数には興味がありません。そういう要素があるということを知っていれば十分です。そこで、最大値を確認します。それが0に等しい場合、つまり、どの要素もクラスタを変更しなかった場合、モデルの訓練が完了したと見なします。配列の各要素のクラスタ識別バッファを読み込んで、ループを抜けます。

      m_bTrained = (c_aFlags.Maximum() == 0);
      if(m_bTrained)
        {
         if(!c_aClasters.BufferRead())
            return false;
         break;
        }

学習がまだ終了していない場合は、3番目のカーネルの呼び出しに進み、クラスタの中心ベクトルを更新します。このカーネルも2次元のタスク空間でチューニングします。したがって、最初のカーネルの呼び出し時に作成された配列を使用することになります。1次元のサイズのみを変更します。

      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_data, data.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_means, c_aMeans.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_clusters, c_aClasters.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_updates, def_k_kmu_total_m, rows))
         return false;
      global_work_size[0] = m_iVectorSize;
      if(!c_OpenCL.Execute(def_k_kmeans_updates, 2, global_work_offset, global_work_size))
         return false;
      if(!c_aMeans.BufferRead())
         return false;
      count++;
      Comment(StringFormat("Study iterations %d", count));
     }
   while(!m_bTrained && !IsStopped());

カーネル実行後、訓練過程を視覚的にコントロールするために、チャートのコメント欄に訓練完了の反復回数を表示し、次のループの反復に移ることにします。

なお、モデルの訓練プロセス全体において、OpenCLコンテキストのメモリをクリアしたり、データを再コピーしたりはしていません。なぜなら、そのような操作にはリソースも必要だからです。リソースの利用効率を高め、モデル全体の訓練時間を短縮するために、これらのコストを排除しました。ただし、この方法は、すべてのデータを保存するのに十分なコンテクストメモリがある場合にのみ可能です。そうでなければ、各カーネルを実行する前に古いデータをアンロードし、新しいデータをロードするという、コンテキストメモリの使い方を再考する必要があるでしょう。

それでも、訓練処理が終了した後、メソッドを終了する前に、コンテキストメモリをクリアし、そこからバッファの一部を削除しています。

   data.BufferFree();
   c_aDistance.BufferFree();
   c_aFlags.BufferFree();
//---
   return true;
  }

モデルの訓練は、それ自体が目的ではありません。訓練結果を生かし、新しいデータにも適用できるようにモデルを訓練するのです。この機能を実装するために、Clusteringメソッドを作成します。実際、そのアルゴリズムは、前述した学習法のうち、学習ループと第3カーネルを除いたものを多少切り詰めたものです。最初の2つのカーネルのみが一度だけ呼び出されます。そのコードは、添付ファイルでご自身で勉強してください。

次に見ていくのは、損失関数(getloss)の値を計算する方法です。モデル訓練時のリソースを節約するため、損失関数の値を計算しないようにしました。したがって、パラメータで、メソッドはデータサンプルへのポインタを受け取り、それに対して誤差が計算されます。先ほどはメソッドの最初にコントロールのブロックを実装していましたが、今はその代わりにクラスタリングメソッドを呼び出しています。もちろん、メソッドの実行結果を確認することも忘れてはいけません。

double CKmeans::GetLoss(CBufferDouble *data)
  {
   if(!Clustering(data))
      return -1;

この手法により、1つのアクションで2つのタスクを同時に解決することができます。最初のタスクは、新しいサンプル自体のクラスタリングです。偏差値を計算するためには、サンプル要素がどのクラスタに属するかを把握する必要があります。

第二に、Clusteringクラスタリングメソッドには、すでに必要なすべてのコントロールが含まれているので、それらを繰り返す必要はありません。

次に、サンプルに含まれるシステム状態の数を数え、バッファを初期化し、偏差を決定します。

   int total = data.Total();
   int rows = total / m_iVectorSize;
//---
   if(CheckPointer(c_aLoss) == POINTER_INVALID)
     {
      c_aLoss = new CBufferDouble();
      if(CheckPointer(c_aLoss) == POINTER_INVALID)
         return -1;
     }
   if(!c_aLoss.BufferInit(rows, 0))
      return -1;

そして、初期データをコンテキストメモリに転送します。なお、平均値やクラスタIDのバッファはコンテキストメモリに渡しません。これは、OpenCLのコンテキストメモリにすでに存在するためです。データクラスタリング後に削除していないため、この段階でリソースを節約することができるのです。

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aLoss.BufferCreate(c_OpenCL))
      return -1;

次に、対応するカーネルを呼び出します。カーネルコールの手順は、前述した例と全く同じです。だから、くよくよするのはやめましょう。すべてのメソッドと関数の完全なコードは、添付ファイルにあります。

ただし、このカーネルでは、個々の状態の偏差値を求めました。次に、平均偏差を求めなければなりません。そのために、バッファの値を単純に合計するループを作成します。そして、その結果を分析した分析済みサンプルに含まれる要素の総数で割るのです。

   m_dLoss = 0;
   for(int i = 0; i < rows; i++)
      m_dLoss += c_aLoss.At(i);
   m_dLoss /= rows;

メソッドの最後には、コンテキストメモリをクリアして、結果の値を返します。

   data.BufferFree();
   c_aLoss.BufferFree();
   return m_dLoss;
  }

ここまでで、モデル訓練とデータクラスタリングに必要な機能一式を作成しました。しかし、モデルの訓練はリソースを必要とするプロセスであり、実用的なモデル使用の開始のたびに繰り返されるわけではないことは分かっています。そこで、モデルをファイルに保存し、そのファイルから機能を完全に復元する機能を追加する必要があります。これらの機能は、SaveメソッドとLoadメソッドで実装されています。この連載では、どのクラスでも使用されるため、すでに複数回、同様のメソッドを作成しています。該当するコードは添付ファイルでご確認いただけます。ご質問は、記事へのコメントでお願します。

最終的なクラスの構成は、以下のようになります。すべてのメソッドとクラスの完全なコードは、以下の添付ファイルにあります。

class CKmeans  : public CObject
  {
protected:
   int               m_iClusters;
   int               m_iVectorSize;
   double            m_dLoss;
   bool              m_bTrained;

   COpenCLMy         *c_OpenCL;       
   //---
   CBufferDouble     *c_aDistance;
   CBufferDouble     *c_aMeans;
   CBufferDouble     *c_aClasters;
   CBufferDouble     *c_aFlags;
   CBufferDouble     *c_aLoss;

public:
                     CKmeans(void);
                    ~CKmeans(void);
   //---
   bool              SetOpenCL(COpenCLMy *context);
   bool              Init(COpenCLMy *context, int clusters, int vector_size);
   bool              Study(CBufferDouble *data, bool init_means = true);
   bool              Clustering(CBufferDouble *data);
   double            GetLoss(CBufferDouble *data);
   //---
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)  { return defUnsupervisedKmeans; }
  };

5.テスト

そして、ここからは処理のクライマックスへと移っていきます。新しいデータクラスタリングクラスを作成したので、その実用的な価値を評価してみましょう。モデルを訓練します。そのためにkmeans.mq5という名前のエキスパートアドバイザー(EA)を作成することにします。EAコード全体は以下の添付ファイルに記載されています。

EAの外部パラメータは、前回使用したものと同じです。唯一の違いはEAの訓練期間が15年に延長されている点です。ラベルの付いていない大量のデータを利用できることは、教師なし学習の利点です。モデルのクラスタ数は、かなり広い範囲で学習処理をループで実装しているため、パラメータに含めませんでした。最適なクラスタ数を見つけるために、50クラスタから1000クラスタまで、いくつかの選択肢を検討しました。手順は50クラスタでした。これらは、前回の記事でPythonスクリプトをテストする際に使用したクラスタリングパラメータと全く同じものです。テストパラメータは、これまでの実験で使用したものです。

• 銘柄：EURUSD
• 時間枠：H1

訓練の結果、損失関数のクラスタ数依存性のグラフを得ることができました。以下に示します。 

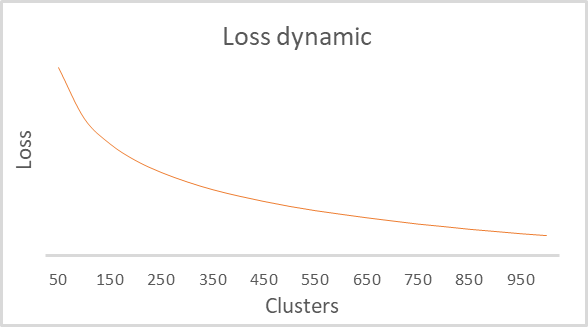
グラフを見ると、100クラスタから500クラスタの範囲で、かなり長いブレイクが発生していることがわかります。このモデルでは、合計で9万2千以上のシステム状態を解析しました。グラフの形は、前回Pythonスクリプトで構築したものと全く同じです。これにより、構築したクラスが正しく動作することを間接的に確認することができます。

終わりに

今回は、最も一般的なk-meansクラスタリング手法の1つを実装するために、新しいクラスCKmeansを作成しました。さらに、クラスタ数を変えてモデルを訓練することにも成功しました。テスト中には約500のパターンを識別することができました。Pythonで同様のテストをおこなったところ、同様の結果が得られました。メソッドのアルゴリズムを正しく繰り返したということです。次回は、クラスタリング結果の実用的な利用方法の可能性について述べる予定です。

参照文献

1. ニューラルネットワークが簡単に
2. ニューラルネットワークが簡単に（第2部）：ネットワークのトレーニングとテスト
3. ニューラルネットワークが簡単に（第3部）：コンボリューションネットワーク
4. ニューラルネットワークが簡単に（第4部）：リカレントネットワーク
5. ニューラルネットワークが簡単に（第5部）：OPENCLでのマルチスレッド計算
6. ニューラルネットワークが簡単に（第6部）：ニューラル ネットワークの学習率の実験
7. ニューラルネットワークが簡単に（第7部）：適応的最適化法
8. ニューラルネットワークが簡単に（第8部）：アテンションメカニズム
9. ニューラルネットワークが簡単に（第9部）：作業の文書化
10. ニューラルネットワークが簡単に（第10部）：Multi-Head Attention
11. ニューラルネットワークが簡単に（第11部）：GPTについて
12. ニューラルネットワークが簡単に（第12部）：ドロップアウト
13. ニューラルネットワークが簡単に（第13部）：Batch Normalization
14. ニューラルネットワークが簡単に（第14部）：データクラスタリング

記事で使用されているプログラム

#	名前	タイプ	詳細
1	kmeans.mq5	EA	モデルを訓練するEA
2	kmeans.mqh	クラスライブラリ	k-means法を整理するためのライブラリ
3	unsupervised.cl	ライブラリ	k-means法を実装するためのOpenCLプログラムコードライブラリ
4	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスライブラリ
5	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ