Algoritmi di ottimizzazione della popolazione

MetaTrader 5 — Esempi | 9 maggio 2023, 10:31

616

"Nulla accade nell’universo
che non faccia capo a qualche criterio di massimo o di minimo"
Leonhard Eulero, XVIII secolo

Contenuti:

1. Prospettiva storica

Gli algoritmi di ottimizzazione sono algoritmi che consentono di trovare punti estremi in un dominio di una funzione, in cui la funzione raggiunge il suo valore minimo o massimo.

I vecchi esperti greci dell'antichità sapevano già che:

— Di tutte le forme con un dato perimetro, il cerchio ha l'area più grande.

— Di tutti i poligoni con un dato numero di lati e un dato perimetro, un poligono regolare ha l'area più grande.

— Di tutte le figure tridimensionali aventi una data area, la sfera ha il volume maggiore.

Il primo problema che ha soluzioni variazionali fu proposto intorno allo stesso periodo. Secondo la leggenda, ciò accadde intorno all'825 a.C. Didone, figlia del re della città fenicia di Tiro, si è trasferita sulla costa meridionale del Mar Mediterraneo chiedendo ad una tribù locale un pezzo di terra che avrebbe ricoperto con pelle di toro. La gente del posto le diede una pelle. La ragazza intraprendente la tagliò in sottili strisce e le legò formando una corda. Con questa corda delimitò il territorio al largo della costa e vi fondò la città di Cartagine.

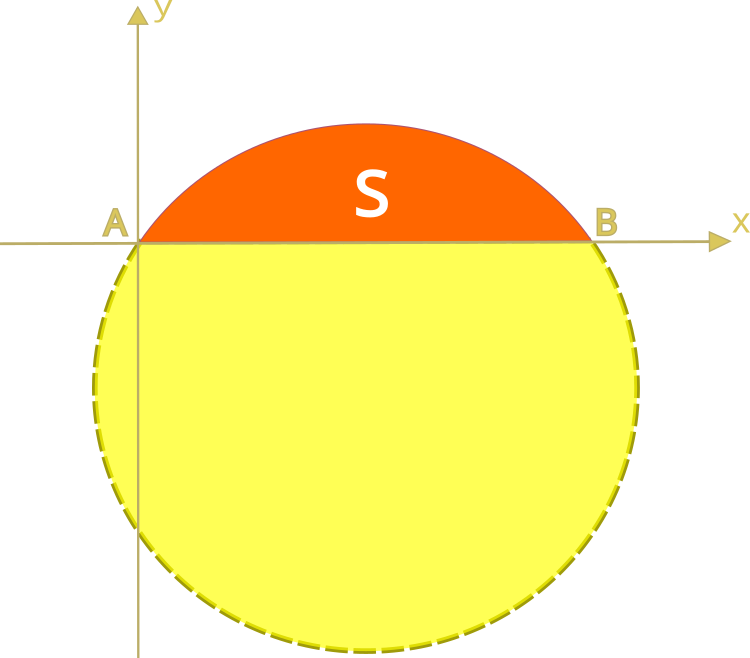
Il problema sta nel trovare la curva più efficiente, che copra la massima superficie, tra curve piane chiuse di una data lunghezza. L'area massima in questo problema è rappresentata dall'area circoscritta da un semicerchio.

didone1

Ora saltiamo un grosso pezzo di storia, compresa l'antica cultura del Mediterraneo, l'oppressione dell'Inquisizione e la cialtroneria del Medioevo, fino al Rinascimento con il suo volo libero del pensiero e le nuove teorie. Nel giugno 1696, Johann Bernoulli pubblica il seguente testo per i lettori di Acta Eruditorum: "Io, Johann Bernoulli, mi rivolgo ai più brillanti matematici del mondo. Niente è più attraente per le persone intelligenti di un problema onesto e impegnativo, la cui possibile soluzione conferirà fama e rimarrà un monumento duraturo. Seguendo l'esempio di Pascal, Fermat, ecc., spero di guadagnarmi la gratitudine dell’intera comunità scientifica ponendo davanti ai migliori matematici del nostro tempo un problema che metterà alla prova i loro metodi e la forza del loro intelletto. Se qualcuno mi comunica la soluzione del problema proposto, lo dichiarerò pubblicamente degno di lode".

Il problema del brachistocrona di Johann Bernulli:

"Dati due punti A e B in un piano verticale, qual è la curva tracciata da un punto su cui agisce solo la gravità, che parte da A e raggiunge B nel tempo più breve". Sorprendentemente, Galileo cercò di risolvere un problema simile già nel 1638, molto prima della pubblicazione di Bernoulli. La risposta: il percorso più veloce di tutti, da un punto all'altro, non è il percorso più breve, come sembra a prima vista, non è una linea retta, ma una curva — una cicloide che determina la curvatura della curva in ogni punto.

Brachistocrona9

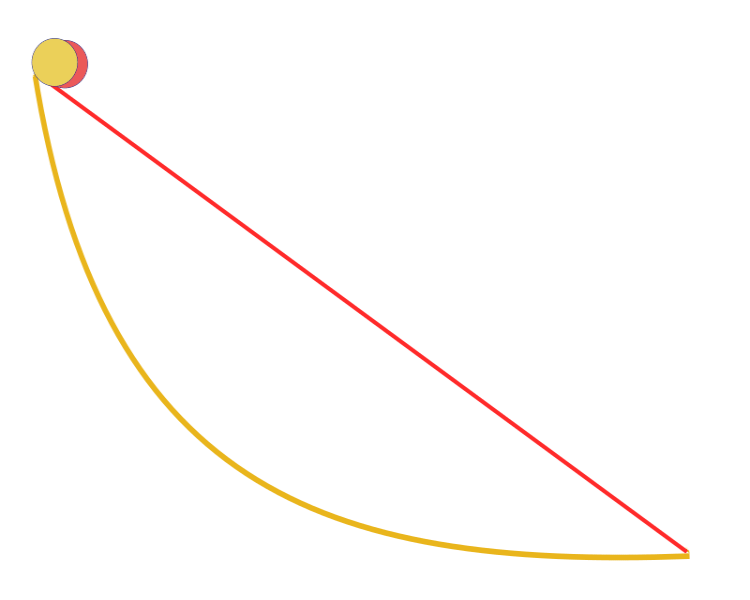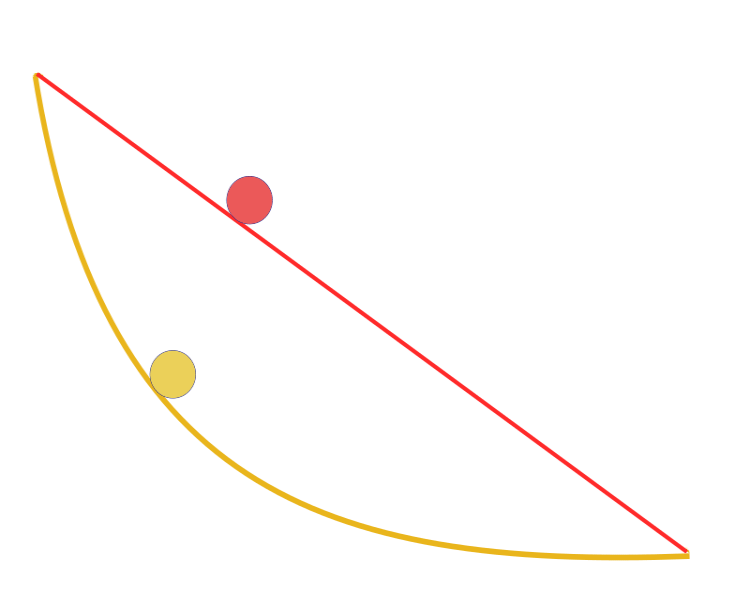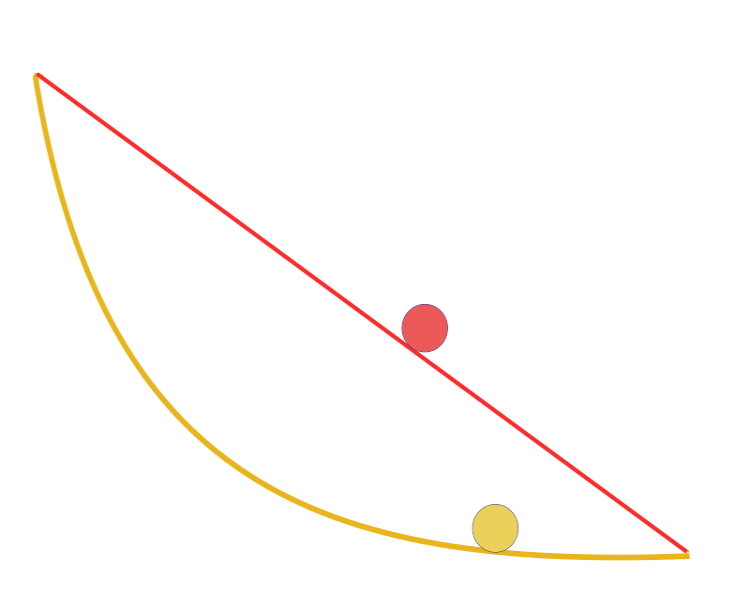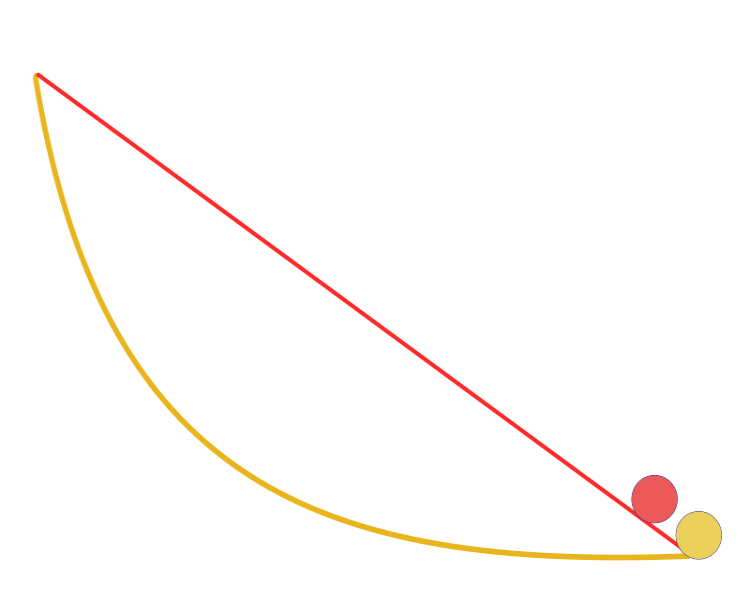
Curva brachistocrona

Tutte le altre soluzioni, inclusa quella di Newton (che all'epoca non fu rivelata), si basano sulla ricerca del gradiente in ciascun punto. Il metodo dietro la soluzione proposta da Isaac Newton costituisce la base del calcolo delle variazioni. I metodi del calcolo delle variazioni sono solitamente applicati nella risoluzione di problemi, in cui i criteri di ottimalità sono presentati sotto forma di funzionali e le cui soluzioni sono funzioni incognite. Tali problemi di solito sorgono nell'ottimizzazione statica di processi con parametri distribuiti o in problemi di ottimizzazione dinamica.

Le condizioni estreme del primo ordine nel calcolo delle variazioni sono state ottenute da Leonard Euler e Joseph Lagrange (le equazioni di Eulero-Lagrange). Queste equazioni sono ampiamente utilizzate nei problemi di ottimizzazione e insieme al principio di minima azione , sono applicate nei calcoli delle traiettorie in meccanica. Ben presto, però, divenne chiaro che le soluzioni di queste equazioni non sempre danno un estremo reale, il che significa che sono necessarie condizioni sufficienti per garantirne il risultato. Il lavoro fu continuato e le condizioni estreme di secondo ordine furono derivate da Legendre e Jacobi, e poi dallo studente di quest'ultimo - Hesse. La questione dell'esistenza di una soluzione nel calcolo delle variazioni fu sollevata per la prima volta da Weierstrass nella seconda metà del XIX secolo.

Nella seconda metà del XVIII secolo, la ricerca di soluzioni ottimali ai problemi formò le basi matematiche e i principi dell'ottimizzazione. Sfortunatamente, i metodi di ottimizzazione in realtà hanno avuto poca utilità in molte aree della scienza e della tecnologia fino alla seconda metà del XX secolo, poiché l'uso pratico dei metodi matematici richiedeva enormi risorse di calcolo. L'avvento delle nuove tecnologie informatiche nel mondo moderno ha finalmente reso possibile l'implementazione di complessi metodi di ottimizzazione dando origine alla disponibilità di una grande varietà di algoritmi.

Il 1980 ha visto l'inizio dell'intenso sviluppo della classe degli algoritmi di ottimizzazione stocastica, che erano il risultato di modelli presi in prestito dalla natura.

2. Classificazione degli OA

Classe

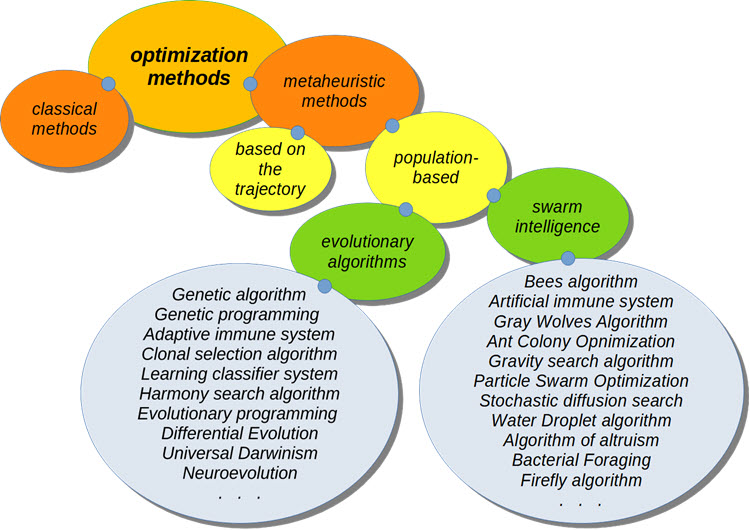
Classificazione AO

Quando si ottimizzano i sistemi di trading, quelli più interessanti sono gli algoritmi di ottimizzazione metaeuristici. Non richiedono la conoscenza della formula della funzione da ottimizzare. La loro convergenza all'optimum globale non è stata dimostrata, ma è stato stabilito sperimentalmente che nella maggior parte dei casi danno una soluzione abbastanza buona e questo è sufficiente per una serie di problemi.

Molti OA sono emersi come modelli presi in prestito dalla natura. Tali modelli sono anche chiamati comportamentali, di sciame o di popolazione, come il comportamento degli uccelli in uno stormo (l'algoritmo dello sciame di particelle) o dei principi del comportamento delle colonie di formiche (algoritmo delle formiche).

Gli algoritmi di popolazione implicano la gestione simultanea di diverse opzioni per risolvere il problema di ottimizzazione e rappresentano un'alternativa ai classici algoritmi basati su traiettorie di movimento la cui area di ricerca ha un solo candidato che si evolve durante la risoluzione del problema.

3. Convergenza e tasso di convergenza. Stabilità della convergenza. Scalabilità dell'algoritmo di ottimizzazione

Efficienza, velocità, convergenza, così come gli effetti delle condizioni del problema e dei parametri dell'algoritmo, richiedono un'attenta analisi per ogni implementazione algoritmica e per ogni classe di problemi di ottimizzazione.

3.1) Convergenza e tasso di convergenza

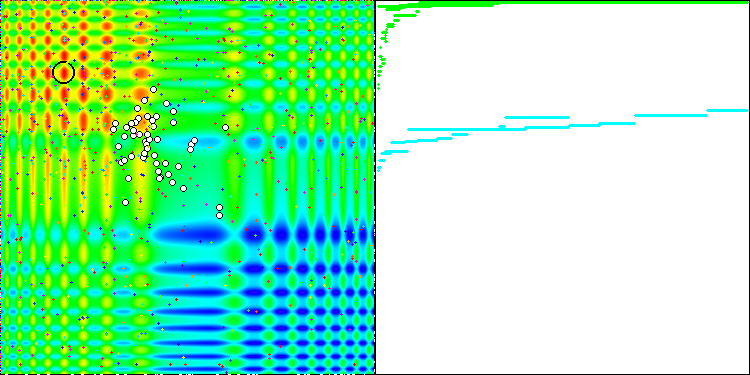
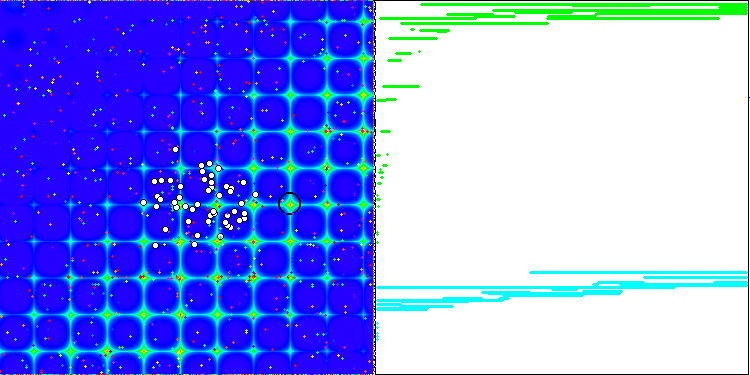
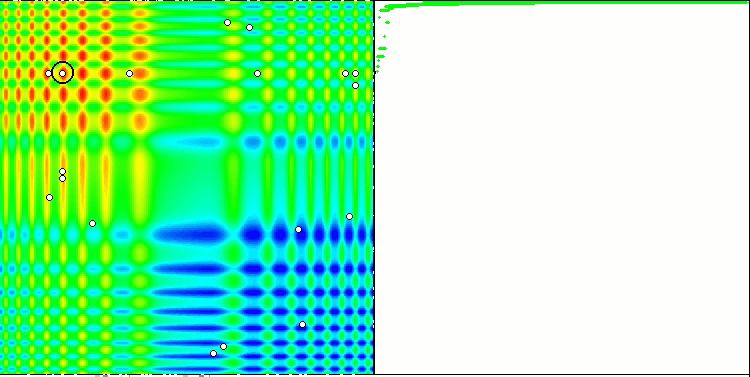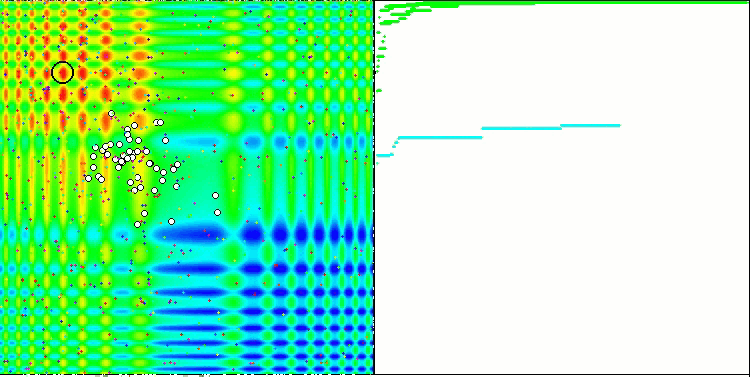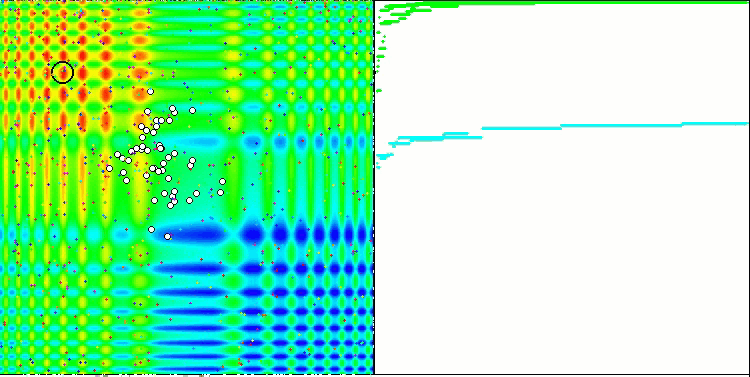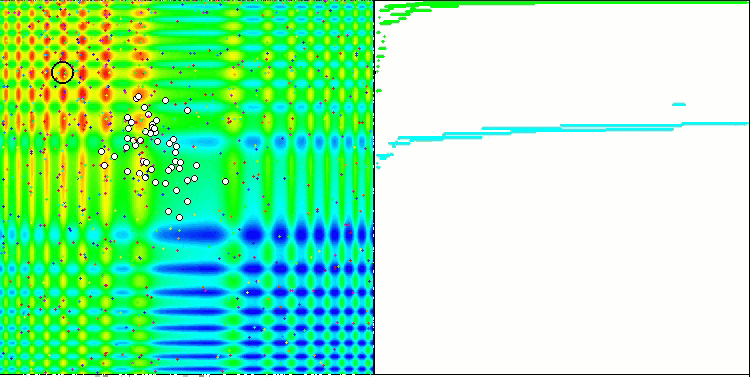
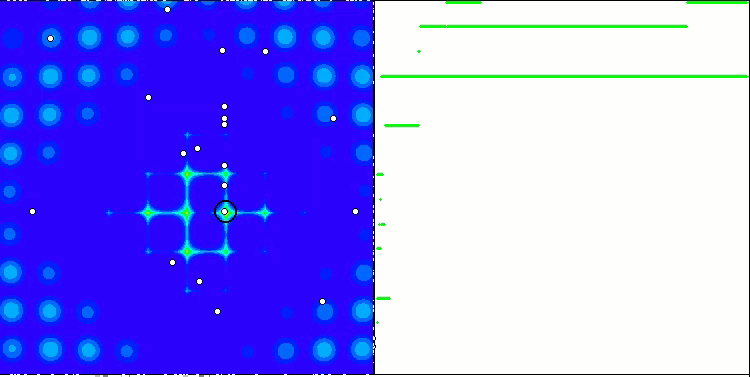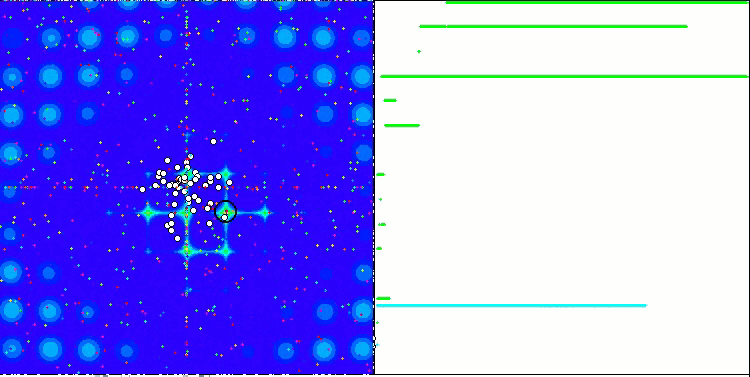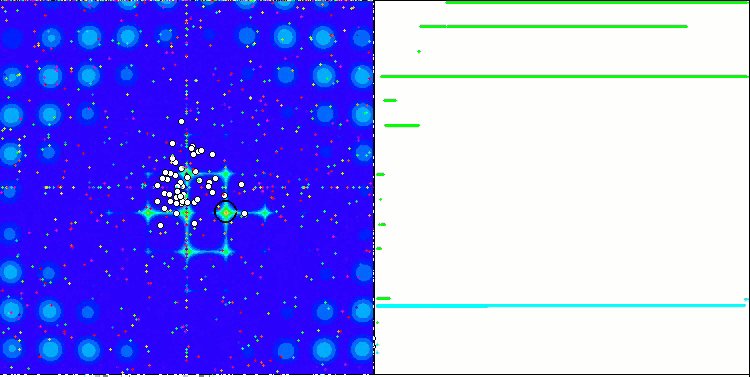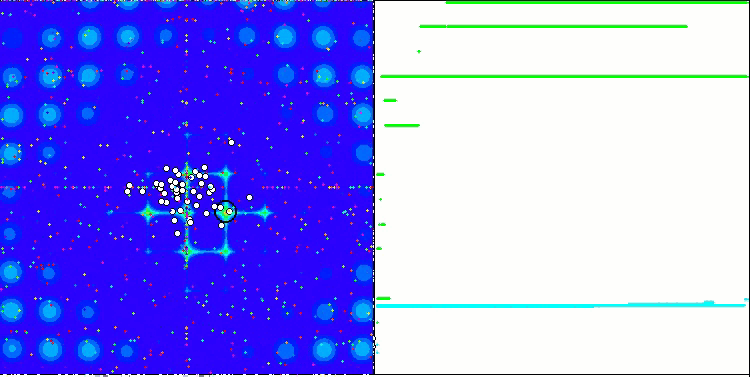
La proprietà di un algoritmo iterativo di raggiungere l’ottimizzazione dell’obiettivo della funzione o di avvicinarsi abbastanza ad esso in un numero finito di passi. Sul lato destro degli screenshot qui sopra, vediamo un grafico costruito in modo iterativo dei risultati ottenuti dalla funzione di test calcolata. Sulla base di queste due immagini, possiamo concludere che la convergenza è influenzata dalla complessità della superficie della funzione. Più è complessa, più è difficile trovare l'estremo globale.

Il tasso di convergenza degli algoritmi è uno dei più importanti indicatori della qualità di un algoritmo di ottimizzazione ed è una delle principali caratteristiche dei metodi di ottimizzazione. Quando sentiamo che un algoritmo è più veloce di un altro, nella maggior parte dei casi si intende il tasso di convergenza. Più il risultato è vicino all'estremo globale e più velocemente lo si ottiene (ovvero le precedenti iterazioni dell'algoritmo), maggiore è questo parametro. Si noti che il tasso di convergenza dei metodi di solito non supera quello quadratico. In rari casi, il metodo può avere un tasso di convergenza cubico.

3.2) Stabilità della convergenza

Il numero di iterazioni necessarie per raggiungere il risultato dipende non solo dalla capacità di ricerca dell'algoritmo stesso, ma anche dalla funzione studiata. Se la funzione è caratterizzata da un'elevata complessità della superficie (presenza di curve strette, discretezza, discontinuità), allora l'algoritmo potrebbe rivelarsi instabile e incapace di fornire una precisione accettabile. Inoltre, la stabilità della convergenza può essere intesa come la ripetibilità dei risultati di ottimizzazione quando vengono eseguiti diversi test consecutivi. Se i risultati presentano discrepanze elevate nei valori, la stabilità dell'algoritmo è bassa.

3.3) Scalabilità dell'algoritmo di ottimizzazione

convergenza7 convergenza6

La scalabilità dell'algoritmo di ottimizzazione è la capacità di mantenere la convergenza all'aumentare della dimensione del problema. In altre parole, all'aumentare del numero di variabili della funzione ottimizzata, la convergenza dovrebbe mantenersi ad un livello accettabile ai fini pratici. Gli algoritmi di popolazione per l'ottimizzazione della ricerca presentano innegabili vantaggi rispetto agli algoritmi classici, soprattutto quando si risolvono problemi di grandi dimensioni e scarsamente formalizzati. In queste condizioni, gli algoritmi di popolazione possono fornire un'alta probabilità di localizzare l'estremo globale della funzione da ottimizzare.

Nel caso di una funzione ottimizzata fluida e unimodale, gli algoritmi di popolazione sono generalmente meno efficienti di qualsiasi classico metodo del gradiente. Inoltre, gli svantaggi degli algoritmi di popolazione includono una forte dipendenza della loro efficienza dai gradi di libertà (il numero di parametri di ottimizzazione), che sono piuttosto numerosi nella maggior parte degli algoritmi.

4. Funzioni di test, costruzione di un criterio di valutazione OA complesso

Non esiste una metodologia generalmente accettata per testare e confrontare gli algoritmi di ottimizzazione. Tuttavia, ci sono molte funzioni di test proposte dai ricercatori in diverse annate. Useremo le funzioni che ho creato prima di pubblicare il primo articolo. Queste funzioni si trovano nella cartella del terminale \MQL5\Experts\Examples\Math 3D\Functions.mqh e \MQL5\Experts\Examples\Math 3D Morpher\Functions.mqh. Queste funzioni soddisfano tutti i criteri di complessità per i test OA. Inoltre, le funzioni Forest e Megacity sono state sviluppate per fornire uno studio più completo delle capacità di ricerca OA.

Funzione test Skin :

La funzione è fluida in tutto il suo dominio e ha molti valori massimi/minimi locali che differiscono in modo insignificante (trappole di convergenza), che causano il blocco degli algoritmi che non raggiungono l'estremo globale.

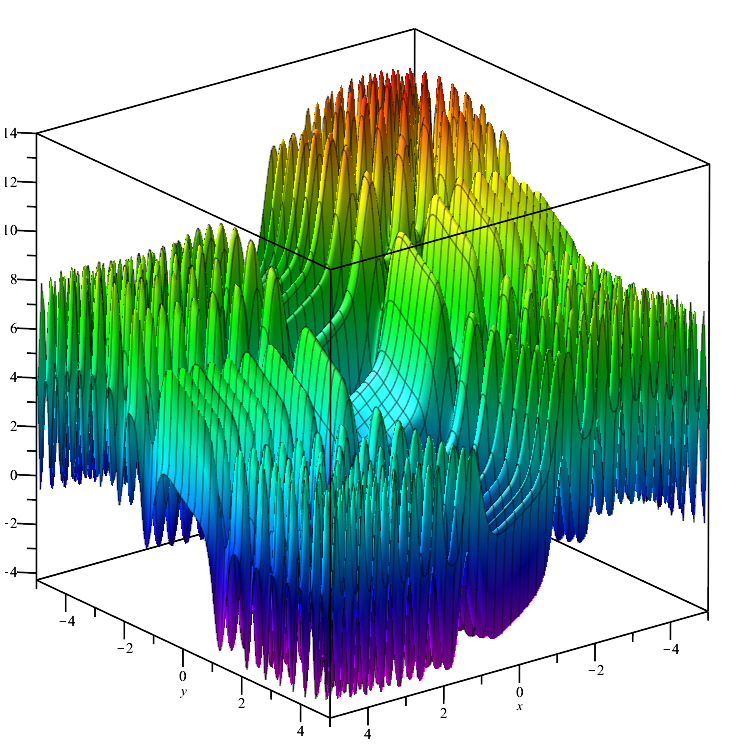
Skin

Funzione di test Forest :

La funzione rappresenta diversi massimi che non hanno un differenziale nei loro punti. Pertanto, potrebbe risultare difficile per gli algoritmi di ottimizzazione, la cui robustezza dipende in modo critico dalla fluidità della funzione in esame.

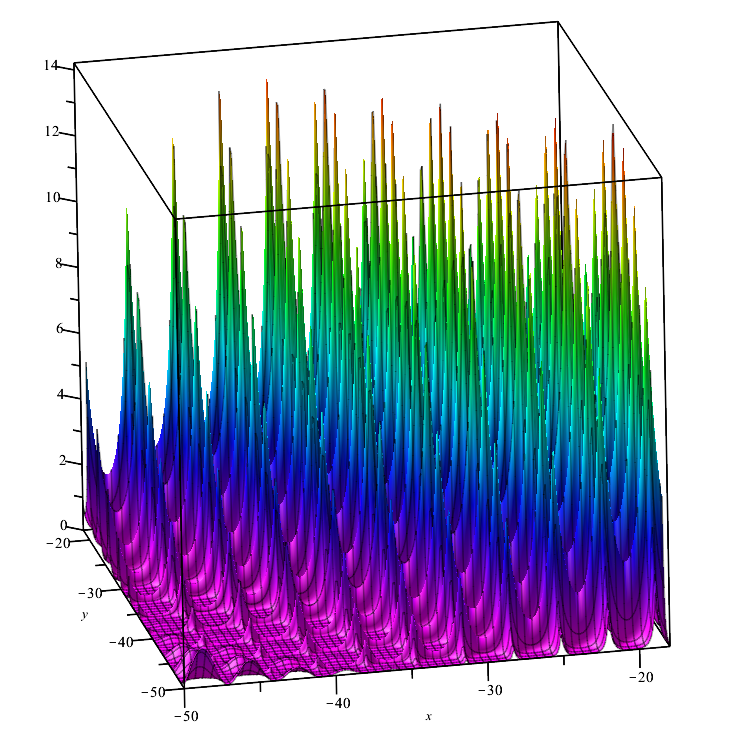
Forest

Funzione di test Megacity :

Una funzione discreta che forma "aree" (dove la modifica delle variabili non comporta un cambiamento significativo nel valore della funzione). Pertanto, pone una difficoltà per gli algoritmi che richiedono un gradiente.

Chinatown

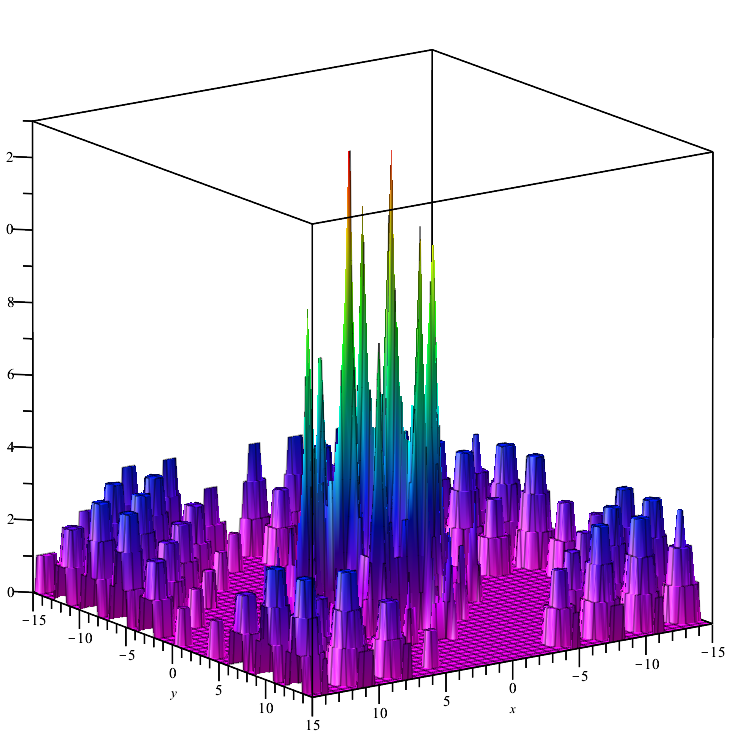
Megacity

5. Banco di prova

Per un confronto completo degli algoritmi di ottimizzazione, si è cercato di creare un criterio di valutazione generale. La complessità di questa idea sta nel fatto che non è chiaro come confrontare gli algoritmi, perché ognuno di essi è buono a modo suo per la corrispondente classe di problemi. Ad esempio, un algoritmo converge rapidamente ma non si adatta bene, mentre un altro si adatta bene ma è instabile.

Convergenza: Per studiare la convergenza, usiamo le tre funzioni presentate sopra. Il loro massimo e minimo sono convertiti in un range da 0.0 (peggior risultato) a 1.0 (miglior risultato), che ci consentirà di valutare la capacità degli algoritmi di garantire la convergenza su diversi tipi di problemi.
Tasso di convergenza: I migliori risultati dell'algoritmo vengono misurati alla 1000a e 10.000a esecuzione della funzione testata. Quindi, possiamo vedere quanto velocemente converge l'OA. Più veloce è la convergenza, più curvo sarà il grafico di convergenza verso il massimo.
Stabilità: Eseguire cinque cicli di ottimizzazione per ciascuna delle funzioni e calcolare il valore medio nell'intervallo da 0,0 a 1,0. Ciò è necessario perché i risultati di alcuni algoritmi possono variare notevolmente da un'esecuzione all'altra. Maggiore è la convergenza di ognuno dei cinque test, maggiore è la stabilità.
Scalabilità: Alcuni OA possono mostrare risultati pratici solo su funzioni con un numero ridotto di variabili, ad esempio non più di due, e alcuni non sono nemmeno in grado di lavorare con più di una variabile. Inoltre, ci sono algoritmi in grado di lavorare con funzioni con mille variabili. Questi algoritmi di ottimizzazione possono essere utilizzati come OA per le reti neurali.

Per comodità d’uso delle funzioni di test, scriviamo una classe genitore e un enumeratore che ci permetteranno in futuro di selezionare un oggetto della classe figlia della corrispondente funzione di test:

//——————————————————————————————————————————————————————————————————————————————
class C_Function
{
  public: //====================================================================
  double CalcFunc (double &args [], //function arguments
                   int     amount)  //amount of runs functions
  {
    double x, y;
    double sum = 0.0;
    for (int i = 0; i < amount; i++)
    {
      x = args [i * 2];
      y = args [i * 2 + 1];

      sum += Core (x, y);
    }

    sum /= amount;

    return sum;
  }
  double GetMinArg () { return minArg;}
  double GetMaxArg () { return maxArg;}
  double GetMinFun () { return minFun;}
  double GetMaxFun () { return maxFun;}
  string GetNamFun () { return fuName;}

  protected: //==================================================================
  void SetMinArg (double min) { minArg = min;}
  void SetMaxArg (double max) { maxArg = max;}
  void SetMinFun (double min) { minFun = min;}
  void SetMaxFun (double max) { maxFun = max;}
  void SetNamFun (string nam) { fuName = nam;}

  private: //====================================================================
  virtual double Core (double x, double y) { return 0.0;}
  
  double minArg;
  double maxArg;
  double minFun;
  double maxFun;
  string fuName;
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
enum EFunc
{
  Skin,
  Forest,
  Megacity,
  
};
C_Function *SelectFunction (EFunc f)
{
  C_Function *func;
  switch (f)
  {
    case  Skin:
      func = new C_Skin (); return (GetPointer (func));
    case  Forest:
      func = new C_Forest (); return (GetPointer (func));
    case  Megacity:
      func = new C_Megacity (); return (GetPointer (func));
    
    default:
      func = new C_Skin (); return (GetPointer (func));
  }
}
//——————————————————————————————————————————————————————————————————————————————

Quindi le classi figlio saranno simili a questa:

//——————————————————————————————————————————————————————————————————————————————
class C_Skin : public C_Function
{
  public: //===================================================================
  C_Skin ()
  {
    SetNamFun ("Skin");
    SetMinArg (-5.0);
    SetMaxArg (5.0);
    SetMinFun (-4.3182);  //[x=3.07021;y=3.315935] 1 point
    SetMaxFun (14.0606);  //[x=-3.315699;y=-3.072485] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a1=2*x*x;
    double a2=2*y*y;
    double b1=MathCos(a1)-1.1;
    b1=b1*b1;
    double c1=MathSin(0.5*x)-1.2;
    c1=c1*c1;
    double d1=MathCos(a2)-1.1;
    d1=d1*d1;
    double e1=MathSin(0.5*y)-1.2;
    e1=e1*e1;

   double res=b1+c1-d1+e1;
   return(res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Forest : public C_Function
{
  public: //===================================================================
  C_Forest ()
  {
    SetNamFun ("Forest");
    SetMinArg (-50.0);
    SetMaxArg (-18.0);
    SetMinFun (0.0);             //many points
    SetMaxFun (15.95123239744);  //[x=-25.132741228718345;y=-32.55751918948773] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = MathPow (f, 4);
    if (res < 0.0) res = 0.0;
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Megacity : public C_Function
{
  public: //===================================================================
  C_Megacity ()
  {
    SetNamFun ("Megacity");
    SetMinArg (-15.0);
    SetMaxArg (15.0);
    SetMinFun (0.0);   //many points
    SetMaxFun (15.0);  //[x=`3.16;y=1.990] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = floor (MathPow (f, 4));
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

Per verificare la validità dei risultati del test OA ottenuti sul banco di prova, possiamo utilizzare uno script che enumera le funzioni X e Y con la dimensione del passo Step. Fare attenzione quando si sceglie il passo, poiché un passo molto piccolo richiederà un lungo tempo per il calcolo. Ad esempio, la funzione Skin ha l'intervallo degli argomenti [-5;5]. Con il passo di 0.00001 lungo l'asse X, sarà (5-(-5))/0.00001=1'000'000 (milioni) di passi, lo stesso numero lungo l'asse Y, rispettivamente, il numero totale di cicli della funzione test per calcolare il valore in ciascuno dei punti sarà pari a 1'000'000 х 1'000'000= 1'000'000'000'000 (10^12, trilioni).

È necessario capire quanto sia difficile il compito per l’OA, poiché è necessario trovare il massimo in soli 10.000 passaggi (approssimativamente questo valore viene utilizzato nell'ottimizzatore MetaTrader 5). Notare che questo calcolo viene eseguito per una funzione con due variabili e il numero massimo di variabili che verranno utilizzate nei test è 1000.

Tieni presente quanto segue: i test dell'algoritmo in questo e nei successivi articoli utilizzano il passo di 0.0! o il minimo possibile per una specifica implementazione dell'OA corrispondente.

//——————————————————————————————————————————————————————————————————————————————
input EFunc  Function          = Skin;
input double Step              = 0.01;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_Function *TestFunc = SelectFunction (Function);

  double argMin = TestFunc.GetMinArg ();
  double argMax = TestFunc.GetMaxArg ();

  double maxFuncValue = 0;
  double xMaxFunc     = 0.0;
  double yMaxFunc     = 0.0;
  
  double minFuncValue = 0;
  double xMinFunc     = 0.0;
  double yMinFunc     = 0.0;
  
  double fValue       = 0.0;

  double arg [2];

  arg [0] = argMin;
  arg [1] = argMin;

  long cnt = 0;

  while (arg [1] <= argMax && !IsStopped ())
  {
    arg [0] = argMin;

    while (arg [0] <= argMax && !IsStopped ())
    {
      cnt++;

      fValue = TestFunc.CalcFunc (arg, 1);

      if (fValue > maxFuncValue)
      {
        maxFuncValue = fValue;
        xMaxFunc = arg [0];
        yMaxFunc = arg [1];
      }
      if (fValue < minFuncValue)
      {
        minFuncValue = fValue;
        xMinFunc = arg [0];
        yMinFunc = arg [1];
      }

      arg [0] += Step;
      
      if (cnt == 1)
      {
       maxFuncValue = fValue;
       minFuncValue = fValue;
      }
    }

    arg [1] += Step;
  }
  
  Print ("======", TestFunc.GetNamFun (), ", launch counter: ", cnt);
  Print ("MaxFuncValue: ", DoubleToString (maxFuncValue, 16), " X: ", DoubleToString (xMaxFunc, 16), " Y: ", DoubleToString (yMaxFunc, 16));
  Print ("MinFuncValue: ", DoubleToString (minFuncValue, 16), " X: ", DoubleToString (xMinFunc, 16), " Y: ", DoubleToString (yMinFunc, 16));
         
  delete TestFunc;
}

//——————————————————————————————————————————————————————————————————————————————

Scriviamo un banco di prova:

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>
#include "AO_RND.mqh"

//——————————————————————————————————————————————————————————————————————————————
input int    Population_P       = 50;
input double ArgumentStep_P     = 0.0;
input int    Test1FuncRuns_P    = 1;
input int    Test2FuncRuns_P    = 20;
input int    Test3FuncRuns_P    = 500;
input int    Measur1FuncValue_P = 1000;
input int    Measur2FuncValue_P = 10000;
input int    NumberRepetTest_P  = 5;
input int    RenderSleepMsc_P   = 0;

//——————————————————————————————————————————————————————————————————————————————
int WidthMonitor = 750;  //monitor screen width
int HeighMonitor = 375;  //monitor screen height

int WidthScrFunc = 375 - 2;  //test function screen width
int HeighScrFunc = 375 - 2;  //test function screen height

CCanvas Canvas;  //drawing table
C_AO_RND AO;     //AO object

C_Skin       SkiF;
C_Forest     ForF;
C_Megacity  ChiF;

struct S_CLR
{
    color clr [];
};

S_CLR FunctScrin []; //two-dimensional matrix of colors
double ScoreAll = 0.0;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  //creating a table -----------------------------------------------------------
  string canvasName = "AO_Test_Func_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, WidthMonitor, HeighMonitor, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }
  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  ArrayResize (FunctScrin, HeighScrFunc);
  for (int i = 0; i < HeighScrFunc; i++)
  {
    ArrayResize (FunctScrin [i].clr, HeighScrFunc);
  }
  
  //============================================================================
  //Test Skin###################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (SkiF, Test1FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrLime);
  FuncTests (SkiF, Test2FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrAqua);
  FuncTests (SkiF, Test3FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrOrangeRed);
  
  //Test Forest#################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ForF, Test1FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrLime);
  FuncTests (ForF, Test2FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrAqua);
  FuncTests (ForF, Test3FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrOrangeRed);
  
  //Test Megacity#############################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ChiF, Test1FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrLime);
  FuncTests (ChiF, Test2FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrAqua);
  FuncTests (ChiF, Test3FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrOrangeRed);
  
  Print ("All score for C_AO_RND: ", ScoreAll / 18.0);
}
//——————————————————————————————————————————————————————————————————————————————

void CanvasErase ()
{
  Canvas.Erase (XRGB (0, 0, 0));
  Canvas.FillRectangle (1,                1, HeighMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
  Canvas.FillRectangle (HeighMonitor + 1, 1, WidthMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
}

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_Function &f,
                int        funcCount,
                double     minFuncVal,
                double     maxFuncVal,
                double     xBest,
                double     yBest,
                color      clrConv)
{
  DrawFunctionGraph (f.GetMinArg (), f.GetMaxArg (), minFuncVal, maxFuncVal, f);
  SendGraphToCanvas (1, 1);
  int x = (int)Scale (xBest, f.GetMinArg (), f.GetMaxArg (), 0, WidthScrFunc - 1, false);
  int y = (int)Scale (yBest, f.GetMinArg (), f.GetMaxArg (), 0, HeighScrFunc - 1, false);
  Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
  Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));
  Canvas.Update ();
  Sleep (1000);

  int xConv = 0.0;
  int yConv = 0.0;

  int EpochCmidl = 0;
  int EpochCount = 0;

  double aveMid = 0.0;
  double aveEnd = 0.0;

  //----------------------------------------------------------------------------
  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    InitAO (funcCount * 2, f.GetMaxArg (), f.GetMinArg (), ArgumentStep_P);

    EpochCmidl = Measur1FuncValue_P / (ArraySize (AO.S_Colony));
    EpochCount = Measur2FuncValue_P / (ArraySize (AO.S_Colony));

    // Optimization-------------------------------------------------------------
    AO.F_EpochReset ();


    for (int epochCNT = 1; epochCNT <= EpochCount && !IsStopped (); epochCNT++)
    {
      AO.F_Preparation ();

      for (int set = 0; set < ArraySize (AO.S_Colony); set++)
      {
        AO.A_FFcol [set] = f.CalcFunc (AO.S_Colony [set].args, funcCount);
      }

      AO.F_Sorting ();

      if (epochCNT == EpochCmidl) aveMid += AO.A_FFpop [0];

      SendGraphToCanvas  (1, 1);

      //draw a population on canvas
      for (int i = 0; i < ArraySize (AO.S_Population); i++)
      {
        if (i > 0) PointDr (AO.S_Population [i].args, f.GetMinArg (), f.GetMaxArg (), clrWhite, 1, 1, funcCount);
      }
      PointDr (AO.S_Population [0].args, f.GetMinArg (), f.GetMaxArg (), clrBlack, 1, 1, funcCount);

      Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
      Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));

      xConv = (int)Scale (epochCNT,       1,          EpochCount, 2, WidthScrFunc - 2, false);
      yConv = (int)Scale (AO.A_FFpop [0], minFuncVal, maxFuncVal, 1, HeighScrFunc - 2, true);

      Canvas.FillCircle (xConv + HeighMonitor + 1, yConv + 1, 1, COLOR2RGB (clrConv));

      Canvas.Update ();
      Sleep (RenderSleepMsc_P);
    }

    aveEnd += AO.A_FFpop [0];

    Sleep (1000);
  }

  aveMid /= (double)NumberRepetTest_P;
  aveEnd /= (double)NumberRepetTest_P;

  double score1 = Scale (aveMid, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  double score2 = Scale (aveEnd, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  
  ScoreAll += score1 + score2;

  Print (funcCount, " ", f.GetNamFun (), "'s; Func runs ", Measur1FuncValue_P, " result: ", aveMid, "; Func runs ", Measur2FuncValue_P, " result: ", aveEnd);
  Print ("Score1: ", DoubleToString (score1, 5), "; Score2: ", DoubleToString (score2, 5));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void InitAO (const int    params,  //amount of the optimized arguments
             const double max,     //maximum of the optimized argument
             const double min,     //minimum of the optimized argument
             const double step)    //step of the optimized argument
{
  AO.F_Init (params, Population_P);
  for (int idx = 0; idx < params; idx++)
  {
    AO.A_RangeMax  [idx] = max;
    AO.A_RangeMin  [idx] = min;
    AO.A_RangeStep [idx] = step;
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void PointDr (double &args [], double Min, double Max, color clr, int shiftX, int shiftY, int count)
{
  double x = 0.0;
  double y = 0.0;
  
  double xAve = 0.0;
  double yAve = 0.0;
  
  int width  = 0;
  int height = 0;
  
  color clrF = clrNONE;
  
  for (int i = 0; i < count; i++)
  {
    xAve += args [i * 2];
    yAve += args [i * 2 + 1];
       
    x = args [i * 2];
    y = args [i * 2 + 1];
    
    width  = (int)Scale (x, Min, Max, 0, WidthScrFunc - 1, false);
    height = (int)Scale (y, Min, Max, 0, HeighScrFunc - 1, false);
    
    clrF = DoubleToColor (i, 0, count - 1, 0, 360);
    Canvas.FillCircle (width + shiftX, height + shiftY, 1, COLOR2RGB (clrF));
  }
  
  xAve /= (double)count;
  yAve /= (double)count;

  width  = (int)Scale (xAve, Min, Max, 0, WidthScrFunc - 1, false);
  height = (int)Scale (yAve, Min, Max, 0, HeighScrFunc - 1, false);

  Canvas.FillCircle (width + shiftX, height + shiftY, 3, COLOR2RGB (clrBlack));
  Canvas.FillCircle (width + shiftX, height + shiftY, 2, COLOR2RGB (clr));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void SendGraphToCanvas (int shiftX, int shiftY)
{
  for (int w = 0; w < HeighScrFunc; w++)
  {
    for (int h = 0; h < HeighScrFunc; h++)
    {
      Canvas.PixelSet (w + shiftX, h + shiftY, COLOR2RGB (FunctScrin [w].clr [h]));
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void DrawFunctionGraph (double     min,
                        double     max,
                        double     fMin,
                        double     fMax,
                        C_Function &f)
{
  double ar [2];
  double fV;

  for (int w = 0; w < HeighScrFunc; w++)
  {
    ar [0] = Scale (w, 0, HeighScrFunc, min, max, false);
    for (int h = 0; h < HeighScrFunc; h++)
    {
      ar [1] = Scale (h, 0, HeighScrFunc, min, max, false);
      fV = f.CalcFunc (ar, 1);
      FunctScrin [w].clr [h] = DoubleToColor (fV, fMin, fMax, 0, 250);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Scaling a number from a range to a specified range
double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
  else
  {
    if (Revers)
    {
      if (In < InMIN) return (OutMAX);
      if (In > InMAX) return (OutMIN);
      return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
    else
    {
      if (In < InMIN) return (OutMIN);
      if (In > InMAX) return (OutMAX);
      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color DoubleToColor (const double in,    //input value
                     const double inMin, //minimum of input values
                     const double inMax, //maximum of input values
                     const int    loH,   //lower bound of HSL range values
                     const int    upH)   //upper bound of HSL range values
{
  int h = (int)Scale (in, inMin, inMax, loH, upH, true);
  return HSLtoRGB (h, 1.0, 0.5);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color HSLtoRGB (const int    h, //0   ... 360
                const double s, //0.0 ... 1.0
                const double l) //0.0 ... 1.0
{
  int r;
  int g;
  int b;
  if (s == 0.0)
  {
    r = g = b = (unsigned char)(l * 255);
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
  else
  {
    double v1, v2;
    double hue = (double)h / 360.0;
    v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
    v1 = 2.0 * l - v2;
    r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
    g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
    b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
}
//——————————————————————————————————————————————————————————————————————————————
//——————————————————————————————————————————————————————————————————————————————
double HueToRGB (double v1, double v2, double vH)
{
  if (vH < 0) vH += 1;
  if (vH > 1) vH -= 1;
  if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
  if ((2 * vH) < 1) return v2;
  if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
  return v1;
}
//——————————————————————————————————————————————————————————————————————————————

Per convertire un numero double da un intervallo ad un colore, è stato utilizzato l'algoritmo di conversione da HSL a RGB (il sistema di colori di MetaTrader 5).

Il banco di prova visualizza un'immagine sul grafico. È diviso a metà.

La funzione di test viene visualizzata sul lato sinistro. Il suo grafico tridimensionale è proiettato su un piano, dove il rosso indica il massimo, mentre il blu indica il minimo. Visualizza la posizione dei punti nella popolazione (il colore corrisponde al numero ordinale della funzione di test con il numero di variabili 40 e 1000, la colorazione non viene eseguita per una funzione con due variabili), i punti le cui coordinate sono mediate sono contrassegnati in bianco, mentre il migliore è contrassegnato in nero.
Il grafico di convergenza è visualizzato sul lato destro, i test con 2 variabili sono contrassegnati in verde, i test con 40 variabili sono blu, mentre i test caratterizzati da 1000 variabili sono in rosso. Ciascuno dei test viene eseguito cinque volte (5 grafici di convergenza per ciascun colore). Qui possiamo osservare quanto la convergenza dell’OA si deteriora con un aumento del numero di variabili.

6. Semplice OA utilizzando RNG

Implementiamo la strategia di ricerca più semplice come esempio di prova. Non ha alcun valore pratico, ma sarà in qualche modo uno standard per confrontare algoritmi di ottimizzazione. La strategia genera un nuovo set di variabili di funzione in una scelta casuale 50/50: copia la variabile da un set genitore selezionato casualmente dalla popolazione o genera una variabile dall'intervallo min/max. Dopo aver ricevuto i valori delle funzioni di test, il nuovo set di variabili risultante viene copiato nella seconda metà della popolazione e ordinato. Pertanto, i nuovi set sostituiscono costantemente metà della popolazione, mentre i migliori set si concentrano nell'altra.

Di seguito è riportato un codice OA basato su RNG:

//+————————————————————————————————————————————————————————————————————————————+
class C_AO_RND
{
  public: //||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

  struct ArrColony
  {
      double args [];
  };

  //----------------------------------------------------------------------------
  double    A_RangeStep []; //Step ranges of genes
  double    A_RangeMin  []; //Min ranges of genes
  double    A_RangeMax  []; //Max ranges of genes

  ArrColony S_Population []; //Population
  ArrColony S_Colony     []; //Colony

  double    A_FFpop [];      //Values of fitness of individuals in population
  double    A_FFcol [];      //Values of fitness of individuals in colony

  //----------------------------------------------------------------------------
  // Initialization of algorithm
  void F_Init (int argCount,       //Number of arguments

               int populationSize) //Population size
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator

    p_argCount  = argCount;
    p_sizeOfPop = populationSize;
    p_sizeOfCol = populationSize / 2;

    p_dwelling  = false;

    f_arrayInitResize (A_RangeStep, argCount, 0.0);
    f_arrayInitResize (A_RangeMin,  argCount, 0.0);
    f_arrayInitResize (A_RangeMax,  argCount, 0.0);

    ArrayResize (S_Population, p_sizeOfPop);
    ArrayResize (s_populTemp, p_sizeOfPop);
    for (int i = 0; i < p_sizeOfPop; i++)
    {
      f_arrayInitResize (S_Population [i].args, argCount, 0.0);
      f_arrayInitResize (s_populTemp [i].args, argCount, 0.0);
    }

    ArrayResize (S_Colony, p_sizeOfCol);
    for (int i = 0; i < p_sizeOfCol; i++)
    {
      f_arrayInitResize (S_Colony [i].args, argCount, 0.0);
    }

    f_arrayInitResize (A_FFpop, p_sizeOfPop, -DBL_MAX);
    f_arrayInitResize (A_FFcol, p_sizeOfCol, -DBL_MAX);

    f_arrayInitResize (a_indexes, p_sizeOfPop, 0);
    f_arrayInitResize (a_valueOnIndexes, p_sizeOfPop, 0.0);
  }

  //----------------------------------------------------------------------------
  void F_EpochReset ()   //Reset of epoch, allows to begin evolution again without initial initialization of variables
  {
    p_dwelling = false;
    ArrayInitialize (A_FFpop, -DBL_MAX);
    ArrayInitialize (A_FFcol, -DBL_MAX);
  }
  //----------------------------------------------------------------------------
  void F_Preparation ();  //Preparation
  //----------------------------------------------------------------------------
  void F_Sorting ();      //The settling of a colony in population and the subsequent sorting of population

  private: //|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  //----------------------------------------------------------------------------
  void F_PopulSorting ();

  //----------------------------------------------------------------------------
  ArrColony          s_populTemp      []; //Temporal population
  int                a_indexes        []; //Indexes of chromosomes
  double             a_valueOnIndexes []; //VFF of the appropriate indexes of chromosomes

  //----------------------------------------------------------------------------
  template <typename T1>
  void f_arrayInitResize (T1 &arr [], const int size, const T1 value)
  {
    ArrayResize     (arr, size);
    ArrayInitialize (arr, value);
  }

  //----------------------------------------------------------------------------
  double f_seInDiSp         (double In, double InMin, double InMax, double step);
  double f_RNDfromCI        (double min, double max);
  double f_scale            (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);

  //---Constants----------------------------------------------------------------
  int  p_argCount;   //Quantity of arguments in a set of arguments
  int  p_sizeOfCol;  //Quantity of set in a colony
  int  p_sizeOfPop;  //Quantity of set in population
  bool p_dwelling;   //Flag of the first settling of a colony in population
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Preparation ()
{
  //if starts of algorithm weren't yet - generate a colony with random arguments
  if (!p_dwelling)
  {
    for (int person = 0; person < p_sizeOfCol; person++)
    {
      for (int arg = 0; arg < p_argCount; arg++)
      {
        S_Colony [person].args [arg] = f_seInDiSp (f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]),
                                                    A_RangeMin  [arg],
                                                    A_RangeMax  [arg],
                                                    A_RangeStep [arg]);
      }
    }

    p_dwelling = true;
  }
  //generation of a colony using with copying arguments from parent sets--------
  else
  {
    int parentAdress = 0;
    double rnd       = 0.0;
    double argVal    = 0.0;

    for (int setArg = 0; setArg < p_sizeOfCol; setArg++)
    {
      //get a random address of the parent set
      parentAdress = (int)f_RNDfromCI (0, p_sizeOfPop - 1);

      for (int arg = 0; arg < p_argCount; arg++)
      {
        if (A_RangeMin [arg] == A_RangeMax [arg]) continue;

        rnd = f_RNDfromCI (0.0, 1.0);

        if (rnd < 0.5)
        {
          S_Colony [setArg].args [arg] = S_Population [parentAdress].args [arg];
        }
        else
        {
          argVal = f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]);
          argVal = f_seInDiSp (argVal, A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]);

          S_Colony [setArg].args [arg] = argVal;
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Sorting ()
{
  for (int person = 0; person < p_sizeOfCol; person++)
  {
    ArrayCopy (S_Population [person + p_sizeOfCol].args, S_Colony [person].args, 0, 0, WHOLE_ARRAY);
  }
  ArrayCopy (A_FFpop, A_FFcol, p_sizeOfCol, 0, WHOLE_ARRAY);

  F_PopulSorting ();
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Ranging of population.
void C_AO_RND::F_PopulSorting ()
{
  //----------------------------------------------------------------------------
  int   cnt = 1, i = 0, u = 0;
  int   t0 = 0;
  double t1 = 0.0;
  //----------------------------------------------------------------------------

  // We will put indexes in the temporary array
  for (i = 0; i < p_sizeOfPop; i++)
  {
    a_indexes [i] = i;
    a_valueOnIndexes [i] = A_FFpop [i];
  }
  while (cnt > 0)
  {
    cnt = 0;
    for (i = 0; i < p_sizeOfPop - 1; i++)
    {
      if (a_valueOnIndexes [i] < a_valueOnIndexes [i + 1])
      {
        //-----------------------
        t0 = a_indexes [i + 1];
        t1 = a_valueOnIndexes [i + 1];
        a_indexes [i + 1] = a_indexes [i];
        a_valueOnIndexes [i + 1] = a_valueOnIndexes [i];
        a_indexes [i] = t0;
        a_valueOnIndexes [i] = t1;
        //-----------------------
        cnt++;
      }
    }
  }

  // On the received indexes create the sorted temporary population
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (s_populTemp [u].args, S_Population [a_indexes [u]].args, 0, 0, WHOLE_ARRAY);

  // Copy the sorted array back
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (S_Population [u].args, s_populTemp [u].args, 0, 0, WHOLE_ARRAY);

  ArrayCopy (A_FFpop, a_valueOnIndexes, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_RND::f_seInDiSp (double in, double inMin, double inMax, double step)
{
  if (in <= inMin) return (inMin);
  if (in >= inMax) return (inMax);
  if (step == 0.0) return (in);
  else return (inMin + step * (double)MathRound ((in - inMin) / step));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Random number generator in the custom interval.
double C_AO_RND::f_RNDfromCI (double min, double max)
{
  if (min == max) return (min);
  double Min, Max;
  if (min > max)
  {
    Min = max;
    Max = min;
  }
  else
  {
    Min = min;
    Max = max;
  }
  return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0)));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
double C_AO_RND::f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return (OutMIN);
    if (In > InMAX) return (OutMAX);
    return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
  }
}
//——————————————————————————————————————————————————————————————————————————————

7. Risultati

AO	Cicli	Skin			Forest			Megacity (discreto)			Risultato finale
AO	Cicli	2 parametri (1 F)	40 parametri (20 F)	1000 parametri (500 F)	2 parametri (1 F)	40 parametri (20 F)	1000 parametri (500 F)	2 parametri (1 F)	40 parametri (20 F)	1000 parametri (500 F)	Risultato finale
RND	1000	0,98744	0,61852	0.49408	0,89582	0.19645	0.14042	0,77333	0.19000	0.14283	0,51254
RND	10.000	0,99977	0,69448	0,50188	0.98181	0.24433	0.14042	0,88000	0.20133	0.14283	0,51254

Dopo i test sul banco di prova, i risultati dell'OA RND si sono rivelati del tutto inaspettati. L'algoritmo è in grado di trovare l'optimum di funzioni di due variabili con altissima precisione, mentre nel caso di Forest e Megacity, i risultati sono notevolmente peggiori. D'altra parte, le mie ipotesi sulle deboli proprietà di ricerca per le funzioni con molte variabili sono state confermate. I risultati sono molto mediocri già a 40 argomenti. Il valore cumulativo finale è 0,51254.

Negli articoli successivi, analizzerò e testerò algoritmi di ottimizzazione conosciuti e ampiamente utilizzati e continuerò a compilare la tabella dei risultati che costituisce la valutazione OA.

Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/8122

File allegati |

Scarica ZIP

MQL5.zip (9.71 KB)

Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

Altri articoli di questo autore

Vai alla discussione

Algoritmi di ottimizzazione della popolazione: Sciame di particelle (PSO)

In questo articolo, prenderò in considerazione il famoso algoritmo Particle Swarm Optimization (PSO). In precedenza, abbiamo discusso caratteristiche così importanti degli algoritmi di ottimizzazione come convergenza, tasso di convergenza, stabilità, scalabilità, nonché sviluppato un banco di prova e considerato il più semplice algoritmo RNG..

Impara come progettare un sistema di trading tramite Chaikin Oscillator

Benvenuti nel nostro nuovo articolo della nostra serie sull'imparare a progettare un sistema di trading tramite gli indicatori tecnici più popolari. Attraverso questo nuovo articolo, impareremo come progettare un sistema di trading tramite l'indicatore Chaikin Oscillator.

Sviluppare un Expert Advisor per il trading da zero (Parte 18): Nuovo sistema di ordini (I)

Questa è la prima parte del nuovo sistema di ordini. Da quando abbiamo iniziato a documentare questo EA nei nostri articoli, ha subito varie modifiche e miglioramenti mantenendo lo stesso modello di sistema degli ordini sul grafico.

Impara come progettare un sistema di trading tramite la Deviazione Standard

Ecco un nuovo articolo della nostra serie su come progettare un sistema di trading con gli indicatori tecnici più popolari nella piattaforma di trading MetaTrader 5. In questo nuovo articolo, impareremo come progettare un sistema di trading tramite l'indicatore Deviazione Standard.