Popülasyon optimizasyon algoritmaları

"Evrende meydana gelen her şeyde 
maksimum/minimum kuralı kendini gösterir.”
Leonhard Euler, 18. yüzyıl

İçindekiler:

1. Tarihsel perspektif
2. Optimizasyon algoritması sınıflandırması
3. Yakınsama ve yakınsama oranı. Yakınsama kararlılığı. Optimizasyon algoritması ölçeklenebilirliği
4. Test fonksiyonları, karmaşık bir optimizasyon algoritması değerlendirme kriterinin oluşturulması
5. Test ortamı
6. RNG kullanan basit bir optimizasyon algoritması örneği
7. Sonuçlar

 

1. Tarihsel perspektif

Optimizasyon algoritmaları, bir fonksiyonun tanım kümesindeki, fonksiyonun maksimum/minimum değerine ulaştığı ekstremumların bulunmasını sağlayan algoritmalardır.

Antik Yunanistan'da uzmanlar şunları çoktan biliyordu:

- Belirli bir çevreye sahip tüm şekiller arasında en büyük alana sahip olan dairedir.

- Belirli bir kenar sayısına ve çevreye sahip tüm çokgenler arasında en büyük alana sahip olan düzgün çokgendir.

- Belirli bir alana sahip tüm üç boyutlu şekiller arasında en büyük hacme sahip olan küredir.

Varyasyonel çözümlere sahip ilk problem de aynı zamanlarda ortaya çıkmıştır. Efsaneye göre bu M.Ö. 825 civarında gerçekleşmiştir. Fenike kenti Sur'un kralının kız kardeşi Dido, Akdeniz'in güney kıyılarına taşınır ve yerel halktan boğa derisiyle çevrelenebilecek kadar bir arsa ister. Yerel halk bunu kabul eder ve ona boğa derisini verir. Becerikli kız onu dar kuşaklar halinde keser ve bu kuşakları birbirine bağlayarak bir ip yapar. Bu iple kıyıda bir arsa alanı çevreler ve orada Kartaca şehrini kurar.

Problem, belirli bir uzunluktaki kapalı düzlem eğrileri arasından maksimum yüzey alanını kapsayan en verimli eğriyi bulmaktır. Bu problemdeki maksimum alan, aşağıda gösterilen yarım daire tarafından çevrelenen alandır.

 

 

 

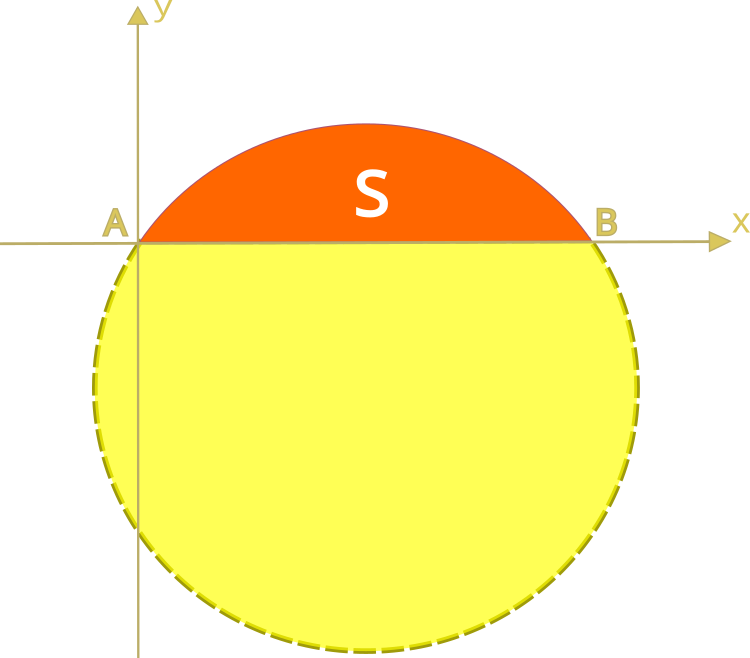
Şimdi, Akdeniz'in antik kültürü, Engizisyon'un baskısı ve Orta Çağ'ın şarlatanlıkları da dahil olmak üzere, düşüncenin özgürce uçuştuğu ve yeni teorilerin ortaya çıktığı Rönesans'a kadar tarihin büyük bir bölümünü atlayalım. Haziran 1696'da Johann Bernoulli, Acta Eruditorum okuyucuları için aşağıdaki metni yayınlar: "Ben, Johann Bernoulli, dünyanın en parlak matematikçilerine sesleniyorum. Zeki insanlar için hiçbir şey, olası çözümü ün kazandıracak ve kalıcı bir anıt olarak kalacak dürüst, zorlu bir problemden daha çekici değildir. Pascal, Fermat, vb. örneğini izleyerek, zamanımızın en iyi matematikçilerinin önüne yöntemlerini ve zekâlarının gücünü sınayacak bir problem koyarak tüm bilim topluluğunun minnettarlığını kazanmayı umuyorum. Bir kişi bana problemin çözümünü iletirse, herkese açık bir şekilde onun övgüye layık olduğunu ilan edeceğim".

Johann Bernoulli'nin en kısa zaman (brakistokron) problemi:

“Dik bir düzlemde iki nokta arasına nasıl bir eğri çizilsin ki bu eğri boyunca sadece yerçekimi etkisiyle sürtünmesiz kayan bir cisim bu yolu en kısa sürede alsın?” Dikkat çekici bir şekilde Galileo, Bernoulli'nin yayınından çok önce, 1638 yılında benzer bir problemi çözmeye çalışmıştır. Cevap: Bir noktadan diğerine giden en hızlı yol, ilk bakışta göründüğü gibi en kısa yol, yani düz bir çizgi değildir, bir eğridir - her noktada eğrinin eğriliğini tanımlayan bir sikloiddir.

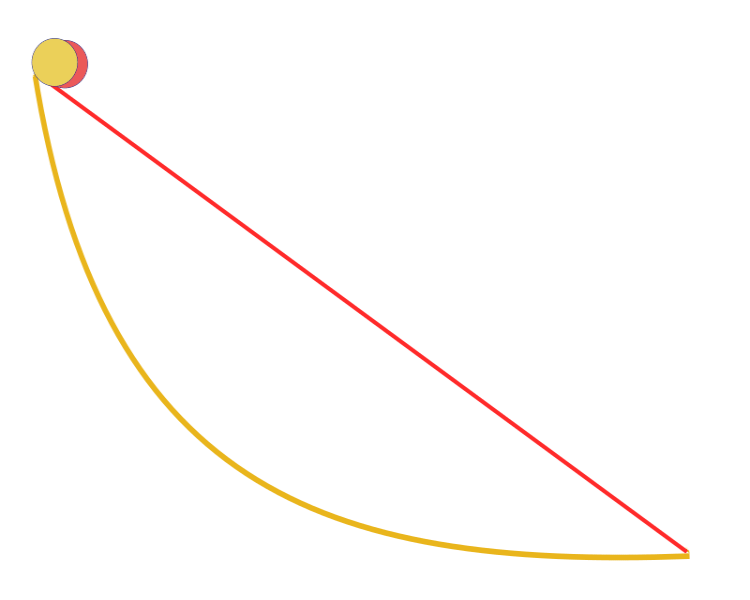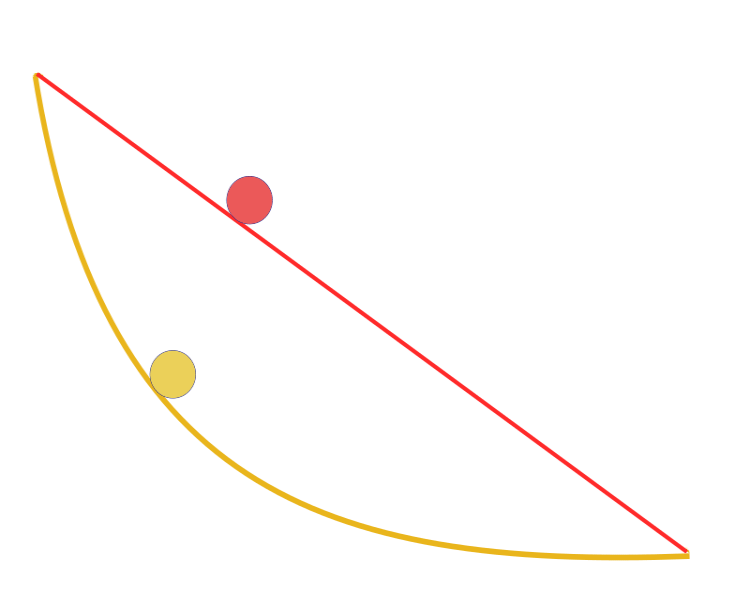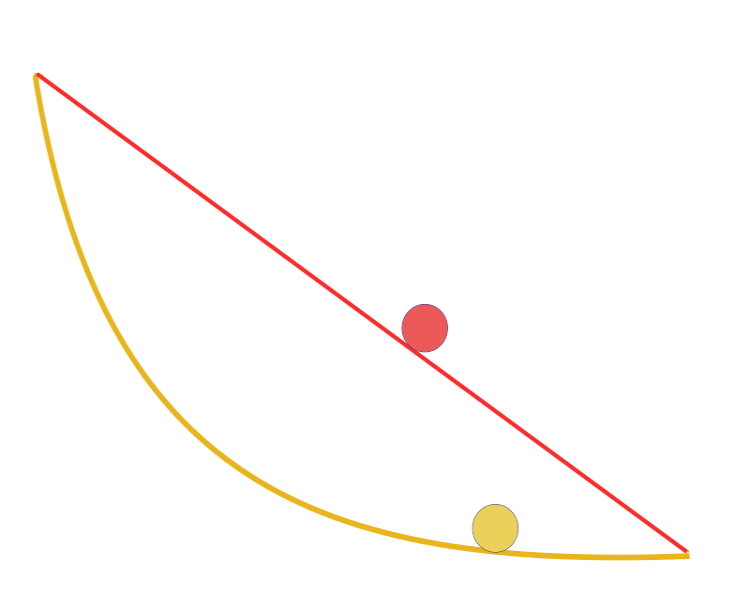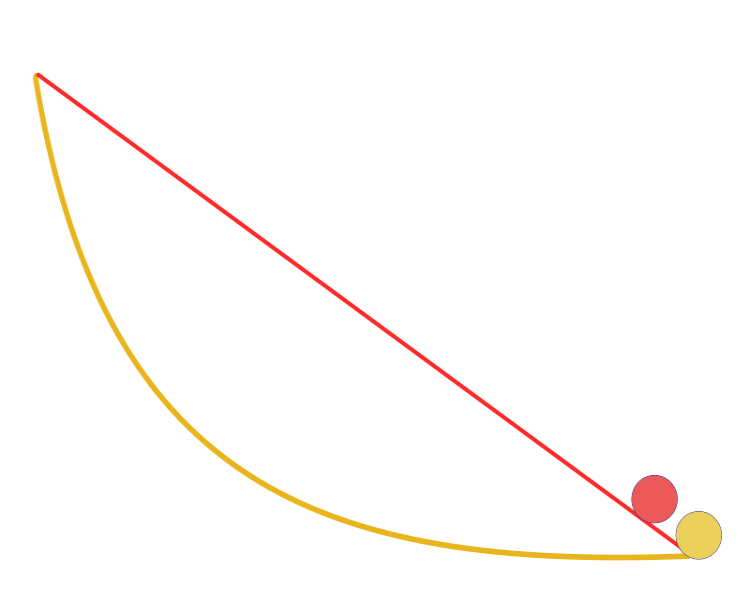
 En kısa zaman eğrisi

Newton'unki de dahil olmak üzere (o sırada açıklanmamış olan) diğer tüm çözümler, her noktadaki gradyanı bulmaya dayanmaktadır. Isaac Newton tarafından sunulan çözümün arkasındaki yöntem, varyasyonel hesaplamanın temelini oluşturmaktadır. Varyasyonel hesaplama yöntemleri genellikle optimallik kriterlerinin fonksiyonel formda ifade edildiği ve çözümleri bilinmeyen fonksiyonlar olan problemlerin çözümünde uygulanır. Bu tür problemler genellikle dağıtılmış parametrelere sahip süreçlerin statik optimizasyonunda veya dinamik optimizasyon problemlerinde ortaya çıkar.

Varyasyonel hesaplamadaki birinci dereceden ekstremum koşulları Leonard Euler ve Joseph Lagrange tarafından elde edilmiştir (Euler-Lagrange denklemleri). Bu denklemler optimizasyon problemlerinde yaygın olarak kullanılır ve en az eylem ilkesiyle birlikte mekanikteki yörüngelerin hesaplanmasında uygulanır. Ancak kısa süre sonra, bu denklemlerin çözümlerinin her zaman gerçek bir ekstremum vermediği ortaya çıktı, dolayısıyla ektremumun bulunmasını garanti eden yeterli koşulların gerekli olduğu anlaşıldı. Çalışmaya devam edildi ve ikinci dereceden ekstremum koşulları Legendre ve Jacobi tarafından ve daha sonra Jacobi’nin öğrencisi Hesse tarafından türetildi. Varyasyonel hesaplamada bir çözümün varlığı sorusu ilk olarak 19. yüzyılın ikinci yarısında Weierstrass tarafından ortaya atılmıştır.

18'inci yüzyılın ikinci yarısına gelindiğinde, problemlere optimal çözümlerin aranması optimizasyonun matematiksel temellerini ve ilkelerini oluşturmuştur. Ne yazık ki, matematiksel yöntemlerin pratik kullanımı büyük hesaplama kaynakları gerektirdiğinden, optimizasyon yöntemleri 20. yüzyılın ikinci yarısına kadar bilim ve teknolojinin birçok alanında çok az kullanılmıştır. Modern dünyada yeni hesaplama teknolojilerinin ortaya çıkması, nihayet karmaşık optimizasyon yöntemlerinin uygulanmasını mümkün kılarak çok çeşitli mevcut algoritmaların ortaya çıkmasına olanak sağlamıştır.

1980'ler, doğadan ilham alınan modellemelerin sonucu olan stokastik optimizasyon algoritmaları sınıfının yoğun gelişiminin başlangıcına tanık olmuştur.

 

2. Optimizasyon algoritması sınıflandırması

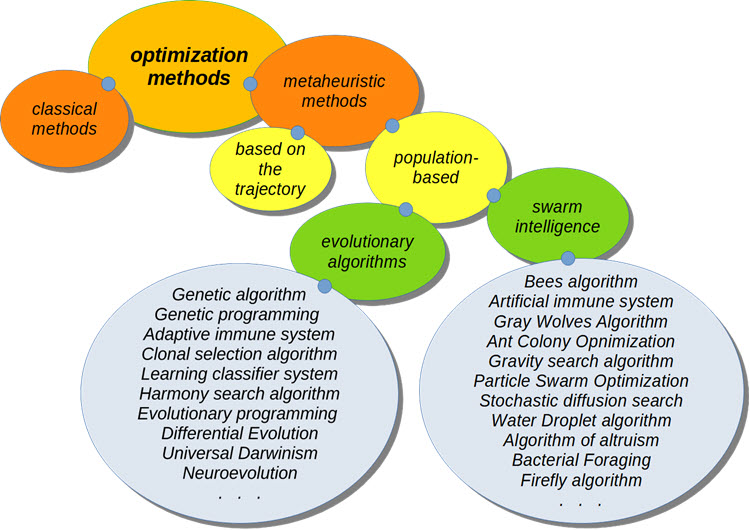
 Optimizasyon algoritması sınıflandırması

Ticaret sistemlerini optimize ederken, en heyecan verici şeyler metasezgisel optimizasyon algoritmalarıdır. Optimize edilen fonksiyonun formülü hakkında bilgi sahibi olmayı gerektirmezler. Global optimuma yakınsadıkları kanıtlanmamıştır, ancak çoğu durumda oldukça iyi bir çözüm sundukları deneysel olarak tespit edilmiştir ve bu da bir takım problemler için yeterlidir.

Pek çok optimizasyon algoritması doğadan ilham alınan modeller olarak ortaya çıkmıştır. Bu tür modeller davranışsal, sürü veya popülasyon olarak da adlandırılır, örneğin bir sürüdeki kuşların davranışı (parçacık sürüsü algoritması) veya bir karınca kolonisinin davranışı (karınca algoritması) gibi.

Popülasyon algoritmaları, optimizasyon problemini çözmek için çeşitli seçeneklerin eşzamanlı olarak işlenmesini içerir ve problem çözümünde arama alanında yalnızca bir adayın evrimleştiği hareket yörüngelerine dayanan klasik algoritmalara bir alternatif teşkil eder.

 

3. Yakınsama ve yakınsama oranı. Yakınsama kararlılığı. Optimizasyon algoritması ölçeklenebilirliği

Her algoritmik uygulama ve optimizasyon problemi sınıfı için, verimlilik, hız, yakınsama ve problem koşullarının ve algoritma parametrelerinin etkileri dikkatli bir analiz gerektirir.

3.1) Yakınsama ve yakınsama oranı

 

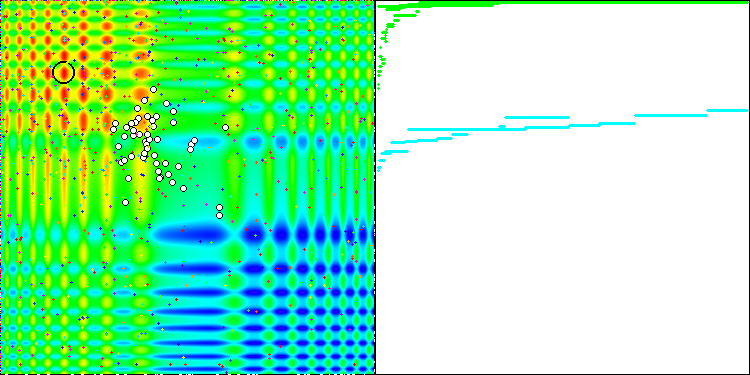
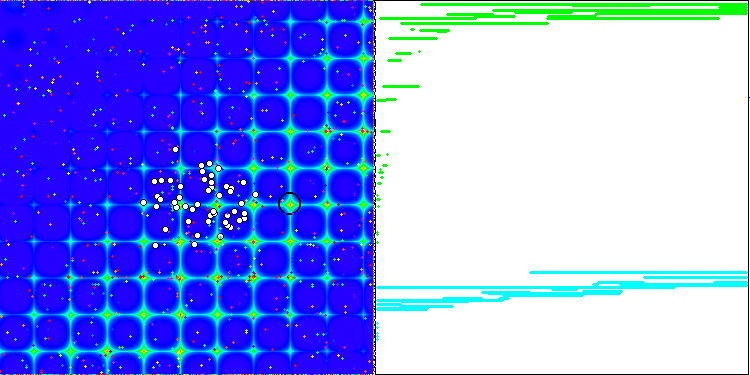
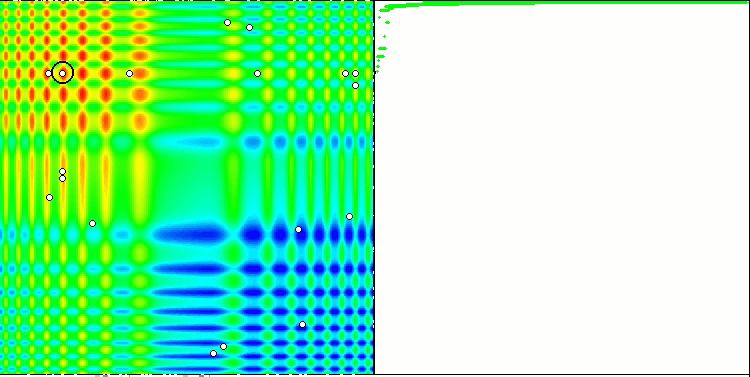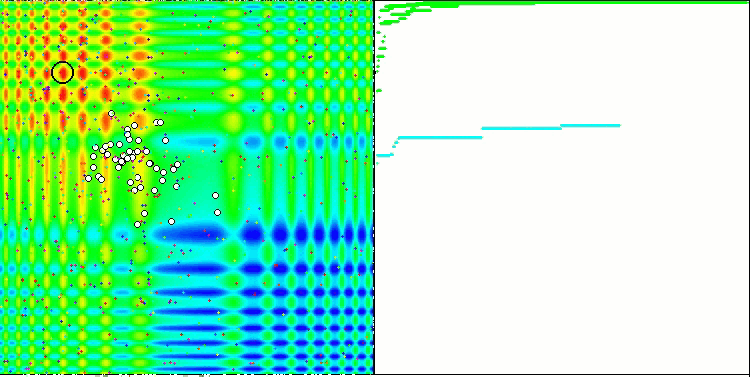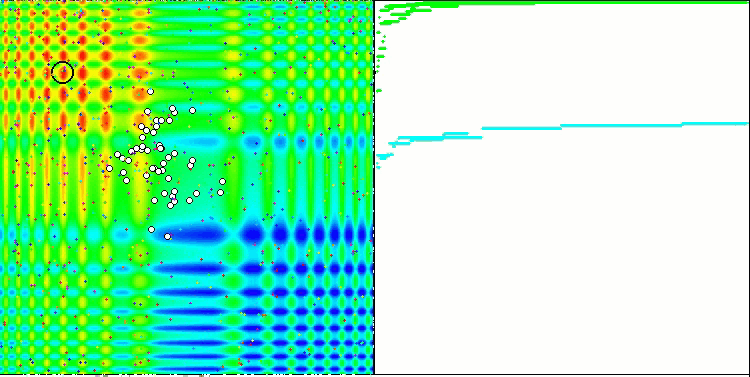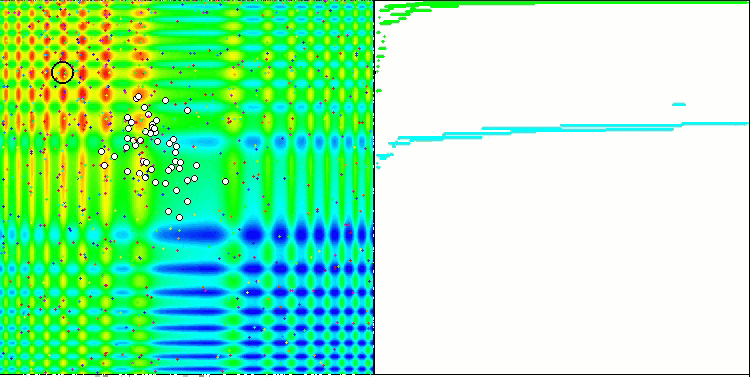
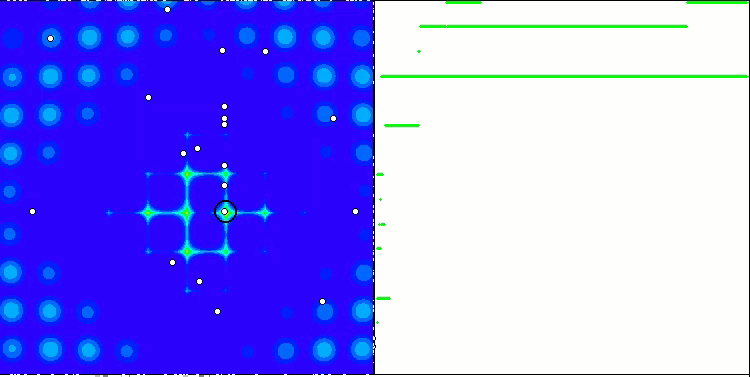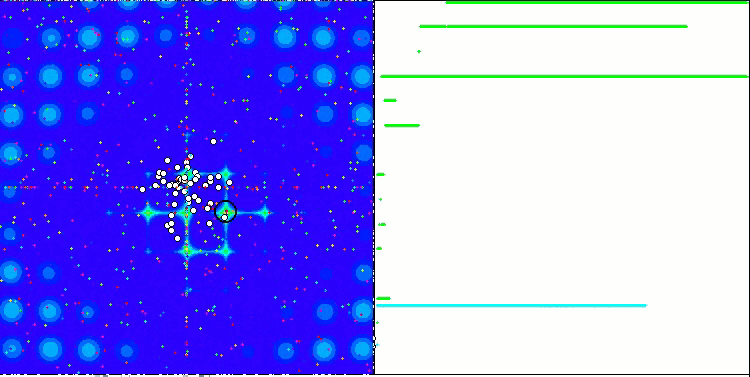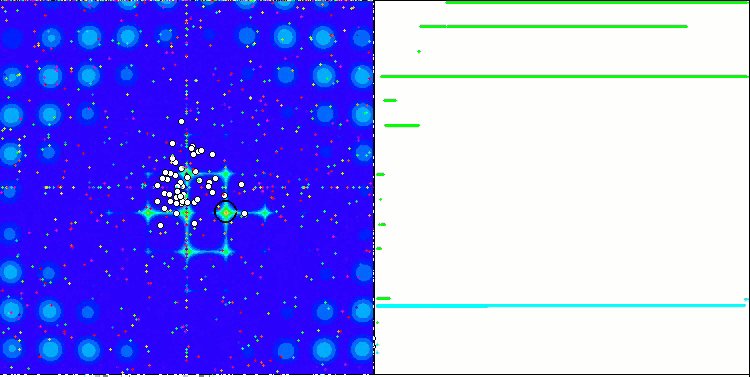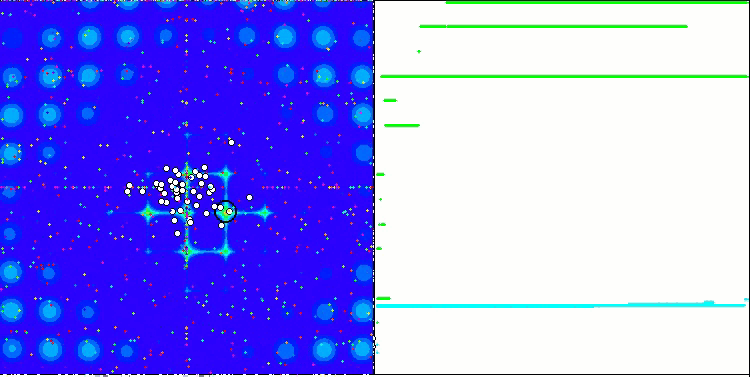
Yinelemeli bir algoritmanın, hedef fonksiyonun optimumuna ulaşma veya sonlu sayıda adımda ona yeterince yaklaşma özelliğidir. Dolayısıyla, yukarıdaki görüntülerde, sağ tarafta, hesaplanan test fonksiyonunun sonuçlarının yinelemeli olarak oluşturulmuş bir grafiğini görüyoruz. Bu iki görüntüye dayanarak, yakınsamanın fonksiyon yüzeyinin karmaşıklığından etkilendiği sonucuna varabiliriz. Ne kadar karmaşık olursa, global ekstremumu bulmak da o kadar zor olur.

Algoritmaların yakınsama oranı, bir optimizasyon algoritmasının kalitesinin en önemli göstergelerinden biridir ve optimizasyon yöntemlerinin temel özelliklerindendir. Bir algoritmanın diğerinden daha hızlı olduğunu duyduğumuzda, çoğu durumda bu yakınsama oranı anlamına gelir. Sonuç global ekstremuma ne kadar yakınsa ve ne kadar hızlı elde edilirse (yani algoritmanın daha erken yinelemelerinde elde edilirse), bu parametre o kadar yüksek olur. Yöntemlerin yakınsama oranının genellikle karesel olanı aşmadığını unutmayın. Nadir durumlarda, yöntem kübik bir yakınsama oranına sahip olabilir.

3.2) Yakınsama kararlılığı

Sonuca ulaşmak için gereken yineleme sayısı sadece algoritmanın arama yeteneğine değil, aynı zamanda üzerinde çalışılan fonksiyona da bağlıdır. Fonksiyon yüzeyi yüksek karmaşıklığa (keskin kıvrımların, ayrıklıkların, süreksizliklerin varlığı) sahipse, algoritma kararsız hale gelebilir ve kabul edilebilir düzeyde bir doğruluk sağlayamayabilir. Buna ek olarak, yakınsamanın kararlılığı, birkaç ardışık test gerçekleştirildiğinde optimizasyon sonuçlarının tekrarlanabilirliği olarak anlaşılabilir. Sonuçlarda yüksek farklılıklar varsa, algoritmanın kararlılığı düşüktür.

3.3) Optimizasyon algoritması ölçeklenebilirliği

Optimizasyon algoritması ölçeklenebilirliği, problemin boyutunda artış olması durumunda da yakınsamayı sürdürme yeteneğidir. Başka bir deyişle, optimize edilen fonksiyonun değişken sayısında artış olmasıyla beraber, yakınsama pratik amaçlar için kabul edilebilir bir seviyede kalmalıdır. Arama optimizasyonunun popülasyon algoritmaları, özellikle yüksek boyutlu ve kötü biçimlendirilmiş problemleri çözerken, klasik algoritmalara kıyasla yadsınamaz avantajlara sahiptir. Bu koşullar altında, popülasyon algoritmaları, optimize edilen fonksiyonun global ekstremumunun lokalize edilmesi için yüksek bir olasılık sağlayabilir.

Düzgün ve tek tepeli optimize edilen bir fonksiyon durumunda, popülasyon algoritmaları genellikle herhangi bir klasik gradyan yönteminden daha az verimlidir. Ayrıca, popülasyon algoritmalarının dezavantajlarından biri de, verimliliklerinin, çoğu algoritmada oldukça yüksek olan serbestlik derecelerine (ayar parametrelerinin sayısı) güçlü bir şekilde bağlı olmasıdır.

 

4. Test fonksiyonları, karmaşık bir optimizasyon algoritması değerlendirme kriterinin oluşturulması

Optimizasyon algoritmalarını test etmek ve karşılaştırmak için genel kabul görmüş bir metodoloji yoktur. Bununla birlikte, farklı yıllarda araştırmacılar tarafından önerilen birçok test fonksiyonu bulunmaktadır. İlk makaleyi yayınlamadan önce oluşturduğum fonksiyonları kullanacağız. Bu fonksiyonlar, MQL5\Experts\Examples\Math 3D\Functions.mqh ve \MQL5\Experts\Examples\Math 3D Morpher\Functions.mqh terminal klasöründen bulunabilir. Bu fonksiyonlar, optimizasyon algoritması testi için tüm karmaşıklık kriterlerini karşılamaktadır. Ayrıca, optimizasyon algoritmasının arama yeteneklerinin daha kapsamlı bir şekilde keşfedilmesini sağlamak için Forest ve Megacity fonksiyonları geliştirilmiştir.

Skin test fonksiyonu:

Fonksiyon, tanım kümesi boyunca düzgündür ve önemsiz derecede farklılık gösteren birçok yerel maksimum/minimum değere (yakınsama tuzakları) sahiptir, bu da global ekstremuma ulaşmayan algoritmaların takılıp kalmasına neden olur.

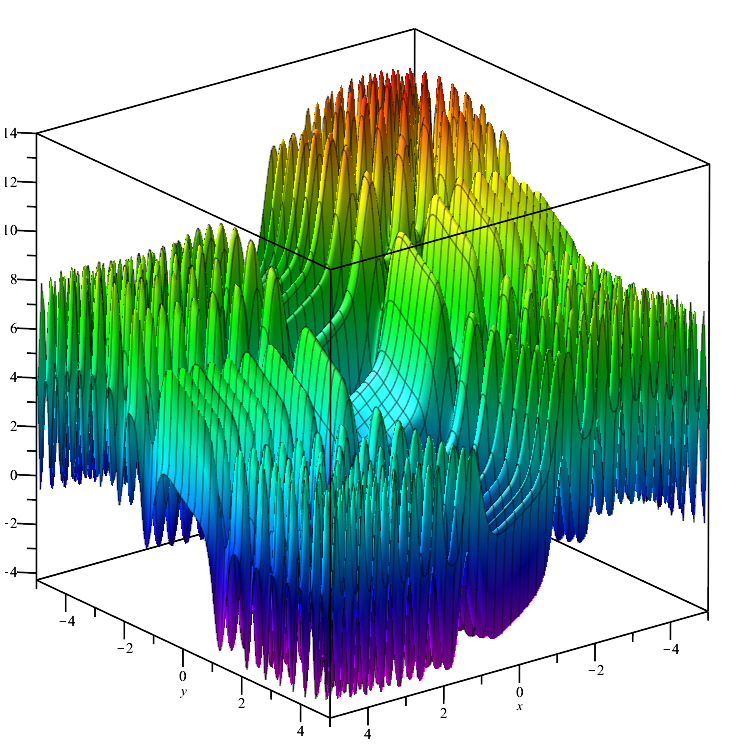
Skin

Forest test fonksiyonu:

Fonksiyon, noktalarında farklılık göstermeyen birkaç maksimuma sahiptir. Bu nedenle, sağlamlığı kritik ölçüde üzerinde çalışılan fonksiyonun düzgünlüğüne bağlı olan optimizasyon algoritmaları için zor olabilir.

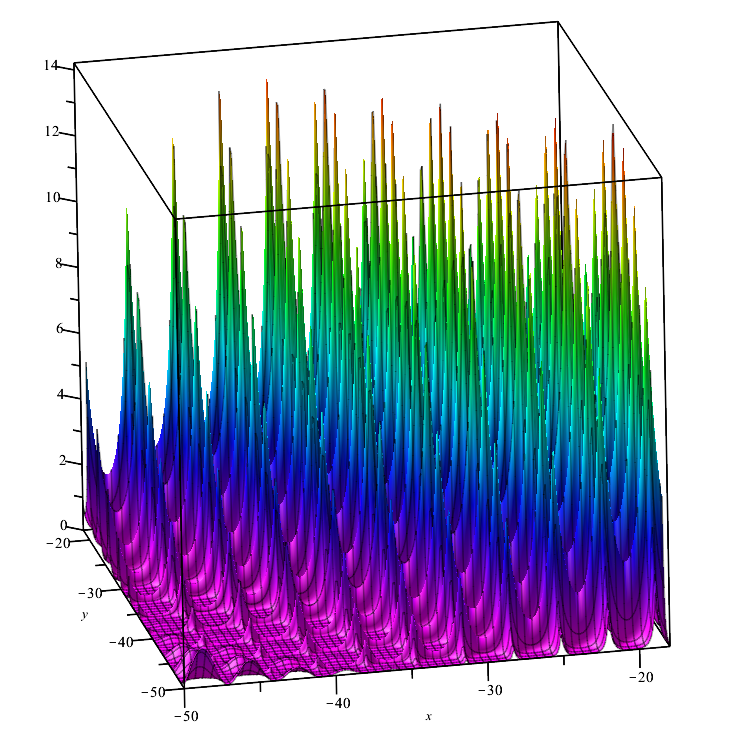
Forest

Megacity test fonksiyonu:

"Alanlar" (bu yerlerde değişkenlerin değiştirilmesi, fonksiyonun değerinde önemli bir değişikliğe yol açmamaktadır) oluşturan ayrık bir fonksiyondur. Bu nedenle gradyan gerektiren algoritmalar için bir zorluk teşkil etmektedir.

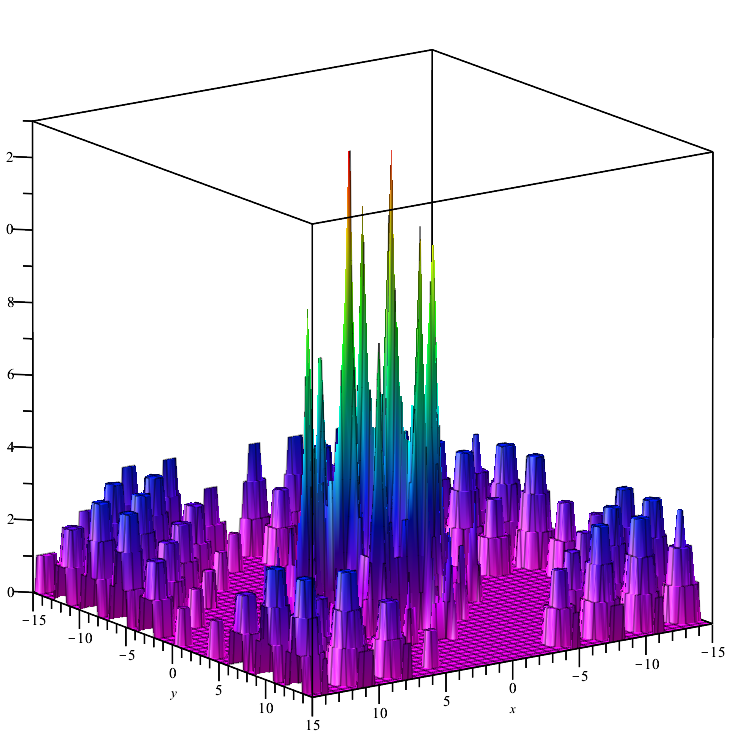
Megacity

5. Test ortamı

Optimizasyon algoritmalarının kapsamlı bir şekilde karşılaştırılması için genel bir değerlendirme kriteri oluşturulmaya çalışılmıştır. Bu fikrin karmaşıklığı, algoritmaların nasıl karşılaştırılacağının net olmaması gerçeğinde yatmaktadır, çünkü onların her biri ilgili problem sınıfı için kendi yolunda iyidir. Örneğin, bir algoritma hızlı bir şekilde yakınsar ancak iyi ölçeklenmezken, bir diğeri iyi ölçeklenir ancak kararsızdır. 

•  Yakınsama: Yakınsamayı incelemek için yukarıda sunulan üç fonksiyonu kullanıyoruz. Maksimum ve minimumu 0.0 (en kötü sonuç) ila 1.0 (en iyi sonuç) aralığına dönüştürüyoruz; bu da algoritmaların farklı türdeki problemlerde yakınsamayı sağlama yeteneğini değerlendirmemize olanak sağlar.
• Yakınsama oranı: Algoritmanın en iyi sonuçları, test edilen fonksiyonun 1000'inci ve 10,000'inci çalıştırmasında ölçülmektedir. Böylece optimizasyon algoritmasının ne kadar hızlı yakınsadığını görebiliriz. Yakınsama ne kadar hızlı olursa, yakınsama grafiği maksimuma doğru o kadar kavisli olacaktır.
•   Kararlılık: Her bir fonksiyon için beş optimizasyon çalıştırması gerçekleştiriyoruz ve 0,0 ila 1,0 aralığındaki ortalama değeri hesaplıyoruz. Bu gereklidir çünkü bazı algoritmaların sonuçları çalıştırmadan çalıştırmaya büyük farklılıklar gösterebilir. Beş testin her birinde yakınsama ne kadar yüksekse, kararlılık da o kadar yüksektir.
•   Ölçeklenebilirlik: Bazı optimizasyon algoritmaları yalnızca az sayıda değişkene sahip olan (örneğin ikiden fazla olmayan) fonksiyonlar üzerinde pratik sonuçlar gösterebilir; bazıları birden fazla değişkenle bile çalışamaz. Buna ek olarak, bin değişkenli fonksiyonlarla çalışabilen algoritmalar da vardır. Bu tür optimizasyon algoritmaları sinir ağları için optimizasyon algoritması olarak kullanılabilir.  

Test fonksiyonlarını kullanırken kolaylık sağlamak için, gelecekte ilgili test fonksiyonunun alt sınıfından bir nesne seçmemize olanak tanıyacak bir üst sınıf ve bir numaralandırıcı yazalım:

//——————————————————————————————————————————————————————————————————————————————
class C_Function
{
  public: //====================================================================
  double CalcFunc (double &args [], //function arguments
                   int     amount)  //amount of runs functions
  {
    double x, y;
    double sum = 0.0;
    for (int i = 0; i < amount; i++)
    {
      x = args [i * 2];
      y = args [i * 2 + 1];

      sum += Core (x, y);
    }

    sum /= amount;

    return sum;
  }
  double GetMinArg () { return minArg;}
  double GetMaxArg () { return maxArg;}
  double GetMinFun () { return minFun;}
  double GetMaxFun () { return maxFun;}
  string GetNamFun () { return fuName;}

  protected: //==================================================================
  void SetMinArg (double min) { minArg = min;}
  void SetMaxArg (double max) { maxArg = max;}
  void SetMinFun (double min) { minFun = min;}
  void SetMaxFun (double max) { maxFun = max;}
  void SetNamFun (string nam) { fuName = nam;}

  private: //====================================================================
  virtual double Core (double x, double y) { return 0.0;}
  
  double minArg;
  double maxArg;
  double minFun;
  double maxFun;
  string fuName;
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
enum EFunc
{
  Skin,
  Forest,
  Megacity,
  
};
C_Function *SelectFunction (EFunc f)
{
  C_Function *func;
  switch (f)
  {
    case  Skin:
      func = new C_Skin (); return (GetPointer (func));
    case  Forest:
      func = new C_Forest (); return (GetPointer (func));
    case  Megacity:
      func = new C_Megacity (); return (GetPointer (func));
    
    default:
      func = new C_Skin (); return (GetPointer (func));
  }
}
//——————————————————————————————————————————————————————————————————————————————

         

Alt sınıflar şu şekilde görünecektir:

//——————————————————————————————————————————————————————————————————————————————
class C_Skin : public C_Function
{
  public: //===================================================================
  C_Skin ()
  {
    SetNamFun ("Skin");
    SetMinArg (-5.0);
    SetMaxArg (5.0);
    SetMinFun (-4.3182);  //[x=3.07021;y=3.315935] 1 point
    SetMaxFun (14.0606);  //[x=-3.315699;y=-3.072485] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a1=2*x*x;
    double a2=2*y*y;
    double b1=MathCos(a1)-1.1;
    b1=b1*b1;
    double c1=MathSin(0.5*x)-1.2;
    c1=c1*c1;
    double d1=MathCos(a2)-1.1;
    d1=d1*d1;
    double e1=MathSin(0.5*y)-1.2;
    e1=e1*e1;

   double res=b1+c1-d1+e1;
   return(res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Forest : public C_Function
{
  public: //===================================================================
  C_Forest ()
  {
    SetNamFun ("Forest");
    SetMinArg (-50.0);
    SetMaxArg (-18.0);
    SetMinFun (0.0);             //many points
    SetMaxFun (15.95123239744);  //[x=-25.132741228718345;y=-32.55751918948773] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = MathPow (f, 4);
    if (res < 0.0) res = 0.0;
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Megacity : public C_Function
{
  public: //===================================================================
  C_Megacity ()
  {
    SetNamFun ("Megacity");
    SetMinArg (-15.0);
    SetMaxArg (15.0);
    SetMinFun (0.0);   //many points
    SetMaxFun (15.0);  //[x=`3.16;y=1.990] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = floor (MathPow (f, 4));
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

Test ortamında elde edilen optimizasyon algoritması testi sonuçlarının geçerliliğini kontrol etmek için, Skin adım büyüklüğüyle X ve Y fonksiyonlarını numaralandıran bir komut dosyası kullanabiliriz. Adımı seçerken dikkatli olun çünkü çok küçük bir adım büyüklüğü hesaplamanın çok uzun sürmesine neden olacaktır. Örneğin, Skin fonksiyonu [-5;5] argüman aralığına sahiptir. X ekseni boyunca 0.00001'lik adımla, (5-(-5))/0.00001=1'000'000 (1 milyon) adım olacaktır. Y ekseni boyunca aynı sayı olacaktır. Böylece, her bir noktadaki değeri hesaplamak için test fonksiyonunun toplam çalıştırma sayısı 1'000'000 х 1'000'000 = 1'000'000'000'000 (10^12, 1 trilyon) olacaktır.

Sadece 10,000 adımda (MetaTrader 5 optimize edicide yaklaşık olarak bu değer kullanılır) maksimumu bulmak gerektiğinden optimizasyon algoritmasının görevinin ne kadar zor olduğu buradan anlaşılmaktadır. Lütfen bu hesaplamanın iki değişkenli bir fonksiyon için yapıldığını ve testlerde kullanılacak maksimum değişken sayısının 1000 olduğunu unutmayın.

Şunu aklınızda bulundurun: Bu ve sonraki makalelerdeki algoritma testlerinde 0.0! adımı veya ilgili optimizasyon algoritmasının belirli bir uygulaması için mümkün olan en küçük adım kullanılmaktadır.

//——————————————————————————————————————————————————————————————————————————————
input EFunc  Function          = Skin;
input double Step              = 0.01;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_Function *TestFunc = SelectFunction (Function);

  double argMin = TestFunc.GetMinArg ();
  double argMax = TestFunc.GetMaxArg ();

  double maxFuncValue = 0;
  double xMaxFunc     = 0.0;
  double yMaxFunc     = 0.0;
  
  double minFuncValue = 0;
  double xMinFunc     = 0.0;
  double yMinFunc     = 0.0;
  
  double fValue       = 0.0;

  double arg [2];

  arg [0] = argMin;
  arg [1] = argMin;

  long cnt = 0;

  while (arg [1] <= argMax && !IsStopped ())
  {
    arg [0] = argMin;

    while (arg [0] <= argMax && !IsStopped ())
    {
      cnt++;

      fValue = TestFunc.CalcFunc (arg, 1);

      if (fValue > maxFuncValue)
      {
        maxFuncValue = fValue;
        xMaxFunc = arg [0];
        yMaxFunc = arg [1];
      }
      if (fValue < minFuncValue)
      {
        minFuncValue = fValue;
        xMinFunc = arg [0];
        yMinFunc = arg [1];
      }

      arg [0] += Step;
      
      if (cnt == 1)
      {
       maxFuncValue = fValue;
       minFuncValue = fValue;
      }
    }

    arg [1] += Step;
  }
  
  Print ("======", TestFunc.GetNamFun (), ", launch counter: ", cnt);
  Print ("MaxFuncValue: ", DoubleToString (maxFuncValue, 16), " X: ", DoubleToString (xMaxFunc, 16), " Y: ", DoubleToString (yMaxFunc, 16));
  Print ("MinFuncValue: ", DoubleToString (minFuncValue, 16), " X: ", DoubleToString (xMinFunc, 16), " Y: ", DoubleToString (yMinFunc, 16));
         
  delete TestFunc;
}

//——————————————————————————————————————————————————————————————————————————————

Bir test ortamı yazalım:

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>
#include "AO_RND.mqh"

//——————————————————————————————————————————————————————————————————————————————
input int    Population_P       = 50;
input double ArgumentStep_P     = 0.0;
input int    Test1FuncRuns_P    = 1;
input int    Test2FuncRuns_P    = 20;
input int    Test3FuncRuns_P    = 500;
input int    Measur1FuncValue_P = 1000;
input int    Measur2FuncValue_P = 10000;
input int    NumberRepetTest_P  = 5;
input int    RenderSleepMsc_P   = 0;

//——————————————————————————————————————————————————————————————————————————————
int WidthMonitor = 750;  //monitor screen width
int HeighMonitor = 375;  //monitor screen height

int WidthScrFunc = 375 - 2;  //test function screen width
int HeighScrFunc = 375 - 2;  //test function screen height

CCanvas Canvas;  //drawing table
C_AO_RND AO;     //AO object

C_Skin       SkiF;
C_Forest     ForF;
C_Megacity  ChiF;

struct S_CLR
{
    color clr [];
};

S_CLR FunctScrin []; //two-dimensional matrix of colors
double ScoreAll = 0.0;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  //creating a table -----------------------------------------------------------
  string canvasName = "AO_Test_Func_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, WidthMonitor, HeighMonitor, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }
  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  ArrayResize (FunctScrin, HeighScrFunc);
  for (int i = 0; i < HeighScrFunc; i++)
  {
    ArrayResize (FunctScrin [i].clr, HeighScrFunc);
  }
  
  //============================================================================
  //Test Skin###################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (SkiF, Test1FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrLime);
  FuncTests (SkiF, Test2FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrAqua);
  FuncTests (SkiF, Test3FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrOrangeRed);
  
  //Test Forest#################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ForF, Test1FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrLime);
  FuncTests (ForF, Test2FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrAqua);
  FuncTests (ForF, Test3FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrOrangeRed);
  
  //Test Megacity#############################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ChiF, Test1FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrLime);
  FuncTests (ChiF, Test2FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrAqua);
  FuncTests (ChiF, Test3FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrOrangeRed);
  
  Print ("All score for C_AO_RND: ", ScoreAll / 18.0);
}
//——————————————————————————————————————————————————————————————————————————————

void CanvasErase ()
{
  Canvas.Erase (XRGB (0, 0, 0));
  Canvas.FillRectangle (1,                1, HeighMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
  Canvas.FillRectangle (HeighMonitor + 1, 1, WidthMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
}

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_Function &f,
                int        funcCount,
                double     minFuncVal,
                double     maxFuncVal,
                double     xBest,
                double     yBest,
                color      clrConv)
{
  DrawFunctionGraph (f.GetMinArg (), f.GetMaxArg (), minFuncVal, maxFuncVal, f);
  SendGraphToCanvas (1, 1);
  int x = (int)Scale (xBest, f.GetMinArg (), f.GetMaxArg (), 0, WidthScrFunc - 1, false);
  int y = (int)Scale (yBest, f.GetMinArg (), f.GetMaxArg (), 0, HeighScrFunc - 1, false);
  Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
  Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));
  Canvas.Update ();
  Sleep (1000);

  int xConv = 0.0;
  int yConv = 0.0;

  int EpochCmidl = 0;
  int EpochCount = 0;

  double aveMid = 0.0;
  double aveEnd = 0.0;

  //----------------------------------------------------------------------------
  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    InitAO (funcCount * 2, f.GetMaxArg (), f.GetMinArg (), ArgumentStep_P);

    EpochCmidl = Measur1FuncValue_P / (ArraySize (AO.S_Colony));
    EpochCount = Measur2FuncValue_P / (ArraySize (AO.S_Colony));

    // Optimization-------------------------------------------------------------
    AO.F_EpochReset ();


    for (int epochCNT = 1; epochCNT <= EpochCount && !IsStopped (); epochCNT++)
    {
      AO.F_Preparation ();

      for (int set = 0; set < ArraySize (AO.S_Colony); set++)
      {
        AO.A_FFcol [set] = f.CalcFunc (AO.S_Colony [set].args, funcCount);
      }

      AO.F_Sorting ();

      if (epochCNT == EpochCmidl) aveMid += AO.A_FFpop [0];

      SendGraphToCanvas  (1, 1);

      //draw a population on canvas
      for (int i = 0; i < ArraySize (AO.S_Population); i++)
      {
        if (i > 0) PointDr (AO.S_Population [i].args, f.GetMinArg (), f.GetMaxArg (), clrWhite, 1, 1, funcCount);
      }
      PointDr (AO.S_Population [0].args, f.GetMinArg (), f.GetMaxArg (), clrBlack, 1, 1, funcCount);

      Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
      Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));

      xConv = (int)Scale (epochCNT,       1,          EpochCount, 2, WidthScrFunc - 2, false);
      yConv = (int)Scale (AO.A_FFpop [0], minFuncVal, maxFuncVal, 1, HeighScrFunc - 2, true);

      Canvas.FillCircle (xConv + HeighMonitor + 1, yConv + 1, 1, COLOR2RGB (clrConv));

      Canvas.Update ();
      Sleep (RenderSleepMsc_P);
    }

    aveEnd += AO.A_FFpop [0];

    Sleep (1000);
  }

  aveMid /= (double)NumberRepetTest_P;
  aveEnd /= (double)NumberRepetTest_P;

  double score1 = Scale (aveMid, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  double score2 = Scale (aveEnd, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  
  ScoreAll += score1 + score2;

  Print (funcCount, " ", f.GetNamFun (), "'s; Func runs ", Measur1FuncValue_P, " result: ", aveMid, "; Func runs ", Measur2FuncValue_P, " result: ", aveEnd);
  Print ("Score1: ", DoubleToString (score1, 5), "; Score2: ", DoubleToString (score2, 5));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void InitAO (const int    params,  //amount of the optimized arguments
             const double max,     //maximum of the optimized argument
             const double min,     //minimum of the optimized argument
             const double step)    //step of the optimized argument
{
  AO.F_Init (params, Population_P);
  for (int idx = 0; idx < params; idx++)
  {
    AO.A_RangeMax  [idx] = max;
    AO.A_RangeMin  [idx] = min;
    AO.A_RangeStep [idx] = step;
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void PointDr (double &args [], double Min, double Max, color clr, int shiftX, int shiftY, int count)
{
  double x = 0.0;
  double y = 0.0;
  
  double xAve = 0.0;
  double yAve = 0.0;
  
  int width  = 0;
  int height = 0;
  
  color clrF = clrNONE;
  
  for (int i = 0; i < count; i++)
  {
    xAve += args [i * 2];
    yAve += args [i * 2 + 1];
       
    x = args [i * 2];
    y = args [i * 2 + 1];
    
    width  = (int)Scale (x, Min, Max, 0, WidthScrFunc - 1, false);
    height = (int)Scale (y, Min, Max, 0, HeighScrFunc - 1, false);
    
    clrF = DoubleToColor (i, 0, count - 1, 0, 360);
    Canvas.FillCircle (width + shiftX, height + shiftY, 1, COLOR2RGB (clrF));
  }
  
  xAve /= (double)count;
  yAve /= (double)count;

  width  = (int)Scale (xAve, Min, Max, 0, WidthScrFunc - 1, false);
  height = (int)Scale (yAve, Min, Max, 0, HeighScrFunc - 1, false);

  Canvas.FillCircle (width + shiftX, height + shiftY, 3, COLOR2RGB (clrBlack));
  Canvas.FillCircle (width + shiftX, height + shiftY, 2, COLOR2RGB (clr));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void SendGraphToCanvas (int shiftX, int shiftY)
{
  for (int w = 0; w < HeighScrFunc; w++)
  {
    for (int h = 0; h < HeighScrFunc; h++)
    {
      Canvas.PixelSet (w + shiftX, h + shiftY, COLOR2RGB (FunctScrin [w].clr [h]));
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void DrawFunctionGraph (double     min,
                        double     max,
                        double     fMin,
                        double     fMax,
                        C_Function &f)
{
  double ar [2];
  double fV;

  for (int w = 0; w < HeighScrFunc; w++)
  {
    ar [0] = Scale (w, 0, HeighScrFunc, min, max, false);
    for (int h = 0; h < HeighScrFunc; h++)
    {
      ar [1] = Scale (h, 0, HeighScrFunc, min, max, false);
      fV = f.CalcFunc (ar, 1);
      FunctScrin [w].clr [h] = DoubleToColor (fV, fMin, fMax, 0, 250);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Scaling a number from a range to a specified range
double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
  else
  {
    if (Revers)
    {
      if (In < InMIN) return (OutMAX);
      if (In > InMAX) return (OutMIN);
      return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
    else
    {
      if (In < InMIN) return (OutMIN);
      if (In > InMAX) return (OutMAX);
      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color DoubleToColor (const double in,    //input value
                     const double inMin, //minimum of input values
                     const double inMax, //maximum of input values
                     const int    loH,   //lower bound of HSL range values
                     const int    upH)   //upper bound of HSL range values
{
  int h = (int)Scale (in, inMin, inMax, loH, upH, true);
  return HSLtoRGB (h, 1.0, 0.5);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color HSLtoRGB (const int    h, //0   ... 360
                const double s, //0.0 ... 1.0
                const double l) //0.0 ... 1.0
{
  int r;
  int g;
  int b;
  if (s == 0.0)
  {
    r = g = b = (unsigned char)(l * 255);
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
  else
  {
    double v1, v2;
    double hue = (double)h / 360.0;
    v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
    v1 = 2.0 * l - v2;
    r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
    g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
    b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
}
//——————————————————————————————————————————————————————————————————————————————
//——————————————————————————————————————————————————————————————————————————————
double HueToRGB (double v1, double v2, double vH)
{
  if (vH < 0) vH += 1;
  if (vH > 1) vH -= 1;
  if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
  if ((2 * vH) < 1) return v2;
  if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
  return v1;
}
//——————————————————————————————————————————————————————————————————————————————

double türündeki bir sayıyı bir aralıktan bir renge dönüştürmek için HSL'i RGB'ye dönüştürme algoritması kullanılmıştır (MetaTrader 5'in renk sistemi).

Test ortamı grafik üzerinde bir görüntü gösterir. İkiye bölünmüştür.

• Sol tarafta test fonksiyonu görüntülenir. Üç boyutlu grafiği bir düzleme yansıtılır; burada kırmızı maksimum, mavi ise minimum anlamına gelir. Popülasyondaki noktaların konumu görüntülenir (renk, değişken sayısı 40 ve 1000 olan test fonksiyonunun sıra sayısına karşılık gelir, iki değişkenli bir fonksiyon için renklendirme yapılmaz), koordinatlarının ortalaması alınan noktalar beyaz renkle işaretlenir ve en iyisi de siyah renkle işaretlenir. 
• Sağ tarafta yakınsama grafiği görüntülenir. 2 değişkenli testler yeşil, 40 değişkenli testler mavi, 1000 değişkenli testler ise kırmızı renkle işaretlenir. Testlerin her biri beş kez gerçekleştirilir (her rengin 5 yakınsama grafiği). Burada, değişken sayısının artmasıyla optimizasyon algoritmasının yakınsamasının ne kadar kötüleştiğini gözlemleyebiliriz.

6. RNG kullanan basit bir optimizasyon algoritması örneği

Test örneği için en basit arama stratejisini uygulayalım. Pratik bir değeri yoktur, ancak gelecekte optimizasyon algoritmalarını karşılaştırmak için bir tür standart olacaktır. Strateji, 50/50 rastgele seçimle yeni bir fonksiyon değişkenleri kümesi oluşturur: popülasyondan rastgele seçilen bir üst kümeden değişken kopyalanır ya da min/maks aralığından bir değişken oluşturur. Test fonksiyonlarının değerleri alındıktan sonra, ortaya çıkan yeni değişkenler kümesi popülasyonun ikinci yarısına kopyalanır ve sıralanır. Böylece, yeni kümeler sürekli olarak popülasyonun yarısının yerini alır ve en iyi kümeler de diğer tarafta yoğunlaşır.

Aşağıda RNG'ye dayalı bir optimizasyon algoritması kodu bulunmaktadır:

//+————————————————————————————————————————————————————————————————————————————+
class C_AO_RND
{
  public: //||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

  struct ArrColony
  {
      double args [];
  };

  //----------------------------------------------------------------------------
  double    A_RangeStep []; //Step ranges of genes
  double    A_RangeMin  []; //Min ranges of genes
  double    A_RangeMax  []; //Max ranges of genes

  ArrColony S_Population []; //Population
  ArrColony S_Colony     []; //Colony

  double    A_FFpop [];      //Values of fitness of individuals in population
  double    A_FFcol [];      //Values of fitness of individuals in colony

  //----------------------------------------------------------------------------
  // Initialization of algorithm
  void F_Init (int argCount,       //Number of arguments

               int populationSize) //Population size
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator

    p_argCount  = argCount;
    p_sizeOfPop = populationSize;
    p_sizeOfCol = populationSize / 2;

    p_dwelling  = false;

    f_arrayInitResize (A_RangeStep, argCount, 0.0);
    f_arrayInitResize (A_RangeMin,  argCount, 0.0);
    f_arrayInitResize (A_RangeMax,  argCount, 0.0);

    ArrayResize (S_Population, p_sizeOfPop);
    ArrayResize (s_populTemp, p_sizeOfPop);
    for (int i = 0; i < p_sizeOfPop; i++)
    {
      f_arrayInitResize (S_Population [i].args, argCount, 0.0);
      f_arrayInitResize (s_populTemp [i].args, argCount, 0.0);
    }

    ArrayResize (S_Colony, p_sizeOfCol);
    for (int i = 0; i < p_sizeOfCol; i++)
    {
      f_arrayInitResize (S_Colony [i].args, argCount, 0.0);
    }

    f_arrayInitResize (A_FFpop, p_sizeOfPop, -DBL_MAX);
    f_arrayInitResize (A_FFcol, p_sizeOfCol, -DBL_MAX);

    f_arrayInitResize (a_indexes, p_sizeOfPop, 0);
    f_arrayInitResize (a_valueOnIndexes, p_sizeOfPop, 0.0);
  }

  //----------------------------------------------------------------------------
  void F_EpochReset ()   //Reset of epoch, allows to begin evolution again without initial initialization of variables
  {
    p_dwelling = false;
    ArrayInitialize (A_FFpop, -DBL_MAX);
    ArrayInitialize (A_FFcol, -DBL_MAX);
  }
  //----------------------------------------------------------------------------
  void F_Preparation ();  //Preparation
  //----------------------------------------------------------------------------
  void F_Sorting ();      //The settling of a colony in population and the subsequent sorting of population

  private: //|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  //----------------------------------------------------------------------------
  void F_PopulSorting ();

  //----------------------------------------------------------------------------
  ArrColony          s_populTemp      []; //Temporal population
  int                a_indexes        []; //Indexes of chromosomes
  double             a_valueOnIndexes []; //VFF of the appropriate indexes of chromosomes

  //----------------------------------------------------------------------------
  template <typename T1>
  void f_arrayInitResize (T1 &arr [], const int size, const T1 value)
  {
    ArrayResize     (arr, size);
    ArrayInitialize (arr, value);
  }

  //----------------------------------------------------------------------------
  double f_seInDiSp         (double In, double InMin, double InMax, double step);
  double f_RNDfromCI        (double min, double max);
  double f_scale            (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);

  //---Constants----------------------------------------------------------------
  int  p_argCount;   //Quantity of arguments in a set of arguments
  int  p_sizeOfCol;  //Quantity of set in a colony
  int  p_sizeOfPop;  //Quantity of set in population
  bool p_dwelling;   //Flag of the first settling of a colony in population
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Preparation ()
{
  //if starts of algorithm weren't yet - generate a colony with random arguments
  if (!p_dwelling)
  {
    for (int person = 0; person < p_sizeOfCol; person++)
    {
      for (int arg = 0; arg < p_argCount; arg++)
      {
        S_Colony [person].args [arg] = f_seInDiSp (f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]),
                                                    A_RangeMin  [arg],
                                                    A_RangeMax  [arg],
                                                    A_RangeStep [arg]);
      }
    }

    p_dwelling = true;
  }
  //generation of a colony using with copying arguments from parent sets--------
  else
  {
    int parentAdress = 0;
    double rnd       = 0.0;
    double argVal    = 0.0;

    for (int setArg = 0; setArg < p_sizeOfCol; setArg++)
    {
      //get a random address of the parent set
      parentAdress = (int)f_RNDfromCI (0, p_sizeOfPop - 1);

      for (int arg = 0; arg < p_argCount; arg++)
      {
        if (A_RangeMin [arg] == A_RangeMax [arg]) continue;

        rnd = f_RNDfromCI (0.0, 1.0);

        if (rnd < 0.5)
        {
          S_Colony [setArg].args [arg] = S_Population [parentAdress].args [arg];
        }
        else
        {
          argVal = f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]);
          argVal = f_seInDiSp (argVal, A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]);

          S_Colony [setArg].args [arg] = argVal;
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Sorting ()
{
  for (int person = 0; person < p_sizeOfCol; person++)
  {
    ArrayCopy (S_Population [person + p_sizeOfCol].args, S_Colony [person].args, 0, 0, WHOLE_ARRAY);
  }
  ArrayCopy (A_FFpop, A_FFcol, p_sizeOfCol, 0, WHOLE_ARRAY);

  F_PopulSorting ();
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Ranging of population.
void C_AO_RND::F_PopulSorting ()
{
  //----------------------------------------------------------------------------
  int   cnt = 1, i = 0, u = 0;
  int   t0 = 0;
  double t1 = 0.0;
  //----------------------------------------------------------------------------

  // We will put indexes in the temporary array
  for (i = 0; i < p_sizeOfPop; i++)
  {
    a_indexes [i] = i;
    a_valueOnIndexes [i] = A_FFpop [i];
  }
  while (cnt > 0)
  {
    cnt = 0;
    for (i = 0; i < p_sizeOfPop - 1; i++)
    {
      if (a_valueOnIndexes [i] < a_valueOnIndexes [i + 1])
      {
        //-----------------------
        t0 = a_indexes [i + 1];
        t1 = a_valueOnIndexes [i + 1];
        a_indexes [i + 1] = a_indexes [i];
        a_valueOnIndexes [i + 1] = a_valueOnIndexes [i];
        a_indexes [i] = t0;
        a_valueOnIndexes [i] = t1;
        //-----------------------
        cnt++;
      }
    }
  }

  // On the received indexes create the sorted temporary population
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (s_populTemp [u].args, S_Population [a_indexes [u]].args, 0, 0, WHOLE_ARRAY);

  // Copy the sorted array back
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (S_Population [u].args, s_populTemp [u].args, 0, 0, WHOLE_ARRAY);

  ArrayCopy (A_FFpop, a_valueOnIndexes, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_RND::f_seInDiSp (double in, double inMin, double inMax, double step)
{
  if (in <= inMin) return (inMin);
  if (in >= inMax) return (inMax);
  if (step == 0.0) return (in);
  else return (inMin + step * (double)MathRound ((in - inMin) / step));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Random number generator in the custom interval.
double C_AO_RND::f_RNDfromCI (double min, double max)
{
  if (min == max) return (min);
  double Min, Max;
  if (min > max)
  {
    Min = max;
    Max = min;
  }
  else
  {
    Min = min;
    Max = max;
  }
  return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0)));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
double C_AO_RND::f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return (OutMIN);
    if (In > InMAX) return (OutMAX);
    return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
  }
}
//——————————————————————————————————————————————————————————————————————————————

7. Sonuçlar

Optimizasyon algoritması	Çalıştırma sayısı	Skin			Forest			Megacity (ayrık)			Nihai sonuç
		2 parametre (1 F)	40 parametre (20 F)	1000 parametre (500 F)	2 parametre (1 F)	40 parametre (20 F)	1000 parametre (500 F)	2 parametre (1 F)	40 parametre (20 F)	1000 parametre (500 F)
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
	10,000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283

Test ortamında yapılan testlerden sonra, RND optimizasyon algoritmasının sonuçlarının oldukça beklenmedik olduğu ortaya çıktı. Algoritma, iki değişkenli fonksiyonların optimumunu çok yüksek doğrulukla bulabilirken, Forest ve Megacity fonksiyonlarının sonuçları belirgin şekilde daha kötüdür. Bununla birlikte, öte yandan, çok değişkenli fonksiyonlar için zayıf arama özellikleri hakkındaki varsayımlarım doğrulandı. Sonuçlar şimdiden 40 argümanda çok vasattır. Nihai kümülatif değer 0.51254’tür.

Sonraki makalelerde, iyi bilinen ve yaygın olarak kullanılan optimizasyon algoritmalarını analiz edip test edeceğiz ve optimizasyon algoritması derecelendirmesini oluşturan sonuç tablosunu doldurmaya devam edeceğiz.