Reti neurali: dalla teoria alla pratica
648
0
Introduzione
Al giorno d'oggi, ogni trader deve aver sentito parlare delle reti neurali e sa quanto sia bello usarle. La maggioranza crede che coloro che possono occuparsi delle reti neurali siano una sorta di super umani. In questo articolo cercherò di spiegarti l'architettura della rete neurale, descriverne le applicazioni e mostrare esempi di utilizzo pratico.
Il concetto di reti neurali
Le reti neurali artificiali sono una delle aree della ricerca sull'intelligenza artificiale che si basa sui tentativi di simulare il sistema nervoso umano nella sua capacità di apprendimento e adattamento che dovrebbe consentirci di costruire una simulazione molto approssimativa del funzionamento del cervello umano.
Curiosamente, le reti neurali artificiali sono costituite da neuroni artificiali.
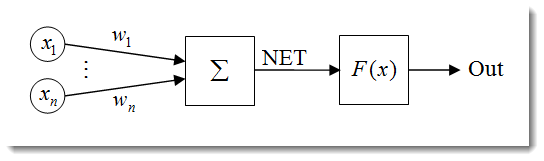
Fig.1. Il modello del neurone artificiale
La struttura di un neurone può essere rappresentata come una composizione delle seguenti unità:
- Input
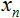; - Pesi
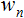; - Funzione di trasferimento
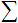e Ingresso netto
; - Funzione di attivazione
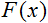; - Output
.
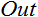Le reti neurali hanno molte proprietà e la capacità di apprendere è la più significativa. Il processo di apprendimento si riduce alla modifica dei pesi .
qui è l'input netto del neurone.
L'input netto viene poi trasformato in output dalla funzione di attivazione, di cui ci occuperemo in seguito. In poche parole, una rete neurale può essere vista come una "scatola nera" che riceve segnali come input ed emette il risultato.
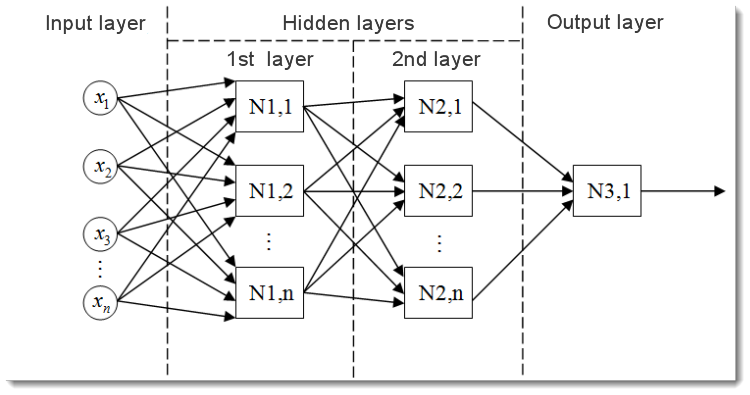
Fig.2. Il modello di una rete neurale multistrato
Ecco come appare una rete neurale multistrato. Comprende:
- Il livello di input, il quale serve a distribuire i dati attraverso la rete e non esegue alcun calcolo. Le uscite di questo livello trasmettono segnali agli ingressi del livello successivo (nascosto o in uscita);
- Il livello di output , il quale di solito contiene un neurone (o talvolta più di uno) che genera l'output dell'intera rete neurale. Questo segnale è alla base della futura logica di controllo dell'EA;
- Gli strati nascosti, strati di neuroni standard che trasmettono segnali dallo strato di input allo strato di output. Il suo input è l'output del livello precedente, mentre il suo output funge da input del livello successivo.
Questo esempio ha mostrato la rete neurale con due livelli nascosti. Ma potrebbero esserci reti neurali che hanno più livelli nascosti.
Normalizzazione dei dati di input
La normalizzazione dei dati di input è il processo mediante il quale tutti i dati di input vengono normalizzati, ovvero ridotti agli intervalli [0,1] o [-1,1]. Se la normalizzazione non viene eseguita, i dati di input avranno un effetto aggiuntivo sul neurone, portando a decisioni sbagliate. In altre parole, come confrontare valori che hanno ordini di grandezza diversi?
La formula di normalizzazione nella sua forma standard è la seguente:
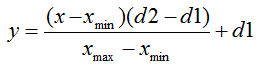
dove:
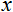: valore da normalizzare;- alt
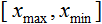altIntervallo di valore хtitle Intervallo di valore xtitle: intervallo di valore x; 
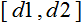: intervallo in cui verrà ridotto il valore di x.
Mi spiego usando un esempio:
Supponiamo di avere n dati di input dall'intervallo [0,10], quindi 
= 0 e 
= 10. Ridurremo i dati nell'intervallo [0,1], quindi 
= 0 e 
= 1. Ora, dopo aver inserito i valori nella formula, possiamo calcolare i valori normalizzati per qualsiasi x da n dati di input.
Ecco come appare quando implementato in MQL5:
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
Specifichiamo prima i limiti superiore e inferiore del valore di output e quindi otteniamo i valori minimo e massimo dell'indicatore (la copia dei dati dall'indicatore viene omessa ma possono esserci, ad esempio, gli ultimi 10 valori). Infine, normalizziamo ogni elemento di input (valori dell'indicatore su barre diverse) e memorizziamo i risultati in un array per un ulteriore utilizzo.
Funzioni di attivazione
La funzione di attivazione è una funzione che calcola l'output di un neurone. L'input che riceve rappresenta la somma di tutti i prodotti degli input e dei rispettivi pesi (di seguito "somma ponderata"):
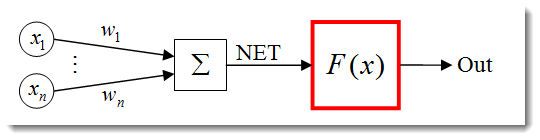
Fig.3. Il modello del neurone artificiale con la funzione di attivazione delineata
La formula della funzione di attivazione nella sua forma standard è la seguente:
dove:
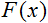- è la funzione di attivazione;
- è la somma pesata ottenuta nella prima fase di calcolo dell'output di un neurone;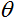
è un valore di soglia della funzione di attivazione. Viene utilizzato solo per la funzione di soglia rigida ed è uguale a zero in altre funzioni.
I principali tipi di funzioni di attivazione sono:
-
Il gradino dell'unità o la funzione di soglia rigida.
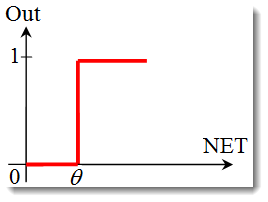
La funzione è descritta dalla seguente formula:
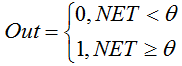
Se la somma ponderata è inferiore al valore specificato, la funzione di attivazione restituisce zero. Se la somma ponderata diventa maggiore, la funzione di attivazione restituisce uno. -
La funzione sigmoidea.
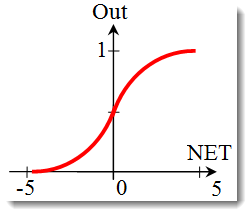
La formula che descrive la funzione sigmoidea è la seguente:
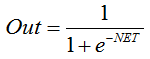
Viene spesso utilizzato nelle reti neurali multistrato e in altre reti con segnali continui. La scorrevolezza e la continuità della funzione sono proprietà molto positive. -
La tangente iperbolica.
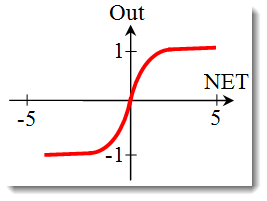
Formula:
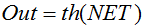o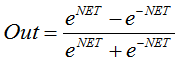 
Viene spesso utilizzato anche in reti con segnali continui. È peculiare in quanto può restituire valori negativi.
Modifica della forma della funzione di attivazione
Nella sezione precedente ci siamo occupati dei tipi di funzioni di attivazione. Tuttavia, c'è un'altra cosa importante da considerare: la pendenza di una funzione (ad eccezione della funzione di soglia rigida). Diamo un'occhiata più da vicino alla funzione sigmoidea.
Guardando il grafico della funzione, si può facilmente vedere che la funzione è liscia nell'intervallo [-5,5]. Supponiamo di avere una rete costituita da un singolo neurone con 10 ingressi e un'uscita. Proviamo ora a calcolare i valori superiore e inferiore della variabile . Ogni ingresso assumerà un valore normalizzato (come già menzionato nella Normalizzazione dei dati di ingresso), ad esempio dall'intervallo [-1,1].
Useremo i valori di input negativi poiché la funzione è differenziabile anche con un argomento negativo. Anche i pesi saranno selezionati dalla stessa gamma. Con tutte le possibili combinazioni di input e pesi, otterremo i valori estremi nell'intervallo [-10,10] come:
In MQL5, la formula apparirà come segue:
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
Ora dobbiamo tracciare la funzione di attivazione nell'intervallo identificato. Prendiamo come esempio la funzione sigmoidea. Il modo più semplice per farlo è usare Excel.
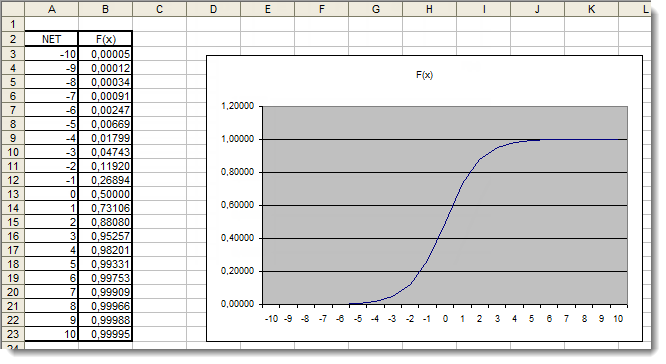
Fig.4. Il grafico Excel della funzione sigmoidea
Qui, possiamo vedere chiaramente che i valori degli argomenti al di fuori dell'intervallo [-5,5] non hanno assolutamente alcun effetto sui risultati. Ciò suggerisce che l'intervallo di valori è incompleto. Proviamo a risolvere questo problema. Aggiungeremo all'argomento un ulteriore coefficiente d che ci permetterà di espandere l'intervallo di valori.
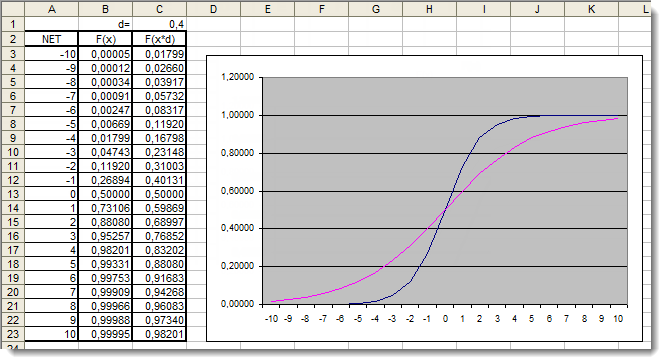
Fig.5. Il grafico Excel della funzione sigmoidea con il coefficiente aggiuntivo applicato
Esaminiamo ancora una volta i grafici. Abbiamo aggiunto un coefficiente aggiuntivo d=0,4 che ha cambiato la forma della funzione. Il confronto dei valori nella tabella suggerisce che ora sono distribuiti in modo più uniforme. Quindi i risultati possono essere espressi come segue:
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
Rivediamo ora la funzione di attivazione della tangente iperbolica. Tralasciando la teoria trattata nella recensione della funzione precedente, si arriva subito all'applicazione pratica. L'unica differenza qui è che l'output può trovarsi nell'intervallo [-1,1]. La somma ponderata può assumere anche valori dell'intervallo [-10,10].
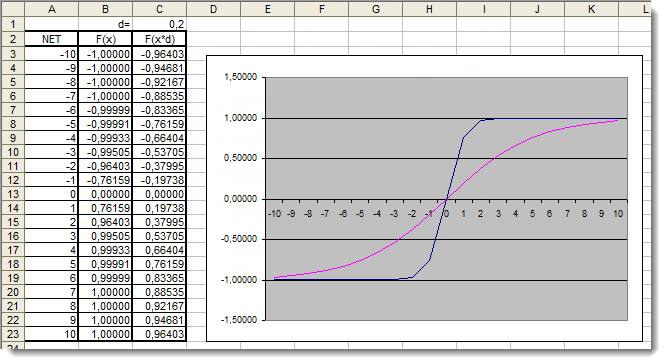
Fig.6. Il grafico Excel della funzione tangente iperbolica con il coefficiente aggiuntivo applicato
Il grafico mostra che la forma della funzione è stata migliorata grazie all'uso del coefficiente aggiuntivo d=0,2. Quindi i risultati possono essere espressi come segue:
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
In questo modo è possibile modificare e migliorare la forma di qualsiasi funzione di attivazione.
Applicazione
Passiamo ora all'applicazione pratica. Per prima cosa cercheremo di implementare il calcolo dell'input netto del neurone, seguito dall'aggiunta della funzione di attivazione. Ricordiamo la formula per calcolare l'input netto del neurone:
double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
Esaminiamolo:
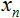- Abbiamo iniziato dichiarando una variabile per memorizzare l'input netto del neurone e due array: input e pesi;
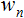- Queste variabili sono state dichiarate all'inizio, al di fuori di tutte le funzioni per dare loro un ambito globale (per essere accessibili da qualsiasi punto del programma);
- Nella funzione di inizializzazione OnInit() (in realtà può essere qualsiasi altra funzione), abbiamo riempito l'array di input e l'array di pesi;
- Questo è stato seguito dal ciclo di somma, n<3 poiché abbiamo solo tre ingressi e tre rispettivi pesi;
- Abbiamo quindi aggiunto valori di input pesati e li abbiamo archiviati nella variabile .
Il primo compito è stato così completato: abbiamo ottenuto la somma. Ora è il turno della funzione di attivazione. Di seguito sono riportati i codici per il calcolo delle funzioni di attivazione esaminati nella sezione Funzioni di attivazione.
La funzione del passo dell'unità o della soglia rigida
double Out; if(NET>=x) Out=1; else Out=0;
La funzione sigmoidea
double Out = 1/(1+exp(-NET));
La funzione tangente iperbolica
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
Mettere tutto insieme
Per rendere l'implementazione più semplice, prenderemo una rete composta da un singolo neurone. È certamente un po' forzato chiamarla rete, ma l'importante è capirne il principio. Dopotutto, una rete neurale multistrato è costituita dagli stessi neuroni in cui l'output dello strato di neuroni precedente funge da input per lo strato successivo.
Utilizzeremo una versione leggermente modificata dell'Expert Advisor sviluppata e introdotta nell'articolo "A Quick Start or a Short Guide for Beginners". Pertanto, ad esempio, sostituiremo l'indicatore di tendenza Moving Average con l'oscillatore Indice di forza relativa. Le informazioni sui parametri dell'indicatore e la loro sequenza sono disponibili nella Guida integrata.
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
La prima cosa che dobbiamo fare è addestrare la nostra rete. Ottimizziamo i pesi.
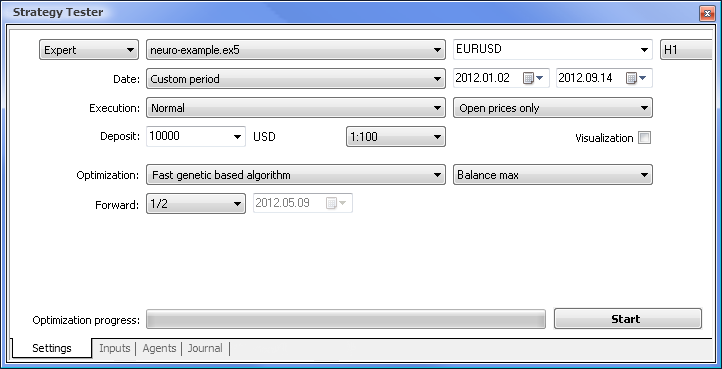
Fig.7. Tester di strategia con i parametri richiesti impostati
Eseguiremo l'ottimizzazione utilizzando i seguenti parametri:
- Data: ad es. dall'inizio dell'anno. Più lungo è il periodo, minore è il verificarsi di curve fitting e migliore è il risultato.
- Esecuzione: normale, solo prezzi di apertura. Non ha senso testare in modalità Ogni tick poiché il nostro Expert Advisor prende solo gli ultimi 10 valori dell'indicatore, ad eccezione del valore corrente.
- L'ottimizzazione può essere impostata per l'esecuzione utilizzando l'algoritmo completo lento. L'ottimizzazione genetica fornirà comunque risultati più rapidi, il che è particolarmente utile quando si valuta un algoritmo. Se il risultato è soddisfacente, puoi anche provare a utilizzare l'algoritmo lento completo per risultati più accurati.
- Forward di 1/2 e oltre ti consente di valutare per quanto tempo il tuo EA può generare i risultati ottenuti fino alla successiva ottimizzazione.
- L'intervallo di tempo e la coppia di valute possono essere impostati come ritieni opportuno.
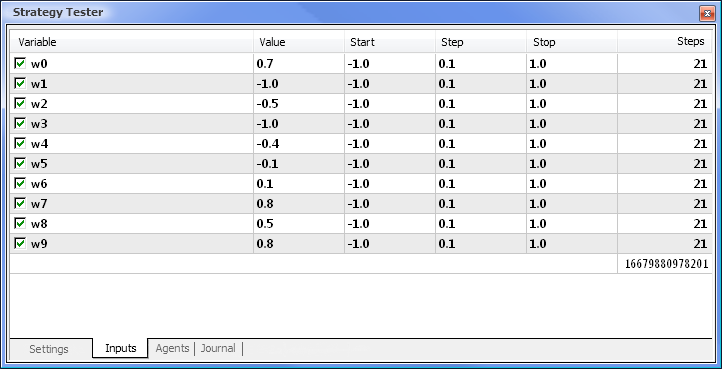
Fig.8. Impostazione dei parametri e dei rispettivi range da ottimizzare
L'ottimizzazione verrà eseguita rispetto a tutti i pesi e ai loro intervalli. Avvia l'ottimizzazione tornando alla scheda Impostazioni e cliccando sul pulsante Avvia.
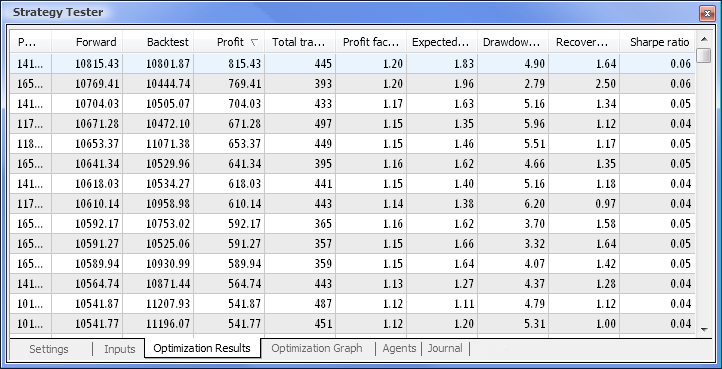
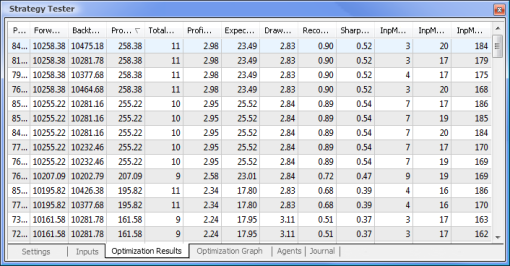
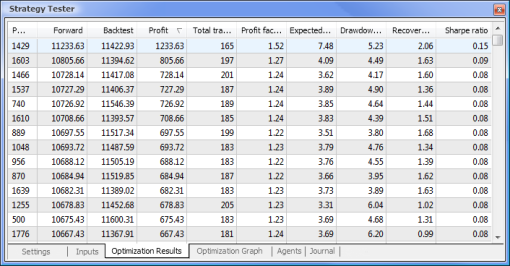
Fig.9. Dati ottenuti a seguito dell'ottimizzazione
Al termine dell'ottimizzazione, selezioniamo il passaggio con il valore di profitto massimo (per ordinare in base a uno dei parametri, clicca sull'intestazione della colonna pertinente) nella scheda Risultati dell'ottimizzazione. È quindi possibile valutare altri parametri e selezionare il passaggio desiderato, se necessario.
Un doppio clic sul passaggio richiesto avvia il test i cui risultati sono mostrati nelle schede Risultati e Grafico.
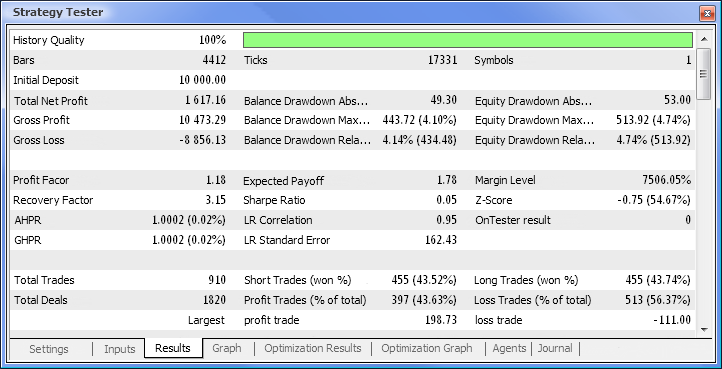
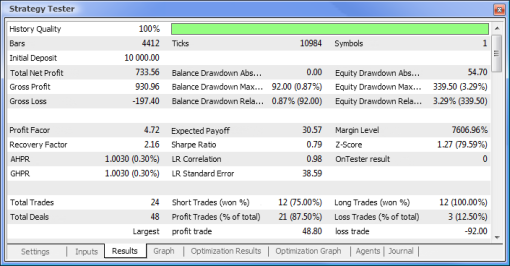
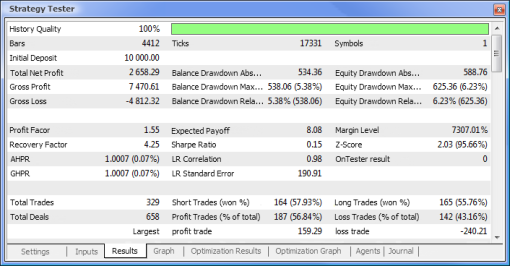
Fig.10. Rapporto di prova
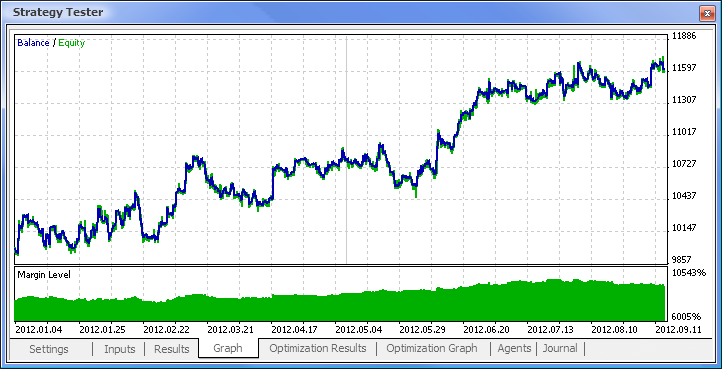
Fig.11. Grafico del saldo
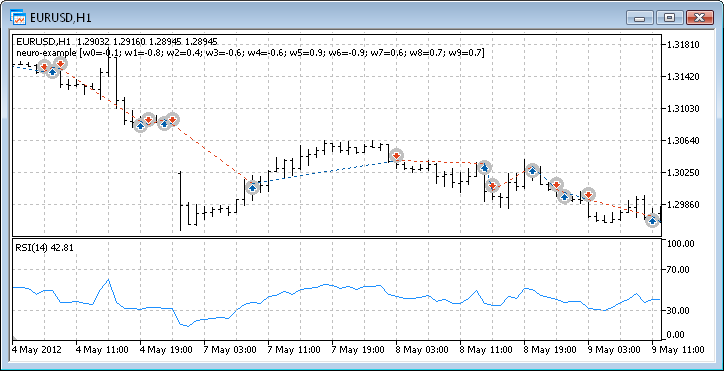
Fig.12. Performance di trading dell'Expert Advisor
Quindi abbiamo finalmente ottenuto i risultati e per cominciare non sono affatto male. Tieni presente che avevamo un solo neurone. L'esempio fornito è chiaramente primitivo, ma bisogna ammettere che anche esso da solo può trarne profitto.
Vantaggi delle reti neurali
Proviamo ora a confrontare un EA basato sulla logica standard con un EA guidato da una rete neurale. Confronteremo i risultati di ottimizzazione e test dell’Expert Advisor campione MACD che viene fornito insieme al terminale con quelli dell'EA basato su rete neurale basata su MACD.
I valori Take Profit e Trailing Stop non saranno coinvolti nell'ottimizzazione in quanto mancano dall'EA guidato dalla rete neurale. Entrambi gli Expert Advisor che andremo a testare sono basati su MACD con i seguenti parametri:
- Periodo della media mobile veloce: 12;
- Periodo della media mobile lenta: 26;
- Periodo di media della differenza: 9;
- Tipo di prezzo: prezzo di chiusura.
Puoi anche impostare la coppia di valute e l'intervallo di tempo richiesti, ma nel nostro caso li lasceremo invariati: rispettivamente EURUSD, H1. Il periodo di prova in entrambi i casi è lo stesso: dall'inizio dell'anno utilizzando i prezzi di apertura.
| Campione MACD | macd-neuro-examle |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
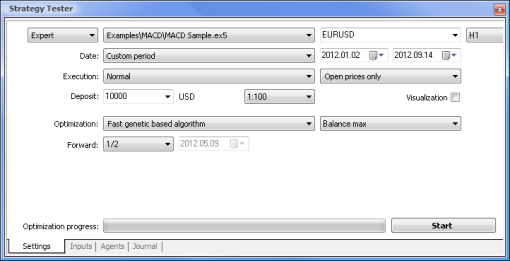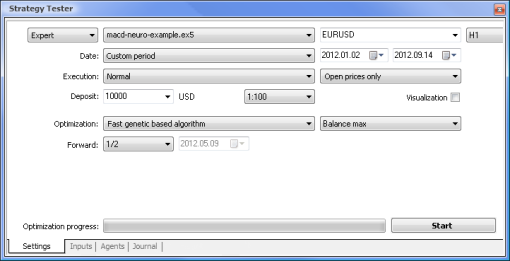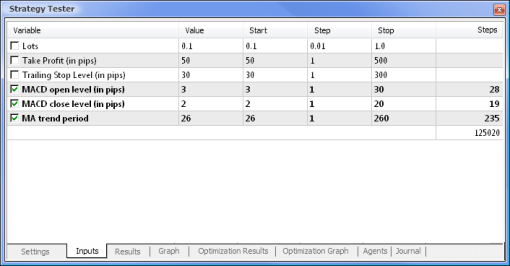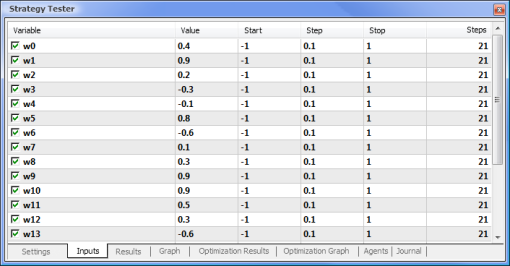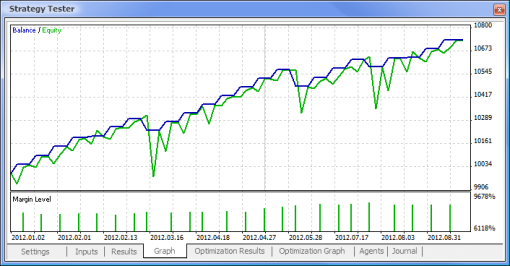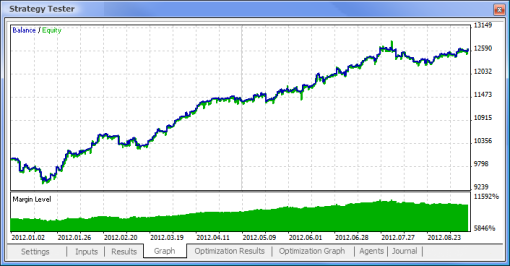Confrontiamo ora i parametri chiave degli Expert Advisor testati:
| Parametro | Campione MACD | macd-neuro-examle |
|---|---|---|
| Utile netto totale | 733,56 | 2 658,29 |
| Saldo Drawdown Assoluto | 0,00 | 534,36 |
| Equità Drawdown Massimo | 339,50 (3,29%) | 625,36 (6,23%) |
| Fattore di profitto | 4,72 | 1,55 |
| Fattore di recupero | 2,16 | 4,25 |
| Profitto previsto | 30,57 | 8,08 |
| Indice di Sharpe | 0,79 | 0,15 |
| Totale operazioni | 24 | 329 |
| Operazioni totali | 48 | 658 |
| Operazioni di profitto (% del totale) | 21 (87,50%) | 187 (56,84%) |
| Trading con profitto medio | 44,33 | 39,95 |
| Media vittorie consecutive | 5 | 2 |
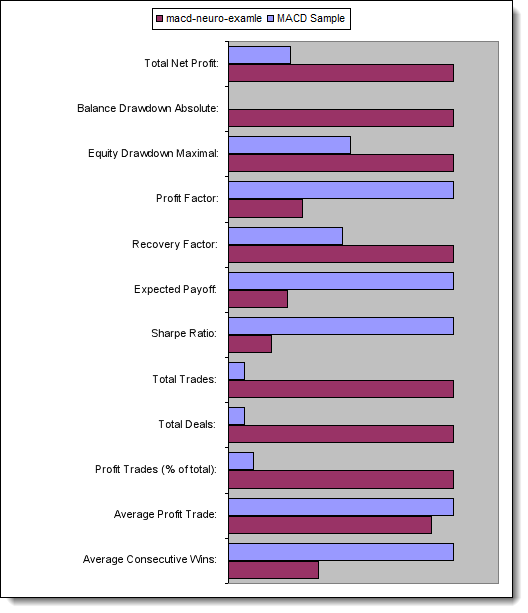
Fig.13. Confronto dei parametri chiave
Conclusione
Questo articolo ha trattato i punti principali che è necessario conoscere quando si progettano EA utilizzando le reti neurali. Ci ha mostrato la struttura di un neurone e un'architettura di rete neurale, ha delineato le funzioni di attivazione e i metodi per cambiare la forma della funzione di attivazione, nonché il processo di ottimizzazione e normalizzazione dei dati di input. Inoltre, abbiamo confrontato un EA basato sulla logica standard con un EA guidato da una rete neurale.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/497
Come acquistare un robot di trading dal Market MetaTrader e installarlo?
Strategia statistica del carry trade
Come preparare le quotazioni MetaTrader 5 per altre applicazioni
Esplorazione delle classi di strategia di trading della libreria standard. Personalizzazione delle strategie
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso