Redes neuronales: de la teoría a la práctica
18 898
0
Introducción
Hoy en día, cualquier operador ha oído hablar de las redes neuronales y conoce las ventajas de su utilización. La mayoría de ellos creen que quien puede trabajar con redes neuronales es una especie de superman. En este artículo intentaré explicarle la arquitectura de la red neuronal, describir sus aplicaciones y dar ejemplos de su uso práctico.
Concepto de redes neuronales
Las redes neuronales artificiales pertenecen a una de esas áreas de la investigación en inteligencia artificial basadas en los intentos de simular el sistema nervioso del ser humano y su capacidad para aprender y adaptarse, lo que nos permitirá crear una simulación muy genérica del funcionamiento del cerebro humano.
Lo más curioso es que las redes neuronales artificiales están formadas por neuronas artificiales.
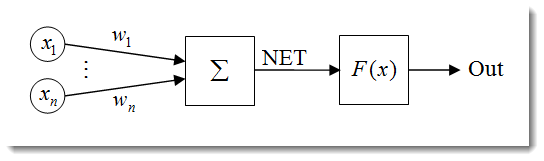
Fig. 1. Modelo de neurona artificial
La estructura de una neurona puede ser representada como una composición de las siguientes unidades:
- Entradas
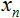; - Pesos
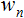; - Función de transferencia
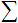y entrada neta 
; - Función de activación
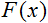; - Salida
.
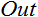Las redes neuronales tienen muchas propiedades y la capacidad de aprender es la más destacada. El proceso de aprendizaje se reduce a cambiar los pesos .
esta es la entrada neta de la neurona.
La entrada neta se transforma luego en la salida mediante la función de activación que veremos más tarde. En pocas palabras, puede considerarse una red neuronal como una "caja negra" que recibe señales como entradas y proporciona resultados como salidas.
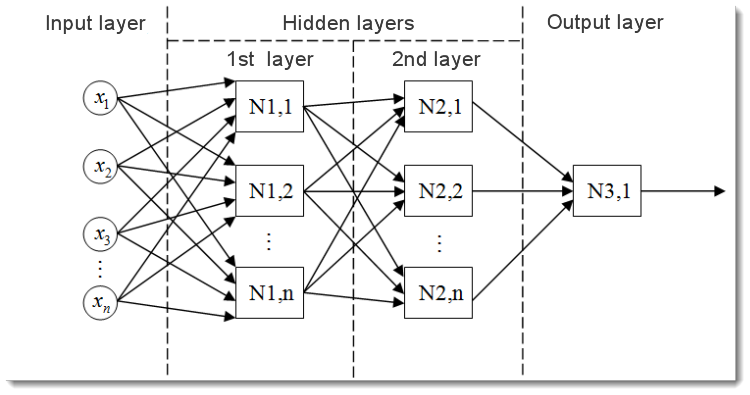
Fig. 2. Modelo de una red neuronal multicapa
Este es el aspecto de una red neuronal multicapa. Comprende:
- La capa de entrada, que sirve para distribuir los datos por la red y no realiza ningún cálculo. Las salidas de esta capa transmiten señales a las entradas de la siguiente capa (oculta o de salida);
- La capa de salida, que normalmente contiene una neurona (o algunas veces más de una) que genera la salida de toda la red neuronal. La señal subyace bajo el control lógico futuro del asesor experto;
- Las capas ocultas, que son capas de neuronas estándar que transmiten señales desde la capa de entrada a la capa de salida. Su entrada es la salida de la capa anterior, mientras que su salida es la entrada de la capa siguiente.
Este ejemplo muestra la red neuronal con dos capas ocultas. Pero puede haber redes neuronales con más capas ocultas.
Normalización de los datos de entrada
La normalización de los datos de entrada es el proceso por el se normalizan todos los datos de entrada, es decir, se reducen a los rangos [0,1] o [-1,1]. Si no se realiza la normalización los datos de entrada tendrán un efecto adicional sobre la neurona, dando lugar a decisiones incorrectas. En otras palabras, ¿cómo podemos comparar los valores con diferentes órdenes de magnitud?
La normalización, en su forma estándar, es como sigue:
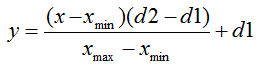
donde:
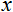- valor a normalizar;
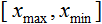- rango de valor х;
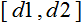- rango al que será reducido el valor de x.
Permítanme explicarlo usando un ejemplo:
Supongamos que tenemos n datos de entrada desde el rango [0, 10], luego 
= 0 y 
= 10. Reduciremos los datos al rango [0, 1], luego 
= 0 y 
= 10. Ahora, una vez introducidos los datos en la fórmula podemos calcular los valores normalizados para cualquier x a partir de n datos de entrada.
Así es queda cuando se implementa en MQL5:
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
Primero especificamos los límites superiores e inferiores del valor de salida y luego obtenemos los valores máximos y mínimos del indicador (se ha obviado el copiado de datos del indicador, aunque pueden ser, por ejemplo, los últimos 10 valores). Por último, normalizamos cada elemento de entrada (valores del indicador en barras distintas) y guardamos los resultados en una matriz para usarlos luego.
Funciones de activación
La función de activación calcula la información de salida de una neurona. La entrada que recibe representa la suma de todos los productos de las entradas y sus respectivos pesos (en adelante "suma ponderada"):
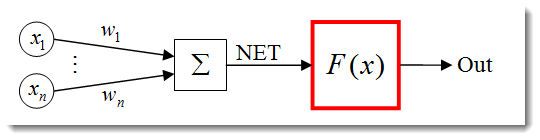
Fig. 3. Modelo de neurona artificial con la descripción de la función de activación
La función de activación, en su forma estándar, es como sigue:
donde:
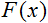- es la función de activación;
- es la suma ponderada obtenida en la primera etapa del cálculo de la información de salida de una neurona;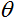
es un valor de umbral de la función de activación. Solo se usa para la función de umbral y es igual a cero en otras funciones.
Los principales tipos de funciones de activación son:
-
El paso unitario o función de umbral dura.
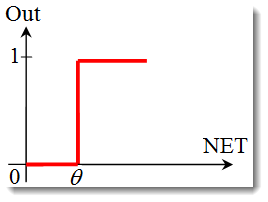
La función se describe en la siguiente fórmula:
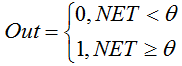
Si la suma ponderada es menor que el valor especificado, la función de activación devuelve cero. Si la suma ponderada es mayor, la función de activación devuelve uno. -
La función sigmoidea
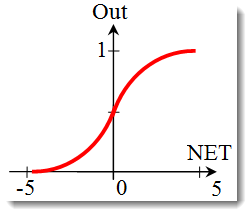
La fórmula que describe la función sigmoidea es la siguiente:
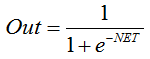
Se usa a menudo en redes neuronales multicapa y otras redes con señales continuas. La suavidad y continuidad de la función son propiedades muy positivas. -
La tangente hiperbólica
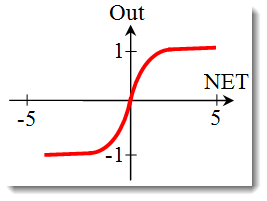
Fórmula:
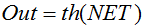o 
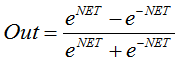
También se usa a menudo en redes con señales continuas. Tiene de especial que puede devolver valores negativos.
Cambiar la forma de la función de activación
En la sección previa hemos trabajado con los distintos tipos de funciones de activación. Ahí hay otra importante cuestión a considerar: la pendiente de la función (excepto para la función umbral dura). Veamos con mayor detenimiento la función sigmoidea.
Al observar el gráfico de la función, uno puede ver fácilmente que la función es suave a lo largo del rango [-5, 5]. Supongamos que tenemos una red con una solo neurona con 10 entradas y una salida. Vamos ahora a intentar calcular los valores superiores e inferiores de la variable . Cada entrada tomará un valor normalizado (como ya se mencionó en la normalización de datos de entrada), por ejemplo, desde el rango [-1,1].
Usaremos los valores de entrada negativos ya que la función no es diferenciable ni siquiera en un argumento negativo. También se elegirán los pesos a partir del mismo rango. Con todas las combinaciones posibles de entradas y pesos, obtendremos los valores extremos en el rango [-10,10] como:
En MQL5, la fórmula será:
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
Ahora necesitamos trazar la función de activación en el rango como identificada. Vamos a tomar como ejemplo la función sigmoidea. La forma más sencilla de hacer esto es utilizar Excel.
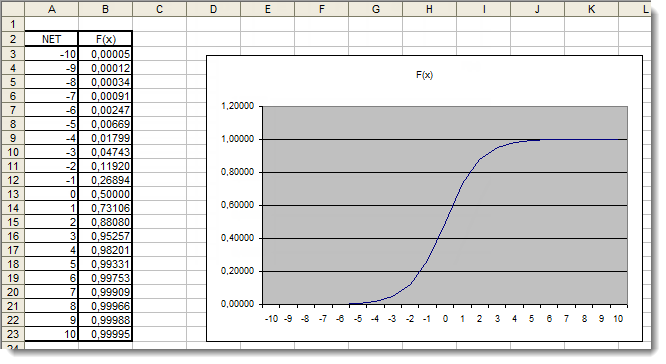
Fig. 4. Gráfico Excel de la función sigmoidea
Aquí podemos ver claramente que los valores del argumento fuera del rango [-5,5] no tienen ningún efecto sobre los resultados. Esto sugiere que el rango de valores es incompleto. Vamos a intentar arreglar esto. Añadiremos al argumento un coeficiente adicional d que nos permitirá ampliar el rango de valores.
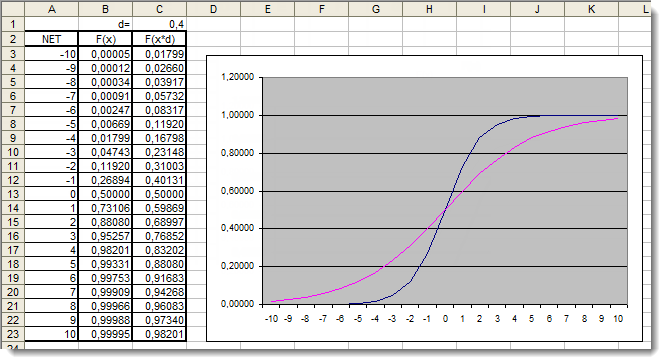
Fig. 5. Gráfico Excel de la función sigmoidea con el coeficiente adicional aplicado.
Vamos a ver una vez más los gráficos. Hemos añadido un coeficiente adicional d=0,4 que ha cambiado la forma de la función. La comparación de los valores en la tabla sugiere que ahora están distribuidos más uniformemente. Los resultados pueden ser expresados de la siguiente forma:
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
Vamos ahora a revisar la función de activación de la tangente hiperbólica. Si no tenemos en cuenta la teoría que vimos con la función previa llegamos a la aplicación práctica de inmediato. La única diferencia aquí es que la salida puede caer en el rango [-1,1]. La suma ponderada puede tomar también valores en el rango [-10, 10].
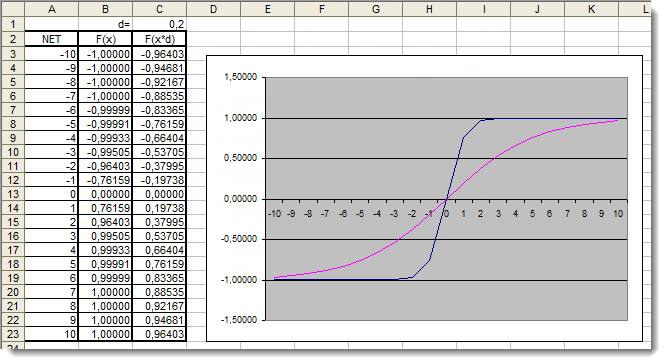
Fig. 6. Gráfico Excel de la función hiperbólica con el coeficiente adicional aplicado.
El gráfico muestra que la forma de la función ha sido mejorada debido al uso del coeficiente adicional d=0,2. Los resultados pueden ser expresados de la siguiente forma:
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
De este modo podemos cambiar y mejorar la forma de cualquier función de activación.
Aplicación
Veamos ahora una aplicación práctica. Primero, intentaremos implementar el cálculo de la entrada neta de la neurona, seguido por la adición de la función de activación. Vamos a recuperar la fórmula para el cálculo de la entrada neta de la neurona:
double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
Examinémoslo más detenidamente:
- Hemos empezado declarando una variable para almacenar la entrada neta de la neurona y dos matrices: entradas 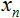y pesos ;
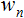- Estas variables han sido declaradas al inicio, fuera de todas las funciones para darle un alcance global (para que sean accesibles desde cualquier punto del programa);
- En la función de inicialización OnInit() (puede ser realmente cualquier otra función) hemos completado la matriz de entrada y la matriz de pesos;
- A continuación se ha realizado el bucle de suma, n<3 ya que solo tenemos tres entradas y tres pesos respectivos;
- Luego hemos añadido los valores de entrada ponderados y los hemos almacenado en la variable .
De esta forma hemos completado la primera tarea y hemos obtenido la suma. Ahora es el turno de la función de activación. A continuación se muestran los códigos para el cálculo de las funciones de activación que hemos visto en la sección funciones de activación.
Paso unitario o función de umbral dura.
double Out; if(NET>=x) Out=1; else Out=0;
La función sigmoidea
double Out = 1/(1+exp(-NET));
La función tangente hiperbólica
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
Reuniéndolo todo
Para hacer más fácil la implementación, tomaremos una red formada por una sola neurona. Sería algo exagerado llamarlo una red, pero lo importante es comprender el principio. Después de todo, una red neuronal multicapa está formada por las mismas neuronas que en la capa anterior de neuronas servían como entrada para la siguiente capa.
Vamos a utilizar una versión ligeramente modificada del asesor experto desarrollado en el artículo "Un inicio rápido o una breve guía para principiantes". Por tanto, vamos a reemplazar el indicador de la media móvil por el oscilador del índice de resistencia relativo. La información sobre los parámetros del indicador y su serie se encuentra disponible en la ayuda.
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
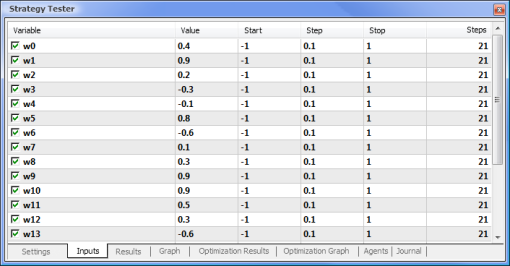
Lo primero que necesitamos hacer es entrenar nuestra red. Vamos a optimizar los pesos.
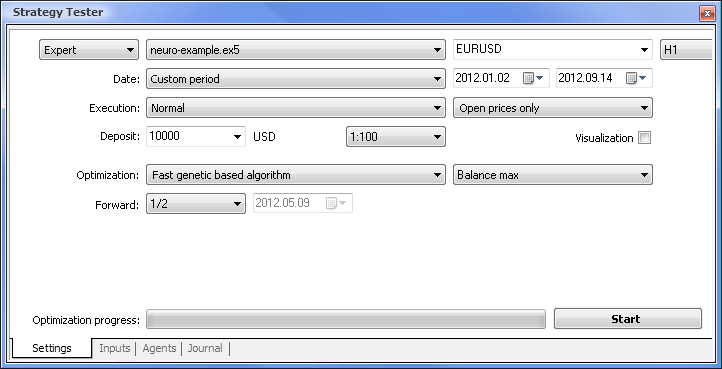
Fig. 7. El probador de estrategias con el conjunto de parámetros requeridos.
Ejecutaremos la optimización usando los siguientes parámetros:
- Fecha: por ejemplo, desde el principio del año, cuanto más largo sea un periodo, con menor frecuencia tiene lugar el ajuste de la curva y mejor será el resultado.
- Ejecución: normal, solo precios de apertura. No hay razón para probar cada modo de tick ya que nuestro asesor experto solo toma los 10 últimos valores del indicador, excepto para el valor actual.
- La optimización puede configurarse para que se ejecute usando un algoritmo completo lento. No obstante, la optimización genética dará resultados más rápidos, lo que resulta especialmente útil al evaluar un algoritmo. Si el resultado es satisfactorio, podemos intentar también el algoritmo completo lento para unos resultados más precisos.
- Si buscamos 1/2 o más podremos evaluar cuánto tiempo puede nuestro asesor experto generar los resultados obtenidos hasta la próxima optimización.
- El marco temporal y el par de divisas pueden los que creamos más adecuados.
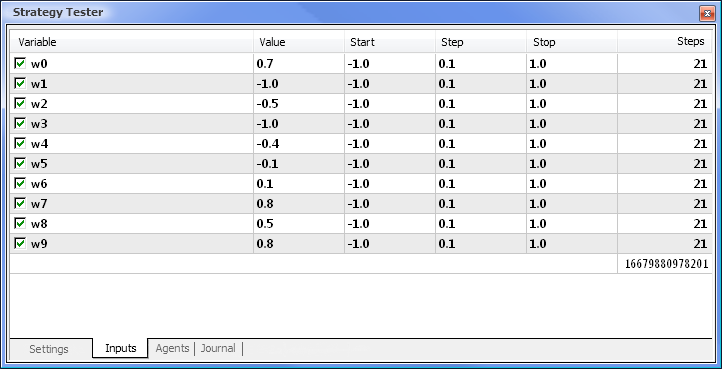
Fig. 8. Establecer los parámetros y sus respectivos rangos a optimizar
Se ejecutará la optimización respecto a todos los pesos y sus rangos. Iniciamos la optimización volviendo a la pestañas Settings (ajustes) y haciendo clic en el botón Start (inicio).
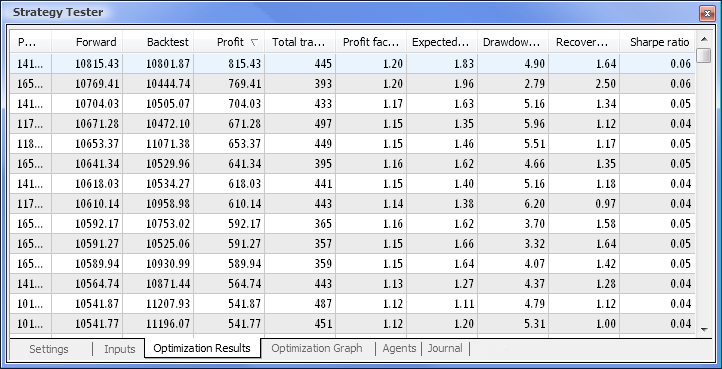
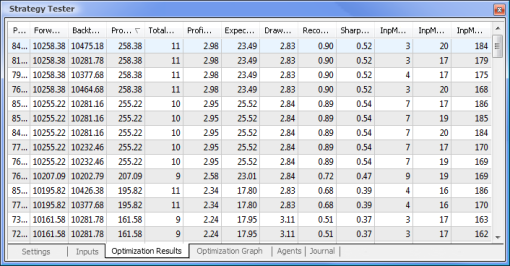
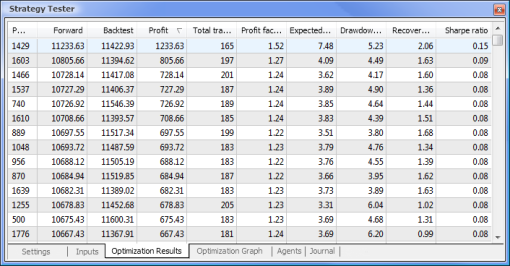
Fig. 9. Datos obtenidos después de la optimización
Después de completar la optimización, seleccionamos la pasada con el mayor beneficio (para ordenarla por uno de los parámetros hacemos clic en el encabezado de la columna correspondiente) en la pestaña Optimization Results (resultados de la optimización). Luego podemos evaluar otros parámetros y seleccionar las pasadas deseadas si el necesario.
Un doble clic en la pasada necesaria inicia la prueba de los resultados mostrados en las pestañas Results (resultados) y Graph (gráfico).
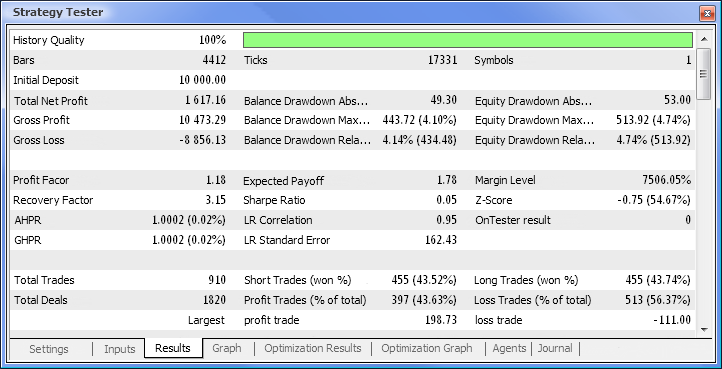
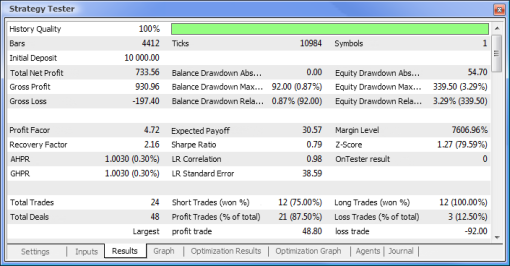
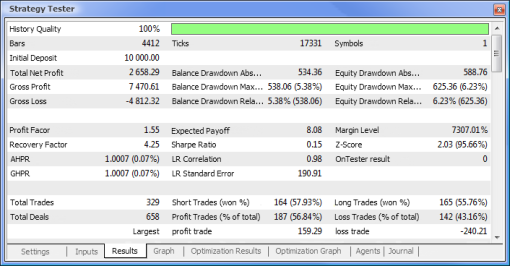
Fig. 10. Informe de prueba
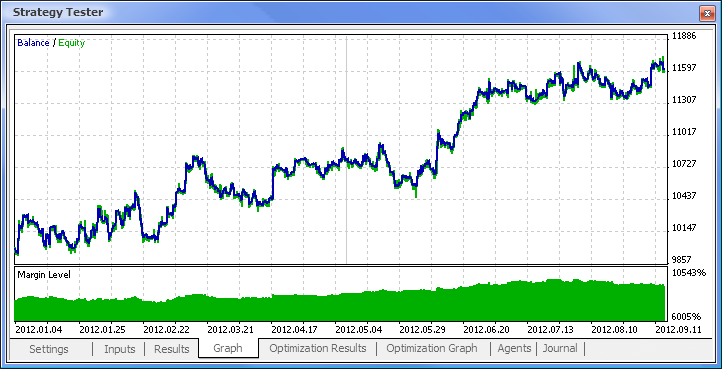
Fig. 11. Gráfico de saldo
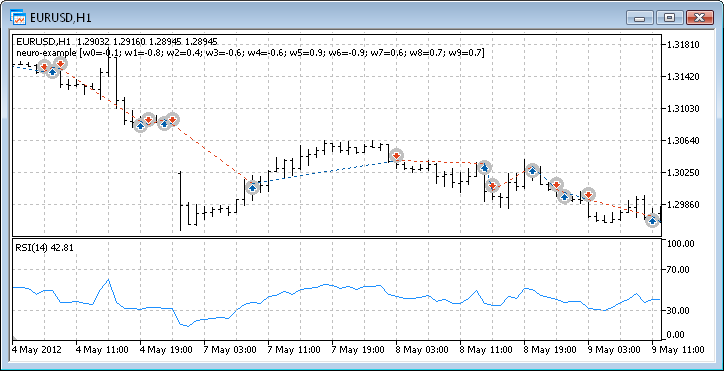
Fig. 12. Funcionamiento del trading del asesor experto
Finalmente obtenemos los resultados y para ser el comienzo no está mal del todo. Tenga en cuenta que solo teníamos una neurona. Este ejemplo es muy primitivo pero hemos de admitir que incluso él solo puede conseguir beneficios.
Ventajas de las redes neuronales
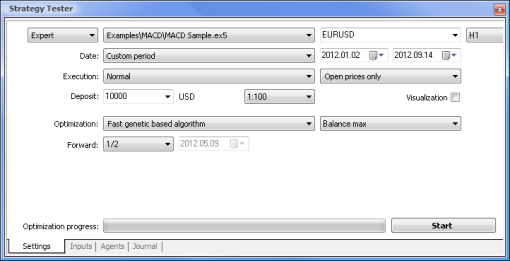
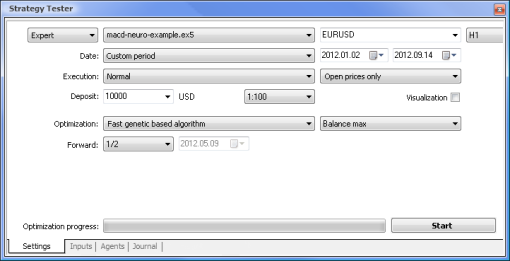
Vamos ahora a intentar comparar un asesor experto basado en la lógica estándar con un asesor experto según una red neuronal. Compararemos los resultados de la optimización y las pruebas del asesor experto de la muestra MACD que viene junto con el terminal con los del asesor experto según una red neuronal basado en MACD.
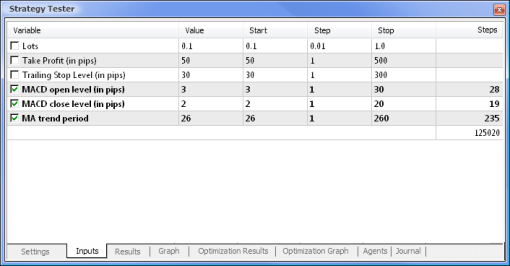
Los valores de Take Profit y Trailing Stop no estarán implicados en la optimización ya que no se encuentran en el asesor experto basado en una red neuronal. Los dos asesores expertos que vamos a probar están basados en MACD con los siguientes parámetros:
- Período de la media móvil rápida: 12;
- Período de la media móvil lenta: 26;
- Periodo de promediación de la diferencia: 9;
- Tipo de precio: precio de cierre.
También puede establecer el par de divisas requerido y el marco temporal, pero en nuestro caso los dejaremos como están: EURUSD y H1, respectivamente. El periodo de prueba es el mismo en ambos casos: desde el principio del año usando precios de apertura.
| Muestra de MACD | macd-neuro-examle |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
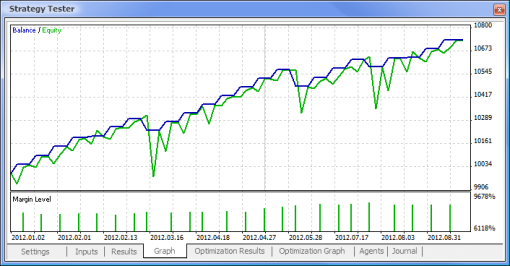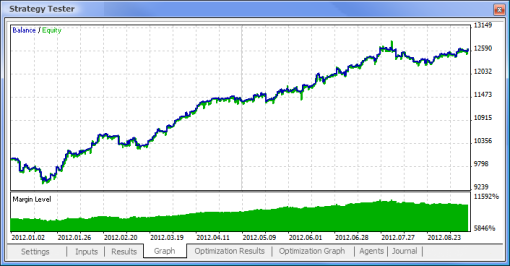Vamos a comparar los parámetros clave de los asesores expertos probados:
| Parámetro | Muestra de MACD | macd-neuro-examle |
|---|---|---|
| Beneficio neto total | 733,56 | 2.658,29. |
| Valor absoluto de reducción del saldo | 0,00 | 534,36 |
| Valor máximo de la reducción del capital | 339,50 (3,29%) | 625,36 (6,23%) |
| Factor de beneficio | 4,72 | 1,55 |
| Factor de recuperación | 2,16 | 4,25 |
| Retribución esperada | 30,57 | 8,08 |
| Ratio de Sharpe | 0,79 | 0,15 |
| Transacciones totales | 24 | 329 |
| Contratos totales | 48 | 658 |
| Transacciones con beneficio (% del total) | 21 (87,50%) | 187 (56,84%) |
| Transacción con beneficio promedio | 44,33 | 39,95 |
| Transacciones con ganancias promedio | 5 | 2 |
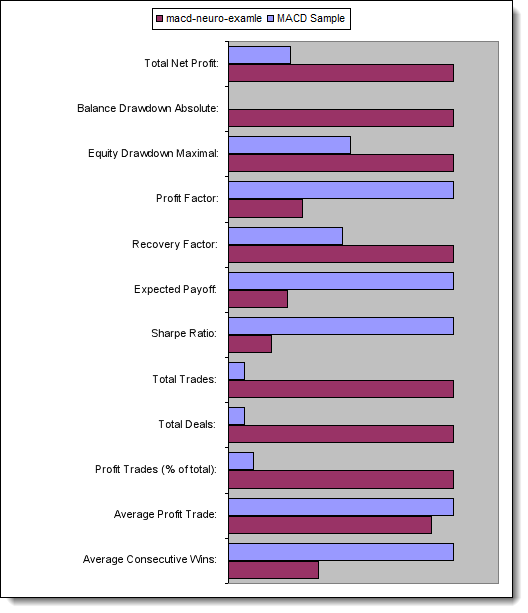
Fig. 13. Comparación de los parámetros clave
Conclusión
Este artículo ha tratado sobre los aspectos que debemos conocer al diseñar asesores expertos usando redes neuronales. Nos ha mostrado la estructura de una neurona y la arquitectura de una red neuronal, ha descrito las funciones de activación y los métodos para cambiar la forma de la función de activación, así como el proceso de optimización y normalización de datos de entrada. Además, hemos comparado un asesor experto basado en la lógica estándar con un asesor experto según una red neuronal.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/497
Comunicándonos con Meta Trader 5 usando conexiones designadas sin utilizar DLL
Introducción al método de descomposición de modo empírico
Simulación Rápida de Ideas de Trading en el Gráfico
Aplicación del método de coordenadas de Eigen al análisis estructural de distribuciones estadísticas no extensivas
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso