Matematica del mercato: profitti, perdite e costi

Contenuto

• Introduzione
• Equazioni per il calcolo dei profitti o delle perdite degli ordini
• Spread all'apertura e alla chiusura
• Il metodo più accurato per calcolare i profitti e le perdite degli ordini
• Funzione di calcolo esatto dello swap
• Parte pratica
• Conclusioni

Introduzione

Durante lo sviluppo degli Expert Advisor, non ho prestato attenzione al significato di alcuni valori nel calcolo dei profitti e delle perdite. La creazione di EA non richiede di approfondire la questione. Infatti, perché dovrei afferrare tutti questi valori considerando che MQL5 e persino MQL4 contengono tutte le funzionalità necessarie per eseguire i calcoli? Tuttavia, dopo un certo periodo di tempo e una certa esperienza, iniziano inevitabilmente a sorgere delle domande. Alla fine cominciamo a notare dettagli che prima ci sembravano insignificanti. Dopo averci riflettuto un po', ci si rende conto che un EA è come una scatola chiusa. Tutti i dati sull'argomento che sono riuscito a trovare su Internet si sono rivelati scarsi e non strutturati. Ho quindi deciso di strutturarlo da solo. Dopo aver letto questo articolo, riceverete un modello matematico completo e funzionante, e imparerete a capire e a calcolare correttamente ogni cosa relativa agli ordini.

Equazioni per il calcolo dei profitti o delle perdite degli ordini

Per sviluppare un sistema di trading efficiente, è necessario innanzitutto capire come viene calcolato il profitto o la perdita di ogni ordine. Tutti noi siamo in grado di calcolare in qualche modo i nostri profitti e le nostre perdite per mantenere il nostro sistema di gestione del denaro. Qualcuno lo fa intuitivamente, qualcuno esegue stime approssimative, ma quasi tutti gli EA hanno i calcoli di tutte le quantità necessarie.

Lo sviluppo di EA disciplina i vostri pensieri e vi fa capire cosa e come viene calcolato, il che non ha prezzo. Arriviamo al punto. Vale la pena partire dall'idea più semplice di come si calcola il profitto di un ordine. Personalmente, ho sempre saputo che il calcolo del profitto è piuttosto complesso nella sua essenza, ma si basa su poche semplici considerazioni. Per semplificare la comprensione, supponiamo che spread, swap e commissioni non esistano. Credo che molte persone non tengano conto di questi valori all'inizio. Naturalmente, il linguaggio MQL5 fornisce funzioni integrate, come OrderCalcProfit, e forse anche altre, ma in questo articolo voglio passare in rassegna le nozioni di base in modo che tutti capiscano cosa viene calcolato e come. Una tale meticolosità può essere sconcertante, ma non prestare attenzione a parametri quali spread, commissioni e swap è un errore fatale che molti trader commettono. Ognuno di questi valori influiscono a modo loro sul profitto o sulla perdita. Nei miei calcoli terrò conto di tutto e mostrerò come queste piccole cose possano essere d'aiuto. Profitto e perdita degli ordini, esclusi spread, commissioni e swap:

• PrBuy = Lot * TickValue * [ ( PE - PS )/Point ] — profitto per un ordine di acquisto
• PrSell = Lot * TickValue * [ ( PS - PE )/Point ] — profitto per un ordine di vendita
• Point — variazione minima possibile del prezzo di un simbolo selezionato
• TickValue — valore del profitto per una posizione profittevole quando il prezzo si muove di "1" Point (Punto)
• PE — prezzo di chiusura del trade (Bid)
• PS — prezzo di apertura del trade (Bid)

Questi valori come Point e TickValue in MQL5 sono definiti a livello di variabili predefinite o sono disponibili all'interno delle funzionalità integrate sotto forma di valore di ritorno delle funzioni di tipo SymbolInfoDouble. Nei miei articoli toccherò regolarmente l'argomento MQL5, in un modo o nell'altro, perché spesso è possibile andare a fondo di molte questioni semplicemente analizzando come è costruito MQL5 o alcune sue funzionalità.

Ora cerchiamo di ampliare leggermente la comprensione di questa equazione. Un ordine Buy viene aperto al valore Ask, mentre un ordine Sell viene aperto al valore Bid. Di conseguenza, un ordine Buy viene chiuso al prezzo Bid, mentre un ordine Sell viene chiuso al prezzo Ask. Riscriviamo le equazioni tenendo conto delle nuove modifiche:

• PrBuy = Lot * TickValue * [ ( Bid2 - Ask1 )/Point ] — profitto per un ordine di acquisto
• PrSell = Lot * TickValue * [ ( Bid1 - Ask2 )/Point ] — profitto per un ordine di vendita
• Bid1 — Prezzo di apertura di un trade Sell
• Ask1 — Prezzo di apertura di un trade Buy
• Bid2 — Prezzo di chiusura di un trade Buy
• Ask2 — Prezzo di chiusura di un trade Sell

Il frammento della specifica qui sotto contiene la maggior parte dei dati di cui avremo bisogno più tardi:

Questa è solo una parte dei dati necessari per il calcolo. Il resto dei dati può essere ottenuto utilizzando varie funzioni integrate in MQL5. Prendiamo come esempio USDJPY. In realtà, non abbiamo bisogno di una specifica per scrivere un codice, ma capire dove vengono visualizzati questi dati può rivelarsi molto utile.

Andiamo avanti e questa volta prendiamo in considerazione la commissione. La commissione per ogni ordine può essere calcolata in vari modi, ma tutti i metodi principali si riducono a una percentuale dei lotti negoziati. Esistono altri modi per addebitare una commissione di trading, ma non li considererò in questa sede poiché non ne avremo bisogno. Considererò due possibili scenari per il calcolo della commissione. Credo siano sufficienti. Se prendiamo come base lo swap, gli esempi di swap possono suggerire un altro metodo di calcolo comune che può essere applicato alla commissione — il calcolo in punti.

Di conseguenza, abbiamo due metodi apparentemente diversi. Tuttavia, come vedremo, questi metodi sono solo una forma conveniente di percepire lo stesso metodo di "tassazione", compreso lo spread. Di seguito sono riportate due equazioni per calcolare la commissione:

1. Commissione = Lot * TickValue * ComissionPoints
2. Commissione = Lot * ContractSize * BidAlpha * ComissionPercent/100

Qui vediamo il nuovo valore "ContractSize", che ha anche un'implementazione in MQL5 a livello di funzionalità integrata che riceve informazioni dal server di negoziazione. Questo valore è uno dei più importanti ed è presente assolutamente in tutti i calcoli dei profitti e delle perdite, anche se in forma implicita, per semplificare i calcoli ai programmatori. Vedo la validità di tali semplificazioni dal punto di vista del programmatore. Ma il nostro obiettivo attuale è capire tutto. Vedrete perché questo è necessario verso la fine dell'articolo. Inoltre, ho introdotto un'ulteriore variabile BidAlpha. Di seguito vi svelerò anche il suo significato. Vengono visualizzati anche i seguenti valori indicati nella specifica del simbolo:

• ComissionPoints - commissione in punti
• ComissionPercent - commissione in percentuale della dimensione del contratto

Il moltiplicatore BidAlpha è necessario per convertire uno swap da unità della valuta di base in uno swap in unità del nostro saldo. Ci sono quattro scenari:

1. BidAlpha = 1 (se la valuta di base è uguale alla valuta di deposito)
2. BidAlpha = Bid (del simbolo selezionato)
3. BidAlpha = Bid (del tasso corrispondente, dove la valuta di base del simbolo selezionato è uguale alla valuta di base del simbolo transitorio e la seconda valuta è uguale alla valuta di deposito)
4. BidAlpha = 1/Ask (del tasso corrispondente, dove la valuta di base del simbolo selezionato è uguale alla seconda valuta del simbolo di transizione e la valuta di base è uguale alla valuta di deposito)

Infatti, se la dimensione del contratto viene applicata alla coppia USDCHF, è chiaro che la valuta di base della coppia selezionata è USD. Supponiamo di avere un deposito in USD, allora la valuta di transizione diventa USDUSD e, di conseguenza, il suo tasso è sempre uno. Il secondo caso è ancora più semplice. Supponiamo di avere una coppia EURUSD, che è anche il tasso di conversione, quindi il suo Bid è il valore richiesto. Il terzo caso potrebbe essere il seguente. Supponiamo che la nostra valuta sia EURNZD. Poi viene fuori che dobbiamo trovare il tasso di conversione tra EUR e USD. Il tasso EURUSD e il Bid di questo tasso sono ciò di cui abbiamo bisogno. Nel quarto caso, le cose sono un po' più complicate. Supponiamo di aver selezionato CHFJPY. È chiaro che la coppia di transizione è USDCHF, poiché non esiste un tasso di cambio CHFUSD sul Forex. Naturalmente, possiamo creare il nostro simbolo sintetico e lavorare con CHFUSD. In questo caso, possiamo utilizzare il caso precedente. Ma in realtà, abbiamo solo bisogno di girare questo simbolo, quindi il suo tasso diventerà uguale a "1/Ask" dell'attuale tasso "scomodo". In effetti, creiamo un simbolo sintetico senza concentrarci su di esso. Lo stesso vale per gli swap. Ci sono anche altre questioni. Ad esempio, quale tasso dovrebbe essere utilizzato nella valuta di transizione - Bid, Ask o Mid? Questo problema non può essere risolto con l'approccio attuale. Troveremo gradualmente l'approccio giusto strada facendo. E ora definiamo, almeno approssimativamente, la struttura per il miglioramento. Per fare ciò, dovremmo scrivere almeno una prima versione approssimativa dell'equazione generale dei profitti e delle perdite, tenendo conto di tutte le opzioni di "tassazione", come spread, swap e commissioni.

Per calcolare gli swap, otteniamo equazioni simili:

1. Swap = Lot * TickValue * SwapPoints * SwapCount(StartTime,EndTime)
2. Swap = Lot * ContractSize * BidAlpha * SwapPercent/100 * SwapCount(StartTime,EndTime)

Le equazioni sono effettivamente molto simili. L'unica differenza è che il moltiplicatore certo è apparso qui sotto forma di funzione SwapCount. Spero mi concediate una certa libertà terminologica. La chiamo "funzione", perché gli swap non vengono addebitati immediatamente, mentre la sua entità dipende dai tempi di apertura e chiusura degli ordini. In un'approssimazione, possiamo naturalmente fare a meno del moltiplicatore e scrivere quanto segue:

• SimpleCount = MathFloor( (EndTime - StartTime) / ( 24 * 60 * 60 ) )

Se assumiamo che EndTime e StartTime siano di tipo 'datetime', la loro differenza è pari al numero di secondi tra i punti di apertura e chiusura dell'ordine. Lo swap viene caricato una volta al giorno, quindi è sufficiente dividere questo valore per il numero di secondi in un giorno. In questo modo possiamo avere una prima idea di come possono essere valutate le posizioni di swap. Naturalmente, questa equazione è tutt'altro che perfetta, ma fornisce una risposta alla domanda su che tipo di funzione sia e cosa restituisca. Inoltre, può suggerire come viene calcolato (almeno approssimativamente) lo swap. Restituisce il numero di swap maturati durante la durata della posizione. Allo stesso modo, la commissione nella specifica sarà uno dei due valori possibili per lo swap con l'indicazione obbligatoria del metodo di calcolo:

• SwapPoints – swap in punti per un rollover di una singola posizione
• SwapPercent – swap per un rollover di una singola posizione in % della dimensione del contratto

Se nel caso della commissione le equazioni sono più semplici e non richiedono chiarimenti, nel caso dello swap tutto è molto più complicato, ma affronteremo le sottigliezze e le sfumature di queste semplificazioni più avanti. In primo luogo, portiamo le equazioni dei profitti e delle perdite, escludendo le commissioni e gli swap, in una forma più coerente:

• PrBuy = Lot * TickValue * [ ( Bid2 - (Bid1+S1*Point) )/Point ] — profitto per un ordine di acquisto
• PrSell = Lot * TickValue * [ ( Bid1 - (Bid2+S2*Point) )/Point ] — profitto per un ordine di vendita
• S1 — spread all'apertura di un ordine di acquisto
• S2 — spread quando si chiude un ordine di vendita

È chiaro che Ask include sia lo spread che il Bid. Separiamo il profitto o la perdita dell'ordine risultante dallo spread, rendendola una somma separata:

• PrBuy = Lot * TickValue * [ ( Bid2 - Bid1)/Point ] + ( - Lot * TickValue * S1 ) — profitto per un ordine di acquisto
• PrSell = Lot * TickValue * [ ( Bid1 - Bid2)/Point ] + ( - Lot * TickValue * S2 ) — profitto per un ordine di vendita

Si può notare che in entrambe le equazioni è stata separata una certa somma, che è la parte addebitata dal broker. Naturalmente, questo non è l'intero importo, ma almeno ora si può vedere più chiaramente cosa riceviamo e cosa prende il broker. Notare che nel primo caso, la nostra "tassa" sullo spread dipende solo dal valore dello spread quando si apre una posizione "Buy", e nel secondo caso, quando si chiude una posizione “Sell”. Si scopre che tutte le volte diamo al broker una parte del nostro profitto sotto forma di spread esattamente al momento dell'acquisto. In effetti, se approfondiamo il trading sul Forex, risulta chiaro che l'apertura di una posizione Buy e la chiusura di una posizione Sell sono azioni equivalenti, confermate dalle nostre equazioni. In questo caso:

• S1 — spread in punti all'apertura di qualsiasi posizione
• S2 — spread in punti alla chiusura di qualsiasi posizione

Questi valori sono esattamente quelli che si possono vedere nella finestra Market Watch se si vuole visualizzare lo spread. La corrispondente funzione MQL5 integrata SymbolInfoInteger con gli ingressi corrispondenti restituisce esattamente gli stessi valori. Gli input sono disponibili nella Guida di MQL5. Il mio compito in questo caso è quello di creare un comodo modello di calcolo matematico legato al linguaggio MQL5 in modo che queste equazioni possano essere immediatamente codificate in qualsiasi EA o in qualsiasi altro codice MQL5 utile. Ecco il nostro sommario, che ora è simile sia allo swap che alla commissione:

• SpreadBuy = - Lot * TickValue * S1
• SpreadSell = - Lot * TickValue * S2

Spread all'apertura e alla chiusura

Convenzionalmente, lo spread viene calcolato al punto Buy, ma ora vi mostrerò perché questo non è corretto. Ho fatto molte ricerche di mercato e il punto di movimento dei prezzi più prevedibile è risultato essere il punto "0:00". È il punto di passaggio da un giorno all'altro. Se osservate attentamente questo punto, vedrete all'incirca la stessa cosa su tutte le coppie di valute — un salto al ribasso del tasso. Ciò avviene a causa di un aumento dello spread in questo punto. Il salto è seguito da un identico rollback. Che cos'è lo spread? Lo spread è il divario tra Bid e Ask. Convenzionalmente, si ritiene che questo divario sia una conseguenza della profondità del mercato. Se la profondità del mercato è saturata dagli ordini limite, lo spread tende a zero, mentre se gli operatori abbandonano il mercato, lo spread aumenta. Possiamo definirla una disintegrazione della profondità del mercato. Anche a prima vista, possiamo dire che il Bid non è l'elemento principale. Si scopre che Ask e Bid sono fondamentalmente uguali. Ciò è facilmente comprensibile se immaginiamo che, ad esempio, è possibile costruire uno strumento speculare USDEUR a partire da "EURUSD", e quindi Bid diventa Ask e, viceversa, Ask diventa Bid. In parole povere, invertiamo la profondità del mercato.

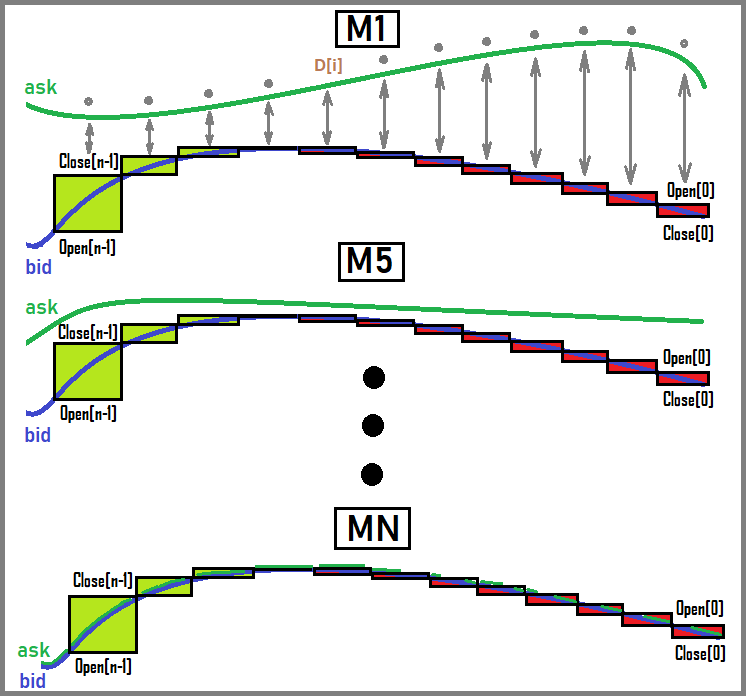
La linea Ask di solito non viene visualizzata sul grafico, anche se sarebbe utile:

alt

Come possiamo vedere, Ask e Bid iniziano a fondersi insieme a un aumento del periodo del grafico. Forse, a causa di queste considerazioni, nessun terminale visualizza entrambe le linee, anche se personalmente ritengo che sia un'opzione necessaria. Tuttavia, conoscere la presenza di questi valori e la loro differenza non è così importante, perché è comunque possibile utilizzarli in un EA. Non ho disegnato la Mid qui, ma credo che tutti capiscano che questa linea si trova esattamente a metà tra Bid e Ask. Chiaramente, per periodi elevati la differenza tra questi valori non ha praticamente alcun ruolo, e sembra che non sia nemmeno necessario tenere conto della presenza di Ask, ma in realtà lo è. Questi dettagli sono molto importanti.

Tenendo conto di ciò, possiamo ora affermare con assoluta certezza che la media della profondità di mercato è un'invariante durante tali trasformazioni. Questo valore può essere calcolato come segue:

• Mid = (Ask + Bid) / 2

Considerando tale rappresentazione e utilizzando l'ultima equazione, si può vedere che:

• Bid = Mid * 2 - Ask
• Ask = Mid * 2 - Bid

Il prossimo:

• Bid = Mid * 2 - (Bid + S*Point) = Mid - (S*Point)/2
• Richiesta = Mid * 2 - (Ask - S*Point) = Mid + (S*Point)/2

Queste espressioni possono ora essere sostituite alle equazioni originali per calcolare il profitto o la perdita degli ordini. Era importante ottenere esattamente queste espressioni, perché voglio mostrarvi qualcosa che non avevate compreso prima. Si scopre che l'importo addebitato dal broker non dipende esclusivamente dal punto di acquisto, ma da entrambi i punti di entrata e di uscita, nonché da qualsiasi posizione. Vediamo come si trasformeranno le nostre equazioni quando vi inseriremo le nuove definizioni estese. Possiamo vedere quanto segue:

• PrBuy = Lot * TickValue * [ ( (Mid2 - (S2*Point)/2) - (Mid1 + (S1*Point)/2) ) )/Point ]
• PrSell = Lot * TickValue * [ ( (Mid1 - (S1*Point)/2) - (Mid2 + (S2*Point)/2) ) )/Point ]

Dopo le opportune trasformazioni, possiamo vedere questo:

• PrBuy = Lot * TickValue * [ (Mid2 – Mid1)/Point ] - Lot * TickValue * (  S1/2 + S2/2  )
• PrSell = Lot * TickValue * [ (Mid1 – Mid2)/Point ] - Lot * TickValue * (  S1/2 + S2/2  )

Considerando che:

• Bid1 = Mid1 - (S1*Point)/2
• Bid2 = Mid2 - (S2*Point)/2
• Ask1 = Mid1 + (S1*Point)/2
• Ask2 = Mid2 + (S2*Point)/2

E tenendo presente che:

• Mid1 — media della profondità di mercato all'apertura di qualsiasi posizione
• Mid2 — media della profondità di mercato quando si chiude una posizione qualsiasi

Per comodità, indichiamo la somma negativa che definisce la perdita da spread come segue:

• Spread = -Lot * TickValue * ( (S1*Punto)/2 + (S2*Punto)/2 )

E, di conseguenza, la somma che indica un profitto o una perdita al netto di spread, commissioni e swap, ad esempio:

• ProfitIdealBuy = Lot * TickValue * [ (Mid2 - Mid1)/Point ]
• ProfitIdealSell = Lot * TickValue * [ (Mid1 - Mid2)/Point ]

Ora possiamo scrivere equazioni convenienti considerando tutte le perdite dovute a spread, commissioni e swap. Iniziamo con il prototipo dell'espressione. Prendiamo come base le ultime equazioni di profitto e perdita degli ordini, considerando solo lo spread qui:

• TotalProfitBuy = ProfitIdealBuy + (Spread + Comission + Swap)
• TotalProfitSell= ProfitIdealSell + (Spread + Comission + Swap)

Forse avrei dovuto scrivere questa equazione all'inizio, ma credo che sia più appropriata qui. Possiamo notare che l’oscuro TickValue è presente quasi ovunque. La questione principale è come viene calcolato e come si può utilizzare uno stesso valore per il calcolo in diversi punti temporali. I punti temporali indicano le entrate e le uscite dalle posizioni. Penso che abbiate capito che questo valore è di natura dinamica e inoltre è diverso per ogni simbolo di trading. Senza scomporre questo valore in componenti, otterremo errori tanto più grandi quanto più distanti sono i "target". In altre parole, le equazioni ottenute sono solo un'approssimazione. Esiste un'equazione assolutamente esatta e priva di questi difetti. I rapporti ottenuti sopra servono come limite. I limiti stessi possono essere espressi come segue:

• Lim[ dP -> 0 ] ( PrBuy(Mid1, Mid1+dP... ) ) = TotalProfitBuy(Mid1, Mid1+dP...)
• Lim[ dP -> 0 ] ( PrSell(Mid1, Mid1+dP... ) ) = TotalProfitSEll(Mid1, Mid1+dP...)
• Mid1+dP = Mid2 — il nuovo prezzo si ottiene da quello precedente più il delta tendente a zero
• TotalProfitBuy = TotalProfitBuy(P1,P2... ) — come è stato determinato, il profitto o la perdita sono una funzione dei valori Mid e di molti altri
• TotalProfitSell = TotalProfitSell(P1,P2… ) — simile

In generale, i limiti equivalenti per una comprensione generale della situazione possono essere elaborati in molti modi. Non è necessario moltiplicarli. Nel nostro caso, uno è sufficiente per chiarezza.

Anche se abbiamo ricevuto alcune equazioni che funzionano, i limiti di applicabilità sono molto condizionati. Successivamente, ci occuperemo di ottenere le equazioni iniziali che implicano tali equazioni approssimate. Senza conoscere gli elementi costitutivi di un profitto o di una perdita, non potremo mai ottenere queste equazioni. A loro volta, queste equazioni ci aiuteranno non solo a trovare i rapporti più precisi per il calcolo dei profitti e delle perdite, ma anche a trovare lo squilibrio dei processi di mercato, che può successivamente produrre un profitto.

Il metodo più accurato per calcolare i profitti e le perdite degli ordini

Per capire come costruire queste equazioni, dobbiamo tornare alle basi, cioè a cosa sono i Buy e i Sell. Ma prima, credo sia importante ricordare che acquistare significa in realtà scambiare il proprio denaro con un prodotto. Un'altra valuta può essere vista come una merce, poiché simboleggia la capacità di possedere determinati beni. È chiaro che la vendita è il processo inverso di scambio della seconda valuta con la prima. Ma se omettiamo tutte le convenzioni, risulta che comprare e vendere sono azioni equivalenti. Una moneta viene scambiata con un'altra e l'unica differenza è quale moneta diamo via e quale riceviamo in cambio.

Cercando informazioni su questi calcoli, ho trovato strane convenzioni che personalmente non sono riuscito a capire per molto tempo, perché non hanno alcun fondamento. Poiché sono un tecnico che ha molta esperienza nello studio di vario materiale tecnico, ho determinato due verità molto semplici. Se il materiale non è chiaro per voi e solleva domande, allora:

• Gli autori non lo comprendono appieno, quindi fanno del loro meglio per convincere l'utente del contrario con tutti i mezzi (di solito utilizzando affermazioni anti-logiche).
• I dettagli sono volutamente omessi per nascondere all'utente informazioni non necessarie.

L'immagine sottostante sviluppa ulteriormente l'idea rendendola più comprensibile. Mostra l'apertura e la chiusura di due tipi di ordini di mercato:

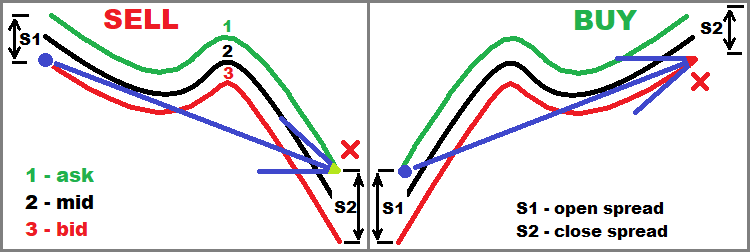
Ora, credo che la sezione degli spread e quella attuale saranno più chiare. In generale, questa immagine è rilevante per l'intero articolo, ma è più utile in questo blocco.

Naturalmente, sono sicuro che nella letteratura specializzata esistono calcoli corretti, ma è ovvio che trovare queste informazioni è più difficile che indovinare da soli ciò che manca. La convenzione prevede che quando acquistiamo, ad esempio, EURUSD, compriamo EUR e vendiamo USD. Scriviamolo:

• EUR = Lot * ContractSize
• USD = - Ask1 * Lot * ContractSize = - (Bid1 + S1*Point) * Lot * ContractSize

In questo caso, si scopre che quando si acquista, si ottiene un importo positivo della valuta di base e un importo negativo della seconda valuta. Credo di non essere l'unico a pensare che questa sia una completa assurdità. Dopo averci riflettuto un po', sono giunto alla conclusione che i rapporti sono corretti, ma sono presentati in modo poco intuitivo. Modifichiamolo nel modo seguente.... Per acquistare EUR, abbiamo bisogno di un'altra valuta, USD, che dovremmo prendere dal nostro saldo, in prestito da un broker o utilizzare entrambi i metodi. In altre parole, per prima cosa prendiamo in prestito USD da un archivio condiviso. Sembra così:

• USD1 = Ask1 * Lot * ContractSize = (Bid1 + S1*Point) * Lot * ContractSize — questo è ciò che abbiamo preso in prestito
• EUR1 = Lot * ContractSize — questo è ciò che abbiamo comprato con fondi presi in prestito al tasso di cambio Ask al momento dell'acquisto.

Il valore negativo apparirà in seguito. In effetti, non può essere qui in questo momento. Il valore negativo appare quando si chiude la posizione. Quindi, se la posizione è aperta, deve essere chiusa. Si scopre che dobbiamo eseguire l'azione Sell utilizzando lo stesso lotto. Se ci atteniamo alle considerazioni standard:

• EUR2 = Lot * ContractSize
• USD2 = Bid2 * Lot * ContractSize

Risulta che vendiamo già EUR e acquistiamo USD. Per quanto riguarda le nostre trasformazioni, si scopre che prendiamo quei EUR che abbiamo scambiato con i fondi presi in prestito e li ricambiamo nella valuta prestata. Il profitto o la perdita si ottengono sottraendo i fondi presi in prestito dai fondi ricevuti:

• Profit_EUR = EUR1 - EUR2 = 0
• Profit_USD = USD2 - USD1 = Bid2 * Lot * ContractSize - (Bid1 + S1*Point) * Lot * ContractSize = Lot * ContractSize * ( Bid2 - Bid1 - S1*Point)

Si scopre che l'EUR scompare e rimangono solo gli USD. Se il nostro deposito viene effettuato in USD, non è necessario convertire la valuta risultante nella valuta del deposito, poiché sono uguali. L'equazione è molto simile a quella che abbiamo preso come base all'inizio, con l'unica differenza che le commissioni e lo swap non vengono presi in considerazione in questo caso perché sono considerati separatamente. Riscriviamo ora questa espressione:

• Profit_USD = Lot * (ContractSize*Point) * [ ( Bid2 - Bid1 - S1*Point) / Point ]

Qui semplicemente dividiamo e moltiplichiamo il lato destro per Point (punto) per ottenere l'equazione originale. La stessa equazione può essere ottenuta se si utilizza il sistema originale di convenzioni che prevede che si venda e si compri nello stesso momento, indipendentemente dalla direzione del trade. In questo caso, tutto ciò che è stato preso in prestito ha un segno meno, a simboleggiare che siamo in debito, mentre l'importo acquistato è lasciato con un segno più. In un tale sistema di convenzioni, non abbiamo bisogno di considerare cosa stiamo cambiando in cosa e da dove. Facciamo lo stesso utilizzando questo approccio:

• EUR1 = Lotto * ContractSize
• USD1 = - Ask1 * Lot * ContractSize = - (Bid1 + S1*Point) * Lot * ContractSize

Questo è un buy. Azione 1.

• EUR2 = - Lot * ContractSize
• USD2 = Bid1 * Lot * ContractSize

Si tratta di un sell. Azione 2.

Inoltre, tutto è semplificato, perché non dobbiamo pensare a cosa sottrarre da cosa e come. È sufficiente sommare separatamente tutti gli EUR e tutti gli USD. La valuta di base scompare comunque, lasciando solo la seconda valuta. Facciamo la somma e assicuriamoci che le equazioni siano identiche alle precedenti:

• Profit_EUR = EUR1 + EUR2 = 0
• Profit_USD = USD1 + USD2 = - (Bid1 + S1*Point) * Lot * ContractSize + Bid2 * Lot * ContractSize = Lot * ContractSize * ( Bid2 - Bid1 - S1*Point)

Si scopre che il profitto di qualsiasi simbolo viene considerato esclusivamente nella seconda valuta (non in quella di base) e che la valuta di base scompare sempre durante l'intero ciclo di apertura-chiusura. Naturalmente, tutto è speculare per la vendita. Scriviamo tutto questo per completare i nostri calcoli. Ora vendiamo EURUSD e chiudiamo la posizione con un "Buy":

• EUR1 = - Lot * ContractSize
• USD1 = Bid1 * Lot * ContractSize

Si tratta di un sell. Azione 1.

• EUR2 = Lot * ContractSize
• USD2 = - (Bid2 + S2*Point) * Lot * ContractSize

Questo è un acquisto, azione due.

Ora aggiungiamo tutti i valori nello stesso modo:

• Profit_EUR = EUR1 + EUR2 = 0
• Profit_USD = USD1 + USD2 = Bid1 * Lot * ContractSize - (Bid2 + S2*Point) * Lot * ContractSize = Lot * ContractSize * ( Bid1 - Bid2 - S2*Point)

Come si può notare, l'equazione differisce solo per lo scambio di Bid1 e Bid2. Naturalmente, lo spread viene addebitato al momento della chiusura della posizione, perché il punto di chiusura è il punto di acquisto. Finora, tutto è rigorosamente conforme alle equazioni originali. Vale la pena notare che ora sappiamo cos'è il TickValue, almeno se la seconda valuta (non quella di base) del nostro simbolo corrisponde alla valuta del nostro deposito. Scriviamo l'equazione di questo valore:

• TickValue = ContractSize * Point

Tuttavia, questo valore è adatto solo ai simboli in cui la valuta del profitto è uguale alla valuta del nostro deposito. Ma cosa succede se utilizziamo, ad esempio, un tasso incrociato, come AUDNZD? L'aspetto principale non è il simbolo in sé, ma il fatto che questo valore è sempre calcolato in relazione alla valuta del nostro deposito e lo riceviamo dal server di trading. Ma se utilizziamo questa equazione in relazione al tasso incrociato, scopriamo che, ovviamente, funziona, ma ci risponderà non nella nostra valuta di deposito, ma nella seconda valuta del simbolo. Per convertire questo valore nella valuta di deposito, è necessario moltiplicarlo per un certo rapporto, che in realtà è il tasso di conversione che abbiamo considerato nel blocco precedente.

• TickValueCross = ContractSize * Point * BidAlphaCross

Il calcolo del tasso di conversione è piuttosto semplice:

1. Guardate la seconda valuta nel nostro simbolo (non quella di base)
2. Cercate un simbolo che contenga questa valuta e la valuta del nostro deposito.
3. Effettuare un cambio al tasso appropriato
4. Se necessario, trasformare il simbolo (percorso speculare)

Ad esempio, se facciamo trading su EURCHF e abbiamo un deposito in USD, il profitto iniziale sarà in CHF, quindi possiamo utilizzare lo strumento USDCHF e il suo tasso. Quindi, dobbiamo scambiare CHF con USD, quindi si scopre che dobbiamo comprare USD per CHF. Ma poiché CHF = PBid * USD, allora USD = (1/PAsk) * CHF e di conseguenza:

• BidAlphaCross = 1/PAsk

Utilizziamo un altro simbolo per il secondo esempio. Ad esempio, se facciamo trading su AUDNZD e otteniamo un profitto in NZD, possiamo prendere il tasso NZDUSD e, poiché USD = PBid * NZD, in questo caso:

• BidAlphaCross = PBid

Vediamo di capirci qualcosa. Convertire CHF in USD significa "+USD ; -CHF". In altre parole, perdiamo una valuta e ne guadagniamo un'altra. Ciò significa acquistare USD, vendendo al tasso USDCHF, al prezzo di PAsk, che in realtà significa proprio quanto segue: "USD = (1/PAsk) * CHF". È più facile percepirlo nel modo seguente: quando acquistiamo, dovremmo ricevere un po' meno USD di quanto potrebbe essere se il broker non prendesse nulla dalla nostra operazione di cambio. Ciò significa che se dividiamo per un PAsk più grande, otterremo un valore inferiore a 1/P.

Nel secondo caso, la situazione è invertita. Convertire NZD in USD significa "+USD ; -NZD", ovvero vendere al prezzo PBid utilizzando il tasso NZDUSD. Impostiamo un rapporto simile per "USD = PBid * NZD". Lo scambio viene nuovamente effettuato a un tasso leggermente peggiore, che è "PBid". Tutto corrisponde. Tutto è trasparente e facile da capire. Tieni presente che il tasso perfetto primario è "PMid", che ho considerato sopra. Considerando questo, è facile capire che lo spread non è altro che la percentuale che il broker addebita sotto forma di valuta scambiata. Pertanto, ogni operazione, sia che si tratti di aprire o chiudere una posizione, è accompagnata da una tassa del broker sullo scambio di valuta, chiamata spread. Il resto di questa imposta è contenuto in commissioni e swap.

Il tasso di conversione non è richiesto e il rapporto è uguale a uno solo se la valuta del profitto corrisponde alla valuta del nostro deposito, quindi il rapporto scompare nel caso delle principali coppie di valute e rende la dimensione del tick fissa per tutte queste coppie. Come nel caso precedente, il nostro simbolo di trading può rivelarsi un tasso transitorio, quindi non dobbiamo cercarlo tra gli altri simboli.

Considerando la presenza del nuovo valore BidAlphaCross, riscrivere le equazioni di profitto e perdita dell'ordine senza commissioni e swap:

• BuyProfit = BidAlphaCross * Lot * ContractSize * ( Bid2 - Bid1 - S1*Point)
• SellProfit = BidAlphaCross * Lot * ContractSize * ( Bid1 - Bid2 - S2*Point)

Tenendo conto che:

• Bid1 = Mid1 - (S1*Point)/2
• Bid2 = Mid2 - (S2*Point)/2

Riscriviamo le equazioni in forma più visiva, sostituendo i tassi con Mid:

• BuyProfit = BidAlphaCross * Lot * ContractSize * ( Mid2 - (S2*Point)/2 - Mid1 + (S1*Point)/2 - S1*Point)
• SellProfit = BidAlphaCross * Lot * ContractSize * ( Mid1 - (S1*Point)/2 - Mid2 + (S2*Point)/2 - S2*Point)

Semplifichiamo tutto questo:

• BuyProfit = Lot * BidAlphaCross * ContractSize * Point * [ ( Mid2 - Mid1 )/ Point - ( S1/2 + S2/2 ) ]
• SellProfit = Lot * BidAlphaCross * ContractSize * Point * [ ( Mid1 – Mid2 )/ Point  - ( S1/2 + S2/2 ) ]

Ancora una semplificazione:

• BuyProfit = Lot * TickValueCross * [ ( Mid2 – Mid1 )/ Point ] - Lot * TickValueCross * ( S1/2 + S2/2 )
• SellProfit = Lot * TickValueCross * [ ( Mid1 – Mid2 )/ Point ] - Lot * TickValueCross * ( S1/2 + S2/2 )

Ora, credo, è diventato più facile e chiaro. Ho volutamente rimosso il sommatore associato allo spread, in modo da poter vedere che si tratta esattamente del valore addebitato, indipendentemente dal tempo in cui la posizione o l'ordine rimangono attivi.

Funzione di calcolo esatto dello swap

Resta ora da chiarire le equazioni di swap. Ricordiamo le equazioni ricevute all'inizio dell'articolo:

• Swap = Lot * TickValue * SwapPoints * SwapCount(StartTime,EndTime)
• Swap = Lot * ContractSize * BidAlpha * SwapPercent/100 * SwapCount(StartTime,EndTime)

Nell'ultimo blocco abbiamo scoperto che TickValue non è un valore a una cifra e viene calcolato in modo diverso per le diverse coppie di valute. È stato stabilito che:

• TickValue = ContractSize * Point

Ma questo funziona solo per quelle coppie in cui la valuta del profitto corrisponde alla valuta del deposito. Nei casi più complessi, si utilizza il seguente valore:

• TickValueCross = ContractSize * Point * BidAlphaCross

dove anche BidAlphaCross è un valore diverso, che dipende dalla valuta di deposito e dal simbolo selezionato. Tutto questo lo abbiamo definito sopra. Su questa base, dobbiamo riscrivere la prima versione dell'equazione sostituendo la costante standard:

• Swap = Lot * TickValueCross * SwapPoints * SwapCount(StartTime,EndTime)

Ma questa equazione è ancora lontana dall'essere perfetta. Questo perché, a differenza di una commissione o di uno spread, uno swap può essere accreditato un numero arbitrariamente elevato di volte mentre la posizione rimane aperta. Si scopre che nel caso dei tassi incrociati, un valore TickValueCross non è sufficiente a descrivere l'intero swap, perché si scopre che a ogni punto di attribuzione dello swap, questo valore è leggermente diverso perché cambia il valore BidAlphaCross. Scriviamo le equazioni complete per il calcolo degli swap per le due opzioni di "tassazione":

1. Swap = SUMM(1 ... D) { Lot * (SwapPoints * K[i]) * TickValueCross[i] } - somma di tutti gli swap maturati in punti, per ogni punto incrociato 0:00
2. Swap = SUMM(1 ... D) { Lot * ContractSize * BidAlpha[i] * (SwapPercent/100 * K[i]) * } — in %

Array da sommare:

• K[i] = 1 o 3 — se il rapporto è "3", significa che era il giorno di attribuzione del triplo swap
• TickValueCross[i] — array di dimensioni dei tick nei punti di swap
• BidAlpha[i] — array di tassi di adeguamento ai punti di ricarica dello swap

Vediamo un esempio di calcolo dello swap per un ordine arbitrario. A tal fine, introdurrò le seguenti brevi notazioni:

• TickValueCross[i] = T[i]
  
• BidAlpha[i] = B[i]
  
• K[i] = K[i]

Ora vediamo graficamente come sommare gli swap:

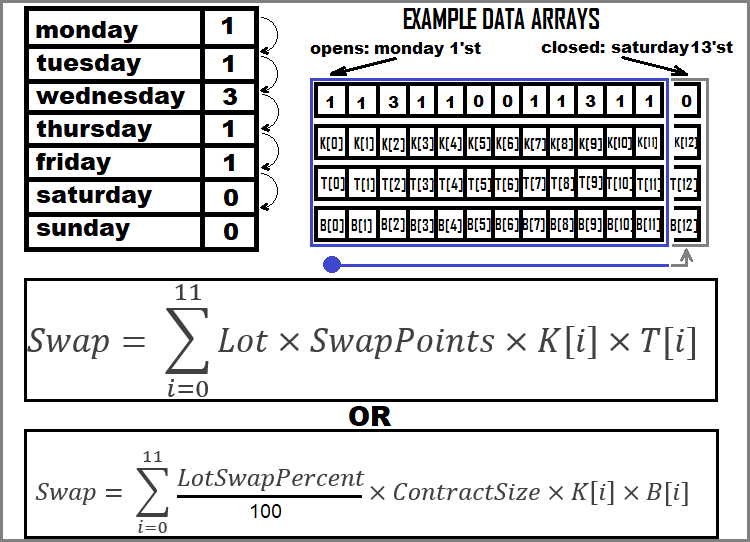
Abbiamo analizzato tutti i possibili esempi di calcolo del profitto e della perdita dell'ordine.

Parte pratica

In questa sezione, testeremo il nostro modello matematico. In particolare, presterei particolare attenzione alle questioni relative al calcolo del profitto o della perdita senza tenere conto delle commissioni e degli swap. Se vi ricordate, mi chiedevo in quale momento dovrei calcolare il valore TickValueCross se calcoliamo il profitto al tasso del cross? Questo momento è l'unica incertezza dell'intero modello che intendo testare. Per farlo, implementiamo prima tutte le funzionalità necessarie per calcolare il profitto o la perdita di qualsiasi ordine utilizzando il nostro modello matematico, testiamolo nel tester di strategia e, infine, confrontiamo i nostri calcoli con i dati degli ordini reali della cronologia di trading. L'obiettivo finale è quello di testare il nostro modello matematico e di confrontarlo con la funzione di riferimento MQL5, come OrderCalcProfit, allo stesso tempo.

Per valutare tutto questo, è necessario introdurre quattro grandezze:

1. Real — profitto dell’ordine dalla cronologia
2. BasicCalculated — lo stesso profitto calcolato all'apertura di un ordine utilizzando la funzione OrderCalcProfit
3. CalculatedStart — profitto calcolato al momento dell'apertura dell'ordine utilizzando il nostro modello matematico
4. CalculatedEnd — profitto calcolato al momento della chiusura dell'ordine utilizzando il nostro modello matematico

Ciò comporta tre tipi di deviazione media del valore del profitto:

1. AverageDeviationCalculatedMQL = Summ(0..n-1) [ 100 * MathAbs(BasicCalculated - Real)/MathAbs(Real) ]  / n : deviazione relativa del profitto tramite codice MQL5
2. AverageDeviationCalculatedStart = Summ(0.. n-1 ) [ 100 * MathAbs(CalculatedStart - Real)/MathAbs(Real) ] / n : deviazione relativa del profitto da parte del nostro codice all'apertura di un ordine
3. AverageDeviationCalculatedEnd =  Summ(0.. n-1 ) [  100 * MathAbs(CalculatedEnd - Real)/MathAbs(Real) ] / n : deviazione relativa del profitto tramite il nostro codice quando si chiude un ordine
   

Analogamente, è possibile inserire tre tipi di deviazione massima:

1. MaxDeviationCalculatedMQL = Max(0.. n-1 ) [ (100 * MathAbs(BasicCalculated - Real)/MathAbs(Real)) ] - deviazione del profitto relativo tramite codice MQL5
2. MaxDeviationCalculatedStart =  Max(0.. n-1 ) [  (100 * MathAbs(CalculatedStart - Real)/MathAbs(Real)) ]  - deviazione relativa del profitto tramite il nostro codice all'apertura di un ordine
3. MaxDeviationCalculatedEnd =  Max(0.. n-1 ) [  (100 * MathAbs(CalculatedEnd - Real)/MathAbs(Real)) ]  - deviazione relativa del profitto da parte del nostro codice quando si chiude un ordine

dove:

• Summ(0..n-1) — somma di tutte le deviazioni relative di tutti gli "n" ordini
• Max(0..n-1) — massima deviazione relativa da tutti gli "n" ordini
  

Possiamo testare il nostro modello matematico implementando questi calcoli nel codice di un EA arbitrario. Cominciamo a implementare la nostra equazione del profitto. L'ho fatto nel modo seguente:

double CalculateProfitTheoretical(string symbol, double lot,double OpenPrice,double ClosePrice,bool bDirection)
   {
   //PrBuy = Lot * TickValueCross * [ ( Bid2 - Ask1 )/Point ]
   //PrSell = Lot * TickValueCross * [ ( Bid1 - Ask2 )/Point ]
   if ( bDirection )
      {
      return lot * TickValueCross(symbol) * ( (ClosePrice-OpenPrice)/SymbolInfoDouble(symbol,SYMBOL_POINT) );
      }
   else
      {
      return lot * TickValueCross(symbol) * ( (OpenPrice-ClosePrice)/SymbolInfoDouble(symbol,SYMBOL_POINT) );
      }   
   }

Qui abbiamo due equazioni in una: per l'acquisto e per la vendita. Il marcatore "bDirection" è responsabile di questo. La funzione aggiuntiva che calcola la dimensione del tick è evidenziata in verde. L'ho implementata nel modo seguente:

double TickValueCross(string symbol,int prefixcount=0)
   {
   if ( SymbolValue(symbol) == SymbolBasic() )
      {
      return TickValue(symbol);
      }
   else
      {
      MqlTick last_tick;
      int total=SymbolsTotal(false);//symbols in Market Watch
      for(int i=0;i<total;i++) Symbols[i]=SymbolName(i,false);
      string crossinstrument=FindCrossInstrument(symbol);
      if ( crossinstrument != "" )
         {
         SymbolInfoTick(crossinstrument,last_tick);
         string firstVAL=StringSubstr(crossinstrument,prefixcount,3);
         string secondVAL=StringSubstr(crossinstrument,prefixcount+3,3);
         if ( secondVAL==SymbolBasic() && firstVAL == SymbolValue(symbol) )
            {
             return TickValue(symbol) * last_tick.bid;
            }
         if ( firstVAL==SymbolBasic() && secondVAL == SymbolValue(symbol) )
            {
            return TickValue(symbol) * 1.0/last_tick.ask;
            }         
         }
      else return TickValue(symbol);  
      }
   return 0.0;   
   }

Sono presenti anche due implementazioni per i casi seguenti:

1. La valuta di profitto del simbolo è la stessa del nostro deposito.
2. Tutti gli altri casi (alla ricerca di un tasso transitorio)

Anche il secondo scenario si divide in due casi:

• La valuta di deposito si trova nella parte superiore del tasso di conversione.
• La valuta di deposito si trova in fondo al tasso di conversione

Tutto è rigorosamente conforme al modello matematico. Per implementare le ultime divisioni, dobbiamo prima trovare lo strumento giusto per calcolare il tasso di conversione:

string FindCrossInstrument(string symbol,int prefixcount=0)
   {
   string firstVAL;
   string secondVAL;
   for(int i=0;i<ArraySize(Symbols);i++)
      {
      firstVAL=StringSubstr(Symbols[i],prefixcount,3);
      secondVAL=StringSubstr(Symbols[i],prefixcount+3,3);
      if ( secondVAL==SymbolBasic() && firstVAL == SymbolValue(symbol) )
         {
         return Symbols[i];
         }
      if ( firstVAL==SymbolBasic() && secondVAL == SymbolValue(symbol) )
         {
         return Symbols[i];
         }      
      }
   return "";
   }

A tal fine è necessario sapere come "togliere" la valuta base dal nome di un simbolo:

string SymbolValue(string symbol,int prefixcount=0)
   {
   return StringSubstr(symbol,prefixcount+3,3);
   }

E ottenere la valuta di profitto utilizzando la funzione MQL5 integrata:

string SymbolBasic()
   {
   return AccountInfoString(ACCOUNT_CURRENCY);
   }

Confrontate tutto questo con le valute di tutti i simboli del Market Watch prima della prima corrispondenza. Ora possiamo utilizzare questa funzionalità al momento dell'apertura e della chiusura degli ordini. Se volete, potete vedere il resto del codice nel file allegato qui sotto. Ho aggiunto il calcolo delle deviazioni dopo la fine del backtest. Vengono scritti nel log del terminale. Ho testato tutte le ventotto principali coppie di valute e i tassi incrociati e messo i risultati in una tabella in modo da poter valutare le prestazioni del nostro modello matematico e confrontarlo con l'implementazione MQL5. I risultati sono stati suddivisi in tre blocchi condizionali. I primi due hanno il seguente aspetto:

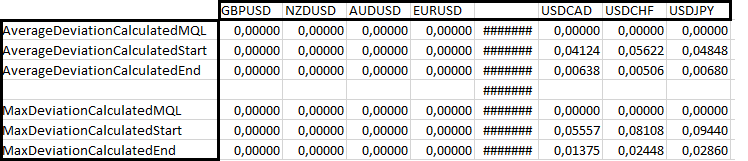
Come si può vedere, per le prime quattro coppie di valute, sia l'MQL5 che la nostra implementazione funzionano perfettamente perché la valuta di profitto è la stessa di quella di deposito. Segue un blocco di tre coppie di valute, in cui la valuta di base è la stessa della valuta di profitto. In questo caso, l'implementazione MQL5 funziona meglio, ma è comunque evidente che l'errore di calcolo all'apertura di un ordine è molto più elevato rispetto allo stesso errore alla chiusura. Questo indica indirettamente che il calcolo deve essere eseguito nel momento in cui l'ordine viene chiuso. Diamo un'occhiata ad altre coppie di valute:

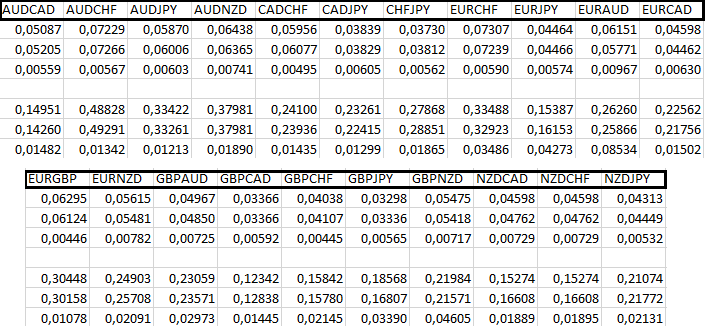
Qui la mia funzionalità non è inferiore a quella di base di MQL5. Inoltre, è evidente che i calcoli effettuati al momento della chiusura di una posizione sono sempre molto più accurati. L'unica cosa che non riesco a spiegare è la presenza di zeri nella prima riga del secondo blocco. Le ragioni possono essere molte, ma mi sembra che non siano legate al mio modello, anche se posso sbagliarmi. Per quanto riguarda il controllo delle equazioni per le commissioni e gli swap, non credo sia necessario. Sono fiducioso in queste equazioni, poiché non c'è nulla di particolarmente complicato in esse.

Conclusioni

In questo articolo ho proposto un modello matematico creato da zero e guidato solo da frammenti di informazioni. Il modello contiene tutto ciò che serve per calcolare gli ordini per le principali coppie di valute e i tassi incrociati. Il modello è stato testato nel tester di strategia ed è pronto per l'uso immediato in qualsiasi EA, indicatore o script utile. In realtà, l'applicabilità di questo modello è molto più ampia del semplice calcolo di profitti, perdite o costi, ma questo è un argomento per un altro articolo. Potete trovare tutte le funzionalità necessarie ed esempi di utilizzo nella ricerca EA che ho utilizzato per compilare la tabella. L'EA è allegato all'articolo. Potete eseguirlo voi stessi e confrontare i risultati con la tabella. Soprattutto, credo di essere riuscito a creare un "manuale" semplice e logico.