Piyasa matematiği: kâr, zarar ve maliyetler

İçindekiler

• Giriş
• Emirlerin kâr veya zararlarını hesaplamak için denklemler
• Açılış ve kapanıştaki makas
• Emirlerin kâr ve zararını hesaplamak için en doğru yöntem
• Swap hesaplama formülü
• Uygulama kısmı
• Sonuç

Giriş

Uzman Danışmanlar geliştirirken, kâr veya zararı hesaplarken belirli değerlerin ne anlama geldiğine hiç dikkat etmedim. Uzman Danışmanların oluşturulması bu konuya derinlemesine girmeyi gerektirmez. Gerçekten de, MQL5 ve hatta MQL4'ün hesaplama yapmak için gerekli tüm fonksiyonları içerdiğini göz önünde bulundurduğumuzda neden tüm bu değerleri öğrenmemiz gerekiyor? Belirli bir süre ve belirli bir deneyimden sonra, kaçınılmaz olarak bazı sorular ortaya çıkmaya başlıyor. Nihayetinde, daha önce bize önemsiz görünen bu tür ayrıntıları fark etmeye başlıyoruz. Biraz düşündükten sonra, bir Uzman Danışmanın kapalı bir kutu olduğunu fark ediyorsunuz. Konuyla ilgili internette bulabildiğim tüm veriler yetersiz ve yapılandırılmamış çıktı. Bu yüzden kendim yapılandırmaya karar verdim. Bu makaleyi okuduktan sonra, eksiksiz ve çalışan bir matematiksel model elde edecek, ayrıca emirlerle ilgili her şeyi anlamayı ve doğru bir şekilde hesaplamayı öğreneceksiniz.

Emirlerin kâr veya zararlarını hesaplamak için denklemler

Verimli bir ticaret sistemi geliştirmek için öncelikle her bir emrin kâr veya zararının nasıl hesaplandığını anlamak gerekir. Hepimiz para yönetim sistemimizi sürdürmek için kâr ve zararlarımızı bir şekilde hesaplayabiliyoruz. Birileri bunu sezgisel olarak yapar, birileri kaba tahminler yürütür, ancak neredeyse her Uzman Danışmanın gerekli tüm miktarların gerekli hesaplamalarına sahiptir.

Uzman Danışmanlar geliştirmek düşüncelerinizi disipline eder ve neyin nasıl hesaplandığını anlamanızı sağlar ki bu paha biçilemez bir şeydir. Şimdi sadede gelelim. Bir emrin kârının nasıl hesaplandığına dair en basit fikirle başlamakta fayda var. Şahsen ben her zaman kâr hesaplamasının özünde oldukça karmaşık olduğunu, ancak birkaç basit hususa dayandığını biliyordum. Anlamayı kolaylaştırmak için makas, swap ve komisyonun var olmadığını varsayalım. Bence pek çok kişi ilk başta bu değerleri dikkate bile almıyor. Elbette, MQL5 dili OrderCalcProfit vb. gibi yerleşik fonksiyonlar içerir, ancak bu makalede herkesin neyin nasıl hesaplandığını anlaması için temelleri gözden geçirmek istiyorum. Bu titizlik şaşırtıcı olabilir, ancak makas, komisyon ve swap gibi parametrelere dikkat etmemek birçok yatırımcının yaptığı ölümcül bir hatadır. Bu değerlerin her biri kâr veya zararı kendi açısından etkiler. Hesaplamalarımda her şeyi dikkate alacağım ve bu tür küçük şeylerin nasıl yardımcı olabileceğini göstereceğim. Makaslar, komisyonlar ve swaplar hariç emirlerin kâr ve zararı:

• PrBuy = Lot*TickValue*[(PE-PS)/Point] - alış emri için kâr
• PrSell = Lot*TickValue*[(PS-PE)/Point] - satış emri için kâr
• Point - seçilen sembolde olası minimum fiyat değişikliği
• TickValue - fiyat "1" Point hareket ettiğinde kârlı bir pozisyon için kâr değeri
• PE - işlem kapanış fiyatı (Bid)
• PS - işlem açılış fiyatı (Bid)

MQL5'teki Point ve TickValue gibi değerler önceden tanımlanmış değişkenler düzeyinde tanımlanır veya SymbolInfoDouble tipi fonksiyonların geri dönüş değeri şeklinde yerleşik fonksiyonlar içerisinde mevcuttur. Makalelerimde düzenli olarak MQL5 konusuna bir şekilde değineceğim çünkü MQL5'in veya belirli fonksiyonlarının nasıl oluşturulduğunu analiz ederek birçok konunun özüne inmek genellikle mümkündür.

Şimdi bu denklemin anlamını biraz daha genişletelim. Bir alış emri Ask fiyatından açılırken, bir satış emri Bid fiyatından açılır. Buna göre, alış emri Bid fiyatından kapatılırken, satış emri de Ask fiyatından kapatılır. Yeni değişiklikleri dikkate alarak denklemleri yeniden yazalım:

• PrBuy = Lot*TickValue*[(Bid2–Ask1)/Point] - alış emri için kâr
• PrSell = Lot*TickValue*[(Bid1–Ask2)/Point] satış emri için kar
• Bid1 - satış işlemi açılış fiyatı
• Ask1 - alış işlemi açılış fiyatı
• Bid2 - alış işlemi kapanış fiyatı
• Ask2 - satış işlemi kapanış fiyatı

Aşağıdaki enstrüman özellikleri penceresi parçası, daha sonra ihtiyaç duyacağımız verilerin çoğunu içermektedir:

Bu, hesaplama için ihtiyaç duyulacak verilerin yalnızca bir kısmıdır. Verilerin geri kalanı çeşitli yerleşik MQL5 fonksiyonları kullanılarak elde edilebilir. Örnek olarak USDJPY'yi ele alalım. Aslında kod yazmak için enstrüman özelliklerine ihtiyacımız yok, ancak bu verilerin nerede gösterildiğini anlamak çok faydalı olabilir.

Devam edelim ve bu kez komisyonu değerlendirelim. Emir başına komisyon çeşitli şekillerde hesaplanabilir, ancak tüm ana yöntemler işlem yaptığımız lot miktarının yüzdesine dayanır. İşlem komisyonu kesmenin başka yolları da vardır, ancak bunlara ihtiyacımız olmayacağı için burada ele almayacağım. Komisyonun hesaplanması için iki olası senaryoyu ele alacağım. Yeterli olduklarına inanıyorum. Swapı temel alırsak, swap örnekleri komisyona uygulanabilecek başka bir yaygın hesaplama yöntemi önerebilir - puan cinsinden hesaplama.

Sonuç olarak, görünüşte farklı iki yöntemimiz var. Ancak, göreceğimiz gibi, bu yöntemler, makas da dahil olmak üzere aynı "ücret alma" yöntemini algılamanın sadece uygun bir şeklidir. Aşağıda komisyonu hesaplamak için iki denklem bulunmaktadır:

1. Comission = Lot*TickValue*ComissionPoints
2. Comission = Lot*ContractSize*BidAlpha*ComissionPercent/100

Burada, işlem sunucusundan bilgi alan yerleşik fonksiyonlar düzeyinde MQL5'te de bir uygulamaya sahip olan yeni "ContractSize" değerini görüyoruz. Bu değer en önemlilerinden biridir ve programcıların hesaplamalarını basitleştirmek için örtük bir biçimde de olsa kesinlikle tüm kâr ve zarar hesaplamalarında bulunur. Programcının bakış açısından bu tür basitleştirmelerin geçerliliğini görüyorum. Ancak şu anki hedefimiz her şeyi anlamak. Bunun neden gerekli olduğunu makalenin sonuna doğru göreceksiniz. Ayrıca, ek bir BidAlpha değişkeni ekledim. Aşağıda anlamını da açıklayacağım. Sembol özelliklerinde belirtilen aşağıdaki değerler de görünmektedir:

• ComissionPoints - puan cinsinden komisyon
• ComissionPercent - sözleşme büyüklüğünün yüzdesi cinsinden komisyon

BidAlpha çarpanı, baz para birimi cinsindeki swapı bakiyemiz cinsinden swapa dönüştürmek için gereklidir. Burada dört senaryo bulunmaktadır:

1. BidAlpha = 1 (baz para birimi mevduat para birimi ile aynıysa)
2. BidAlpha = Bid (seçilen sembolün)
3. BidAlpha = Bid (seçilen sembolün baz para biriminin geçiş sembolünün baz para birimi ile aynı olduğu ve ikinci para biriminin mevduat para birimi ile aynı olduğu ilgili kurun)
4. BidAlpha = 1/Ask (seçilen sembolün baz para biriminin geçiş sembolünün ikinci para birimi ile aynı olduğu ve baz para biriminin mevduat para birimi ile aynı olduğu ilgili kurun)

Nitekim, sözleşme büyüklüğü USDCHF çiftine uygulanırsa, seçilen çiftin baz para biriminin USD olduğu açıktır. Diyelim ki USD cinsinden bir bakiyemiz var, o zaman geçiş dövizi USDUSD olur ve oranı her zaman birdir. İkinci durum daha da basittir. Aynı zamanda dönüşüm oranı olan EURUSD çiftimiz olduğunu varsayalım, o halde bu döviz çiftinin Bid değeri gerekli değerdir. Üçüncü durum şu şekilde olabilir. Döviz çiftimizin EURNZD olduğunu varsayalım. O zaman EUR ve USD arasındaki dönüşüm oranını bulmamız gerektiği ortaya çıkıyor. EURUSD kuru ve bu kurun Bid fiyatı ihtiyacımız olan şeydir. Dördüncü durumda işler biraz daha karmaşıktır. CHFJPY'yi seçtiğimizi varsayalım. Forex'te CHFUSD döviz kuru olmadığı için geçiş çifti USDCHF olacaktır. Elbette kendi sentetik sembolümüzü oluşturabilir ve CHFUSD ile çalışabiliriz. Bu durumda, önceki durumu kullanabiliriz. Ama aslında, sadece bu sembolü ters çevirmemiz gerekiyor, o zaman oranı mevcut "uygunsuz" oranın "1/Ask" değerine eşit olacaktır. Aslında, ona odaklanmadan sentetik bir sembol yaratıyoruz. Aynı şeyler swaplar için de geçerlidir. Başka sorular da var. Örneğin, geçiş dövizinde hangi fiyat kullanılmalıdır - Bid, Ask veya Mid? Bu soru mevcut yaklaşım çerçevesinde çözülemez. Yol boyunca yavaş yavaş doğru yaklaşımı bulacağız. Şimdi iyileştirme çerçevesini en azından yaklaşık olarak tanımlayalım. Bunu yapmak için, makas, swap ve komisyon gibi tüm "ücret alma" seçeneklerini hesaba katarak genel kâr ve zarar denkleminin en azından ilk yaklaşık versiyonunu yazmalıyız.

Swapları hesaplamak için benzer denklemler elde ederiz:

1. Swap = Lot*TickValue*SwapPoints*SwapCount(StartTime, EndTime)
2. Swap = Lot*ContractSize*BidAlpha*SwapPercent/100*SwapCount(StartTime, EndTime)

Denklemler gerçekten de oldukça benzerdir. Tek fark, belirli çarpanın burada SwapCount fonksiyonu şeklinde ortaya çıkmış olmasıdır. Umarım terminoloji konusunda bana biraz özgürlük tanırsınız. Buna "fonksiyon" diyorum, çünkü swaplar hemen tahsil edilmez ve büyüklüğü emir açılış ve kapanış zamanlarına bağlıdır. Kabaca bir yaklaşımla, elbette çarpan olmadan yapabilir ve aşağıdakileri yazabiliriz:

• SimpleCount = MathFloor((EndTime-StartTime)/(24*60*60))

EndTime ve StartTime'ın 'datetime' tipinde olduğunu varsayarsak, aralarındaki fark emir açılış ve kapanış noktaları arasındaki saniye sayısına eşittir. Swap günde bir kez ücretlendirilir, bu nedenle bu değeri bir gündeki saniye sayısına bölmeniz yeterlidir. Bu şekilde swapların nasıl değerlendirilebileceğine dair ilk fikri edinebiliriz. Elbette bu denklem mükemmel olmaktan uzaktır, ancak ne tür bir fonksiyon olduğu ve ne geri döndürdüğü sorusunun cevabını verir. Ayrıca, swapın nasıl (en azından yaklaşık olarak) hesaplandığı hakkında bir fikir verebilir. Pozisyon ömrü boyunca tahakkuk eden swap sayısını geri döndürür. Komisyona benzer şekilde, sembol özellerinde hesaplama yönteminin zorunlu olarak belirtilmesiyle birlikte swap için olası iki değer vardır:

• SwapPoints - puan cinsinden tek bir pozisyon taşıma için swap
• SwapPercent - sözleşme büyüklüğünün yüzdesi cinsinden tek bir pozisyon taşıma için swap

Komisyon durumunda denklemler daha basit ve açıklama gerektirmezken, swap durumunda her şey çok daha karmaşıktır, ancak basitleştirmelerin inceliklerini ve nüanslarını daha sonra ele alacağız. İlk olarak, komisyonlar ve swaplar hariç olmak üzere kâr ve zarar denklemlerini daha tutarlı bir forma getirelim:

• PrBuy = Lot*TickValue*[(Bid2-(Bid1+S1*Point))/Point] - alış emri için kâr
• PrSell = Lot*TickValue*[(Bid1-(Bid2+S2*Point))/Point] - satış emri için kâr
• S1 - alış emri açarken makas
• S2 - satış emri açarken makas

Ask'in hem makas hem de Bid'i içerdiği açıktır. Emrin sonucunda oluşan kâr veya zararı makastan ayırarak ayrı bir toplam haline getirelim:

• PrBuy = Lot*TickValue*[(Bid2-Bid1)/Point] + (-Lot*TickValue*S1) - alış emri için kâr
• PrSell = Lot*TickValue*[(Bid1-Bid2)/Point] + (-Lot*TickValue*S2) - satış emri için kâr

Her iki denklemde de broker tarafından tahsil edilen kısım olan belirli bir toplamın ayrıldığı görülebilir. Elbette bu miktarın tamamı değildir, ancak en azından şimdi ne elde ettiğimizi ve brokerın ne aldığını daha net görebiliyoruz. İlk durumda, makas üzerindeki "ücret", "alış" pozisyonu açarken ve ikinci durumda da "satış" pozisyonunu kapatırken makas değerine bağlı olduğunu unutmayın. Brokera kârımızın bir kısmını tam olarak her zaman satın alma sırasında bir makas şeklinde verdiğimiz ortaya çıktı. Gerçekten de, forex ticaretini daha derinlemesine incelersek, bir alış pozisyonu açmanın ve bir satış pozisyonunu kapatmanın denklemlerimiz tarafından onaylanan eşdeğer bir eylem olduğu anlaşılır. Bu durumda:

• S1 - herhangi bir pozisyon açarken puan cinsinden makas
• S2 - herhangi bir pozisyonu kapatırken puan cinsinden makas

Bu değerler, makası görüntülemek istiyorsanız Piyasa Gözlemi penceresinde görebileceğiniz değerlerdir. Karşılık gelen girdilere sahip yerleşik SymbolInfoInteger MQL5 fonksiyonu tam olarak aynı değerleri geri döndürür. Girdileri MQL5 Yardımında bulabilirsiniz. Bu durumda benim görevim, MQL5 diline bağlı uygun bir matematiksel hesaplama modeli oluşturmaktır, böylece bu denklemler herhangi bir Uzman Danışmana veya başka bir yararlı MQL5 koduna hemen kodlanabilir. İşte şimdi hem swap hem de komisyona benzeyen toplamımız:

• SpreadBuy = -Lot*TickValue*S1
• SpreadSell = -Lot*TickValue*S2

Açılış ve kapanıştaki makas

Geleneksel olarak, makas alış noktasında hesaplanır, ancak şimdi size bunun neden yanlış olduğunu göstereceğim. Çok sayıda piyasa araştırması yaptım ve fiyat hareketinin en tahmin edilebilir noktasının "0:00" noktası olduğu ortaya çıktı. Bu, bir günden diğerine geçiş noktasıdır. Bu noktayı dikkatle gözlemlerseniz, tüm döviz çiftlerinde yaklaşık olarak aynı şeyi göreceksiniz - fiyatın aşağı yönde doğru bir sıçraması. Bu, bu noktada makastaki bir artış nedeniyle gerçekleşir. Sıçramayı eşit bir geri dönüş takip eder. Makas nedir? Makas, alış ve satış fiyatları arasındaki boşluktur. Geleneksel olarak, bu boşluğun piyasa derinliğinin bir sonucu olduğuna inanılmaktadır. Piyasa derinliği limit emirlerle doygun hale gelirse, makas sıfır olma eğilimindedir ve katılımcılar piyasadan ayrılırsa makas artar. Buna piyasa derinliğinin dağılması da diyebiliriz. İlk bakışta bile burada asıl önemli olanın Bid olmadığını söyleyebiliriz. Ask ve Bid'in temelde eşit olduğu ortaya çıktı. Örneğin, "EURUSD"den bir USDEUR ayna enstrümanı oluşturmanın mümkün olduğunu ve ardından Bid'in Ask'e ve tam tersi olarak Ask'in de Bid'e dönüştüğünü hayal edersek bunu anlamak kolaydır. Basitçe söylemek gerekirse, piyasa derinliğini tersine çeviriyoruz.

Faydalı olsa da, Ask çizgisi genellikle grafikte gösterilmez:

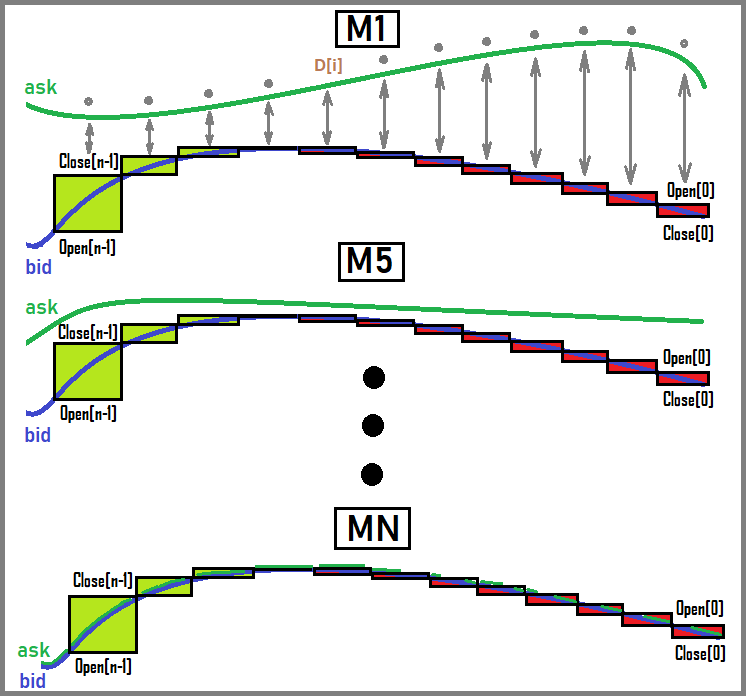
Gördüğümüz gibi, grafik zaman dilimindeki artışla birlikte Bid ve Ask fiyatları birleşmeye başlıyor. Belki de bu hususlar nedeniyle hiçbir terminal her iki satırı da göstermiyor, ancak ben şahsen bunun gerekli bir seçenek olduğunu düşünüyorum. Ancak, bu değerlerin varlığını ve aralarındaki farkı bilmek o kadar da önemli değildir, çünkü bunları yine de bir Uzman Danışmanda kullanabilirsiniz. Burada Mid’i çizmedim, ancak herkesin bu çizginin Bid ve Ask arasında tam ortada olduğunu anladığını düşünüyorum. Açıkçası, yüksek zaman dilimleri için bu değerler arasındaki fark pratikte bir rol oynamaz ve Ask'in varlığını hesaba katmanıza bile gerek yok gibi görünür, ancak aslında gereklidir. Bu ayrıntılar çok önemlidir.

Bunu akılda tutarak, artık piyasa derinliğinin ortasının bu tür dönüşümler sırasında değişmez olduğunu kesin olarak söyleyebiliriz. Bu değer aşağıdaki gibi hesaplanabilir:

• Mid = (Ask+Bid)/2

Böyle bir gösterimi göz önünde bulundurarak ve son denklemi kullanarak şunu görebiliriz:

• Bid = Mid*2 -Ask
• Ask = Mid*2 - Bid

Devamında:

• Bid = Mid*2 - (Bid+S*Point) = Mid - (S*Point)/2
• Ask = Mid*2 - (Ask-S*Point) = Mid + (S*Point)/2

Bu ifadeler artık emirlerin kâr veya zararını hesaplamak için orijinal denklemlere yerleştirilebilir. Tam olarak bu ifadeleri elde etmek önemliydi, çünkü size daha önce anlamadığınız bir şeyi göstermek istiyorum. Broker tarafından tahsil edilen tutarın aslında yalnızca alış noktasına değil, herhangi bir pozisyonun hem giriş hem de çıkış noktalarına bağlı olduğu ortaya çıktı. Yeni genişletilmiş tanımları eklediğimizde denklemlerimizin neye dönüşeceğini görelim. Şunu elde ederiz:

• PrBuy = Lot*TickValue*[((Mid2 - (S2*Point)/2) - (Mid1 + (S1*Point)/2)))/Point]
• PrSell = Lot*TickValue*[((Mid1 - (S1*Point)/2) - (Mid2 + (S2*Point)/2)))/Point]

Uygun dönüşümlerden sonra:

• PrBuy = Lot*TickValue*[(Mid2-Mid1)/Point] - Lot*TickValue*(S1/2+S2/2)
• PrSell = Lot*TickValue*[(Mid1-Mid2)/Point] - Lot*TickValue*(S1/2+S2/2)

Şunu göz önünde bulundurarak:

• Bid1 = Mid1 - (S1*Point)/2
• Bid2 = Mid2 - (S2*Point)/2
• Ask1 = Mid1 + (S1*Point)/2
• Ask2 = Mid2 + (S2*Point)/2

Ve şunu da aklınızda bulundurun:

• Mid1 - herhangi bir pozisyon açarken piyasa derinliğinin ortası
• Mid2 - herhangi bir pozisyonu kapatırken piyasa derinliğinin ortası

Kolaylık olması açısından, makaslardan kaynaklanan zararı tanımlayan negatif toplamı aşağıdaki gibi gösteriyoruz:

• Spread = -Lot*TickValue*((S1*Point)/2 + (S2*Point)/2)

Ve buna göre, makas, komisyon ve swap hariç kâr veya zararı gösteren toplam:

• ProfitIdealBuy = Lot*TickValue*[(Mid2-Mid1)/Point]
• ProfitIdealSell = Lot*TickValue*[(Mid1-Mid2)/Point]

Şimdi makas, komisyon ve swaplardan kaynaklanan tüm zararları dikkate alarak uygun denklemler yazabiliriz. İfade prototipi ile başlayalım. Burada dikkate alınan tek şey makas olacak şekilde son emir kâr ve zarar denklemlerini temel alalım:

• TotalProfitBuy = ProfitIdealBuy+(Spread+Comission+Swap)
• TotalProfitSell= ProfitIdealSell+(Spread+Comission+Swap)

Belki de bu denklemi en başta yazmalıydım ama burada yazmamın daha uygun olduğunu düşünüyorum. Belirsiz TickValue'nun neredeyse her yerde mevcut olduğunu görebiliriz. Asıl soru, bunun nasıl hesaplandığı ve farklı zaman noktalarında hesaplama için tek ve aynı değerin nasıl kullanılabileceğidir. Zaman noktaları pozisyonlara giriş ve çıkışlar anlamına gelir. Sanırım, bu değerin doğası gereği dinamik olduğunu ve dahası, her ticaret sembolü için farklı olduğunu anlıyorsunuz. Bu değeri bileşenlerine ayırmadan, ne kadar uzak "hedeflerimiz" varsa o kadar büyük hatalar elde edeceğiz. Başka bir deyişle, elde edilen denklemler sadece bir yaklaşımdır. Bu eksiklikleri içermeyen, mutlak kesin bir denklem vardır. Yukarıda elde edilen oranlar onların limiti olarak hizmet eder. Limitlerin kendileri aşağıdaki gibi ifade edilebilir:

• Lim[dP -> 0](PrBuy(Mid1, Mid1+dP…)) = TotalProfitBuy(Mid1, Mid1+dP…)
• Lim[dP -> 0](PrSell(Mid1, Mid1+dP…)) = TotalProfitSEll(Mid1, Mid1+dP…)
• Mid1+dP = Mid2 - yeni fiyat, ‘önceki fiyat’ artı ‘sıfıra eğilimli delta’dan elde edilir
• TotalProfitBuy = TotalProfitBuy(P1, P2…) - tanımlandığı üzere, kâr veya zarar, Mid değerlerinin ve diğer birçok değerin bir fonksiyonudur
• TotalProfitSell = TotalProfitSell(P1, P2…) - benzer

Genel olarak, durumun anlaşılması için eşdeğer limitler birçok şekilde oluşturulabilir. Ancak onları çoğaltmaya gerek yoktur. Bizim durumumuzda, netlik için bir tanesi yeterlidir.

Her ne kadar bazı denklemlere sahip olsak ve hatta çalışıyor olsalar da, uygulanabilirlikleri çok koşulludur. Daha sonra, bu tür yaklaşık denklemleri gerektiren başlangıç denklemlerini elde etmekle meşgul olacağız. Bir kâr ya da zararın hangi yapı taşlarından oluştuğunu bilmeden bu denklemleri asla elde edemeyiz. Buna karşılık, bu denklemler sadece kâr ve zararı hesaplamak için en doğru oranları bulmamıza değil, aynı zamanda daha sonra kâr sağlayabilecek piyasa süreçlerinin dengesizliğini bulmamıza da yardımcı olacaktır.

Emirlerin kâr ve zararını hesaplamak için en doğru yöntem

Bu denklemlerin nasıl oluşturulacağını anlamak için temellere, yani alış ve satışın ne olduğuna geri dönmemiz gerekir. Ancak öncelikle, alışın aslında paranızı bir ürünle (emtiayla) değiştirmek anlamına geldiğini hatırlamanın önemli olduğunu düşünüyorum. Başka bir para birimi, belirli mallara sahip olma kabiliyetini sembolize ettiği için bir emtia olarak görülebilir. O halde satışın, ikinci para biriminin birincisiyle değiştirilmesinin tersi bir süreç olduğu açıktır. Ancak tüm yorumları bir kenara bırakırsak, alış ve satışın eşdeğer eylemler olduğu ortaya çıkar. Bir para birimi diğeriyle değiştirilir ve tek fark hangi para birimini verdiğimiz ve karşılığında hangisini aldığımızdır.

Bu hesaplamalar hakkında bilgi ararken, kişisel olarak uzun süre kavrayamadığım garip ifadeler buldum, çünkü bunların hiçbir dayanağı yoktu. Çeşitli teknik materyalleri inceleme konusunda oldukça fazla deneyime sahip bir teknik bilim meraklısı olduğum için, çok basit iki gerçek belirledim. Eğer materyal sizin için açık değilse ve soru işaretleri uyandırıyorsa, o zaman:

• Yazarlar bunu kendileri de tam olarak anlamıyor, bu yüzden sizi tam tersine ikna etmek için ellerinden geleni yapıyorlar (bu genellikle mantık karşıtı ifadeler kullanılarak yapılır)
• Gereksiz bilgileri sizden saklamak için ayrıntılar kasıtlı olarak atlanır

Aşağıdaki şekil fikri daha da geliştirerek anlaşılmasını kolaylaştırmaktadır. İki tür piyasa emrinin açılışını ve kapanışını göstermektedir:

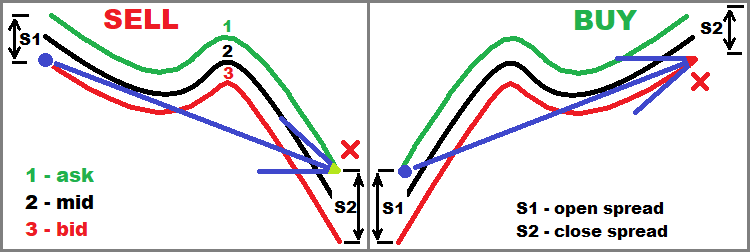
Şimdi, makaslar bölümünün ve mevcut bölümün daha net hale geleceğini düşünüyorum. Genel olarak, bu şekil tüm makale için geçerlidir, ancak en çok bu blokta kullanışlıdır.

Elbette, özelleşmiş literatürde doğru hesaplamalar olduğundan eminim, ancak bu bilgiyi bulmanın kendi başınıza neyin eksik olduğunu tahmin etmekten daha zor olduğu açıktır. Geleneksel olarak, örneğin EURUSD satın aldığımızda, EUR alıp USD sattığımız varsayılır. Bunu yazalım:

• EUR = Lot*ContractSize
• USD = - Ask1*Lot*ContractSize = -(Bid1 + S1*Point)*Lot*ContractSize

Bu durumda, alış yaparken, baz para biriminden pozitif bir miktar ve ikinci para biriminden negatif bir miktar elde ettiğimiz ortaya çıkar. Sanırım bunun tamamen saçmalık olduğunu düşünen tek kişi ben değilim. Biraz düşündükten sonra, oranların doğru olduğu, ancak oldukça anlaşılır olmayan bir şekilde sunulduğu sonucuna vardım. Bunu şu şekilde değiştirelim... EUR satın almak için başka bir para birimi olan USD'ye ihtiyacımız var, onu ya bakiyemizden, ya brokerdan borç alarak ya da her iki yöntemi de kullanarak edinebiliriz. Başka bir deyişle, önce USD’yi bir tür ortak kasadan borç alıyoruz. Bu, şu şekilde görünür:

• USD1 = Ask1*Lot*ContractSize = (Bid1 + S1*Point)*Lot*ContractSize - bu, borç aldığımız şey
• EUR1 = Lot*ContractSize - bu, satın alma sırasındaki Ask döviz kuru üzerinden borç parayla satın aldığımız şey

Negatif değer daha sonra görünecektir. Aslında, şu anda burada olamaz. Pozisyonumuzu kapattığımızda negatif değer görünür. Dolayısıyla, pozisyon açıksa kapatılmalıdır. Aynı lotu kullanarak satış eylemini gerçekleştirmemiz gerektiği ortaya çıktı. Eğer standart değerlendirmelere bağlı kalırsak:

• EUR2 =  Lot*ContractSize
• USD2 = Bid2*Lot*ContractSize

Görünüşe göre zaten EUR satıyor ve USD alıyoruz. Dönüşümlerimizle ilgili olarak, borç aldığımız parayla değiştirdiğimiz EUR'ları kendimizden tekrar borç alınan para birimine çevirdiğimiz ortaya çıkmaktadır. Edinilen paradan (şimdi, borç alınan para cinsinde) borç alınan paranın çıkarılmasıyla kâr veya zarar elde edilecektir:

• Profit_EUR = EUR1-EUR2 = 0
• Profit_USD = USD2-USD1 = Bid2*Lot*ContractSize - (Bid1 + S1*Point)*Lot*ContractSize = Lot*ContractSize*(Bid2 - Bid1 - S1*Point)

EUR'nun kaybolduğu ve sadece USD'nin kaldığı görülmektedir. Bakiyemiz USD cinsindeyse, elde edilen para birimini bakiyemizin para birimine dönüştürmemize gerek yoktur, çünkü bunlar aynıdır. Denklem en başta temel aldığımız denkleme çok benzemektedir, tek fark komisyon ve swapın burada dikkate alınmamasıdır çünkü bunlar ayrı olarak değerlendirilmektedir. Şimdi bu ifadeyi biraz yeniden yazalım:

• Profit_USD = Lot*(ContractSize*Point)*[(Bid2 - Bid1 - S1*Point)/Point]

Burada basitçe sağ tarafı Point ile bölüp çarpıyoruz ve orijinal denklemimizi elde ediyoruz. Aynı denklem, ticaret işlemi yönünden bağımsız olarak aynı anda satış ve alış yaptığımızı belirten geleneksel sistemi kullanırsak da elde edilebilir. Bu durumda, borç alınan her şey borçlu olduğumuzu simgeleyen eksi işaretine sahipken, satın alınan miktar artı işaretiyle bırakılır. Böyle bir sistemde, neyi neye ve nereden değiştirdiğimizi düşünmemize gerek yoktur. Aynı şeyi bu yaklaşımı kullanarak yapalım:

• EUR1 = Lot*ContractSize
• USD1 = -Ask1*Lot*ContractSize = -(Bid1 + S1*Point)*Lot*ContractSize

Bu bir alış. Birinci eylem.

• EUR2 = -Lot*ContractSize
• USD2 = Bid1*Lot*ContractSize

Bu bir satış. İkinci eylem.

Dahası, her şey basitleştirildi, çünkü neyin neyden ve nasıl çıkarılacağını düşünmemize gerek yoktur. Sadece tüm EUR ve tüm USD'yi ayrı ayrı toplamamız gerekiyor. Baz para birimi her halükarda kaybolur ve geriye yalnızca ikinci para birimi kalır. Toplayalım ve denklemlerin öncekilerle aynı olduğundan emin olalım:

• Profit_EUR = EUR1+EUR2 = 0
• Profit_USD = USD1+USD2 = -(Bid1 + S1*Point)*Lot*ContractSize + Bid2*Lot*ContractSize = Lot*ContractSize*(Bid2 - Bid1 - S1*Point)

Herhangi bir sembolün kârının yalnızca ikinci para biriminde dikkate alındığı (baz para biriminde değil) ve baz para biriminin tam açılış-kapanış döngüsünde her zaman kaybolduğu ortaya çıktı. Doğal olarak, satış için her şey yansıtılır. Hesaplamalarımızı tamamlamak için tümünü yazalım. Şimdi EURUSD satıyoruz ve ardından bir "alış” yaparak bu pozisyonu kapatıyoruz:

• EUR1 =  -Lot*ContractSize
• USD1 = Bid1*Lot*ContractSize

Bu bir satış. Birinci eylem.

• EUR2 = Lot*ContractSize
• USD2 = -(Bid2 + S2*Point)*Lot*ContractSize

Bu bir alış, ikinci eylem.

Şimdi tüm değerleri aynı şekilde toplayalım:

• Profit_EUR = EUR1+EUR2 = 0
• Profit_USD = USD1+USD2 = Bid1*Lot*ContractSize - (Bid2 + S2*Point)*Lot*ContractSize = Lot*ContractSize*(Bid1 - Bid2 - S2*Point)

Gördüğünüz gibi, denklem sadece Bid1 ve Bid2'nin yer değiştirmesiyle farklılık göstermektedir. Ve tabii ki, makas pozisyonun kapanış noktasında tahsil edilir, çünkü kapanış noktası alış noktasıdır. Şimdiye kadar her şey orijinal denklemlere tam olarak uyuyor. Ayrıca, artık TickValue'nun ne olduğunu bildiğimizi de belirtmek gerekir, en azından sembolümüzün ikinci para birimi (baz para birimi değil) bakiyemizin para birimiyle eşleşiyorsa. Bu değerin denklemini yazalım:

• TickValue = ContractSize*Point

Ancak, bu değer yine yalnızca kâr para biriminin mevduat para birimine eşit olduğu semboller için uygundur. Peki ya AUDNZD gibi bir çapraz kur kullanırsak ne olur? Buradaki en önemli şey sembolün kendisi değil, bu değerin her zaman mevduat para birimine göre hesaplanması ve bunu işlem sunucusundan elde etmemizdir. Ancak bu denklemi çapraz kurla ilişkili olarak kullanırsak, o zaman elbette işe yaradığı ortaya çıkar, ancak bize mevduat para birimimizde değil, sembolün ikinci para biriminde yanıt verecektir. Bunu mevduat para birimine dönüştürmek için, bu değeri belirli bir oranla çarpmak gerekir, bu da aslında bir önceki blokta ele aldığımız dönüşüm oranıdır.

• TickValueCross = ContractSize*Point*BidAlphaCross

Dönüşüm oranı hesaplaması oldukça basittir:

1. Sembolümüzdeki ikinci para birimine bakarız (baz olana değil)
2. Bu para birimini ve mevduat para birimini içeren bir sembol ararız
3. Uygun kur üzerinden dönüşüm yaparız
4. Gerekirse sembolü tersine çeviririz (ayna görüntüsü)

Örneğin, EURCHF üzerinde işlem yaparsak ve USD cinsinden bir bakiyemiz varsa, ilk kâr CHF cinsinden olacaktır, bu nedenle USDCHF enstrümanını ve oranını kullanabiliriz. Yani, CHF'i USD'ye çevirmemiz gerekiyor. Ancak CHF = PBid*USD olduğundan, USD = (1/PAsk)*CHF ve buna göre:

• BidAlphaCross = 1/PAsk

İkinci örnek için başka bir sembol kullanalım. Örneğin, AUDNZD üzerinde işlem yapıyoruz ve NZD cinsinde kâr elde ediyoruz, o zaman NZDUSD oranını kullanabiliriz ve USD = PBid*NZD olduğundan, bu durumda:

• BidAlphaCross = PBid

Hadi çözelim. CHF'i USD'ye dönüştürmek "+USD; -CHF" anlamına gelir. Başka bir deyişle, bir para birimini kaybedip diğerini kazanıyoruz. Bu, USD satın almak (USDCHF kurunu PAsk fiyatından satmak) anlamına gelir, ki bu aslında sadece şudur: "USD = (1/PAsk)*CHF". Bunu şu şekilde algılamak daha kolaydır: satın alırken, brokerın dönüştürme işlemimizden hiçbir şey almaması durumunda olabileceğinden biraz daha az USD elde etmeliyiz. Bu, daha büyük bir PAsk'e bölersek 1/P'den daha küçük bir değer elde edeceğimiz anlamına gelir.

İkinci durumda ise durum tersine dönmektedir. NZD'yi USD'ye dönüştürmek "+USD; -NZD" anlamına gelir, bu da NZDUSD kurunu PBid fiyatından satmaktır. Burada da benzer bir oran belirliyoruz: "USD = PBid*NZD". Dönüştürme yine biraz daha kötü bir fiyat olan "PBid" üzerinden yapılır. Her şey eşleşiyor. Her şey şeffaf ve anlaşılması kolay. Birincil mükemmel oranın yukarıda ele aldığım "PMid" olduğunu unutmayın. Bunu göz önünde bulundurarak, makasın, brokerın dönüştürülen para birimi biçiminde tahsil ettiği yüzdeden başka bir şey olmadığını anlamak kolaydır. Bu nedenle, ister bir pozisyon açılıyor ister kapatılıyor olsun, her ticaret işlemine, makas adı verilen bir broker döviz çevirme ücreti eşlik eder. Bu ücretin geri kalanı komisyon ve swapta yer alır.

Kâr para biriminin mevduat para birimi ile aynı olduğu durumda, dönüşüm oranı gerekli değildir (oran bire eşittir), bu nedenle majör döviz çiftleri durumunda oran kaybolur ve tüm bu çiftler için tik büyüklüğünü sabit hale getirir. Önceki durumda olduğu gibi, ticaret sembolümüz bir geçiş oranı olabilir, bu nedenle onu diğer semboller arasında aramak zorunda değiliz.

Yeni BidAlphaCross değerinin varlığını göz önünde bulundurarak, emir kâr ve zarar denklemlerini komisyon ve swap olmadan yeniden yazalım:

• BuyProfit = BidAlphaCross*Lot*ContractSize*(Bid2 - Bid1 - S1*Point)
• SellProfit = BidAlphaCross*Lot*ContractSize*(Bid1 - Bid2 - S2*Point)

Şunları dikkate alarak:

• Bid1 = Mid1 - (S1*Point)/2
• Bid2 = Mid2 - (S2*Point)/2

Oradaki Mid yerine oranları koyarak denklemleri daha görsel bir biçimde yeniden yazalım:

• BuyProfit = BidAlphaCross*Lot*ContractSize*(Mid2 - (S2*Point)/2 - Mid1 + (S1*Point)/2 - S1*Point)
• SellProfit = BidAlphaCross*Lot*ContractSize*(Mid1 - (S1*Point)/2 - Mid2 + (S2*Point)/2 - S2*Point)

Tüm bunları basitleştirelim:

• BuyProfit = Lot*BidAlphaCross*ContractSize*Point*[(Mid2-Mid1)/Point - (S1/2+S2/2)]
• SellProfit = Lot*BidAlphaCross*ContractSize*Point*[(Mid1-Mid2)/Point - (S1/2+S2/2)]

Daha fazla basitleştirme:

• BuyProfit = Lot*TickValueCross*[(Mid2-Mid1)/Point] - Lot*TickValueCross*(S1/2+S2/2)
• SellProfit = Lot*TickValueCross*[(Mid1-Mid2)/Point] - Lot*TickValueCross*(S1/2+S2/2)

Şimdi, sanırım, daha kolay ve net hale geldi. Makas ile ilişkili toplamı kasıtlı olarak kaldırdım, böylece pozisyonumuzun veya emrimizin ne kadar süre aktif kaldığına bakılmaksızın bunun tam olarak tahsil edilen değer olduğunu görebiliriz.

Swap hesaplama formülü

Şimdi geriye swap denklemlerini açıklığa kavuşturmak kalıyor. Makalenin başında elde ettiğimiz denklemleri hatırlayalım:

• Swap = Lot*TickValue*SwapPoints*SwapCount(StartTime, EndTime)
• Swap = Lot*ContractSize*BidAlpha*SwapPercent/100*SwapCount(StartTime, EndTime)

Son blokta, TickValue'nun tek basamaklı bir değer olmadığını ve farklı döviz çiftleri için farklı şekilde hesaplandığını öğrendik. Şu tespit edildi:

• TickValue = ContractSize*Point

Ancak bu yalnızca kâr para biriminin mevduat para birimiyle eşleştiği çiftler için geçerlidir. Daha karmaşık durumlarda aşağıdaki değeri kullanırız:

• TickValueCross = ContractSize*Point*BidAlphaCross

Burada BidAlphaCross da mevduat para birimine ve seçilen sembole bağlı olan farklı bir değerdir. Tüm bunları yukarıda tanımladık. Buna dayanarak, standart sabiti değiştirerek denklemin ilk versiyonunu yeniden yazmamız gerekir:

• Swap = Lot*TickValueCross*SwapPoints*SwapCount(StartTime, EndTime)

Ancak bu denklem hala mükemmel olmaktan uzaktır. Bunun nedeni, komisyon veya makasın aksine, pozisyonunuz açık kalırken swapın değişken sayılarda tahsil edilebilmesidir. Çapraz kurlar söz konusu olduğunda, TickValueCross değerinin toplam swapı tanımlamak için yeterli olmadığı ortaya çıkmaktadır, çünkü her swap tahakkuk noktasında, BidAlphaCross değeri değiştiği için bu değerin biraz farklı olduğu anlaşılmaktadır. İki "ücret alma" seçeneği için swap hesaplama denklemlerinin tamamını yazalım:

1. Swap = Summ(1…D){Lot*(SwapPoints*K[i])*TickValueCross[i]} - puan cinsinden tahakkuk eden tüm swapların toplamı, her geçilen 0:00 noktası için
2. Swap = Summ(1…D){Lot*ContractSize*BidAlpha[i]*(SwapPercent/100*K[i])} - yüzde cinsinden

Toplanacak diziler:

• K[i] = 1 veya 3 - oran "3" ise, bu üçlü swap tahakkukunun yapıldığı gün olduğu anlamına gelir
• TickValueCross[i] - swap noktalarındaki tik büyüklükleri dizisi
• BidAlpha[i] - swap noktalarındaki ayarlama oranları dizisi

Rastgele bir emir için swap hesaplama örneğine bakalım. Bunu yapmak için, aşağıdaki kısa notasyonları tanıtacağım:

• TickValueCross[i] = T[i]
  
• BidAlpha[i] = B[i]
  
• K[i] = K[i]

Şimdi swapları nasıl toplayacağımızı grafiksel olarak gösterelim:

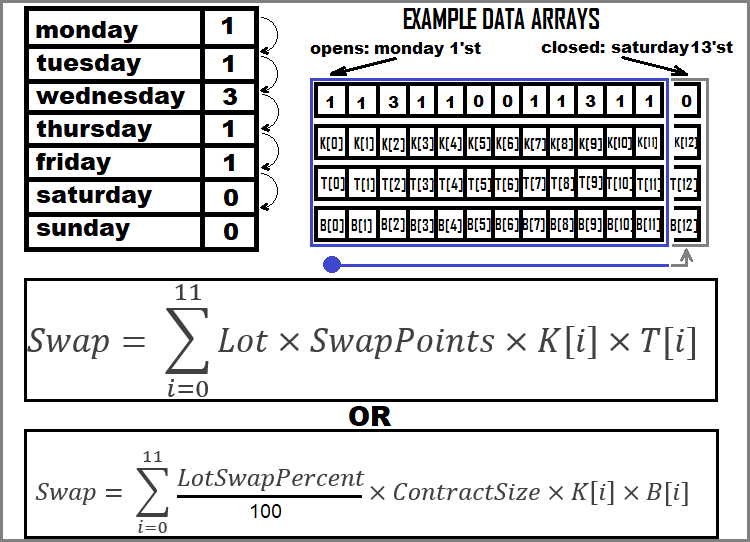
Emir kâr ve zararının hesaplanmasına ilişkin tüm olası örnekleri analiz ettik.

Uygulama kısmı

Bu bölümde matematiksel modelimizi test edeceğiz. Özellikle, komisyonları ve swapları hesaba katmadan kâr veya zarar hesaplama konularına özel dikkat göstereceğim. Hatırlarsanız, kârı çapraz kur üzerinden hesaplarsak TickValueCross değerini hangi zaman noktasında hesaplamam gerektiğini merak ediyordum? Bu, test edeceğim tüm modeldeki tek belirsizliktir. Bunu yapmak için, önce matematiksel modelimizi kullanarak herhangi bir emrin kâr veya zararını hesaplamak için gerekli tüm fonksiyonları uygulayalım, strateji sınayıcıda test edelim ve tüm bunlardan sonra hesaplamalarımızı işlem geçmişindeki gerçek emir verileriyle karşılaştıralım. Nihai hedef, matematiksel modelimizi test etmek ve aynı zamanda OrderCalcProfit gibi MQL5 referans fonksiyonu ile karşılaştırmaktır.

Tüm bunları değerlendirebilmek için dört niceliğin tanıtılması gerekmektedir:

1. Real - geçmişten emrin kârı
2. BasicCalculated - aynı kâr, ancak OrderCalcProfit fonksiyonu kullanılarak emrin açılması sırasında hesaplanır
3. CalculatedStart - matematiksel modelimiz kullanılarak emrin açılması sırasında hesaplanan kâr
4. CalculatedEnd - matematiksel modelimiz kullanılarak emrin kapatılması sırasında hesaplanan kâr

Bu, kâr değerinin üç tür ortalama sapmasını gerektirir:

1. AverageDeviationCalculatedMQL = Summ(0...n-1)[100*MathAbs(BasicCalculated-Real)/MathAbs(Real)]/n - MQL5 koduna göre göreceli kâr sapması
2. AverageDeviationCalculatedStart = Summ(0...n-1)[100*MathAbs(CalculatedStart-Real)/MathAbs(Real)]/n - bir emir açarken kodumuz tarafından göreceli kâr sapması
3. AverageDeviationCalculatedEnd = Summ(0...n-1)[100*MathAbs(CalculatedEnd-Real)/MathAbs(Real)]/n - bir emri kapatırken kodumuz tarafından göreceli kâr sapması
   

Buna benzer şekilde, üç tür maksimum sapma girebiliriz:

1. MaxDeviationCalculatedMQL = Max(0...n-1)[(100*MathAbs(BasicCalculated-Real)/MathAbs(Real))] - MQL5 koduna göre göreceli kâr sapması
2. MaxDeviationCalculatedStart =Max(0...n-1)[(100*MathAbs(CalculatedStart-Real)/MathAbs(Real))]- bir emir açarken kodumuz tarafından göreceli kâr sapması
3. MaxDeviationCalculatedEnd = Max(0...n-1)[(100*MathAbs(CalculatedEnd-Real)/MathAbs(Real))] - bir emri kapatırken kodumuz tarafından göreceli kâr sapması

Tanımlamalar:

• Summ(0...n-1) - tüm "n" emrin göreceli sapmalarının toplamı
• Max(0...n-1) - tüm "n" emrin maksimum göreceli sapması
  

Bu hesaplamaları rastgele bir Uzman Danışmanın koduna uygulayarak matematiksel modelimizi test edebiliriz. Kâr denklemimizi uygulayarak başlayalım. Ben bunu şu şekilde yaptım:

double CalculateProfitTheoretical(string symbol, double lot,double OpenPrice,double ClosePrice,bool bDirection)
   {
   //PrBuy = Lot * TickValueCross * [ ( Bid2 - Ask1 )/Point ]
   //PrSell = Lot * TickValueCross * [ ( Bid1 - Ask2 )/Point ]
   if ( bDirection )
      {
      return lot * TickValueCross(symbol) * ( (ClosePrice-OpenPrice)/SymbolInfoDouble(symbol,SYMBOL_POINT) );
      }
   else
      {
      return lot * TickValueCross(symbol) * ( (OpenPrice-ClosePrice)/SymbolInfoDouble(symbol,SYMBOL_POINT) );
      }   
   }

Burada bir arada iki denklemimiz var: alış ve satış için. "bDirection" işaretleyicisi bundan sorumludur. Tik büyüklüğünü hesaplayan ek fonksiyon yeşil renkle vurgulanmıştır. Bunu aşağıdaki şekilde uyguladım:

double TickValueCross(string symbol,int prefixcount=0)
   {
   if ( SymbolValue(symbol) == SymbolBasic() )
      {
      return TickValue(symbol);
      }
   else
      {
      MqlTick last_tick;
      int total=SymbolsTotal(false);//symbols in Market Watch
      for(int i=0;i<total;i++) Symbols[i]=SymbolName(i,false);
      string crossinstrument=FindCrossInstrument(symbol);
      if ( crossinstrument != "" )
         {
         SymbolInfoTick(crossinstrument,last_tick);
         string firstVAL=StringSubstr(crossinstrument,prefixcount,3);
         string secondVAL=StringSubstr(crossinstrument,prefixcount+3,3);
         if ( secondVAL==SymbolBasic() && firstVAL == SymbolValue(symbol) )
            {
             return TickValue(symbol) * last_tick.bid;
            }
         if ( firstVAL==SymbolBasic() && secondVAL == SymbolValue(symbol) )
            {
            return TickValue(symbol) * 1.0/last_tick.ask;
            }         
         }
      else return TickValue(symbol);  
      }
   return 0.0;   
   }

Ayrıca aşağıdaki durumlar için içeride iki uygulama vardır:

1. Sembolün kâr para birimi mevduat para birimi ile aynı
2. Diğer tüm durumlar (geçiş oranı aranır)

İkinci senaryo da kendi içinde ikiye ayrılır:

• Mevduat para birimi dönüştürme oranının üstündedir
• Mevduat para birimi dönüştürme oranının altındadır

Her şey matematiksel modelle tam bir uyum içinde. İkinci senaryo için öncelikle dönüşüm oranını hesaplayacak doğru aracı bulmamız gerekiyor:

string FindCrossInstrument(string symbol,int prefixcount=0)
   {
   string firstVAL;
   string secondVAL;
   for(int i=0;i<ArraySize(Symbols);i++)
      {
      firstVAL=StringSubstr(Symbols[i],prefixcount,3);
      secondVAL=StringSubstr(Symbols[i],prefixcount+3,3);
      if ( secondVAL==SymbolBasic() && firstVAL == SymbolValue(symbol) )
         {
         return Symbols[i];
         }
      if ( firstVAL==SymbolBasic() && secondVAL == SymbolValue(symbol) )
         {
         return Symbols[i];
         }      
      }
   return "";
   }

Bunu yapmak için sembol adından baz para birimini nasıl "çıkaracağımızı" bilmemiz gerekir:

string SymbolValue(string symbol,int prefixcount=0)
   {
   return StringSubstr(symbol,prefixcount+3,3);
   }

Ve yerleşik MQL5 fonksiyonunu kullanarak kâr para birimini elde ederiz:

string SymbolBasic()
   {
   return AccountInfoString(ACCOUNT_CURRENCY);
   }

Tüm bunları ilk eşleşmeye kadar tüm Piyasa Gözlemi sembollerindeki para birimleriyle karşılaştırırız. Artık bu fonksiyonu emirleri açarken ve kapatırken kullanabiliriz. Dilerseniz kodun geri kalanını aşağıda ekli dosyada görebilirsiniz. Geriye dönük testin bitiminden sonra sapmaların hesaplanmasını ekledim. Terminal günlüğüne yazılırlar. Yirmi sekiz majör döviz çiftinin ve çapraz kurların tümünü test ettim ve sonucu bir tabloya koydum, böylece matematiksel modelimizin performansını değerlendirebilir ve MQL5 uygulamasıyla karşılaştırabiliriz. Sonuçları üç koşullu bloğa ayırdım. İlk ikisi aşağıdaki gibidir:

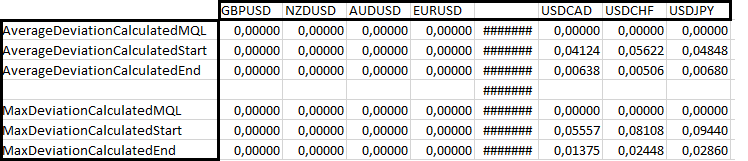
Gördüğünüz gibi, ilk dört döviz çifti için hem MQL5 hem de bizim uygulamamız mükemmel çalışıyor çünkü kâr para birimi mevduat para birimiyle aynı. Ardından, baz para biriminin kâr para birimi ile aynı olduğu üç döviz çiftinden oluşan bir blok geliyor. Bu durumda, MQL5 uygulaması en iyi şekilde çalışmaktadır, ancak yine de, emir açarken hesaplama hatasının, kapatırken aynı hatadan çok daha yüksek olduğu açıktır. Bu dolaylı olarak hesaplamanın gerçekten emir kapatıldığı anda yapılması gerektiğini gösterir. Diğer döviz çiftlerine göz atalım:

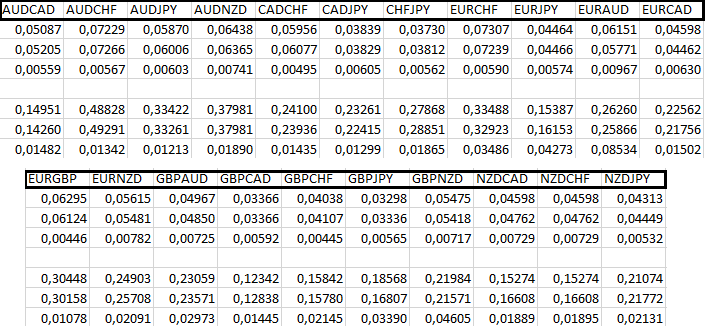
Burada fonksiyonum temel MQL5'ten daha düşük değil. Ayrıca, pozisyon kapatılırken yapılan hesaplamaların her zaman çok daha doğru olduğu açıktır. Açıklayamadığım tek şey, ikinci bloğun ilk satırında sıfırların bulunması. Birçok nedeni olabilir, ancak bana öyle geliyor ki bunlar benim modelimle ilgili değil, yine de yanılıyor olabilirim. Komisyonlar ve swaplar için denklemleri kontrol etmeye gelince, bunun gerekli olduğunu düşünmüyorum. Bu denklemlerde özellikle kafa karıştırıcı bir şey olmadığı için onlara güveniyorum.

Sonuç

Bu makalede, sıfırdan oluşturulmuş ve sadece bilgi kırıntıları tarafından yönlendirilen bir matematiksel model ortaya koydum. Model, majör döviz çiftleri ve çapraz kurlar için emirleri hesaplamak için ihtiyacınız olan her şeyi içermektedir. Model, strateji sınayıcıda test edilmiştir ve herhangi bir Uzman Danışman, gösterge veya faydalı komut dosyasında hemen kullanıma hazırdır. Aslında bu modelin uygulanabilirliği sadece kâr, zarar veya maliyetleri hesaplamaktan çok daha geniştir, ancak bu başka bir makalenin konusudur. Tabloyu derlemek için kullandığım araştırma Uzman Danışmanında gerekli tüm fonksiyonları ve kullanım örneklerini bulabilirsiniz. Uzman Danışman makaleye eklenmiştir. Kendiniz çalıştırabilir ve sonuçları tablo ile karşılaştırabilirsiniz. En önemlisi, basit ve mantıklı bir "kılavuz" oluşturmayı başardığıma inanıyorum.