Redes neuronales: así de sencillo (Parte 93): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo (Parte final)

MetaTrader 5 — Sistemas comerciales | 9 diciembre 2024, 12:10

Introducción

En el artículo anterior, nos familiarizamos con el algoritmo ATFNet, que es un conjunto de 2 modelos de predicción de series temporales. Uno de ellos trabaja en el ámbito temporal y construye valores predictivos de las series temporales estudiadas basándose en el análisis de las amplitudes de las señales. El segundo modelo trabaja con las características frecuenciales de la serie temporal analizada y registra sus dependencias globales, su periodicidad y su espectro. La fusión adaptativa de dos predicciones independientes, según el autor del método, genera resultados impresionantes.

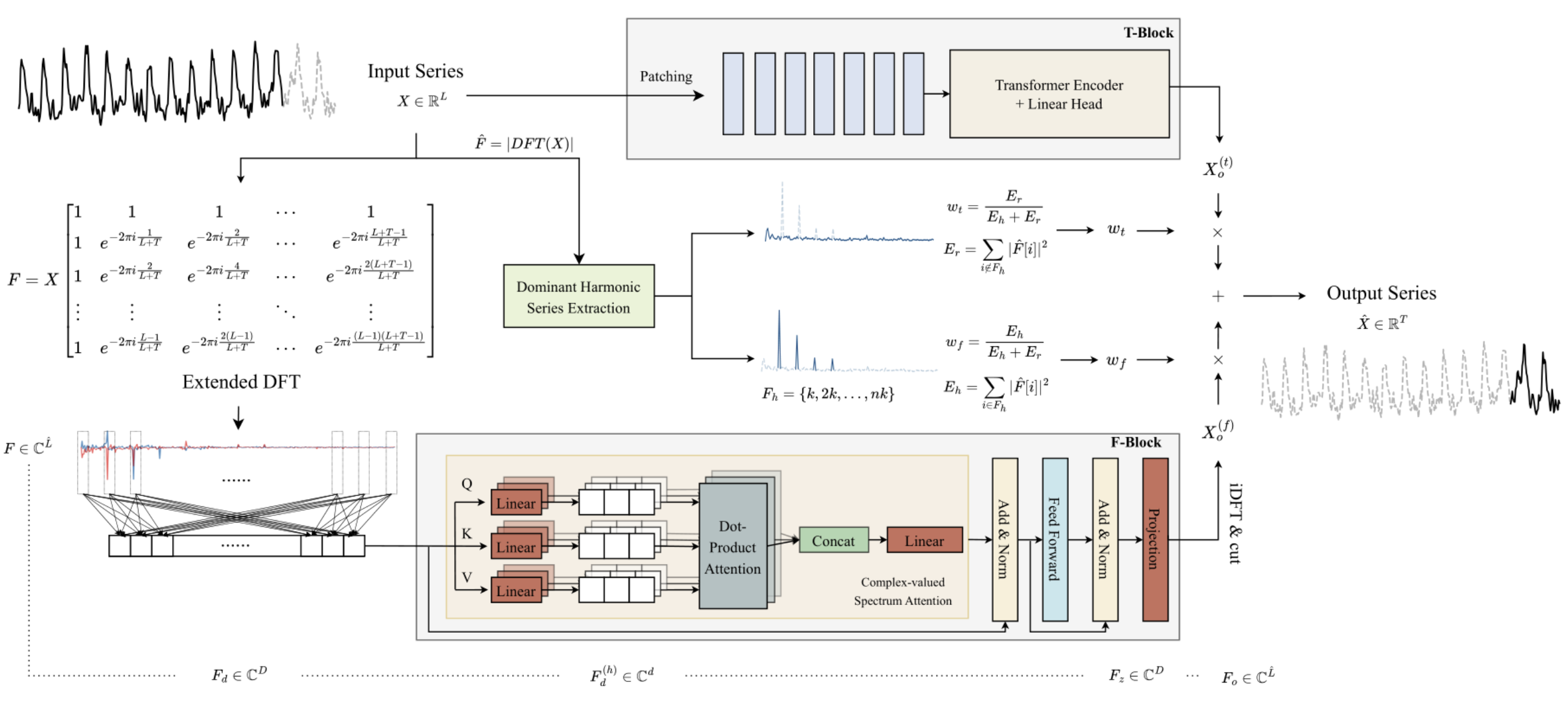
La característica clave del bloque de frecuencia F es una construcción completa del algoritmo utilizando las matemáticas de números complejos. Para cumplir este requisito, en el artículo anterior construimos la clase CNeuronComplexMLMHAttention. Repite por completo los algoritmos del Transformer codificador multicapa con elementos de Self-Attention multicabezal. La clase de atención integrada que construimos es la base del bloque F. En este artículo, seguiremos aplicando los planteamientos propuestos por los autores del método ATFNet.

1. Creación de la clase ATFNet

Después de implementar la base del bloque de frecuencia F, que es la clase de atención compleja CNeuronComplexMLMHAttention, subimos un nivel y creamos la clase CNeuronATFNetOCL, en la que implementaremos todo el algoritmo ATFNet.

Debo admitir que la implementación de un algoritmo tan complejo como ATFNet dentro de una única clase de capa neuronal puede no ser la solución más óptima. Pero el modelo de red neuronal secuencial que construimos antes no contempla la posibilidad de organizar el trabajo de varios procesos paralelos diferentes, que es exactamente nuestro caso: utilizamos el bloque T y el bloque F. La implantación de esta funcionalidad requerirá cambios más globales. Por lo tanto, decidí crear una solución con costes mínimos, es decir, implementar todo el algoritmo como una clase de capa neuronal. A continuación se muestra la estructura de la clase CNeuronATFNetOCL.

class CNeuronATFNetOCL  :  public CNeuronBaseOCL
  {
protected:
   uint              iHistory;
   uint              iForecast;
   uint              iVariables;
   uint              iFFT;
   //--- T-Block
   CNeuronBatchNormOCL  cNorm;
   CNeuronTransposeOCL  cTranspose;
   CNeuronPositionEncoder  cPositionEncoder;
   CNeuronPatching      cPatching;
   CLayer               caAttention;
   CLayer               caProjection;
   CNeuronRevINDenormOCL cRevIN;
   //--- F-Block
   CBufferFloat      *cInputs;
   CBufferFloat      cInputFreqRe;
   CBufferFloat      cInputFreqIm;
   CNeuronBaseOCL    cInputFreqComplex;
   CBufferFloat      cMainFreqWeights;
   CNeuronBaseOCL    cNormFreqComplex;
   CBufferFloat      cMeans;
   CBufferFloat      cVariances;
   CNeuronComplexMLMHAttention cFreqAtteention;
   CNeuronBaseOCL    cUnNormFreqComplex;
   CBufferFloat      cOutputFreqRe;
   CBufferFloat      cOutputFreqIm;
   CBufferFloat      cOutputTimeSeriasRe;
   CBufferFloat      cOutputTimeSeriasIm;
   CBufferFloat      cOutputTimeSeriasReGrad;
   CBufferFloat      cReconstructInput;
   CBufferFloat      cForecast;
   CBufferFloat      cReconstructInputGrad;
   CBufferFloat      cForecastGrad;
   CBufferFloat      cZero;
   //---
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, 
                         bool reverse = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      ComplexNormalize(void);
   virtual bool      ComplexUnNormalize(void);
   virtual bool      ComplexNormalizeGradient(void);
   virtual bool      ComplexUnNormalizeGradient(void);
   virtual bool      MainFreqWeights(void);
   virtual bool      WeightedSum(void);
   virtual bool      WeightedSumGradient(void);
   virtual bool      calcReconstructGradient(void);

public:
                     CNeuronATFNetOCL(void) {};
                    ~CNeuronATFNetOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[], 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronATFNetOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *net, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual CBufferFloat   *getWeights(void);
  };

En la estructura de clase CNeuronATFNetOCL presentada, preste atención a las cuatro variables internas:

iHistory: la profundidad del historial analizado;
iForecast: horizonte de planificación;
iVariables: el número de variables analizadas (series temporales unitarias);
iFFT: el tamaño del tensor de descomposición rápida de Fourier (Discrete Fourier Transform, DFT).

Como hemos visto anteriormente, el algoritmo DFT requiere que el tamaño del vector de datos inicial sea igual a una de las potencias de «2». Por lo tanto, completamos el tensor de datos inicial con valores cero hasta alcanzar el tamaño requerido.

Los objetos internos del método se dividen en dos bloques dependiendo del bloque del algoritmo ATFNet al que pertenezcan. Tendremos en cuenta su propósito, así como la funcionalidad de los métodos de clase, mientras implementamos el algoritmo.

Todos los objetos internos se declaran estáticamente, por lo que podemos dejar vacíos el constructor y el destructor de la clase CNeuronATFNetOCL.

1.1 Inicialización de objetos

La inicialización de los objetos internos de nuestra nueva clase se realiza en el método Init. Aquí nos encontramos con la primera consecuencia de nuestra decisión de implementar todo el algoritmo ATFNet dentro de una clase: necesitamos pasar un gran número de parámetros desde el llamador.

En realidad, dentro de la clase CNeuronATFNetOCL, tenemos que construir dos modelos multicapa paralelos utilizando mecanismos de atención tanto en el bloque temporal T como en el bloque frecuencial F. Para cada uno de los modelos, necesitamos especificar la arquitectura.

Para resolver este problema, decidimos utilizar parámetros «universales» siempre que fuera posible, es decir, parámetros que pueden ser utilizados por igual por ambos modelos. Pues bien, disponemos de parámetros para describir el tensor de entrada y salida: la profundidad del historial analizado, el número de series temporales unitarias y el horizonte de planificación. Estos parámetros se utilizan por igual en el bloque T y en el bloque F.

Además, ambos modelos se construyen en torno al Encoder del Transformer y explotan la arquitectura multicabezal Self-Attention con varias capas. Decidimos utilizar el mismo número de cabezas de atención y capas de codificador en ambos bloques.

Sin embargo, necesitamos pasar parámetros adicionales para la capa de segmentación de datos que se utiliza en el bloque T y no tiene análogo en el bloque F. Para no aumentar mucho el número de parámetros del método, decidí utilizar un array de 3 elementos. El primer elemento de esta matriz contiene el tamaño de la ventana de un segmento, y el segundo elemento contiene el paso de esta ventana en el búfer de datos de origen. En el último elemento de la matriz, escribimos el tamaño de un parche a la salida de la capa de segmentación de datos.

bool CNeuronATFNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[],
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch))
      return false;

En el cuerpo del método, como es habitual, llamamos al método de inicialización de la clase padre del mismo nombre. Tenga en cuenta que para el método de la clase padre especificamos el tamaño de la capa como el producto del número de variables analizadas (series temporales unitarias) y el horizonte de planificación. En otras palabras, esperamos que la salida de la capa CNeuronATFNetOCL sea un resultado listo de la continuación predicha de la serie temporal analizada.

Una vez inicializados correctamente los objetos heredados, guardamos los parámetros clave de la arquitectura en variables.

   iHistory = MathMax(history, 1);
   iForecast = forecast;
   iVariables = variables;

A continuación, calcularemos el tamaño del tensor para la descomposición rápida de Fourier. Los autores de ATFNet proponen una descomposición de Fourier ampliada que determina las características de frecuencia de la serie temporal completa dados los datos históricos y de previsión.

   uint size = iHistory + iForecast;
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) < size)
      power++;
   iFFT = uint(MathPow(2, power));

El siguiente paso es inicializar los objetos internos de nuestra clase. Empecemos por la presentación prevista de los datos iniciales. Dado que nuestro modelo supone el análisis de series temporales unitarias en los dominios temporal y frecuencial, esperamos recibir una matriz de series temporales unitarias como entrada a nuestra capa. CNeuronATFNetOCL devolverá un mapa similar de valores predichos a la salida.

Otro punto es la normalización de los datos. Ambos bloques del modelo utilizan la normalización de los datos de entrada. La diferencia es que el bloque T utiliza la normalización en el dominio del tiempo y el bloque F en el ámbito de la frecuencia. Por lo tanto, en esta implementación, decidí introducir datos no normalizados en la capa. La normalización y la adición inversa de características estocásticas se llevan a cabo dentro de bloques individuales según las dimensiones correspondientes.

Para facilitar la lectura y la transparencia del código, inicializaremos los objetos internos por bloques de su uso y en el orden del algoritmo construido. Empecemos por el bloque T.

Como ya se ha mencionado, los datos no normalizados se introducen en la capa. Por lo tanto, primero debemos convertir los datos obtenidos en una forma comparable.

//--- T-Block
   if(!cNorm.Init(0, 0, OpenCL, iHistory * iVariables, batch, optimization))
      return false;

Los autores del método ATFNet no utilizan la codificación de datos posicionales en el ámbito de la frecuencia, pero la emplean cuando analizan datos en el ámbito del tiempo. Añadamos una capa de codificación posicional.

   if(!cPositionEncoder.Init(0, 1, OpenCL, iVariables, iHistory, optimization, batch))
      return false;

Al construir una capa de segmentación de datos, incorporamos a su algoritmo una especie de transposición de datos. Ahora tenemos que preparar la entrada antes de alimentarla a la capa CNeuronPatching. Para realizar esta operación, añadimos una capa de transposición de datos.

   if(!cTranspose.Init(0, 2, OpenCL, iHistory, iVariables, optimization, batch))
      return false;
   cTranspose.SetActivationFunction(None);

A continuación, hay que calcular el número de parches a la salida de la capa de segmentación en función del tamaño de la ventana de un segmento y de su paso, obtenidos en los parámetros del método a partir del programa externo.

   uint count = (iHistory - patch[0] + 2 * patch[1] - 1) / patch[1];

Tras realizar el trabajo preparatorio necesario, inicializamos la capa de segmentación de datos.

   if(!cPatching.Init(0, 3, OpenCL, patch[0], patch[1], patch[2], count, iVariables, optimization, batch))
      return false;

Al construir el método PatchTST, utilizamos Conformer como bloque de atención. Aquí utilizaremos la misma solución. En el siguiente paso, creamos el número necesario de capas anidadas CNeuronConformer.

   caAttention.SetOpenCL(OpenCL);
   for(uint l = 0; l < layers; l++)
     {
      CNeuronConformer *temp = new CNeuronConformer();
      if(!temp)
         return false;
      if(!temp.Init(0, 4 + l, OpenCL, patch[2], 32, heads, iVariables, count, optimization, batch))
        {
         delete temp;
         return false;
        }
      if(!caAttention.Add(temp))
        {
         delete temp;
         return false;
        }
     }

Al bloque de atención que analiza las series temporales de entrada le sigue un bloque de 3 capas convolucionales que realizará la previsión de los datos posteriores en toda la profundidad de planificación en el contexto de series temporales unitarias individuales.

   int total = 3;
   caProjection.SetOpenCL(OpenCL);
   uint window = patch[2] * count;
   for(int l = 0; l < total; l++)
     {
      CNeuronConvOCL *temp = new CNeuronConvOCL();
      if(!temp)
         return false;
      if(!temp.Init(0, 4+layers+l, OpenCL, window, window, (total-l)*iForecast, iVariables, optimization, batch))
        {
         delete temp;
         return false;
        }
      temp.SetActivationFunction(TANH);
      if(!caProjection.Add(temp))
        {
         delete temp;
         return false;
        }
      window = (total - l) * iForecast;
     }

Obsérvese que en cada capa especificamos el mismo número de elementos de secuencia, igual al número de series temporales unitarias de la serie temporal analizada. En cada capa posterior, el número de filtros a la salida de la capa neuronal disminuye y llega a ser igual a la profundidad de predicción especificada en la última capa.

A la salida del bloque T, añadimos a los valores de previsión parámetros estadísticos de la serie temporal de entrada utilizando la capa CNeuronRevINDenormOCL.

   if(!cRevIN.Init(0, 4 + layers + total, OpenCL, iForecast * iVariables, 1, cNorm.AsObject()))
      return false;

En este punto, hemos inicializado todos los objetos internos relacionados con el bloque T con la predicción en el ámbito temporal. Ahora pasamos a trabajar con objetos del bloque de frecuencia F.

Según el algoritmo ATFNet, los datos de entrada introducidos en el bloque F se convierten al ámbito de la frecuencia mediante la descomposición rápida de Fourier (DFT). Como recordará, la implementación del algoritmo DFT que construimos anteriormente escribe el espectro de frecuencias en dos búferes de datos. Una para la parte real del espectro, la segunda para la parte imaginaria.

//--- F-Block
   if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL))
      return false;

Para facilitar el procesamiento posterior, combinaremos la información del espectro en un solo búfer.

   if(!cInputFreqComplex.Init(0, 0, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

También tenemos que preparar un búfer para escribir la parte de la frecuencia dominante. Cabe señalar aquí que determinamos la frecuencia dominante por separado para cada serie de tiempo unitaria.

   if(!cMainFreqWeights.BufferInit(iVariables, 0) || !cMainFreqWeights.BufferCreate(OpenCL))
      return false;

La entrada a nuestra capa son datos sin procesar, que generan espectros bastante diferentes de series de tiempo unitarias. Para convertir los espectros en una forma comparable antes del procesamiento posterior, los autores del método recomiendan normalizar las características de frecuencia. Guardaremos los datos normalizados en los búferes de la capa cNormFreqComplex.

   if(!cNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

En este caso, guardaremos las características estadísticas del espectro original en los búferes de datos correspondientes.

   if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL))
      return false;
   if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL))
      return false;

Procesaremos las características de frecuencia de los datos de entrada preparados utilizando el bloque de atención compleja. En el artículo anterior, realizamos una gran implementación de la clase CNeuronComplexMLMHAttention. Ahora sólo tenemos que inicializar el objeto interno de la clase especificada.

   if(!cFreqAtteention.Init(0, 2, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch))
      return false;

Según el algoritmo, tras procesar el espectro de entrada en el bloque de atención compleja, hay que ejecutar procedimientos inversos. En primer lugar, añadimos indicadores estadísticos de las características de la frecuencia de entrada al espectro procesado.

   if(!cUnNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

Separemos las partes real e imaginaria del espectro.

   if(!cOutputFreqRe.BufferInit(iFFT*iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputFreqIm.BufferInit(iFFT*iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL))
      return false;

A continuación, devolvemos los datos al área temporal.

   if(!cOutputTimeSeriasRe.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputTimeSeriasIm.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasIm.BufferCreate(OpenCL))
      return false;

A efectos del paso de retropropagación, creamos un búfer de gradiente para la parte real de la serie temporal.

   if(!cOutputTimeSeriasReGrad.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasReGrad.BufferCreate(OpenCL))
      return false;

Tenga en cuenta que no creamos un búfer de gradiente para la parte imaginaria de la serie temporal. La cuestión es que para una serie temporal, los valores objetivo de la parte imaginaria son «0». Por lo tanto, el gradiente de error de la parte imaginaria es igual a los valores de la parte imaginaria con signo opuesto. En el paso de retropropagación, podemos utilizar el búfer de resultados del paso de avance para la parte imaginaria de la serie temporal procesada.

Tenga en cuenta que tras la DFT inversa (iDFT), tenemos previsto recibir una serie temporal completa procesada consistente en una reconstrucción de los datos de entrada y los valores de previsión para un horizonte de planificación determinado. Para extraer la parte necesaria de los valores de previsión, dividimos la serie temporal completa en dos búferes: datos reconstruidos y valores de previsión.

   if(!cReconstructInput.BufferInit(iHistory*iVariables, 0) || !cReconstructInput.BufferCreate(OpenCL))
      return false;
   if(!cForecast.BufferInit(iForecast*iVariables, 0) || !cForecast.BufferCreate(OpenCL))
      return false;

Añada búferes para los gradientes de error correspondientes.

   if(!cReconstructInputGrad.BufferInit(iHistory*iVariables, 0) || !cReconstructInputGrad.BufferCreate(OpenCL))
      return false;
   if(!cForecastGrad.BufferInit(iForecast*iVariables, 0) || !cForecastGrad.BufferCreate(OpenCL))
      return false;

Tenga en cuenta que el método propuesto por los autores de ATFNet no proporciona ningún análisis de las desviaciones de los datos reconstruidos respecto a los valores de entrada de las series temporales analizadas. Añadimos esta funcionalidad en un intento de implementar un ajuste más afinado del complejo bloque de atención. Potencialmente, una mejor comprensión de los datos analizados mejorará la calidad de predicción del modelo.

Además, creamos un búfer de valores cero que se utilizará para rellenar los valores que faltan en los datos de entrada y los gradientes de error.

   if(!cZero.BufferInit(iFFT*iVariables, 0) || !cZero.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

No olvide supervisar los procesos operativos en cada etapa. Una vez finalizada la inicialización de todos los objetos declarados, devolvemos al llamante el valor lógico de la ejecución de las operaciones del método.

1.2 Pase de avance

Una vez finalizada la inicialización de los objetos de clase, pasamos a construir el algoritmo de avance. Empecemos por construir kernels adicionales en el programa OpenCL.

En primer lugar, piense en la normalización de los espectros de respuesta en frecuencia de las series temporales unitarias. Si utilizamos algoritmos de normalización de datos reales previamente implementados, esto puede distorsionar enormemente los datos. Por lo tanto, necesitamos aplicar la normalización de datos en un entorno complejo. Implementamos esta funcionalidad en el kernel ComplexNormalize. En los parámetros del kernel, pasaremos punteros a 4 búferes de datos y el tamaño de la secuencia unitaria. Utilizaremos este kernel en un espacio de problemas unidimensional en el contexto de espectros de series temporales unitarias.

__kernel void ComplexNormalize(__global float2 *inputs,
                               __global float2 *outputs,
                               __global float2 *means,
                               __global float *vars,
                               int dimension)
  {
   if(dimension <= 0)
      return;

Fíjate en la declaración de los búferes de datos. Los búferes de datos de entrada, salida y media son de tipo vectorial float2. Decidimos utilizar este tipo de datos en OpenCL para trabajar con cantidades complejas. Sin embargo, también existe un búfer de dispersiones que se declara con un tipo real float. Las dispersiones muestran la desviación típica de un valor respecto a la media. La distancia entre dos puntos es una cantidad real.

En el cuerpo del método, comprobamos la dimensión obtenida del vector normalizado. Obviamente, debe ser mayor que «0». A continuación, identificamos el hilo actual en el espacio de tareas, determinamos el desplazamiento en los búferes de datos y creamos una representación compleja de la dimensionalidad de la secuencia analizada.

   size_t n = get_global_id(0);
   const int shift = n * dimension;
   const float2 dim = (float2)(dimension, 0);

A continuación, organizamos un bucle en el que determinamos el valor medio del espectro analizado.

   float2 mean = 0;
   for(int i = 0; i < dimension; i++)
     {
      float2 val = inputs[shift + i];
      if(isnan(val.x) || isinf(val.x) ||
         isnan(val.y) || isinf(val.y))
         inputs[shift + i] = (float2)0;
      else
         mean += val;
     }
   means[n] = mean = ComplexDiv(mean, dim);

Guardamos inmediatamente el resultado obtenido en el elemento correspondiente del búfer de valores medios.

En la etapa siguiente, organizamos un bucle para determinar la dispersión de la secuencia analizada.

   float variance = 0;
   for(int i = 0; i < dimension; i++)
      variance += pow(ComplexAbs(inputs[shift + i] - mean), 2);
   vars[n] = variance = sqrt((isnan(variance) || isinf(variance) ? 1.0f : variance / dimension));

Hay dos puntos que señalar aquí. En primer lugar, a pesar de guardar el valor medio en el búfer de datos externo, utilizamos el valor de la variable local al realizar operaciones, ya que acceder a un elemento del búfer situado en la memoria global del contexto es mucho más lento que acceder a una variable local del kernel.

El segundo punto es metódico: al calcular la varianza de una secuencia de números complejos, a diferencia de los números reales, elevamos al cuadrado el valor absoluto de la desviación de un elemento de la secuencia compleja respecto al valor medio. Es el valor absoluto de una cantidad compleja que mostrará la distancia entre puntos en el espacio bidimensional de las partes real e imaginaria. Mientras que una simple diferencia de cantidades complejas sólo nos mostrará un desplazamiento de coordenadas.

En la última etapa de la operación kernel, organizamos el último bucle, en el que normalizamos los datos del espectro de entrada. Escribimos los valores obtenidos en los elementos correspondientes del búfer de resultados.

   float2 v=(float2)(variance, 0);
   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexDiv((inputs[shift + i] - mean), v);
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      outputs[shift + i] = val;
     }
  }

Aquí también trabajamos con variables locales de media y desviación típica.

E inmediatamente crearemos un kernel de normalización inversa ComplexUnNormalize, en el que devolveremos los indicadores estadísticos extraídos del espectro de entrada.

__kernel void ComplexUnNormalize(__global float2 *inputs,
                                 __global float2 *outputs,
                                 __global float2 *means,
                                 __global float *vars,
                                 int dimension)
  {
   if(dimension <= 0)
      return;

Este kernel recibe el mismo conjunto de parámetros de 4 punteros a búferes de datos y una variable. También tenemos previsto ejecutar el kernel en un espacio de tareas unidimensional para el número de series temporales unitarias.

En el cuerpo del kernel, identificamos el hilo en el espacio de tareas y definimos los desplazamientos en los búferes de datos.

   size_t n = get_global_id(0);
   const int shift = n * dimension;

Carga variables estadísticas de los búferes y convierte inmediatamente la desviación estándar en un valor complejo.

   float v= vars[n];
   float2 variance=(float2)((v > 0 ? v : 1.0f), 0)
   float2 mean = means[n];

A continuación, organizar el único bucle de conversión de datos en este kernel.

   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexMul(inputs[shift + i], variance) + mean;
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      outputs[shift + i] = val;
     }
  }

Los valores obtenidos se escriben en los elementos correspondientes del búfer de resultados.

Para llamar a los kernels creados anteriormente en el lado del programa principal, utilizamos los métodos ComplexNormalize y ComplexUnNormalize. El algoritmo para su construcción no difiere de los métodos considerados anteriormente para poner en cola los kernels del programa OpenCL. Por lo tanto, no nos detendremos en estos métodos. De todos modos, se proporcionan en el archivo adjunto.

Además, para combinar de forma adaptativa los resultados de las previsiones de tiempo y frecuencia, necesitamos coeficientes de influencia. Los autores del método ATFNet proponen determinarlas por la cuota de la frecuencia dominante en el espectro global. En consecuencia, en el lado OpenCL crearemos dos kernels para el programa:

MainFreqWeight - determinar la parte de la frecuencia dominante;
WeightedSum - calcula la suma ponderada de las previsiones en los dominios de la frecuencia y el tiempo.

Planificamos ambos kernels en un espacio de tareas unidimensional en función del número de series temporales unitarias analizadas.

En los parámetros del kernel MainFreqWeight, pasamos punteros a dos búferes de datos (características de frecuencia y resultados) y la dimensión de la serie analizada.

__kernel void MainFreqWeight(__global float2 *freq,
                             __global float *weight,
                             int dimension
                            )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

En el cuerpo del kernel, identificamos el hilo actual en el espacio de tareas y determinamos los desplazamientos en los búferes de datos. Después preparamos las variables locales.

   float max_f = 0;
   float total = 0;
   float energy;

A continuación, ejecutamos un bucle para determinar la energía de la frecuencia dominante y de todo el espectro.

   for(int i = 0; i < dimension; i++)
     {
      energy = ComplexAbs(freq[shift + i]);
      total += energy;
      max_f = fmax(max_f, energy);
     }

Para completar las operaciones del kernel, dividimos la energía de la frecuencia dominante por la energía total del espectro. El valor resultante se guarda en el elemento correspondiente del búfer de salida.

   weight[n] = max_f / (total > 0 ? total : 1);
  }

El algoritmo del kernel WeightedSum para determinar la suma ponderada de las predicciones en el dominio del tiempo y la frecuencia es bastante sencillo. En los parámetros, el kernel recibe 4 punteros a búferes de datos y la dimensión del vector de una secuencia (en nuestro caso, la profundidad de predicción).

__kernel void WeightedSum(__global float *inputs1,
                          __global float *inputs2,
                          __global float *outputs,
                          __global float *weight,
                          int dimension
                         )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

En el cuerpo del kernel, identificamos el hilo actual en el espacio unidimensional de tareas y determinamos los desplazamientos en los búferes de datos: A continuación, creamos un bucle de suma ponderada de elementos. Los resultados de las operaciones se escriben en el elemento correspondiente del búfer de resultados.

   float w = weight[n];
   for(int i = 0; i < dimension; i++)
      outputs[shift + i] = inputs1[shift + i] * w + inputs2[shift + i] * (1 - w);
  }

Para colocar kernels en la cola de ejecución en el lado del programa principal, creamos métodos del mismo nombre. Encontrará estos códigos en el anexo.

Una vez completado el trabajo preparatorio, pasamos a construir el método de paso de avance feedForward de nuestra clase CNeuronATFNetOCL. En los parámetros de este método, al igual que en el método similar de la clase padre, recibimos un puntero al objeto de la capa neuronal anterior, que en este caso actúa como dato inicial para las operaciones posteriores.

bool CNeuronATFNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !NeuronOCL.getOutput())
      return false;

En el cuerpo del método, primero comprobamos la relevancia del puntero recibido. Aquí también guardamos un puntero al búfer de resultados de la capa neuronal obtenida en la variable interna del objeto actual.

   if(cInputs != NeuronOCL.getOutput())
      cInputs = NeuronOCL.getOutput();

A continuación, realizamos primero operaciones de previsión sobre los datos posteriores de la serie temporal analizada en el dominio temporal. Normalizar los datos obtenidos.

//--- T-Block
   if(!cNorm.FeedForward(NeuronOCL))
      return false;;

A continuación, añada la codificación posicional.

   if(!cPositionEncoder.FeedForward(cNorm.AsObject()))
      return false;

Transponga el tensor resultante y divida los datos en parches.

   if(!cTranspose.FeedForward(cPositionEncoder.AsObject()))
      return false;
   if(!cPatching.FeedForward(cTranspose.AsObject()))
      return false;

Los datos preparados pasan por el bloque de atención.<

   int total = caAttention.Total();
   CNeuronBaseOCL *prev = cPatching.AsObject();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *att = caAttention.At(i);
      if(!att.FeedForward(prev))
         return false;
      prev = att;
     }

Los valores posteriores se predicen.

   total = caProjection.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *proj = caProjection.At(i);
      if(!proj.FeedForward(prev))
         return false;
      prev = proj;
     }

A la salida del bloque T, añadimos valores estadísticos de las series temporales de entrada a los valores de previsión.

   if(!cRevIN.FeedForward(prev))
      return false;

Una vez obtenidos los valores predichos en el dominio del tiempo, pasamos a trabajar con el dominio de la frecuencia. En primer lugar, transformamos las series temporales obtenidas en un espectro de características frecuenciales. Para ello utilizamos el algoritmo FFT.

//--- F-Block
   if(!FFT(cInputs, cInputs, GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), false))
      return false;

Tras obtener dos búferes de las partes real e imaginaria del espectro de frecuencias, los combinamos en un único tensor.

   if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(), 1, 1,
                                                                                     iFFT * iVariables))
      return false;

Tenga en cuenta que al concatenar para ambos búferes de datos utilizamos un tamaño de ventana de 1 elemento. Así, obtenemos un tensor en el que las partes real e imaginaria de la característica de frecuencia correspondiente están próximas entre sí.

Normalizamos el tensor resultante de la frecuencia de entrada.

   if(!ComplexNormalize())
      return false;

Determinar la parte de la frecuencia dominante.

   if(!MainFreqWeights())
      return false;

Pasamos los datos de frecuencia preparados por el bloque de atención. Aquí sólo necesitamos llamar al método de paso de avance de la clase de atención compleja multicapa creada en el artículo anterior.

   if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject()))
      return false;

Una vez ejecutadas con éxito las operaciones del bloque de atención, devolvemos los parámetros estadísticos la frecuencia de la serie de entrada a los datos procesados.

   if(!ComplexUnNormalize())
      return false;

Divide el tensor del espectro de frecuencias en las partes real e imaginaria que lo componen.

   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getOutput(), 1, 1,
                                                                                          iFFT * iVariables))
      return false;

Vuelve a transformar el espectro de frecuencias en una serie temporal.

   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm),

           GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), true))
      return false;

Creo que deberíamos explicar las operaciones anteriores del bloque F. A primera vista, puede parecer extraño realizar un gran número de transformaciones de una serie temporal en respuestas en frecuencia, normalizarlas y, a continuación, realizar operaciones inversas devolviendo los datos a la misma serie temporal, sólo para realizar operaciones de atención. Además, todas estas operaciones, excepto la atención, no tienen parámetros entrenables y, en teoría, deberían devolver las series temporales originales. Pero todo es cuestión del bloque de atención.

Permítanme recordarles que los autores del método propusieron utilizar la transformada discreta de Fourier ampliada. En la práctica, simplemente utilizamos una base exponencial compleja para una DFT de una serie temporal completa. Pero al transformar la serie temporal original en su característica de frecuencia, no tenemos valores predichos y simplemente los sustituimos por valores cero. Por lo tanto, la ejecución de una DFT inversa devolverá, como es de esperar, valores predichos cercanos a «0», lo que no es adecuado. Por lo tanto, normalizamos los espectros de las series temporales unitarias para que sean comparables. Al compararlos entre sí en el bloque de atención, intentamos enseñar al modelo a restaurar los datos que faltan de las características de frecuencia analizadas.

Así, a la salida del bloque de atención compleja, esperamos recibir espectros modificados y coherentes entre sí de características de frecuencia de series temporales completas unitarias con datos perdidos restaurados. Al restaurar las series temporales a partir de los espectros modificados, podemos obtener valores de previsión de las series temporales analizadas que difieren de cero.

Para completar las operaciones de paso de avance, sólo tenemos que extraer los valores predichos de la serie temporal completa.

   if(!DeConcat(GetPointer(cReconstructInput), GetPointer(cForecast), GetPointer(cOutputTimeSeriasReGrad),

                GetPointer(cOutputTimeSeriasRe), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables))
      return false;

Y suma las predicciones realizadas en los dominios temporal y frecuencial, teniendo en cuenta el coeficiente de significación.

//--- Output
   if(!WeightedSum())
      return false;
//---
   return true;
  }

No olvides controlar los resultados de las operaciones en cada fase. Una vez completadas las operaciones del método, devolvemos el resultado lógico de todas las operaciones a la persona que ha realizado la llamada.

1.3 Distribución del gradiente de error

Después de realizar el paso de avance, necesitamos distribuir el gradiente de error a todos los parámetros de entrenamiento del modelo. En nuestra nueva clase, ambos están en el bloque T y en el bloque F. Por lo tanto, necesitamos implementar un mecanismo para propagar el gradiente de error a través de los bloques T y F. A continuación, tenemos que combinar el gradiente de error de los dos flujos y pasar el gradiente resultante a la capa anterior.

Al igual que con el paso de avance, antes de construir el método calcInputGradients, tenemos que hacer algo de trabajo preparatorio. Durante el paso de avance, en el lado de OpenCL, creamos kernels para la normalización y el retorno inverso de los valores de la distribución estadística: ComplexNormalize y ComplexUnNormalize. En el paso de retropropagación, necesitamos crear kernels de distribución de gradiente de error a través de las operaciones especificadas ComplexNormalizeGradient y ComplexUnNormalizeGradient, respectivamente.

En el kernel de distribución del gradiente de error, mediante el bloque de normalización de frecuencias, sólo dividimos el gradiente de error obtenido por la desviación estándar del espectro correspondiente.

__kernel void ComplexNormalizeGradient(__global float2 *inputs_gr,
                                       __global float2 *outputs_gr,
                                       __global float *vars,
                                       int dimension)
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;
//---
   float v = vars[n];
   float2 variance = (float2)((v > 0 ? v : 1.0f), 0);
   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexDiv(outputs_gr[shift + i], variance);
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      inputs_gr[shift + i] = val;
     }
  }

Debo decir que este es un enfoque bastante simplificado para resolver este problema. Aquí tomamos el valor medio y la desviación típica como constantes. De hecho, son funciones y, según las reglas del descenso de gradiente, también tenemos que ajustar su influencia y propagar el gradiente de error a los elementos influyentes del modelo. Pero, como demuestra la práctica, la influencia de estos elementos en los datos iniciales es bastante pequeña. Por lo tanto, para reducir el coste de formación del modelo, omitiremos estas operaciones.

El kernel para la distribución del gradiente mediante operaciones de desnormalización de datos es similar, con la única diferencia de que aquí multiplicamos el gradiente de error resultante por la desviación típica.

__kernel void ComplexUnNormalizeGradient(__global float2 *inputs_gr,
      __global float2 *outputs_gr,
      __global float *vars,
      int dimension)
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;
//---
   float v = vars[n];
   float2 variance = (float2)((v > 0 ? v : 1.0f), 0);
   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexMul(outputs_gr[shift + i], variance);
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      inputs_gr[shift + i] = val;
     }
  }

A continuación, necesitamos implementar un kernel para distribuir el gradiente de error total entre los bloques de predicción en los dominios del tiempo y la frecuencia. Implementamos esta funcionalidad en el kernel WeightedSumGradient. En los parámetros, este kernel recibe punteros a 4 búferes de datos y 1 parámetro, de forma similar al kernel de avance correspondiente.

__kernel void WeightedSumGradient(__global float *inputs_gr1,
                                  __global float *inputs_gr2,
                                  __global float *outputs_gr,
                                  __global float *weight,
                                  int dimension
                                 )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

En el cuerpo del kernel, como de costumbre, identificamos el hilo actual en el espacio unidimensional de tareas y determinamos el desplazamiento en los búferes de datos. A continuación, prepararemos las variables de ponderación locales para las previsiones de frecuencias y series temporales.

   float w = weight[n];
   float w1 = 1 - weight[n];

A continuación, creamos un bucle para propagar el gradiente de error a través de los búferes de datos correspondientes.

   for(int i = 0; i < dimension; i++)
     {
      float grad = outputs_gr[shift + i];
      inputs_gr1[shift + i] = grad * w;
      inputs_gr2[shift + i] = grad * w1;
     }
  }

Los kernels de propagación del gradiente de error anteriores se colocan en la cola de ejecución dentro de los métodos pertinentes en el lado del programa principal. Puedes familiarizarte con el código de estos métodos en el archivo adjunto.

Otro punto al que debemos prestar atención es el cálculo del gradiente de error de la serie temporal reconstruida de valores históricos. Implementaremos esta funcionalidad en el método calcReconstructGradient.

Aunque las operaciones se realizan en el lado del contexto OpenCL, para realizar las operaciones especificadas no creamos un nuevo kernel. En su lugar, utilizaremos un kernel ya preparado que determina el gradiente de error en función de los valores objetivo. Sólo tenemos que crear un método para poner el kernel en la cola de ejecución utilizando los búferes de datos de nuestro bloque F.

El kernel que utilizamos se ejecuta en un espacio de tareas unidimensional en función del número de elementos del tensor. En nuestro caso, el tamaño del vector analizado es igual al producto de la profundidad del historial analizado y el número de series temporales unitarias.

bool CNeuronATFNetOCL::calcReconstructGradient(void)
  {
   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = iHistory * iVariables;

Nuestros datos objetivo incluyen los valores de los datos originales que obtuvimos durante el paso de avance de la capa neuronal anterior. Durante el paso de avance, guardamos un puntero al búfer de datos que necesitábamos.

   if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_t, cInputs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Determinamos el gradiente de error de los datos reconstruidos a partir del espectro procesado.

   if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_o, cReconstructInput.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Escribiremos los resultados de las operaciones en el búfer de gradiente de los datos recuperados.

   if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_ig, cReconstructInputGrad.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

No utilizamos funciones de activación en el paso hacia delante.

   if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_activation, (int)None))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Ponemos el kernel en la cola de ejecución, comprobamos el resultado de las operaciones y completamos el método, devolviendo al llamante el resultado lógico de las operaciones realizadas.

   if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_error, 1))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   ResetLastError();
   if(!OpenCL.Execute(def_k_CalcOutputGradient, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel CalcOutputGradient: %d", GetLastError());
      return false;
     }
//---
   return true;
  }

Una vez completado el trabajo preparatorio, pasamos directamente a la construcción del método de propagación de gradientes de error calcInputGradients.

En los parámetros de este método, similar al mismo método de la clase padre, recibimos un puntero al objeto de la capa neuronal anterior, a la que debemos propagar el gradiente de error.

bool CNeuronATFNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !NeuronOCL.getGradient() || !cInputs)
      return false;

En el cuerpo del método, comprobamos inmediatamente la relevancia del puntero recibido. Después, distribuimos el gradiente de error obtenido de la capa posterior en 2 flujos entre los bloques de predicción en los dominios del tiempo y la frecuencia.

//--- Output
   if(!WeightedSumGradient())
      return false;

En primer lugar, propagamos el gradiente de error a través del bloque T de predicción en el dominio del tiempo. Aquí, en el orden inverso al paso de avance, llamamos a los métodos relevantes de los objetos anidados.

//--- T-Block
   if(cRevIN.Activation() != None && 
     !DeActivation(cRevIN.getOutput(), cRevIN.getGradient(), cRevIN.getGradient(), cRevIN.Activation()))
      return false;
   CNeuronBaseOCL *next = cRevIN.AsObject();
   for(int i = caProjection.Total() - 1; i >= 0; i--)
     {
      CNeuronBaseOCL *proj = caProjection.At(i);
      if(!proj || !proj.calcHiddenGradients((CObject *)next))
         return false;
      next = proj;
     }
   for(int i = caAttention.Total() - 1; i >= 0; i--)
     {
      CNeuronBaseOCL *att = caAttention.At(i);
      if(!att || !att.calcHiddenGradients((CObject *)next))
         return false;
      next = att;
     }
   if(!cPatching.calcHiddenGradients((CObject*)next))
      return false;
   if(!cTranspose.calcHiddenGradients(cPatching.AsObject()))
      return false;
   if(!cPositionEncoder.calcHiddenGradients(cTranspose.AsObject()))
      return false;
   if(!cNorm.calcHiddenGradients(cPositionEncoder.AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(cNorm.AsObject()))
      return false;

El algoritmo de propagación del gradiente en el bloque de predicción de frecuencia es un poco más complicado. En primer lugar, definimos el gradiente de error para la parte imaginaria de la serie temporal reconstruida. Como ya se ha mencionado, el valor objetivo de la parte imaginaria de la serie temporal es 0. Por lo tanto, para determinar el gradiente de error, simplemente cambiamos el signo de los resultados del paso de avance.

//--- F-Block
   if(!CNeuronBaseOCL::SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm), 
                                       GetPointer(cOutputTimeSeriasIm), iFFT*iVariables, false, 0, 0, 0, -0.5))
      return false;

A continuación, definimos el gradiente del error de recuperación de datos históricos.

   if(!calcReconstructGradient())
      return false;

Después combinamos los tensores de gradiente del error de recuperación de datos históricos (definidos en el método calcReconstructGradient), el gradiente del error de previsión de la serie temporal (obtenido dividiendo el gradiente del error de la capa posterior en dos corrientes) y lo complementamos con valores cero hasta el tamaño del espectro de la serie completa.

   if(!Concat(GetPointer(cReconstructInputGrad), GetPointer(cForecastGrad), GetPointer(cZero), 
              GetPointer(cOutputTimeSeriasReGrad), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables))
      return false;

Añadimos valores cero al final del tensor del gradiente de error de la serie temporal completa, ya que no disponemos de datos sobre los valores objetivo más allá del horizonte de planificación. Esto significa que simplemente no los corregimos.

El gradiente de error resultante para la serie temporal completa construida utilizando los datos del bloque de predicción de frecuencia se traduce al dominio de la frecuencia aplicando FFT.

   if(!FFT(GetPointer(cOutputTimeSeriasReGrad), GetPointer(cOutputTimeSeriasIm),





           GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), false))
      return false;

Combinamos los datos obtenidos de las partes real e imaginaria del espectro de frecuencias del gradiente de error en un único tensor.

   if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getGradient(),
                                                                              1, 1, iFFT * iVariables))
      return false;

Corregir el gradiente de error de la derivada de las operaciones de desnormalización de datos.

   if(!ComplexUnNormalizeGradient())
      return false;

Propagar el gradiente de error a través del bloque de atención compleja.

   if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject()))
      return false;

A continuación, corrige el gradiente de error mediante la derivada de la función de normalización de datos.

   if(!ComplexNormalizeGradient())
      return false;

Separa las partes real e imaginaria del espectro.

   if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getGradient(),
                                                                             1, 1, iFFT * iVariables))
      return false;

Devuelve el gradiente de error al dominio del tiempo utilizando IFFT.

   if(!FFT(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm),



           GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), false))
      return false;

Obsérvese que hemos obtenido el gradiente de error para la serie temporal completa. Pero sólo necesitamos propagar el gradiente del error de los datos históricos a la capa anterior. Por lo tanto, primero seleccionamos los datos para el horizonte histórico analizado.

   if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasRe), 
                                                                        iHistory, iFFT-iHistory, iVariables))
      return false;

A continuación, sumamos los valores obtenidos a los resultados de la distribución del gradiente de error del bloque T.

   if(!CNeuronBaseOCL::SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cInputFreqRe), 
                                       NeuronOCL.getGradient(), iHistory*iVariables, false, 0, 0, 0, 0.5))
      return false;
//---
   return true;
  }

Como siempre, en cada iteración controlamos el proceso de realización de las operaciones. Una vez completadas con éxito todas las operaciones, devolvemos el resultado lógico del método a la instancia que lo ha invocado.

1.4 Actualización de los parámetros del modelo

El gradiente de error de cada parámetro entrenado del modelo determina su influencia en el resultado global. En el siguiente paso, ajustamos los parámetros del modelo para minimizar el error. Esta funcionalidad se realiza en el método updateInputWeights. Dentro de la implementación de nuestra clase, la actualización de los parámetros indica llamar a los métodos del mismo nombre de los objetos anidados que contienen los parámetros que se están entrenando. En el bloque F, sólo se trata de una clase de atención compleja.

bool CNeuronATFNetOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
//--- F-Block
   if(!cFreqAtteention.UpdateInputWeights(cNormFreqComplex.AsObject()))
      return false;

El bloque T tiene más objetos de este tipo.

//--- T-Block
   if(!cPatching.UpdateInputWeights(cPositionEncoder.AsObject()))
      return false;
   int total = caAttention.Total();
   CNeuronBaseOCL *prev = cPatching.AsObject();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *att = caAttention.At(i);
      if(!att.UpdateInputWeights(prev))
         return false;
      prev = att;
     }
   total = caProjection.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *proj = caProjection.At(i);
      if(!proj.UpdateInputWeights(prev))
         return false;
      prev = proj;
     }
//---
   return true;
  }

Con esto concluimos nuestro examen de los algoritmos de aplicación de los enfoques propuestos por los autores del método ATFNet. Puedes encontrar el código completo de la clase CNeuronATFNetOCL en el archivo adjunto.

2. Arquitectura del modelo

Hemos completado nuestra clase que implementa los planteamientos del método ATFNet. Pasemos a construir la arquitectura de nuestros modelos. Como seguramente ya habrás deducido, implementaremos una nueva capa neuronal en el codificador de estados del entorno. Por supuesto, es difícil referirse a la clase CNeuronATFNetOCL como una capa neuronal. Implementa una arquitectura bastante compleja para construir un modelo completo.

Alimentaremos nuestro codificador con un conjunto de entradas brutas, como hicimos con los modelos construidos anteriormente.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Sin embargo, en este caso no normalizamos los datos obtenidos. Tanto el bloque T como el bloque F cuentan con normalización de datos en sus arquitecturas. Así que nos saltamos este paso. Sin embargo, nuestras entradas se forman según vectores que describen estados individuales del entorno. Antes del tratamiento posterior, transponemos las entradas para permitir el análisis en términos de series temporales unitarias.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, utilizamos nuestra nueva clase para pronosticar los datos posteriores de la serie temporal analizada.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronATFNetOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.window_out = NForecast;
   descr.step = 8;
   descr.layers = 4;
     {
      int temp[] = {5, 1, 16};
      ArrayCopy(descr.windows, temp);
     }
   descr.activation = None;
   descr.batch = 10000;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

En realidad, esta capa contiene todo nuestro modelo. A su salida, obtenemos los valores de previsión que necesitamos para toda la profundidad de planificación. Sólo tenemos que transponerlos a la dimensión requerida.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Para la coherencia del espectro de valores predichos, utilizaremos las aproximaciones del método FreDF.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(false);
   descr.probability = 0.8f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Dejamos los modelos Actor y Critic sin cambios.

Los programas de entrenamiento y prueba de los modelos entrenados también se copiaron de los artículos anteriores. Puede estudiar el código usted mismo en el archivo adjunto.

3. Pruebas

Hemos trabajado bastante para implementar los enfoques propuestos por los autores del método ATFNet utilizando MQL5. La cantidad de trabajo realizado ha ido incluso más allá del alcance de un solo artículo. Finalmente, pasamos a la etapa final de nuestro trabajo: entrenar y probar modelos.

Para entrenar los modelos, utilizaremos el EA que creamos anteriormente para entrenar los modelos anteriores. Por lo tanto, también se pueden utilizar datos de entrenamiento recopilados previamente.

Los modelos se entrenan con los datos históricos del EURUSD con el marco temporal H1 durante todo el año 2023.

En la primera etapa, entrenamos el modelo Encoder para pronosticar estados posteriores del entorno en un horizonte de planificación que viene determinado por la constante NForecast.

Al igual que antes, el modelo Encoder analiza únicamente el movimiento de los precios, por lo que durante la primera etapa de entrenamiento no necesitamos actualizar el conjunto de entrenamiento.

En la segunda etapa de nuestro proceso de aprendizaje, buscamos la política de acción Actor más óptima. Aquí ejecutamos un entrenamiento iterativo de los modelos Actor y Critic, que se alterna con la actualización del conjunto de datos de entrenamiento. El proceso de actualización del conjunto de datos de entrenamiento nos permite refinar las recompensas ambientales en el dominio de la política actual del Actor, lo que a su vez nos permitirá afinar la política deseada.

Durante el proceso de entrenamiento, pudimos obtener una política de Actor capaz de generar beneficios tanto en los conjuntos de datos de entrenamiento como en los de prueba. A continuación se muestran los resultados de las pruebas del modelo.

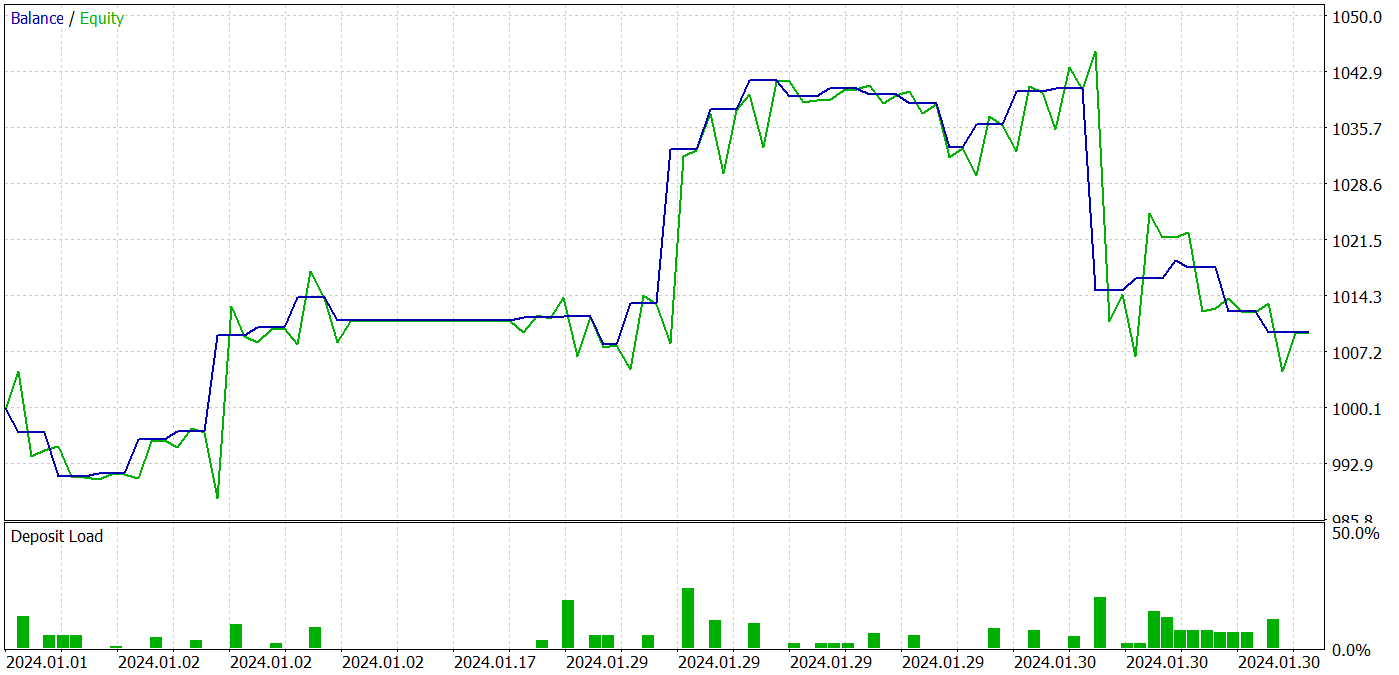
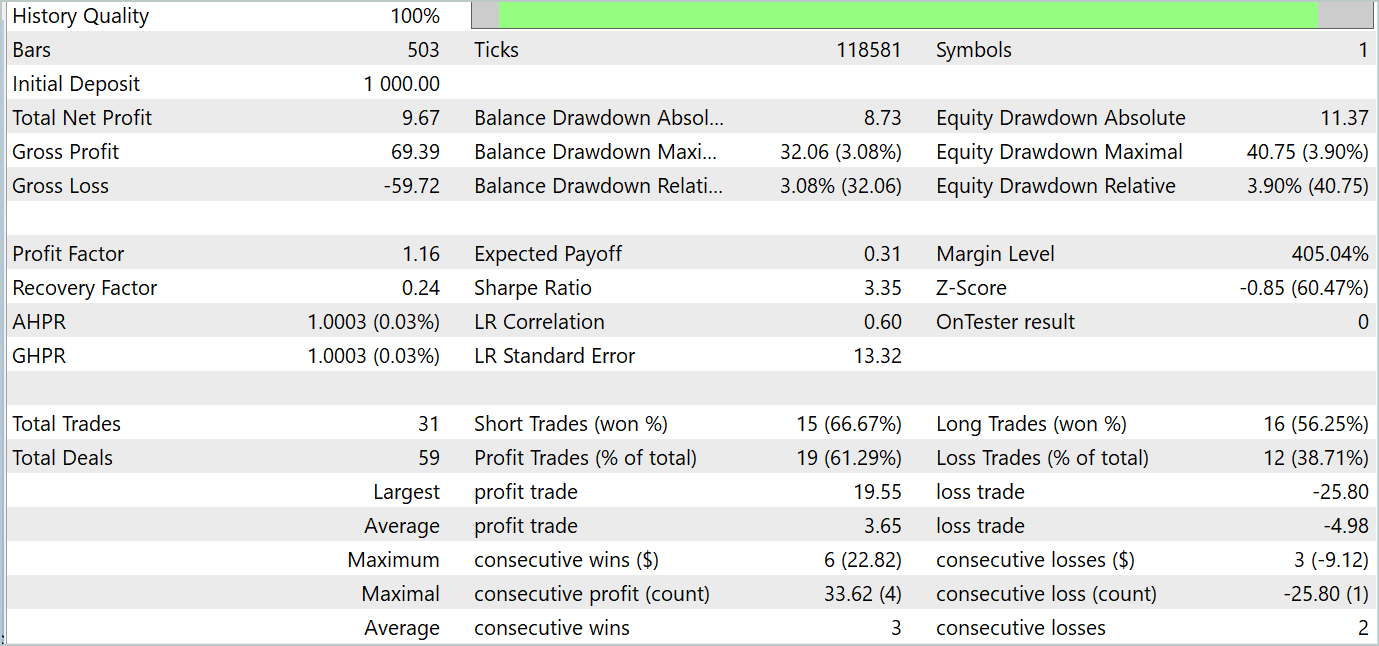
Durante el periodo de prueba, el modelo realizó 31 operaciones, 19 de las cuales se cerraron con beneficios. El porcentaje de operaciones rentables superó el 61%. Cabe destacar que el modelo tenía casi el mismo número de posiciones largas y cortas (15 frente a 16).

Conclusión

Los dos últimos artículos se dedicaron al método ATFNet, que se propuso para la previsión de series temporales multivariantes y se presentó en el artículo «ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting». El modelo ATFNet combina módulos de dominio temporal y frecuencial para analizar dependencias en datos de series temporales. Se utiliza el bloque T para capturar las dependencias locales en el dominio temporal y el bloque F para analizar las ciclicidades de las series temporales en el dominio de la frecuencia.

ATFNet aplica la ponderación de energía de la serie armónica dominante, la transformada de Fourier ampliada y la atención al espectro complejo para adaptarse a la periodicidad y los desfases de frecuencia en las series temporales de entrada.

En la parte práctica del artículo, implementamos nuestra visión de los enfoques propuestos utilizando MQL5. Entrenamos y probamos modelos con datos reales. Los resultados de las pruebas indican el potencial de los enfoques propuestos para construir estrategias de negociación rentables.

Referencias

Programas utilizados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Expert Advisor	Colección de ejemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para la recolección de ejemplos utilizando el método Real-ORL
3	Study.mq5	Expert Advisor	EA para el entrenamiento del modelo
4	StudyEncoder.mq5	Expert Advisor	EA de entrenamiento del codificador
5	Test.mq5	Expert Advisor	EA de prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Código base	Biblioteca OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15024

Archivos adjuntos |

Descargar ZIP

MQL5.zip (1298.75 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Desarrollo de un sistema de repetición (Parte 60): Presionando play en el servicio (I)

Llevamos bastante tiempo trabajando únicamente con los indicadores. Pero ahora ha llegado el momento de hacer que el servicio vuelva a ejecutar su trabajo y podamos ver el gráfico construyéndose con los datos proporcionados. Sin embargo, como no todo es tan simple, será necesario observar para entender lo que nos espera.

Algoritmo de búsqueda cooperativa artificial (Artificial Cooperative Search, ACS)

La búsqueda cooperativa artificial (Artificial Cooperative Search, ACS) es un método innovador que utiliza una matriz binaria y múltiples poblaciones dinámicas basadas en relaciones de mutualismo y cooperación para encontrar soluciones óptimas de forma rápida y precisa. El enfoque único de ACS sobre depredadores y presas le permite obtener excelentes resultados en problemas de optimización numérica.

Desarrollo de un sistema de repetición (Parte 61): Presionando play en el servicio (II)

En este artículo, analizaremos las modificaciones necesarias para que el sistema de repetición/simulación pueda operar de manera más eficiente y segura. También mostraré algo de interés para quienes deseen aprovechar al máximo el uso de clases. Además, abordaré un problema específico de MQL5 que reduce el rendimiento del código al trabajar con clases y explicaré cómo resolverlo.

Redes neuronales: así de sencillo (Parte 92): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo

Los autores del método FreDF confirmaron experimentalmente la ventaja de la previsión combinada en los ámbitos de la frecuencia y el tiempo. Sin embargo, el uso del hiperparámetro de peso no es óptimo para series temporales no estacionarias. En este artículo, nos familiarizaremos con el método de combinación adaptativa de previsiones en los ámbitos de la frecuencia y el tiempo.