
Calculating mathematical expressions (Part 2). Pratt and shunting yard parsers
In this article, we continue to study various mathematical expression parsing methods and their implementation in the MQL language. In the first part we considered recursive descent parsers. The main advantage of such parsers is their user-friendly structure, which is directly related to specific grammar of expressions. But when it comes to efficiency and technical features, there are other types of parsers that are worth paying attention to.
Parsers Using Operator Precedence
The next parser type which we are going to consider is the precedence parser. They have a more compact implementation because class methods are created not based on grammar rules (on which case each rule is converted to a separate method), but in a more generalized form taking into account only the precedence of operators.
The precedence of operations was already present in an implicit form in the EBNF grammar description: its rules execute from operations with lower priority to operations with higher priority, up to terminal entities — constants and variables. This is because precedence determines the sequence in which operations should be performed when there is no explicit parenthesis grouping. For example, the precedence of the multiplication operation is higher than that of the addition. But the unary minus takes precedence over multiplication. The closer the syntax tree element to the root (to the whole expression), the later it will be evaluated.
To implement the parsers, we need two tables with numeric values corresponding to the precedence of each operation. The higher the value, the higher the priority.
We have two tables, because unary and binary operations will be logically separated in algorithms. Actually, we are talking not only about operations, but we are talking more generally about the symbols which can be found in expressions as prefixes and infixes (more information about types of operators in Wikipedia).
As the name implies, the prefix is the symbol that precedes the operand (for example, '!' in the "!var" expression), and the infix is the character between the operands (for example, '+' in the expression "a + b"). There are also postfixes (such as a pair of '+' in the increment operator, which is also available in MQL — "i++"), but they are not used in our expressions and thus we will not consider them.
In addition to unary operations '!', '-', '+', prefixes can be an open parenthesis '(' — indicates the beginning of a group, a letter or an underscore — indicate the beginning of an identifier, as well as a digit or a period '.' — indicate the beginning of a numeric constant.
Let us describe the tables in the ExpressionPrecedence class, from which certain parser classes based on priorities will be inherited. All these parsers will work with Promise.
class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *> { protected: static uchar prefixes[128]; static uchar infixes[128]; static ExpressionPrecedence epinit; static void initPrecedence() { // grouping prefixes['('] = 9; // unary prefixes['+'] = 9; prefixes['-'] = 9; prefixes['!'] = 9; // identifiers prefixes['_'] = 9; for(uchar c = 'a'; c <= 'z'; c++) { prefixes[c] = 9; } // numbers prefixes['.'] = 9; for(uchar c = '0'; c <= '9'; c++) { prefixes[c] = 9; } // operators // infixes['('] = 9; // parenthesis is not used here as 'function call' operator infixes['*'] = 8; infixes['/'] = 8; infixes['%'] = 8; infixes['+'] = 7; infixes['-'] = 7; infixes['>'] = 6; infixes['<'] = 6; infixes['='] = 5; infixes['!'] = 5; infixes['&'] = 4; infixes['|'] = 4; infixes['?'] = 3; infixes[':'] = 2; infixes[','] = 1; // arg list delimiter } ExpressionPrecedence(const bool init) { initPrecedence(); } public: ExpressionPrecedence(const string vars = NULL): AbstractExpressionProcessor(vars) {} ExpressionPrecedence(VariableTable &vt): AbstractExpressionProcessor(vt) {} }; static uchar ExpressionPrecedence::prefixes[128] = {0}; static uchar ExpressionPrecedence::infixes[128] = {0}; static ExpressionPrecedence ExpressionPrecedence::epinit(true);
Precedence tables are created in an "economical" way, using sparse arrays of 128 elements (this is enough, because characters with codes from other ranges are not supported). Precedence is specified in cells corresponding to symbol codes. Thus, the precedence can be easily accessed by direct addressing by the token code.
Two additional helper method will be used in child classes, allowing to check the symbols that follow in the input string: _lookAhead simply returns the next token (as if looking a step ahead), _matchNext — reads the token if it matches or throws an error otherwise.
class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *> { protected: ... ushort _lookAhead() { int i = 1; while(_index + i < _length && isspace(_expression[_index + i])) i++; if(_index + i < _length) { return _expression[_index + i]; } return 0; } void _matchNext(ushort c, string message, string context = NULL) { if(_lookAhead() == c) { _nextToken(); } else if(!_failed) // prevent chained errors { error(message, context); } } ... };
Let us start with the first precedence-based parser: the Pratt parser.
Pratt Parser (ExpressionPratt)
Pratt parser is top-down, just like the recursive descent parser. This means that it will also have recursive calls of some methods which analyze individual constructs in the expressions. However, there will be much fewer of these methods.
The constructors and the main public 'evaluate' method look familiar.
class ExpressionPratt: public ExpressionPrecedence { public: ExpressionPratt(const string vars = NULL): ExpressionPrecedence(vars) { helper = new ExpressionHelperPromise(&this); } ExpressionPratt(VariableTable &vt): ExpressionPrecedence(vt) { helper = new ExpressionHelperPromise(&this); } virtual Promise *evaluate(const string expression) override { Promise::environment(&this); AbstractExpressionProcessor<Promise *>::evaluate(expression); if(_length > 0) { return parseExpression(); } return NULL; }
The new parseExpression method is the heart of the Pratt algorithm. It starts by setting the current precedence equal to 0 by default, which means that any signal can be read.
virtual Promise *parseExpression(const int precedence = 0) { if(_failed) return NULL; // cut off subexpressions in case of errors _nextToken(); if(prefixes[(uchar)_token] == 0) { this.error("Can't parse " + ShortToString(_token), __FUNCTION__); return NULL; } Promise *left = _parsePrefix(); while((precedence < infixes[_token]) && !_failed) { left = _parseInfix(left, infixes[(uchar)_token]); } return left; }
The idea of the method is simple: start parsing the expression by reading the next symbol which must be a prefix (otherwise it is an error), and pass control to the _parsePrefix method which can read any prefix construct as a whole. After that, as long as the precedence of the next symbol is higher than the current precedence, pass control to the _parseInfix method which can read any infix construct as a whole. Thus, the entire parser consists of only three methods. In a sense, the Pratt parser represents an expression as a hierarchy of prefix and infix constructs.
Note that if the current _token is not found in the infix table, its precedence will be zero and the 'while' loop will stop (or not start at all).
The specific feature of the _parseInfix method is that the current Promise (left) object is passed inside in the first parameter becomes a part of the subexpression, while the allowable minimal precedence of operations, which the method is allowed to read, is set in the second parameter as the precedence of the current infix token. The method will return the new Promise object for the whole subexpression. This object is saved in the same variable (and the previous reference to Promise will somehow be available by reference fields from the new object).
Let us consider methods _parsePrefix and _parseInfix in more detail.
The _parsePrefix method expects the current token from allowed prefixes and handles it using 'switch'. The already familiar method parseExpression is called for the opening parenthesis '(', to calculate the nested expression. The precedence parameter is omitted, which means parsing from the lowest zero precedence (because it is like a separate expression in brackets). A 'helper' object is used for '!', in order to receive a logical negation from the next fragment. It is read by the parseExpression method, but this time the precedence of the current token is passed into it. It means that the fragment to be negated will end before the first symbol with a precedence lower than '!'. For example, if the expression has "!a*b", then parseExpression will stop after reading the 'a' variable, because multiplication '*' has a lower priority than negation '!'. Unary '+' and '-' are processed in a similar way, but 'helper' is not used in this case. For '+', we only need to read the subexpression in parseExpression. For '-', call the overridden 'minus' for the received result (as you remember, the results are Promise objects).
The _parsePrefix method sorts all other symbols by their belonging to the 'isalpha' category. It is assumed that a letter is the beginning of an identifier, and a digit or a period is the beginning of a number. In all other cases the method will return NULL.
Promise *_parsePrefix()
{
Promise *result = NULL;
switch(_token)
{
case '(':
result = parseExpression();
_match(')', ") expected!", __FUNCTION__);
break;
case '!':
result = helper._negate(parseExpression(prefixes[_token]));
break;
case '+':
result = parseExpression(prefixes[_token]);
break;
case '-':
result = -parseExpression(prefixes[_token]);
break;
default:
if(isalpha(_token))
{
string variable;
while(isalnum(_token))
{
variable += ShortToString(_token);
_nextToken();
}
if(_token == '(')
{
const string name = variable;
const int index = _functionTable.index(name);
if(index == -1)
{
error("Function undefined: " + name, __FUNCTION__);
return NULL;
}
const int arity = _functionTable[index].arity();
if(arity > 0 && _lookAhead() == ')')
{
error("Missing arguments for " + name + ", " + (string)arity + " required!", __FUNCTION__);
return NULL;
}
Promise *params[];
ArrayResize(params, arity);
for(int i = 0; i < arity; i++)
{
params[i] = parseExpression(infixes[',']);
if(i < arity - 1)
{
if(_token != ',')
{
_match(',', ", expected (param-list)!", __FUNCTION__);
break;
}
}
}
_match(')', ") expected after " + (string)arity + " arguments!", __FUNCTION__);
result = helper._call(index, params);
}
else
{
return helper._variable(variable); // get index and if not found - optionally reserve the name with nan
}
}
else // digits are implied, must be a number
{
string number;
if(_readNumber(number))
{
return helper._literal(number);
}
}
}
return result;
}
An identifier followed by a parenthesis '(' is interpreted as a function call. We additionally parse for it a list of arguments (according to the function arity), separated by commas. Every argument is obtained by calling parseExpression with the comma ',' precedence. The Promise object for the function is generated using helper._call(). If there is no identifier after the parenthesis, a Promise object for the helper._variable() variable is created.
When the first token is not a letter, the _parsePrefix method tries to read a number using _readNumber and creates Promise for it by calling helper._literal().
The _parseInfix method expects the current token to be one of the allowed infixes. Moreover, in the first parameter it receives the left operand which has already been read into the Promise *left object. The second parameter specifies the minimal precedence of tokens to be parsed. Once something with a lower precedence is encountered, the subexpression is considered ended. The purpose of _parseInfix is to call parseExpression with 'precedence', in order to read the right operand, after which we can create a Promise object for a binary operation corresponding to the infix.
Promise *_parseInfix(Promise *left, const int precedence = 0) { Promise *result = NULL; const ushort _previous = _token; switch(_previous) { case '*': case '/': case '%': case '+': case '-': result = new Promise((uchar)_previous, left, parseExpression(precedence)); break; case '>': case '<': if(_lookAhead() == '=') { _nextToken(); result = new Promise((uchar)(_previous == '<' ? '{' : '}'), left, parseExpression(precedence)); } else { result = new Promise((uchar)_previous, left, parseExpression(precedence)); } break; case '=': case '!': _matchNext('=', "= expected after " + ShortToString(_previous), __FUNCTION__); result = helper._isEqual(left, parseExpression(precedence), _previous == '='); break; case '&': case '|': _matchNext(_previous, ShortToString(_previous) + " expected after " + ShortToString(_previous), __FUNCTION__); result = new Promise((uchar)_previous, left, parseExpression(precedence)); break; case '?': { Promise *truly = parseExpression(infixes[':']); if(_token != ':') { _match(':', ": expected", __FUNCTION__); } else { Promise *falsy = parseExpression(infixes[':']); if(truly != NULL && falsy != NULL) { result = helper._ternary(left, truly, falsy); } } } case ':': case ',': // just skip break; default: error("Can't process infix token " + ShortToString(_previous)); } return result; }
It is important that the current infix token at the beginning of the method is remembered in the _previous variable. This is done because, in case of success, parseExpression call shifts the position in the string to some other token, an arbitrary number of symbols to the right.
We have considered only 3 methods, each having a fairly transparent structure, and this is the entire Pratt parser as a whole.
Its application is similar to the ExpressionCompiler parser: create the ExpressionPratt object, set a table of variables, launch the 'evaluate' method for the expression string and receive Promise with a syntax tree which can be calculated using resolve().
Of course, using a syntax tree is not the only method for lazy evaluation. The next parser type which we are going to consider runs without using a tree, while it writes the evaluation algorithm into the so-called bytecode. So, let's see first how a bytecode works.
Bytecode Generation
Bytecode is a sequence of commands describing the entire calculation algorithm in a "fast" binary representation. Bytecode creation resembles a real compilation; however, the result contains not the processor instructions, but variables or structures of the applied language that control a certain calculator class. In our case, the execution unit is the following ByteCode structure:
struct ByteCode { uchar code; double value; int index; ByteCode(): code(0), value(0.0), index(-1) {} ByteCode(const uchar c): code(c), value(0.0), index(-1) {} ByteCode(const double d): code('n'), value(d), index(-1) {} ByteCode(const uchar c, const int i): code(c), value(0.0), index(i) {} string toString() const { return StringFormat("%s %f %d", CharToString(code), value, index); } };
Its fields repeat the fields of Promise objects — not all but only some of them, which represent a minimum set required for streaming calculations. The calculations are streaming because the commands will be read and executed sequentially, from left to right, without switching between hierarchical structures.
The 'code' field contains the essence of the command (the value corresponds to Promise codes), the 'value' field contains a number (constant), and the 'index' field contains the index of a variable/function in the table of variables/functions.
One of the methods for writing calculation instructions is the Reverse Polish Notation, also known as postfix notation. The idea of this notation is that operators follow their operands. For example, the usual infix notation "a + b" becomes postfix "a b +", and a more complex case of "a + b * sqrt(c)" becomes "a b c 'sqrt' * +".
RPN is good for bytecode because it enables easy implementation of calculation using the stack. When a program "sees" a digit or a variable reference in the input stream, it pushes this value onto the stack. If an operator or function is encountered in the input stream, the program pops the required number of values from the stack, performs the specified operation with the values and pushes the result back onto the stack. At the end of the process, the expression evaluation result will remain the only number on the stack.
Since RPN provides an alternative description of the same expressions for which we build syntax trees, these two presentations can be converted to each other. Let's try to generate a bytecode based on a Promise tree. To do so, add the exportToByteCode method to the Promise class.
class Promise { ... public: void exportToByteCode(ByteCode &codes[]) { if(left) left.exportToByteCode(codes); const int truly = ArraySize(codes); if(code == '?') { ArrayResize(codes, truly + 1); codes[truly].code = code; } if(right) right.exportToByteCode(codes); const int falsy = ArraySize(codes); if(last) last.exportToByteCode(codes); const int n = ArraySize(codes); if(code != '?') { ArrayResize(codes, n + 1); codes[n].code = code; codes[n].value = value; codes[n].index = index; } else // (code == '?') { codes[truly].index = falsy; // jump over true branch codes[truly].value = n; // jump over both branches } } ... };
The method receives as a parameter an array of ByteCode structures, into which it should save the contents of the current Promise object. First it analyzes all subordinate nodes, for which the method is recursively called for 'left', 'right' and 'last' pointers if there are non-zero. After that, when all operands have been saved, the properties of the Promise object are written to the bytecode.
Since the expression grammar has a conditional operator, the method additionally remembers the size of the bytecode array at points where the true and false instruction branches begin, as well as the end of the conditional expression. This allows writing to the conditional operator bytecode structure the offset in the array, to which it should jump during calculations if the condition is true or false. The instruction branch for the true condition starts immediately after the byte code '?'. After the execution of the instructions, we should jump by an offset to the 'value' field. The branch of instructions for a false condition starts by the offset in the 'index' field, immediately the field of "true" instructions.
Please note that when we evaluate the expression in interpretation mode or by the syntax tree, both branches of the conditional operator are calculated before one of their values is selected, depending on the condition, which means that one of the branches is calculated to no purpose. In bytecode, we skip the unnecessary branch calculation.
To convert the entire expression tree to bytecode, call exportToByteCode for a root object returned by 'evaluate'. Here is an example for the Pratt parser:
ExpressionPratt e(vars);
Promise *p = e.evaluate(expr);
ByteCode codes[];
p.exportToByteCode(codes);
for(int i = 0; i < ArraySize(codes); i++)
{
Print(i, "] ", codes[i].toString());
}
Now, we need to write a function which will perform calculations based on the bytecode. Let's add it to the same Promise class because bytecode uses variable and function indices, and Promise has links to these tables by default.
#define STACK_SIZE 100 // stack imitation #define push(S,V,N) S[N++] = V #define pop(S,N) S[--N] #define top(S,N) S[N-1] class Promise { ... public: static double execute(const ByteCode &codes[], VariableTable *vt = NULL, FunctionTable *ft = NULL) { if(vt) variableTable = vt; if(ft) functionTable = ft; double stack[]; int ssize = 0; ArrayResize(stack, STACK_SIZE); int jumps[]; int jsize = 0; ArrayResize(jumps, STACK_SIZE / 2); const int n = ArraySize(codes); for(int i = 0; i < n; i++) { if(jsize && top(jumps, jsize) == i) { --jsize; // fast "pop & drop" i = pop(jumps, jsize); continue; } switch(codes[i].code) { case 'n': push(stack, codes[i].value, ssize); break; case 'v': push(stack, variableTable[codes[i].index], ssize); break; case 'f': { IFunctor *ptr = functionTable[codes[i].index]; double params[]; ArrayResize(params, ptr.arity()); int psize = 0; for(int j = 0; j < ptr.arity(); j++) { push(params, pop(stack, ssize), psize); } ArrayReverse(params); push(stack, ptr.execute(params), ssize); } break; case '+': push(stack, pop(stack, ssize) + pop(stack, ssize), ssize); break; case '-': push(stack, -pop(stack, ssize) + pop(stack, ssize), ssize); break; case '*': push(stack, pop(stack, ssize) * pop(stack, ssize), ssize); break; case '/': push(stack, Promise::safeDivide(1, pop(stack, ssize)) * pop(stack, ssize), ssize); break; case '%': { const double second = pop(stack, ssize); const double first = pop(stack, ssize); push(stack, fmod(first, second), ssize); } break; case '!': push(stack, (double)(!pop(stack, ssize)), ssize); break; case '~': push(stack, (double)(-pop(stack, ssize)), ssize); break; case '<': { const double second = pop(stack, ssize); const double first = pop(stack, ssize); push(stack, (double)(first < second), ssize); } break; case '>': { const double second = pop(stack, ssize); const double first = pop(stack, ssize); push(stack, (double)(first > second), ssize); } break; case '{': { const double second = pop(stack, ssize); const double first = pop(stack, ssize); push(stack, (double)(first <= second), ssize); } break; case '}': { const double second = pop(stack, ssize); const double first = pop(stack, ssize); push(stack, (double)(first >= second), ssize); } break; case '&': push(stack, (double)(pop(stack, ssize) && pop(stack, ssize)), ssize); break; case '|': { const double second = pop(stack, ssize); const double first = pop(stack, ssize); push(stack, (double)(first || second), ssize); // order is important } break; case '`': push(stack, _precision < fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break; case '=': push(stack, _precision > fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break; case '?': { const double first = pop(stack, ssize); if(first) // true { push(jumps, (int)codes[i].value, jsize); // to where the entire if ends push(jumps, codes[i].index, jsize); // we jump from where true ends } else // false { i = codes[i].index - 1; // -1 is needed because of forthcoming ++ } } break; default: Print("Unknown byte code ", CharToString(codes[i].code)); } } return pop(stack, ssize); } ... };
Working with the stack is implemented through macros on the 'stack' array, in which a certain number of elements STACK_SIZE is allocated in advance. This is done to accelerate execution by avoiding ArrayResize calls during push and pop operations. STACK_SIZE equal to 100 seems sufficient for the most of real one-line expressions. Otherwise we will have a stack overflow.
To control the execution of conditional operators which can be nested, we need to use an additional 'jumps' stack.
All these operations are already familiar from the Promise and Pratt parser codes above. The only difference is the widespread use of the stack as a source of operands and as a place to store an intermediate result. The bytecode is executed in a loop, in a single method call, without recursion.
This functionality enables us to calculate expressions using bytecode received by exporting syntax trees from Pratt parser or from ExpressionCompiler.
ExpressionPratt e(vars);
Promise *p = e.evaluate(expr);
ByteCode codes[];
p.exportToByteCode(codes);
double r = Promise::execute(codes);
Later, when testing all parsers, we will compare the performance speed of calculations using a tree and bytecode.
But the main purpose of introducing a bytecode was to enable the implementation of another parser type, the "Shunting Yard" parser.
Shunting Yard Parser (ExpressionShuntingYard)
The Shunting Yard parser name stems from the method used to divide the stream of input tokens into those which can instantly be passed to the output, and those which should be pushed onto a special stack, from which tokens are retrieved by certain rules concerning the combination of token precedences (that of the token in the stack and of the next token in the input stream). The parser converts an input expression back to RPN (Reverse Polish Notation). This is convenient for us because we can immediately generate bytecode, without a syntax tree. As can be seen from the general description, the shunting method is based on the precedence of operators, that is why this parser is related to Pratt parser. So, it will be implemented as an ExpressionPrecedence child class.
This parser belongs to the bottom-up category.
In general terms, the algorithm is as follows (we omit here specifics of right associativity, which we don't have, as well as the complications related to the ternary conditional operator):
Read the next token form the expression in a loop (until the expression end)
if the toke is a unary operation, save it on the stack
if it is a number, write it to the bytecode
if it is a variable, write its index to bytecode
if it is a function identifier, save its index on the stack
if the token is an infix operator
as long as '(' is not at the top of the stack and ((the precedence of the operator at the stack top >= current operator precedence) or a function is at the top)
push the top of the stack into the output bytecode
save operator on stack
if the token is '(', save it on the stack
if the token is ')'
as long as the top of the stack is not '('
push the top of the stack into the output bytecode
if '(' is on top of the stack, remove and discard
if there are tokens left on the stack, move them sequentially into the output bytecode
Obviously, the implementation of this parser requires only one method.
The whole ExpressionShuntingYard class is presented below. The main public method convertToByteCode starts parsing which is executed in exportToByteCode. Since our expressions support conditional operators, a recursive call of exportToByteCode is used to parse their subexpressions.
class ExpressionShuntingYard: public ExpressionPrecedence { public: ExpressionShuntingYard(const string vars = NULL): ExpressionPrecedence(vars) { } ExpressionShuntingYard(VariableTable &vt): ExpressionPrecedence(vt) { } bool convertToByteCode(const string expression, ByteCode &codes[]) { Promise::environment(&this); AbstractExpressionProcessor<Promise *>::evaluate(expression); if(_length > 0) { exportToByteCode(codes); } return !_failed; } protected: template<typename T> static void _push(T &stack[], T &value) { const int n = ArraySize(stack); ArrayResize(stack, n + 1, STACK_SIZE); stack[n] = value; } void exportToByteCode(ByteCode &output[]) { ByteCode stack[]; int ssize = 0; string number; uchar c; ArrayResize(stack, STACK_SIZE); const int previous = ArraySize(output); while(_nextToken() && !_failed) { if(_token == '+' || _token == '-' || _token == '!') { if(_token == '-') { _push(output, ByteCode(-1.0)); push(stack, ByteCode('*'), ssize); } else if(_token == '!') { push(stack, ByteCode('!'), ssize); } continue; } number = ""; if(_readNumber(number)) // if a number was read, _token has changed { _push(output, ByteCode(StringToDouble(number))); } if(isalpha(_token)) { string variable; while(isalnum(_token)) { variable += ShortToString(_token); _nextToken(); } if(_token == '(') { push(stack, ByteCode('f', _functionTable.index(variable)), ssize); } else // variable name { int index = -1; if(CheckPointer(_variableTable) != POINTER_INVALID) { index = _variableTable.index(variable); if(index == -1) { if(_variableTable.adhocAllocation()) { index = _variableTable.add(variable, nan); _push(output, ByteCode('v', index)); error("Unknown variable is NaN: " + variable, __FUNCTION__, true); } else { error("Unknown variable : " + variable, __FUNCTION__); } } else { _push(output, ByteCode('v', index)); } } } } if(infixes[_token] > 0) // operator, including least significant '?' { while(ssize > 0 && isTop2Pop(top(stack, ssize).code)) { _push(output, pop(stack, ssize)); } if(_token == '?' || _token == ':') { if(_token == '?') { const int start = ArraySize(output); _push(output, ByteCode((uchar)_token)); exportToByteCode(output); // subexpression truly, _token has changed if(_token != ':') { error("Colon expected, given: " + ShortToString(_token), __FUNCTION__); break; } output[start].index = ArraySize(output); exportToByteCode(output); // subexpression falsy, _token has changed output[start].value = ArraySize(output); if(_token == ':') { break; } } else { break; } } else { if(_token == '>' || _token == '<') { if(_lookAhead() == '=') { push(stack, ByteCode((uchar)(_token == '<' ? '{' : '}')), ssize); _nextToken(); } else { push(stack, ByteCode((uchar)_token), ssize); } } else if(_token == '=' || _token == '!') { if(_lookAhead() == '=') { push(stack, ByteCode((uchar)(_token == '!' ? '`' : '=')), ssize); _nextToken(); } } else if(_token == '&' || _token == '|') { _matchNext(_token, ShortToString(_token) + " expected after " + ShortToString(_token), __FUNCTION__); push(stack, ByteCode((uchar)_token), ssize); } else if(_token != ',') { push(stack, ByteCode((uchar)_token), ssize); } } } if(_token == '(') { push(stack, ByteCode('('), ssize); } else if(_token == ')') { while(ssize > 0 && (c = top(stack, ssize).code) != '(') { _push(output, pop(stack, ssize)); } if(c == '(') // must be true unless it's a subexpression (then 'c' can be 0) { ByteCode disable_warning = pop(stack, ssize); } else { if(previous == 0) { error("Closing parenthesis is missing", __FUNCTION__); } return; } } } while(ssize > 0) { _push(output, pop(stack, ssize)); } } bool isTop2Pop(const uchar c) { return (c == 'f' || infixes[c] >= infixes[_token]) && c != '(' && c != ':'; } };
The usage of a shunting-yard parser is different from previous types. We skip here the step in which a tree is received by calling 'evaluate'. Instead, the convertToByteCode method immediately returns the bytecode for the passed expression.
ExpressionShuntingYard sh; sh.variableTable().adhocAllocation(true); ByteCode codes[]; bool success = sh.convertToByteCode("x + y", codes); if(success) { sh.variableTable().assign("x=10;y=20"); double r = Promise::execute(codes); }
This concludes the overview of different types of parsers. The diagram of classes looks like this:
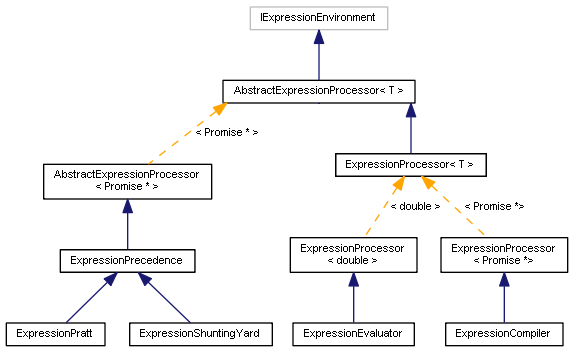
Parser class diagram
To test and compare different parsers, we will create a test script later.
Since the ultimate application field is trading, let is view how the list of standard functions can be expanded with technical indicators.
Embedding Indicators in Expressions as Functions
When calculating expressions, the trader may need some specific information, such as the balance, the number of positions, indicator readings and so on. All this can be made available within expressions by expanding the list of functions. To demonstrate this approach, let's add the Moving Average indicator to the set of functions.
The mechanism for embedding an indicator to expressions is based on the earlier considered functors and is therefore implemented as a class derived from AbstractFunc. As we already know, all AbstractFunc family class instances are automatically registered in AbstractFuncStorage and become available in the table of functions.
class IndicatorFunc: public AbstractFunc { public: IndicatorFunc(const string n, const int a = 1): AbstractFunc(n, a) { // the single argument is the bar number, // two arguments are bar number and buffer index } static IndicatorFunc *create(const string name); };
The specific feature of indicators in MetaTrader 5 is that they also require two application stages: first we need to create the indicator (to obtain its description) and then to request data from it. In the context of expression processing, the first step should be performed during parsing and the second step should be performed during evaluation. Since the indicator creation requires the specification of all parameters, they must be implemented in the name instead of being passed in function parameters. For example, if we created the "iMA" function with parameters (period, method, price_type), then at the parsing stage we would receive only its name, while the definition of parameters would be postponed until the execution stage, when it is too late to create an indicator (since we should read data from the indicator at this stage).
As a solution, we can reserve a set of names for the Moving Average indicator. The names are composed according to the following rule: method_price_period. Here, 'method' is one of the meaningful words of the ENUM_MA_METHOD enumeration (SMA, EMA, SMMA, LWMA); 'price' is one of the price types from the enumerations ENUM_APPLIED_PRICE (CLOSE, OPEN, HIGH, LOW, MEDIAN, TYPICAL, WEIGHTED); 'period' is an integer. Thus, the use of the "SMA_OPEN_10" function should create a simple moving average based on open price, with a period of 10.
The indicator function arity is equal to 1 by default. The only parameter is used to pass the bar number. If the arity is set to 2, then the second parameter can be used to indicate the buffer number. It is not needed for the moving average.
The MAIndicatorFunc class is used for creating indicator instances with parameters corresponding to the requested names.
class MAIndicatorFunc: public IndicatorFunc { protected: const int handle; public: MAIndicatorFunc(const string n, const int h): IndicatorFunc(n), handle(h) {} ~MAIndicatorFunc() { IndicatorRelease(handle); } static MAIndicatorFunc *create(const string name) // SMA_OPEN_10(0) { string parts[]; if(StringSplit(name, '_', parts) != 3) return NULL; ENUM_MA_METHOD m = -1; ENUM_APPLIED_PRICE t = -1; static string methods[] = {"SMA", "EMA", "SMMA", "LWMA"}; for(int i = 0; i < ArraySize(methods); i++) { if(parts[0] == methods[i]) { m = (ENUM_MA_METHOD)i; break; } } static string types[] = {"NULL", "CLOSE", "OPEN", "HIGH", "LOW", "MEDIAN", "TYPICAL", "WEIGHTED"}; for(int i = 1; i < ArraySize(types); i++) { if(parts[1] == types[i]) { t = (ENUM_APPLIED_PRICE)i; break; } } if(m == -1 || t == -1) return NULL; int h = iMA(_Symbol, _Period, (int)StringToInteger(parts[2]), 0, m, t); if(h == INVALID_HANDLE) return NULL; return new MAIndicatorFunc(name, h); } double execute(const double ¶ms[]) override { const int bar = (int)params[0]; double result[1] = {0}; if(CopyBuffer(handle, 0, bar, 1, result) != 1) { Print("CopyBuffer error: ", GetLastError()); } return result[0]; } };
The 'create' factory method parses the name passed to it, extracts parameters from the name and creates an indicator with 'handle'. The indicator value is obtained in the standard method of functors — execute.
Since other indicators can be added to the function in the future, the IndicatorFunc class provides a single entry point for requests of any indicators, which is the 'create' method. So far, it contains only a redirection to the MAIndicatorFunc::create() call.
static IndicatorFunc *IndicatorFunc::create(const string name) { // TODO: support more indicator types, dispatch calls based on the name return MAIndicatorFunc::create(name); }
This method must be called from the table of functions, so add the required code to the FunctionTable class.
class FunctionTable: public Table<IFunctor *> { public: ... #ifdef INDICATOR_FUNCTORS virtual int index(const string name) override { int i = _table.getIndex(name); if(i == -1) { i = _table.getSize(); IFunctor *f = IndicatorFunc::create(name); if(f) { Table<IFunctor *>::add(name, f); return i; } return -1; } return i; } #endif };
The new version of the 'index' method tries to find a suitable indicator, if the passed name is not found in the list of built-in 25 functions. To connect this additional functionality, we need to define the INDICATOR_FUNCTORS macro.
With this option enabled, we can calculate, for example, the following expression: "EMA_OPEN_10(0)/EMA_OPEN_21(0)".
In practice, the parameters of the called indicators are often provided in settings. This means that they must be somehow dynamically inserted into the expression line. To simplify this task, the AbstractExpressionProcessor class supports a special expression preprocessing option. Its description is omitted in the article for brevity. Enabling of preprocessing is managed by the optional second parameter of the 'evaluate' method (which is equal to false by default, i.e. preprocessing is disabled).
The option operates as follows. In an expression, we can specify in curly braces a variable name, which will be replaced with the variable value of before parsing. For example, if the expression is equal to "EMA_TYPICAL_{Period}(0)" and the variables table contains the Period variable with the value of 11, then "EMA_TYPICAL_11(0)" will be analyzed.
To test indicator functions, we will later create an Expert Advisor, whose trading signals will be generated based on the evaluated expressions, including the moving average.
But first we need to make sure that the parsers are working correctly.
Test Script (ExpresSParserS)
The test scrip ExpresSParserS.mq5 includes a set of functional tests and measurement if calculation speed for 4 parser types, as well as a demonstration of various mode, logging of syntax tree and byte code, use of indicators as built-in functions.
The functional tests include both correct applications and deliberately wrong ones (undeclared variables, zero division, and so on). The correctness of a test is determined by the correspondence of the actual and expected result, which means that errors can also be "correct". For example, here is what the Pratt parser testing log looks like.
Running 19 tests on ExpressionPratt* … 1 passed, ok: a > b ? b > c ? 1 : 2 : 3 = 3.0; expected = 3.0 2 passed, ok: 2 > 3 ? 2 : 3 > 4 ? 3 : 4 = 4.0; expected = 4.0 3 passed, ok: 4 > 3 ? 2 > 4 ? 2 : 4 : 3 = 4.0; expected = 4.0 4 passed, ok: (a + b) * sqrt(c) = 8.944271909999159; expected = 8.944271909999159 5 passed, ok: (b == c) > (a != 1.5) = 0.0; expected = 0.0 6 passed, ok: (b == c) >= (a != 1.5) = 1.0; expected = 1.0 7 passed, ok: (a > b) || sqrt(c) = 1.0; expected = 1.0 8 passed, ok: (!1 != !(b - c/2)) = 1.0; expected = 1.0 9 passed, ok: -1 * c == -sqrt(-c * -c) = 1.0; expected = 1.0 10 passed, ok: pow(2, 5) % 5 = 2.0; expected = 2.0 11 passed, ok: min(max(a,b),c) = 2.5; expected = 2.5 12 passed, ok: atan(sin(0.5)/cos(0.5)) = 0.5; expected = 0.5 13 passed, ok: .2 * .3 + .1 = 0.16; expected = 0.16 14 passed, ok: (a == b) + (b == c) = 0.0; expected = 0.0 15 passed, ok: -(a + b) * !!sqrt(c) = -4.0; expected = -4.0 16 passed, ok: sin ( max ( 2 * 1.5, 3 ) / 3 * 3.14159265359 ) = -2.068231111547469e-13; expected = 0.0 lookUpVariable error: Variable is undefined: _1c @ 7: 1 / _1c^ 17 passed, er: 1 / _1c = nan; expected = nan safeDivide error: Error : Division by 0! @ 15: 1 / (2 * b - c)^ 18 passed, er: 1 / (2 * b - c) = inf; expected = inf 19 passed, ok: sqrt(b-c) = -nan(ind); expected = -nan(ind) 19 tests passed of 19 17 for correct expressions, 2 for invalid expressions
As you can see, all 19 tests completed successfully. In two tests we received expected errors.
Speed is measured only for multiple calculations in a cycle. When working with the interpreter, this includes the expression parsing stage, because it is performed for every calculation. For all other parser types, the parsing stage is done "outside". One-time expression parsing takes approximately equal time for all methods. Here is one of the results of measuring 10,000 cycles (microseconds).
>>> Performance tests (timing per method) Evaluation: 104572 Compilation: 25011 Pratt bytecode: 23738 Pratt: 24967 ShuntingYard: 23147
As expected, previously "compiled" expressions are evaluated several times faster than interpreted ones. We can also conclude that the fastest calculations are those based on a byte code. In this case, the method for obtaining the bytecode makes no substantial difference, so we can use either Pratt parser or the shunting yard method. You can select a parser according to your personal reference and to how well you understand the algorithm, or choose the one which is best adaptable for your specific tasks, such as syntax expansion or integration with existing programs.
Using expressions to set up Expert Advisor signals (ExprBot)
Expressions can be used in trading robots to generate trading signals. This provides greater flexibility as compared to simple changing of parameters. Due to the expandable list of functions, this provides practically the same capabilities as MQL, however no compilation is needed here. In addition, routine operations can be easily hidden inside ready-made functors. This provides a balance between product setup flexibility and complexity.
We have a set of moving average indicators, so our trading system will be based on these indicators (though, we can add to expressions time functions, risk management, tick prices and other data).
To demonstrate the principle, let's create a simple Expert Advisor, ExprBot. The variables SignalBuy and SignalSell will contain expressions with the conditions for executing Buy and Sell trades. The following formulas can be used for a strategy based on the intersection of two MAs.
#define INDICATOR_FUNCTORS #include <ExpresSParserS/ExpressionCompiler.mqh> input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold"; input string Variables = "Threshold=0.01"; input int Fast = 10; input int Slow = 21;
The threshold is set as a constant only to demonstrate input of random variables. Parameters with the Fast and Slow averaging periods are used for inserting into expressions before they are parsed, as a part of the indicator name.
Since there are two signals, we instantiate two recursive descent parsers. In general, we could use one, but the tables of variables in two expressions can be potentially different, in which case we would need to switch this context before each calculation.
ExpressionCompiler ecb(Variables), ecs(Variables); Promise *p1, *p2;
In the OnInit handler, save the parameters in variable tables and build syntax trees.
int OnInit() { ecb.variableTable().set("Fast", Fast); ecb.variableTable().set("Slow", Slow); p1 = ecb.evaluate(SignalBuy, true); if(!ecb.success()) { Print("Syntax error in Buy signal:"); p1.print(); return INIT_FAILED; } ecs.variableTable().set("Fast", Fast); ecs.variableTable().set("Slow", Slow); p2 = ecs.evaluate(SignalSell, true); if(!ecs.success()) { Print("Syntax error in Sell signal:"); p2.print(); return INIT_FAILED; } return INIT_SUCCEEDED; }
The entire strategy is written in the OnTick handler (auxiliary functions are omitted here; it is also necessary to include the MT4Orders library).
#define _Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK) #define _Bid SymbolInfoDouble(_Symbol, SYMBOL_BID) void OnTick() { if(!isNewBar()) return; bool buy = p1.resolve(); bool sell = p2.resolve(); if(buy && sell) { buy = false; sell = false; } if(buy) { OrdersCloseAll(_Symbol, OP_SELL); if(OrdersTotalByType(_Symbol, OP_BUY) == 0) { OrderSend(_Symbol, OP_BUY, Lot, _Ask, 100, 0, 0); } } else if(sell) { OrdersCloseAll(_Symbol, OP_BUY); if(OrdersTotalByType(_Symbol, OP_SELL) == 0) { OrderSend(_Symbol, OP_SELL, Lot, _Bid, 100, 0, 0); } } else { OrdersCloseAll(); } }
These two expressions are calculated by "promises" p1 and p2. As a result, we have two flags 'buy' and 'sell', which initiate the opening or closing of a position in the corresponding directions. The MQL code guarantees that there can only be one open position at a time, and thus if signals are opposite (this can happen if you use more complex expressions or if a negative threshold is set by mistake), any existing position is closed. Signal conditions can be edited in different ways, within the parser functions.
If you launch the EA in the Strategy Tester, the result will most likely be not very good. However, what's important, is that the EA trades and trading is managed by parsers. They do not give ready-made profitable systems but provide and additional tool for finding strategies.
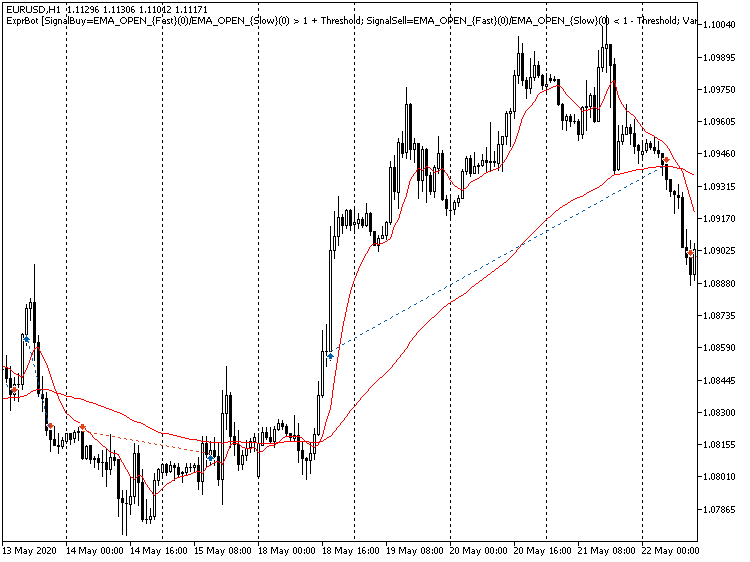
An example of trading using signals calculated by expressions
Conclusion
In these two articles, we examined four parser types, compared their capabilities and implemented classes which can be embedded into MQL programs. All parsers used the same grammar with the most frequently used mathematical operations and 25 functions. If necessary, the grammar can be expanded by extending the list of supported operators, by adding new built-in application functions (indicators, prices, trade statistics) and syntax structures (in particular, arrays and functions for their processing).
The technology enables a more flexible separation of settings and immutable MQL code. The ability to customize algorithms by editing expressions in input parameters seems easier for end users, while there is no need to learn the basics of MQL programming which are required in order to find the desired code fragment, to edit it following rules and to deal with potential compilation errors. From the point of view of MQL program developers, parsing and expression evaluation support provides other advantages, such as its potential ability to be transformed to a "script on top of MQL", which would allow to avoid using libraries and versioning of the MQL compiler.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/8028
 Quick Manual Trading Toolkit: Working with open positions and pending orders
Quick Manual Trading Toolkit: Working with open positions and pending orders
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use