数式の計算(第2部)Prattパーサーおよび操車場パーサー

本稿では、さまざまな数式の解析方法と、MQL言語でのそれらの実装について引き続き調査します。第1部では、再帰下降パーサーについて検討しました。このようなパーサーの主な利点はユーザーフレンドリーな構造で、これは特定の式の文法に直接関連しています。しかし、効率と技術的機能に関しては、注意を払う価値のある他のタイプのパーサーがあります。

演算子の優先順位を使用するパーサー

次に検討するパーサータイプは、優先度パーサーです。クラスメソッドは文法ルールに基づいて作成されるのではなく(この場合、各ルールは個別のメソッドに変換されます)、演算子の優先順位のみを考慮したより一般化された形式で作成されるため、実装はよりコンパクトになります。

操作の優先順位は、EBNF文法記述に暗黙の形式ですでに存在していました。そのルールは、優先度の低い操作から優先度の高い操作まで、最終エンティティ(定数と変数)まで実行されます。これは、明示的な括弧のグループ化がない場合に、操作を実行する順序が優先順位によって決まるためです。たとえば、乗算演算の優先順位は加算の優先順位よりも高くなります。ただし、単項マイナスは乗算よりも優先されます。構文木要素がルート(式全体)に近いほど、後で評価されます。

パーサーを実装するには、各操作の優先順位に対応する数値を持つ2つのテーブルが必要です。値が高いほど、優先度が高くなります。

単項演算と二項演算はアルゴリズムで論理的に分離されるため、2つのテーブルがあります。実際、ここでお話しするのは、操作についてだけでなく、より一般的には、接頭辞や中置辞として式に含まれる記号についてでです(演算子の種類の詳細はウィキペディアでご覧ください)。

名前が示すように、接頭辞は被演算子の前にある記号(例: 式「!var」の「!」)であり、中置辞は演算子間の文字(例: 式「 a + b」の「+」)。後置辞もありますが(インクリメント演算子の「+」のペアなど、MQLでも「i ++」のように使用できます)、式では使用されないため、考慮しません。

単項演算「!」、「-」、「+」に加えて、接頭辞は、グループの始まりを示す開き括弧(()、文字、識別子の始まりを示すアンダースコア(—)にすることができます。また、数字または数値定数の始まりを示めすピリオド(.) にもなりえます。

ExpressionPrecedenceクラスのテーブルについて説明します。このクラスから、優先度に基づく特定のパーサークラスが継承されます。これらのパーサーはすべてPromiseで動作します。

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      static uchar prefixes[128];
      static uchar infixes[128];
      
      static ExpressionPrecedence epinit;
      
      static void initPrecedence()
      {
        // グループ化
        prefixes['('] = 9;
  
        // 単項
        prefixes['+'] = 9;
        prefixes['-'] = 9;
        prefixes['!'] = 9;
        
        // 識別子
        prefixes['_'] = 9;
        for(uchar c = 'a'; c <= 'z'; c++)
        {
          prefixes[c] = 9;
        }
        
        // 数値
        prefixes['.'] = 9;
        for(uchar c = '0'; c <= '9'; c++)
        {
          prefixes[c] = 9;
        }
        
        // 演算子
        // infixes['('] = 9; // ここでは、括弧は「関数呼び出し」演算子として使用されていない
        infixes['*'] = 8;
        infixes['/'] = 8;
        infixes['%'] = 8;
        infixes['+'] = 7;
        infixes['-'] = 7;
        infixes['>'] = 6;
        infixes['<'] = 6;
        infixes['='] = 5;
        infixes['!'] = 5;
        infixes['&'] = 4;
        infixes['|'] = 4;
        infixes['?'] = 3;
        infixes[':'] = 2;
        infixes[','] = 1; // 引数リストの区切り文字
      }
  
      ExpressionPrecedence(const bool init)
      {
        initPrecedence();
      }
  
    public:
      ExpressionPrecedence(const string vars = NULL): AbstractExpressionProcessor(vars) {}
      ExpressionPrecedence(VariableTable &vt): AbstractExpressionProcessor(vt) {}
  };
  
  static uchar ExpressionPrecedence::prefixes[128] = {0};
  static uchar ExpressionPrecedence::infixes[128] = {0};
  static ExpressionPrecedence ExpressionPrecedence::epinit(true);

優先順位テーブルは、128要素のスパース配列を使用して、「経済的な」方法で作成されます(他の範囲のコードを持つ文字はサポートされていないため、これで十分です)。優先順位は、シンボルコードに対応するセルで指定されます。したがって、トークンコードによる直接アドレス指定により、優先順位に簡単にアクセスできます。

2つの追加のヘルパーメソッドが子クラスで使用され、入力文字列に続くシンボルをチェックできます。_lookAheadは単に次のトークンを返します(一歩先を見ているかのように)、_matchNextは、トークンが一致する場合はトーケンを読み、それ以外の場合ではエラーをスローします。

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      ...
      ushort _lookAhead()
      {
        int i = 1;
        while(_index + i < _length && isspace(_expression[_index + i])) i++;
        if(_index + i < _length)
        {
          return _expression[_index + i];
        }
        return 0;
      }
      
      void _matchNext(ushort c, string message, string context = NULL)
      {
        if(_lookAhead() == c)
        {
          _nextToken();
        }
        else if(!_failed) // エラーの連鎖を防止
        {
          error(message, context);
        }
      }
      ...
  };

最初の優先順位ベースのパーサーであるPrattパーサーから始めましょう。

Prattパーサー(ExpressionPratt)

Prattパーサーは、再帰下降パーサー同様に、トップダウンです。つまり、式の個々の構成を分析するいくつかのメソッドの再帰呼び出しはありますが、これらのメソッドははるかに少なくなります。

コンストラクタとメインのpublic「evaluate」メソッドには見覚えがあります。

  class ExpressionPratt: public ExpressionPrecedence
  {
    public:
      ExpressionPratt(const string vars = NULL): ExpressionPrecedence(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionPratt(VariableTable &vt): ExpressionPrecedence(vt) { helper = new ExpressionHelperPromise(&this); }
  
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          return parseExpression();
        }
        return NULL;
      }

新しいparseExpressionメソッドは、Prattアルゴリズムの中心です。このメソッドは現在の優先順位をデフォルトで0に設定することから始まり、任意のシグナルを読み取ることができます。

      virtual Promise *parseExpression(const int precedence = 0)
      {
        if(_failed) return NULL; // エラーの場合は部分式を切り取る
      
        _nextToken();
        if(prefixes[(uchar)_token] == 0)
        {
          this.error("Can't parse " + ShortToString(_token), __FUNCTION__);
          return NULL;
        }
        
        Promise *left = _parsePrefix();
        
        while((precedence < infixes[_token]) && !_failed)
        {
          left = _parseInfix(left, infixes[(uchar)_token]);
        }
        
        return left;
      }

このメソッドの考え方は単純です。接頭辞である必要がある次のシンボルを読み取ることで式の解析を開始し(そうでない場合はエラーです)、接頭辞構造全体を読み取ることができる_parsePrefixメソッドに制御を渡します。その後、次のシンボルの優先順位が現在の優先順位よりも高い限り、任意のインフィックス構造全体を読み取ることができる_parseInfixメソッドに制御を渡します。したがって、パーサー全体は3つのメソッドのみで構成されます。ある意味で、Prattパーサーは、式を接頭辞と中置辞の構造の階層として表されます。

現在の_tokenが中置辞テーブルに見つからない場合、その優先順位はゼロになり、「while」ループは停止します(またはまったく開始しません)。

_parseInfixメソッドの特定の機能は、最初のパラメータで渡された現在のPromise(左)オブジェクトが部分式の一部になる一方で、メソッドが読み取ることを許可されている操作の許容最小優先順位が現在のインフィックストークンの優先順位としての2番目のパラメーターで設定されていることです。このメソッドは、部分式全体の新しいPromiseオブジェクトを返します。このオブジェクトは同じ変数に保存されます(そして、Promiseへの以前の参照は、新しいオブジェクトの参照フィールドによって何らかの形で利用可能になります)。

メソッド_parsePrefixと_parseInfixについてさらに詳しく考えてみましょう。

_parsePrefixメソッドは、許可された接頭辞から現在のトークンを予期し、「switch」を使用してそれを処理します。ネストされた式を計算するために、すでにおなじみのメソッドparseExpressionが開き括弧(()に対して呼び出されます。優先順位パラメータは省略され、最小のゼロ優先順位から解析されます(括弧内の別個の式のようなものであるため)。次のフラグメントから論理否定を受け取るために、「!」には「ヘルパー」オブジェクトが使用されます。parseExpressionメソッドによって読み取られますが、今回は現在のトークンの優先順位が渡されます。つまり、否定されるフラグメントは、優先順位が「!」よりも低い最初のシンボルより前で終了します。たとえば、式に「!a*b」が含まれている場合、parseExpressionは「a」変数を読み取った後に停止します。単項の「+」と「-」は同様の方法で処理されますが、この場合「ヘルパー」は使用されません。「+」の場合、parseExpressionで部分式を読み取るだけで済みます。「-」の場合、受信した結果のオーバーライドされた「マイナス」を呼び出します(覚えていらっしゃるように、結果はPromiseオブジェクトです)。

_parsePrefixメソッドは、他のすべてのシンボルを「isalpha」カテゴリに属するもので並び替えます。文字は識別子の始まりであり、数字またはピリオドは数字の始まりであると想定されています。それ以外の場合、メソッドはNULLを返します。

      Promise *_parsePrefix()
      {
        Promise *result = NULL;
        switch(_token)
        {
          case '(':
            result = parseExpression();
            _match(')', ") expected!", __FUNCTION__);
            break;
          case '!':
            result = helper._negate(parseExpression(prefixes[_token]));
            break;
          case '+':
            result = parseExpression(prefixes[_token]);
            break;
          case '-':
            result = -parseExpression(prefixes[_token]);
            break;
          default:
            if(isalpha(_token))
            {
              string variable;
            
              while(isalnum(_token))
              {
                variable += ShortToString(_token);
                _nextToken();
              }
              
              if(_token == '(')
              {
                const string name = variable;
                const int index = _functionTable.index(name);
                if(index == -1)
                {
                  error("Function undefined: " + name, __FUNCTION__);
                  return NULL;
                }
                
                const int arity = _functionTable[index].arity();
                if(arity > 0 && _lookAhead() == ')')
                {
                  error("Missing arguments for " + name + ", " + (string)arity + " required!", __FUNCTION__);
                  return NULL;
                }
                
                Promise *params[];
                ArrayResize(params, arity);
                for(int i = 0; i < arity; i++)
                {
                  params[i] = parseExpression(infixes[',']);
                  if(i < arity - 1)
                  {
                    if(_token != ',')
                    {
                      _match(',', ", expected (param-list)!", __FUNCTION__);
                      break;
                    }
                  }
                }
              
                _match(')', ") expected after " + (string)arity + " arguments!", __FUNCTION__);
                
                result = helper._call(index, params);
              }
              else
              {
                return helper._variable(variable); // インデックスを取得し、できない場合はオプションで名前をnanとして予約する
              }
            }
            else // 数字が示唆され、数字である必要がある
            {
              string number;
              if(_readNumber(number))
              {
                return helper._literal(number);
              }
            }
        }
        return result;
      }

識別子の後に続いた括弧(()は、関数呼び出しとして解釈されます。さらに、コンマで区切られた引数のリスト(関数のアリティに従って)を解析します。すべての引数は、コンマ(,)の優先順位を指定してparseExpressionを呼び出すことによって取得されます。関数のPromiseオブジェクトは、helper._call()を使用して生成されます。括弧の後に識別子がない場合は、helper._variable()変数のPromiseオブジェクトが作成されます。

最初のトークンが文字でない場合、_parsePrefixメソッドは_readNumberを使用して数値の読み取りを試み、helper._literal()を呼び出してその数値のPromiseを作成します。

_parseInfixメソッドは、現在のトークンが許可された中置辞の1つであることを想定しています。さらに、最初のパラメータでは、Promise *leftオブジェクトに既に読み込まれている左の被演算子を受け取ります。2番目のパラメータは、解析されるトークンの最小優先順位を指定します。優先度の低いものが検出されると、部分式は終了したと見なされます。_parseInfixの目的は、右の被演算子を読み取るために「precedence」を指定してparseExpressionを呼び出すことです。その後、中置辞に対応する2項演算のPromiseオブジェクトを作成できます。

      Promise *_parseInfix(Promise *left, const int precedence = 0)
      {
        Promise *result = NULL;
        const ushort _previous = _token;
        switch(_previous)
        {
          case '*':
          case '/':
          case '%':
          case '+':
          case '-':
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '>':
          case '<':
            if(_lookAhead() == '=')
            {
              _nextToken();
              result = new Promise((uchar)(_previous == '<' ? '{' : '}'), left, parseExpression(precedence));
            }
            else
            {
              result = new Promise((uchar)_previous, left, parseExpression(precedence));
            }
            break;
          case '=':
          case '!':
            _matchNext('=', "= expected after " + ShortToString(_previous), __FUNCTION__);
            result = helper._isEqual(left, parseExpression(precedence), _previous == '=');
            break;
          case '&':
          case '|':
            _matchNext(_previous, ShortToString(_previous) + " expected after " + ShortToString(_previous), __FUNCTION__);
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '?':
            {
              Promise *truly = parseExpression(infixes[':']);
              if(_token != ':')
              {
                _match(':', ": expected", __FUNCTION__);
              }
              else
              {
                Promise *falsy = parseExpression(infixes[':']);
                if(truly != NULL && falsy != NULL)
                {
                  result = helper._ternary(left, truly, falsy);
                }
              }
            }
          case ':':
          case ',': // ただスキップする
            break;
          default:
            error("Can't process infix token " + ShortToString(_previous));
          
        }
        return result;
      }

メソッドの先頭にある現在の中置辞トークンが_previous変数に記憶されていることが重要です。これは、成功した場合、parseExpression呼び出しが文字列内の位置を他のトークン、つまり任意の数のシンボルの右側にシフトするためです。

ここでは3つのメソッドのみを検討し、それぞれがかなり透明な構造を持っていますが、これがPrattパーサー全体です。

その適用は、ExpressionCompilerパーサーに似ています。ExpressionPrattオブジェクトを作成し、変数のテーブルを設定し、式文字列の「evaluate」メソッドを起動して、resolve()を使用して計算できる構文木でPromiseを受け取ります。

もちろん、構文木を使用することだけが遅延評価の方法ではありません。次に検討するパーサータイプは、木を使用せずに実行されますが、評価アルゴリズムはいわゆるバイトコードに書き込まれます。それでは、最初にバイトコードがどのように機能するかを見てみましょう。

バイトコードの生成

バイトコードは、計算アルゴリズム全体を「高速」バイナリ表現で記述する一連のコマンドです。バイトコードの作成は実際のコンパイルに似ています。 ただし、結果にはプロセッサ命令ではなく、特定の計算機クラスを制御する適用言語の変数または構造が含まれます。この場合、実行ユニットは次のByteCode構造体です。

  struct ByteCode
  {
      uchar code;
      double value;
      int index;
  
      ByteCode(): code(0), value(0.0), index(-1) {}
      ByteCode(const uchar c): code(c), value(0.0), index(-1) {}
      ByteCode(const double d): code('n'), value(d), index(-1) {}
      ByteCode(const uchar c, const int i): code(c), value(0.0), index(i) {}
      
      string toString() const
      {
        return StringFormat("%s %f %d", CharToString(code), value, index);
      }
  };

そのフィールドは、ストリーミング計算に必要な最小セットを表す、Promiseオブジェクトの一部のフィールドを繰り返したものです。ストリーミング計算となるのは、階層構造を切り替えることなく、コマンドが左から右に順番に読み取られて実行されるためです。

「code」フィールドにはコマンドの本質(値はPromiseコードに対応します)、「value」フィールドには数値(定数)、「index」フィールドには変数/関数テーブル内の変数/関数のインデックスがそれぞれ含まれます。

計算命令を作成する方法の1つは、逆ポーランド記法です。これは後置記法とも呼ばれます。この表記の考え方は、演算子が被演算子の後に来るというものです。たとえば、通常の中置記法「a + b」は接尾辞「a b +」になり、より複雑な「a + b * sqrt(c)」は「a b c 'sqrt' * +」になります。

RPNは、スタックを使用して計算を簡単に実装できるため、バイトコードに適しています。入力ストリーム内の数字または変数参照が「認識」されると、この値はスタックにプッシュされます。入力ストリームで演算子または関数が検出された場合、必要な数の値がスタックからポップされ、その値を使用して指定された操作が実行され、結果がスタックにプッシュされます。プロセスの終了時に、式の評価結果はスタックに残った唯一の数値となります。

RPNは、構文木を構築するのと同じ式の代替記述を提供するため、これら2つのプレゼンテーションを相互に変換できます。Promiseの木に基づいてバイトコードを生成してみましょう。 これを行うには、exportToByteCodeメソッドをPromiseクラスに追加します。

  class Promise
  {
    ...
    public:
      void exportToByteCode(ByteCode &codes[])
      {
        if(left) left.exportToByteCode(codes);
        const int truly = ArraySize(codes);
        
        if(code == '?')
        {
          ArrayResize(codes, truly + 1);
          codes[truly].code = code;
        }
        
        if(right) right.exportToByteCode(codes);
        const int falsy = ArraySize(codes);
        if(last) last.exportToByteCode(codes);
        const int n = ArraySize(codes);
        
        if(code != '?')
        {
          ArrayResize(codes, n + 1);
          codes[n].code = code;
          codes[n].value = value;
          codes[n].index = index;
        }
        else // (code == '?')
        {
          codes[truly].index = falsy; // true分岐を飛び越える
          codes[truly].value = n;     // 両方の分岐を飛び越える
        }
      }
      ...
  };

このメソッドは、パラメータとしてByteCode構造体の配列を受け取り、現在のPromiseオブジェクトのコンテンツをそこに保存します。まず、すべての従属ノードを分析します。ゼロ以外の場合は、メソッドが「left」、「right」、および「last」のポインターに対して再帰的に呼び出されます。その後、すべての被演算子が保存されると、Promiseオブジェクトのプロパティがバイトコードに書き込まれます。

式の文法には条件演算子があるため、このメソッドは、条件式の終了だけでなく、trueとfalseの命令分岐が始まるポイントでのバイトコード配列のサイズをさらに記憶します。これにより、条件演算子のバイトコード構造体に配列内のオフセットを書き込むことができます。条件がtrueまたはfalseの場合、計算中にそこにジャンプする必要があります。true条件の命令分岐は、バイトコード「?」の直後から始まります。命令の実行後、「value」フィールドにオフセットでジャンプします。false条件の命令分岐は、「index」フィールドのオフセットから始まり、すぐに「true」命令のフィールドになります。

解釈モードまたは構文木で式を評価する場合、条件に応じて、値の1つが選択される前に、条件演算子の両方の分岐が計算されます。つまり、分岐の1つは目的なしに計算されます。バイトコードでは、不要な分岐計算をスキップします。

式木全体をバイトコードに変換するには、「evaluate」によって返されるルートオブジェクトに対してexportToByteCodeを呼び出します。Prattパーサーの例を次に示します。

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
  
    for(int i = 0; i < ArraySize(codes); i++)
    {
      Print(i, "] ", codes[i].toString());
    }

次に、バイトコードに基づいて計算を実行する関数を作成する必要があります。バイトコードは変数と関数のインデックスを使用し、Promiseにはデフォルトでこれらのテーブルへのリンクがあるため、同じPromiseクラスに追加しましょう。

  #define STACK_SIZE 100
  
  // スタックの模造
  #define push(S,V,N) S[N++] = V
  #define pop(S,N) S[--N]
  #define top(S,N) S[N-1]
  
  class Promise
  {
    ...
    public:
      static double execute(const ByteCode &codes[], VariableTable *vt = NULL, FunctionTable *ft = NULL)
      {
        if(vt) variableTable = vt;
        if(ft) functionTable = ft;
  
        double stack[]; int ssize = 0; ArrayResize(stack, STACK_SIZE);
        int jumps[]; int jsize = 0; ArrayResize(jumps, STACK_SIZE / 2);
        const int n = ArraySize(codes);
        for(int i = 0; i < n; i++)
        {
          if(jsize && top(jumps, jsize) == i)
          {
            --jsize; // 素早く「ポップ&ドロップ」する
            i = pop(jumps, jsize);
            continue;

          }
          switch(codes[i].code)
          {
            case 'n': push(stack, codes[i].value, ssize); break;
            case 'v': push(stack, variableTable[codes[i].index], ssize); break;
            case 'f':
              {
                IFunctor *ptr = functionTable[codes[i].index];
                double params[]; ArrayResize(params, ptr.arity()); int psize = 0;
                for(int j = 0; j < ptr.arity(); j++)
                {
                  push(params, pop(stack, ssize), psize);
                }
                ArrayReverse(params);
                push(stack, ptr.execute(params), ssize);
              }
              break;
            case '+': push(stack, pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '-': push(stack, -pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '*': push(stack, pop(stack, ssize) * pop(stack, ssize), ssize); break;
            case '/': push(stack, Promise::safeDivide(1, pop(stack, ssize)) * pop(stack, ssize), ssize); break;
            case '%':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, fmod(first, second), ssize);
              }
              break;
            case '!': push(stack, (double)(!pop(stack, ssize)), ssize); break;
            case '~': push(stack, (double)(-pop(stack, ssize)), ssize); break;
            case '<':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first < second), ssize);
              }
              break;
            case '>':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first > second), ssize);
              }
              break;
            case '{':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first <= second), ssize);
              }
              break;
            case '}':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first >= second), ssize);
              }
              break;
            case '&': push(stack, (double)(pop(stack, ssize) && pop(stack, ssize)), ssize); break;
            case '|':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first || second), ssize); // 順番は重要
              }
              break;
            case '`': push(stack, _precision < fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '=': push(stack, _precision > fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '?':
              {
                const double first = pop(stack, ssize);
                if(first) // true
                {
                  push(jumps, (int)codes[i].value, jsize); // if全体が終了する場所へ
                  push(jumps, codes[i].index, jsize);      // trueが終了する場所からジャンプする
                }
                else // false
                {
                  i = codes[i].index - 1; // ++が続くので-1が必要
                }
              }
              break;
            default:
              Print("Unknown byte code ", CharToString(codes[i].code));
          }
        }
        return pop(stack, ssize);
      }
      ...
  };

スタックの操作は、「stack」配列のマクロを介して実装されます。この配列では、特定の数の要素STACK_SIZEが事前に割り当てられています。これは、プッシュおよびポップ操作中のArrayResize呼び出しを回避することにより、実行を高速化するために行われます。実際の1行の式のほとんどには、100に等しいSTACK_SIZEで十分なようです。さもないと、スタックオーバーフローが発生します。

ネストできる条件演算子の実行を制御するには、追加の「jumps」スタックを使用する必要があります。

これらの操作はすべて、上記のPromiseおよびPrattパーサーコードからすでによく知られています。唯一の違いは、被演算子のソースとして、および中間結果を格納する場所としてスタックが広く使用されていることです。バイトコードは、再帰なしで、単一のメソッド呼び出しでループで実行されます。

この機能により、PrattパーサーまたはExpressionCompilerから構文木をエクスポートして受け取ったバイトコードを使用して式を計算できます。

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
    double r = Promise::execute(codes);

後で、すべてのパーサーをテストするときに、木とバイトコードを使用した計算のパフォーマンス速度を比較します。

しかし、バイトコードを導入する主な目的は、別のパーサータイプである「操車場」パーサーの実装を可能にすることでした。

操車場パーサー(ExpressionShuntingYard)

操車場パーサーという名前は、入力トークンのストリームを、出力に即座に渡すことができるものと、トークンの優先順位(スタック内のトークンと入力ストリーム内の次のトークンの優先順位)の組み合わせに関する特定のルールによってトークンが取得存在される特別なスタックにプッシュする必要があるものに分割するために使用されるメソッドに由来します。パーサーは、入力式をRPN(逆ポーランド記法)に変換し直します。これは、構文文なしでバイトコードをすぐに生成できるため便利です。一般的な説明からわかるように、操車場法は演算子の優先順位に基づいているため、このパーサーはPrattパーサーに関連しています。したがって、ExpressionPrecedence子クラスとして実装されます。

このパーサーは、ボトムアップカテゴリに属しています。

一般的に、アルゴリズムは次のとおりです(ここでは、使用しない右結合性の詳細と、三項条件演算子に関連する複雑さを省略しています)。

  ループ内の式から次のトークンを読み取ります(式が終了するまで)
    トークンが単項演算の場合は、スタックに保存します
    数値の場合は、バイトコードに書き込みます
    変数の場合は、そのインデックスをバイトコードに書き込みます
    関数識別子の場合は、そのインデックスをスタックに保存します
    トークンが中置演算子の場合
      「(」がスタックの最上位になく、((スタック最上位の演算子の優先順位> =現在の演算子の優先順位)または関数が最上位にある限り)
        スタックの最上位を出力バイトコードにプッシュします
      演算子をスタックに保存します
    トークンが「(」の場合、スタックに保存します
    トークンが「)」の場合
      スタックの最上位が「(」でない限り
        スタックの最上位を出力バイトコードにプッシュします
      「(」がスタックの一番上にある場合は、削除して破棄します
  スタックにトークンが残っている場合は、それらを順番に出力バイトコードに移動します

明らかに、このパーサーの実装に必要なメソッドは1つだけです。

ExpressionShuntingYardクラス全体を以下に示します。メインのpublicメソッドconvertToByteCodeは、exportToByteCodeで実行される解析を開始します。式は条件演算子をサポートしているため、exportToByteCodeの再帰呼び出しを使用して部分式を解析します。

  class ExpressionShuntingYard: public ExpressionPrecedence
  {
    public:
      ExpressionShuntingYard(const string vars = NULL): ExpressionPrecedence(vars) { }
      ExpressionShuntingYard(VariableTable &vt): ExpressionPrecedence(vt) { }
  
      bool convertToByteCode(const string expression, ByteCode &codes[])
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          exportToByteCode(codes);
        }
        return !_failed;
      }
  
    protected:
      template<typename T>
      static void _push(T &stack[], T &value)
      {
        const int n = ArraySize(stack);
        ArrayResize(stack, n + 1, STACK_SIZE);
        stack[n] = value;
      }
  
      void exportToByteCode(ByteCode &output[])
      {
        ByteCode stack[];
        int ssize = 0;
        string number;
        uchar c;
        
        ArrayResize(stack, STACK_SIZE);
        
        const int previous = ArraySize(output);
        
        while(_nextToken() && !_failed)
        {
          if(_token == '+' || _token == '-' || _token == '!')
          {
            if(_token == '-')
            {
              _push(output, ByteCode(-1.0));
              push(stack, ByteCode('*'), ssize);
            }
            else if(_token == '!')
            {
              push(stack, ByteCode('!'), ssize);
            }
            continue;
          }
          
          number = "";
          if(_readNumber(number)) // 数値が読まれたら、_tokenが変更されている
          {
            _push(output, ByteCode(StringToDouble(number)));
          }
          
          if(isalpha(_token))
          {
            string variable;
            while(isalnum(_token))
            {
              variable += ShortToString(_token);
              _nextToken();
            }
            if(_token == '(')
            {
              push(stack, ByteCode('f', _functionTable.index(variable)), ssize);
            }
            else // 変数名
            {
              int index = -1;
              if(CheckPointer(_variableTable) != POINTER_INVALID)
              {
                index = _variableTable.index(variable);
                if(index == -1)
                {
                  if(_variableTable.adhocAllocation())
                  {
                    index = _variableTable.add(variable, nan);
                    _push(output, ByteCode('v', index));
                    error("Unknown variable is NaN: " + variable, __FUNCTION__, true);
                  }
                  else
                  {
                    error("Unknown variable : " + variable, __FUNCTION__);
                  }
                }
                else
                {
                  _push(output, ByteCode('v', index));
                }
              }
            }
          }
          
          if(infixes[_token] > 0) // 最下位の「？」を含む演算子
          {
            while(ssize > 0 && isTop2Pop(top(stack, ssize).code))
            {
              _push(output, pop(stack, ssize));
            }
            
            if(_token == '?' || _token == ':')
            {
              if(_token == '?')
              {
                const int start = ArraySize(output);
                _push(output, ByteCode((uchar)_token));
                exportToByteCode(output); // true部分式、_tokenが変更されている
                if(_token != ':')
                {
                  error("Colon expected, given: " + ShortToString(_token), __FUNCTION__);
                  break;
                }
                output[start].index = ArraySize(output);
                exportToByteCode(output); // false 部分式、_tokenが変更されている
                output[start].value = ArraySize(output);
                if(_token == ':')
                {
                  break;
                }
              }
              else
              {
                break;
              }
            }
            else
            {
              if(_token == '>' || _token == '<')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '<' ? '{' : '}')), ssize);
                  _nextToken();
                }
                else
                {
                  push(stack, ByteCode((uchar)_token), ssize);
                }
              }
              else if(_token == '=' || _token == '!')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '!' ? '`' : '=')), ssize);
                  _nextToken();
                }
              }
              else if(_token == '&' || _token == '|')
              {
                _matchNext(_token, ShortToString(_token) + " expected after " + ShortToString(_token), __FUNCTION__);
                push(stack, ByteCode((uchar)_token), ssize);
              }
              else if(_token != ',')
              {
                push(stack, ByteCode((uchar)_token), ssize);
              }
            }
          }
          
          if(_token == '(')
          {
            push(stack, ByteCode('('), ssize);
          }
          else if(_token == ')')
          {
            while(ssize > 0 && (c = top(stack, ssize).code) != '(')
            {
              _push(output, pop(stack, ssize));
            }
            if(c == '(') // 部分式でない限りtrue(その場合、「c」は0)
            {
              ByteCode disable_warning = pop(stack, ssize);
            }
            else
            {
              if(previous == 0)
              {
                error("Closing parenthesis is missing", __FUNCTION__);
              }
              return;
            }
          }
        }
        
        while(ssize > 0)
        {
          _push(output, pop(stack, ssize));
        }
      }
      
      bool isTop2Pop(const uchar c)
      {
        return (c == 'f' || infixes[c] >= infixes[_token]) && c != '(' && c != ':';
      }
  };

操車場パーサーの使用法は、以前のタイプとは異なります。ここで、「evaluate」を呼び出して木を受け取る手順をスキップして、代わりに、convertToByteCodeメソッドは、渡された式のバイトコードをすぐに返します。

  ExpressionShuntingYard sh;
  sh.variableTable().adhocAllocation(true);
  
  ByteCode codes[];
  bool success = sh.convertToByteCode("x + y", codes);
  if(success)
  {
    sh.variableTable().assign("x=10;y=20");
    double r = Promise::execute(codes);
  }

これで、さまざまなタイプのパーサーの概要は終わりです。クラスの図は次のようになります。

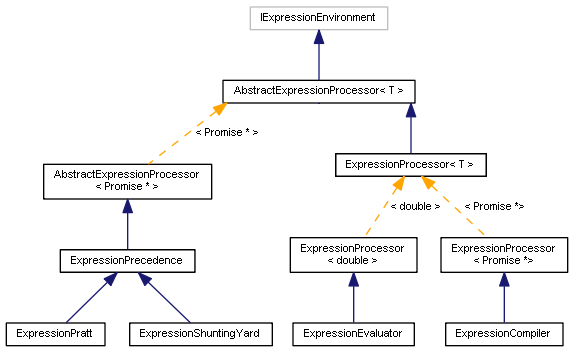
パーサークラス図

さまざまなパーサーをテストして比較するために、後でテストスクリプトを作成します。

究極の適用分野は取引であるため、標準機能のリストをテクニカル指標で拡張する方法を見てみましょう。

関数としての式への指標の埋め込み

式を計算するとき、トレーダーは、残高、ポジション数、指標の読み取り値など、特定の情報を必要とする場合があります。関数のリストを拡張することにより、これらすべてを式内で使用できるようにすることができます。このアプローチを示すために、一連の関数に移動平均指標を追加しましょう。

式に指標を埋め込むメカニズムは、以前に検討された関手に基づいているため、AbstractFuncから派生したクラスとして実装されます。すでにわかっているように、すべてのAbstractFuncファミリクラスインスタンスは自動的にAbstractFuncStorageに登録され、関数のテーブルで使用できるようになります。

  class IndicatorFunc: public AbstractFunc
  {
    public:
      IndicatorFunc(const string n, const int a = 1): AbstractFunc(n, a)
      {
        // 単一の引数は小節番号
        // 2つの引数はバー番号とバッファインデックス
      }
      static IndicatorFunc *create(const string name);
  };

MetaTrader 5指標の特定の機能は、2つのアプリケーションステージも必要とすることです。最初に指標を作成し(説明を取得するため)、次に指標からデータをリクエストする必要があります。式の処理のコンテキストでは、最初の手順は解析中、2番目の手順は評価中に実行する必要があります。指標の作成にはすべてのパラメータの指定が必要なため、関数パラメータで渡すのではなく、名前で実装する必要があります。たとえば、パラメータ(period、method、price_type)を持つ「iMA」関数を作成した場合、解析段階ではその名前のみを受け取り、パラメータの定義は実行段階まで延期されるため、指標を作成するには遅すぎます(この段階で指標からデータを読み取る必要があるため)。

解決策として、移動平均指標の名前のセットを予約できます。名前は、method_price_periodのルールに従って構成されます。ここで、「method」はENUM_MA_METHOD列挙(SMA、EMA、SMMA、LWMA)の意味のある単語の1つです。 「price」は、列挙型ENUM_APPLIED_PRICE(CLOSE、OPEN、HIGH、LOW、MEDIAN、TYPICAL、WEIGHTED)の価格タイプの1つです。 「period」は整数です。したがって、「SMA_OPEN_10」関数を使用すると、始値に基づいて、期間が10の単純な移動平均が作成されます。

指標関数のアリティは、デフォルトで1に等しくなります。唯一のパラメータは、バー番号を渡すために使用されます。アリティが2に設定されている場合、2番目のパラメータを使用してバッファ番号を示すことができます。移動平均には必要ありません。

MAIndicatorFuncクラスは、要求された名前に対応するパラメータを持つ指標インスタンスを作成するために使用されます。

  class MAIndicatorFunc: public IndicatorFunc
  {
    protected:
      const int handle;
      
    public:
      MAIndicatorFunc(const string n, const int h): IndicatorFunc(n), handle(h) {}
      
      ~MAIndicatorFunc()
      {
        IndicatorRelease(handle);
      }
      
      static MAIndicatorFunc *create(const string name) // SMA_OPEN_10(0)
      {
        string parts[];
        if(StringSplit(name, '_', parts) != 3) return NULL;
        
        ENUM_MA_METHOD m = -1;
        ENUM_APPLIED_PRICE t = -1;
        
        static string methods[] = {"SMA", "EMA", "SMMA", "LWMA"};
        for(int i = 0; i < ArraySize(methods); i++)
        {
          if(parts[0] == methods[i])
          {
            m = (ENUM_MA_METHOD)i;
            break;
          }
        }
  
        static string types[] = {"NULL", "CLOSE", "OPEN", "HIGH", "LOW", "MEDIAN", "TYPICAL", "WEIGHTED"};
        for(int i = 1; i < ArraySize(types); i++)
        {
          if(parts[1] == types[i])
          {
            t = (ENUM_APPLIED_PRICE)i;
            break;
          }
        }
        
        if(m == -1 || t == -1) return NULL;
        
        int h = iMA(_Symbol, _Period, (int)StringToInteger(parts[2]), 0, m, t);
        if(h == INVALID_HANDLE) return NULL;
        
        return new MAIndicatorFunc(name, h);
      }
      
      double execute(const double &params[]) override
      {
        const int bar = (int)params[0];
        double result[1] = {0};
        if(CopyBuffer(handle, 0, bar, 1, result) != 1)
        {
          Print("CopyBuffer error: ", GetLastError());
        }
        return result[0];
      }
  };

「create」ファクトリメソッドは、渡された名前を解析し、名前からパラメータを抽出して、「handle」を使用して指標を作成します。指標値は、関手の標準的なメソッド(execute)で取得されます。

将来、他の指標が関数に追加される可能性があるため、IndicatorFuncクラスは、指標の要求に対して単一のエントリポイントを提供します。これは「create」メソッドです。これまでのところ、MAIndicatorFunc::create()呼び出しへのリダイレクトのみが含まれています。

  static IndicatorFunc *IndicatorFunc::create(const string name)
  {
    // TODO: より多くの指標タイプをサポートし、名前に基づいて呼び出しをディスパッチ
    return MAIndicatorFunc::create(name);
  }

このメソッドは関数のテーブルから呼び出す必要があるため、必要なコードをFunctionTableクラスに追加します。

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      ...
      #ifdef INDICATOR_FUNCTORS
      virtual int index(const string name) override
      {
        int i = _table.getIndex(name);
        if(i == -1)
        {
          i = _table.getSize();
          IFunctor *f = IndicatorFunc::create(name);
          if(f)
          {
            Table<IFunctor *>::add(name, f);
            return i;
          }
          return -1;
        }
        return i;
      }
      #endif
  };

組み込みの25関数のリストに渡された名前が見つからない場合、新しいバージョンの「index」メソッドは適切な指標を見つけようとします。この追加機能を接続するには、INDICATOR_FUNCTORSマクロを定義する必要があります。

このオプションを有効にすると、たとえば、「EMA_OPEN_10(0)/ EMA_OPEN_21(0)」という式を計算できます。

実際には、呼び出された指標のパラメータは、多くの場合、設定で提供されます。これは、それらを何らかの方法で式の行に動的に挿入する必要があることを意味します。このタスクを簡素化するために、AbstractExpressionProcessorクラスは特別な式の前処理オプションをサポートしています。簡潔にするために、その説明は記事では省略されています。前処理の有効化は、「evaluate」メソッドのオプションの2番目のパラメータによって管理されます(これはデフォルトでfalseに等しく、つまり前処理は無効になっています)。

このオプションは次のように動作します。式では、中括弧で変数名を指定できます。変数名は、解析前の変数値に置き換えられます。たとえば、式が「EMA_TYPICAL_ {Period}(0)」に等しく、変数テーブルに値11のPeriod変数が含まれている場合、「EMA_TYPICAL_11(0)」が分析されます。

インディケータ機能をテストするために、後でエキスパートアドバイザーを作成します。エキスパートアドバイザーの取引シグナルは、移動平均を含む評価された式に基づいて生成されます。

ただし、最初に、パーサーが正しく機能していることを確認する必要があります。

テストスクリプト(ExpresSParserS)

テストスクリプトExpresSParserS.mq5には、4つのパーサータイプの計算速度の場合の機能テストと測定のセット、さまざまなモードのデモンストレーション、構文木とバイトコードのロギング、組み込み関数としての指標の使用が含まれています。

機能テストには、正しいアプリケーションと意図的に間違ったアプリケーション(宣言されていない変数、ゼロ除算など)の両方が含まれます。テストの正しさは、実際の結果と期待される結果の対応によって決定されます。つまり、エラーも「正しい」可能性があります。たとえば、Prattパーサのテストログは次のようになります。

  Running 19 tests on ExpressionPratt* …
  1 passed, ok: a > b ? b > c ? 1 : 2 : 3 = 3.0; expected = 3.0
  2 passed, ok: 2 > 3 ? 2 : 3 > 4 ? 3 : 4 = 4.0; expected = 4.0
  3 passed, ok: 4 > 3 ? 2 > 4 ? 2 : 4 : 3 = 4.0; expected = 4.0
  4 passed, ok: (a + b) * sqrt(c) = 8.944271909999159; expected = 8.944271909999159
  5 passed, ok: (b == c) > (a != 1.5) = 0.0; expected = 0.0
  6 passed, ok: (b == c) >= (a != 1.5) = 1.0; expected = 1.0
  7 passed, ok: (a > b) || sqrt(c) = 1.0; expected = 1.0
  8 passed, ok: (!1 != !(b - c/2)) = 1.0; expected = 1.0
  9 passed, ok: -1 * c == -sqrt(-c * -c) = 1.0; expected = 1.0
  10 passed, ok: pow(2, 5) % 5 = 2.0; expected = 2.0
  11 passed, ok: min(max(a,b),c) = 2.5; expected = 2.5
  12 passed, ok: atan(sin(0.5)/cos(0.5)) = 0.5; expected = 0.5
  13 passed, ok: .2 * .3 + .1 = 0.16; expected = 0.16
  14 passed, ok: (a == b) + (b == c) = 0.0; expected = 0.0
  15 passed, ok: -(a + b) * !!sqrt(c) = -4.0; expected = -4.0
  16 passed, ok: sin ( max ( 2 * 1.5, 3 ) / 3 * 3.14159265359 ) = -2.068231111547469e-13; expected = 0.0
  lookUpVariable error: Variable is undefined: _1c @ 7: 1 / _1c^
  17 passed, er: 1 / _1c = nan; expected = nan
  safeDivide error: Error : Division by 0! @ 15: 1 / (2 * b - c)^
  18 passed, er: 1 / (2 * b - c) = inf; expected = inf
  19 passed, ok: sqrt(b-c) = -nan(ind); expected = -nan(ind)
  19 tests passed of 19
  17 for correct expressions, 2 for invalid expressions

ご覧のとおり、19のテストすべてが正常に完了しました。2つのテストで、予想されるエラーが発生しました。

速度は、サイクル内の複数の計算に対してのみ測定されます。 インタープリターを使用する場合、すべての計算に対して実行されるため、これには式の解析段階が含まれます。他のすべてのパーサータイプの場合、解析段階は「外部」で実行されます。1回限りの式の解析には、すべてのメソッドでほぼ同じ時間がかかります。これは、10,000サイクル(マイクロ秒)を測定した結果の1つです。

  >>> Performance tests (timing per method)
  Evaluation: 104572
  Compilation: 25011
  Pratt bytecode: 23738
  Pratt: 24967
  ShuntingYard: 23147

予想どおり、以前に「コンパイルされた」式は、解釈された式よりも数倍速く評価されます。また、最速の計算はバイトコードに基づく計算であると結論付けることもできます。 この場合、バイトコードを取得する方法に実質的な違いはないため、Prattパーサーまたは操車法のいずれかを使用できます。個人的な参照とアルゴリズムの理解度に応じてパーサーを選択することも、構文の拡張や既存のプログラムとの統合などの特定のタスクに最適なパーサーを選択することもできます。

式を使用したエキスパートアドバイザーシグナルの設定(ExprBot)

式は、自動売買ロボットで取引シグナルを生成するために使用して、パラメータを単純に変更する場合に比べて柔軟性が高まります。関数の拡張可能なリストにより、これはMQLと実質的に同じ機能を提供しますが、ここではコンパイルは必要ありません。さらに、日常的な操作は既製の関手の中に簡単に隠すことができるので、製品設定の柔軟性と複雑さのバランスがとれます。

移動平均指標のセットがあるため、取引システムはこれらの指標に基づいています(ただし、式に時間関数、リスク管理、ティック価格、その他のデータを追加できます)。

原理を示すために、簡単なエキスパートアドバイザーであるExprBotを作成しましょう。SignalBuy変数とSignalSell変数にはそれぞれ、買いと売りの取引を実行するための条件を持つ式が含まれます。次の式は、2つのMAの共通部分に基づく戦略に使用できます。

  #define INDICATOR_FUNCTORS
  #include <ExpresSParserS/ExpressionCompiler.mqh>
  
  input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
  input string Variables = "Threshold=0.01";
  input int Fast = 10;
  input int Slow = 21;

閾値は、確率変数の入力を示すために定数としてのみ設定されます。高速および低速の平均化期間を持つパラメータは、指標名の一部として、解析される前に式に挿入するために使用されます。

2つのシグナルがあるため、2つの再帰下降パーサーをインスタンス化します。一般に、1つを使用できますが、2つの式の変数のテーブルは潜在的に異なる可能性があります。その場合、各計算の前にこのコンテキストを切り替える必要があります。

  ExpressionCompiler ecb(Variables), ecs(Variables);
  Promise *p1, *p2;

OnInitハンドラーで、パラメータを変数テーブルに保存し、構文木を構築します。

  int OnInit()
  {
    ecb.variableTable().set("Fast", Fast);
    ecb.variableTable().set("Slow", Slow);
    p1 = ecb.evaluate(SignalBuy, true);
    if(!ecb.success())
    {
      Print("Syntax error in Buy signal:");
      p1.print();
      return INIT_FAILED;
    }
    ecs.variableTable().set("Fast", Fast);
    ecs.variableTable().set("Slow", Slow);
    p2 = ecs.evaluate(SignalSell, true);
    if(!ecs.success())
    {
      Print("Syntax error in Sell signal:");
      p2.print();
      return INIT_FAILED;
    }
    
    return INIT_SUCCEEDED;
  }

戦略全体はOnTickハンドラーで記述されます(ここでは補助関数は省略されています。MT4Ordersライブラリも含める必要があります)。

  #define _Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
  #define _Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)
  
  void OnTick()
  {
    if(!isNewBar()) return;
    
    bool buy = p1.resolve();
    bool sell = p2.resolve();
    
    if(buy && sell)
    {
      buy = false;
      sell = false;
    }
    
    if(buy)
    {
      OrdersCloseAll(_Symbol, OP_SELL);
      if(OrdersTotalByType(_Symbol, OP_BUY) == 0)
      {
        OrderSend(_Symbol, OP_BUY, Lot, _Ask, 100, 0, 0);
      }
    }
    else if(sell)
    {
      OrdersCloseAll(_Symbol, OP_BUY);
      if(OrdersTotalByType(_Symbol, OP_SELL) == 0)
      {
        OrderSend(_Symbol, OP_SELL, Lot, _Bid, 100, 0, 0);
      }
    }
    else
    {
      OrdersCloseAll();
    }
  }

これらの2つの式は、「promises」p1とp2によって計算されます。その結果、対応する方向でポジションのオープンまたは決済を開始する「買い」と「売り」の2つのフラグがあります。MQLコードは、一度に1つのポジションしか存在できないことを保証します。したがって、シグナルが反対の場合(これは、より複雑な式を使用した場合、または負の閾値が誤って設定された場合に発生する可能性があります)、既存のポジションはすべて決済されます。シグナル条件は、パーサー関数内でさまざまな方法で編集できます。

ストラテジーテスターでEAを起動した場合、結果はあまり良くない可能性があります。ただし、重要なのは、EAの取引と取引はパーサーによって管理されるということです。既製の収益性の高いシステムを提供するものではありませんが、戦略を見つけるための追加のツールを提供します。

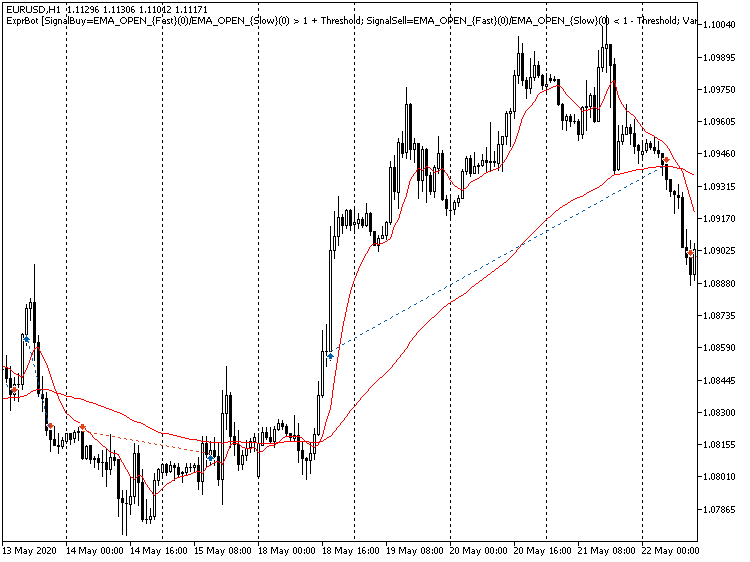
式で計算されたシグナルを使用した取引の例

終わりに

これらの2つの記事では、4つのパーサータイプを調べ、それらの機能を比較し、MQLプログラムに埋め込むことができるクラスを実装しました。すべてのパーサーは、最も頻繁に使用される数学演算および25の関数と同じ文法を使用します。必要に応じて、サポートされている演算子のリストを拡張し、新しい組み込みアプリケーション関数(指標、価格、取引統計)と構文構造(特に、それらの処理のための配列と関数)を追加することにより、文法を拡張できます。

このテクノロジーにより、設定と不変のMQLコードをより柔軟に分離できます。入力パラメータの式を編集してアルゴリズムをカスタマイズする機能は、エンドユーザーにとっては簡単に思えますが、目的のコードフラグメントを見つけ、ルールに従って編集し、潜在的なコンパイルエラーを処理するために必要なMQLプログラミングの基本を学ぶ必要はありません。MQLプログラム開発者の観点からは、解析と式の評価のサポートにより、ライブラリの使用やMQLコンパイラのバージョン管理を回避できる「MQL上のスクリプト」に変換できる可能性など、他の利点が得られます。