Cálculo de expressões matemáticas (Parte 2). Analisadores Pratt e estação de triagem

Neste artigo, continuamos a estudar diferentes métodos de análise de expressões matemáticas e sua implementação na linguagem MQL. Na primeira parte, vimos analisadores de descendência recursiva. Sua principal vantagem é que se tratam de uma colocação intuitiva diretamente relacionada à gramática específica de uma expressão. Mas quando se fala de eficiência e nível tecnológico, existem outros tipos de analisadores aos quais vale a pena prestar atenção.

Analisadores usando precedência de operadores

O próximo tipo de analisador que estudaremos é os de precedência (precedence) de operadores. Eles são caracterizados por uma implementação mais compacta devido ao fato de que os métodos das classes são criados não com base em regras gramaticais (como vimos, neste caso, cada regra é convertida em seu próprio método), mas de uma forma mais generalizada que leva em consideração apenas a precedência dos operadores.

A precedência (ou prioridade) das operações já estava presente de forma implícita na escrita de gramática EBNF: suas regras estão organizadas desde operações com menor prioridade para aquelas com maior prioridade, até entidades terminais, isto é, constantes e variáveis. Isso ocorre porque a precedência dita a sequência em que as operações devem ser realizadas quando não existe agrupamento explícito entre parênteses. Por exemplo, a precedência da operação de multiplicação é maior do que a da de adição. Porém, o menos unário tem precedência sobre a multiplicação. Quanto mais próximo o elemento da árvore sintática estiver da raiz (a expressão inteira), mais tarde será avaliado.

Para implementar analisadores, precisamos de duas tabelas com valores numéricos correspondentes à prioridade de cada operação. Quanto maior for o valor, maior será a prioridade.

Existem duas tabelas, porque, assim, as operações unárias e binárias são logicamente separadas nos algoritmos. Particularmente, estamos falando não apenas sobre operações, mas, num sentido mais geral, sobre caracteres que podem ser encontrados em expressões na forma de prefixos e infixos (veja os tipos de operadores na Wikipedia)

Como o nome indica, o prefixo é o caractere que precede o operando (por exemplo, '!' na expressão "!var"), e o infixo é o caractere entre os operandos (por exemplo, '+' na expressão "a + b"). Também existem posfixos (por exemplo, um par de '+' no operador de incremento, que também está em MQL, isto é, "i++"), que, porém, não são usados em nossas expressões e, portanto, permanecem nos bastidores.

Como prefixos, além das operações unárias '!', '-', '+', pode haver um parêntese de abertura '(', isto é, um sinal do início de um grupo, uma letra ou sublinhado que é um sinal de início de um identificador, bem como um dígito ou ponto '.' sendo um sinal o início de uma constante numérica.

Descrevemos as tabelas na classe ExpressionPrecedence, a partir desta serão herdadas as classes de analisadores concretas baseadas em prioridade. Todos esses analisadores funcionarão com base no Promise.

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      static uchar prefixes[128];
      static uchar infixes[128];
      
      static ExpressionPrecedence epinit;
      
      static void initPrecedence()
      {
        // grouping
        prefixes['('] = 9;
  
        // unary
        prefixes['+'] = 9;
        prefixes['-'] = 9;
        prefixes['!'] = 9;
        
        // identifiers
        prefixes['_'] = 9;
        for(uchar c = 'a'; c <= 'z'; c++)
        {
          prefixes[c] = 9;
        }
        
        // numbers
        prefixes['.'] = 9;
        for(uchar c = '0'; c <= '9'; c++)
        {
          prefixes[c] = 9;
        }
        
        // operators
        // infixes['('] = 9; // parenthesis is not used here as 'function call' operator
        infixes['*'] = 8;
        infixes['/'] = 8;
        infixes['%'] = 8;
        infixes['+'] = 7;
        infixes['-'] = 7;
        infixes['>'] = 6;
        infixes['<'] = 6;
        infixes['='] = 5;
        infixes['!'] = 5;
        infixes['&'] = 4;
        infixes['|'] = 4;
        infixes['?'] = 3;
        infixes[':'] = 2;
        infixes[','] = 1; // arg list delimiter
      }
  
      ExpressionPrecedence(const bool init)
      {
        initPrecedence();
      }
  
    public:
      ExpressionPrecedence(const string vars = NULL): AbstractExpressionProcessor(vars) {}
      ExpressionPrecedence(VariableTable &vt): AbstractExpressionProcessor(vt) {}
  };
  
  static uchar ExpressionPrecedence::prefixes[128] = {0};
  static uchar ExpressionPrecedence::infixes[128] = {0};
  static ExpressionPrecedence ExpressionPrecedence::epinit(true);

As tabelas de prioridade são feitas de forma "econômica" usando matrizes esparsas com um tamanho de 128 elementos (isso é o suficiente, porque caracteres com códigos de outras faixas não são suportados). As células correspondentes aos códigos de caracteres indicam suas prioridades. Assim, a prioridade é facilmente obtida por endereçamento direto pelo código de token.

As classes herdadas também exigem dois novos métodos auxiliares para verificar os caracteres que seguem na string de entrada: _lookAhead simplesmente retorna o próximo token (como se estivesse olhando um passo à frente) e _matchNext o lê se ele corresponde ao esperado ou emite um erro caso contrário.

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      ...
      ushort _lookAhead()
      {
        int i = 1;
        while(_index + i < _length && isspace(_expression[_index + i])) i++;
        if(_index + i < _length)
        {
          return _expression[_index + i];
        }
        return 0;
      }
      
      void _matchNext(ushort c, string message, string context = NULL)
      {
        if(_lookAhead() == c)
        {
          _nextToken();
        }
        else if(!_failed) // prevent chained errors
        {
          error(message, context);
        }
      }
      ...
  };

O primeiro analisador baseado em precedência que veremos é o analisador Pratt.

Analisador Pratt (ExpressionPratt)

O analisador Pratt é decrescente, assim como o analisador descendente recursivo. Isso significa que ele também conterá chamadas recursivas para certos métodos que analisam construções individuais na expressão, mas haverá muito menos desses métodos.

Os construtores e o principal método público evaluate parecem familiares.

  class ExpressionPratt: public ExpressionPrecedence
  {
    public:
      ExpressionPratt(const string vars = NULL): ExpressionPrecedence(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionPratt(VariableTable &vt): ExpressionPrecedence(vt) { helper = new ExpressionHelperPromise(&this); }
  
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          return parseExpression();
        }
        return NULL;
      }

O novo método parseExpression está no centro do algoritmo do Pratt. Ele começa definindo a prioridade atual igual a 0, por padrão, o que significa que pode ler qualquer caractere.

      virtual Promise *parseExpression(const int precedence = 0)
      {
        if(_failed) return NULL; // cut off subexpressions in case of errors
      
        _nextToken();
        if(prefixes[(uchar)_token] == 0)
        {
          this.error("Can't parse " + ShortToString(_token), __FUNCTION__);
          return NULL;
        }
        
        Promise *left = _parsePrefix();
        
        while((precedence < infixes[_token]) && !_failed)
        {
          left = _parseInfix(left, infixes[(uchar)_token]);
        }
        
        return left;
      }

A essência do método é simples: começamos a analisar a expressão lendo o seguinte caractere que deve ser um prefixo (caso contrário, dá erro) e transferimos o controle para o método _parsePrefix que pode ler qualquer construção de prefixo em sua totalidade. Depois disso, enquanto a prioridade do próximo caractere é maior do que a prioridade atual, transferimos o controle para o método _parseInfix que pode ler qualquer construção de infixo inteiramente. Por tal razão, todo o analisador consiste em apenas 3 métodos. Em certo sentido, o analisador Pratt representa uma expressão como uma hierarquia de construções de prefixo e infixo.

Observe que se o _token atual não estiver na tabela de infixos, sua prioridade será zero e o ciclo while irá parar (ou nem iniciar).

O truque do método _parseInfix é que o objeto Promise (left) atual é passado para dentro no primeiro parâmetro e se torna parte da subexpressão, enquanto a prioridade mínima permitida de operações que o método pode ler é definida no segundo parâmetro como a prioridade do token infixo atual. O método retorna um novo objeto Promise para toda a subexpressão, com a particularidade de que ele é armazenado na mesma variável (e a referência antiga para a Promise estará disponível de uma forma ou de outra através dos campos de referência do novo objeto).

Vejamos como estão organizados os métodos _parsePrefix e _parseInfix.

É lógico que _parsePrefix espera o token atual entre os prefixos permitidos e os processa com ajuda de switch. No caso do parêntese de abertura '(', é chamado o conhecido método parseExpression para ler a expressão aninhada. O parâmetro de prioridade é omitido, indicando análise a partir da prioridade zero mais baixa (afinal, há uma expressão separada entre colchetes). No caso de '!', é usado o objeto helper para obter uma negação lógica do fragmento seguinte e é novamente lido pelo método parseExpression, mas desta vez a prioridade do token atual é passada para dentro. Isso significa que o fragmento a ser negado terminará antes do primeiro caractere com uma prioridade menor que a de '!'. Por exemplo, se a expressão diz "!a*b", então parseExpression irá parar após a leitura do nome da variável 'a', porque a multiplicação '*' tem uma precedência menor do que a negação '!'. Os unários '+' e '-' são tratados de maneira semelhante, mas aqui não precisamos do objeto helper. Para '+' basta ler a subexpressão em parseExpression, já para '-' chamamos para o resultado o operador menos substituído (lembre-se de que os resultados são objetos Promise).

O método _parsePrefix classifica todos os outros caracteres com base na associação à categoria isalpha. Supõe-se que uma letra é o início de um identificador e um dígito ou ponto é o início de um número. Em todos os outros casos, o método retornará NULL.

      Promise *_parsePrefix()
      {
        Promise *result = NULL;
        switch(_token)
        {
          case '(':
            result = parseExpression();
            _match(')', ") expected!", __FUNCTION__);
            break;
          case '!':
            result = helper._negate(parseExpression(prefixes[_token]));
            break;
          case '+':
            result = parseExpression(prefixes[_token]);
            break;
          case '-':
            result = -parseExpression(prefixes[_token]);
            break;
          default:
            if(isalpha(_token))
            {
              string variable;
            
              while(isalnum(_token))
              {
                variable += ShortToString(_token);
                _nextToken();
              }
              
              if(_token == '(')
              {
                const string name = variable;
                const int index = _functionTable.index(name);
                if(index == -1)
                {
                  error("Function undefined: " + name, __FUNCTION__);
                  return NULL;
                }
                
                const int arity = _functionTable[index].arity();
                if(arity > 0 && _lookAhead() == ')')
                {
                  error("Missing arguments for " + name + ", " + (string)arity + " required!", __FUNCTION__);
                  return NULL;
                }
                
                Promise *params[];
                ArrayResize(params, arity);
                for(int i = 0; i < arity; i++)
                {
                  params[i] = parseExpression(infixes[',']);
                  if(i < arity - 1)
                  {
                    if(_token != ',')
                    {
                      _match(',', ", expected (param-list)!", __FUNCTION__);
                      break;
                    }
                  }
                }
              
                _match(')', ") expected after " + (string)arity + " arguments!", __FUNCTION__);
                
                result = helper._call(index, params);
              }
              else
              {
                return helper._variable(variable); // get index and if not found - optionally reserve the name with nan
              }
            }
            else // digits are implied, must be a number 
            {
              string number;
              if(_readNumber(number))
              {
                return helper._literal(number);
              }
            }
        }
        return result;
      }

Um identificador seguido por um parêntese '(' é interpretado como uma chamada de função. Para isso, opcionalmente é analisada a lista de argumentos (de acordo com a aridade da função) separados por vírgulas. Cada argumento é obtido chamando parseExpression com a prioridade da vírgula ','. O objeto Promise para a função ]e gerada com ajuda de helper._call(). Se não houver parênteses após o identificador, é criado o objeto Promise para a variável helper._variable().

Quando o primeiro token não é uma letra, o método _parsePrefix tenta ler o número com ajuda de _readNumber e cria para ele um Promise chamando helper._literal().

O método _parseInfix aguarda que o token atual seja um dos infixos permitidos, com a particularidade de que no primeiro parâmetro ele recebe o primeiro operando já lido no objeto Promise *left. O segundo parâmetro especifica a prioridade mínima dos tokens a serem analisados, assim que algo com uma prioridade inferior for encontrado, a subexpressão termina. A tarefa de _parseInfix é a de chamar parseExpression com prioridade precedence, para ler o operando direito, após isso é possível criar o objeto Promise para a operação binária que corresponde ao infixo.

      Promise *_parseInfix(Promise *left, const int precedence = 0)
      {
        Promise *result = NULL;
        const ushort _previous = _token;
        switch(_previous)
        {
          case '*':
          case '/':
          case '%':
          case '+':
          case '-':
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '>':
          case '<':
            if(_lookAhead() == '=')
            {
              _nextToken();
              result = new Promise((uchar)(_previous == '<' ? '{' : '}'), left, parseExpression(precedence));
            }
            else
            {
              result = new Promise((uchar)_previous, left, parseExpression(precedence));
            }
            break;
          case '=':
          case '!':
            _matchNext('=', "= expected after " + ShortToString(_previous), __FUNCTION__);
            result = helper._isEqual(left, parseExpression(precedence), _previous == '=');
            break;
          case '&':
          case '|':
            _matchNext(_previous, ShortToString(_previous) + " expected after " + ShortToString(_previous), __FUNCTION__);
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '?':
            {
              Promise *truly = parseExpression(infixes[':']);
              if(_token != ':')
              {
                _match(':', ": expected", __FUNCTION__);
              }
              else
              {
                Promise *falsy = parseExpression(infixes[':']);
                if(truly != NULL && falsy != NULL)
                {
                  result = helper._ternary(left, truly, falsy);
                }
              }
            }
          case ':':
          case ',': // just skip
            break;
          default:
            error("Can't process infix token " + ShortToString(_previous));
          
        }
        return result;
      }

É importante que o token infixo atual no início do método seja lembrado na variável _previous. Isso é assim porque a chamada de parseExpression, se for bem-sucedida, move na string a posição para outro token um número arbitrário de caracteres à direita.

Bem, embora tivéssemos considerado apenas 3 métodos com uma estrutura razoavelmente transparente, na verdade isso é todo o analisador Pratt.

Seu uso é semelhante ao do analisador ExpressionCompiler: criamos um objeto ExpressionPratt, configuramos a tabela de variáveis, executamos o método evaluate na string de expressão e obtemos na saída um Promise com uma árvore de sintaxe que pode ser calculada usando resolve().

Usar uma árvore de sintaxe, obviamente, não é a única maneira de adiar a avaliação da expressão. O próximo tipo de analisador que vamos considerar dispensa a árvore e grava o algoritmo de cálculo no chamado bytecode. Portanto, devemos primeiro nos familiarizar com essa abordagem.

Geração de Bytecode

Bytecode é uma sequência de comandos que descreve todo o algoritmo de cálculo usando uma representação binária "rápida". A criação de um bytecode pode lembrar a da uma compilação de programa, mas com a particularidade de que o resultado não contém instruções do processador, senão variáveis ou estruturas de uma linguagem aplicada que controlam uma determinada calculadora-classe. Em nosso caso, a unidade de execução será uma estrutura ByteCode.

  struct ByteCode
  {
      uchar code;
      double value;
      int index;
  
      ByteCode(): code(0), value(0.0), index(-1) {}
      ByteCode(const uchar c): code(c), value(0.0), index(-1) {}
      ByteCode(const double d): code('n'), value(d), index(-1) {}
      ByteCode(const uchar c, const int i): code(c), value(0.0), index(i) {}
      
      string toString() const
      {
        return StringFormat("%s %f %d", CharToString(code), value, index);
      }
  };

Seus campos repetem os dos objetos Promise, mas não todos, apenas o conjunto mínimo necessário para cálculos de "fluxo". Eles são de fluxo no sentido de que os comandos serão lidos e executados sequencialmente da esquerda para a direita, sem passar por nenhuma estrutura hierárquica.

O campo code contém a essência do comando (o valor corresponde aos códigos Promise), o campo, o número (constante), o campo index, o número da variável ou da função nas tabelas de variáveis ou funções, respectivamente.

Uma maneira de escrever instruções computacionais é a polonesa inversa (Reverse Polish Notation), conhecida também como postfixa. Basicamente, nela os operandos são escritos primeiro e, em seguida, o código da operação. Por exemplo, a conhecida notação infixa "a + b" se torna postfixa "a b +", já o caso mais complexo "a + b * sqrt(c)" se converte em "a b c 'sqrt' * +".

RPN é bom para bytecode porque é fácil de implementar computação com ajuda de uma pilha. Quando o programa "vê" um número ou uma referência a uma variável no fluxo de caracteres de entrada, ele coloca esse valor numa pilha. Se no fluxo de entrada for encontrado um operador ou função, o programa retira da pilha o número de valores necessário, executa a operação especificada neles e coloca o resultado de volta na pilha. No final do processo, o resultado da avaliação da expressão será o único número na pilha.

Visto que RPN descreve de forma alternativa as mesmas expressões para as quais estamos construindo árvores de sintaxe, essas duas representações podem ser convertidas uma na outra. Vamos tentar gerar um bytecode baseado na árvore Promise. Para fazer isso, adicionamos o método exportToByteCode à classe Promise.

  class Promise
  {
    ...
    public:
      void exportToByteCode(ByteCode &codes[])
      {
        if(left) left.exportToByteCode(codes);
        const int truly = ArraySize(codes);
        
        if(code == '?')
        {
          ArrayResize(codes, truly + 1);
          codes[truly].code = code;
        }
        
        if(right) right.exportToByteCode(codes);
        const int falsy = ArraySize(codes);
        if(last) last.exportToByteCode(codes);
        const int n = ArraySize(codes);
        
        if(code != '?')
        {
          ArrayResize(codes, n + 1);
          codes[n].code = code;
          codes[n].value = value;
          codes[n].index = index;
        }
        else // (code == '?')
        {
          codes[truly].index = falsy; // jump over true branch
          codes[truly].value = n;     // jump over both branches
        }
      }
      ...
  };

O método recebe como parâmetro uma matriz de estruturas ByteCode nas quais deve armazenar o conteúdo do objeto Promise atual. Primeiro, todos os nós subordinados são analisados, para isso, o método é chamado recursivamente para os ponteiros left, right, last, se eles não forem nulos. Só depois disso, quando todas as partes (operandos) são salvas, as propriedades do próprio objeto Promise são gravadas no bytecode.

Uma vez que a gramática das expressões contém uma instrução condicional, o método adicionalmente lembra o tamanho da matriz de bytecode nos pontos onde as ramificações verdadeira e falsa da instrução começam, bem como o final da expressão condicional. Isso permite gravar na estrutura de bytecode da instrução condicional na matriz, onde devemos pular durante o avaliação se a condição for verdadeira ou falsa. A ramificação das instruções para a condição verdadeira começa imediatamente após o bytecode '?', e depois que elas são executadas, precisamos ir para o deslocamento no campo value. A ramificação de instruções para uma condição falsa começa no deslocamento no campo index, imediatamente após o campo de instruções "verdadeiras".

Observe que quando avaliamos a expressão no modo de interpretação ou pela árvore sintática, ambas as ramificações da instrução condicional são calculadas antes que um de seus valores seja selecionado dependendo da condição, ou seja, uma das ramificações é considerada inativa. No caso do bytecode, pulamos as avaliações de ramificação desnecessárias.

Para converter toda a árvore de expressão em bytecode, devemos chamar exportToByteCode para o objeto raiz retornado como resultado evaluate. Por exemplo, para o analisador Pratt:

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
  
    for(int i = 0; i < ArraySize(codes); i++)
    {
      Print(i, "] ", codes[i].toString());
    }

Agora resta escrever uma função que realize as avaliações com base no bytecode. Também vamos colocá-la na classe Promise, porque os índices de variáveis e funções são usados em bytecodes e o Promise tem links para essas tabelas por padrão.

  #define STACK_SIZE 100
  
  // stack imitation
  #define push(S,V,N) S[N++] = V
  #define pop(S,N) S[--N]
  #define top(S,N) S[N-1]
  
  class Promise
  {
    ...
    public:
      static double execute(const ByteCode &codes[], VariableTable *vt = NULL, FunctionTable *ft = NULL)
      {
        if(vt) variableTable = vt;
        if(ft) functionTable = ft;
  
        double stack[]; int ssize = 0; ArrayResize(stack, STACK_SIZE);
        int jumps[]; int jsize = 0; ArrayResize(jumps, STACK_SIZE / 2);
        const int n = ArraySize(codes);
        for(int i = 0; i < n; i++)
        {
          if(jsize && top(jumps, jsize) == i)
          {
            --jsize; // fast "pop & drop"
            i = pop(jumps, jsize);
            continue;

          }
          switch(codes[i].code)
          {
            case 'n': push(stack, codes[i].value, ssize); break;
            case 'v': push(stack, variableTable[codes[i].index], ssize); break;
            case 'f':
              {
                IFunctor *ptr = functionTable[codes[i].index];
                double params[]; ArrayResize(params, ptr.arity()); int psize = 0;
                for(int j = 0; j < ptr.arity(); j++)
                {
                  push(params, pop(stack, ssize), psize);
                }
                ArrayReverse(params);
                push(stack, ptr.execute(params), ssize);
              }
              break;
            case '+': push(stack, pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '-': push(stack, -pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '*': push(stack, pop(stack, ssize) * pop(stack, ssize), ssize); break;
            case '/': push(stack, Promise::safeDivide(1, pop(stack, ssize)) * pop(stack, ssize), ssize); break;
            case '%':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, fmod(first, second), ssize);
              }
              break;
            case '!': push(stack, (double)(!pop(stack, ssize)), ssize); break;
            case '~': push(stack, (double)(-pop(stack, ssize)), ssize); break;
            case '<':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first < second), ssize);
              }
              break;
            case '>':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first > second), ssize);
              }
              break;
            case '{':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first <= second), ssize);
              }
              break;
            case '}':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first >= second), ssize);
              }
              break;
            case '&': push(stack, (double)(pop(stack, ssize) && pop(stack, ssize)), ssize); break;
            case '|':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first || second), ssize); // order is important
              }
              break;
            case '`': push(stack, _precision < fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '=': push(stack, _precision > fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '?':
              {
                const double first = pop(stack, ssize);
                if(first) // true
                {
                  push(jumps, (int)codes[i].value, jsize); // to where the entire if ends
                  push(jumps, codes[i].index, jsize);      // we jump from where true ends
                }
                else // false
                {
                  i = codes[i].index - 1; // -1 is needed because of forthcoming ++
                }
              }
              break;
            default:
              Print("Unknown byte code ", CharToString(codes[i].code));
          }
        }
        return pop(stack, ssize);
      }
      ...
  };

O trabalho com a pilha é levado a cabo por meio de macros na matriz stack, na qual um número predefinido de elementos STACK_SIZE é alocado antecipadamente. Isso é feito para acelerar as coisas, eliminando chamadas para ArrayResize ao executar operações push e pop. Um STACK_SIZE de 100 parece ser suficiente para a maioria das expressões de uma linha do mundo real. Caso contrário, haverá um excedente de pilha.

Para controlar a execução de instruções condicionais, que podem ser aninhadas, devemos usar uma pilha jumps adicional.

Todas as operações já nos são familiares graças aos códigos Promise e ao analisador Pratt discutidos acima. A única diferença é o uso generalizado da pilha como uma fonte de operandos e um local para armazenar um resultado intermediário. Todo o bytecode é executado num ciclo, numa única chamada de método, sem recursão.

Com esta funcionalidade, já podemos calcular expressões a partir do bytecode obtido exportando árvores de sintaxe desde o analisador Pratt ou ExpressionCompiler.

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
    double r = Promise::execute(codes);

Um pouco mais tarde, ao testar todos os analisadores, compararemos o desempenho das avaliações com base numa árvore e bytecode.

Mas o objetivo principal da introdução de bytecodes foi possibilitar a implementação de outro tipo de analisador, a da estação de triagem.

Analisador estação de triagem (ExpressionShuntingYard)

O analisador estação de triagem (Shunting Yard) deve seu nome à maneira como divide o fluxo de tokens de saída em aqueles que podem ser logo pulados na saída e em aqueles que devem ser colocados numa pilha especial, de onde são recuperados os tokens de acordo com regras particulares relacionadas com a combinação de precedências dos tokens (do que vai na pilha e do que vem a seguir no fluxo de entrada). O analisador converte a expressão de entrada em notação polonesa inversa (RPN na sigla em inglês). Isso é conveniente para nós, porque podemos gerar bytecode imediatamente, ignorando a árvore de sintaxe. Como podemos ver na descrição geral, a maneira como se classifica é baseada na precedência dos operadores, por isso dado analisador é aparentado com o Pratt e será implementado como uma classe-herdeira de ExpressionPrecedence.

Dado analisador pertence aos da classe dos ascendentes (bottom-up).

O algoritmo, em termos gerais, é o seguinte (aqui não tocamos nuances relacionadas com a associação à direita, uma vez que não temos complicações associadas à instrução condicional):

  Num ciclo, lemos o seguinte token da expressão (até que termine)
    se o token for uma operação unária, vamos salvá-lo na pilha
    se for um número, vamos gravá-lo em bytecode
    se for uma variável, vamos escrever seu índice em bytecode
    se for um identificador de função, salvamos seu índice na pilha
    se o token for um operador infixo
      até que o topo da pilha não seja '(' e ((precedência do operador no topo da pilha >= precedência do operador atual) ou no topo houver uma função)
        vamos transferir o topo da pilha para o bytecode de saída
      salvamos o operador na pilha
    se o token for '(', vamos armazená-lo no pilha
    se o token for ')'
      até que no topo não haja '('
        vamos transferir o topo da pilha para o bytecode de saída
      se no topo da pilha houver '(', devemos remover e descartar
  se na pilha restarem tokens, vamos transferi-los para o bytecode de saída

Obviamente, a implementação desse analisador exige apenas um método.

Abaixo é mostrada toda a classe ExpressionShuntingYard. O método público principal convertToByteCode inicia a analise que é realizado em exportToByteCode. Como nossas expressões suportam instruções condicionais, usamos uma chamada recursiva para exportToByteCode para analisar suas subexpressões.

  class ExpressionShuntingYard: public ExpressionPrecedence
  {
    public:
      ExpressionShuntingYard(const string vars = NULL): ExpressionPrecedence(vars) { }
      ExpressionShuntingYard(VariableTable &vt): ExpressionPrecedence(vt) { }
  
      bool convertToByteCode(const string expression, ByteCode &codes[])
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          exportToByteCode(codes);
        }
        return !_failed;
      }
  
    protected:
      template<typename T>
      static void _push(T &stack[], T &value)
      {
        const int n = ArraySize(stack);
        ArrayResize(stack, n + 1, STACK_SIZE);
        stack[n] = value;
      }
  
      void exportToByteCode(ByteCode &output[])
      {
        ByteCode stack[];
        int ssize = 0;
        string number;
        uchar c;
        
        ArrayResize(stack, STACK_SIZE);
        
        const int previous = ArraySize(output);
        
        while(_nextToken() && !_failed)
        {
          if(_token == '+' || _token == '-' || _token == '!')
          {
            if(_token == '-')
            {
              _push(output, ByteCode(-1.0));
              push(stack, ByteCode('*'), ssize);
            }
            else if(_token == '!')
            {
              push(stack, ByteCode('!'), ssize);
            }
            continue;
          }
          
          number = "";
          if(_readNumber(number)) // if a number was read, _token has changed
          {
            _push(output, ByteCode(StringToDouble(number)));
          }
          
          if(isalpha(_token))
          {
            string variable;
            while(isalnum(_token))
            {
              variable += ShortToString(_token);
              _nextToken();
            }
            if(_token == '(')
            {
              push(stack, ByteCode('f', _functionTable.index(variable)), ssize);
            }
            else // variable name
            {
              int index = -1;
              if(CheckPointer(_variableTable) != POINTER_INVALID)
              {
                index = _variableTable.index(variable);
                if(index == -1)
                {
                  if(_variableTable.adhocAllocation())
                  {
                    index = _variableTable.add(variable, nan);
                    _push(output, ByteCode('v', index));
                    error("Unknown variable is NaN: " + variable, __FUNCTION__, true);
                  }
                  else
                  {
                    error("Unknown variable : " + variable, __FUNCTION__);
                  }
                }
                else
                {
                  _push(output, ByteCode('v', index));
                }
              }
            }
          }
          
          if(infixes[_token] > 0) // operator, including least significant '?'
          {
            while(ssize > 0 && isTop2Pop(top(stack, ssize).code))
            {
              _push(output, pop(stack, ssize));
            }
            
            if(_token == '?' || _token == ':')
            {
              if(_token == '?')
              {
                const int start = ArraySize(output);
                _push(output, ByteCode((uchar)_token));
                exportToByteCode(output); // subexpression truly, _token has changed
                if(_token != ':')
                {
                  error("Colon expected, given: " + ShortToString(_token), __FUNCTION__);
                  break;
                }
                output[start].index = ArraySize(output);
                exportToByteCode(output); // subexpression falsy, _token has changed
                output[start].value = ArraySize(output);
                if(_token == ':')
                {
                  break;
                }
              }
              else
              {
                break;
              }
            }
            else
            {
              if(_token == '>' || _token == '<')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '<' ? '{' : '}')), ssize);
                  _nextToken();
                }
                else
                {
                  push(stack, ByteCode((uchar)_token), ssize);
                }
              }
              else if(_token == '=' || _token == '!')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '!' ? '`' : '=')), ssize);
                  _nextToken();
                }
              }
              else if(_token == '&' || _token == '|')
              {
                _matchNext(_token, ShortToString(_token) + " expected after " + ShortToString(_token), __FUNCTION__);
                push(stack, ByteCode((uchar)_token), ssize);
              }
              else if(_token != ',')
              {
                push(stack, ByteCode((uchar)_token), ssize);
              }
            }
          }
          
          if(_token == '(')
          {
            push(stack, ByteCode('('), ssize);
          }
          else if(_token == ')')
          {
            while(ssize > 0 && (c = top(stack, ssize).code) != '(')
            {
              _push(output, pop(stack, ssize));
            }
            if(c == '(') // must be true unless it's a subexpression (then 'c' can be 0)
            {
              ByteCode disable_warning = pop(stack, ssize);
            }
            else
            {
              if(previous == 0)
              {
                error("Closing parenthesis is missing", __FUNCTION__);
              }
              return;
            }
          }
        }
        
        while(ssize > 0)
        {
          _push(output, pop(stack, ssize));
        }
      }
      
      bool isTop2Pop(const uchar c)
      {
        return (c == 'f' || infixes[c] >= infixes[_token]) && c != '(' && c != ':';
      }
  };

O uso co analisador de classificação é diferente dos tipos anteriores. Para fazer isso, é excluído o passo para obter uma árvore com ajuda da chamada de evaluate. Em vez disso, o método convertToByteCode retorna imediatamente o bytecode para a expressão transferida.

  ExpressionShuntingYard sh;
  sh.variableTable().adhocAllocation(true);
  
  ByteCode codes[];
  bool success = sh.convertToByteCode("x + y", codes);
  if(success)
  {
    sh.variableTable().assign("x=10;y=20");
    double r = Promise::execute(codes);
  }

Assim concluímos a visão geral dos diferentes tipos de analisadores. O diagrama de classes fica algo assim.

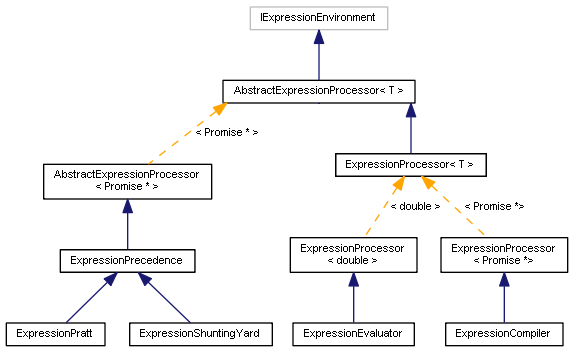
Diagrama de classes de analisadores

Para testar e comparar os diferentes analisadores, criaremos um script de teste posteriormente.

Para tornar a tarefa mais aplicável ao trading, daremos o toque final e mostraremos como se pode complementar a lista de funções embutidas usando indicadores técnicos.

Incorporando indicadores em expressões como funções

Ao calcular expressões, um trader pode precisar de informações específicas, como o tamanho do saldo, o número de posições, leituras de indicadores, etc. Tudo isso pode ser disponibilizado dentro de expressões, expandindo a lista de funções integradas. Para mostrar essa abordagem, vamos adicionar um indicador de média móvel ao conjunto de recursos.

O mecanismo para incorporar um indicador numa expressão usa como fundamento os functores considerados anteriormente e, portanto, é implementado como uma classe derivada de AbstractFunc. Lembre-se de que todas as instâncias de classes da família AbstractFunc são automaticamente registradas em AbstractFuncStorage e ficam disponíveis na tabela de funções.

  class IndicatorFunc: public AbstractFunc
  {
    public:
      IndicatorFunc(const string n, const int a = 1): AbstractFunc(n, a)
      {
        // the single argument is the bar number,
        // two arguments are bar number and buffer index
      }
      static IndicatorFunc *create(const string name);
  };

Uma característica dos indicadores no MetaTrader 5 é que eles requerem dois estágios para serem aplicados: primeiro, o indicador precisa ser criado (obter seu descritor) e só então solicitar dados dele. Quanto ao processamento de expressões, a primeira etapa deve ser executada durante a análise e a segunda, durante a avaliação. Visto que a criação de um indicador requer a especificação de todos os parâmetros, eles devem ser codificados no nome e não passados nos parâmetros da função. Por exemplo, se criássemos a função "iMA" com parâmetros (período, método, tipo_preço), na fase de análise receberíamos apenas o seu nome, enquanto a definição de parâmetros seria adiada até a fase de execução, quando é tarde demais para criar um indicador (uma vez que é hora de ler seus dados).

Nesse sentido, optou-se por reservar para o indicador de média móvel todo um conjunto de nomes formados assim: método_preço_período. Aqui, o método é uma das palavras importantes da enumeração ENUM_MA_METHOD (SMA, EMA, SMMA, LWMA), o preço é um dos tipos de preço da enumeração ENUM_APPLIED_PRICE (CLOSE, OPEN, HIGH, LOW, MEDIAN, TYPICAL, WEIGHTED), o período é um número inteiro. Assim, o uso da função "SMA_OPEN_10" deve gerar uma média móvel simples de acordo com os preços de abertura com período 10.

A aridade da função do indicador é igual a 1 por padrão. O número da barra é transferido como parâmetro único. Se a aridade for definida como 2, o segundo parâmetro deverá indicar o número do buffer. Não precisamos disso para a média móvel.

A classe MAIndicatorFunc é responsável por criar instâncias de indicadores com parâmetros correspondentes aos nomes solicitados.

  class MAIndicatorFunc: public IndicatorFunc
  {
    protected:
      const int handle;
      
    public:
      MAIndicatorFunc(const string n, const int h): IndicatorFunc(n), handle(h) {}
      
      ~MAIndicatorFunc()
      {
        IndicatorRelease(handle);
      }
      
      static MAIndicatorFunc *create(const string name) // SMA_OPEN_10(0)
      {
        string parts[];
        if(StringSplit(name, '_', parts) != 3) return NULL;
        
        ENUM_MA_METHOD m = -1;
        ENUM_APPLIED_PRICE t = -1;
        
        static string methods[] = {"SMA", "EMA", "SMMA", "LWMA"};
        for(int i = 0; i < ArraySize(methods); i++)
        {
          if(parts[0] == methods[i])
          {
            m = (ENUM_MA_METHOD)i;
            break;
          }
        }
  
        static string types[] = {"NULL", "CLOSE", "OPEN", "HIGH", "LOW", "MEDIAN", "TYPICAL", "WEIGHTED"};
        for(int i = 1; i < ArraySize(types); i++)
        {
          if(parts[1] == types[i])
          {
            t = (ENUM_APPLIED_PRICE)i;
            break;
          }
        }
        
        if(m == -1 || t == -1) return NULL;
        
        int h = iMA(_Symbol, _Period, (int)StringToInteger(parts[2]), 0, m, t);
        if(h == INVALID_HANDLE) return NULL;
        
        return new MAIndicatorFunc(name, h);
      }
      
      double execute(const double &params[]) override
      {
        const int bar = (int)params[0];
        double result[1] = {0};
        if(CopyBuffer(handle, 0, bar, 1, result) != 1)
        {
          Print("CopyBuffer error: ", GetLastError());
        }
        return result[0];
      }
  };

O método de fábrica create analisa o nome passado a ele, extrai parâmetros e cria um indicador com um descritor handle. O valor do indicador é obtido no método padrão dos functores, execute.

Como no futuro à função podem ser adicionados outros indicadores, a classe IndicatorFunc tem um ponto de entrada para solicitações de quaisquer indicadores, o método create. Até agora, ele contém apenas um redirecionamento para a chamada MAIndicatorFunc::create().

  static IndicatorFunc *IndicatorFunc::create(const string name)
  {
    // TODO: support more indicator types, dispatch calls based on the name
    return MAIndicatorFunc::create(name);
  }

Este método deve ser chamado a partir da tabela de funções, portanto, iremos complementar a classe FunctionTable.

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      ...
      #ifdef INDICATOR_FUNCTORS
      virtual int index(const string name) override
      {
        int i = _table.getIndex(name);
        if(i == -1)
        {
          i = _table.getSize();
          IFunctor *f = IndicatorFunc::create(name);
          if(f)
          {
            Table<IFunctor *>::add(name, f);
            return i;
          }
          return -1;
        }
        return i;
      }
      #endif
  };

A nova versão do método index tenta encontrar um indicador adequado se o nome passado não for encontrado na lista das 25 funções integradas. Para anexar esta funcionalidade adicional, precisamos definir a macro INDICATOR_FUNCTORS.

Com esta opção habilitada, podemos calcular, por exemplo, a seguinte expressão: "EMA_OPEN_10(0)/EMA_OPEN_21(0)".

Na prática, os parâmetros dos indicadores chamados são frequentemente movidos para as configurações. Isso significa que eles devem, de alguma forma, serem embutidos dinamicamente na string de expressão. Para simplificar essa tarefa, a classe AbstractExpressionProcessor oferece suporte a uma opção especial de pré-processamento de expressão. Não tocamos essa nuance por questões de brevidade. A inclusão do pré-processamento é controlada pelo segundo parâmetro opcional do método evaluate (por padrão, false, pré-processamento desativado).

O princípio de operação desta opção é o seguinte. Numa expressão, é possível entre chaves especificar o nome de variável que será substituído pelo valor da variável antes da análise. Por exemplo, se a expressão for igual a "EMA_TYPICAL_{Period}(0)" e na tabela de variáveis houver uma variável Period com valor 11, será analisada a expressão "EMA_TYPICAL_11(0)".

Para testar as funções-indicadores, criaremos posteriormente um Expert Advisor, cujos sinais de negociação serão gerados com base em expressões calculadas, incluindo a média móvel.

Mas primeiro precisamos ter certeza de que os próprios analisadores estão funcionando corretamente.

Script de teste (ExpresSParserS)

O script de teste ExpresSParserS.mq5 inclui um conjunto de testes funcionais, bem como uma medição da velocidade de computação para 4 tipos de analisadores, além disso tem uma demonstração de alguns modos, saída de uma árvore de sintaxe e bytecode para o log, uso de indicadores como funções integradas.

Entre os testes funcionais, há tanto expressões corretas como deliberadamente errôneas (variáveis não declaradas, divisão por zero na etapa de cálculo, etc.). Pode-se dizer que o teste é correto se os resultados reais corresponderem com os esperados, o que implica que os erros também podem ser "corretos". Por exemplo, assim fica o log de teste do analisador Pratt.

  Running 19 tests on ExpressionPratt* …
  1 passed, ok: a > b ? b > c ? 1 : 2 : 3 = 3.0; expected = 3.0
  2 passed, ok: 2 > 3 ? 2 : 3 > 4 ? 3 : 4 = 4.0; expected = 4.0
  3 passed, ok: 4 > 3 ? 2 > 4 ? 2 : 4 : 3 = 4.0; expected = 4.0
  4 passed, ok: (a + b) * sqrt(c) = 8.944271909999159; expected = 8.944271909999159
  5 passed, ok: (b == c) > (a != 1.5) = 0.0; expected = 0.0
  6 passed, ok: (b == c) >= (a != 1.5) = 1.0; expected = 1.0
  7 passed, ok: (a > b) || sqrt(c) = 1.0; expected = 1.0
  8 passed, ok: (!1 != !(b - c/2)) = 1.0; expected = 1.0
  9 passed, ok: -1 * c == -sqrt(-c * -c) = 1.0; expected = 1.0
  10 passed, ok: pow(2, 5) % 5 = 2.0; expected = 2.0
  11 passed, ok: min(max(a,b),c) = 2.5; expected = 2.5
  12 passed, ok: atan(sin(0.5)/cos(0.5)) = 0.5; expected = 0.5
  13 passed, ok: .2 * .3 + .1 = 0.16; expected = 0.16
  14 passed, ok: (a == b) + (b == c) = 0.0; expected = 0.0
  15 passed, ok: -(a + b) * !!sqrt(c) = -4.0; expected = -4.0
  16 passed, ok: sin ( max ( 2 * 1.5, 3 ) / 3 * 3.14159265359 ) = -2.068231111547469e-13; expected = 0.0
  lookUpVariable error: Variable is undefined: _1c @ 7: 1 / _1c^
  17 passed, er: 1 / _1c = nan; expected = nan
  safeDivide error: Error : Division by 0! @ 15: 1 / (2 * b - c)^
  18 passed, er: 1 / (2 * b - c) = inf; expected = inf
  19 passed, ok: sqrt(b-c) = -nan(ind); expected = -nan(ind)
  19 tests passed of 19
  17 for correct expressions, 2 for invalid expressions

Aqui vemos que todos os 19 testes foram realizados com êxito e que duas vezes foram recebidos erros esperados.

A velocidade é medida apenas para vários cálculos num ciclo. No caso do intérprete, isto inclui a etapa de análise da expressão, uma vez que isso é feito com todos os cálculos e, para todos os outros tipos de analisadores, o estágio de análise está "fora dos colchetes". Analisar uma expressão uma dura aproximadamente o mesmo tempo para todos os métodos. Aqui está um dos resultados medidos de 10.000 ciclos (microssegundos).

  >>> Performance tests (timing per method)
  Evaluation: 104572
  Compilation: 25011
  Pratt bytecode: 23738
  Pratt: 24967
  ShuntingYard: 23147

Como esperado, as expressões previamente "compiladas" são avaliadas várias vezes mais rápido do que as interpretadas. Também podemos concluir que os cálculos mais rápidos são baseados em bytecode e que o tipo de analisador para obtenção do bytecode não desempenha um papel especial, pois podemos usar tanto Pratt quanto classificação. A escolha do analisador pode ser feita com base numa avaliação subjetiva de quão compreensível é o algoritmo e de quão fácil se adapta às nossas tarefas, como expandir a sintaxe ou integrar com desenvolvimentos em andamento.

Usando expressões para configurar sinais do EA (ExprBot)

As expressões podem ser usadas em robôs para gerar sinais de negociação. Isso dá mais flexibilidade do que apenas alterar parâmetros. Graças a uma lista expansível de funções, os recursos praticamente não diferem do que a MQL permite. Adicionalmente, não precisamos compilar tudo isso. Além disso, é fácil ocultar operações de rotina dentro de functores já prontos. Assim, o programador dá ao usuário um equilíbrio entre flexibilidade e complexidade de configuração do produto.

Visto que dispomos de um conjunto de indicadores de média móvel, vamos construir um sistema de negociação baseado neles (embora nada nos impeça de integrar nas expressões funções de tempo, gerenciamento de riscos, preços de tick, etc.).

Para mostrar o princípio, vamos criar um Expert Advisor simples, ExprBot. Nas variáveis de entrada SignalBuy e SignalSell, serão inseridas expressões com as condições de realização de compras e vendas, respectivamente. Para uma estratégia na interseção de duas MAs, podem ser propostas as seguintes fórmulas.

  #define INDICATOR_FUNCTORS
  #include <ExpresSParserS/ExpressionCompiler.mqh>
  
  input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
  input string Variables = "Threshold=0.01";
  input int Fast = 10;
  input int Slow = 21;

O limite é estabelecido como uma constante apenas para mostrar a entrada de variáveis arbitrárias. Os parâmetros com períodos de média Fast e Slow são destinados à inserção em expressões antes de analisá-los, como um fragmento do nome do indicador.

Como há dois sinais, instanciamos dois analisadores descendentes recursivos. Em princípio, era possível pegar um, mas em duas expressões as tabelas de variáveis podem diferir potencialmente, e, portanto, seria necessário mudar este contexto antes de cada cálculo.

  ExpressionCompiler ecb(Variables), ecs(Variables);
  Promise *p1, *p2;

No manipulador OnInit, salvamos os parâmetros nas tabelas de variáveis e construímos árvores de sintaxe.

  int OnInit()
  {
    ecb.variableTable().set("Fast", Fast);
    ecb.variableTable().set("Slow", Slow);
    p1 = ecb.evaluate(SignalBuy, true);
    if(!ecb.success())
    {
      Print("Syntax error in Buy signal:");
      p1.print();
      return INIT_FAILED;
    }
    ecs.variableTable().set("Fast", Fast);
    ecs.variableTable().set("Slow", Slow);
    p2 = ecs.evaluate(SignalSell, true);
    if(!ecs.success())
    {
      Print("Syntax error in Sell signal:");
      p2.print();
      return INIT_FAILED;
    }
    
    return INIT_SUCCEEDED;
  }

A estratégia se encaixa num pequeno manipulador OnTick (omitimos funções auxiliares; também é preciso anexar a biblioteca MT4Orders).

  #define _Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
  #define _Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)
  
  void OnTick()
  {
    if(!isNewBar()) return;
    
    bool buy = p1.resolve();
    bool sell = p2.resolve();
    
    if(buy && sell)
    {
      buy = false;
      sell = false;
    }
    
    if(buy)
    {
      OrdersCloseAll(_Symbol, OP_SELL);
      if(OrdersTotalByType(_Symbol, OP_BUY) == 0)
      {
        OrderSend(_Symbol, OP_BUY, Lot, _Ask, 100, 0, 0);
      }
    }
    else if(sell)
    {
      OrdersCloseAll(_Symbol, OP_BUY);
      if(OrdersTotalByType(_Symbol, OP_SELL) == 0)
      {
        OrderSend(_Symbol, OP_SELL, Lot, _Bid, 100, 0, 0);
      }
    }
    else
    {
      OrdersCloseAll();
    }
  }

Ambas as expressões são calculadas com base nas "promessas" p1 e p2. O resultado é os dois sinalizadores Buy e Sell, que iniciam a abertura ou fechamento de uma posição nas direções correspondentes. O código MQL garante que possa ser aberta apenas uma posição por vez, e se os sinais se contradizerem (isso é possível se as expressões forem alteradas para algo mais complexo do que um sistema de reversão, ou se por engano o limite for definido como negativo), qualquer posição ativa será fechada. As condições para sinais podem ser editadas conforme desejado dentro dos limites do que é definido nas funções dos analisadores.

Se executarmos o Expert Advisor no testador, provavelmente teremos um relatório com indicadores abaixo da média, mas algo mais é importante é que o trading estará sendo realizado e é gerenciado por analisadores. Eles não proporcionam sistemas lucrativos prontos, mas, sim, uma ferramenta adicional para buscá-los.

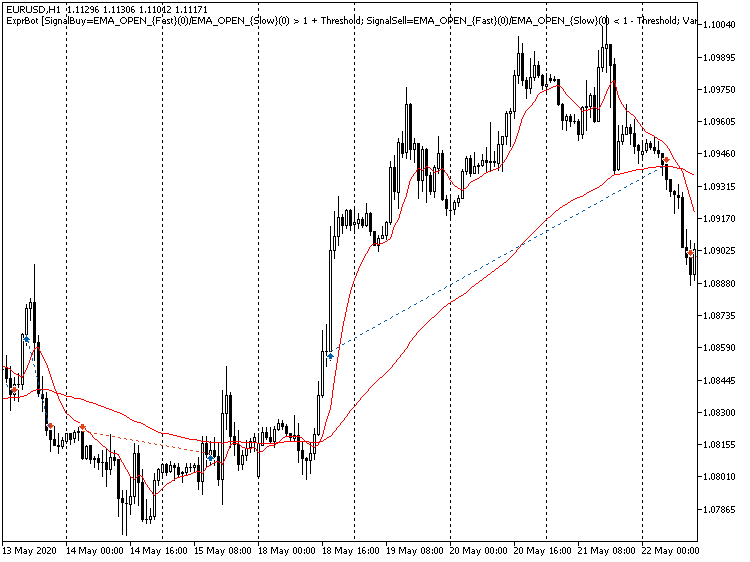
Exemplo de negociação usando sinais calculados por expressões

Fim do artigo

Neste artigo (em duas partes), examinamos 4 tipos de analisadores, comparamos seus recursos e implementamos classes prontas para serem incorporadas a programas em linguagem MQL. Todos os analisadores usam a mesma gramática com as operações matemáticas mais populares e 25 funções. Se necessário, a gramática pode ser expandida, complementado a lista de operadores suportados, adicionando novas funções integradas aplicáveis (indicadores, preços, estatísticas financeiras) e estruturas sintáticas (em particular, matrizes e funções para seu processamento).

Esta abordagem permite separar de maneira mais flexível configurações e código MQL imutável. Poder personalizar algoritmos através da edição de expressões nos parâmetros de entrada parece ser mais fácil para os usuários finais do que ter de aprender os fundamentos da programação em MQL, a fim de localizar o fragmento necessário, editá-lo em conformidade com todas as convenções e lidar com possíveis erros de compilação. Do ponto de vista dos autores de programas MQL, o suporte para análise e avaliação de expressões promete outras vantagens, em particular, pode, se bem trabalhado, ser transformado no conceito de "script acima de MQL", o que torna possível se livrar de bibliotecas e versionamento do compilador MQL.