
Deep Neural Networks (Part VIII). Increasing the classification quality of bagging ensembles
Contents
- Introduction
- Preparing Initial Data
- Processing noise samples in the pretrain subset
- Training ensembles of neural network classifiers on denoised initial data and calculating continuous predictions of neural networks on test subsets
- Determining the thresholds for the obtained continuous predictions, converting them into class labels, and calculating metrics for neural networks
- Testing ensembles
- Optimizing hyperparameters of ensembles of neural network classifiers
- Optimizing postprocessing hyperparameters
- Combining several best ensembles into a superensemble as well as their outputs
- Analyzing experimental results
- Conclusion
- Attachments
Introduction
In the previous two articles (1, 2), we created an ensemble of ELM neural network classifiers. That time we discussed how the classification quality could be improved. Among the many possible solutions, two were chosen: reduce the impact of noise samples and select the optimal threshold, by which the continuous predictions of the ensemble's neural networks are converted into class labels. In this article, I propose to experimentally test how the classification quality is affected by:
- data denoising methods,
- threshold types,
- optimization of hyperparameters the ensemble's neural networks and postprocessing.
Then compare the quality of classification obtained by averaging and by a simple majority voting of the superensemble composed of the best ensembles following the optimization results. All computations are performed in the R 3.4.4 environment.
1. Preparing Initial Data
To prepare the initial data, we will use the scripts described previously.
In the first block (Library), load the necessary functions and libraries.
In the second block (prepare), using the quotes with timestamps passed from the terminal, calculate the indicator values (in this case, these are digital filters) and additional variables based on OHLC. Combine this data set into dataframe dt. Then define the parameters of outliers in these data and impute them. Then define the normalization parameters and normalize the data. We get the resulting set of input data DTcap.n.
In the third block (Data X1), generate two sets:
- data1 — contains all 13 indicators with the Data timestamps and the Class target;
- X1 — the same set of predictors but without a timestamp. The target is converted to a numeric value (0, 1).
In the fourth block (Data X2), also generate two sets:
- data2 — contains 7 predictors and a timestamp (Data, CO, HO, LO, HL, dC, dH, dL);
- Х2 — the same predictors but without a timestamp.
#--1--Library------------- patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/" source(file = paste0(patch,"importar.R")) source(file = paste0(patch,"Library.R")) source(file = paste0(patch,"FunPrepareData_VII.R")) source(file = paste0(patch,"FUN_Stacking_VIII.R")) import_fun(NoiseFiltersR, GE, noise) #--2-prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign", preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) DTcap.n <- NormData(DTcap, preproc = preproc) }, env) #--3-Data X1------------- evalq({ subset <- qc(pretrain, train, test, test1) foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 names(data1) <- subset X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 names(X1) <- subset }, env) #--4-Data-X2------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 names(data2) <- subset X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 names(X2) <- subset rm(dt, DT, pre.outl, DTcap, meth, preproc) }, env)
In the fifth block (bestF), sort the predictors of the Х1 set in ascending order of their importance (orderX1). Select those of them with the coefficient above 0.5 (featureX1). Print the coefficients and names of the selected predictors.
#--5--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") -> rx1 rx1$stopri[ ,1] -> orderX1 featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% dp$select(V1) %>% unlist() %>% unname() }, env) print(env$rx1$stopri) [,1] [,2] [1,] 6 1.0423206 [2,] 12 1.0229287 [3,] 7 0.9614459 [4,] 10 0.9526798 [5,] 5 0.8884596 [6,] 1 0.8055126 [7,] 3 0.7959655 [8,] 11 0.7594309 [9,] 8 0.6960105 [10,] 2 0.6626440 [11,] 4 0.4905196 [12,] 9 0.3554887 [13,] 13 0.2269289 colnames(env$X1$pretrain$x)[env$featureX1] [1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl" [10] "stlm"
The same calculations are performed for the second data set Х2. We obtain orderX2 and featureX2.
evalq({
orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx2
rx2$stopri[ ,1] -> orderX2
featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
[,1] [,2]
[1,] 1 1.6650259
[2,] 5 1.6636689
[3,] 3 0.7751799
[4,] 2 0.7751351
[5,] 6 0.5692846
[6,] 7 0.5496889
[7,] 4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL"
This completes the preparation of the initial data for the experiments. We have prepared two data sets X1/data1, X2/data2 and predictors orderX1, orderX2 ranked by importance. All the above scripts are located in the Prepare_VIII.R file.
2. Processing noise samples in the pretrain subset
Many authors of articles, including myself, devoted their publications to the filtering of noise predictors. Here I propose to explore another, equally important, but less used feature — the identification and processing of noise samples in data sets. So why are some examples in data sets considered noise and what methods can be used to process them? I will try to explain.
Thus, we are faced with the task of classification, while we have a training set of predictors and a target. The target is considered to correspond well to the internal structure of the training set. But in reality, the data structure of the predictors set is much more complicated than the proposed structure of the target. It turns out that the set contains examples that correspond to the target well, while there are some that do not correspond to it at all, greatly distorting the model when learning. As a result, this leads to a decrease in the quality of the model classification. The approaches to identifying and processing the noise samples have already been considered in detail. Here we check how the classification quality is affected by three processing methods:
- correction of the mistakenly labeled examples;
- removing them from the set;
- allocating them to a separate class.
The noise samples will be identified and processed using the NoiseFiltersR::GE() function. It looks for the noise samples and modifies their labels (corrects erroneous labeling). Examples that cannot be relabeled are removed. The identified noise samples can also be removed from the set manually, or moved to a separate class, assigning a new label to them. All the calculations above are performed on the 'pretrain' subset, since it will be used for training the ensemble. See the result of the function:
#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
out <- noise(x = data1[[1]] %>% dp$select(-Data))
summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset
Call:
GE(x = data1[[1]] %>% dp$select(-Data))
Parameters:
k: 5
kk: 3
Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)
Explicit indexes for removed instances:
.......
Output structure of the out function:
> str(env$out) List of 7 $ cleanData :'data.frame': 4001 obs. of 14 variables: ..$ ftlm : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ... ..$ stlm : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ... ..$ rbci : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ... ..$ pcci : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... ..$ fars : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ... ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ... ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ... ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ... ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ... ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ... ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ... ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ... $ remIdx : int(0) $ repIdx : int [1:819] 16 27 30 31 32 34 36 38 46 58 ... $ repLab : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ... $ parameters:List of 2 ..$ k : num 5 ..$ kk: num 3 $ call : language GE(x = data1[[1]] %>% dp$select(-Data)) $ extraInf : NULL - attr(*, "class")= chr "filter"
Where:
- out$cleanData — the data set after correcting the labeling of the noise samples,
- out$remIdx — indexes of the removed samples (none in our example),
- out$repIdx — indexes of the samples with targets relabeled,
- out$repLab — new labels of these noise samples. Thus, we can remove them from the set or assign a new label to them using out$repIdx.
Once the indexes of the noise samples are determined, prepare four data sets for training the ensembles combined into the denoiseX1pretrain structure.
- denoiseX1pretrain$origin — the original pretraining set;
- denoiseX1pretrain$repaired — data set with the labeling of the noise samples corrected;
- denoiseX1pretrain$removed — data set with the noise samples removed;
- denoiseX1pretrain$relabeled — data set with the noise samples assigned a new label (i.e., the target now has three classes).
#--2-Data Xrepair-------------
#library(NoiseFiltersR)
evalq({
out <- noise(x = data1$pretrain %>% dp$select(-Data))
Yrelab <- X1$pretrain$y
Yrelab[out$repIdx] <- 2L
X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data)
denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x, y = X1$pretrain$y),
repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>%
as.numeric() %>% subtract(1)),
removed = list(x = X1rem %>% dp$select(-Class),
y = X1rem$Class %>% as.numeric() %>% subtract(1)),
relabeled = list(x = X1$pretrain$x, y = Yrelab))
rm(out, Yrelab, X1rem)
}, env)
The subsets denoiseX1pretrain$origin|repaired|relabeled have the identical predictors х, but the target у is different in every set. Let us have a look at their structure:
#------------------------- env$denoiseX1pretrain$repaired$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$relabeled$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$repaired$y %>% table() . 0 1 1888 2113 env$denoiseX1pretrain$removed$y %>% table() . 0 1 1509 1673 env$denoiseX1pretrain$relabeled$y %>% table() . 0 1 2 1509 1673 819
Since the number of samples in the set denoiseX1pretrain$removed has changed, let us check how the significance of the predictors has changed:
evalq({
orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(),
type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx1rem
rx1rem$stopri[ ,1] -> orderX1rem
featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(),
rx1rem$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
[,1] [,2]
[1,] 6 1.0790642
[2,] 12 1.0320772
[3,] 7 0.9629750
[4,] 10 0.9515987
[5,] 5 0.8426669
[6,] 1 0.8138830
[7,] 3 0.7934568
[8,] 11 0.7682185
[9,] 8 0.6720211
[10,] 2 0.6355753
[11,] 4 0.5159589
[12,] 9 0.3670544
[13,] 13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl"
[10] "stlm" "pcci"
The order and composition of the best predictors has changed. This will need to be considered when training ensembles.
So, we have 4 subsets ready: denoiseX1pretrain$origin, repaired, removed, relabeled. They will be used for training the ELM ensembles. Scripts for denoising the data are located in the Denoise.R file. The structure of the initial data Х1 and denoiseX1pretrain looks as follows:

Fig. 1. The structure of the initial data.
3. Training ensembles of neural network classifiers on denoised initial data and calculating continuous predictions of neural networks on test subsets
Let us write a function for training the ensemble and receiving predictions which will later serve as the input data for the trainable combiner in the stacking ensemble.
Such calculations have already been performed in the previous article, therefore, their details will not be discussed. In short:
- in block 1 (Input), define the constants;
- in block 2 (createEns), define the function CreateEns(), that would create an ensemble of individual neural network classifiers with constant parameters and reproducible initialization;
- in block 3 (GetInputData), the GetInputData() function calculates the predictions of three subsets Х1$ train/test/test1 using the ensemble Ens.
#--1--Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 r = 7L SEED <- 12345 #--2-createENS---------------------- createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){ Xtrain <- X[ , featureX1] k <- 1 rng <- RNGseq(n, SEED) #---creste Ensemble--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #--3-GetInputData -FUN----------- GetInputData <- function(Ens, X, Y){ #---predict-InputPretrain-------------- Xtrain <- X[ ,featureX1] k <- 1 rng <- RNGseq(n, SEED) #---create Ensemble--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 predict(Ens[[i]], newdata = Xtrain[-idx, ]) } %>% unname() -> InputPretrain #---predict-InputTrain-- Xtest <- X1$train$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> InputTrain #[ ,n] #---predict--InputTest---- Xtest1 <- X1$test$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X1$test1$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputPretrain = InputPretrain, InputTrain = InputTrain, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
We already have the denoiseX1pretrain set with four groups of data for training ensembles: original (origin), with corrected labeling (repaired), with removed (removed) and relabeled (relabeled) noise samples. After training the ensemble on each of these groups of data, we obtain four ensembles. Using these ensembles with the GetInputData() function, we obtain four groups of predictions in three subsets: train, test and test1. Below are the scripts separately for each ensemble in the expanded form (only for debugging and ease of understanding).
#---4--createEns--origin-------------- evalq({ Ens.origin <- vector(mode = "list", n) res.origin <- vector("list", 4) x <- denoiseX1pretrain$origin$x %>% as.matrix() y <- denoiseX1pretrain$origin$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin }, env) #---4--createEns--repaired-------------- evalq({ Ens.repaired <- vector(mode = "list", n) res.repaired <- vector("list", 4) x <- denoiseX1pretrain$repaired$x %>% as.matrix() y <- denoiseX1pretrain$repaired$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.repaired GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired }, env) #---4--createEns--removed-------------- evalq({ Ens.removed <- vector(mode = "list", n) res.removed <- vector("list", 4) x <- denoiseX1pretrain$removed$x %>% as.matrix() y <- denoiseX1pretrain$removed$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed GetInputData(Ens = Ens.removed, X = x, Y = y) -> res.removed }, env) #---4--createEns--relabeled-------------- evalq({ Ens.relab <- vector(mode = "list", n) res.relab <- vector("list", 4) x <- denoiseX1pretrain$relabeled$x %>% as.matrix() y <- denoiseX1pretrain$relabeled$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab GetInputData(Ens = Ens.relab, X = x, Y = y) -> res.relab }, env)
The structure of the ensemble predictions results is shown below:
> env$res.origin %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ... $ InputTrain : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ... $ InputTest : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ... $ InputTest1 : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ... > env$res.repaired %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ... $ InputTrain : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ... $ InputTest : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ... $ InputTest1 : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ... > env$res.removed %>% str() List of 4 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ... $ InputTrain : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ... $ InputTest : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ... $ InputTest1 : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ... > env$res.relab %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ... $ InputTrain : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ... $ InputTest : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ... $ InputTest1 : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...
Let us see how the distribution of these outputs/inputs looks like. See the first 10 outputs of the InputTrain[ ,1:10] sets:
#------Ris InputTrain------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
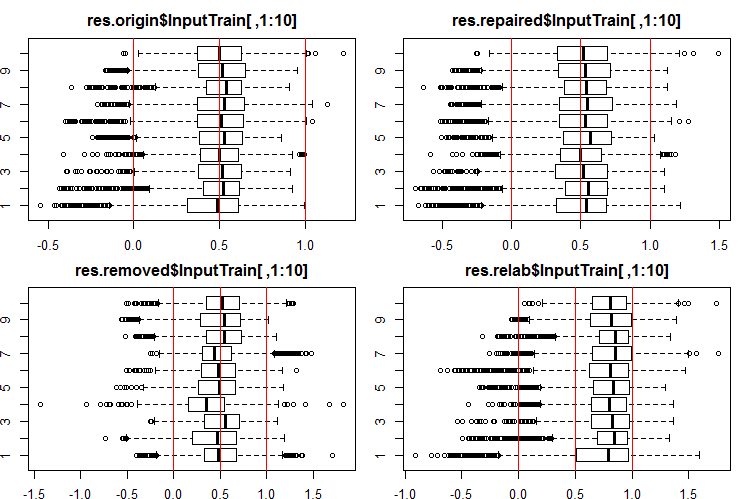
Fig. 2. Distribution of predictions of the InputTrain outputs using four different ensembles.
See the 10 first outputs of the InputTest[ ,1:10] sets:
#------Ris InputTest------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1) boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
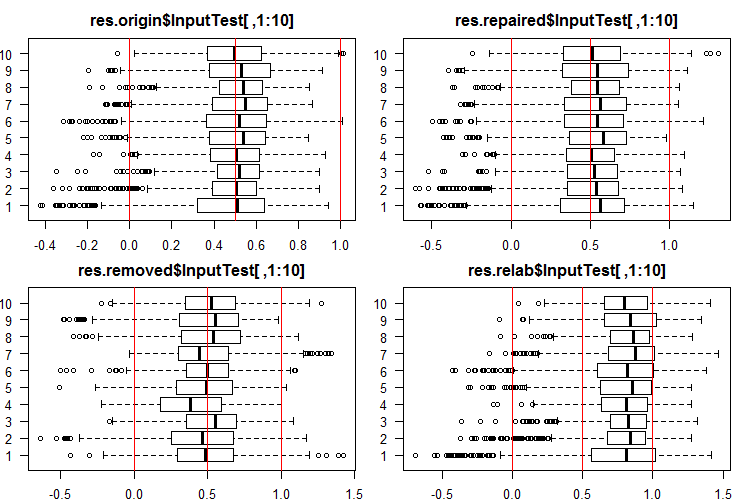
Fig. 3. Distribution of predictions of the InputTest outputs using four different ensembles.
See the 10 first outputs of the InputTest1[ ,1:10] sets:
#------Ris InputTest1------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
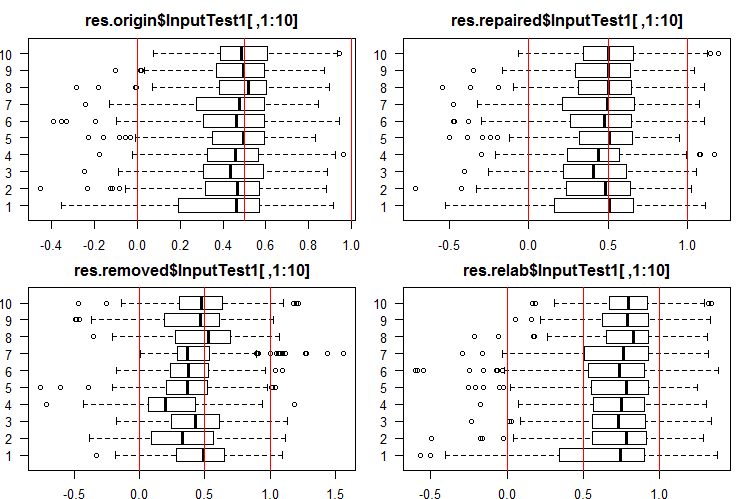
Fig. 4. Distribution of predictions of the InputTest1 outputs using four different ensembles.
Distribution of all predictions differs greatly from the predictions obtained from the data normalized by the SpatialSign method in the previous experiments. You can experiment with different normalization methods on your own.
After calculating the prediction of subsets X1$train/test/test1 using each ensemble, we obtain four groups of data — res.origin, res.repaired, res.removed and res.relab, with distributions shown in Figures 2 — 4.
Let us determine the classification quality of each ensemble, converting the continuous predictions into class labels.
4. Determining the thresholds for the obtained continuous predictions, converting them into class labels, and calculating metrics for neural networks
To convert the continuous data into class labels, one or several thresholds of division into these classes are used. The continuous predictions of the InputTrain sets, obtained from the fifth neural network of all ensembles, look as follows:
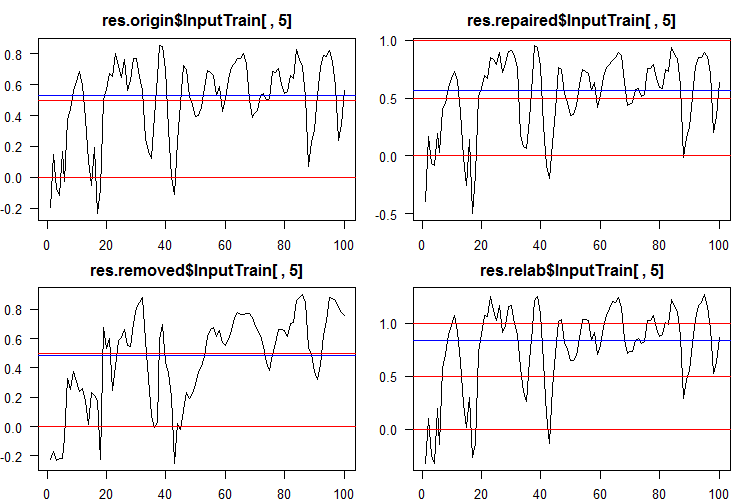
Fig. 5. Continuous predictions of the fifth neural network of various ensembles.
As you can see, the graphs of continuous prediction of the origin, repaired, relabeled models are similar in shape, but have a different range. The line of the removed model's prediction is considerably different in shape.
To simplify the subsequent calculations, collect all models and their predictions in one structure predX1. To do this, write a compact function that will repeat all calculations in a cycle. There is the script and a picture of the predX1 structure:
library("doFuture")
#---predX1------------------
evalq({
group <- qc(origin, repaired, removed, relabeled)
predX1 <- vector("list", 4)
foreach(i = 1:4, .packages = "elmNN") %do% {
x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
y <- denoiseX1pretrain[[i]]$y
SEED = 12345
createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens
GetInputData(Ens = ens, X = x, Y = y) -> pred
return(list(ensemble = ens, pred = pred))
} -> predX1
names(predX1) <- group
}, env)
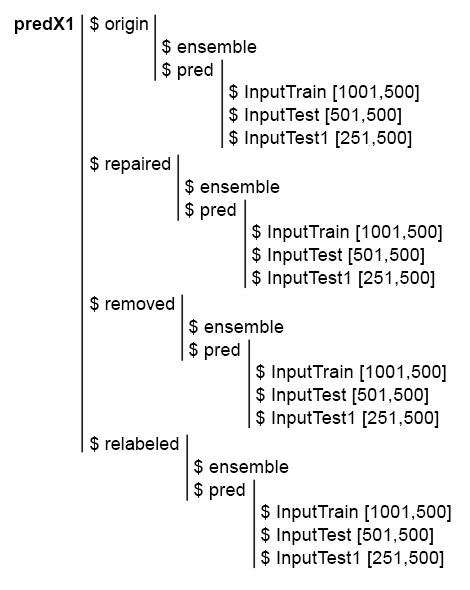
Fig. 6. Structure of the predX1 set
Remember that to obtain the metrics of the ensemble's prediction quality, two operations need to be performed: pruning and averaging (or simple majority voting). For pruning, it is necessary to convert all outputs of the ensemble's every neural network from the continuous form into class labels. Then define the metrics of each neural network and select a certain number of them with the best scores. Then average the continuous predictions of these best neural networks and obtain a continuous average prediction of the ensemble. Once more, define the threshold, convert the averaged prediction into class labels and calculate the final scores of the ensemble's classification quality.
Thus, it is necessary to convert the continuous prediction into class labels twice. The conversion thresholds at these two stages can either be the same or different. Which variants of thresholds can be used?
- The default threshold. In this case, it is equal to 0.5.
- Threshold equal to the median. I think it is more reliable. But the median can be determined only on the validation set, while it can be applied only when testing the subsequent subsets. For example, we define the thresholds on the InputTrain subset, which will later be used on the InputTest and InputTest1 subsets.
- Threshold optimized for various criteria. For example, it can be the minimum classification error, the maximum accuracy "1", or "0", etc. The optimal thresholds are always determined on the InputTrain subset, and used on the InputTest and InputTest1 subsets.
- When averaging the outputs of the best neural networks, calibration can be used. Some authors write that only well-calibrated outputs can be averaged. Confirming this statement is beyond the scope of this article.
The optimal threshold will be determined using the InformationValue::optimalCutoff() function. It is described in detail in the package.
To determine the thresholds for points 1 and 2, additional calculations are not required. To calculate the optimal thresholds for point 3, let us write the function GetThreshold().
#--function------------------------- evalq({ import_fun("InformationValue", optimalCutoff, CutOff) import_fun("InformationValue", youdensIndex, th_youdens) GetThreshold <- function(X, Y, type){ switch(type, half = 0.5, med = median(X), mce = CutOff(Y, X, "misclasserror"), both = CutOff(Y, X,"Both"), CutOff(Y, X, "Ones"), zeros = CutOff(Y, X, "Zeros") ) } }, env)
Only the first four types of thresholds described in this function (half, med, mce, both) will be calculated. The first two are the half and median thresholds. The mce threshold provides the minimum classification error, the both threshold — the maximum value of the coefficient youdensIndex = (sensitivity + specificity —1). The calculation order will be as follows:
1. In the predX1 set, calculate the four types of thresholds for each of 500 neural networks of the ensemble on the InputTrain subset, separately in each group of data (origin, repaired, removed and relabeled).
2. Then, using these thresholds, convert the continuous predictions of all neural network ensembles in all subsets (train|test|test1) into classes and determine the average values F1. We obtain four groups of metrics containing three subsets each. Below is a step-by-step script for the origin group.
Define 4 types of thresholds on the predX1$origin$pred$InputTrain subset:
#--threshold--train--origin--------
evalq({
Ytest = X1$train$y
Ytest1 = X1$test$y
Ytest2 = X1$test1$y
testX1 <- vector("list", 4)
names(testX1) <- group
type <- qc(half, med, mce, both)
registerDoFuture()
cl <- makeCluster(4)
plan(cluster, workers = cl)
foreach(i = 1:4, .combine = "cbind") %dopar% {# type
foreach(j = 1:500, .combine = "c") %do% {
GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
}
} -> testX1$origin$Threshold
stopCluster(cl)
dimnames(testX1$origin$Threshold) <- list(NULL,type)
}, env)
We use two nested loops in each calculation. In the outer loop, select the threshold type, create a cluster, and parallelize the calculation to 4 cores. In the inner loop, iterate over the InputTrain predictions of each of 500 neural networks comprising the ensemble. 4 types of thresholds are defined for each one. The structure of the obtained data will be as follows:
> env$testX1$origin$Threshold %>% str() num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "half" "med" "mce" "both" > env$testX1$origin$Threshold %>% head() half med mce both [1,] 0.5 0.5033552 0.3725180 0.5125180 [2,] 0.5 0.4918041 0.5118821 0.5118821 [3,] 0.5 0.5005034 0.5394191 0.5394191 [4,] 0.5 0.5138439 0.4764055 0.5164055 [5,] 0.5 0.5241393 0.5165478 0.5165478 [6,] 0.5 0.4673319 0.4508287 0.4608287
Using the obtained thresholds, covert the continuous predictions of the origin group of the subsets train, test and test1 into class labels and calculate the metrics (mean(F1)).
#--train--------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTrainScore
dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTestScore
dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTest1Score
dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env)
See the distribution of metrics in the origin group and three of its subsets. The script below for the origin group:
k <- 1L #origin # k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
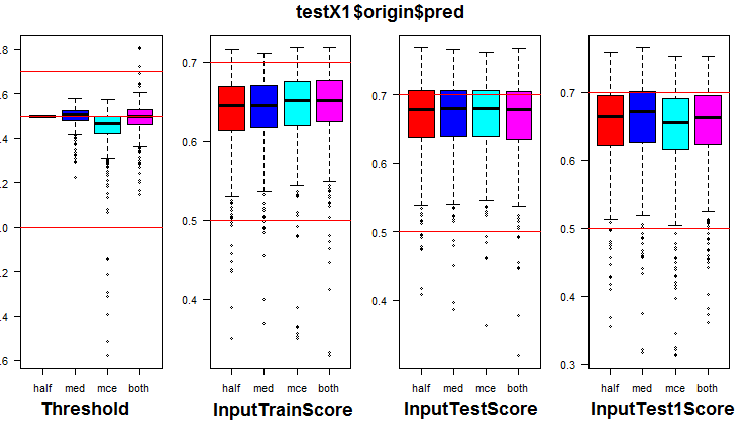
Fig. 7. Distribution of thresholds and metrics in the origin group
The visualization showed that using "med" as the threshold for the origin group of data does not give a visible improvement in quality compared to the "half" threshold.
Calculate all 4 types of thresholds in all groups (be prepared for it to take quite a lot of time and memory).
library("doFuture") #--threshold--train--------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y registerDoFuture() cl <- makeCluster(4) plan(cluster, workers = cl) while (k <= 4) { # group foreach(i = 1:4, .combine = "cbind") %dopar% {# type foreach(j = 1:500, .combine = "c") %do% { GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i]) } } -> testX1[[k]]$Threshold dimnames(testX1[[k]]$Threshold) <- list(NULL,type) k <- k + 1 } stopCluster(cl) }, env)
Using the obtained thresholds, calculate the metrics in all groups and subsets:
#--train-------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTrainScore dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type k <- k + 1 } }, env) #--test----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTestScore dimnames(testX1[[k]]$InputTestScore)[[2]] <- type k <- k + 1 } }, env) #--test1----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTest1Score dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type k <- k + 1 } }, env)
To each group of data, we added metrics of each of the ensemble's 500 neural networks with four different thresholds on three subsets.
Let us see how the metrics are distributed in each group and subset. The script is provided for the repaired subset. It is similar for other groups, only the group number changes. For clarity, the graphs of all groups will be presented in one.
# k <- 1L #origin k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
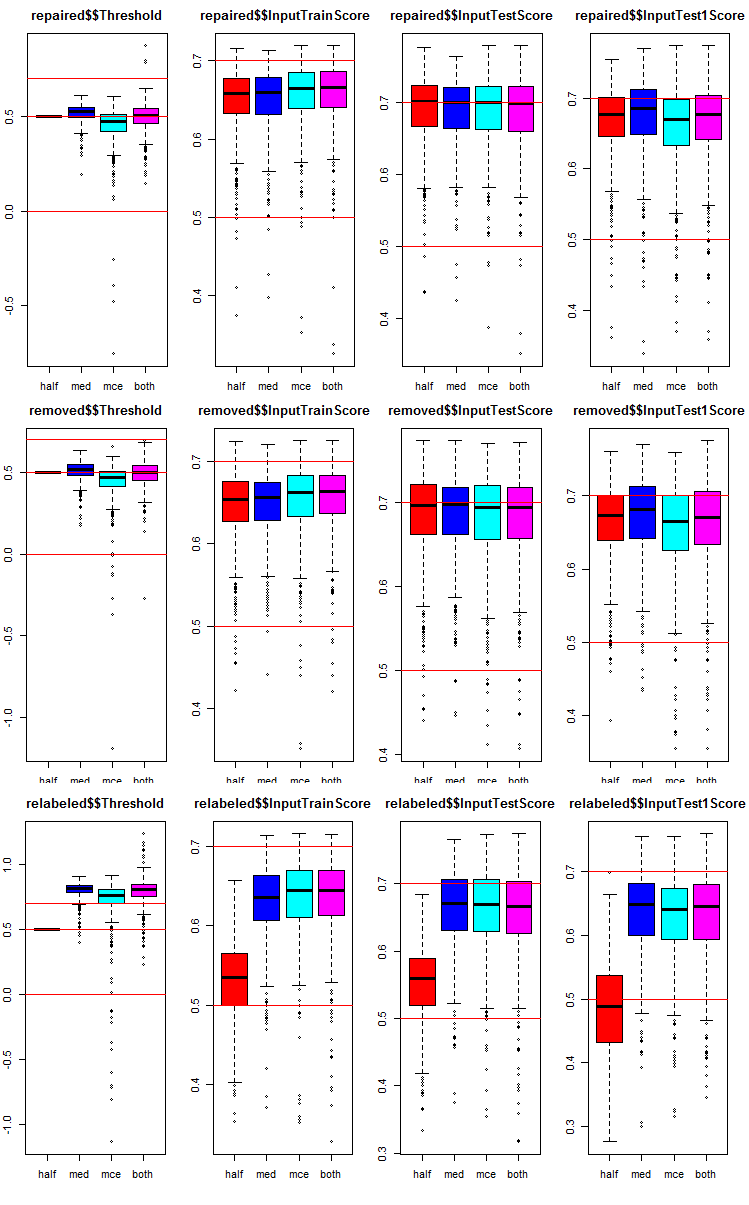
Fig. 8. Distribution graphs of prediction metrics of the ensemble's each neural network in three groups of data with three subsets and four different thresholds.
Common in all groups:
- metrics of the test subset (InputTestScore) are much better than metrics of the validation set (InputTrainScore);
- metrics of the second test subset (InputTest1Score) are noticeably worse than metrics of the first test subset;
- threshold of type "half" shows results not worse than others on all subsets, except relabeled.
5. Testing ensembles
5.1. Determining 7 neural networks with the best metrics in each ensemble and in each group of data in the InputTrain subset
Perform pruning. In each group of data of the testX1 subset, it is necessary to select 7 InputTrainScore values with the largest values of the mean F1. Their indexes will be the indexes of the best neural networks in the ensemble. The script is given below, and can also be found in the Test.R file.
#--bestNN---------------------------------------- evalq({ nb <- 3L k <- 1L while (k <= 4) { foreach(j = 1:4, .combine = "cbind") %do% { testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1) } -> testX1[[k]]$bestNN dimnames(testX1[[k]]$bestNN) <- list(NULL, type) k <- k + 1 } }, env)
We obtained indexes of the neural networks with the best scores in four groups of data (origin, repaired, removed, relabeled). Let us take a closer look at them and compare how much these best neural networks differ depending on the group of data and threshold type.
> env$testX1$origin$bestNN half med mce both [1,] 415 75 415 415 [2,] 191 190 220 220 [3,] 469 220 191 191 [4,] 220 469 469 469 [5,] 265 287 57 444 [6,] 393 227 393 57 [7,] 75 322 444 393 > env$testX1$repaired$bestNN half med mce both [1,] 393 393 154 154 [2,] 415 92 205 205 [3,] 205 154 220 220 [4,] 462 190 393 393 [5,] 435 392 287 287 [6,] 392 220 90 90 [7,] 265 287 415 415 > env$testX1$removed$bestNN half med mce both [1,] 283 130 283 283 [2,] 207 110 300 300 [3,] 308 308 110 110 [4,] 159 134 192 130 [5,] 382 207 207 192 [6,] 192 283 130 308 [7,] 130 114 134 207 env$testX1$relabeled$bestNN half med mce both [1,] 234 205 205 205 [2,] 69 287 469 469 [3,] 137 191 287 287 [4,] 269 57 191 191 [5,] 344 469 415 415 [6,] 164 75 444 444 [7,] 184 220 57 57
You can see that the indexes of neural networks with the "mce" and "both" threshold types coincide very often.
5.2. Averaging continuous predictions of these 7 best neural networks.
After choosing the 7 best neural networks, average them in each group of data, in subsets InputTrain, InputTest, InputTest1 and by each threshold type. Script for processing the InputTrain subset in 4 groups:
#--Averaging--train------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTrain[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TrainYpred dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Let us take a look at the structure and statistical scores of the obtained averaged continuous predictions in the data group repaired:
> env$testX1$repaired$TrainYpred %>% str() num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both" > env$testX1$repaired$TrainYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.2202 Min. :-0.4021 Min. :-0.4106 Min. :-0.4106 1st Qu.: 0.3348 1st Qu.: 0.3530 1st Qu.: 0.3512 1st Qu.: 0.3512 Median : 0.5323 Median : 0.5462 Median : 0.5462 Median : 0.5462 Mean : 0.5172 Mean : 0.5010 Mean : 0.5012 Mean : 0.5012 3rd Qu.: 0.7227 3rd Qu.: 0.7153 3rd Qu.: 0.7111 3rd Qu.: 0.7111 Max. : 1.1874 Max. : 1.0813 Max. : 1.1039 Max. : 1.1039
The statistics of the last two threshold types is identical here as well. Here are the scripts for the two remaining subsets InputTest, InputTest1:
#--Averaging--test------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TestYpred dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env) #--Averaging--test1------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest1[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$Test1Ypred dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Let us take a look at the statistics of the InputTest subset of the repaired data group:
> env$testX1$repaired$TestYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.1524 Min. :-0.5055 Min. :-0.5044 Min. :-0.5044 1st Qu.: 0.2888 1st Qu.: 0.3276 1st Qu.: 0.3122 1st Qu.: 0.3122 Median : 0.5177 Median : 0.5231 Median : 0.5134 Median : 0.5134 Mean : 0.5114 Mean : 0.4976 Mean : 0.4946 Mean : 0.4946 3rd Qu.: 0.7466 3rd Qu.: 0.7116 3rd Qu.: 0.7149 3rd Qu.: 0.7149 Max. : 1.1978 Max. : 1.0428 Max. : 1.0722 Max. : 1.0722
The statistics of the last two threshold types is identical here too.
5.3. Defining the thresholds for the averaged continuous predictions
Now we have averaged predictions of each ensemble. They need to be converted into class labels and the final metrics of quality for all data groups and threshold types. To do this, similar to the previous calculations, determine the best thresholds using only the InputTrain subsets. The script provided below calculates the thresholds in each group and in each subset:
#-th_aver------------------------------ evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i]) } } -> testX1[[k]]$th_aver dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env)
5.4. Converting the averaged continuous predictions of the ensembles into class labels and calculating the metrics of the ensembles on the InputTrain, InputTest and InputTest1 subsets of all data groups.
With the th_aver thresholds calculated above, determine the metrics:
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TrainScore dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TestScore dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred)) k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$Test1Score dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred)) k <- k + 1 } }, env)
Create a summary table and analyze the obtained metrics. Let us start with the origin group (its noise samples were not processed in any way). We are looking for the scores TestScore and Test1Score. The scores of the TestTrain subset are indicative, they are needed for comparison with the test scores:
> env$testX1$origin$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.711 0.708 0.712 0.712 med 0.711 0.713 0.707 0.707 mce 0.712 0.704 0.717 0.717 both 0.711 0.706 0.717 0.717 > env$testX1$origin$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.750 0.738 0.745 0.745 med 0.748 0.742 0.746 0.746 mce 0.742 0.720 0.747 0.747 both 0.748 0.730 0.747 0.747 > env$testX1$origin$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.735 0.732 0.716 0.716 med 0.733 0.753 0.745 0.745 mce 0.735 0.717 0.716 0.716 both 0.733 0.750 0.716 0.716
What does the proposed table show?
The best result of 0.750 in TestScore was shown by the variant with the "half" threshold in both transformations (both when pruning and averaging). However, the quality drops to 0.735 in the Test1Score subset.
A more stable result of ~0.745 in both subsets are shown by the threshold variants (med, mce, both) when pruning and med when averaging.
See the next data group — repaired (with the corrected labeling of the noise samples):
> env$testX1$repaired$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.711 0.717 0.717 med 0.709 0.709 0.713 0.713 mce 0.728 0.714 0.709 0.709 both 0.728 0.711 0.717 0.717 > env$testX1$repaired$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.759 0.761 0.756 0.756 med 0.754 0.748 0.747 0.747 mce 0.758 0.755 0.743 0.743 both 0.758 0.732 0.754 0.754 > env$testX1$repaired$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.744 0.724 0.724 med 0.738 0.748 0.744 0.744 mce 0.697 0.720 0.677 0.677 both 0.697 0.743 0.731 0.731
The best result displayed in the table is 0.759 in the half/half combination. A more stable result of ~0.750 in both subsets are shown by the threshold variants (half, med, mce, both) when pruning and med when averaging.
See the next data group — removed (with the noise samples removed from the set):
> env$testX1$removed$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.720 0.724 0.718 med 0.715 0.717 0.715 0.717 mce 0.721 0.722 0.725 0.723 both 0.721 0.720 0.725 0.723 > env$testX1$removed$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.761 0.769 0.761 0.751 med 0.752 0.749 0.760 0.752 mce 0.749 0.755 0.753 0.737 both 0.749 0.736 0.753 0.760 > env$testX1$removed$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.712 0.732 0.716 0.720 med 0.729 0.748 0.740 0.736 mce 0.685 0.724 0.721 0.685 both 0.685 0.755 0.721 0.733
Analyze the table. The best result of 0.769 in TestScore was shown by the variant with the med/half thresholds. However, the quality drops to 0.732 in the Test1Score subset. For the TestScore subset, the best combination of thresholds when pruning (half, med, mce, both) and half when averaging produces the best scores of all groups.
See the last data group — relabeled (with the noise samples isolated to a separate class):
> env$testX1$relabeled$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.672 0.559 0.529 0.529 med 0.715 0.715 0.711 0.711 mce 0.712 0.715 0.717 0.717 both 0.710 0.718 0.720 0.720 > env$testX1$relabeled$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.572 0.555 0.555 med 0.736 0.748 0.746 0.746 mce 0.739 0.747 0.745 0.745 both 0.710 0.756 0.754 0.754 > env$testX1$relabeled$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.664 0.498 0.466 0.466 med 0.721 0.748 0.740 0.740 mce 0.739 0.732 0.716 0.716 both 0.734 0.737 0.735 0.735
The best results for this group are produced by the following combination of thresholds: (med, mce, both) when pruning and both or med when averaging.
Keep in mind that you can get values different from mine.
The figure below shows the data structure of testX1 after all the above calculations:

Fig. 9. The data structure of testX1.
6. Optimizing hyperparameters of ensembles of neural network classifiers
All the previous calculations have been carried out on ensembles with the same hyperparameters of neural networks, set based on personal experience. As you may know, the hyperparameters of neural networks, like other models, need to be optimized for a specific data set to obtain better results. For training, we use the denoised data separated into 4 groups (origin, repaired, removed and relabeled). Therefore, it is necessary to obtain optimal hyperparameters of the ensemble's neural networks precisely for these sets. All questions regarding the Bayesian optimization have been thoroughly discussed in the previous article, so their details will not be considered here.
4 hyperparameters of neural networks will be optimized:
- the number of predictors — numFeature = c(3L, 13L) in the range from 3 to 13;
- the percentage of samples used in training — r = c(1L, 10L) in the range from 10 % to 100%;
- the number of neurons in the hidden layer — nh = c(1L, 51L) in the range from 1 to 51;
- type of the activation function — fact = c(1L, 10L) index in the list of activation functions Fact.
Set the constants:
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L) ) }, env)
Write a fitness function that will return the quality indicator Score = meаn(F1) and the ensemble's prediction in class labels. Pruning (selection of the best neural networks in the ensemble) and averaging of the continuous prediction will be performed using the same threshold = 0.5. It proved to be a very good option earlier — at least for the first approximation. Here is the script:
#---Fitnes -FUN----------- evalq({ n <- 500 numEns <- 3 # SEED <- c(12345, 1235809) fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) k <- 1 rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
The SEED variable commented out has two values. This is necessary for checking the impact of this parameter on the result experimentally. I have performed the optimization with the same initial data and parameters, but with two different values of SEED. The best result was shown by SEED = 1235809. This value will be used in the scripts below. But the obtained hyperparameters and classification quality scores will be provided for both values of SEED. You can experiment with other values.
Let us check if the fitness function works, how long one pass of its calculations takes and see the result:
evalq({
Ytrain <- X1$pretrain$y
Ytest <- X1$train$y
Ytest1 <- X1$test$y
Xtrain <- X1$pretrain$x
Xtest <- X1$train$x
Xtest1 <- X1$test$x
orderX <- orderX1
SEED <- 1235809
system.time(
res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
)
}, env)
user system elapsed
5.89 0.00 5.99
env$res$Score
[1] 0.741
Below is the script for optimizing the hyperparameters of neural networks successively for each group of denoised data. Use 20 points of the starting random initialization and 20 subsequent iterations.
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) } -> OPT_Res1 group <- qc(origin, repaired, removed, relabeled) names(OPT_Res1) <- group }, env)
Once you start the execution of the script, be patient for about half an hour (it depends on your hardware). Sort the obtained Score values in descending order and choose the three best ones. These scores are assigned to the variables best.res (for SEED = 12345) and best.res1 (for SEED = 1235809).
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res
names(best.res) <- group
}, env)
evalq({
foreach(i = 1:4) %do% {
OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res1
names(best.res1) <- group
}, env)
See the best.res scores:
env$best.res # $origin # Round numFeature r nh fact Value # 1 39 10 7 20 2 0.769 # 2 12 6 4 38 2 0.766 # 3 38 4 3 15 2 0.766 # # $repaired # Round numFeature r nh fact Value # 1 5 10 5 20 7 0.767 # 2 7 5 2 36 9 0.766 # 3 28 5 10 6 8 0.766 # # $removed # Round numFeature r nh fact Value # 1 1 11 6 44 9 0.764 # 2 8 8 6 26 7 0.764 # 3 19 12 1 40 5 0.763 # # $relabeled # Round numFeature r nh fact Value # 1 24 9 10 1 10 0.746 # 2 7 9 9 2 8 0.745 # 3 32 4 1 1 10 0.738
The same for the best.res1 scores:
> env$best.res1 $origin Round numFeature r nh fact Value 1 19 8 3 41 2 0.777 2 32 8 1 33 2 0.777 3 23 6 1 35 1 0.770 $repaired Round numFeature r nh fact Value 1 26 9 4 17 3 0.772 2 33 11 9 30 9 0.771 3 38 5 4 17 2 0.770 $removed Round numFeature r nh fact Value 1 30 5 4 17 2 0.770 2 8 8 2 13 6 0.769 3 32 5 3 22 7 0.766 $relabeled Round numFeature r nh fact Value 1 34 12 5 8 9 0.777 2 33 9 5 4 9 0.763 3 36 12 7 4 9 0.760
As you can see, these results look better. For comparison, you can print not the first three results, but ten: the differences will be even more noticeable.
Each optimization run will generate different hyperparameter values and results. The hyperparameters can be optimized using different initial RNG settings, as well as with a specific starting initialization.
Let us collect the best hyperparameters of the ensembles' neural networks for 4 data groups. They will be needed later for creating ensembles with optimal hyperparameters.
#---best.param-------------------
evalq({
foreach(i = 1:4, .combine = "rbind") %do% {
OPT_Res1[[i]]$Best_Par %>% unname()
} -> best.par1
dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env)
The hyperparameters:
> env$best.par1 numFeature r nh fact origin 8 3 41 2 repaired 9 4 17 3 removed 5 4 17 2 relabeled 12 5 8 9
All scripts from this script are available in the Optim_VIII.R file.
7. Optimizing postprocessing hyperparameters (thresholds for pruning and averaging)
Optimization of the neural networks' hyperparameters provides a small increase in the classification quality. As proven earlier, the combination of threshold types when pruning and averaging has a stronger impact on the classification quality.
We have already optimized the hyperparameters with a constant combination of thresholds half/half. Perhaps this combination is not optimal. Let us repeat the optimization with two additional optimized parameters th1 = c(1L, 2L)) — threshold type when pruning the ensemble (selecting the best neural networks) — and th2 = c(1L, 4L) — threshold type when converting the averaged prediction of the ensemble into class labels. Define the constants and the value ranges of the hyperparameters to be optimized.
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds_m <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L), th1 = c(1L, 2L), th2 = c(1L, 4L) ) }, env)
On to the fitness function. It was slightly modified: added two formal parameters th1, th2. In the function body and in the 'best' block, calculate the threshold depending on th1. In the 'test-average' block, determine the threshold using the GetThreshold() function depending on the threshold type th2.
#---Fitnes -FUN----------- evalq({ n <- 500L numEns <- 3L # SEED <- c(12345, 1235809) fitnes_m <- function(numFeature, r, nh, fact, th1, th2){ bestF <- orderX %>% head(numFeature) k <- 1L rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- ifelse(th1 == 1L, 0.5, median(y.pr)) -> th foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred th <- GetThreshold(ensPred, Yts$Ytest1, type[th2]) ifelse(ensPred > th, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Check how much time one iteration of this function takes and if it works:
#---res fitnes------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Xtrain <- X1$pretrain$x Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 th1 <- 1 th2 <- 4 system.time( res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2) ) }, env) user system elapsed 6.13 0.04 6.32 > env$res_m$Score [1] 0.748
The execution time of the function has changed insignificantly. After that, run the optimization and wait for the result:
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res1 <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes_m, bounds = bonds_m, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100) #, control = c(100, 50, 8)) } -> OPT_Res_m group <- qc(origin, repaired, removed, relabeled) names(OPT_Res_m) <- group }, env)
Select the 10 best hyperparameters obtained for each data group:
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
} -> best.res_m
names(best.res_m) <- group
}, env)
$origin
Round numFeature r nh fact th1 th2 Value
1 19 8 3 41 2 2 4 0.778
2 25 6 8 51 8 2 4 0.778
3 39 9 1 22 1 2 4 0.777
4 32 8 1 21 2 2 4 0.772
5 10 6 5 32 3 1 3 0.769
6 22 7 2 30 9 1 4 0.769
7 28 6 10 25 5 1 4 0.769
8 30 7 9 33 2 2 4 0.768
9 40 9 2 48 10 2 4 0.768
10 23 9 1 2 10 2 4 0.767
$repaired
Round numFeature r nh fact th1 th2 Value
1 39 7 8 39 8 1 4 0.782
2 2 5 8 50 3 2 3 0.775
3 3 12 6 7 8 1 1 0.769
4 24 5 10 45 5 2 3 0.769
5 10 7 8 40 2 1 4 0.768
6 13 5 8 40 2 2 4 0.768
7 9 6 9 13 2 2 3 0.766
8 19 5 7 46 6 2 1 0.765
9 40 9 8 50 6 1 4 0.764
10 20 9 3 28 9 1 3 0.763
$removed
Round numFeature r nh fact th1 th2 Value
1 40 7 2 39 8 1 3 0.786
2 13 5 3 48 3 2 3 0.776
3 8 5 6 18 1 1 1 0.772
4 5 5 10 24 3 1 3 0.771
5 29 13 7 1 1 1 4 0.771
6 9 7 3 25 7 1 4 0.770
7 17 9 2 17 1 1 4 0.770
8 19 7 7 25 2 1 3 0.768
9 4 10 6 19 7 1 3 0.765
10 2 4 4 47 7 2 3 0.764
$relabeled
Round numFeature r nh fact th1 th2 Value
1 7 8 1 13 1 2 4 0.778
2 26 8 1 19 6 2 4 0.768
3 3 6 3 45 4 2 2 0.766
4 20 6 2 40 10 2 2 0.766
5 13 4 3 18 2 2 3 0.762
6 10 10 6 4 8 1 3 0.761
7 31 11 10 16 1 2 4 0.760
8 15 13 7 7 1 2 3 0.759
9 5 7 3 20 2 1 4 0.758
10 9 9 3 22 8 2 3 0.758
There is a slight improvement in quality. The best hyperparameters for each data group are very different from the hyperparameters obtained during the previous optimization with no consideration of different combination of thresholds. The best quality scores are demonstrated by data groups with relabeled (repaired) and removed (removed) noise samples.
#---best.param------------------- evalq({ foreach(i = 1:4, .combine = "rbind") %do% { OPT_Res_m[[i]]$Best_Par %>% unname() } -> best.par_m dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2)) }, env) # > env$best.par_m------------------------ # numFeature r nh fact th1 th2 # origin 8 3 41 2 2 4 # repaired 7 8 39 8 1 4 # removed 7 2 39 8 1 3 # relabeled 8 1 13 1 2 4
The scripts used in this section are available in the Optim_mVIII.R file.
8. Combining several best ensembles into a superensemble as well as their outputs
Combine several best ensembles into a superensemble, and their outputs are cascaded by simple majority voting.
First, combine the results of several best ensembles obtained during the optimization. After the optimization, the function returns not only the best hyperparameters, but also the history of predictions in class labels at all iterations. Generate a superensemble from the 5 best ensembles in each data group, and use simple majority voting to check if the classification quality scores improve in that variant.
Calculations are performed in the following sequence:
- sequentially iterate over 4 data groups in a loop;
- determine the indexes of the 5 best predictions in each data group;
- combine the predictions with these indexes into a dataframe;
- change the class label from "0" to "-1" in all predictions;
- sum these predictions row by row;
- convert these summed values into class labels (-1, 0, 1) according to the condition: if the value is greater than 3, then class = 1; if less than -3, then class = -1; otherwise class = 0
Here is the script that performs these calculations:
#--Index-best-------------------
evalq({
prVot <- vector("list", 4)
foreach(i = 1:4) %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x)) ->.;
ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
} -> prVot
names(prVot) <- group
}, env)
We have an additional third class "0". If "-1", it is "Sell", "1" is "Buy", and "0" is "not sure". How the Expert Advisor reacts to this signal is up to the user. It can stay out of the market, or it can be in the market and do nothing, waiting for a new signal to action. The behavior models should be built and checked when testing the expert.
To obtain the metrics, it is necessary to:
- sequentially iterate over each data group in a loop;
- in the actual value of the target Ytest1, replace the "0" class label with the label "-1";
- combine the actual and predicted target prVot obtained above into a dataframe;
- remove the rows with the value of prVot = 0 from the dataframe;
- calculate the metrics.
Calculate and see the result.
evalq({
foreach(i = 1:4) %do% { #group
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred)
} -> Score
names(Score) <- group
}, env)
env$Score
$origin
$origin$metrics
Accuracy Precision Recall F1
-1 0.806 0.809 0.762 0.785
1 0.806 0.804 0.845 0.824
$origin$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 49
1 37 201
Accuracy : 0.8063
95% CI : (0.7664, 0.842)
No Information Rate : 0.5631
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6091
Mcnemar's Test P-Value : 0.2356
Sensitivity : 0.8093
Specificity : 0.8040
Pos Pred Value : 0.7621
Neg Pred Value : 0.8445
Prevalence : 0.4369
Detection Rate : 0.3536
Detection Prevalence : 0.4640
Balanced Accuracy : 0.8066
'Positive' Class : -1
$repaired
$repaired$metrics
Accuracy Precision Recall F1
-1 0.82 0.826 0.770 0.797
1 0.82 0.816 0.863 0.839
$repaired$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 147 44
1 31 195
Accuracy : 0.8201
95% CI : (0.7798, 0.8558)
No Information Rate : 0.5731
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6358
Mcnemar's Test P-Value : 0.1659
Sensitivity : 0.8258
Specificity : 0.8159
Pos Pred Value : 0.7696
Neg Pred Value : 0.8628
Prevalence : 0.4269
Detection Rate : 0.3525
Detection Prevalence : 0.4580
Balanced Accuracy : 0.8209
'Positive' Class : -1
$removed
$removed$metrics
Accuracy Precision Recall F1
-1 0.819 0.843 0.740 0.788
1 0.819 0.802 0.885 0.841
$removed$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 145 51
1 27 207
Accuracy : 0.8186
95% CI : (0.7789, 0.8539)
No Information Rate : 0.6
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6307
Mcnemar's Test P-Value : 0.009208
Sensitivity : 0.8430
Specificity : 0.8023
Pos Pred Value : 0.7398
Neg Pred Value : 0.8846
Prevalence : 0.4000
Detection Rate : 0.3372
Detection Prevalence : 0.4558
Balanced Accuracy : 0.8227
'Positive' Class : -1
$relabeled
$relabeled$metrics
Accuracy Precision Recall F1
-1 0.815 0.809 0.801 0.805
1 0.815 0.820 0.828 0.824
$relabeled$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 39
1 37 178
Accuracy : 0.8151
95% CI : (0.7741, 0.8515)
No Information Rate : 0.528
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6292
Mcnemar's Test P-Value : 0.9087
Sensitivity : 0.8093
Specificity : 0.8203
Pos Pred Value : 0.8010
Neg Pred Value : 0.8279
Prevalence : 0.4720
Detection Rate : 0.3820
Detection Prevalence : 0.4769
Balanced Accuracy : 0.8148
'Positive' Class : -1
#---------------------------------------
The quality has improved significantly in all groups. The best scores of 'Balanced Accuracy' have been obtained in the groups removed (0.8227) and repaired (0.8209).
Let us combine the group predictions using simple majority voting as well. Perform the combining in cascade:
- iterate over all data groups in a loop;
- determine the indexes of the passes with the best results;
- select the predictions of these best passes;
- in each column, replace the class label "0" with the label "-1";
- sum the predictions in the group row by row.
See the result obtained:
#--Index-best-------------------
evalq({
foreach(i = 1:4, .combine = "+") %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x))
} -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
166 12 4 6 7 6 5 3 6 1 4 4 5 6 5 10 7 3 8 24 209
Leave only the largest values of voting and calculate the metrics:
evalq({
pred <- {prVotSum ->.;
ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = pred) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env)
env$ScoreSum
> env$ScoreSum
$metrics
Accuracy Precision Recall F1
-1 0.835 0.849 0.792 0.820
1 0.835 0.823 0.873 0.847
$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 141 37
1 25 172
Accuracy : 0.8347
95% CI : (0.7931, 0.8708)
No Information Rate : 0.5573
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6674
Mcnemar's Test P-Value : 0.1624
Sensitivity : 0.8494
Specificity : 0.8230
Pos Pred Value : 0.7921
Neg Pred Value : 0.8731
Prevalence : 0.4427
Detection Rate : 0.3760
Detection Prevalence : 0.4747
Balanced Accuracy : 0.8362
'Positive' Class : -1
This produced a very good score of Balanced Accuracy = 0.8362.
The scripts described in this section are available in the Voting.R file.
But we must not forget about one nuance. When optimizing the hyperparameters, we used the InputTest testing set. This means that we can start working with the next testing set InputTest1. Combining the ensembles in cascade is most likely to produce the same positive effect without optimization of the hyperparameters. Check it on the averaging results obtained earlier.
Combine the averaged outputs of the ensembles obtained in section 5.2.
Reproduce the calculations described in section 5.4, with one change. When converting the continuous averaged prediction into class labels, these labels will be [-1, 0, 1]. The sequence of calculation in each subset train/test/test1:
- sequentially iterate over 4 data groups in a loop;
- by 4 types of pruning thresholds;
- by 4 types of averaging thresholds;
- convert the continuous averaged prediction of the ensemble into class labels [-1, 1];
- sum them by 4 types of averaging thresholds;
- relabel the summed with new labels [-1, 0, 1];
- add the obtained result to the VotAver structure.
#---train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) VotAver <- vector("list", 4) names(VotAver) <- group while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Train.clVoting dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test------------------------------ evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test.clVoting dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test1------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test1.clVoting dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type) k <- k + 1 } }, env)
Once the relabeled averaged predictions in subsets and groups are determined, calculate their metrics. Sequence of calculations:
- iterate over the groups in a loop;
- iterate over 4 types of averaging thresholds;
- change the class label in the actual prediction from "0" to "-1";
- combine the actual and relabeled prediction to the dataframe;
- remove the rows with the prediction equal to 0 from the dataframe;
- calculate the metrics and add them to the VotAver structure.
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TrainScoreVot names(VotAver[[k]]$TrainScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest1 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TestScoreVot names(VotAver[[k]]$TestScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest2 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$Test1ScoreVot names(VotAver[[k]]$Test1ScoreVot) <- type k <- k + 1 } }, env)
Collect the data in a readable form and view them:
#----TrainScoreVot-------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
} -> TrainScoreVot
dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
half med mce both
origin 0.738 0.750 0.742 0.752
repaired 0.741 0.743 0.741 0.741
removed 0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
} -> TestScoreVot
dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
half med mce both
origin 0.774 0.789 0.797 0.804
repaired 0.777 0.788 0.778 0.778
removed 0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
} -> Test1ScoreVot
dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
half med mce both
origin 0.737 0.757 0.757 0.755
repaired 0.756 0.743 0.754 0.754
removed 0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713
The best results were shown on the testing subset in the 'removed' data group, with processing of noise samples.
Once again, combine the results in each subset of each data group by averaging types.
#==Variant-2========================================== #--TrainScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Train.clVoting ->.; apply(., 1, function(x) sum(x)) ->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum ifelse(Ytest == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--TestScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum ifelse(Ytest1 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--Test1ScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test1.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum ifelse(Ytest2 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env)
Collect the results in a readable form.
evalq({
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
} -> TrainScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
} -> TestScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
} -> Test1ScoreVotSum
ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum,
Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin 0.763 0.807 0.762
repaired 0.752 0.802 0.748
removed 0.761 0.810 0.765
relabeled 0.766 0.825 (!!) 0.711
Consider the results of the testing set. Surprisingly, the relabeled method had the best result. The results in all groups are much better than those obtained in section 5.4. The method of combining the ensemble outputs in cascade by simple majority voting gives an improvement in classification quality (Accuracy) from 5% to 7%.
The scripts from this section are located in the Voting_aver.R file. The structure of the data obtained is shown in the figure below:

Fig. 10. The data structure of VotAver.
The figure below provides a simplified scheme of all calculations: it shows the stages, the used scripts and data structures.
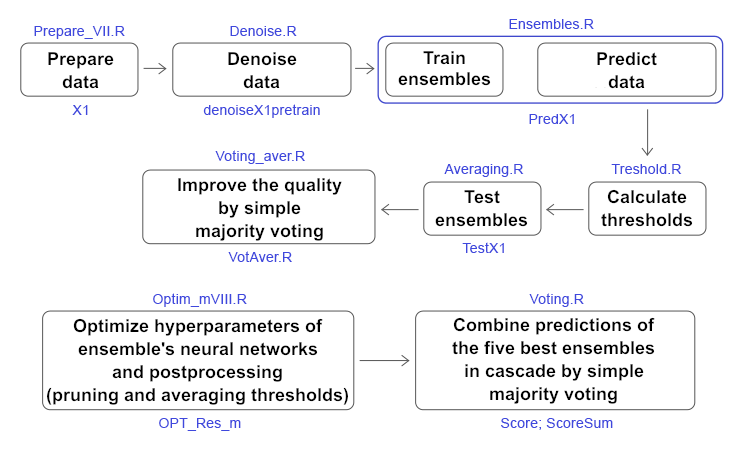
Fig. 11. Structure and sequence of the main calculations in the article.
8. Analyzing experimental results
We have processed the noise samples from the initial data sets in the pretrain subsets (!) in three ways:
- reallocated the "erroneously" labeled data without changing the number of classes (repaired);
- removed the "noise" samples from the subset (removed);
- isolated the "noise" samples in a separate class (relabeled).
Four groups of data (origin, repaired, removed, relabeled) were obtained in the denoiseX1pretrain structure. Use them to train the ensemble consisting of 500 ELM neural network classifiers. Obtain four ensembles. Calculate the continuous predictions of three subsets Х1$train/test/test1 using these 4 ensembles and collect them into the predX1 structure.
Then calculate 4 types of thresholds for continuous predictions of each of the 500 neural networks of each ensemble on the InputTrain subset (!). Using these thresholds, convert the continuous predictions into class labels (0, 1). Calculate the metrics (mean(F1)) for each neural network of the ensembles and collect them in the structure testX1$$(InputTrainScore|InputTestScore|InputTest1Score). Visualization of the metrics' distribution in 4 data groups and 3 subsets shows:
- first, the metrics on the first test subset are higher than on InputTrainS in all groups;
- second, the metrics are visually higher in the repaired and removed groups than in two others.
Now select the 7 best neural networks with the largest values of mean(F1) in each ensemble and average their continuous predictions. Add their values to the structure testX1$$(TrainYpred|TestYpred|Test1Ypred). Calculate the thresholds th_aver on the subset TrainYpred, determine the metrics of all averaged continuous predictions and add them to the structure testX1$$(TrainScore|TestScore|Test1Score). Now they can be analyzed.
With different combination of the pruning and averaging thresholds in different data groups, we obtain metrics in the range of 0.75 — 0.77. The best result has been obtained in the removed group with the "noise" samples removed.
Optimization of the neural networks' hyperparameters provides a stable increase in metrics of 0.77+ in all groups.
Optimization of the neural networks' hyperparameters and postprocessing (pruning and averaging) thresholds provides a stably high result of about 0.78+ in all groups with the processed "noise" samples.
Create a superensemble from several ensembles with the optimal hyperparameters, take the predictions of these ensembles and combine them by a simple majority voting in each data group. As a result, obtain the metrics in groups repaired and removed in the range of 0.82+. Combining these predictions of the superensembles by simple majority voting as well, obtain the final metric value of 0.836. Thus, combining the predictions in cascade by simple majority voting gives an improvement in quality of 6-7%.
Verify this statement on the averaged predictions of the ensemble received early. After repeating the calculations and conversions in the groups, receive metrics of 0.8+ in the removed group of the Test subset. Continuing the combination in cascade, receive metrics with values of 0,8+ in the Test subset in all data groups.
It can be concluded that combining the ensemble predictions in cascade by simple voting improves the classification quality indeed.
Conclusion
In this article, three methods for improving the quality of bagging ensembles have been considered, as well as optimization of hyperparameters of the ensemble's neural networks and postprocessing. Based on the results of the experiments, the following conclusions can be drawn:
- processing the noise samples using the repaired and removed methods significantly improves the classification quality of ensembles;
- selecting the threshold type for pruning and averaging, as well as their combination significantly affect the classification quality;
- combining several ensembles into a superensemble with their predictions combined in cascade by simple majority voting gives the greatest increase in the classification quality;
- optimizing the hyperparameters of ensembles' neural networks and post processing slightly improves the classification quality scores. It is advisable to perform the first optimization on new data, and them repeat it periodically when the quality decreases. Periodicity is determined experimentally.
Attachments
GitHub/PartVIII contains the following files:
- Importar.R — package import functions.
- Library.R — required libraries.
- FunPrepareData_VII.R — functions for preparing initial data.
- FunStacking_VIII.R — functions for creating and testing the ensemble.
- Prepare_VIII.R — functions and scripts for preparing the initial data for trainable combiners.
- Denoise.R — scripts for processing noise samples.
- Ensemles.R — scripts for creating ensembles.
- Threshold.R — scripts for determining thresholds.
- Test.R — scripts for testing ensembles.
- Averaging.R — scripts for averaging continuous outputs of ensembles.
- Voting_aver.R — combining averaged outputs in cascade by simple majority voting.
- Optim_VIII.R — scripts for optimization the hyperparameters of neural networks.
- Optim_mVIII.R — scripts for optimization the hyperparameters of neural networks and postprocessing.
- Voting.R — combining outputs of the superensemble in cascade by simple majority voting.
- SessionInfo_VII.txt — list of packages used in the article scripts.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/4722
 Combining trend and flat strategies
Combining trend and flat strategies
 PairPlot graph based on CGraphic for analyzing correlations between data arrays (time series)
PairPlot graph based on CGraphic for analyzing correlations between data arrays (time series)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
After choosing the best 7 ensembles and classifying it[=1,0,1] ,I would like to extract the data to train it on a Keras model, but I can't seem to find the specific dataframes.
Figure 11 shows the structural scheme of calculations. Above each stage is the name of the script. Under each stage is the name of the resulting data structure. What data do you want to use?
If you want to use the averaged continuous predictions of the seven best ensembles, then they are in the structure
k = c(origin/repaired/removed/relabeled)
j = c( half, mean, med, both)
If you need the predictions of the seven best in binary form, then they are in the structure
Hello again,
I am getting the following errors, which I cant resolve - any tips?
Error 1: "in { : task 1 failed - "object 'History' not found" , when I run the following code segment:
#---OptPar------ evalq({ foreach(i = 1:4) %do% { OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3) } -> best.res names(best.res) <- group }, env) evalq({ foreach(i = 1:4) %do% { OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3) } -> best.res1 names(best.res1) <- group }, env)Not sure where the History object is created, and couldnt find it at all in the github repo in the various .R files for this article
Error 2: "Yts" not found, when I run the following code segment:
Also not sure when/how the "Yts" is being created
I think both of these might be resolved by a piece of code that may be missing from the github repo?
Would appreciate any help you can provide, many thanks in advance