MQL5における動的時間伸縮を用いたパターン認識

MetaTrader 5 — 例 | 21 10月 2024, 12:24

167

Francis Dube

はじめに

パターン認識はトレーダーにとって常に貴重なツールです。ローソク足のユニークな組み合わせを特定したり、チャートに想像上の線を引いたりする際、これらのパターンはテクニカル分析の不可欠な要素となっています。人間は常にパターンを見つけて認識する能力に優れており、時には存在しないパターンを見てしまうこともあると言われています。したがって、金融時系列における潜在的に利益をもたらすパターンを特定する際には、より客観的な手法を適用することが有益です。本稿では、価格データからユニークなパターンを見つけるための客観的手法として、Dynamic Time Warping(DTW)（英語）（動的時間伸縮）の応用について議論します。その起源や仕組み、金融時系列分析への適用を探るとともに、純粋なMQL5でのアルゴリズムの実装を紹介し、実践的な例を通じてその使用を実証します。

動的時間伸縮

動的時間伸縮(DTW)は、時間と共に変化する2つのデータシーケンスの類似性を測定するために設計された高度なアルゴリズムです。このアルゴリズムは、速度やリズムが異なっていても、データポイント間の厳密な整列を必要とせずに類似性を測定します。従来の手法とは異なり、DTWはシーケンス間の最適なマッチングを見つけるためにワーピングや時間のストレッチを可能にする、より柔軟なアプローチを提供します。例えば、2人の人間が森の中を別々の道を歩いているとしましょう。2人とも同じ場所から出発し、同じ場所で歩き終わりますが、一方は他方より速く歩き、何らかの理由で任意に立ち止まるかもしれません。DTWは、異なる道を歩んでいても、2人の歩みを一致させる最善の方法を見つける手助けをします。この手法は、歩行速度、加速度、減速度の違いを効果的に考慮し、類似性の尺度を提供することができます。この汎用性により、DTWはオーディオ、ビデオ、グラフィックスを含む幅広いデータタイプに適用でき、シーケンシャルな形式に変換可能なデータはすべてDTW分析の候補となる可能性があります。

動的時間伸縮

DTWは、1968年にVintsyuk（英語）によって音声認識のために開発され、その後1978年に迫江博昭や千葉成美などの研究者によって改良されました。この手法は、類似したパターンを整列させるために時間次元を伸縮させることで、異なる長さのシーケンスを比較できるため、様々な分野で広く支持されています。DTWはその後、バイオインフォマティクスや歩行分析など、多岐にわたる分野で応用されています。金融市場は非線形で非定常な時系列データによって特徴付けられますが、ユークリッド距離のような従来の距離尺度では、このようなデータの複雑さや歪みを捉えることが難しい場合があります。しかし、DTWは時間的歪みを持つ時系列間の類似性を識別するのに優れており、金融市場の分析に適したツールとなっています。DTWは、時間的な整合性ではなく、シーケンスの形状に基づいて整列させることで、金融データにおける独自のパターンを発見することが可能です。

しくみ

DTWアルゴリズムを適用する目的は、候補シーケンスがあらかじめ定義された参照シーケンスにどれほど類似しているかを判断することです。アルゴリズムによって算出される最終的な指標は、候補シーケンスと参照シーケンスの類似度を示します。この値が低いほど、シーケンス同士が似ていることを意味し、完全に一致する場合はこの値は0になります。DTWアルゴリズムは、候補シーケンスと参照データセットとの間で最適な整列を見つけるために、特定の原則に従います。候補シーケンスのすべての点は、参照シーケンスの少なくとも1つのデータ点に対応しなければならず、その逆も同様です。また、一方のシーケンスの始まりは他方の始まりと一致し、終わりも同様に一致しなければなりません。さらに、シーケンスをトラバースする際には、対応する点は前方にのみ進む必要があります。これにより、一方のシーケンスのいかなる点も、もう一方のシーケンスのその点の前にある点と整列することができなくなります。

このプロセスは、2つのシーケンスの要素間のペアワイズ距離をキャプチャする距離行列の構築から始まります。この行列の各要素は、1番目のシーケンスの点と2番目のシーケンスの対応する点との間の距離を表します。この段階では、従来の空間距離測定のいずれかを使用できます。空間距離測定は、与えられた空間内のデータ点間の距離または非類似度を定量化するために用いられる数学的手法です。どの距離尺度を選択するかは、データの具体的な特性と手元のタスクに依存します。以下の表は、最も一般的な空間距離測定とそれぞれの簡単な説明を示しています。

ユークリッド距離

距離メトリック	詳細
ユークリッド距離	ユークリッド距離とは、ユークリッド空間における2点間の直線距離のことです。最も直感的で、広く使われている距離尺度です。
マンハッタン距離	マンハッタン距離は、タクシー距離や街区距離としても知られ、2点間の座標の差の絶対値を合計することで2点間の距離を測定します。
ミンコフスキー距離	ミンコフスキー距離は、ユークリッド距離とマンハッタン距離を一般化したものです。これは、異なる距離測定を切り替えるために調整できるパラメータを含んでいます。
チェビシェフ距離	チェビシェフ距離は、最大距離またはチェス盤距離とも呼ばれ、一対の点の座標間の最も大きな差を測定します。
コサイン類似度	コサイン類似度は、2つの非ゼロベクトル間の角度の余弦を測定し、大きさではなく方向の類似性を表します。

空間距離尺度の選択は、データの性質とタスクの特定の要件に依存します。これらの尺度の違いと用途を理解することは、有意義な分析のために最も適切な尺度を選択するのに役立ちます。

累積コスト計算式

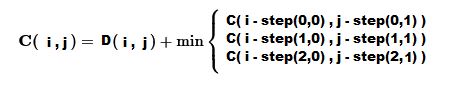
次の手順では、距離行列を使用して累積コスト行列を計算します。ここで各要素は、シーケンスの整列にかかる最小コストを表します。この整列プロセスでは、候補シーケンスが参照シーケンスにより酷似するように変換されます。累積コスト行列は、候補シーケンスの各点を参照シーケンスに合わせるために必要な変更の程度を定量化します。コストが大きいほど、より有意な変換が必要であり、シーケンス間の非類似性が大きいことを意味します。これらの累積コスト行列の値は、最適なワーピングパスを決定するために使用されます。ワーピングパスは、時系列間の距離を最小化しつつ、ある時系列を別の時系列にマッピングする整列のシーケンスを示します。基本的には、ワーピングパスはシーケンスの一部が他のシーケンスとできるだけ密接に整列するために、どのように伸張または圧縮されるかを示しています。

累積コスト行列のグリッド

ワーピングパスを見つけるには、シーケンスをグリッド状に配置し、一方のシーケンスをx軸に、もう一方のシーケンスをy軸に沿わせます。このグリッド上の各点は、1番目のシーケンスの要素と2番目のシーケンスの要素が一致する可能性を表します。ワーピングパスは、2つのシーケンス間の最良の整列を実現するグリッドを通るルートです。このパスは、両方のシーケンスの最初の要素に対応するグリッドの左下隅から始まり、両シーケンスの最後の要素に対応する右上隅で終わります。パスが進む際には、3つの方向に移動できます。すなわち、両方のシーケンスの要素にマッチする斜め方向、最初のシーケンスの要素を繰り返す水平方向、そして2番目のシーケンスの要素を繰り返す垂直方向です。この動きにより、整列プロセスは常に時間的に前進し、シーケンス内の要素をスキップしないことが保証されます。

ワーピングパスは、2つのシーケンスの整列要素間の累積距離またはコストを最小化するように選択されます。そのために、距離行列の値を、点の位置合わせに使用されるグリッドに重ね合わせます。グリッド上の各点におけるコストは、時間的に前進する際に考慮される3つの方向（斜め、水平、垂直）に従い、前の点からの隣接する累積距離の最小値に対応する距離メトリックを加算することで計算されます。各グリッド点は、対応するシーケンス値の距離メトリックに関連付けられているため、最小値は候補シーケンスを変換して参照シーケンスに一致させるために必要な操作を示します。もし累積距離の最小値が現在の点の対角線上にある場合、それはマッチング操作を表します。前の点からの最小の累積距離が現在の点まで水平であれば、それは挿入操作を示し、参照シーケンスからの値が候補シーケンスに効果的に挿入されることになります。逆に、累積距離の最小値が現在の点に対して垂直であれば、それは削除操作を意味し、候補シーケンスから値が削除されることになります。最小値を見つけるために考慮される事前の累積距離値の選択は、特定のステップパターンに支配されます。

ステップパターンは、整列中にシーケンス内の点の間で許容される移動や遷移を決定します。これらは、最小累積距離を計算する際に考慮される有効な方向（対角、水平、垂直）のいずれかの点の数を指定します。ステップパターンの選択は、整列プロセスと全体の距離計算に大きく影響を与えます。さまざまなステップパターンが存在し、それぞれが特定の用途に合わせて調整されています。また、前進と継続の原則を遵守する限り、独自のステップパターンを作成することも可能です。このテキストでは、さまざまな領域で効果的であることが実証されている、最も一般的かつ汎用的なステップパターンに焦点を当てます。他のステップパターンを探ることに興味がある方には、Sakoe-Chiba、Rabiner-Juang、Rabiner-Myersの論文が深い洞察を与えてくれるでしょう。

古典的対照的ステップパターン

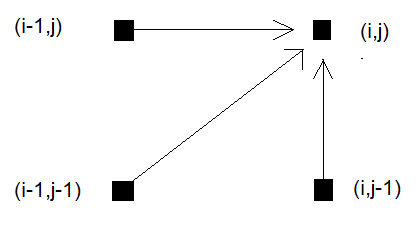
最も一般的なステップパターンは標準ステップパターンであり、対照的ステップパターンや古典的ステップパターンとも呼ばれています。このパターンの主な利点は、両方の時系列が完全にカバーされることを保証する点です。標準ステップパターンでは、現在の点の上、右、対角線上にある直近の値のみを考慮するため、グリッド上での対角線、水平、垂直の1ステップ移動が可能となります。

クラシック非対称ステップパターン

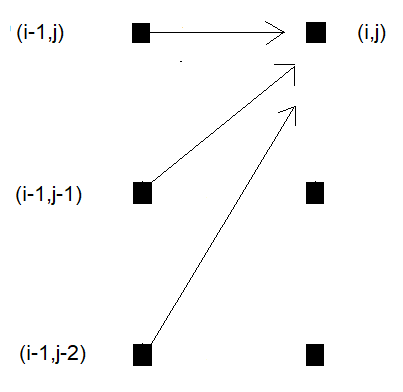
もう1つの人気のあるステップパターンは、古典的非対称パターンです。このパターンは、標準的なステップパターンと同様に3方向への遷移を定義しますが、1つのシーケンスに偏りが生じます。アルゴリズムは斜めに進むことが可能ですが、点がスキップされた場合、一方のシーケンスで進むことが他方よりも有利になる場合があります。このパターンは、グリッド上でのアルゴリズムの動きを制限する追加の制約と組み合わせて使用されることが一般的です。非対称ステップパターンでは、さらに勾配制約が適用され、ワーピングパスの急勾配や平坦度が制限されます。この制約は、一方のシーケンスが他方のシーケンスに対して過度に引き伸ばされたり圧縮されたりするのを防ぎ、シーケンスの長さやシフトが類似していると予想される場合に特に有効です。

技術的に完璧であるが無意味な整列を防ぐために、追加の制約を適用することができますが、これはデータの過剰適合を引き起こす可能性があります。これらの制約は、シーケンスの過剰な伸張や圧縮を防ぎ、分析対象のデータの文脈において整列が論理的に意味をなすことを保証します。このような制約は「グローバル制約」として知られ、実用的なアプリケーションにおけるDTWアルゴリズムの有効性と解釈可能性を高めます。2つの一般的なグローバル制約には、Sakoe-ChibaバンドとItakura平行四辺形があります。

Sakoe-Chibaバンド

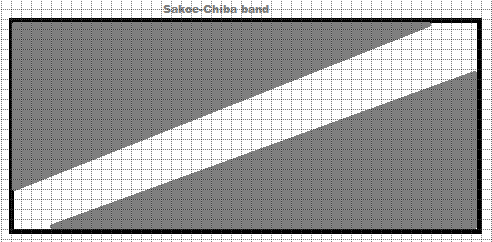
Sakoe-Chibaバンドは、整列行列の対角線を中心に固定されたバンド内にワーピングパスを制限します。これにより、整列が元のタイミングやシフトから大きくずれるのを防ぎます。この手法は、わずかなタイミングの違いが想定される一方で、大きなずれが発生することは想定されない作業において特に有効です。

Itakura

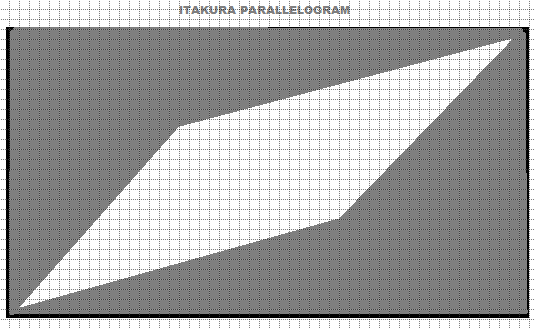
Itakura平行四辺形拘束は、ワーピングパスが収まるべき平行四辺形状の領域を定義します。この領域は両端が狭く、中間が広くなっています。これは、シーケンスの最初と最後がより密接に整列し、中間部分がある程度フレキシブルであることが期待される場合に特に効果的です。グローバル制約はワーピングプロセスを制御し、得られた整列が特定のタスクに関連することを保証するため、DTWにとって不可欠です。データセットの特性や分析の目的に基づいて、最も適切な制約を選択することが重要です。

累積コスト行列が完成すると、それを用いて最適なワーピングパスを決定します。アルゴリズムは、累積コスト行列の最後の要素から最初の要素まで遡り、整列コストの合計を最小化するパスを特定します。このパスは、シーケンス間の最適な整列を表します。累積コスト行列の最終値は総合距離スコアとなり、正規化距離スコアの算出にも使用されます。ワーピングパスは、両シーケンスの整列点を表すインデックスのペアをリストアップします。整列手順を評価するには、最適なワーピングパスをプロットすることが一般的です。満足のいく結果が得られれば、ほぼ対角線上にプロットされるはずです。この対角線プロットは、シーケンスがうまく整列していることを示し、完全に直線の対角線は2つの同一シーケンスに対応します。以下のセクションでは、動的時間伸縮のMQL5ネイティブ実装について詳しく説明します。

MQL5での実装

DTW MQL5の実装は、インクルードファイルdtw.mqhに示されています。動的時間伸縮の全側面が完全に、あるいは広範囲にカバーされているわけではありません。後ほど、より多くの機能を提供するDTWのPython実装を見てみましょう。このライブラリを作成した目的は、距離スコアを計算するための基本的な機能を提供することです。このライブラリはdtw-pythonモジュールの部分的なフォークです。

コードはまず、ステップパターンやさまざまな距離測定、グローバル制約の列挙体を定義することから始まる。

//+------------------------------------------------------------------+
//|  step patterns                                                   |
//+------------------------------------------------------------------+
enum ENUM_STEP_PATTERN
  {
   STEP_SYMM1=0,//symmetric1
   STEP_SYMM2,//symmetric2
   STEP_ASYMM//asymmetric
  };

ENUM_STEP_PATTERN：DTWアルゴリズムのパス探索フェーズで許容される遷移パターンを制限する列挙体のセットを定義します。これらのパターンは、ワーピング処理の指針となり、時系列間の許容される整列に影響を与えます。

//+------------------------------------------------------------------+
//|  distance metric                                                 |
//+------------------------------------------------------------------+
enum ENUM_DIST_METRIC
  {
   DIST_EUCLIDEAN=0,//euclidean
   DIST_CITYBLOCK,//city block
   DIST_COSINE,//cosine
   DIST_CORRELATION,//correlation
   DIST_CHEBYSHEV,//chebyshev
   DIST_SQEUCLIDEAN//squared euclidean
  };

ENUM_DIST_METRIC：サポートされる距離メトリクスに対応する列挙体のコレクションを提供します。これらのメトリクスは、ユークリッド距離、シティブロック距離などのオプションで、時系列のデータポイント間の非類似度を定量化します。

//+------------------------------------------------------------------+
//|   window function                                                |
//+------------------------------------------------------------------+
enum ENUM_GLOBAL_CONSTRAINT
  {
   CONSTRAINT_NONE=0,// no constrains applied
   CONSTRAINT_SAKOECHIBA,// sakoe chiba
   CONSTRAINT_SLATEDBAND,// slated band
   CONSTRAINT_ITAKURA// itakura
  };

ENUM_GLOBAL_CONSTRAINT：パス検索中に制約を課すさまざまなグローバル制約を包含します。これらは反りの柔軟性に影響を与え、整列精度を向上させる可能性があります。

//+------------------------------------------------------------------+
//| lists the transitions allowed while searching                    |
//|for the minimum-distance path                                     |
//+------------------------------------------------------------------+
class CStepPattern
  {
private:
   matrix            m_mx,m_stepsMatrix;
   ENUM_HINT         m_stephint;
public:
                     CStepPattern(matrix &mx, matrix &stepmatrix, ENUM_HINT hint=HINT_NA)
     {
      m_mx = mx;
      m_stepsMatrix = stepmatrix;
      m_stephint = hint;
     }
                    ~CStepPattern(void)
     {

     }
   matrix            getStepMatrix(void)
     {
      return m_stepsMatrix;
     }
   ulong             getNRows(void)
     {
      return m_mx.Rows();
     }
   int               getNPatterns(void)
     {
      vector vec = m_mx.Col(0);
      return (int(vec.Max()));
     }

   CStepPattern*     T(void)
     {
      ulong cols[] = {0, 2, 1, 3};

      matrix cpy = np::selectMatrixCols(m_mx,cols);
      ENUM_HINT hint = m_stephint;

      if(m_stephint == HINT_N)
         hint = HINT_M;
      else
         if(m_stephint == HINT_M)
            hint = HINT_N;

      CStepPattern* out = new CStepPattern(cpy,m_stepsMatrix,hint);

      return out;
     }

   matrix            extractPattern(vector &sn)
     {
      vector col  =  m_mx.Col(0);
      matrix out = matrix::Ones(1,1);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == sn[j])
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols()-1,100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               vector vv = np::sliceVector(v,1);
               if(!out.Row(vv,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      if(!np::reverseMatrixRows(out))
        {
         Print(__FUNCTION__, " Reverse Matrix failure ");
         return matrix::Zeros(1,1);
        }
      return out;
     }

   matrix            mkDIrDeltas(void)
     {
      matrix out = matrix::Zeros(1,1);
      vector col = m_mx.Col(3);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == -1.0)
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols(),100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               if(!out.Row(v,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      return np::sliceMatrixCols(out,1,3);
     }

   matrix             getP(void)
     {
      ulong sel[] = {0, 2, 1, 3};
      matrix s = np::selectMatrixCols(m_mx,sel);
      return s;
     }

   matrix            getMx(void)
     {
      return m_mx;
     }
  };

CStepPatternは、許容される遷移と操作を定義する行列を管理することで、さまざまなステップパターンを扱うように設計されたクラスです。特定のシーケンスに基づいてパターンを抽出し、DTWの計算に不可欠な方向性デルタの行列を操作するメソッドを提供します。

//+------------------------------------------------------------------+
//| Global constraints                                               |
//+------------------------------------------------------------------+
class CConstraint
  {
public:
                     CConstraint(void)
     {

     }
                    ~CConstraint(void)
     {

     }

   static matrix       noConstraint(ulong iw,ulong jw)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      for(ulong i = 0; i<mats[0].Rows(); i++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            long value = long(mats[0][i][j]);
            mats[0][i][j] = (double)(value|1);
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       sakoeChibaConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize, ulong winsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      matrix abs = MathAbs(mats[1]-mats[0]);

      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;
     }

   static matrix       itakuraConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      long a,b,c,d;

      for(ulong i = 0, k = 0; i<mats[0].Rows() && k<mats[1].Rows(); i++,k++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            a = long(mats[1][k][j]) < (2*long(mats[0][i][j]))?1:0;
            b = long(mats[0][i][j]) <=(2*long(mats[1][k][j]))?1:0;
            c = long(mats[0][i][j]) >=(long(qsize)-1-2*(long(refsize)-long(mats[1][k][j])))?1:0;
            d = long(mats[1][k][j]) > (long(refsize)-1-2*(long(qsize)-long(mats[0][i][j])))?1:0;
            mats[0][i][j] = double(ulong(a&b&c&d));
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       slantedBandConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize,ulong winsize)
     {

      matrix mats[];

      np::indices(iw,jw,mats);

      matrix  diagj = (mats[0]*refsize/qsize);

      matrix abs = MathAbs(mats[1]-diagj);


      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;

     }

  };

CConstraintクラスには、Sakoe-Chiba、Itakura、Slanted Bandなど、さまざまなタイプの制約を有効にするための静的メソッドが含まれています。これらは、あらかじめ定義された基準に基づいて探索空間を制限することにより、計算効率と関連性を向上させるためにDTW整列を制約するのに役立ちます。

noConstraint()メソッド：制約がないことを意味する1で満たされた行列を生成します。

sakoeChibaConstraint()メソッド：指定されたウィンドウサイズと時系列の長さに基づいて、Sakoe-Chiba制約を課します。

itakuraWindow()メソッド：時系列の長さを用いてItakura制約を強制します。

slantedBandConstraint()メソッド：ウィンドウサイズと時系列の長さに基づいたSlanted Band制約を実装します。

Cdtwクラスは、DTWの計算を担当するコアクラスです。

   //+------------------------------------------------------------------+
   //|     main interface method for dtw                                |
   //+------------------------------------------------------------------+

   bool              dtw(matrix&x, matrix&y, ENUM_DIST_METRIC dist_method,ENUM_STEP_PATTERN step_pattern=STEP_SYMM2, ENUM_GLOBAL_CONSTRAINT win_type=CONSTRAINT_NONE,ulong winsize=0)
     {
      if(y.Cols()!=x.Cols())
        {
         Print(__FUNCTION__, " invalid input parameters, size containers donot match. ");
         return false;
        }

      if(CheckPointer(m_stepPattern)==POINTER_DYNAMIC)
         delete m_stepPattern;

      switch(step_pattern)
        {
         case STEP_SYMM1:
            m_stepPattern = new CStepPattern(_symmetric1,Symmetric);
            m_stephint = HINT_NA;
            break;

         case STEP_SYMM2:
            m_stepPattern = new CStepPattern(_symmetric2,Symmetric,HINT_NM);
            m_stephint = HINT_NM;
            break;

         case STEP_ASYMM:
            m_stepPattern = new CStepPattern(_asymmetric,Asymmetric,HINT_N);
            m_stephint = HINT_N;
            break;
        }

      if(CheckPointer(m_stepPattern)==POINTER_INVALID)
        {
         Print(__FUNCTION__," failed step pointer initialization ", GetLastError());
         return false;
        }

      matrix stepsMatrix = m_stepPattern.getStepMatrix();
      m_query = x;
      m_qlen = x.Rows();
      m_ref = y;
      m_reflen = y.Rows();
      m_distMetric = dist_method;
      m_winMethod = win_type;
      m_winsize = winsize;

      if(y.Rows())
        {
         if(!m_distance.Resize(m_qlen,m_reflen))
           {
            Print(__FUNCTION__," resize error ", GetLastError());
            return false;
           }
         for(ulong i = 0; i<m_qlen; i++)
            for(ulong j =0; j<m_reflen; j++)
               m_distance[i][j]=dist(m_query.Row(i),m_ref.Row(j));
        }
      else
         m_distance = m_query;

      ulong n,m;
      n=m_distance.Rows();
      m=m_distance.Cols();
      matrix wm;
      if(m_winMethod == CONSTRAINT_NONE)
         wm = matrix::Ones(m_distance.Rows(), m_distance.Cols());
      else
        {
         switch(m_winMethod)
           {
            case CONSTRAINT_ITAKURA:
               wm = CConstraint::itakuraConstraint(n,m,m_qlen,m_reflen);
               break;
            case CONSTRAINT_SAKOECHIBA:
               wm = CConstraint::sakoeChibaConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            case CONSTRAINT_SLATEDBAND:
               wm = CConstraint::slantedBandConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            default:
               wm = CConstraint::noConstraint(n,m);
               break;
           }
        }

      if(m_winMethod!=CONSTRAINT_NONE)
        {
         for(ulong i = 0; i<wm.Rows(); i++)
            for(ulong j = 0; j<wm.Cols(); j++)
               if((i+j)>0 && wm[i][j] != 1.0)
                  m_distance[i][j] = wm[i][j];
        }


      m_costMatrix = matrix::Zeros(m_distance.Rows()+ulong(stepsMatrix.Col(0).Max()),m_distance.Cols()+ulong(stepsMatrix.Col(1).Max()));
      m_costMatrix.Fill(double("inf"));
      m_costMatrix[ulong(stepsMatrix.Col(0).Max())][ulong(stepsMatrix.Col(1).Max())] = m_distance[0][0];

      m_dirMatrix = matrix::Zeros(m_costMatrix.Rows(),m_costMatrix.Cols());
      m_dirMatrix.Fill(double(INT_MIN));
      for(ulong i = 0; i<m_dirMatrix.Cols(); i++)
         m_dirMatrix[0][i] = double(1);
      for(ulong i = 0; i<m_dirMatrix.Rows(); i++)
         m_dirMatrix[i][0] = double(2);

      if(!calCM(m_distance,stepsMatrix,m_costMatrix,m_dirMatrix))
        {
         Print(__FUNCTION__, " computeCM() failed ");
         return false;
        }

      m_jmin = m_costMatrix.Cols() - 1;

      return true;
     }

DTWを実行する主要な関数としてdtw()メソッドを提供します。このメソッドは、一変量（ベクトル）と多変量（行列）の時系列に対応するようにオーバーロードされています。入力引数として、2つの時系列（行列またはベクトルとして表現）、距離メトリック、ステップパターン、グローバル制約、ウィンドウサイズを取ります。呼び出されると、メソッドは入力データと選択されたステップパターンの妥当性について様々な確認を実行することから始まります。続いて、選択された距離メトリックに基づいて距離行列が計算されます。グローバル制約が指定された場合、DTWアルゴリズムで使用されるコスト行列と方向行列はそれに応じて準備されます。その後、calCM()関数が呼び出され、累積コスト行列が計算されます。最後に、dtw()関数は成功または失敗を示すブール値を返します。

   //+------------------------------------------------------------------+
   //|    Get the optimal path: corresponding points from both series   |
   //+------------------------------------------------------------------+

   matrix            warpPath(bool openEnd=false)
     {
      matrix stmatrix = m_stepPattern.getStepMatrix();
      return backtrack(m_dirMatrix,stmatrix,openEnd,openEnd?long(m_costMatrix.Row(m_costMatrix.Rows()-1).ArgMin()):-1);
     }

warpPath()メソッドは、パスの終了（オープンまたはクローズ）を制御するオプションの'openEnd'引数に基づいて、両方の時系列から識別された最適なパス（対応する点）を取得します。

   //+------------------------------------------------------------------+
   //|     Get the accumulated cost matrix                              |
   //+------------------------------------------------------------------+

   matrix            costMatrix(void)
     {
      return m_costMatrix;
     }

costMatrix()メソッドは、DTW アルゴリズムの主要な出力である累積コスト行列へのアクセスを提供します。

   //+------------------------------------------------------------------+
   //|       Get the cost matrix                                        |
   //+------------------------------------------------------------------+

   matrix            localCostMatrix(void)
     {
      return m_distance;
     }

localCostMatrix()メソッドは、時系列のデータポイント間のペアワイズ距離を表すローカル距離行列を返します。

   //+------------------------------------------------------------------+
   //|        Get the direction matrix                                  |
   //+------------------------------------------------------------------+

   matrix            directionMatrix(void)
     {
      return m_dirMatrix;
     }

directionMatrix()メソッドは、方向行列へのアクセスを許可します。方向行列は、DTW中のパス探索プロセスを導く役割を果たします。

   //+------------------------------------------------------------------+
   //|  private method implementing accumulated cost calculation        |
   //+------------------------------------------------------------------+

   bool              calCM(matrix &distMatrix,matrix &stepMatrix,matrix &costMatrix,matrix &dirMatrix)
     {
      ulong max0,max1;
      max0 = ulong(stepMatrix.Col(0).Max());
      max1 = ulong(stepMatrix.Col(1).Max());
      double curCost,curd;

      for(ulong i = max0; i<costMatrix.Rows(); i++)
        {
         for(ulong j = max1; j<costMatrix.Cols(); j++)
           {
            for(ulong k = 0; k<stepMatrix.Rows(); k++)
              {
               curd = costMatrix[i-ulong(stepMatrix[k][0])][j-ulong(stepMatrix[k][1])];
               curCost = curd + distMatrix[i-max0][j-max1];
               if(curCost<costMatrix[i][j])
                 {
                  costMatrix[i][j] = curCost;
                  dirMatrix[i][j] = double(k);
                 }
              }
           }
        }
      costMatrix = np::sliceMatrix(costMatrix,max0,END,1,max1);
      dirMatrix  = np::sliceMatrix(dirMatrix,max0,END,1,max1);
      return true;

     }

calCM() privateメソッドは、DTWアルゴリズムの中核をなす累積コスト行列を計算します。距離行列、ステップパターン、コスト行列、方向行列を入力として利用します。

   //+------------------------------------------------------------------+
   //|  distance metric calculation                                     |
   //+------------------------------------------------------------------+


   double            dist(vector &u,vector &v)
     {
      switch(m_distMetric)
        {
         case DIST_EUCLIDEAN:
            return euclidean(u,v);
         case DIST_CITYBLOCK:
            return cityblock(u,v);
         case DIST_CHEBYSHEV:
            return chebyshev(u,v);
         case DIST_CORRELATION:
            return correlation(u,v);
         case DIST_COSINE:
            return cosine(u,v);
         case DIST_SQEUCLIDEAN:
            return sqeuclidean(u,v);
         default:
            Print(__FUNCTION__, " invalid parameter ");
            return EMPTY_VALUE;
        }
     }

dist() private関数は、選択された距離メトリックに基づいて2つのデータ点間の距離を計算します。

Cdtwクラスのテスト

このセクションでは、Cdtwクラスの能力を、PythonベースのDTW実装によって生成された出力と比較することによって示します。dtw-pythonモジュールは、Pythonにおける数多くのDTW実装の1つです。Pythonで簡単なスクリプトを実行し、その結果がMQL5の実装で再現できるかどうかを確認します。まずPythonスクリプトをリストアップします。

import numpy as np
import matplotlib.pyplot as plt
import dtw

len = 10
add_noise = True
noise = np.random.uniform(size=len)if add_noise else np.zeros((len,))
arx = np.linspace(start = 1, stop = 6.28,num = len)
query = np.sin(arx) + noise
ref = np.cos(arx)

alignment =  dtw.dtw(query,ref,dist_method='cosine',step_pattern='symmetric2', window_type=None,keep_internals=True)
print( f'Accumulated Cost Matrix is {alignment.costMatrix}')
print(f'Distance is {alignment.distance}, \n normalize distance is {alignment.normalizedDistance}')
print(f'Warp Path is {alignment.index1[:]}:{alignment.index2[:]}')
plt.plot(alignment.index1,alignment.index2)
plt.show()

このスクリプトは、DTWアルゴリズムを使用して2つの時系列を整列し、その整列を視覚化する方法を示します。最初に、数値演算のためのnumpy、プロットのためのmatplotlib.pyplot、そしてDTWアルゴリズムの実装のためのdtwという必要なライブラリをインポートします。時系列の長さは10に設定され、1から6.28の間に等間隔で配置された10個の値からなる配列arxが作成されます。時系列queryはarxの正弦を取り、ランダムなノイズを加えて生成されます。一方、参照時系列refはarxの余弦をとって生成されます。次に、DTW整列がquery系列とref系列の間で実行されます。時系列間の距離は余弦距離法を用いて測定され、対称的なステップパターンがワーピングパスに適用されます。ウィンドウの制約は使用されず、コスト行列やワーピングパスのような内部の詳細も保持されます。

その後、このコードは累積コスト行列、合計整列距離、正規化距離、および2つの系列間のワーピングパスのインデックスを表示します。最後に、2つの時系列のインデックスがどのように整列しているかを示す整列インデックスをプロットすることで、ワーピングパスが可視化されます。この方法により、位相がずれていたり、長さが異なっていたりする2つの時系列を詳細に比較することができ、一方の時系列が他方の時系列と整合するためにどのようにゆがむかを観察することができます。

今説明したPythonコードと同等のMQL5コードを以下に示します。

//+------------------------------------------------------------------+
//|                                                      dtwTest.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Uniform.mqh>
#include<dtw.mqh>
//---
input ulong series_len = 10;
input bool  AddRandomNoise = false;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input bool WarpPathConstraint = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(series_len<10)
     {
      Alert(" Invalid input for series_len parameter. Should be >=10 ");
      return;
     }
//---
   vector arg = np::linspace(1.0,6.28,series_len);
   vector noise = vector::Zeros(series_len);

   if(AddRandomNoise)
     {
      double array[];
      if(!MathRandomUniform(0.0,1.0,int(series_len),array))
        {
         Print(__LINE__, " MathRandomUniform() failed ", GetLastError());
         return;
        }

      if(!noise.Assign(array))
        {
         Print(__LINE__, " vector assignment failure ", GetLastError());
         return;
        }
     }

   vector q = sin(arg) + noise; // candidate sequence
   vector rf =  cos(arg);       // reference sequence

   Cdtw cdtw;

   cdtw.dtw(q,rf,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize);

   Print(" local cm ", cdtw.localCostMatrix());
   Print(" final cm ", cdtw.costMatrix());
   Print(" direction matrix \n", cdtw.directionMatrix());
   matrix path = cdtw.warpPath();
   Print(" Warp path \n", cdtw.warpPath());
   Print(" Distance metric ", cdtw.distance());
   Print(" Normalized Distance metric ", cdtw.normalizedDistance());

   vector xx = path.Col(0);
   vector yy = path.Col(1);

   CGraphic *g = np::plotXY(xx,yy,"Warp Plot", " Query ", " Reference ");

   Sleep(20000);
   g.Destroy();
   ChartRedraw();
   delete g;
  }
//+------------------------------------------------------------------+

以下は、Pythonスクリプトからの出力です。

KQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Accumulated Cost Matrix is [[ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
RD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
FH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
JL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
NQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
GD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 2.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
QH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 4.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
KL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
GS      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  2.  2.  2.  2.  2.  2.  0.  0.  0.]
PJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  4.  4.  4.  4.  4.  4.  0.  0.  0.]]
LJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Distance is 0.0, 
MM      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  normalize distance is 0.0
CH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Warp Path is [0 1 2 3 4 5 5 5 5 6 7 8 8 9]:[0 0 0 0 0 1 2 3 4 5 6 7 8 9]

Python出力からのワーピングパス

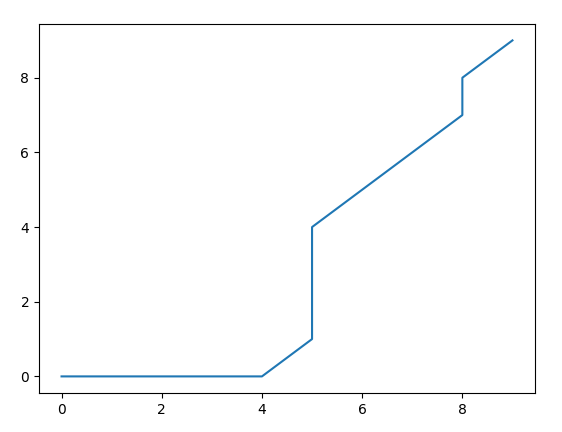
以下は、MQL5スクリプトからの出力です。

NE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         local cm [[0,2,2,2,2,2,2,0,0,0]
LH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
HE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
RL      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
DF      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,0,0,2.220446049250313e-16,0,0,2,2,2]
ND      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,2,2,2]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,2.220446049250313e-16,2,2,2]
RS      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
OH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]]
ML      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         final cm [[0,2,4,6,8,10,12,12,12,12]
JR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
EI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16,2,4,6]
CP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2,4,6]
EH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,2,4,6]
IN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2,2,2,2,2,2,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4,4,4,4,4,4,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]]
MO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         direction matrix 
QK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[-2147483648,1,1,1,1,1,1,1,1,1]
GN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
QQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
CK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
MR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
OE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,1,1,1,1,1,1,1,1]
HO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,1,1,1,0,0]
MF      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,0,0]
CH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,1,1]
LN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,2,0,0]]
PK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Warp path 
HM      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[9,9]
GJ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,8]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,7]
DK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [7,6]
HP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,5]
QI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4]
GQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,3]
RN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,2]
MG      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,1]
CO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,0]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [3,0]
EL      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0]
JE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [1,0]
DO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,0]]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Distance metric 4.440892098500626e-16
NR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Normalized Distance metric 2.2204460492503132e-17

MT5スクリプトからのワーピングパス

両スクリプトの出力を比較すると、コードは十分に機能しているようです。そのため、より実用的なことに使うことができます。そこで、DTWを戦略策定にどのように活用できるかを考えてみます。

動的時間伸縮の適用

DTWは、金融時系列における柔軟なパターン認識と比較技術を可能にし、自動化された戦略開発に活用することができます。例えば、DTWは異なるスケールやさまざまな時間軸で発生する場合でも、繰り返し発生する価格パターンを識別できます。これらのパターンを過去のデータと整合させることで、市場の大きな動きに先行する微妙なシフトやアノマリーを検出することが可能になります。

バックテストにおいては、DTWを適用して、それぞれの時系列結果を揃えることで、異なる市場環境下での戦略のパフォーマンスを比較できます。このアプローチは、市場行動の変化に対する戦略の適応度を評価するのに役立ち、戦略の頑健性をより深く理解する手助けとなります。さらに、DTWは類似の売買シグナルや市場状態をクラスタリングするためにも使用でき、これを分析することで高確率の売買機会を特定することが可能です。こうしたクラスタを認識することで、繰り返し起こる市場行動をより効果的に利用するために戦略を微調整できます。

また、アルゴリズム戦略の最適化において、DTWは最も有望なパラメータセットと、現在の市場ダイナミクスに酷似した過去の市場状況とのマッチングを支援します。これにより、進化する市場環境によりダイナミックに適応する戦略が可能になります。DTWを活用することで、自動化された戦略はより適応的になり、文脈を認識し、金融データにおける複雑な時間的関係を理解できるようになります。しかし、DTWは便利なツールである一方で、魔法の杖ではありません。特に経験の浅いユーザーにとっては、扱いが難しいかもしれません。

DTWの最大の課題のひとつは、その動作パラメータの設定です。グローバル制約とローカル制約の適切な組み合わせは、このメソッドを最大限に活用するために極めて重要です。DTWは偽の一致を生み出しやすく、最良の結果を得るためには多くの試行錯誤が必要です。これは、以下に示すMQL5スクリプトで具体的に示されます。

//+------------------------------------------------------------------+
//|                                             dtwPatternSearch.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\LogReturns.ex5"
#property script_show_inputs
#include<dtw.mqh>
#include<ErrorDescription.mqh>
enum ENUM_PRICE
  {
   CLOSE=0,//close price
   MEDIAN,//median price
   TYPICAL//typical price
  };

enum ENUM_TRANSFORM_TYPE
  {
   PERCENT_DIFF=0,//percent difference
   LOG_DIFF//log difference
  };
//--- input parameters
input string   Pattern = "0.0469,0.0093,0.0697,-0.0699";
input string   SymbolName="BTCUSD";
input datetime SearchStartDate=D'2024.06.01';
input datetime SearchStopDate=D'2018.04.22';
input double   NormalizedDistanceThreshold=0.01;
input ENUM_TIMEFRAMES      TimeFrame=PERIOD_D1;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input ENUM_PRICE AppliedPrice=CLOSE;
input ENUM_TRANSFORM_TYPE AppliedTransform=LOG_DIFF;
input int Lag = 1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   string pattern_values[];
//---
   int len = StringSplit(Pattern,StringGetCharacter(",",0),pattern_values);
   if(pattern_values[len-1]=="")
      len--;
//---
   if(len<3)
     {
      Alert("Pattern sequence is inadequately defined");
      return;
     }
//---
   vector pattern(len);
   for(ulong i = 0; i<pattern.Size(); i++)
      pattern[i]=StringToDouble(pattern_values[i]);
//---set prices handle
   int handle = INVALID_HANDLE;
   handle=iCustom(SymbolName!=""?SymbolName:NULL,TimeFrame,"::Indicators\\LogReturns.ex5",AppliedPrice,AppliedTransform,1);
   if(handle==INVALID_HANDLE)
     {
      Print("invalid handle ",ErrorDescription(GetLastError()));
      return;
     }
//---
   vector searchBuffer;
   if(!searchBuffer.CopyIndicatorBuffer(handle,0,SearchStartDate,SearchStopDate))
     {
      Print("History loading error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   ulong stop = searchBuffer.Size()-pattern.Size();
   vector subv;
   Cdtw cdtw;
   ulong counter=0;
   for(ulong i = 0; i<stop; i++)
     {
      subv = np::sliceVector(searchBuffer,i,i+pattern.Size());

      if(!cdtw.dtw(subv,pattern,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize))
        {
         Print(" dtw failed ");
         return;
        }

      if(cdtw.normalizedDistance()<NormalizedDistanceThreshold)
        {
         counter++;
         Print(" pattern found  ", datetime(SearchStopDate+(PeriodSeconds(TimeFrame)*(i+pattern.Size()-1))));
        }
     }
//---
   Print(" SearchBuffer size ", searchBuffer.Size());
   Print(" Reference pattern found ", counter, " times.");
  }
//+------------------------------------------------------------------+

このスクリプトでは、指標「LogReturns.ex5」によって計算された一連のログリターンから構成される任意のパターンを定義できます。できます。このスクリプトは、比較のために動的時間伸縮(DTW)を使用して、金融商品の価格データ内の特定のパターンを検索するように設計されています。DTWアルゴリズム用のdtw.mqhやエラー記述を処理するためのErrorDescription.mqhなど、必要なライブラリが含まれています。スクリプトは2つの列挙体を定義しています。ENUM_PRICEは使用する価格の種類（終値、中央値、典型値）を指定し、ENUM_TRANSFORM_TYPEは価格データの変換方法（パーセント差または対数差）を指定します。

入力パラメータには、マッチさせるパターン、銘柄名（例：BTCUSD）、検索の日付範囲、正規化距離のしきい値、データの時間枠、距離メトリック、ステップパターン、グローバル制約、制約のウィンドウサイズ、使用する価格のタイプ、適用する変換のタイプ、ラグ値など、検索の詳細を指定できます。スクリプトが起動すると、まず入力されたパターン文字列を値の配列に分割し、パターンが少なくとも3つの値で適切に定義されていることを確認します。パターンが有効であれば、次の処理のためにベクトル形式に変換されます。次に、スクリプトはiCustom関数を使用して、選択した価格タイプと変換をデータに適用するカスタム指標（LogReturns.ex5）を呼び出し、価格データのロードを試みます。iCustomから返されたハンドルが無効な場合、エラーメッセージが出力され、スクリプトは終了します。

価格データが正常にロードされると、そのデータはsearchBufferベクトルに格納されます。次に、スクリプトはsearchBufferを反復処理して、パターンと同じサイズの小さなサブベクトルにスライスし、DTWアルゴリズムを使って各サブベクトルをパターンと比較します。DTW比較は、指定された距離メトリック、ステップパターン、およびグローバル制約を使用しておこないます。各比較について、サブベクトルとパターンとの間の正規化された距離が指定されたしきい値より小さい場合、スクリプトは価格データのその時点でパターンが見つかったとみなします。パターンが見つかったタイムスタンプを示すメッセージを表示し、カウンタをインクリメントします。最後に、スクリプトはsearchBufferのサイズと、指定された日付範囲内でパターンが見つかった合計回数を表示します。このスクリプトは、過去の価格データから特定のパターンを自動検出することができ、パターン認識に基づく取引戦略の開発に役立ちます。

デフォルトのシーケンスは以下のようなパターンです。

検索するパターン

異なる制約を適用してスクリプトを実行すると、さまざまな数のマッチが生成されます。これはデフォルトの設定での出力です。

RN      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Chosen Parameters
IJ      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Distance Threshold 0.01
CS      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    DIST_EUCLIDEAN
ND      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    STEP_SYMM2
CN      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    CONSTRAINT_NONE
HG      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     WinSize 0
OO      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     pattern found  2018.04.25 00:00:00
NJ      0       22:00:09.221    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.04.28 00:00:00
KD      0       22:00:09.222    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.07.01 00:00:00
QO      0       22:00:09.230    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.04.27 00:00:00
II      0       22:00:09.234    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.10.26 00:00:00
PD      0       22:00:09.237    dtwPatternSearch (BTCUSD,D1)     pattern found  2021.02.06 00:00:00
RN      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     pattern found  2024.01.29 00:00:00
DH      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     SearchBuffer size 2197
PQ      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     Reference pattern found 7 times.

NormalizedDistanceThresholdパラメータが、マッチが存在するかどうかの判断に重要な役割を果たすことは明らかです。それでも、制約条件が変われば結果はかなり違ってきます。制約だけでなく、ユーザーは適切な距離メトリックを選択しなければなりません。明らかに、DTWアルゴリズムを採用する際には、かなりのドメイン知識が不可欠です。

結論

動的時間伸縮(DTW)は、金融時系列分析におけるパターン認識に対して洗練されたアプローチを提供しますが、考慮すべきいくつかの欠点も伴います。まず、DTWは特に長い時系列や大規模なデータセットを扱う際に計算量が増加します。このアルゴリズムでは、ある時系列の各点を別の時系列の各点と比較する必要があり、そのため処理時間とメモリ使用量が大きくなる可能性があります。これは特に、高頻度の金融データを分析したり、リアルタイムでの分析を試みる際に問題となります。次に、DTWは金融データのノイズや外れ値に対して敏感です。

金融時系列は市場の変動によりノイズが多く、小さな変動や異常がDTWアルゴリズムによる誤った整列を引き起こすことがあります。この感度は、パターン認識において、有意な予測力を持たないパターンを特定する偽陽性を引き起こす可能性があります。最後に、DTWには解釈性の面で課題があります。DTWは時系列間の類似度を測定しますが、ワーピングパスや結果として得られる距離指標は、特に明確で実行可能なインサイトが重要な金融分析の文脈において、意味のある方法で解釈するのが難しいことがあります。これらの課題から、DTWは金融時系列のパターン認識において有用なツールであるものの、その適用には注意が必要であり、多くの場合、その限界に対処できる他の分析手法と組み合わせる必要があることが示唆されます。

ファイル	詳細
Mql5\include\np.mqh	様々なベクトルおよび行列ユーティリティ関数のヘッダファイル
Mql5\include\dtw.mqh	動的時間伸縮アルゴリズムのMQL5実装を含むインクルードファイル
Mql5\indicators\LogReturns.mq5	価格系列の対数リターンの指標
Mql5\scripts\dwTest.mq5	DTWのMQL5実装のテストとデモンストレーションに使用されるスクリプト
Mql5\scripts\dtwPatternSearch.mq5	データのサンプルから任意のパターンを検索するスクリプト
Mql5\scripts\DTW.py	dtw-pythonモジュールを使用して、DTWアルゴリズムを使用して2つの系列を整列するPythonスクリプト