
An introduction to Receiver Operating Characteristic curves
Introduction
The Receiver Operating Characteristic (ROC) graph serves as a method for visualizing, organizing, and selecting classifiers based on their performance. Originating in signal detection theory, ROC graphs have been employed to illustrate the trade-off between true positive rates and false positive rates of classifiers. Beyond their general utility as a performance graphing method, ROC curves exhibit properties that render them particularly valuable in domains characterized by skewed class distributions and disparate classification error costs. Which is especially relevant to classifiers applied to financial time series datasets.
While the conceptual framework of ROC graphs is straightforward, practical application reveals complexities that warrant careful consideration. Furthermore, common misconceptions and potential pitfalls exist in their empirical use. This article aims to provide a foundational introduction to ROC curves and serve as a practical guide for their application in evaluating classifier performance.
Binary classification formulation
Many real-world applications involve binary classification problems, where instances belong to one of two mutually exclusive and collectively exhaustive classes. A prevalent instance of this scenario arises when a single target class is defined, and each instance is categorized as either a member of this class or its complement. Consider, for example, radar signal classification, where a detected outline on a screen is categorized as either a tank (the target class) or a non-tank object. Similarly, a credit card transaction can be classified as either fraudulent (the target class) or legitimate.
This specific formulation of the binary classification problem, characterized by the identification of a single target class, forms the basis for subsequent analysis. Rather than explicitly assigning instances to one of two distinct classes, the approach adopted here focuses on determining whether an instance belongs to the designated target class. While the terminology employed, referencing "target" and its complement, may evoke military connotations, the concept is broadly applicable. The target class can represent various entities, such as a malignant tumor, a successful financial trade, or, as previously mentioned, a fraudulent credit card transaction. The essential characteristic is the duality of the class of primary interest and all other possibilities.
The confusion matrix
For a given classifier applied to a test dataset, four distinct outcomes are possible. If an instance belonging to the positive class is classified as positive, it is designated as a true positive, (TP). Conversely, if it is classified as negative, it is designated as a false negative, (FN). Similarly, if an instance belonging to the negative class is classified as negative, it is designated as a true negative, (TN); if classified as positive, it is designated as a false positive, (FP). These four values, make up, a two-by-two confusion matrix, also referred to as a contingency table.
This matrix encapsulates the distribution of instances across these four outcomes and serves as the foundational basis for numerous commonly employed performance metrics, some of which, include:
- Hit Rate or Sensitivity or Recall: The proportion of target instances correctly classified as targets, calculated as TP / (TP + FN).
- False Alarm Rate (Type I Error Rate): The proportion of non-target instances incorrectly classified as targets, calculated as FP / (TN + FP).
- Miss Rate (Type II Error Rate): The proportion of target instances incorrectly classified as non-targets, calculated as FN / (TP + FN).
- Specificity: The proportion of non-target instances correctly classified as non-targets, calculated as TN / (TN + FP).
Wikipedia has a useful graphic that displays an extensive list of performance metrics derived from a confusion matrix.
ROC curves
The inner workings of most binary classification models, make a numerical prediction and subsequently compare it to a predetermined threshold. If the prediction equals or surpasses this threshold, the instance is classified as a target; otherwise, it is classified as a non-target. It is evident that the threshold value influences all the aforementioned performance measures. Setting the threshold at or below the minimum possible prediction results in all instances being classified as targets, yielding a perfect hit rate but a correspondingly poor false alarm rate.
Conversely, setting the threshold above the maximum possible prediction leads to all instances being classified as non-targets, resulting in a zero hit rate and a perfect zero false alarm rate. The optimal threshold value lies between these extremes. By systematically varying the threshold across its entire range, both the hit rate and false alarm rate traverse their respective ranges from 0 to 1, with one metric improving at the expense of the other. The curve generated by plotting these two rates against each other (with the threshold acting as a latent parameter) is termed the Receiver Operating Characteristic curve.
The ROC curve is conventionally depicted with the false alarm rate along the horizontal axis and the hit rate along the vertical axis. Consider a classification model that yields random numeric predictions, uncorrelated with the true class of a case.
In such a scenario, the hit rate and false alarm rate will, on average, be equivalent across all thresholds, resulting in an ROC curve that approximates a diagonal line extending from the lower-left to the upper-right corner of the graph. For instance, should a classifier randomly assign an instance to the positive class with a 50% probability, it is expected to correctly classify 50% of both positive and negative instances, resulting in the coordinate point (0.5, 0.5) within the ROC space.
Similarly, if the classifier assigns an instance to the positive class with a 90% probability, it is anticipated to correctly classify 90% of the positive instances; however, the false positive rate will concomitantly increase to 90%, yielding the coordinate point (0.9, 0.9). Consequently, a random classifier will generate an ROC point that traverses along the diagonal, its position determined by the frequency with which it predicts the positive class. To achieve performance exceeding that of random guessing, as indicated by a location within the upper triangular region of the ROC space, the classifier must leverage informative patterns present within the data.
Conversely, a perfect model, characterized by the existence of a threshold that precisely separates targets (predictions equal to or exceeding the threshold) from non-targets (predictions below the threshold), exhibits a distinct ROC curve. As the parametric threshold transitions from its minimum to the optimal threshold, the false alarm rate decreases from 1 to 0, while the hit rate remains consistently at 1. Subsequent increases in the parametric threshold cause the hit rate to diminish from 1 to 0, with the false alarm rate remaining at 0. This results in an ROC curve that forms a path from the upper-right to the upper-left corner, and then to the lower-left corner.
Models of intermediate performance, exhibiting accuracy between these extremes, will produce ROC curves situated between the diagonal and the upper-left corner. The degree to which the curve deviates from the diagonal towards the upper-left corner signifies the model's performance. In a general sense, a point on an ROC plot is considered superior to another if it has a higher true positive rate, a lower false positive rate, or both. Classifiers situated on the left-hand side of an ROC plot, proximal to the abscissa, may be characterized as conservative.
These classifiers exhibit a tendency to issue positive classifications only when presented with substantial evidence, resulting in a low false positive rate but often accompanied by a diminished true positive rate. Conversely, classifiers located on the upper right-hand side of the ROC graph, characterized as less conservative, tend to issue positive classifications even with minimal evidence, leading to a high true positive rate but frequently accompanied by an elevated false positive rate. In numerous real-world domains, where negative instances predominate, the performance of classifiers in the left-hand region of the ROC plot becomes increasingly pertinent.
Classifiers residing within the lower right triangular region of the ROC space exhibit performance inferior to that of random guessing. Consequently, this region is typically devoid of data points in ROC graphs. The negation of a classifier, defined as the reversal of its classification decisions for all instances, results in its true positive classifications becoming false negative errors and its false positive classifications becoming true negative classifications. Therefore, any classifier yielding a point within the lower right triangle can be transformed, through negation, to produce a corresponding point within the upper left triangle. A classifier situated along the diagonal can be characterized as possessing no discernible information regarding class membership. Conversely, a classifier positioned below the diagonal can be interpreted as possessing informative patterns, albeit applying them in an erroneous manner.
ROC performance metrics
While visual inspection of an ROC curve plot may offer preliminary insights, a more comprehensive understanding of model performance is achieved through the analysis of relevant performance measures. Before detailed analysis, it is necessary to elucidate the data constructs that characterize a ROC curve. To facilitate comprehension, an illustrative example is provided.
The subsequent table presents a hypothetical sample of ROC performance metrics derived from a classification model. This example employs the iris dataset, accessible via the Sklearn Python library. Adhering to the target/non-target paradigm, the classification objective was restricted to the identification of a singular iris variant. Specifically, if setosa is designated as the target, all other variants are categorized as non-targets. Consistent with conventional classification methodologies, the model was trained to generate an output of 0 for non-targets and 1 for targets. The sample labels were accordingly transformed. It is noteworthy that alternative labeling schemes are also viable.
For each threshold value within the decision threshold range, a confusion matrix is generated to compute the true positive rate and false positive rate. These computations utilize the output probability or decision function value from the trained prediction model, with the corresponding threshold determining class membership. The table presented herein was generated utilizing the script ROC_curves_table_demo.mq5.
KG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) TPR FPR FNR TNR PREC NPREC M_E ACC B_ACC THRESH NF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.038 0.000 0.962 1.000 1.000 0.000 0.481 0.667 0.519 0.98195 DI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.077 0.000 0.923 1.000 1.000 0.000 0.462 0.680 0.538 0.97708 OI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.115 0.000 0.885 1.000 1.000 0.000 0.442 0.693 0.558 0.97556 GI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.154 0.000 0.846 1.000 1.000 0.000 0.423 0.707 0.577 0.97334 GH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.192 0.000 0.808 1.000 1.000 0.000 0.404 0.720 0.596 0.97221 RH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.231 0.000 0.769 1.000 1.000 0.000 0.385 0.733 0.615 0.97211 IK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.269 0.000 0.731 1.000 1.000 0.000 0.365 0.747 0.635 0.96935 CK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.308 0.000 0.692 1.000 1.000 0.000 0.346 0.760 0.654 0.96736 NK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.346 0.000 0.654 1.000 1.000 0.000 0.327 0.773 0.673 0.96715 EJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.385 0.000 0.615 1.000 1.000 0.000 0.308 0.787 0.692 0.96645 DJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.423 0.000 0.577 1.000 1.000 0.000 0.288 0.800 0.712 0.96552 HJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.462 0.000 0.538 1.000 1.000 0.000 0.269 0.813 0.731 0.96534 NM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.500 0.000 0.500 1.000 1.000 0.000 0.250 0.827 0.750 0.96417 GM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.538 0.000 0.462 1.000 1.000 0.000 0.231 0.840 0.769 0.96155 CL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.577 0.000 0.423 1.000 1.000 0.000 0.212 0.853 0.788 0.95943 LL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.615 0.000 0.385 1.000 1.000 0.000 0.192 0.867 0.808 0.95699 NL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.654 0.000 0.346 1.000 1.000 0.000 0.173 0.880 0.827 0.95593 KO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.692 0.000 0.308 1.000 1.000 0.000 0.154 0.893 0.846 0.95534 NO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.731 0.000 0.269 1.000 1.000 0.000 0.135 0.907 0.865 0.95258 NO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.769 0.000 0.231 1.000 1.000 0.000 0.115 0.920 0.885 0.94991 EN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.808 0.000 0.192 1.000 1.000 0.000 0.096 0.933 0.904 0.94660 CN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.846 0.000 0.154 1.000 1.000 0.000 0.077 0.947 0.923 0.94489 OQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.885 0.000 0.115 1.000 1.000 0.000 0.058 0.960 0.942 0.94420 NQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.923 0.000 0.077 1.000 1.000 0.000 0.038 0.973 0.962 0.93619 GQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.962 0.000 0.038 1.000 1.000 0.000 0.019 0.987 0.981 0.92375 PP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.000 0.000 1.000 1.000 0.000 0.000 1.000 1.000 0.92087 OP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.020 0.000 0.980 0.963 0.037 0.010 0.987 0.990 0.12257 RP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.041 0.000 0.959 0.929 0.071 0.020 0.973 0.980 0.07124 RS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.061 0.000 0.939 0.897 0.103 0.031 0.960 0.969 0.05349 KS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.082 0.000 0.918 0.867 0.133 0.041 0.947 0.959 0.04072 KR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.102 0.000 0.898 0.839 0.161 0.051 0.933 0.949 0.03502 KR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.122 0.000 0.878 0.812 0.188 0.061 0.920 0.939 0.02523 JR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.143 0.000 0.857 0.788 0.212 0.071 0.907 0.929 0.02147 HE 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.163 0.000 0.837 0.765 0.235 0.082 0.893 0.918 0.01841 QE 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.184 0.000 0.816 0.743 0.257 0.092 0.880 0.908 0.01488 DE 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.204 0.000 0.796 0.722 0.278 0.102 0.867 0.898 0.01332 PD 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.224 0.000 0.776 0.703 0.297 0.112 0.853 0.888 0.01195 PD 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.245 0.000 0.755 0.684 0.316 0.122 0.840 0.878 0.01058 MG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.265 0.000 0.735 0.667 0.333 0.133 0.827 0.867 0.00819 JG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.286 0.000 0.714 0.650 0.350 0.143 0.813 0.857 0.00744 EG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.306 0.000 0.694 0.634 0.366 0.153 0.800 0.847 0.00683 LF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.327 0.000 0.673 0.619 0.381 0.163 0.787 0.837 0.00635 CF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.347 0.000 0.653 0.605 0.395 0.173 0.773 0.827 0.00589 KF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.367 0.000 0.633 0.591 0.409 0.184 0.760 0.816 0.00578 JI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.388 0.000 0.612 0.578 0.422 0.194 0.747 0.806 0.00556 JI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.408 0.000 0.592 0.565 0.435 0.204 0.733 0.796 0.00494 NH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.429 0.000 0.571 0.553 0.447 0.214 0.720 0.786 0.00416 PH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.449 0.000 0.551 0.542 0.458 0.224 0.707 0.776 0.00347 LH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.469 0.000 0.531 0.531 0.469 0.235 0.693 0.765 0.00244 KK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.490 0.000 0.510 0.520 0.480 0.245 0.680 0.755 0.00238 HK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.510 0.000 0.490 0.510 0.490 0.255 0.667 0.745 0.00225 LK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.531 0.000 0.469 0.500 0.500 0.265 0.653 0.735 0.00213 PJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.551 0.000 0.449 0.491 0.509 0.276 0.640 0.724 0.00192 CJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.571 0.000 0.429 0.481 0.519 0.286 0.627 0.714 0.00189 EM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.592 0.000 0.408 0.473 0.527 0.296 0.613 0.704 0.00177 IM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.612 0.000 0.388 0.464 0.536 0.306 0.600 0.694 0.00157 HM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.633 0.000 0.367 0.456 0.544 0.316 0.587 0.684 0.00132 EL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.653 0.000 0.347 0.448 0.552 0.327 0.573 0.673 0.00127 DL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.673 0.000 0.327 0.441 0.559 0.337 0.560 0.663 0.00119 KL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.694 0.000 0.306 0.433 0.567 0.347 0.547 0.653 0.00104 DO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.714 0.000 0.286 0.426 0.574 0.357 0.533 0.643 0.00102 RO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.735 0.000 0.265 0.419 0.581 0.367 0.520 0.633 0.00085 DN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.755 0.000 0.245 0.413 0.587 0.378 0.507 0.622 0.00082 EN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.776 0.000 0.224 0.406 0.594 0.388 0.493 0.612 0.00069 HN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.796 0.000 0.204 0.400 0.600 0.398 0.480 0.602 0.00062 HQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.816 0.000 0.184 0.394 0.606 0.408 0.467 0.592 0.00052 DQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.837 0.000 0.163 0.388 0.612 0.418 0.453 0.582 0.00048 FQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.857 0.000 0.143 0.382 0.618 0.429 0.440 0.571 0.00044 MP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.878 0.000 0.122 0.377 0.623 0.439 0.427 0.561 0.00028 LP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.898 0.000 0.102 0.371 0.629 0.449 0.413 0.551 0.00026 NS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.918 0.000 0.082 0.366 0.634 0.459 0.400 0.541 0.00015 ES 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.939 0.000 0.061 0.361 0.639 0.469 0.387 0.531 0.00012 MS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.959 0.000 0.041 0.356 0.644 0.480 0.373 0.520 0.00007 QR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.980 0.000 0.020 0.351 0.649 0.490 0.360 0.510 0.00004 CR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 1.000 0.000 0.000 0.347 0.653 0.500 0.347 0.500 0.00002
An examination of the tabulated ROC curve data reveals a discernible trend: both the TPR and FPR exhibit a decline from 1 to 0 as the decision threshold increases. Given the model's inherent predictive capacity, the FPR demonstrates a more rapid reduction than the TPR. Notably, the FPR reaches zero while the TPR maintains a value of 1. Consequently, unless the relative costs of Type I and Type II errors are substantially disparate, the optimal threshold is expected to reside within the interval defined by these extrema. It is also important to observe that the table includes specificity, which is equivalent to the True Negative Rate (TNR), and represents the complement of the FPR.
In numerous instances, the determination of the optimal threshold can be achieved through direct inspection of the True Positive Rate and False Positive Rate columns. The interpretability of this process is enhanced by the inclusion of target and non-target sample sizes. Where the costs associated with Type I and Type II errors are approximately equivalent, the mean error serves as a suitable scalar performance metric. This metric, denoted as M_E in the table, is calculated as the arithmetic mean of the False Alarm Rate and the Miss Rate.
However, in scenarios where the costs of these error types diverge significantly, the mean error metric diminishes in relevance. Precision, in particular, is a critical performance indicator in various applications. Typically, the precision of target detection is of primary interest. In certain contexts, the precision of non-target identification may also be pertinent. For the objective of accurate target detection, the column labeled PREC provides pertinent information. Conversely, the column labeled NPREC is relevant for the precise identification of non-targets.
The table presents additional performance metrics, including accuracy (ACC) and balanced accuracy (B_ACC). Accuracy is defined as the proportion of correctly classified instances, encompassing both true positives and true negatives, within the total dataset. Balanced accuracy, calculated as the arithmetic mean of sensitivity and specificity, is employed to mitigate the impact of class imbalance, a condition characterized by a significant disparity in the sample sizes of target and non-target classes. Before the discussion of the area under the ROC curve, an examination of the computational procedures used to generate the aforementioned table of ROC metrics is warranted. Specifically, the code responsible for the calculation of these ROC-related metrics will be analyzed.
The relevant code is encapsulated within the header file roc_curves.mqh, which defines a series of functions and the data structure conf_stats. The conf_stats structure serves as a container for the storage of various parameters derived from the confusion matrix.
//+------------------------------------------------------------------+ //| confusion matrix stats | //+------------------------------------------------------------------+ struct conf_stats { double tn; //true negatives double tp; //true positives double fn; //false negatives double fp; //false positives double num_targets; //number of actual positive labels(target) double num_non_targets; //number of acutal negative labels(non targets) double tp_rate; //true positives rate - hit rate - recall - sensitivity double fp_rate; //false positives rate - fall out - type 1 error double fn_rate; //false negatives rate - miss rate - type 2 error double tn_rate; //true negatives rate - specificity double precision; //precision - positive predictve value double null_precision; //null precision - false discovery rate double prevalence; //prevalence double lr_plus; //positive likelihood ratio double lr_neg; //negative likelihood ratio double for_rate; //false omission rate double npv; //negative predictive value double acc; //accuracy double b_acc; //balanced accuracy double f1_score; //f1 score double mean_error; //mean error };
The conf_stats structure functions as the primary parameter within the roc_stats() function, facilitating the storage of evaluation results derived from the confusion matrix. This evaluation is conducted on a dataset comprising true labels, corresponding predictions, and a designated threshold. The true labels are provided as a vector, denoted as targets, serving as the second parameter. The third argument, probas, represents the vector of predicted probabilities or decision variables.
//+------------------------------------------------------------------+ //| defines | //+------------------------------------------------------------------+ bool roc_stats(conf_stats &cmat, vector &targets, vector &probas, double threshold, long target_label = 1, long non_target_label= 0) { vector all_labels = np::unique(targets); if(all_labels.Size()!=2 || long(all_labels[all_labels.ArgMin()])!=non_target_label || long(all_labels[all_labels.ArgMax()])!=target_label || target_label<=non_target_label) { Print(__FUNCTION__, " ", __LINE__, " invalid inputs "); return false; } //--- cmat.tp=cmat.fn=cmat.tn=cmat.fp = 0.0; //--- for(ulong i = 0; i<targets.Size(); i++) { if(probas[i]>=threshold && long(targets[i]) == target_label) cmat.tp++; else if(probas[i]>=threshold && long(targets[i]) == non_target_label) cmat.fp++; else if(probas[i]<threshold && long(targets[i]) == target_label) cmat.fn++; else cmat.tn++; } //--- cmat.num_targets = cmat.tp+cmat.fn; cmat.num_non_targets = cmat.fp+cmat.tn; //--- cmat.tp_rate = (cmat.tp+cmat.fn>0.0)?(cmat.tp/(cmat.tp+cmat.fn)):double("na"); cmat.fp_rate = (cmat.tn+cmat.fp>0.0)?(cmat.fp/(cmat.tn+cmat.fp)):double("na"); cmat.fn_rate = (cmat.tp+cmat.fn>0.0)?(cmat.fn/(cmat.tp+cmat.fn)):double("na"); cmat.tn_rate = (cmat.tn+cmat.fp>0.0)?(cmat.tn/(cmat.tn+cmat.fp)):double("na"); cmat.precision = (cmat.tp+cmat.fp>0.0)?(cmat.tp/(cmat.tp+cmat.fp)):double("na"); cmat.null_precision = 1.0 - cmat.precision; cmat.for_rate = (cmat.tn+cmat.fn>0.0)?(cmat.fn/(cmat.tn+cmat.fn)):double("na"); cmat.npv = 1.0 - cmat.for_rate; cmat.lr_plus = (cmat.fp_rate>0.0)?(cmat.tp_rate/cmat.fp_rate):double("na"); cmat.lr_neg = (cmat.tn_rate>0.0)?(cmat.fn_rate/cmat.tn_rate):double("na"); cmat.prevalence = (cmat.num_non_targets+cmat.num_targets>0.0)?(cmat.num_targets/(cmat.num_non_targets+cmat.num_targets)):double("na"); cmat.acc = (cmat.num_non_targets+cmat.num_targets>0.0)?((cmat.tp+cmat.tn)/(cmat.num_non_targets+cmat.num_targets)):double("na"); cmat.b_acc = ((cmat.tp_rate+cmat.tn_rate)/2.0); cmat.f1_score = (cmat.tp+cmat.fp+cmat.fn>0.0)?((2.0*cmat.tp)/(2.0*cmat.tp+cmat.fp+cmat.fn)):double("na"); cmat.mean_error = ((cmat.fp_rate+cmat.fn_rate)/2.0); //--- return true; //--- }
The threshold parameter defines the critical value used to delineate class membership. The final two parameters enable the explicit specification of the target and non-target labels, respectively. The function returns a boolean value, indicating successful execution with true and error occurrence with false.
//+------------------------------------------------------------------+ //| roc table | //+------------------------------------------------------------------+ matrix roc_table(vector &true_targets,matrix &probas,ulong target_probs_col = 1, long target_label = 1, long non_target_label= 0) { matrix roctable(probas.Rows(),10); conf_stats mts; vector probs = probas.Col(target_probs_col); if(!np::quickSort(probs,false,0,probs.Size()-1)) return matrix::Zeros(1,1); for(ulong i = 0; i<roctable.Rows(); i++) { if(!roc_stats(mts,true_targets,probas.Col(target_probs_col),probs[i],target_label,non_target_label)) return matrix::Zeros(1,1); roctable[i][0] = mts.tp_rate; roctable[i][1] = mts.fp_rate; roctable[i][2] = mts.fn_rate; roctable[i][3] = mts.tn_rate; roctable[i][4] = mts.precision; roctable[i][5] = mts.null_precision; roctable[i][6] = mts.mean_error; roctable[i][7] = mts.acc; roctable[i][8] = mts.b_acc; roctable[i][9] = probs[i]; } //--- return roctable; }
The roc_table() function generates a matrix encapsulating ROC curve data. Input parameters include a vector of true class labels, a matrix of predicted probabilities or decision variables, and an unsigned long integer specifying the column index for class membership determination in multi-column matrices. The final two parameters define the target and non-target labels. In the event of an error, the function returns a 1x1 matrix of zeros. It is imperative to note that both roc_stats() and roc_table() are specifically designed for binary classification models. Non-conformance to this requirement will result in an error message.
//+------------------------------------------------------------------+ //| roc curve table display | //+------------------------------------------------------------------+ string roc_table_display(matrix &out) { string output,temp; if(out.Rows()>=10) { output = "TPR FPR FNR TNR PREC NPREC M_E ACC B_ACC THRESH"; for(ulong i = 0; i<out.Rows(); i++) { temp = StringFormat("\n%5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.5lf", out[i][0],out[i][1],out[i][2],out[i][3],out[i][4],out[i][5],out[i][6],out[i][7],out[i][8],out[i][9]); StringAdd(output,temp); } } return output; }
The roc_table_display() function accepts a single matrix parameter, ideally the output from a previous invocation of roc_table(), and formats the data into a tabular string representation.
Area under an ROC curve
The Area Under the ROC Curve (AUC) provides a concise, single-value metric for classifier performance, addressing the excessive detail of the full ROC curve. While the ROC curve visually depicts the trade-off between true and false positive rates, the AUC quantifies the overall ability of the model to distinguish between classes. A useless model, represented by a diagonal line on the ROC graph, yields an AUC of 0.5, indicating random performance. Conversely, a perfect model, with an ROC curve hugging the top-left corner, achieves an AUC of 1.0. Therefore, a higher AUC signifies better model performance. Calculating the AUC involves determining the area beneath the ROC curve, and due to the inherent statistical variation in test datasets, simple summation is typically sufficient for accurate estimation, foregoing the need for complex numerical integration.
The AUC possesses a significant statistical interpretation: it represents the probability that a classifier will assign a higher rank to a randomly selected positive instance compared to a randomly selected negative instance. This characteristic establishes an equivalence between the AUC and the Wilcoxon rank-sum test, also known as the Mann-Whitney U test.
The Wilcoxon rank-sum test, a non-parametric statistical method, assesses the difference between two independent groups without assuming normality. It operates by ranking all observations and comparing the rank sums between the groups, thereby evaluating differences in medians.
Furthermore, the AUC is intrinsically linked to the Gini coefficient. Specifically, the Gini coefficient is derived as twice the area between the diagonal line of chance and the ROC curve. The Gini coefficient, a measure of distributional inequality, quantifies the degree of dispersion within a distribution, ranging from 0 (perfect equality) to 1 (maximal inequality). In the context of income distribution, it reflects the disparity in income levels. Graphically, the Gini coefficient is defined as the ratio of the area between the Lorenz curve and the line of perfect equality to the area under the line of perfect equality.
The function, roc_auc(), defined in roc_curves.mqh calculates the AUC for a binary classification problem, with the option to limit the calculation to a specific maximum FPR. It takes the true class labels and predicted probabilities as input, along with an optional target label and maximum FPR. If the maximum FPR is 1.0, it computes the standard AUC. Otherwise, it calculates the ROC curve, finds the point on the curve corresponding to the maximum FPR using searchsorted, interpolates the TPR at that point, and then calculates the partial AUC up to that maximum FPR using the trapezoidal rule. Finally, it normalizes this partial AUC to a score between 0.5 and 1.0, effectively providing a measure of classifier performance within the specified FPR range.
//+------------------------------------------------------------------+ //| area under the curve | //+------------------------------------------------------------------+ double roc_auc(vector &true_classes, matrix &predicted_probs,long target_label=1,double max_fpr=1.0) { vector all_labels = np::unique(true_classes); if(all_labels.Size()!=2|| max_fpr<=0.0 || max_fpr>1.0) { Print(__FUNCTION__, " ", __LINE__, " invalid inputs "); return EMPTY_VALUE; } if(max_fpr == 1.0) { vector auc = true_classes.ClassificationScore(predicted_probs,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY); return auc[0]; } matrix tpr,fpr,threshs; if(!true_classes.ReceiverOperatingCharacteristic(predicted_probs,AVERAGE_BINARY,fpr,tpr,threshs)) { Print(__FUNCTION__, " ", __LINE__, " invalid inputs "); return EMPTY_VALUE; } vector xp(1); xp[0] = max_fpr; vector stop; if(!np::searchsorted(fpr.Row(0),xp,true,stop)) { Print(__FUNCTION__, " ", __LINE__, " searchsorted failed "); return EMPTY_VALUE; } vector xpts(2); vector ypts(2); xpts[0] = fpr[0][long(stop[0])-1]; xpts[1] = fpr[0][long(stop[0])]; ypts[0] = tpr[0][long(stop[0])-1]; ypts[1] = tpr[0][long(stop[0])]; vector vtpr = tpr.Row(0); vtpr = np::sliceVector(vtpr,0,long(stop[0])); vector vfpr = fpr.Row(0); vfpr = np::sliceVector(vfpr,0,long(stop[0])); if(!vtpr.Resize(vtpr.Size()+1) || !vfpr.Resize(vfpr.Size()+1)) { Print(__FUNCTION__, " ", __LINE__, " error ", GetLastError()); return EMPTY_VALUE; } vfpr[vfpr.Size()-1] = max_fpr; vector yint = np::interp(xp,xpts,ypts); vtpr[vtpr.Size()-1] = yint[0]; double direction = 1.0; vector dx = np::diff(vfpr); if(dx[dx.ArgMin()]<0.0) direction = -1.0; double partial_auc = direction*np::trapezoid(vtpr,vfpr); if(partial_auc == EMPTY_VALUE) { Print(__FUNCTION__, " ", __LINE__, " trapz failed "); return EMPTY_VALUE; } double minarea = 0.5*(max_fpr*max_fpr); double maxarea = max_fpr; return 0.5*(1+(partial_auc-minarea)/(maxarea-minarea)); }
The max_fpr parameter facilitates the computation of the partial Area Under the ROC Curve (AUC), thereby enabling the evaluation of classifier performance within a defined range of FPR values. This functionality is particularly salient in scenarios where emphasis is placed on performance at lower FPR thresholds. Furthermore, it proves advantageous when analyzing imbalanced datasets, where the ROC curve may be disproportionately influenced by a substantial quantity of true negatives. Employing this parameter allows for a focused assessment of the curve's pertinent region.
While Receiver Operating Characteristic (ROC) curves provide a useful framework for classifier evaluation, their application in determining definitive classifier superiority warrants careful consideration, particularly when incorporating the cost of misclassification. Although the AUC offers a metric for assessing classifier quality, comparative performance evaluations necessitate a more nuanced approach. To adequately address cost considerations, a return to the foundational confusion matrix is necessary.
Conventional classification paradigms frequently prioritize accuracy maximization, implicitly assuming uniform costs for all misclassifications. In contrast, cost-sensitive classification acknowledges the differential costs associated with various error types, aiming to minimize the aggregate cost of errors rather than solely optimizing accuracy. For instance, in a classifier designed to identify promising investment stocks, the cost of a missed opportunity (false negative) may be deemed less consequential than the cost of a false positive. The assignment of costs to each misclassification type yields a cost matrix. This matrix articulates the costs associated with diverse prediction outcomes, specifying the penalties or losses incurred for incorrect predictions, such as false positives and false negatives, and potentially including costs for correct predictions. A hypothetical confusion matrix, accompanied by its corresponding cost matrix, is shown below.
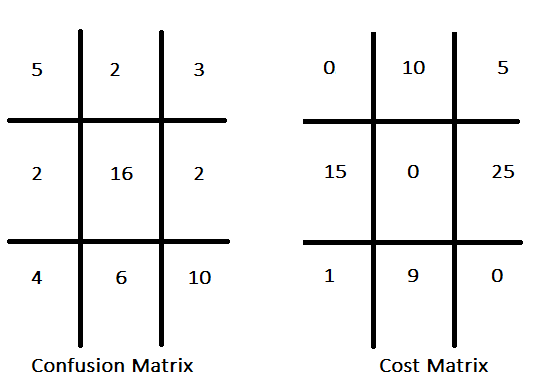
The cost matrix typically features null values along its diagonal, signifying a zero cost associated with correct predictions, a convention that, while prevalent, is not obligatory. Given a defined cost structure for all misclassification types, the information encapsulated within the confusion matrix can be aggregated into a singular performance metric. A rudimentary approach involves multiplying the frequency of each misclassification type by its corresponding cost and subsequently summing these products. However, the efficacy of this metric is contingent upon the dataset's class proportions accurately mirroring those encountered in real-world applications.
A more robust measure of cost-sensitive performance is the expected cost per sample. This metric is derived by normalizing the confusion matrix's sample counts by their respective row totals, yielding the conditional probabilities of classified classes given true classes. These probabilities are then multiplied by their corresponding costs from the cost matrix, and the products are summed across each row, resulting in the expected cost for a member of each class. Subsequently, these class-specific costs are weighted by the expected proportions of samples in each class and summed, producing the overall expected cost per sample. Estimating the expected class proportions in real-world scenarios necessitates a comprehensive understanding of the data's underlying distribution within the deployment environment. Methodologies for this estimation include:
- Analysis of historical data, wherein existing records are examined to provide reliable estimates of class proportions. For instance, in medical diagnostics, patient records can elucidate disease prevalence.
- Consultation with domain experts, whose specialized knowledge can refine or validate estimates obtained through other means.
- Implementation of representative sampling techniques when new data collection is feasible, ensuring that the sample accurately reflects the real-world distribution, particularly in imbalanced datasets. Stratified sampling can further ensure adequate representation of all classes, even in cases of uneven distribution.
The expected proportions of samples within a class are formally equivalent to prior probabilities. In the specific context of binary classification, let
q denote the prior probability of a sample belonging to the target class. Further, define p1 as the probability of a Type I error (false positive), with c1 representing its associated cost, and p2 as the probability of a Type II error (false negative), with c2 representing its associated cost. In numerous applications, q is ascertainable through theoretical or empirical means, and the costs c1 and c2 are known, either precisely or with reasonable approximation. Consequently, these three quantities can be treated as fixed parameters. The error probabilities p1 and p2 are determined by the classification threshold. The expected cost is expressed by the following equation.
Rearranging this equation yields.
Demonstrating a linear relationship between p1 and p2 for any given expected cost. When this linear relationship is graphically represented on the ROC curve, its slope is determined by the prior probability q and the cost ratio c2/c1. Variation of the expected cost generates a family of parallel lines, with lines positioned lower and to the right signifying higher costs. Intersection of this line with the ROC curve at two points indicates two thresholds yielding equivalent, albeit suboptimal, costs. Lines situated entirely above and to the left of the ROC curve represent performance unattainable by the model. The line tangent to the ROC curve signifies the optimal achievable cost.
This analysis underscores that the AUC does not necessarily provide a definitive measure of a classification model's practical performance. While the AUC is a valid overall quality metric, its utility is diminished when operational costs are considered, as it can yield misleading conclusions in cost-sensitive applications.
Decision problems with more than two classes
Extending the ROC curve framework to multi-class classification necessitates the adoption of specific adaptation strategies. Predominantly, two methodologies are employed: the One-vs-Rest (OvR), also known as One-vs-All (OvA), and the One-vs-One (OvO) approaches. The OvR strategy transforms the multi-class problem into multiple binary classification tasks by treating each class as the positive class against the combined remaining classes, resulting in n ROC curves for n classes. Conversely, the OvO method constructs binary classification problems for all possible class pairs, yielding n(n-1)/2 ROC curves.
To aggregate the performance metrics derived from these binary classifications, averaging techniques are utilized. Micro-averaging calculates global TPR and FPR by considering all instances across all classes, thus assigning equal weight to each instance. Macro-averaging, on the other hand, computes TPR and FPR for each class independently and then averages them, thereby assigning equal weight to each class, a method particularly useful when class-specific performance is paramount. Consequently, the interpretation of multi-class ROC curves hinges on the chosen decomposition strategy (OvR or OvO) and averaging method (micro or macro), as these choices significantly influence the resultant performance evaluation.
MQL5 built-in functions for ROC curves and AUC
In MQL5, the computation of Receiver Operating Characteristic (ROC) curves and Area Under the Curve (AUC) is facilitated through dedicated functionality. The
ReceiverOperatingCharacteristic() vector method is employed to generate the necessary values for ROC curve visualization. This method operates on a vector representing the true class labels. The first argument is a matrix of probabilities or decision values, structured with columns corresponding to the number of classes. The second argument, a variable of the ENUM_AVERAGE_MODE enumeration, specifies the averaging methodology. Notably, this function supports only AVERAGE_NONE, AVERAGE_BINARY, and AVERAGE_MICRO. Upon successful execution, the false positive rate (FPR), true positive rate (TPR), and associated thresholds are written to designated matrices, the final three parameters. The method returns a boolean value indicating execution success.
AUC calculation is performed via the ClassificationScore() vector method. Similar to the ROC method, it is invoked on the vector of true class labels and requires a matrix of predicted probabilities or decision values. The second parameter, an ENUM_CLASSIFICATION_METRIC enumeration, must be set to CLASSIFICATION_ROC_AUC to specify AUC computation. Unlike the ROC method, this function accommodates all values of ENUM_AVERAGE_MODE. The method returns a vector of calculated areas, the cardinality of which is contingent upon the averaging mode and the number of classes present in the dataset.
To elucidate the impact of various averaging modes, the ROC_Demo.mq5 script was developed. This script utilizes the Iris dataset and a logistic regression model to address user-configurable binary or multi-class classification problems. The complete script code is provided below.
//+------------------------------------------------------------------+ //| ROC_Demo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<logistic.mqh> #include<ErrorDescription.mqh> #include<Generic/SortedSet.mqh> //--- enum CLASSIFICATION_TYPE { BINARY_CLASS = 0,//binary classification problem MULITI_CLASS//multiclass classification problem }; //--- input parameters input double Train_Test_Split = 0.5; input int Random_Seed = 125; input CLASSIFICATION_TYPE classification_problem = BINARY_CLASS; input ENUM_AVERAGE_MODE av_mode = AVERAGE_BINARY; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- CHighQualityRandStateShell rngstate; CHighQualityRand::HQRndSeed(Random_Seed,Random_Seed+Random_Seed,rngstate.GetInnerObj()); //--- matrix data = np::readcsv("iris.csv"); data = np::sliceMatrixCols(data,1); //--- if(classification_problem == BINARY_CLASS) data = np::sliceMatrixRows(data,0,100); //--- ulong rindices[],trainset[],testset[]; np::arange(rindices,int(data.Rows())); //--- //--- if(!np::shuffleArray(rindices,GetPointer(rngstate)) || ArrayCopy(trainset,rindices,0,0,int(ceil(Train_Test_Split*rindices.Size())))<0 || !ArraySort(trainset)) { Print(__LINE__, " error ", ErrorDescription(GetLastError())); return; } //--- CSortedSet<ulong> test_set(rindices); //--- test_set.ExceptWith(trainset); //--- test_set.CopyTo(testset); //--- matrix testdata = np::selectMatrixRows(data,testset); matrix test_predictors = np::sliceMatrixCols(testdata,0,4); vector test_targets = testdata.Col(4); matrix traindata = np::selectMatrixRows(data,trainset); matrix train_preditors = np::sliceMatrixCols(traindata,0,4); vector train_targets = traindata.Col(4); //--- logistic::Clogit logit; //-- if(!logit.fit(train_preditors,train_targets)) { Print(" error training logistic model "); return; } //--- matrix y_probas = logit.probas(test_predictors); vector y_preds = logit.predict(test_predictors); //--- vector auc = test_targets.ClassificationScore(y_probas,CLASSIFICATION_ROC_AUC,av_mode); //--- if(auc.Size()>0) Print(" AUC ", auc); else Print(" AUC error ", ErrorDescription(GetLastError())); //--- matrix fpr,tpr,threshs; if(!test_targets.ReceiverOperatingCharacteristic(y_probas,av_mode,fpr,tpr,threshs)) { Print(" ROC error ", ErrorDescription(GetLastError())); return; } //--- string legend; for(ulong i = 0; i<auc.Size(); i++) { string temp = (i!=int(auc.Size()-1))?StringFormat("%.3lf,",auc[i]):StringFormat("%.3lf",auc[i]); StringAdd(legend,temp); } CGraphic* roc = np::plotMatrices(fpr, tpr,"ROC",false,"FPR","TPR",legend,true,0,0,10,10,600,500); if(CheckPointer(roc)!=POINTER_INVALID) { Sleep(7000); roc.Destroy(); delete roc; ChartRedraw(); } } //+------------------------------------------------------------------+
Initially, a binary classification problem is examined, with the averaging mode set to AVERAGE_BINARY. This mode calculates the ROC curve and AUC under the assumption that the target class is labeled as 1, adhering to the fundamental target/non-target paradigm inherent in ROC curve generation. The output resulting from the script execution with these configurations demonstrates that the AUC value vector contains a single element. Furthermore, the FPR, TPR, and threshold matrices each comprise a single row.
MK 0 12:45:28.930 ROC_Demo (Crash 1000 Index,M5) AUC [1]
To examine the ROC curve and associated AUC for target classes other than label 1, the averaging mode should be set to AVERAGE_NONE. In this mode, the ReceiverOperatingCharacteristic() and ClassificationScore() functions evaluate each class independently as the target, providing corresponding results. Executing the script with AVERAGE_NONE and a binary classification problem yields the following output. In this instance, the ROC graph displays two curves, representing the plots of the respective rows in the FPR and TPR matrices. Two AUC values are also computed.
CK 0 16:42:43.249 ROC_Demo (Crash 1000 Index,M5) AUC [1,1]
The results are presented in correspondence with the class label order. For instance, in the binary classification problem depicted in the aforementioned script, where labels are 0 and 1, the first rows of the TPR, FPR, and threshold matrices represent the ROC curve values when label 0 is considered the target class, while the second rows pertain to label 1 as the target. This ordering convention also applies to the AUC values. It is pertinent to note that this result format is consistent across ROC stats calculated from multi-class datasets. In binary classification scenarios, employing averaging options other than AVERAGE_NONE and AVERAGE_BINARY invokes computational methods that correspond with multi-class dataset handling. Conversely, in multi-class classification, AVERAGE_BINARY triggers an error. However, AVERAGE_MICRO, AVERAGE_MACRO, and AVERAGE_WEIGHTED all yield a single, aggregated AUC value.
LL 0 17:27:13.673 ROC_Demo (Crash 1000 Index,M5) AUC [1,0.9965694682675815,0.9969135802469137]
The AVERAGE_MICRO averaging mode computes ROC curves and AUC globally by treating each element of the one-hot encoded true class matrix as a distinct label. This approach transforms the multi-class problem into a binary classification problem through initial one-hot encoding of the true class labels, generating a matrix with columns corresponding to the number of classes. This matrix, along with the predicted decision values or probabilities matrix, is then flattened into a single-column structure. Subsequent ROC curve and AUC calculations are performed on these flattened containers. This methodology produces comprehensive performance metrics that encompass all classes, assigning equal weight to each instance. This is particularly advantageous in scenarios with significant class imbalance, mitigating bias towards the majority class. Empirical results from the demonstration script illustrate this behavior.
RG 0 17:26:51.955 ROC_Demo (Crash 1000 Index,M5) AUC [0.9984000000000001]
The AVERAGE_MACRO averaging mode adopts a distinct strategy to address class imbalance. Each class is evaluated independently, calculating the AUC based on its respective class probabilities. The final AUC is then derived as the arithmetic mean of these individual AUC values. Notably, MQL5 documentation indicates that AVERAGE_MACRO is not supported by the ReceiverOperatingCharacteristic() method. The ClassificationScore(), method implements the OvR technique for AUC calculation in multi-class datasets. Script execution with AVERAGE_MACRO confirms the successful AUC calculation, while the ROC curve generation fails as anticipated.
ER 0 17:26:09.341 ROC_Demo (Crash 1000 Index,M5) AUC [0.997827682838166] NF 0 17:26:09.341 ROC_Demo (Crash 1000 Index,M5) ROC error Wrong parameter when calling the system function
The AVERAGE_WEIGHTED averaging mode operates analogously to AVERAGE_MACRO, except for the final aggregation step. Instead of a simple arithmetic mean, a weighted average is computed, where the weights are determined by the class distribution of the true class labels. This approach yields a final AUC value that accounts for the dominant classes within the dataset. Similar to AVERAGE_MACRO, ReceiverOperatingCharacteristic() does not support AVERAGE_WEIGHTED. The script output exemplifies this behavior.
IN 0 17:26:28.465 ROC_Demo (Crash 1000 Index,M5) AUC [0.9978825995807129] HO 0 17:26:28.465 ROC_Demo (Crash 1000 Index,M5) ROC error Wrong parameter when calling the system function
Conclusion
ROC curves are effective tools for the visualization and evaluation of classifiers. They afford a more comprehensive assessment of classification performance compared to scalar metrics such as accuracy, error rate, or error cost. By decoupling classifier performance from class skew and error costs, they offer advantages over alternative evaluation methodologies, including precision and recall curves. However, as with any evaluation metric, the judicious application of ROC graphs necessitates a thorough understanding of their inherent characteristics and limitations. It is anticipated that this article will contribute to the augmentation of general knowledge pertaining to ROC curves and foster the adoption of improved evaluation practices within the community.
| File Name | File Description |
|---|---|
| MQL5/Scripts/ROC_Demo.mq5 | Script used demonstrate built-in MQL5 functions related ROC curves. |
| MQL5/Scripts/ ROC_curves_table_demo.mq5 | Script demonstrating the generation of various ROC-based performance metrics. |
| MQL5/Include/logisitc.mqh | Header file containing definition of Clogit class that implements logistic regression. |
| MQL5/Include/roc_curves.mqh | Header of custom functions that implement various utilities for binary classification performance evaluation. |
| MQL5/Include/np.mqh | Header file of various vector and matrix utility functions. |
| MQL5/Files/iris.csv | CSV file of iris dataset. |
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Automating Trading Strategies in MQL5 (Part 11): Developing a Multi-Level Grid Trading System
Automating Trading Strategies in MQL5 (Part 11): Developing a Multi-Level Grid Trading System
 Developing a Replay System (Part 60): Playing the Service (I)
Developing a Replay System (Part 60): Playing the Service (I)
 Data Science and ML (Part 34): Time series decomposition, Breaking the stock market down to the core
Data Science and ML (Part 34): Time series decomposition, Breaking the stock market down to the core
 Neural Networks in Trading: State Space Models
Neural Networks in Trading: State Space Models
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use