Implementing the Generalized Hurst Exponent and the Variance Ratio test in MQL5

Introduction

In the article Calculating the Hurst Exponent , we were introduced to the concept of fractal analysis and how it can be  applied to financial markets. In that article the author described the rescaled range method (R/S) of estimating the Hurst Exponent. In this article we take a different approach by demonstrating the implementation of the Generalized Hurst Exponent (GHE) to classify the nature of a series. We will focus on using the GHE to identify forex symbols that exhibit a tendency to mean revert, in the hope of exploiting this behaviour.

To begin we briefly discuss the underpinnings of the GHE and how it differs from the original Hurst Exponent. In relation to that we will describe a statistical test that may be used to affirm results from GHE analysis, called the Variance Ratio Test (VRT). From there, we move on to the application of the GHE in identifying candidate forex symbols for mean reversion trading. Here, we present an indicator for generating entry and exit signals. Which we will finally put to the test in a basic Expert Advisor.

Understanding the Generalized Hurst Exponent

The Hurst exponent measures the scaling properties of time series. Scaling properties are fundamental characteristics that describe how a system behaves as its size or time scale changes. In the context of time series data, scaling properties provide insights into the relationship between different time scales and the patterns present in the data. For a stationary series, the changes in subsequent values over time occur more gradually compared to what would happen in a geometric random walk. To quantify this behaviour mathematically, we analyze the rate of diffusion in the series. The variance serves as a metric for expressing the rate of at which other values diverge from the first in the series.

In the formula above "K" represents an arbitrary lag at which the analysis is conducted. To get a better picture of the nature of the series we would have to assess the variance at other lags as well. So "K" can be assigned any positive integer value less than the length of the series. The largest lag applied is discretionary. Its important to keep this in mind. The Hurst exponent is therefore associated with the scaling behaviour of the variance at different lags. Using the power law it is defined by:

The GHE is a generalization of the original where the 2 is substituted for a variable usually denoted as "q". Thereby changing the above formulas to:

and

The GHE expands the original Hurst by analyzing how different statistical features of the changes between consecutive points in a time series vary with different orders of moments. In mathematical terms, moments are statistical measures that describe the shape and characteristics of a distribution. The qth-order moment is a specific type of moment, where "q" is a parameter determining the order. The GHE emphasizes different characteristics of a time series for each value of "q". Specifically, when q=1 the result depicts the scaling properties of absolute deviation. Whilst the q=2 is most important when investigating long range dependence.

Implementation of the GHE in MQL5

In this section we go over the implementation of the GHE in MQL5. After which, we will test it by analyzing random samples of artificially generated time series. Our implementation is contained in the file GHE.mqh. The file starts by including VectorMatrixTools.mqh, which contains definitions for various functions for initializing common types of vectors and matrices. The contents of this file are shown below.

//+------------------------------------------------------------------+
//|                                            VectorMatrixTools.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
//+------------------------------------------------------------------+
//|Vector arange initialization                                      |
//+------------------------------------------------------------------+
template<typename T>
void arange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization                                     |
//+------------------------------------------------------------------+
template<typename T>
void slice(vector<T> &vec,const vector<T> &toCopyfrom,ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;
   if(!vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<toCopyfrom.Size() && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization  using array                        |
//+------------------------------------------------------------------+
template<typename T>
void assign(vector<T> &vec,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;

   if(size != vec.Size() &&  !vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<ulong(toCopyfrom.Size()) && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Matrix initialization                                            |
//+------------------------------------------------------------------+
template<typename T>
void rangetrend(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   ulong r = mat.Rows();

   vector col1(r,arange,value,step);

   vector col2 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col1,0) || !mat.Col(col2,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+-------------------------------------------------------------------------------------+
//| ols design Matrix initialization with constant and first column from specified array|
//+-------------------------------------------------------------------------------------+
template<typename T>
void olsdmatrix(matrix<T> &mat,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   vector col0(1,assign,toCopyfrom,start,stop,step);

   ulong r = col0.Size();

   if(!r)
     {
      Print(__FUNCTION__," failed to initialize first column ");
      return;
     }

   vector col1 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col0,0) || !mat.Col(col1,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+------------------------------------------------------------------+
//|vector to array                                                   |
//+------------------------------------------------------------------+
bool vecToArray(const vector &in, double &out[])
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return false;
     }
//---
   if(ulong(out.Size())!=in.Size() && ArrayResize(out,int(in.Size()))!=int(in.Size()))
     {
      Print(__FUNCTION__," resize error ", GetLastError());
      return false;
     }
//---
   for(uint i = 0; i<out.Size(); i++)
      out[i]=in[i];
//---
   return true;
//---
  }
//+------------------------------------------------------------------+
//| difference a vector                                               |
//+------------------------------------------------------------------+
vector difference(const vector &in)
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return vector::Zeros(1);
     }
//---
   vector yy,zz;
//---
   yy.Init(in.Size()-1,slice,in,1,in.Size()-1,1);
//---
   zz.Init(in.Size()-1,slice,in,0,in.Size()-2,1);
//---
   return yy-zz;
  }
//+------------------------------------------------------------------+

 GHE.mqh, contains the definition for the "gen_hurst()" function and its overload. One works by supplying the data to be analyzed in a vector and the other expects it in an array. The function also takes an integer "q", and optional integer parameters "lower" and "upper" with default values. This is the same "q" mentioned in the previous section's description of the GHE. The last two parameters are optional, "lower" and "upper" together define the range of lags at which the analysis will be conducted, analogous to the range of "K" values in the formulas above.  

//+--------------------------------------------------------------------------+
//|overloaded gen_hurst() function that works with series contained in vector|
//+--------------------------------------------------------------------------+
double general_hurst(vector &data, int q, int lower=0,int upper=0)
  {
   double series[];

   if(!vecToArray(data,series))
      return EMPTY_VALUE;
   else
      return general_hurst(series,q,lower,upper);
  }

When an error occurs, the function will return the equivalent of the built in constant EMPTY_VALUE, along with a helpful string message output to the terminal's Experts tab. Within, "gen_hurst()", the routine begins by checking the arguments passed to it. Making sure they conform to the following conditions:

• "q" cannot to be less than 1.
• "lower" cannot be set to anything less than 2 and also cannot be larger than or equal to "upper".
• Whilst the "upper" argument cannot be more than half the size of the data series being analyzed. If any of these conditions are not met, the function will immediately flag an error.

if(data.Size()<100)
     {
      Print("data array is of insufficient length");
      return EMPTY_VALUE;
     }

   if(lower>=upper || lower<2 ||  upper>int(floor(0.5*data.Size())))
     {
      Print("Invalid input for lower and/or upper");
      return EMPTY_VALUE;
     }

   if(q<=0)
     {
      Print("Invalid input for q");
      return EMPTY_VALUE;
     }

   uint len = data.Size();

   int k =0;

   matrix H,mcord,lmcord;
   vector n_vector,dv,vv,Y,ddVd,VVVd,XP,XY,PddVd,PVVVd,Px_vector,Sqx,pt;
   double dv_array[],vv_array[],mx,SSxx,my,SSxy,cc1,cc2,N;

   if(!H.Resize(ulong(upper-lower),1))
     {
      Print(__LINE__," ",__FUNCTION__," ",GetLastError());
      return EMPTY_VALUE;
     }

   for(int i=lower; i<upper; i++)
     {
      vector x_vector(ulong(i),arange,1.0,1.0);

      if(!mcord.Resize(ulong(i),1))
        {
         Print(__LINE__," ",__FUNCTION__," ",GetLastError());
         return EMPTY_VALUE;
        }

      mcord.Fill(0.0);

The function's inner workings start with a "for" loop from 'lower' to 'upper', and for each 'i', it creates a vector 'x_vector' with 'i' elements using the 'arange' function. It then resizes the matrix 'mcord' to have 'i' rows and one column.

 for(int j=1; j<i+1; j++)
        {
         if(!diff_array(j,data,dv,Y))
            return EMPTY_VALUE;

The inner loop begins by using the helper function "diff_array()" to calculate the differences in the 'data' array and store them in vectors 'dv' and 'Y'.

 N = double(Y.Size());

         vector X(ulong(N),arange,1.0,1.0);

         mx = X.Sum()/N;

         XP = MathPow(X,2.0);

         SSxx = XP.Sum() - N*pow(mx,2.0);

         my = Y.Sum()/N;

         XY = X*Y;

         SSxy = XY.Sum() - N*mx*my;

         cc1 = SSxy/SSxx;

         cc2 = my - cc1*mx;

         ddVd = dv - cc1;

         VVVd = Y - cc1*X - cc2;

         PddVd = MathAbs(ddVd);

         PddVd = pow(PddVd,q);

         PVVVd = MathAbs(VVVd);

         PVVVd = pow(PVVVd,q);

         mcord[j-1][0] = PddVd.Mean()/PVVVd.Mean();
        }

Its here that the variance at a specific lag is calculated. The results of which are stored in the matrix "mcord".

 Px_vector = MathLog10(x_vector);

      mx = Px_vector.Mean();

      Sqx = MathPow(Px_vector,2.0);

      SSxx = Sqx.Sum() - i*pow(mx,2.0);

      lmcord = log10(mcord);

      my = lmcord.Mean();

      pt = Px_vector*lmcord.Col(0);

      SSxy = pt.Sum() - i*mx*my;

      H[k][0]= SSxy/SSxx;

      k++;

Outside the inner loop, in the final leg of the outer loop, the main "H" matrix values are updated. Finally, the function returns the mean of the 'H' matrix divided by 'q'.

 return H.Mean()/double(q);

To test our GHE function, the application GHE.ex5, implemented as an Expert Advisor has been prepared. It allows one to visualize, random series with predefined characteristics and observe how the GHE works. Full interactivity enables adjusting the all parameters of the GHE, as well as the length of the series within  limits. An interesting feature is the ability to log transform the series before applying the GHE, to test if there are any benefits to preprocessing the data in this manner.

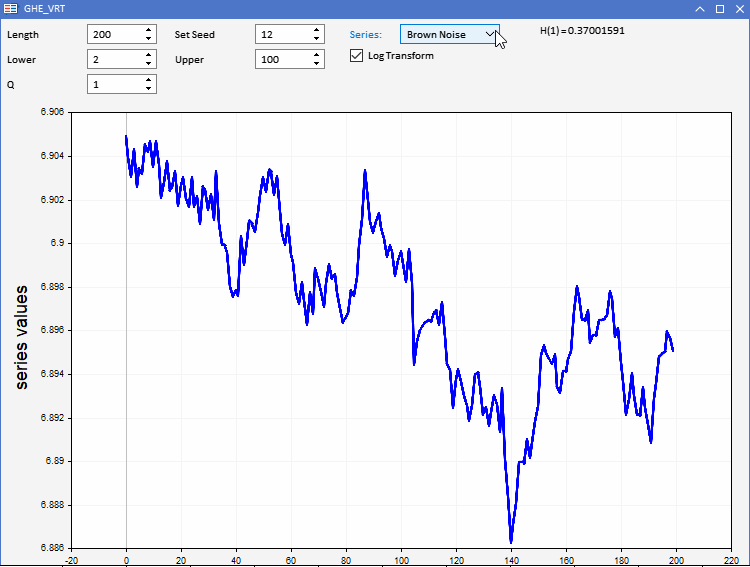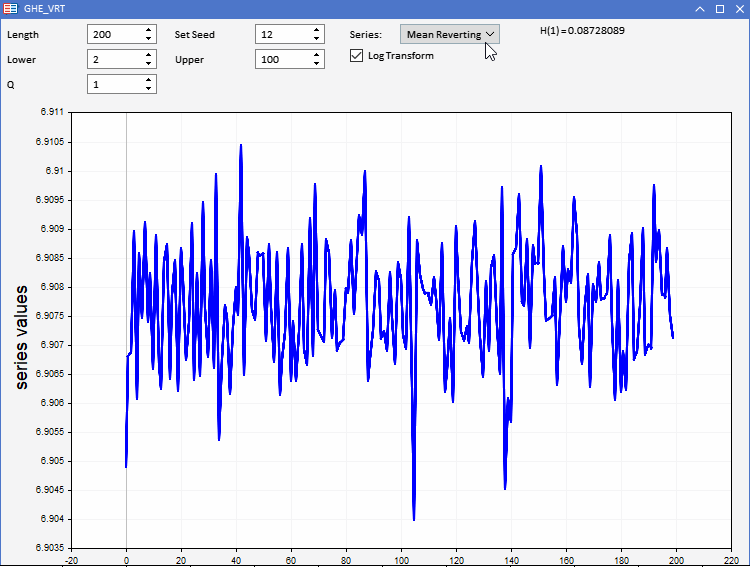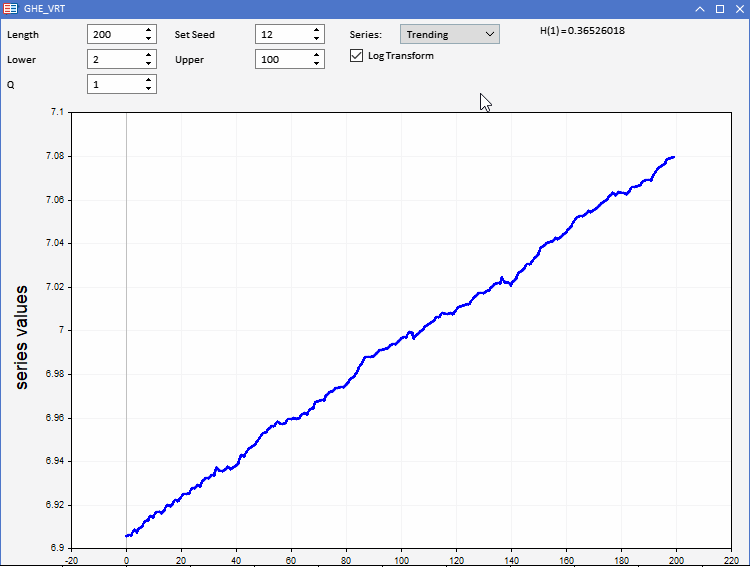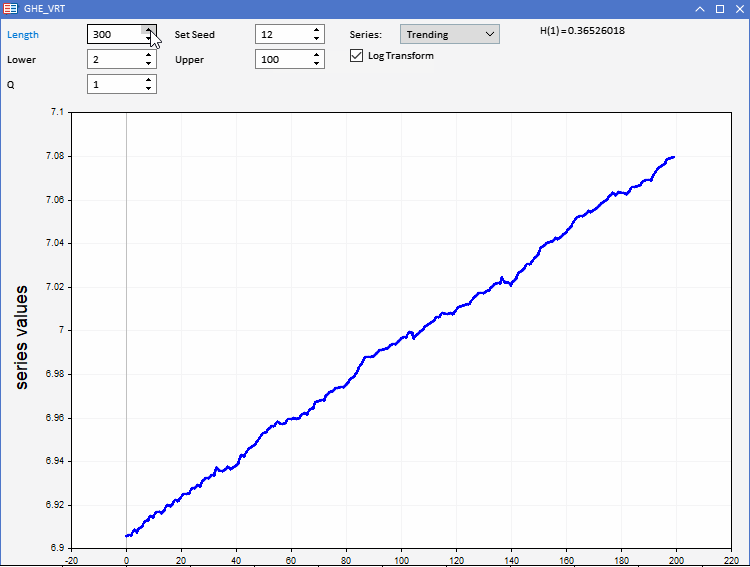
We all know that when it comes to real world application, data sets are plagued by excessive noise. Since the GHE produces an estimate, that is sensitive to sample size, we need to test the significance of the result. This can be done by conducting a hypothesis test called the Variance Ratio (VR) test.

The Variance Ratio Test

The Variance Ratio Test is a statistical test used to assess the randomness of a time series by examining whether the variance of the series increases proportionally with the length of the time interval. The test is based on the idea that if the series to be tested follows a random walk, the variance of the series  changes over a given time interval should increase linearly with the length of the interval. If the variance increases at a slower rate, it may indicate serial correlation in the series changes, suggesting that the series is predictable. The Variance Ratio tests whether:

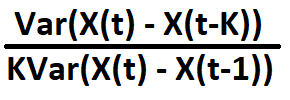
is equal to 1, where:
- X() is the time series of interest.
- K is an arbitrary lag.
- Var() denotes the variance.

The null hypothesis of the test is that the time series follows a random walk, and thus the variance ratio should be equal to 1. A variance ratio significantly different from 1 may lead to rejecting the null hypothesis, suggesting the presence of some form of predictability or serial correlation in the time series.

Implementation of the Variance Ratio Test

The VR test is implemented as the CVarianceRatio class defined in VRT.mqh. There are two methods that can be called to conduct a VR test "Vrt()" , one works with vectors and the other with arrays. The method parameters are described below:

• "lags" specifies the number of periods or lags used in the variance calculation, in the context of how we want to use the VR test to assess the significance of our GHE estimate , we could set "lags" to either the corresponding "lower" or "upper" parameters of "gen_hurst()". This value cannot be set to less than 2. 
• "trend" is an enumeration allowing the specification of the type of random walk we want to test for. Only two options have an effect, TREND_CONST_ONLY and TREND_NONE.
• "debiased" indicates whether to use a debiased version of the test, which is applicable only if "overlap" is true. When set to true, the function employs a bias correction technique to adjust the variance ratio estimate, aiming for a more accurate representation of the true relationship between variances. This is mostly beneficial when working with small sample sized series.
  
• "overlap" Indicates whether to use all overlapping blocks. If false, the length of the series minus one, must be an exact multiple of "lags".  If this condition is not satisfied, some values at the end of the input series will be discarded.
• "robust" selects whether to account for either heteroskedasticity (true) or only homoskedasticity (false). In statistical analysis, a process that is heteroskedastic has non-constant variance, whereas a homoskedastic series is charactized by constant variance. 
  

The "Vrt()" method returns true on successful execution, after which, any of the getter methods can be called to retrieve all aspects of the test result.

//+------------------------------------------------------------------+
//| CVarianceRatio  class                                            |
//| Variance ratio hypthesis test for a random walk                  |
//+------------------------------------------------------------------+
class CVarianceRatio
  {
private:
   double            m_pvalue;     //pvalue
   double            m_statistic;  //test statistic
   double            m_variance;   //variance
   double            m_vr;         //variance ratio
   vector            m_critvalues; //critical values

public:
                     CVarianceRatio(void);
                    ~CVarianceRatio(void);

   bool              Vrt(const double &in_data[], ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);
   bool              Vrt(const vector &in_vect, ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);

   double            Pvalue(void) { return m_pvalue;}
   double            Statistic(void) { return m_statistic;}
   double            Variance(void) { return m_variance;}
   double            VRatio(void) { return m_vr;}
   vector            CritValues(void) { return m_critvalues;}
  };

Inside "Vrt()" , if "overlap" is false, we check if the length of input series is divisible by "lags". If not, we trim the end of the series and issue a warning about the data length. We then reassign "nobs" based on the updated length of the series. And calculate "mu", the trend term. Here we calculate the differences of adjacent elements in the series and save them to "delta_y". Using "delta_y" the variance is computed and saved in the variable "sigma2_1". If there's no overlap, we calculate the variance for non-overlapping blocks. Otherwise, we calculate the variance for overlapping blocks. If "debiased" is enabled along with "overlap", we adjust the variances. Here  "m_varianced" is calculated depending on "overlap" and "robust". Finally, the variance ratio, test statistic and p-value are calculated.

//+------------------------------------------------------------------+
//| main method for computing Variance ratio test                    |
//+------------------------------------------------------------------+
bool CVarianceRatio::Vrt(const vector &in_vect,ulong lags,ENUM_TREND trend=1,bool debiased=true,bool robust=true,bool overlap=true)
  {
   ulong nobs = in_vect.Size();

   vector y = vector::Zeros(2),delta_y;

   double mu;

   ulong nq = nobs - 1;

   if(in_vect.Size()<1)
     {
      Print(__FUNCTION__, "Invalid input, no data supplied");
      return false;
     }

   if(lags<2 || lags>=in_vect.Size())
     {
      Print(__FUNCTION__," Invalid input for lags");
      return false;
     }

   if(!overlap)
     {
      if(nq % lags != 0)
        {
         ulong extra = nq%lags;
         if(!y.Init(5,slice,in_vect,0,in_vect.Size()-extra-1))
           {
            Print(__FUNCTION__," ",__LINE__);
            return false;
           }
         Print("Warning:Invalid length for input data, size is not exact multiple of lags");
        }
     }
   else
      y.Copy(in_vect);

   nobs = y.Size();

   if(trend == TREND_NONE)
      mu = 0;
   else
      mu = (y[y.Size()-1] - y[0])/double(nobs - 1);

   delta_y = difference(y);

   nq = delta_y.Size();

   vector mudiff = delta_y - mu;

   vector mudiff_sq = MathPow(mudiff,2.0);

   double sigma2_1 = mudiff_sq.Sum()/double(nq);

   double sigma2_q;

   vector delta_y_q;

   if(!overlap)
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1,lags) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1,lags))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq);
     }
   else
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq*lags);
     }


   if(debiased && overlap)
     {
      sigma2_1 *= double(nq)/double(nq-1);
      double mm = (1.0-(double(lags)/double(nq)));
      double m = double(lags*(nq - lags+1));// * (1.0-double(lags/nq));
      sigma2_q *= double(nq*lags)/(m*mm);
     }

   if(!overlap)
      m_variance = 2.0 * (lags-1);
   else
      if(!robust)
         m_variance = double((2 * (2 * lags - 1) * (lags - 1)) / (3 * lags));
      else
        {
         vector z2, o, p;
         z2=MathPow((delta_y-mu),2.0);
         double scale = pow(z2.Sum(),2.0);
         double theta = 0;
         double delta;
         for(ulong k = 1; k<lags; k++)
           {
            if(!o.Init(3,slice,z2,k,z2.Size()-1) ||
               !p.Init(3,slice,z2,0,z2.Size()-k-1))
              {
               Print(__FUNCTION__," ",__LINE__);
               return false;
              }
            o*=double(nq);
            p/=scale;
            delta = o.Dot(p);
            theta+=4.0*pow((1.0-double(k)/double(lags)),2.0)*delta;
           }
         m_variance = theta;
        }
   m_vr = sigma2_q/sigma2_1;

   m_statistic = sqrt(nq) * (m_vr - 1)/sqrt(m_variance);

   double abs_stat = MathAbs(m_statistic);

   m_pvalue = 2 - 2*CNormalDistr::NormalCDF(abs_stat);

   return true;
  }

To test the class we modify the application GHE.ex5 used to demonstrate the "gen_hurst()" function. Because the GHE is defined by a range of lags that the analysis is concentrated on. We can calibrate the VRT to test the significance of the GHE results over the same range of lags. By running the VRT at the minimum and maximum lags we should a obtain sufficient information. In GHE.ex5 variance ratio at the "lower" is displayed first before the variance ratio at the "upper" lag.
Remember that a variance ratio that diverges significantly is an indication of predictability in the data. Variance ratios close to 1, suggest the series is not far off from a random walk. By playing around with the application, testing different combinations of parameters, we notice that both the GHE and VRT results are affected by the sample size.

For series lengths less than  1000, both sometimes gave unexpected results.

Also,  there were instances where the results of the GHE would differ significantly when comparing tests using raw values and log transformed values.

Now that we are familiar with the VRT and GHE we can apply them to our mean reversion strategy. If it is known that a price series is mean reverting, we can roughly estimate what the price will do based on its current deviation from the mean. The basis of our strategy will rely on analyzing the characteristics of a prices series over a given period of time. Using this analysis we form a model that estimates points at which price is likely to snap back after diverging too far from the norm. We need some way to measure and quantify this diversion to generate entry and exit signals.

The Z-score

The z-score measures the number of standard deviations the price is from its mean. By normalizing the prices, the z-score oscillates about zero. Lets see what a plot of the z-score looks like by implementing it as an indicator. The full code is shown below.

//+------------------------------------------------------------------+
//|                                                       Zscore.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<VectorMatrixTools.mqh>
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
//--- plot Zscore
#property indicator_label1  "Zscore"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input int      z_period = 10;
//--- indicator buffers
double         ZscoreBuffer[];
vector vct;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,ZscoreBuffer,INDICATOR_DATA);
//----
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0);
//---
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,z_period-1);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(rates_total<z_period)
     {
      Print("Insufficient history");
      return -1;
     }
//---
   int limit;
   if(prev_calculated<=0)
      limit = z_period - 1;
   else
      limit = prev_calculated - 1;
//---
   for(int i = limit; i<rates_total; i++)
     {
      vct.Init(ulong(z_period),assign,close,ulong(i-(z_period-1)),i,1);
      if(vct.Size()==ulong(z_period))
         ZscoreBuffer[i] = (close[i] - vct.Mean())/vct.Std();
      else
         ZscoreBuffer[i]=0.0;
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

From this plot, it can seen that the indicator values now look more normally distributed.

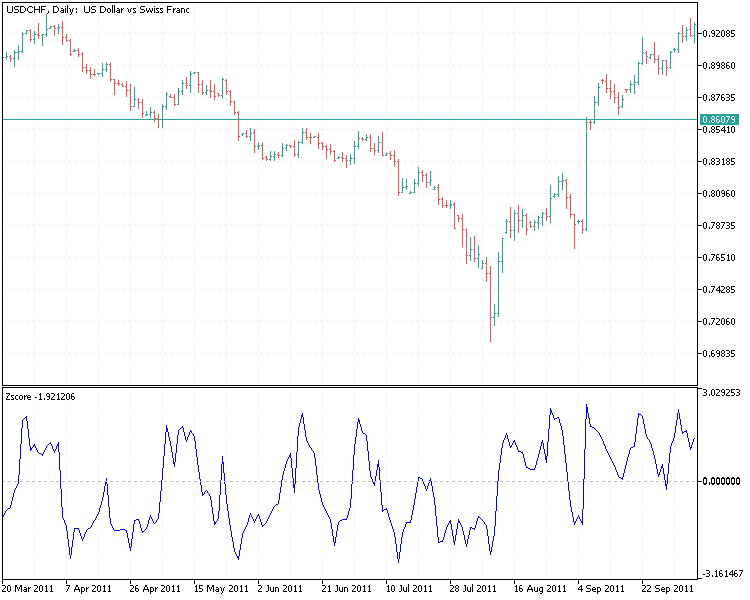
Trading signals are generated when the z-score deviates significantly from 0, exceeds some historically derived threshold. An extremely negative z-score signals an appropriate time to go long, whilst the opposite indicates a good time to go short. That means we need two thresholds for buy and sell signals. One negative (for buy) and one positive (for sell). With our entries covered, we move onto determining one exists. One option is to derive another set of thresholds that work when in a specific position (long or short). When short we may look to close our position as the z-score traverses back towards 0. Similarly, we close a long position when the z-score climbs towards 0 from the extreme level we bought at.

We now have our entries and exits defined using the indicator Zscore.ex5. Lets put all this together in an EA. The code is shown below.

//+------------------------------------------------------------------+
//|                                                MeanReversion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Zscore.ex5"
#include<ExpertTools.mqh>
//---Input parameters
input int  PeriodLength  = 10;
input double LotsSize = 0.01;
input double  LongOpenLevel = -2.0;
input double  ShortOpenLevel = 2.0;
input double  LongCloseLevel = -0.5;
input double  ShortCloseLevel = 0.5;
input ulong  SlippagePoints = 10;
input ulong  MagicNumber    = 123456;
//---
 int indi_handle;
//---
 double zscore[2];
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(PeriodLength<2)
    {
     Print("Invalid parameter value for PeriodLength");
     return INIT_FAILED;
    }
//---
   if(!InitializeIndicator())
    return INIT_FAILED;
//---        
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---    
      int signal = GetSignal();
//---      
      if(SumMarketOrders(MagicNumber,_Symbol,-1))
       {
        if(signal==0)
         CloseAll(MagicNumber,_Symbol,-1);
        return; 
       }
      else
        OpenPosition(signal);
//---   
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Initialize indicator                                             |
//+------------------------------------------------------------------+
bool InitializeIndicator(void)
{
 indi_handle = INVALID_HANDLE;
//---
 int try = 10;
//---
 while(indi_handle == INVALID_HANDLE && try>0)
  {
   indi_handle = (indi_handle==INVALID_HANDLE)?iCustom(NULL,PERIOD_CURRENT,"::Indicators\\Zscore.ex5",PeriodLength):indi_handle;
   try--;
  }
//---
 if(try<0)
  {
   Print("Failed to initialize Zscore indicator ");
   return false;
  }
//---
 return true;
}
//+------------------------------------------------------------------+
//|Get the signal to trade or close                                  |
//+------------------------------------------------------------------+
int GetSignal(const int sig_shift=1)
{
//---
 if( CopyBuffer(indi_handle,int(0),sig_shift,int(2),zscore)<2)
   {
    Print(__FUNCTION__," Error copying from indicator buffers: ", GetLastError());
    return INT_MIN;
   } 
//---   
 if(zscore[1]<LongOpenLevel && zscore[0]>LongOpenLevel)
     return (1);
//---   
 if(zscore[1]>ShortOpenLevel && zscore[0]<ShortOpenLevel)
     return (-1);          
//---   
 if((zscore[1]>LongCloseLevel && zscore[0]<LongCloseLevel) ||
    (zscore[1]<ShortCloseLevel && zscore[0]>ShortCloseLevel))
     return (0);
//---
 return INT_MIN;
//--- 
}
//+------------------------------------------------------------------+
//|  Go long or short                                                |
//+------------------------------------------------------------------+
bool OpenPosition(const int sig)
{

 long pid;
//--- 
 if(LastOrderOpenTime(pid,NULL,MagicNumber)>=iTime(NULL,0,0))
   return false;
//---   
 if(sig==1)
   return SendOrder(_Symbol,0,ORDER_TYPE_BUY,LotsSize,SlippagePoints,0,0,NULL,MagicNumber);
 else
  if(sig==-1)
    return SendOrder(_Symbol,0,ORDER_TYPE_SELL,LotsSize,SlippagePoints,0,0,NULL,MagicNumber); 
//--- 
  return false;                   
}

It is very basic, there are no stoploss or takeprofit levels defined. Our goal is to first optimize the EA to get the optimal period for the Zscore indicator, as well as the optimal entry and exit thresholds. We will optimize over several years of data and test the optimal paramters out of sample, but before we do that, we take short detour to introduce another interesting tool. In the book Algorithmic Trading: Winning Strategies And Their Rationale, the author Ernest Chan describes an interesting tool for developing mean reverting strategies, its called the Half life of mean reversion.

Half life of mean reversion

The half-life of mean reversion represents the time it takes for a deviation from the mean to diminish by half. In the context of an asset's price, the half-life of mean reversion indicates how quickly the price tends to revert to its historical average after deviating from it. It is a measure of the speed at which the mean-reverting process occurs. Mathematically, the half-life can be related to the speed of mean reversion by the equation:

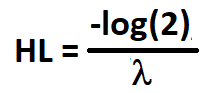
Where:
- HL is the half-life.
- log() is the natural logarithm.
- lambda is the speed of mean reversion.

In practical terms, a shorter half-life implies a faster mean reversion process, while a longer half-life suggests a slower mean reversion. The half-life concept can be used to fine-tune parameters in mean-reverting trading strategies, helping to optimize entry and exit points based on historical data and the observed speed of mean reversion. The half-life of mean reversion is derived from the mathematical representation of a mean-reverting process, typically modeled as an Ornstein-Uhlenbeck process. The Ornstein-Uhlenbeck process is a stochastic differential equation that describes a continuous-time version of mean-reverting behaviour.

According to Chan, its is possible to determine whether mean reversion is an appropriate strategy to employ by calculating the half life of mean reversion. First, if lambda is positive then mean reversion should not be applied at all. Even when lambda is negative and very close to zero, applying mean reversion is discouraged as it indicates that the half life will be long. Mean reversion should be employed only when the half life is reasonably short.

The half life of mean reversion is implemented as a function in MeanReversionUtilities.mqh, the code is given below. It is calculated by regressing the price series against the series of differences between subsequent values. Lambda is equal to the beta parameter of the regression model and the half life is computed by dividing -log(2) by lambda.

//+------------------------------------------------------------------+
//|Calculate Half life of Mean reversion                             |
//+------------------------------------------------------------------+
double mean_reversion_half_life(vector &data, double &lambda)
  {
//---
   vector yy,zz;
   matrix xx;
//---
   OLS ols_reg;
//---
   yy.Init(data.Size()-1,slice,data,1,data.Size()-1,1);
//---
   zz.Init(data.Size()-1,slice,data,0,data.Size()-2,1);
//---
   if(!xx.Init(zz.Size(),2) || !xx.Col(zz,0) || !xx.Col(vector::Ones(zz.Size()),1) || !ols_reg.Fit(yy-zz,xx))
     {
      Print(__FUNCTION__," Error in calculating half life of mean reversion ", GetLastError());
      return 0;
     }
//---
   vector params = ols_reg.ModelParameters();
   lambda = params[0];
//---
   return (-log(2)/lambda);
//---
  }

We will use it in conjuction with the GHE and VRT to test a sample of prices over a selected period of years, for a few forex symbols. We will use the test results to select an appropriate symbol to which will will apply the EA we built earlier. It will be optimized on the same period of years and finally tested out of sample.  The script below accepts a list of candidate symbols that will be tested using the GHE, VRT and the half life.

//+------------------------------------------------------------------+
//|                                                 SymbolTester.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<MeanReversionUtilities.mqh>
#include<GHE.mqh>
#include<VRT.mqh>

//--- input parameters
input string   Symbols = "EURUSD,GBPUSD,USDCHF,USDJPY";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2020.01.02 00:00:01';
input datetime StopDate=D'2015.01.18 00:00:01';
input int Q_parameter = 2;
input int MinimumLag = 2;
input int MaximumLag = 100;
input bool ApplyLogTransformation = true;
//---
CVarianceRatio vrt;
double ghe,hl,lb,vlower,vupper;
double prices[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(StartDate<=StopDate)
     {
      Print("Invalid input for StartDater or StopDate");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;
//---in case there are less than two symbols specified
   if(num_symbols<1)
     {
      Print("Invalid input. Please list at least one symbol");
      return;
     }
//---loop through all paired combinations from list
   for(uint i=0; i<symbols.Size(); i++)
     {

      //--- get prices for the pair of symbols
      if(CopyClose(symbols[i],TimeFrame,StartDate,StopDate,prices)<1)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //---
      if(ApplyLogTransformation && !MathLog(prices))
        {
         Print("Mathlog error ", GetLastError());
         return;
        }
      //---
      if(!vrt.Vrt(prices,MinimumLag))
         return;
      //---
      vlower = vrt.VRatio();
      //---
      if(!vrt.Vrt(prices,MaximumLag))
         return;
      //---
      vupper = vrt.VRatio();
      //---
      ghe = general_hurst(prices,Q_parameter,MinimumLag,MaximumLag);
      //---
      hl = mean_reversion_half_life(prices,lb);
      //--- output the results
      Print(symbols[i], " GHE:  ", DoubleToString(ghe)," | Vrt: ",DoubleToString(vlower)," ** ",DoubleToString(vupper)," | HalfLife ",DoubleToString(hl)," | Lambda: ",DoubleToString(lb));
     }
  }
//+------------------------------------------------------------------+

Running the script produces the following results:

19:31:03.143    SymbolTester (USDCHF,D1)        EURUSD GHE:  0.44755644 | Vrt: 0.97454284 ** 0.61945905 | HalfLife 85.60548208 | Lambda: -0.00809700
19:31:03.326    SymbolTester (USDCHF,D1)        GBPUSD GHE:  0.46304381 | Vrt: 1.01218672 ** 0.82086185 | HalfLife 201.38001205 | Lambda: -0.00344199
19:31:03.509    SymbolTester (USDCHF,D1)        USDCHF GHE:  0.42689382 | Vrt: 1.02233286 ** 0.47888803 | HalfLife 28.90550869 | Lambda: -0.02397976
19:31:03.694    SymbolTester (USDCHF,D1)        USDJPY GHE:  0.49198795 | Vrt: 0.99875744 ** 1.06103587 | HalfLife 132.66433924 | Lambda: -0.00522482

The USDCHF symbol has the most promising test results over the selected date period. So we will optimize the EA's parameters trading the USDCHF. An interesting exercise would be to select the Zscore period for optimization and see if it differs from the calculated half life.

Here we can see the optimal Zscore period, it is very close to the calculated half life of mean reversion. Which is encouraging. Of course, more extensive testing would be necessary to determine the usefullness of the half life.

Finally we test the EA out of sample with the optimal parameters.

The results donot look good. Likely due to the fact that the market is in continuous flux, so the characteristics observed over the period the EA was optimized over, no longer apply. We need more dynamic entry and exit thresholds that account for changes in underlying market dynamics.

We can use what was learned here as a basis for further development. One avenue we can explore is the application of the tools described here to implement a pairs trading strategy. Instead of the Zscore indicator being based in a single price series, it can be based on the spread of two cointegrated or correlated instruments.

Conclusion

In this article we have demonstrated the implementation of the Generalized Hurst Exponent in MQL5 and shown how it can be used to determine the characteristics of a price series.  We also looked at the application of the Variance Ratio test, as well as the half life of mean reversion.  The table that follows is a description of all the files attached with the article.

File	Description
Mql5\include\ExpertTools.mqh	Contains function definitions for conducting trade operation used in MeanReversion EA
Mql5\include\GHE.mqh	Contains definition of function implementing the Generalized Hurst Exponent
Mql5\include\OLS.mqh	Contains definition of OLS class implementing ordinary least squares regression
Mql5\include\VRT.mqh	Contains definition of CVarianceRatio class that encapsulates the Variance ratio test
Mql5\include\VectorMatrixTools.mqh	Has various function definitions for quickly initializing common vectors and matrices
Mql5\include\TestUtilities.mqh	Has a number of declarations used in OLS class definition
Mql5\include\MeanReversionUtilities.mqh	Contains various function definitions including one implementing the half life of mean reversion
Mql5\Indicators\Zscore.mq5	indicator used in MeanReversion EA
Mql5\scripts\SymbolTester.mq5	Script that can be used to test symbols for mean reversion
Mql5\Experts\GHE.ex5	Expert advisor app that can be used to explore and experiment with the GHE and VRT tools
Mql5\scripts\MeanReversion.mq5	EA demonstrates a simple mean reversion strategy