A Generic Optimization Formulation (GOF) to Implement Custom Max with Constraints

Introduction — Basics of Optimization

Optimization problems have two phases: 1) problem formulation, and 2) problem solution. In phase one there are three main components: the input variables, the objective functions, and the constraint functions. In phase two, the solution of the problem is carried out numerically with an optimization algorithm.

Variables (notation x_1 , x_2 , x_3 , …, x_n):  Variables are the “knobs” we can change to maximize the objective function. There are variables of different types: integer, real, and Boolean. In expert advisors we could use variables such as: the moving average period, the TP/SL ratio at entry, the SL in pips, etc.

Objective Functions (notation f_i (x)): If there is more than one objective function, the problem is called a multi-objective optimization problem. MetaTrader 5 optimization algorithm expects just one objective function, hence, in order to consider more than one objective, we need to combine them into one. The simplest way to combine objective functions is by creating a weighted sum of them. Some developers have proposed to use multiplication operation to combine them, and it may work in some situations, but we prefer the summation as a better approach. In this article we use a "targeted and weighted" summation of objectives as will be explained below. As examples of objective functions  we have: balance, profit target, win rate, annual return, net profit, etc.

Constraint Functions (notation g_i (x)): These are functions that generate a value that the user wants to bound. The bound could be an upper bound, like in g_i(x) ≤ U_i , where g_i(x) is the i_th constraint, and U_i is the upper bound. Similarly, a lower bound constraint is like g_i(x) ≥ L_i , where L_i is the lower bound.

MetaTrader 5 optimization algorithm only takes the constraints imposed on the input variables (also known as side constraints), for instance, 3 <= x_1 <= 4, but no other constraint type can be used. Hence, we need to include the presence of any additional constraint g_i(x) into the final and single objective function, F(x), as will be shown below. Examples of constraint functions g_i(x) are: limiting the number of consecutive losses, or the Sharpe ratio, or the win rate, etc.

Optimization Algorithms

In general terms, there are two main types of optimization algorithms. The first type is the more classical, based on the calculation of gradients of all functions involved in the optimization problem (this dates back to Isaac Newton’s times). The second type is more recent (since the ~1970’s) that does not use gradient information at all. In between, there may be algorithms that combine the two approaches mentioned, but we don’t need to address them here. The MetaTrader 5 algorithm called “Fast Genetic based Algorithm”---in the MetaTrader 5 terminal Settings tab---belongs to the second type. This allows us to skip the need for the computation gradients for objective and constraint functions. Even more, thanks to the gradient-less nature of the MetaTrader 5 algorithm, we were able to account for constraints functions that would not had been appropriate with gradient-based algorithms. More on this will be discussed below.

One important point is that the MetaTrader 5 algorithm called “Slow Complete Algorithm” is not actually an optimization algorithm but a brute force, exhaustive evaluation of all possible combinations of values for all the input variables within the side constraints.

The Objective Function F(x) Built from Multiple Objectives f_i(x)

In this section we will go over the combination of multiple objective functions into one single objective function F.

As mentioned in the Introduction, we use summation to combine multiple objectives. The reader is welcome to change the source code to use a multiplicative combination is so desired. The summation combination formula is:

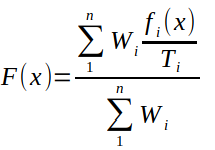
where 

• x is the vector of n input variables
• f_i(x) is the i_th objective function
• W_i     is the i_th weight
• T_i is the i_th target desired for the i_th objective function

The target serves as a normalization (dividing) value such that a given objective is comparable to  other objectives in the summation. In other words, the weighted sum is for “normalized” objective functions. The weight serves as such, as a weight that multiplies the normalized objective ( f_i(x)/T_i ) such that the user is able to emphasize which normalized objective is more important than the other. The weights W_i’s are convexified by dividing the sum of W_i*f_i(x)/T_i by the sum of the W_i’s.

Selection of W_i: The convexification of weights allows the user to focus on their relative value, rather than in their absolute value. For instance, suppose there are three objectives: annual return, recovery factor, and profit factor. These weights: W_1=10, W_2=5, W_3=1, have the same effect of W_1=100, W_2=50, W_3=10, that is to say, normalized objective 1 (annual return/T_1) is considered twice as important as the normalized objective 2 (recovery factor/T_2), and ten times more important than the normalized objective 3 (profit factor/T_3). There is no right or wrong values of  as long as they are positive, and express the relative importance based on the user’s criterion.

Selection of T_i: The selection of targets T_i must me done carefully after a few simulations, before doing the full fleshed optimization. The reason for doing so is to estimate the ranges of each objective function and set T_i values that will render normalized functions (f_i(x)/T_i) of comparable magnitude. For example, suppose that your account has an initial balance of 10,000; your EA algorithm makes the final balance to be around 20,000 before it is optimized; the profit factor is 0.9. If you set up your optimization problem with two objectives: f_1 = balance, f_2 = profit factor, then a good value for targets are: T_1 = 30k, T_2 = 2, which will make both normalized functions of the same order of magnitude (comparable values). Once you run a full optimization you may find that the EA gives a very large final balance, and a similar profit factor. At this point, you could adjust the T_i values if the normalized function are of different orders of magnitude. Target values must also be positive real numbers. Use your judgment. More on this topic will be discussed when we cover the output from the GOF code.

Adding Constraints 

The formulation of the objective function as the weighted sum of individual objectives is pretty much standard. Now we introduce a simple way to include constraint functions in the optimization problem in such a way that the Fast-Genetic-based-Algorithm of MetaTrader 5 still works. We are going to use a modified version of the Lagrange method which subtract a penalty from the single optimization objective.  For that purpose we will define new penalty functions that measure the amount of violation for each constraint:

As you can check, P_i(x) is positive when g_i(x) is violated, and zero otherwise. If U_i or L_i are zero, we replace them by 1 to avoid division by zero.

In the Lagrange multiplier method, there is one multiplier per constraint, and their values are the solution of a system of equations. In our modified version, we assume all multipliers are the same and have a constant value k_p (see formula below). This simplification works here because the optimization algorithm does not need to compute gradients of any function in the optimization problem.

The final single objective function F(x) is

Note: the symbol “:=” means assignment, not mathematical definition. 

Multiplier k_p plays the role of the Lagrange multipliers, and is used to force infeasible designs (those who violate at least one constraint) to have a very low objective. This lowering of the objective value will make the genetic algorithm in MetaTrader 5 to rank that design very low and unlikely to be used to for reproduction in the next generation of designs.

Multiplier k_o is not part of the Lagrange multiplier method. It is used to increase the objective function for feasible designs to expand the positive side of the Y axis in the optimization plots in the MetaTrader 5 terminal. 

The user may change K_o and K_p values in the input Miscellaneous section. We recommend the values of k_o and K_p to be powers of 10 (e.g., 10, 100, 1000, etc.).

Screenshot of the MetaTrader 5 terminal Inputs Tab

There are three input sections in GOF: objective functions, constraint functions, and miscellaneous.

Below is the Objective Functions section. There are up 5 objectives that can be included in the problem formulation, out of 18 possible functions that will be shown later. Adding more than 5 objectives can be done following the code, but anything beyond 3 objectives makes the selection of weights and target more difficult. Adding more than 18 possible functions can be done following the code.

Below is the hard constraint function section. There are up to 10 constraint that can be added to the optimization formulation, out of 14 constraint functions implemented in GOF. Adding more than 10 constraints can be done following the code. Adding new constraints to the list of 14 can also be done by following the code.

Below is the Miscellaneous Optimization Parameter Section. More on this section will be discussed in next paragraphs.

Using GenericOptimizationFormulation.mqh in your EA

If you are a person that have little patience to read the whole article, we first provide the steps to use this code in your EA so you can play with it first, and then read the rest of the article with more insight. Below are the initial comments in the GenericOptimizationFormulation.mqh file:

/*

In order to use this file in your EA you must do the following:

- Edit the EA .mq5 file

- Insert the following two lines after the input variables and before OnInit()

     ulong gof_magic= an_ulong_value;

     #include <YOUR_INCLUDE_LOCATION\GenericOptimizationFormulation.mqh>

- Save and compile your EA file

If you get compiler's errors, make sure you did:

- replace an_ulong_value by the variable containing the magic number, or by the magic numeric value

- replace YOUR_INCLUDE_LOCATION by the folder name where your include files are

*/

Hopefully the insert above is self-explanatory. We will show an example using the MetaTrader 5 Moving Average EA later. Now let's continue with the explanation of the source code.

The Source Code: GenericOptimizationFormulation.mqh

Now that we presented formulas for the objective function and constraints, we discuss the mql5 implementation with snippets of the code.

 Requests to readers:

• It is said that a software with more than seven lines of code has a non-zero probability of having a bug. GOF has more than a thousand lines, so the probability are definitely non-zero. We encourage the reader to provide feedback in the comments to make improvements in the code.
• If you find a better way to write the code, we are looking forward to see your better lines of code to improve GOF.
• Add and enhance the code with your own objective functions and constraints. Please share them in the comments as well.

Libraries Included

First, we need to include some libraries to do some statistics and algebra:

#include <Math\Stat\Lognormal.mqh>
#include <Math\Stat\Uniform.mqh>
#include <Math\Alglib\alglib.mqh>

Objective Functions to choose from:

enum gof_FunctionDefs {        // functions to build objective
   MAX_NONE=0,                 // 0] None
   MAX_AnnRetPct,              // 1] Annual Return %
   MAX_Balance,                // 2] Balance
   MAX_NetProfit,              // 3] Net Profit
   MAX_SharpeRatio,            // 4] Sharpe Ratio
   MAX_ExpPayOff,              // 5] Expected Payoff
   MAX_RecovFact,              // 6] Recovery Factor
   MAX_ProfFact,               // 7] Profit Factor
   MAX_LRcrr3,                 // 8] LRcrr^3
   MAX_NbrTradesPerWeek,       // 9] #Trades/week
   MAX_WinRatePct,             // 10] Win Rate %
   MAX_Rew2RiskRatio,          // 11] Reward/Risk(RRR=AvgWin/AvgLoss)
   MAX_OneOverLRstd,           // 12] 1/(LR std%)
   MAX_OneHoverWorstTradePct,  // 13] 100/(1+|WorstLoss/Init.Dep*100|)
   MAX_LR,                     // 14] LRslope*LRcorr/LRstd
   MAX_OneHoverEqtyMaxDDpct,   // 15] 100/(1+EqtyMaxDD%))
   MAX_StratEfficiency,        // 16] Seff=Profit/(TotalTrades*AvgLot)
   MAX_KellyCrit,              // 17] Kelly Criterion
   MAX_OneOverRoRApct          // 18] 1/Max(0.01,RoRA %)
};

There are 18 possible objectives to choose a maximum of 5 in order to formulate the optimization problem. The user can add more functions to the source code following the same implementation pattern. Names of the objective functions are meant to be self-explanatory, except for a few ones mentioned below:

• LRcrr^3: the linear regression correlation coefficient to the power of 3.
• 1/(LR std%): LR std is the linear regression standard deviation. The inverse measures how tight the equity line is to a straight line.
• 100/(1+|WorstLoss/Init.Dep*100|): worst loss divided by the initial deposit is a measure of poor performance. The inverse of that is a measure of good performance.
• LRslope*LRcorr/LRstd: this is a multiplicative objective of three functions from the linear regression: the slope, the correlation coefficient and the standard deviation.
• Seff=Profit/(TotalTrades*AvgLot): is a measure of strategy efficiency. We prefer strategies with high profit, small number of trades with small lot size.
• 1/Max(0.01,RoRA %): RoRA is the Risk of Ruin your Account. This is computed using a Monte Carlo simulation that we will discuss later.

Hard Constraints to choose from:

enum gof_HardConstrains {
   hc_NONE=0,                     // 0] None
   hc_MaxAccountLoss_pct,         // 1] Account Loss % InitDep
   hc_maxAllowed_DDpct,           // 2] Equity DrawDown %
   hc_maxAllowednbrConLossTrades, // 3] Consecutive losing trades
   hc_minAllowedWin_pct,          // 4] Win Rate %
   hc_minAllowedNbrTradesPerWeek, // 5] # trades/week
   hc_minAllowedRecovFactor,      // 6] Recov Factor
   hc_minAllowedRRRFactor,        // 7] Reward/Risk ratio
   hc_minAllowedAnnualReturn_pct, // 8] Annual Return in %
   hc_minAllowedProfFactor,       // 9] Profit Factor
   hc_minAllowedSharpeFactor,     // 10] Sharpe Factor
   hc_minAllowedExpPayOff,        // 11] Expected PayOff
   hc_minAllowedMarginLevel,      // 12] Smallest Margin Level
   hc_maxAllowedTradeLoss,        // 13] Max Loss trade
   hc_maxAllowedRoRApct           // 14] Risk of Ruin(%)
};
enum gof_HardConstType {
   hc_GT=0, // >=     Greater or equal to
   hc_LT    // <=     Less or equal to
};

There are 14 possible constraints to choose a maximum of 10 in order to formulate the optimization problem. The user can add more constraints to the source code following the same implementation pattern. Names of the constraint functions are meant to be self-explanatory. There are two types of constraints, hc_GT for constraints with a lower bound, and ht_LT for constraints with an upper boung. More on this when we show how to use them.

Risk Of Ruin Options

enum gof_RoRaCapital {
   roraCustomPct=0,  // Custom % of Ini.Dep.
   roraCustomAmount, // Custom Capital amount
   roraIniDep        // Initial deposit
};

when computing the risk of ruin your account, there are three ways to define the "account" money. The first option is as a percentage of the initial deposit. The second option is a fixed capital amount given in your account currency. The third one is the special case of the first option if the percentage is 100%. Risk of ruin is explained later with the code.

Objective function decimals

As mentioned earlier, we can choose to display additional information from the simulation using the two decimals in the result column. Here are the options:

enum gof_objFuncDecimals {
   fr_winRate=0, // WinRate %
   fr_MCRoRA,    // MonteCarlo Sim Risk of Ruin Account %
   fr_LRcorr,    // LR correlation
   fr_ConLoss,   // Max # Consecutive losing Trades
   fr_NONE       // None
};

fr_winRate is the percent win rate of the simulation in percentage. For instance, if the win rate is 34%, the result objective will be 0.39. If the win rate is 100%, it will display 0.99.

fr_MCRoRA is the risk of ruin the account in percentage. For instance, if the risk of ruin the account is 11%, the result objective will be 0.11.

fr_LRcorr is the linear regression correlation coefficient. For instance, if the coefficient is 0.88, the result objective will be 0.88.

fr_ConLoss is the largest number of continuous losing trades. For instance, if number is 7, the result objective will be 0.07. If the number is more than 99, it will display 0.99.

fr_NONE is used when you don't want to see any information in the decimals.

Objective Functions

The next section in the code is the selection of individual objective functions (maximum 5). Below is a snippet of only the first function, along with its target and weight.

input group   "- Build Custom Objective to Maximize:"
sinput gof_FunctionDefs gof_Func1   = MAX_AnnRetPct;          // Select Objective Function to Maximize 1:
sinput double gof_Target1           = 200;                    // Target 1
sinput double gof_Weight1           = 1;                      // Weight 1

Constraint functions

input group   "- Hard Constraints:"
sinput bool   gof_IncludeHardConstraints     = true;//if false, all constraints are ignored

sinput gof_HardConstrains gof_HC_1=hc_minAllowedAnnualReturn_pct; // Select Constraint Function 1:
sinput gof_HardConstType gof_HCType_1=hc_GT; // Type 1
sinput double gof_HCBound_1=50; // Bound Value 1

There is an option to turn off all hard constraint by setting gof_IncludeHardConstraints=false. Next there is the selection of the first constraint, its type, and its bound value. All ten constraints use the same format.

Miscellaneous Optimization Parameters

input group   "------ Misc Optimization Params -----"
sinput gof_objFuncDecimals gof_fr                  = fr_winRate;     // Choose Result-column's decimals
sinput gof_RoRaCapital  gof_roraMaxCap             = roraCustomPct;  // Choose capital method for Risk of Ruin
sinput double           gof_RoraCustomValue        = 10;             // Custom Value for Risk of Ruin (if needed)
sinput bool             gof_drawSummary            = false;          // Draw summary on chart
sinput bool             gof_printSummary           = true;           // Print summary on journal
sinput bool             gof_discardLargestProfit   = false;          // Subtract Largest Profit from Netprofit
sinput bool             gof_discardLargestLoss     = false;          // Add Largest Loss to Net profit
sinput double           gof_PenaltyMultiplier      = 100;            // Multiplier for Penalties (k_p)
sinput double           gof_ObjMultiplier          = 100;            // Multiplier for Objectives (k_o)

In the section above, the user will choose:

• gof_fr: The quantity to display as decimals in the Result column. 
• gof_roraMaxCap: The method to compute the RoRA capital.
• gof_RoraCustomValue: The value of capital or % of initial deposit for RoRA. This depend on your selection in the previous line.
• gof_drawSummary: You may choose to draw the GOF report summary on the chart.
• gof_printSummary: You may choose to print the GOF report summary on the Journal Tab.
• gof_discardLargestProfit: You may subtract the largest profit from the net profit to discourage strategies that favor a single large gain.
• gof_discardLargestLoss: You may add the largest lost to the net profit to discourage strategies that have a big loss. 
• gof_PenaltyMultiplier: the multiplier "K_p" shown above in the objective function definition earlier.
• gof_ObjMultiplier: the multiplier "K_o" shown above in the objective function definition earlier.

Default values in the miscellaneous section should work well.

The next lines in the code are to define variables, and to fetch values from the MetaTrader 5 TesterStatistics() function. After that, the GOF main section comes:

//------------ GOF ----------------------
// Printing and displaying results from the simulation
   GOFsummaryReport();

// calculate the single objective function
   double SingleObjective = calcObjFunc();

// calculate the total penalty from constraint violations
   if(gof_IncludeHardConstraints) gof_constraintTotalPenalty=calcContraintTotalPenalty(gof_displayContraintFlag);

// Compute customMaxCriterion
// gof_PenaltyMultiplier pushes infeasible designs to have low objective values
// gof_PenaltyMultiplier expand the positive side of the Y axis
   double customMaxCriterion=gof_constraintTotalPenalty>0?
                             SingleObjective-gof_PenaltyMultiplier*gof_constraintTotalPenalty:
                             gof_ObjMultiplier*SingleObjective;

// add additional simulation result as two decimal digits in the result column
   customMaxCriterion=AddDecimalsToCustomMax(customMaxCriterion);

// Printing and displaying more results from GOF
   FinishGOFsummaryReport(customMaxCriterion);

   return (NormalizeDouble(customMaxCriterion,2));

The code above shows: 

• GOFsummaryReport() to prepare the GOF summary report that goes in the Journal tab and on the chart.
• calcObjFunc() to calculate the combined single objective function.
• calcContraintTotalPenalty() to calculate the total penalty due to constraint violations.
• customMaxCriterion is then calculated as shown in the Introduction as the sum of the single objective minus the total penalty of constraint violations.
• AddDecimalsToCustomMax() is used to add the information in the decimals of customMaxCriterion.
• FinishGOFsummaryReport() is to finish and print the GOF Summary Report.

The rest of the code is a direct implementation of the formulas given in the introduction. The only part that is worth discussing is the risk of ruin calculation.

Risk of Ruin using Monte Carlo Simulations

The risk of ruin could be computed with a simple formula, but we chose to use a Monte Carlo simulation instead because the simple formula was not given sensible results. For the Monte Carlo approach we need the average win and loss, the standard deviations of such wins and losses, the win rate, and the number of trades in the simulation. Additionally we need to provide the capital that defines the ruin of the account. 

double MonteCarlo_RiskOfRuinAccount(double WinRatePct, double AvgWin, double AvgLoss, double limitLoss_money, int nTrades) {
// 10000 Montecarlo simulations, each with at least 100 trades.
// Ideally, if we had lots of trades in the history, we could use a Markov Chain transfer probability matrix
//  we are limiting the statistics to mean & stdev, without knowledge of a transfer probability information

   double posDealsMean,posDealsStd,negDealsMean,negDealsStd;
   CalcDealStatistics(gof_dealsEquity, posDealsMean,posDealsStd,negDealsMean,negDealsStd);

// seeding the random number generator
   MathSrand((int)TimeLocal()+1);

// ignore posDealsMean and negDealsMean. Use AvgWin and AvgLoss instead
   AvgLoss=MathAbs(AvgLoss);
   WinRatePct=MathMin(100,MathMax(0,WinRatePct));

// case when win rate is 100%:
   if((int)(WinRatePct*nTrades/100)>=nTrades) {
      WinRatePct=99;          // just to be a bit conservative if winrate=100%
      AvgLoss=AvgWin/2;       // a guessengineering value
      negDealsStd=posDealsStd;// a guessengineering value
   }

// Use log-normal distribution function. Mean and Std are estimated as:
   double win_lnMean =log(AvgWin*AvgWin/sqrt(AvgWin*AvgWin+posDealsStd*posDealsStd));
   double loss_lnMean=log(AvgLoss*AvgLoss/sqrt(AvgLoss*AvgLoss+negDealsStd*negDealsStd));
   double win_lnstd  =sqrt(log(1+(posDealsStd*posDealsStd)/(AvgWin*AvgWin)));
   double loss_lnstd =sqrt(log(1+(negDealsStd*negDealsStd)/(AvgLoss*AvgLoss)));

   double rand_Win[],rand_Loss[];
   double r[];

// limit amount of money that defines Ruin
   limitLoss_money=MathAbs(limitLoss_money);
   bool success;
   int ruinCount=0; // counter of ruins
   int successfulMCcounter=0;
   int nTradesPerSim=MathMax(100,nTrades);// at least 100 trades per sim
   int nMCsims=10000; // MC sims, each one with nTradesPerSim

   for(int iMC=0; iMC<nMCsims; iMC++) {
      success=MathRandomUniform(0,1,nTradesPerSim,r);

      // generate nTradesPerSim wins and losses for each simulation
      // use LogNormal distribution
      success&=MathQuantileLognormal(r,win_lnMean,win_lnstd,true,false,rand_Win);
      success&=MathQuantileLognormal(r,loss_lnMean,loss_lnstd,true,false,rand_Loss);
      if(!success)continue;
      successfulMCcounter++;
      //simulate nTradesPerSim
      double eqty=0; // start each simulation with zero equity
      for(int i=0; i<nTradesPerSim; i++) {

         // draw a random number in [0,1]
         double randNumber=(double)MathRand()/32767.;

         // select a win or a loss depending on the win rate and the random number
         // and add to the equity
         eqty+=randNumber*100 < WinRatePct?
               rand_Win[i]:
               -rand_Loss[i];

         // check if equity is below the limit (ruin)
         // count the number of times there is a ruin
         if(eqty<= -limitLoss_money) {
            ruinCount++;
            break;
         }
      }
   }
// compute risk of ruin as percentage
   double RiskOfRuinPct=(double)(ruinCount)/successfulMCcounter*100.;
   return(RiskOfRuinPct);
}

We inserted many comment lines in the code above for easy understanding. The function CalcDealStatistics(), also included in the source code, is where the standard deviations of wins and losses are computed. The main assumption in the Risk of Ruin calculation is that the history of deals follows a Log-Normal distribution to make sure samples of the distribution are positive and negative values for wins and losses, respectively.

Ideally, if we had lots of trades in the history, we could use a Markov Chain transfer probability matrix instead of assuming the "log-normality" of the deal history.  Because deal histories have around a few hundred deals (at most) there is not enough information to build the Markov Chain transition probability matrix with good accuracy. 

Interpreting MC Risk of Ruin

A Monte Carlo simulation result needs to be interpreted as a probability of the risk of losing the capital, not as a predictive value. For instance, if the returning value from the Monte Carlo simulation is 1%, it means that there is a 1% chance (probability) that your trading strategy will wipe out your total capital at risk. It does not mean that you will lose 1% of the capital at risk.

Adding Decimals to Custom Max

This is a tricky thing to do. If the reader finds a better way, please share it. Once the decimal values are computed (named dec in the code) the objective (obj) is modified in the following way:

  obj=obj>0?
       MathFloor(obj*gof_ObjPositiveScalefactor)+dec/100.:
       -(MathFloor(-obj*gof_ObjNegativeScalefactor)+dec/100.);

As you can see, if obj is a positive value it is multiplied by a large number (gof_ObjPositiveScalefactor=1e6), truncated, and then the value "dec" is divided by 100, and added as decimal. When the obj value is negative (implying that there are many constraints violated) the obj is multiplied by a different number (gof_ObjPositiveScalefactor =1e3) to compress the vertical axis for negative values.

Implementing GOF in the MetaTrader 5 Moving Average EA

Here is an example to show how to implement GOF in the MetaTrader 5 Moving Averages.mq5 expert advisor:

//+------------------------------------------------------------------+
//|                                              Moving Averages.mq5 |
//|                             Copyright 2000-2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2000-2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;

#define MA_MAGIC 1234501

// changes needed to use the GenericOptimizationFormulation (GOF):
ulong gof_magic= MA_MAGIC;
#include <GenericOptimizationFormulation.mqh>
// end of changes

That's it! Just two lines need to be added to the EA file.

Optimization Examples using GOF

Example 1: One objective, no constraints (as if we were using MetaTrader 5 Max Balance in the Settings tab):

The input tab is below. Since there is only one objective, the target and weight it not relevant at all.  Notice how all constraints are turned off with the first Boolean variable in the Hard Constraints section:

The miscellaneous sections is:

Results are shown below. See how the "Result" column is not the account balance, but the modified objective with the win rate as decimals.

We can see that the best combination of variables (9,9,3) produces a profit of 939.81 and a win rate of 41%.

We simulated the optimal combination (first line) in the table. The GOF Summary Report printed in the Journal tab is:

We will review the GOF summary report in more detail in the next example.

Example 2: Three objectives and five constraints

The settings tab is the same as before. The input variables and ranges are also the same. The input tab for GOF variables is shown below.

Objectives:

• Annual return with target of 50% and weight of 100
• The recovery factor with target of 10 and weight of 10
• The win rate percentage with target of 100% and weight 10 

Constraints:

• Account loss as % of initial deposit to be less than or equal to 10%
• Equity Drawdown % to be less than  or equal to 10%
• Number of consecutive losing trades to be less than or equal to 5
• Win rate to be greater than or equal to 35%
• Risk of Ruin account to be less than or equal to 0.5%

The capital for calculating the Risk of Ruin was set to 10% of the Initial Deposit, or 1000 units of the account currency, as shown in the Miscellaneous section above.

The best design turned out to be (10,6,6) as you can see in the first line in the optimization table.

Notice that the optimizer found a solution with lower profit compared to the first example (805.64 vs 839.81), but this new design satisfies all five constraints and maximizes three objective combined.

The GOF Summary Report 

By simulating the first line in the optimization table above, we get the GOF summary report below:

There are three sections in the GOF Summary. The first section has many quantities from the BackTest tab. There are some additional quantities that are not present in the BackTest tab: annualized profit, test length in years, Reward/Risk ratio (RRR),  Average and largest volume, win and loss standard deviations, and minimum margin level attained during the simulation.

The second section is for the Objective functions. Here there are four values for each objective: the value of the objective, the target, the weight, and the contribution percentage. The contribution percentage is the contribution of that objective function to the total single objective. In this example, the annual return contributed 95.1%, the recovery factor contributed 1.4% and  the win rate contributed 3.5% for a total of 100% of the total single objective. Target and Weights affect these contributions. 

The third section is for Constraints. A "pass" or "Fail" message is printed for each constraint, and a comparison between the actual value of the constraint vs the bound input is shown as well.

For comparison purposes, we ran the first design from example #1 (9, 9, 3) through the same optimization formulation of example 2. Below is the summary for this simulation. Notice how there is a violation of one constraint. The number of consecutive losses is 6 which is greater than the bound value of 5 given in the optimization formulation. Hence, even though the MaxBalance design (9,9,3) has better profit than the MultiObjective/Constrained design (10,6,6), it is the (10,6,6) design that satisfies all constraints. 

Recommendations when using GenericOptimizationFormulation.mqh

The greater freedom to choose multiple objectives and multiple constraints should be exercised with care. Here are some general recommendations:

1. Use no more than 3 objectives. The code allows for up to 5 objectives, but the selection of targets and weights, which affect the final outcome, becomes more difficult as the number of objectives is more than 3.
2. Use constraints based on your preferences and don't set them too tight when selecting upper (U_i) and lower (L_i) bounds. If your bounds are too tight, you won't get any feasible combination of input variables.
3. If you don't know what bound value to give for a given constraint, you may move the constraint to the objective section, and see how it behaves (magnitude, sign, etc.) by inspecting the GOF Summary report.
4. Adjust k_o and k_p if you want better plots, or if you find the optimizer is not producing the results you expected.
5. Remember, the optimal design (the top line in the Optimization table) it not necessarily the most profitable design, but the design with the highest objective function based on your selection of individual objectives and constraints.
6. We recommend that after the optimization is done, you sort designs by other columns such as profit, recovery factor, drawdown, expected payoff, profit factor, etc. The top line on each sorting could be a candidate you may consider to simulate to review the GOF summary report.
7. A good selection of objectives and constraints was shown in example #2. Use them as initial point for your experimentation.

Things Gone Wrong

You may set up an optimization formulation that is not providing the result you expected. Here are some reasons this may be happening:

1. Constraints are too tight and the MetaTrader 5 genetic optimization algorithm will take many generations to get to a positive objective function, and in some cases, it may not get there. Solution: relax your constraints.
2. Constraints are in conflict with each other. Solution: check that constraints are logically consistent.
3. Plots in the optimization have a bias toward the negative values in the y axis (meaning, the negative side occupies more space than the positive side). Solution: increase K_o or decrease K_p, or both.
4. Some designs that you like do not appear near the top in the optimization table. Keep in mind that targets and weights affect the optimization objective, and also, a single constraint violation may send the objective downward in the table. Solution: reformulate your optimization problem by adjusting targets and weights and constraints.

   

Conclusion

We hope that this Generic Optimization Formulation is useful to you. Now you have the extra freedom to choose multiple objectives and multiple constraints to set up the optimization problem you like.