Универсальная формула оптимизации (GOF) при реализации режима Custom Max с ограничениями

Введение — Основы оптимизации

Задачи оптимизации состоят из двух этапов: 1) формулировка задачи и 2) решение задачи. На первом этапе имеются три основных компонента: входные переменные, целевые функции и функции ограничений. На втором этапе решение задачи осуществляется численно с использованием алгоритма оптимизации.

Переменные (x_1 , x_2 , x_3 , …, x_n):  Переменные — это "регуляторы", которые мы можем изменять, чтобы максимизировать целевую функцию. Существуют переменные разных типов: целочисленные, вещественные и логические. В советниках мы могли бы использовать такие переменные, как: период скользящей средней, соотношение TP/SL при входе, SL в пунктах и т. д.

Целевые функции (f_i (x)): Если имеется более одной целевой функции, задача называется задачей многоцелевой оптимизации. Алгоритм оптимизации MetaTrader 5 ожидает только одну целевую функцию, поэтому для рассмотрения более одной цели нам необходимо объединить их в одну. Самый простой способ объединения целевых функций — создание их взвешенной суммы. Некоторые разработчики предлагают использовать умножение для их объединения, и в некоторых ситуациях такой подход может сработать, но я предпочитаю суммирование. В этой статье мы используем "целевое и взвешенное" ("targeted and weighted") суммирование целей. Я объясню его ниже. В качестве примеров целевых функций у нас есть: баланс, целевая прибыль, процент выигрышей, годовая доходность, чистая прибыль и т. д.

Функции ограничений (g_i (x)): Эти функции генерируют значение, которое необходимо ограничить. Это может быть верхняя граница, например g_i(x) ≤ U_i, где g_i(x) - i_е ограничение, а U_i - верхняя граница. Аналогично, нижняя граница выглядит как g_i(x) ≥ L_i, где L_i - нижняя граница.

Алгоритм оптимизации MetaTrader 5 учитывает только ограничения, наложенные на входные переменные (также известные как побочные ограничения), например, 3 <= x_1 <= 4, но никакой другой тип ограничений использоваться не может. Следовательно, нам необходимо включить наличие любого дополнительного ограничения g_i(x) в конечную и единственную целевую функцию, F(x), как будет показано ниже. Примерами функций ограничений g_i(x) являются: ограничение количества последовательных проигрышей, коэффициента Шарпа, процента выигрышей и т. д.

Алгоритмы оптимизации

В общем виде существуют два основных типа алгоритмов оптимизации. Первый тип — более классический, основанный на вычислении градиентов всех функций, участвующих в задаче оптимизации (он восходит к временам Исаака Ньютона). Второй тип появился позднее (примерно в 1970-х годах) и вообще не использует информацию о градиенте. Между ними могут существовать алгоритмы, объединяющие два упомянутых подхода, но нам нет необходимости рассматривать их здесь. "Быстрый генетический алгоритм" ("Fast Genetic based Algorithm") в настройках терминала MetaTrader 5. Это позволяет нам отказаться от необходимости вычисления градиентов для целевых и ограничительных функций. Более того, благодаря безградиентной природе алгоритма MetaTrader 5 мы смогли учесть функции ограничений. Мы не смогли бы этого сделать при использовании градиентных алгоритмов. Подробнее об этом будет сказано ниже.

Важным моментом является то, что алгоритм MetaTrader 5, называемый "медленным полным алгоритмом" ("Slow Complete Algorithm"), на самом деле не является алгоритмом оптимизации, а представляет собой грубую, исчерпывающую оценку всех возможных комбинаций значений для всех входных переменных в пределах побочных ограничений.

Целевая функция F(x), построенная из нескольких целевых функций f_i(x)

В этом разделе мы рассмотрим объединение нескольких целевых функций в одну целевую функцию F.

Как упоминалось во введении, мы используем суммирование для объединения нескольких целей. Вы можете изменить исходный код, если хотите использовать объединение на основе умножения. Формула объединения при суммировании имеет вид:

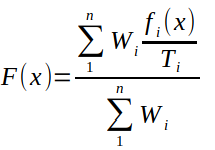
где 

• x - вектор из n входных переменных
• f_i(x) - i-я целевая функция
• W_i - i-й вес
• T_i — это i-я цель, желаемая для i-й целевой функции

Цель служит нормализующим (разделительным) значением, позволяющим сопоставить данную цель с другими целями при суммировании. Другими словами, взвешенная сумма относится к "нормализованным" целевым функциям. Вес умножает нормализованную цель (f_i(x)/T_i) таким образом, что пользователь может подчеркнуть, какая нормализованная цель важнее другой. Веса W_i становятся выпуклыми путем деления суммы W_i*f_i(x)/T_i на сумму W_i.

Выбор W_i: Выпуклость весов позволяет пользователю сосредоточиться на их относительном значении, а не на абсолютном. Например, предположим, что есть три цели: годовая доходность, коэффициент восстановления и коэффициент прибыли. Эти веса (W_1=10, W_2=5, W_3=1) имеют тот же эффект, что и W_1=100, W_2=50, W_3=10, то есть нормализованная цель 1 (годовая доходность/T_1) считается в два раза важнее нормализованной цели 2 (фактор восстановления/T_2) и в десять раз важнее нормализованной цели 3 (фактор прибыли/T_3). Не существует правильных или неправильных значений, если они положительны и выражают относительную важность на основе критерия пользователя.

Выбор T_i: Прежде чем выполнять полноценную оптимизацию, необходимо тщательно выбрать цели T_i на основе нескольких симуляций. Причиной этого является необходимость оценить диапазоны каждой целевой функции и задать значения T_i, которые позволят получить нормализованные функции (f_i(x)/T_i) сопоставимой величины. Например, предположим, что начальный баланс вашего счета составляет 10 000. Алгоритм вашего советника устанавливает конечный баланс около 20 000 перед его оптимизацией, фактор прибыли составляет 0,9. Если вы ставите перед собой задачу оптимизации с двумя целями: f_1 = баланс, f_2 = фактор прибыли, то хорошими значениями для целей будут: T_1 = 30 000, T_2 = 2, что сделает обе нормализованные функции одного порядка величины (сравнимые значения). После проведения полной оптимизации вы можете обнаружить, что советник показывает очень большой итоговый баланс и аналогичный фактор прибыли. На этом этапе можно скорректировать значения T_i, если нормализованные функции имеют разные порядки величин. Целевые значения также должны быть положительными вещественными числами. Решение за вами. Подробнее эта тема будет обсуждаться, когда мы рассмотрим выходные данные кода универсальной формулы оптимизации (Generic Optimization Formulation, GOF).

Добавление ограничений 

Формулировка целевой функции как взвешенной суммы отдельных целей является довольно стандартной. Теперь рассмотрим простой способ включения функций ограничения в задачу оптимизации таким образом, чтобы быстрый генетический алгоритм MetaTrader 5 продолжал работать. Мы собираемся использовать модифицированную версию метода множителей Лагранжа, который вычитает штраф из единственной цели оптимизации. Для этой цели мы определим новые функции штрафа, которые измеряют величину нарушения для каждого ограничения:

Как видим, P_i(x) положительно, когда нарушается g_i(x), и равно нулю в противном случае. Если U_i или L_i равны нулю, мы заменяем их на 1, чтобы избежать деления на ноль.

В методе множителей Лагранжа на каждое ограничение приходится один множитель, а их значения являются решением системы уравнений. В нашей модифицированной версии мы предполагаем, что все множители одинаковы и имеют постоянное значение k_p (см. формулу ниже). Это упрощение работает здесь, поскольку алгоритму оптимизации не нужно вычислять градиенты какой-либо функции в задаче оптимизации.

Окончательная целевая функция F(x) равна

Примечание: символ ":=" означает присваивание, а не математическое определение. 

Множитель k_p играет роль множителей Лагранжа и используется для того, чтобы заставить невыполнимые варианты (те, которые нарушают хотя бы одно ограничение) иметь очень низкую цель. Из-за такого снижения целевого значения генетический алгоритм в MetaTrader 5, оценивающий этот вариант, будет оценен очень низко и вряд ли будет использоваться для воспроизведения в следующем поколении.

Множитель k_o не является частью метода множителей Лагранжа. Он используется для увеличения целевой функции для возможных вариантов с целью расширения положительной стороны оси Y на графиках оптимизации в терминале MetaTrader 5. 

Пользователь может изменить значения K_o и K_p в разделе Miscellaneous (разное). Я рекомендую сделать значения k_o и K_p степенями числа 10 (например, 10, 100, 1000 и т.д.).

Скриншот вкладки с входными данными в терминале MetaTrader 5

В GOF имеется три входных раздела: целевые функции, функции ограничений и прочее.

Ниже представлен раздел целевых функций. В формулировку задачи можно включить до 5 целей из 18 возможных функций, которые будут показаны позже. Добавление более 5 целей может быть выполнено в соответствии с кодом, но если число целей превышает 3, выбор весов и целевого показателя усложняются. Добавление более 18 возможных функций можно выполнить, следуя коду.

Ниже представлен раздел функций с жесткими ограничениями. В формулу оптимизации можно добавить до 10 ограничений из 14 функций ограничений, реализованных в GOF. Добавление более 10 ограничений можно выполнить, следуя коду. Добавление новых ограничений в список из 14 также можно выполнить, следуя коду.

Ниже представлен раздел с разными параметрами оптимизации. Подробнее этот раздел будет рассмотрен ниже.

Применение GenericOptimizationFormulation.mqh в советнике

Если вам не хочется читать всю статью, мы сначала предоставим вам шаги по использованию этого кода в вашем советнике, чтобы вы могли сначала поэкспериментировать с ним, а затем прочитать остальную часть статьи с более глубоким пониманием. Ниже приведены начальные комментарии в файле GenericOptimizationFormulation.mqh:

/*

In order to use this file in your EA you must do the following:

- Edit the EA .mq5 file

- Insert the following two lines after the input variables and before OnInit()

     ulong gof_magic= an_ulong_value;

     #include <YOUR_INCLUDE_LOCATION\GenericOptimizationFormulation.mqh>

- Save and compile your EA file

If you get compiler's errors, make sure you did:

- replace an_ulong_value by the variable containing the magic number, or by the magic numeric value

- replace YOUR_INCLUDE_LOCATION by the folder name where your include files are

*/

Позже я приведу пример использования советника MetaTrader 5 Moving Average. Теперь рассмотрим исходный код.

Исходный код - GenericOptimizationFormulation.mqh

Теперь, когда мы представили формулы для целевой функции и ограничений, обсудим реализацию на MQL5 с фрагментами кода.

 Просьбы к читателям:

• Говорят, что программа, содержащая более семи строк кода, имеет ненулевую вероятность наличия ошибки. В GOF более тысячи строк, поэтому вероятность определенно ненулевая. Мы призываем читателей оставлять отзывы в комментариях для улучшения кода.
• Если вы знаете лучший способ написать код, пожалуйста, поделитесь им со мной.
• Добавляйте и улучшайте код с помощью собственных целевых функций и ограничений. Пожалуйста, поделитесь ими в комментариях.

Используемые библиотеки

Во-первых, нам нужно включить несколько библиотек для выполнения статистических и алгебраических вычислений:

#include <Math\Stat\Lognormal.mqh>
#include <Math\Stat\Uniform.mqh>
#include <Math\Alglib\alglib.mqh>

Целевые функции на выбор:

enum gof_FunctionDefs {        // functions to build objective
   MAX_NONE=0,                 // 0] None
   MAX_AnnRetPct,              // 1] Annual Return %
   MAX_Balance,                // 2] Balance
   MAX_NetProfit,              // 3] Net Profit
   MAX_SharpeRatio,            // 4] Sharpe Ratio
   MAX_ExpPayOff,              // 5] Expected Payoff
   MAX_RecovFact,              // 6] Recovery Factor
   MAX_ProfFact,               // 7] Profit Factor
   MAX_LRcrr3,                 // 8] LRcrr^3
   MAX_NbrTradesPerWeek,       // 9] #Trades/week
   MAX_WinRatePct,             // 10] Win Rate %
   MAX_Rew2RiskRatio,          // 11] Reward/Risk(RRR=AvgWin/AvgLoss)
   MAX_OneOverLRstd,           // 12] 1/(LR std%)
   MAX_OneHoverWorstTradePct,  // 13] 100/(1+|WorstLoss/Init.Dep*100|)
   MAX_LR,                     // 14] LRslope*LRcorr/LRstd
   MAX_OneHoverEqtyMaxDDpct,   // 15] 100/(1+EqtyMaxDD%))
   MAX_StratEfficiency,        // 16] Seff=Profit/(TotalTrades*AvgLot)
   MAX_KellyCrit,              // 17] Kelly Criterion
   MAX_OneOverRoRApct          // 18] 1/Max(0.01,RoRA %)
};

Для формулировки задачи оптимизации существует 18 возможных целей, из которых можно выбрать максимум 5. Пользователь может добавлять больше функций в исходный код, следуя той же схеме реализации. Названия целевых функций должны быть очевидными, за исключением нескольких, упомянутых ниже:

• LRcrr^3 - коэффициент корреляции линейной регрессии в степени 3.
• 1/(LR std%) - стандартное отклонение линейной регрессии. Обратное значение измеряет, насколько линия эквити близка к прямой линии.
• 100/(1+|WorstLoss/Init.Dep*100|) - наибольший убыток, поделенный на первоначальный депозит, является показателем плохой работы. Обратное значение — мера хорошей работы.
• LRslope*LRcorr/LRstd - мультипликативная цель трех функций линейной регрессии: наклона, коэффициента корреляции и стандартного отклонения.
• Seff=Profit/(TotalTrades*AvgLot) - мера эффективности стратегии. Мы предпочитаем стратегии с высокой прибылью, небольшим количеством сделок и небольшим размером лота.
• 1/Max(0.01,RoRA %) - риск разорения счета. Вычисляется с помощью метода моделирования Монте-Карло, которое мы обсудим позже.

Жесткие ограничения на выбор:

enum gof_HardConstrains {
   hc_NONE=0,                     // 0] None
   hc_MaxAccountLoss_pct,         // 1] Account Loss % InitDep
   hc_maxAllowed_DDpct,           // 2] Equity DrawDown %
   hc_maxAllowednbrConLossTrades, // 3] Consecutive losing trades
   hc_minAllowedWin_pct,          // 4] Win Rate %
   hc_minAllowedNbrTradesPerWeek, // 5] # trades/week
   hc_minAllowedRecovFactor,      // 6] Recov Factor
   hc_minAllowedRRRFactor,        // 7] Reward/Risk ratio
   hc_minAllowedAnnualReturn_pct, // 8] Annual Return in %
   hc_minAllowedProfFactor,       // 9] Profit Factor
   hc_minAllowedSharpeFactor,     // 10] Sharpe Factor
   hc_minAllowedExpPayOff,        // 11] Expected PayOff
   hc_minAllowedMarginLevel,      // 12] Smallest Margin Level
   hc_maxAllowedTradeLoss,        // 13] Max Loss trade
   hc_maxAllowedRoRApct           // 14] Risk of Ruin(%)
};
enum gof_HardConstType {
   hc_GT=0, // >=     Greater or equal to
   hc_LT    // <=     Less or equal to
};

Существует 14 возможных ограничений, из которых можно выбрать максимум 10, чтобы сформулировать задачу оптимизации. Пользователь может добавлять больше ограничений в исходный код, следуя той же схеме реализации. Существует два типа ограничений: hc_GT для ограничений с нижней границей и ht_LT для ограничений с верхней границей. Подробнее об этом мы поговорим, когда будем обсуждать их использование.

Варианты риска разорения

enum gof_RoRaCapital {
   roraCustomPct=0,  // Custom % of Ini.Dep.
   roraCustomAmount, // Custom Capital amount
   roraIniDep        // Initial deposit
};

При расчете риска разорения счета существует три способа определения денег на "счете". Первый вариант — процент от первоначального депозита. Второй вариант — фиксированная сумма капитала в валюте вашего счета. Третий вариант является частным случаем первого варианта, если процент равен 100%. Риск разорения поясняется далее в коде.

Дробные значения целевой функции

Как упоминалось ранее, мы можем отобразить дополнительную информацию из моделирования, используя два десятичных знака в столбце результата. Варианты следующие:

enum gof_objFuncDecimals {
   fr_winRate=0, // WinRate %
   fr_MCRoRA,    // MonteCarlo Sim Risk of Ruin Account %
   fr_LRcorr,    // LR correlation
   fr_ConLoss,   // Max # Consecutive losing Trades
   fr_NONE       // None
};

fr_winRate - процент выигрышей симуляции. Например, если процент выигрышей составляет 34%, целевой результат составит 0,39. Если процент выигрышей составляет 100%, он будет отображаться как 0,99.

fr_MCRoRA - риск разорения счета в процентах. Например, если риск разорения счета составляет 11%, целевой результат составит 0,11.

fr_LRcorr - коэффициент корреляции линейной регрессии. Например, если коэффициент равен 0,88, целевой результат будет равен 0,88.

fr_ConLoss - наибольшее количество убыточных сделок подряд. Например, если число равно 7, целевой результат будет равен 0,07. Если число больше 99, будет отображено 0,99.

fr_NONE - используется, когда вы не хотите видеть никакой информации в десятичных знаках.

Целевые функции

Следующий раздел кода — выбор индивидуальных целевых функций (максимум 5). Ниже приведен фрагмент только первой функции, а также ее цель и вес.

input group   "- Build Custom Objective to Maximize:"
sinput gof_FunctionDefs gof_Func1   = MAX_AnnRetPct;          // Select Objective Function to Maximize 1:
sinput double gof_Target1           = 200;                    // Target 1
sinput double gof_Weight1           = 1;                      // Weight 1

Функции ограничения

input group   "- Hard Constraints:"
sinput bool   gof_IncludeHardConstraints     = true;//if false, all constraints are ignored

sinput gof_HardConstrains gof_HC_1=hc_minAllowedAnnualReturn_pct; // Select Constraint Function 1:
sinput gof_HardConstType gof_HCType_1=hc_GT; // Type 1
sinput double gof_HCBound_1=50; // Bound Value 1

Можно отключить все жесткие ограничения, установив gof_IncludeHardConstraints=false. Далее следует выбор первого ограничения, его типа и ограничительного значения. Все десять ограничений используют один и тот же формат.

Разные параметры оптимизации

input group   "------ Misc Optimization Params -----"
sinput gof_objFuncDecimals gof_fr                  = fr_winRate;     // Choose Result-column's decimals
sinput gof_RoRaCapital  gof_roraMaxCap             = roraCustomPct;  // Choose capital method for Risk of Ruin
sinput double           gof_RoraCustomValue        = 10;             // Custom Value for Risk of Ruin (if needed)
sinput bool             gof_drawSummary            = false;          // Draw summary on chart
sinput bool             gof_printSummary           = true;           // Print summary on journal
sinput bool             gof_discardLargestProfit   = false;          // Subtract Largest Profit from Netprofit
sinput bool             gof_discardLargestLoss     = false;          // Add Largest Loss to Net profit
sinput double           gof_PenaltyMultiplier      = 100;            // Multiplier for Penalties (k_p)
sinput double           gof_ObjMultiplier          = 100;            // Multiplier for Objectives (k_o)

В разделе выше пользователь выбирает:

• gof_fr - количество, которое будет отображаться в виде десятичных знаков в столбце Result (результат). 
• gof_roraMaxCap - метод расчета капитала для риска разорения.
• gof_RoraCustomValue - величина капитала или % от первоначального депозита для риска разорения. Зависит от значения в предыдущей строке.
• gof_drawSummary - показать отчет GOF на графике.
• gof_printSummary - показать отчет GOF на вкладке "Журнал".
• gof_discardLargestProfit - вычесть самую большую прибыль из чистой прибыли, чтобы исключить стратегии, которые отдают предпочтение одному крупному выигрышу.
• gof_discardLargestLoss - добавить самый большой убыток к чистой прибыли, чтобы исключить стратегии, склонные к большим убыткам. 
• gof_PenaltyMultiplier - множитель K_p, показанный в определении целевой функции выше.
• gof_ObjMultiplier - множитель K_o, показанный в определении целевой функции выше.

Значения по умолчанию в разделе Miscellaneous должны работать хорошо.

Следующие строки кода предназначены для определения переменных и извлечения значений из функции MetaTrader 5 TesterStatistics(). Далее следует основная часть GOF:

//------------ GOF ----------------------
// Printing and displaying results from the simulation
   GOFsummaryReport();

// calculate the single objective function
   double SingleObjective = calcObjFunc();

// calculate the total penalty from constraint violations
   if(gof_IncludeHardConstraints) gof_constraintTotalPenalty=calcContraintTotalPenalty(gof_displayContraintFlag);

// Compute customMaxCriterion
// gof_PenaltyMultiplier pushes infeasible designs to have low objective values
// gof_PenaltyMultiplier expand the positive side of the Y axis
   double customMaxCriterion=gof_constraintTotalPenalty>0?
                             SingleObjective-gof_PenaltyMultiplier*gof_constraintTotalPenalty:
                             gof_ObjMultiplier*SingleObjective;

// add additional simulation result as two decimal digits in the result column
   customMaxCriterion=AddDecimalsToCustomMax(customMaxCriterion);

// Printing and displaying more results from GOF
   FinishGOFsummaryReport(customMaxCriterion);

   return (NormalizeDouble(customMaxCriterion,2));

Приведенный выше код позволяет: 

• GOFsummaryReport() - подготовить сводный отчет GOF, который будет отображаться на вкладке "Журнал" и на графике.
• calcObjFunc() - рассчитать объединенную целевую функцию.
• calcContraintTotalPenalty() - рассчитать общую сумму штрафа за нарушение ограничений.
• customMaxCriterion - отобразить сумму единственного целевого значения за вычетом общего штрафа за нарушение ограничений.
• AddDecimalsToCustomMax() - показать customMaxCriterion в десятичном виде.
• FinishGOFsummaryReport() - подготовить и распечатать сводный отчет GOF.

Остальная часть кода представляет собой прямую реализацию формул, приведенных во введении. Единственное, что стоит обсудить, — это расчет риска разорения.

Риск разорения с использованием моделирования Монте-Карло

Риск разорения можно рассчитать с помощью простой формулы, но вместо этого мы решили использовать моделирование Монте-Карло, поскольку простая формула не давала внятных результатов. Для метода Монте-Карло нам нужны средние выигрыши и проигрыши, стандартные отклонения таких выигрышей и проигрышей, процент выигрышей и количество сделок в симуляции. Кроме того, нам необходимо предоставить капитал, который определяет разорение счета. 

double MonteCarlo_RiskOfRuinAccount(double WinRatePct, double AvgWin, double AvgLoss, double limitLoss_money, int nTrades) {
// 10000 Montecarlo simulations, each with at least 100 trades.
// Ideally, if we had lots of trades in the history, we could use a Markov Chain transfer probability matrix
//  we are limiting the statistics to mean & stdev, without knowledge of a transfer probability information

   double posDealsMean,posDealsStd,negDealsMean,negDealsStd;
   CalcDealStatistics(gof_dealsEquity, posDealsMean,posDealsStd,negDealsMean,negDealsStd);

// seeding the random number generator
   MathSrand((int)TimeLocal()+1);

// ignore posDealsMean and negDealsMean. Use AvgWin and AvgLoss instead
   AvgLoss=MathAbs(AvgLoss);
   WinRatePct=MathMin(100,MathMax(0,WinRatePct));

// case when win rate is 100%:
   if((int)(WinRatePct*nTrades/100)>=nTrades) {
      WinRatePct=99;          // just to be a bit conservative if winrate=100%
      AvgLoss=AvgWin/2;       // a guessengineering value
      negDealsStd=posDealsStd;// a guessengineering value
   }

// Use log-normal distribution function. Mean and Std are estimated as:
   double win_lnMean =log(AvgWin*AvgWin/sqrt(AvgWin*AvgWin+posDealsStd*posDealsStd));
   double loss_lnMean=log(AvgLoss*AvgLoss/sqrt(AvgLoss*AvgLoss+negDealsStd*negDealsStd));
   double win_lnstd  =sqrt(log(1+(posDealsStd*posDealsStd)/(AvgWin*AvgWin)));
   double loss_lnstd =sqrt(log(1+(negDealsStd*negDealsStd)/(AvgLoss*AvgLoss)));

   double rand_Win[],rand_Loss[];
   double r[];

// limit amount of money that defines Ruin
   limitLoss_money=MathAbs(limitLoss_money);
   bool success;
   int ruinCount=0; // counter of ruins
   int successfulMCcounter=0;
   int nTradesPerSim=MathMax(100,nTrades);// at least 100 trades per sim
   int nMCsims=10000; // MC sims, each one with nTradesPerSim

   for(int iMC=0; iMC<nMCsims; iMC++) {
      success=MathRandomUniform(0,1,nTradesPerSim,r);

      // generate nTradesPerSim wins and losses for each simulation
      // use LogNormal distribution
      success&=MathQuantileLognormal(r,win_lnMean,win_lnstd,true,false,rand_Win);
      success&=MathQuantileLognormal(r,loss_lnMean,loss_lnstd,true,false,rand_Loss);
      if(!success)continue;
      successfulMCcounter++;
      //simulate nTradesPerSim
      double eqty=0; // start each simulation with zero equity
      for(int i=0; i<nTradesPerSim; i++) {

         // draw a random number in [0,1]
         double randNumber=(double)MathRand()/32767.;

         // select a win or a loss depending on the win rate and the random number
         // and add to the equity
         eqty+=randNumber*100 < WinRatePct?
               rand_Win[i]:
               -rand_Loss[i];

         // check if equity is below the limit (ruin)
         // count the number of times there is a ruin
         if(eqty<= -limitLoss_money) {
            ruinCount++;
            break;
         }
      }
   }
// compute risk of ruin as percentage
   double RiskOfRuinPct=(double)(ruinCount)/successfulMCcounter*100.;
   return(RiskOfRuinPct);
}

Функция CalcDealStatistics(), также включенная в исходный код, используется для вычисления стандартного отклонения выигрышей и проигрышей. Основное предположение при расчете риска разорения заключается в том, что история сделок следует логнормальному распределению, чтобы гарантировать, что выборки распределения имеют положительные и отрицательные значения для выигрышей и проигрышей соответственно.

В идеале, если бы у нас было много сделок в истории, мы могли бы использовать матрицу вероятностей перехода цепи Маркова вместо предположения о "логарифмической нормальности" истории сделок. Поскольку истории сделок содержат около нескольких сотен сделок (максимум), информации для построения матрицы вероятностей перехода цепи Маркова с хорошей точностью недостаточно. 

Интерпретация риска разорения счета

Результат моделирования Монте-Карло необходимо интерпретировать как вероятность риска потери капитала, а не как прогностическое значение. Например, если возвращаемое значение моделирования Монте-Карло составляет 1%, это означает, что существует 1%-ная вероятность того, что ваша торговая стратегия уничтожит весь используемый вами капитал. Это значение не означает, что вы потеряете 1% от используемого капитала.

Добавление десятичных знаков к Custom Max

Это непростая задача. Если читатель найдет лучший способ, пожалуйста, поделитесь им. После вычисления десятичных значений (dec) целевое значение (obj) изменяется следующим образом:

  obj=obj>0?
       MathFloor(obj*gof_ObjPositiveScalefactor)+dec/100.:
       -(MathFloor(-obj*gof_ObjNegativeScalefactor)+dec/100.);

Как видите, если obj — положительное значение, оно умножается на большое число (gof_ObjPositiveScalefactor=1e6), усекается, а затем значение dec делится на 100 и добавляется как десятичное. Если значение obj отрицательное (что означает, что нарушено много ограничений), obj умножается на другое число (gof_ObjPositiveScalefactor = 1e3), чтобы сжать вертикальную ось для отрицательных значений.

Реализация GOF в советнике Moving Average EA

Приведенный ниже пример показывает, как реализовать GOF в советнике Moving Averages.mq5:

//+------------------------------------------------------------------+
//|                                              Moving Averages.mq5 |
//|                             Copyright 2000-2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2000-2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;

#define MA_MAGIC 1234501

// changes needed to use the GenericOptimizationFormulation (GOF):
ulong gof_magic= MA_MAGIC;
#include <GenericOptimizationFormulation.mqh>
// end of changes

Это всё! В файл советника нужно добавить всего две строки.

Примеры оптимизации с использованием GOF

Пример 1: Одна цель, никаких ограничений (как если бы мы установили Max Balance в настройках MetaTrader 5):

Ниже приведена вкладка "Параметры". Поскольку есть только одна цель, то цель и вес вообще не имеют значения. Обратите внимание, как все ограничения отключаются с первой булевой переменной в разделе Hard Constraints (жесткие ограничения):

Раздел Miscellaneous (разное):

Результаты показаны ниже. Обратите внимание, что столбец Result (результат) — это не остаток на счете, а измененная цель с показателем выигрыша в виде десятичных дробей.

Мы видим, что наилучшая комбинация переменных (9,9,3) дает прибыль 939,81 и процент выигрышей 41%.

Мы смоделировали оптимальную комбинацию (первая строка) в таблице. Сводный отчет GOF на вкладке "Журнал" выглядит так:

Мы рассмотрим сводный отчет GOF более подробно в следующем примере.

Пример 2: Три цели и пять ограничений

Вкладка настроек та же, что и раньше. Входные переменные и диапазоны также одинаковы. Вкладка ввода переменных GOF показана ниже.

Цели:

• Годовой доход с целевым показателем 50% и весом 100
• Фактор восстановления с целевым значением 10 и весом 10
• Процент выигрышей при цели 100% и весе 10 

Ограничения:

• Потеря счета от первоначального депозита должна быть меньше или равна 10%
• Просадка капитала должна быть меньше или равна 10%
• Количество последовательных убыточных сделок должно быть меньше или равно 5
• Процент выигрышей должен быть больше или равен 35%
• Риск разорения счета должен быть меньше или равен 0,5%

Капитал для расчета риска разорения был установлен в размере 10% от первоначального депозита или 1000 единиц валюты счета, как показано в разделе Miscellaneous (разное) выше.

Как вы можете видеть в первой строке таблицы оптимизации, наилучшим вариантом оказался (10,6,6).

Обратите внимание, что оптимизатор нашел решение с меньшей прибылью по сравнению с первым примером (805,64 против 839,81), однако новый вариант удовлетворяет всем пяти ограничениям и максимизирует три объединенные цели.

Сводный отчет GOF 

Мы получаем сводный отчет GOF, представленный ниже, путем моделирования первой строки в приведенной выше таблице оптимизации:

Отчет GOF состоит из трех разделов. В первом разделе содержится множество величин из вкладки "Бэктест". Есть некоторые дополнительные величины, которые отсутствуют на вкладке "Бэктест": годовая прибыль, продолжительность теста в годах, соотношение прибыли к риску (Reward/Risk ratio, RRR), средний и максимальный объем, стандартные отклонения выигрышей и проигрышей и минимальный уровень маржи, достигнутый в ходе моделирования.

Второй раздел посвящен целевым функциям. Здесь для каждой цели есть четыре значения: цели, контрольного показателя (target), веса и процента вклада. Процент вклада — это вклад данной целевой функции в общую цель. В этом примере годовой доход составил 95,1%, фактор восстановления — 1,4%, а процент выигрышей — 3,5%, что в общей сложности составляет 100% от общей цели. Цель и веса влияют на эти вклады. 

Третий раздел посвящен ограничениям. Сообщение "Pass" (успех) или "Fail" (неудача) выводится для каждого ограничения, а также отображается сравнение фактического значения ограничения с входными данными.

Для сравнения мы прогнали первую конструкцию из примера 1 (9, 9, 3) через ту же формулу оптимизации из примера 2. Ниже приведено краткое описание этого моделирования. Обратите внимание - одно ограничение нарушается. Число последовательных проигрышей равно 6, что превышает граничное значение 5, заданное в формуле оптимизации. Следовательно, даже несмотря на то, что MaxBalance (9,9,3) обеспечивает большую прибыль, чем MultiObjective/Constrained (10,6,6), именно (10,6,6) удовлетворяет всем ограничениям. 

Рекомендации по использованию GenericOptimizationFormulation.mqh

Большую свободу выбора множественных целей и множественных ограничений следует использовать с осторожностью. Вот несколько общих рекомендаций:

1. Используйте не более 3 целей. Код допускает до 5 целей, но выбор целей и весов, влияющих на конечный результат, усложняется, если количество целей превышает 3.
2. Используйте ограничения, основанные на ваших предпочтениях, и не устанавливайте их слишком жестко при выборе верхней (U_i) и нижней (L_i) границ. Если ваши границы слишком узкие, вы не получите никакой разумной комбинации входных переменных.
3. Если вы не знаете, какое граничное значение задать для данного ограничения, вы можете переместить ограничение в раздел целей и посмотреть, как оно себя ведет (величина, знак и т. д.), изучив отчет GOF.
4. Отрегулируйте k_o и k_p, если вам нужны лучшие графики или если вы обнаружили, что оптимизатор не выдает ожидаемых вами результатов.
5. Помните, что оптимальный вариант (верхняя строка в таблице оптимизации) — не обязательно самый прибыльный. Это вариант с наивысшей целевой функцией на основе вашего выбора индивидуальных целей и ограничений.
6. Мы рекомендуем после завершения оптимизации отсортировать варианты по другим столбцам, таким как прибыль, фактор восстановления, просадка, матожидание выигрыша, фактор прибыли и т. д. Верхняя строка в каждой сортировке может быть кандидатом для моделирования при работе со сводным отчетом GOF.
7. Хороший выбор целей и ограничений показан в примере 2. Используйте их как отправную точку для своих экспериментов.

Что может пойти не так?

Вы можете задать формулу оптимизации, которая не дает ожидаемого вами результата. Вот несколько причин, по которым это может происходить:

1. Ограничения слишком жесткие, и генетическому алгоритму оптимизации MetaTrader 5 потребуется много поколений, чтобы достичь положительной целевой функции, а в некоторых случаях он может ее и вовсе не достичь. Решение: ослабьте ограничения.
2. Ограничения противоречат друг другу. Решение: проверьте, что ограничения логически непротиворечивы.
3. Графики оптимизации имеют смещение в сторону отрицательных значений по оси Y (то есть отрицательная сторона занимает больше места, чем положительная). Решение: увеличьте K_o или уменьшите K_p, или сделайте и то, и другое.
4. Некоторые понравившиеся вам варианты не отображаются в верхней части таблицы оптимизации. Помните, что цели и веса влияют на цель оптимизации, а также, что одно нарушение ограничения может сместить цель вниз в таблице. Решение: переформулируйте задачу оптимизации, скорректировав цели, веса и ограничения.

   

Заключение

Я надеюсь, что показанная здесь универсальная формула оптимизации окажется для вас полезной. Теперь у вас есть дополнительная свобода выбора нескольких целей и нескольких ограничений для постановки нужной вам задачи оптимизации.