Modelli di regressione della libreria Scikit-learn e la loro esportazione in ONNX
MetaTrader 5
—
Integrazione
| 27 agosto 2024, 18:13
296
0
ONNX (Open Neural Network Exchange) è un formato per la descrizione e lo scambio di modelli di apprendimento automatico, che offre la possibilità di trasferire modelli tra diversi framework di apprendimento automatico. Nell'apprendimento profondo e nelle reti neurali, si utilizzano spesso tipi di dati come float32. Sono ampiamente utilizzati perché di solito forniscono un'accuratezza e un'efficienza accettabili per l'addestramento dei modelli di deep learning.
Alcuni modelli classici di apprendimento automatico sono difficili da rappresentare come operatori ONNX. Per questo motivo, sono stati introdotti ulteriori operatori ML (ai.onnx.ml) per implementarli in ONNX. Vale la pena notare che, secondo le specifiche ONNX, gli operatori chiave di questo set (LinearRegressor, SVMRegressor, TreeEnsembleRegressor) possono accettare vari tipi di dati in ingresso (tensore(float), tensore(double), tensore(int64), tensore(int32)), ma restituiscono sempre il tipo tensore(float) in uscita. Anche la parametrizzazione di questi operatori viene eseguita utilizzando numeri in virgola mobile, il che può limitare l'accuratezza dei calcoli, soprattutto se sono stati utilizzati numeri a doppia precisione per definire i parametri del modello originale.
Ciò può comportare una perdita di precisione quando si convertono i modelli o si utilizzano tipi di dati differenti nel processo di conversione ed elaborazione dei dati in ONNX. Molto dipende dal convertitore, come vedremo più avanti; alcuni modelli riescono a bypassare queste limitazioni e a garantire la piena portabilità dei modelli ONNX, consentendo di lavorare con essi in doppia precisione senza perdere in accuratezza. È importante considerare queste caratteristiche quando si lavora con i modelli e la loro rappresentazione in ONNX, soprattutto nei casi in cui la precisione della rappresentazione dei dati è importante.
Scikit-learn è una delle librerie per l'apprendimento automatico più popolare e utilizzata dalla comunità Python. Offre un'ampia gamma di algoritmi, un'interfaccia facile da usare e una buona documentazione. L'articolo precedente, "Modelli di Classificazione della Libreria Scikit-learn e Loro Esportazione in ONNX", copriva i modelli di classificazione.
In questo articolo esploreremo l'applicazione dei modelli di regressione nel pacchetto Scikit-learn, calcoleremo i loro parametri con doppia precisione per il set di dati di prova, proveremo a convertirli nel formato ONNX con precisione double e float e utilizzeremo i modelli ottenuti in programmi MQL5. Inoltre, confronteremo l'accuratezza dei modelli originali e delle loro versioni ONNX per la precisione float e double. Inoltre, esamineremo la rappresentazione ONNX dei modelli di regressione, che ci forniranno una migliore comprensione della loro struttura interna e il loro funzionamento.
Contenuto
- Se ti dà fastidio, ben venga il tuo contributo
- 1. Set dei dati di prova
Lo script per la visualizzazione del set di dati di prova - 2. Modelli di Regressione
2.0. Elenco dei Modelli di Regressione di Scikit-learn - 2.1. Modelli di Regressione Scikit-learn convertiti in modelli ONNX float e double
- 2.1.1. sklearn.linear_model.ARDRegression
2.1.1.1. Codice per la creazione di ARDRegression
2.1.1.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.1.3. Rappresentazione ONNX di ard_regression_float.onnx e ard_regression_double.onnx - 2.1.2. sklearn.linear_model.BayesianRidge
2.1.2.1. Codice per la creazione del modello BayesianRidge ed esportazione in ONNX per float e double
2.1.2.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.2.3. Rappresentazione ONNX di bayesian_ridge_float.onnx e bayesian_ridge_double.onnx - 2.1.3. sklearn.linear_model.ElasticNet
2.1.3.1. Codice per la creazione del modello ElasticNet e esportazione in ONNX per float e double
2.1.3.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.3.3. Rappresentazione ONNX di elastic_net_float.onnx e elastic_net_double.onnx - 2.1.4. sklearn.linear_model.ElasticNetCV
2.1.4.1. Codice per la creazione del modello ElasticNet e esportazione in ONNX per float e double
2.1.4.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.4.3. Rappresentazione ONNX di elastic_net_cv_float.onnx e elastic_net_cv_double.onnx - 2.1.5. sklearn.linear_model.HuberRegressor
2.1.5.1. Codice per creare il modello HuberRegressor ed esportarlo in ONNX per float e double
2.1.5.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.5.3. Rappresentazione ONNX di huber_regressor_float.onnx e huber_regressor_double.onnx - 2.1.6. sklearn.linear_model.Lars
2.1.6.1. Codice per creare il modello Lars ed esportarlo in ONNX per float e double
2.1.6.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.6.3. Rappresentazione ONNX di lars_float.onnx e lars_double.onnx - 2.1.7. sklearn.linear_model.LarsCV
2.1.7.1. Codice per creare il modello LarsCV ed esportarlo in ONNX per float e double
2.1.7.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.7.3. Rappresentazione ONNX di lars_cv_float.onnx e lars_cv_double.onnx - 2.1.8. sklearn.linear_model.Lasso
2.1.8.1. Codice per creare il modello Lasso ed esportarlo in ONNX per float e double
2.1.8.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.8.3. Rappresentazione ONNX di lasso_float.onnx e lasso_double.onnx - 2.1.9. sklearn.linear_model.LassoCV
2.1.9.1. Codice per creare il modello LassoCV ed esportarlo in ONNX per float e double
2.1.9.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.9.3. Rappresentazione ONNX di lasso_cv_float.onnx e lasso_cv_double.onnx - 2.1.10. sklearn.linear_model.LassoLars
2.1.10.1. Codice per la creazione del modello LassoLars e esportazione in ONNX per float e double
2.1.10.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.10.3. Rappresentazione ONNX di lasso_lars_float.onnx e lasso_lars_double.onnx - 2.1.11. sklearn.linear_model.LassoLarsCV
2.1.11.1. Codice per la creazione del modello LassoLarsCV e per esportazione in ONNX per float e double
2.1.11.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.11.3. Rappresentazione ONNX di lasso_lars_cv_float.onnx e lasso_lars_cv_double.onnx - 2.1.12. sklearn.linear_model.LassoLarsIC
2.1.12.1. Codice per creare il modello LassoLarsIC ed esportarlo in ONNX per float e double
2.1.12.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.12.3. Rappresentazione ONNX di lasso_lars_ic_float.onnx e lasso_lars_ic_double.onnx - 2.1.13. sklearn.linear_model.LinearRegression
2.1.13.1. Codice per creare il modello LinearRegression ed esportarlo in ONNX per float e double
2.1.13.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.13.3. Rappresentazione ONNX di linear_regression_float.onnx e linear_regression_double.onnx - 2.1.14. sklearn.linear_model.Ridge
2.1.14.1. Codice per creare il modello Ridge ed esportarlo in ONNX per float e double
2.1.14.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.14.3. Rappresentazione ONNX di ridge_float.onnx e ridge_double.onnx - 2.1.15. sklearn.linear_model.RidgeCV
2.1.15.1. Codice per la creazione del modello RidgeCV e per l'esportazione in ONNX per float e double
2.1.15.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.15.3. Rappresentazione ONNX di ridge_cv_float.onnx e ridge_cv_double.onnx - 2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
2.1.16.1. Codice per creare il modello OrthogonalMatchingPursuit ed esportarlo in ONNX per float e double
2.1.16.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.16.3. Rappresentazione ONNX di orthogonal_matching_pursuit_float.onnx e orthogonal_matching_pursuit_double.onnx - 2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
2.1.17.1. Codice per la creazione del modello PassiveAggressiveRegressor e per la sua esportazione in ONNX per float e double
2.1.17.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.17.3. Rappresentazione ONNX di passive_aggressive_regressor_float.onnx e passive_aggressive_regressor_double.onnx - 2.1.18. sklearn.linear_model.QuantileRegressor
2.1.18.1. Codice per creare il modello QuantileRegressor ed esportarlo in ONNX per float e double
2.1.18.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.18.3. Rappresentazione ONNX del quantile_regressor_float.onnx e del quantile_regressor_double.onnx - 2.1.19. sklearn.linear_model.RANSACRegressor
2.1.19.1. Codice per la creazione del modello RANSACRegressor ed esportazione in ONNX per float e double
2.1.19.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.19.3. Rappresentazione ONNX di ransac_regressor_float.onnx e ransac_regressor_double.onnx - 2.1.20. sklearn.linear_model.TheilSenRegressor
2.1.20.1. Codice per la creazione del modello TheilSenRegressor ed esportazione in ONNX per float e double
2.1.20.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.20.3. Rappresentazione ONNX di theil_sen_regressor_float.onnx e theil_sen_regressor_double.onnx - 2.1.21. sklearn.linear_model.LinearSVR
2.1.21.1. Codice per creare il modello LinearSVR ed esportarlo in ONNX per float e double
2.1.21.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.21.3. Rappresentazione ONNX di linear_svr_float.onnx e linear_svr_double.onnx - 2.1.22. sklearn.linear_model.MLPRegressor
2.1.22.1. Codice per creare il modello MLPRegressor ed esportarlo in ONNX per float e double
2.1.22.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.22.3. Rappresentazione ONNX di mlp_regressor_float.onnx e mlp_regressor_double.onnx - 2.1.23. sklearn.cross_decomposition.PLSRegression
2.1.23.1. Codice per la creazione del modello PLSRegression ed esportazione in ONNX per float e double
2.1.23.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.23.3. Rappresentazione ONNX di pls_regression_float.onnx e pls_regression_double.onnx - 2.1.24. sklearn.linear_model.TweedieRegressor
2.1.24.1. Codice per creare il modello TweedieRegressor ed esportarlo in ONNX per float e double
2.1.24.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.24.3. Rappresentazione ONNX di tweedie_regressor_float.onnx e tweedie_regressor_double.onnx - 2.1.25. sklearn.linear_model.PoissonRegressor
2.1.25.1. Codice per creare il modello PoissonRegressor ed esportarlo in ONNX per float e double
2.1.25.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.25.3. Rappresentazione ONNX di poisson_regressor_float.onnx e poisson_regressor_double.onnx - 2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
2.1.26.1. Codice per creare il modello RadiusNeighborsRegressor ed esportarlo in ONNX per float e double
2.1.26.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.26.3. Rappresentazione ONNX di radius_neighbors_regressor_float.onnx e radius_neighbors_regressor_double.onnx - 2.1.27. sklearn.neighbors.KNeighborsRegressor
2.1.27.1. Codice per la creazione del modello KNeighborsRegressor ed esportazione in ONNX per float e double
2.1.27.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.27.3. Rappresentazione ONNX di kneighbors_regressor_float.onnx e kneighbors_regressor_double.onnx
- 2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
2.1.28.1. Codice per la creazione del modello GaussianProcessRegressor ed esportazione in ONNX per float e double
2.1.28.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.28.3. Rappresentazione ONNX di gaussian_process_regressor_float.onnx e gaussian_process_regressor_double.onnx
- 2.1.29. sklearn.linear_model.GammaRegressor
2.1.29.1. Codice per creare il modello GammaRegressor ed esportarlo in ONNX per float e double
2.1.29.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.29.3. Rappresentazione ONNX di gamma_regressor_float.onnx e gamma_regressor_double.onnx - 2.1.30. sklearn.linear_model.SGDRegressor
2.1.30.1. Codice per la creazione del modello SGDRegressor ed esportazione in ONNX per float e double
2.1.30.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.1.30.3. Rappresentazione ONNX di sgd_regressor_float.onnx e sgd_rgressor_double.onnx
- 2.2. Modelli di regressione dalla libreria Scikit-learn che vengono convertiti solo in modelli ONNX con precisione float
- 2.2.1. sklearn.linear_model.AdaBoostRegressor
2.2.1.1. Codice per creare il modello AdaBoostRegressor ed esportarlo in ONNX per float e double
2.2.1.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.1.3. Rappresentazione ONNX di adaboost_regressor_float.onnx e adaboost_regressor_double.onnx - 2.2.2. sklearn.linear_model.BaggingRegressor
2.2.2.1. Codice per la creazione del modello BaggingRegressor e l'esportazione in ONNX per float e double
2.2.2.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.2.3. Rappresentazione ONNX di bagging_regressor_float.onnx e bagging_regressor_double.onnx - 2.2.3. sklearn.linear_model.DecisionTreeRegressor
2.2.3.1. Codice per creare il modello DecisionTreeRegressor ed esportarlo in ONNX per float e double
2.2.3.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.3.3. Rappresentazione ONNX decision_tree_regressor_float.onnx and decision_tree_regressor_double.onnx - 2.2.4. sklearn.linear_model.ExtraTreeRegressor
2.2.4.1. Codice per la creazione del modello ExtraTreeRegressor e per l'esportazione in ONNX per float e double
2.2.4.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.4.3. Rappresentazione ONNX di extra_tree_regressor_float.onnx e extra_tree_regressor_double.onnx - 2.2.5. sklearn.ensemble.ExtraTreesRegressor
2.2.5.1. Codice per creare il modello ExtraTreesRegressor ed esportarlo in ONNX per float e double
2.2.5.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.5.3. Rappresentazione ONNX di extra_trees_regressor_float.onnx e extra_trees_regressor_double.onnx - 2.2.6. sklearn.svm.NuSVR
2.2.6.1. Codice per la creazione del modello NuSVR ed esportazione in ONNX per float e double
2.2.6.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.6.3. Rappresentazione ONNX di nu_svr_float.onnx e nu_svr_double.onnx - 2.2.7. sklearn.ensemble.RandomForestRegressor
2.2.7.1. Codice per la creazione del modello RandomForestRegressor ed esportazione in ONNX per float e double
2.2.7.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.7.3. Rappresentazione ONNX di random_forest_regressor_float.onnx e random_forest_regressor_double.onnx
- 2.2.8. sklearn.ensemble.GradientBoostingRegressor
2.2.8.1. Codice per la creazione del modello GradientBoostingRegressor ed esportazione in ONNX per float e double
2.2.8.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.8.3. Rappresentazione ONNX del gradient_boosting_regressor_float.onnx e gradient_boosting_regressor_double.onnx
- 2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
2.2.9.1. Codice per la creazione del modello HistGradientBoostingRegressor ed esportazione in ONNX per float e double
2.2.9.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.9.3. Rappresentazione ONNX di hist_gradient_boosting_regressor_float.onnx e hist_gradient_boosting_regressor_double.onnx - 2.2.10. sklearn.svm.SVR
2.2.10.1. Codice per la creazione del modello SVR ed esportazione in ONNX per float e double
2.2.10.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
2.2.10.3. Rappresentazione ONNX di svr_float.onnx e svr_double.onnx
- 2.3. Modelli di regressione che hanno riscontrato problemi durante la conversione in ONNX
- 2.3.1. sklearn.dummy.DummyRegressor
Codice per la creazione di DummyRegressor - 2.3.2. sklearn.kernel_ridge.KernelRidge
Codice per la creazione di KernelRidge - 2.3.3. sklearn.isotonic.IsotonicRegression
Codice per la creazione di IsotonicRegression - 2.3.4. sklearn.cross_decomposition.PLSCanonical
Codice per la creazione di PLSCanonical - 2.3.5. sklearn.cross_decomposition.CCA
Codice per la creazione di CCA - Conclusione
- Riepilogo
Se ti dà fastidio, ben venga il tuo contributo
Sul forum degli sviluppatori di ONNX Runtime, uno degli utenti ha segnalato un errore "[ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Impossibile trovare un'implementazione per il nodo LinearRegressor:LinearRegressor(1)" durante l'esecuzione di un modello tramite ONNX Runtime.
Ciao a tutti, ricevo questo errore quando provo a dedurre un modello di regressione lineare. Vi prego di aiutarmi a risolvere questo problema.
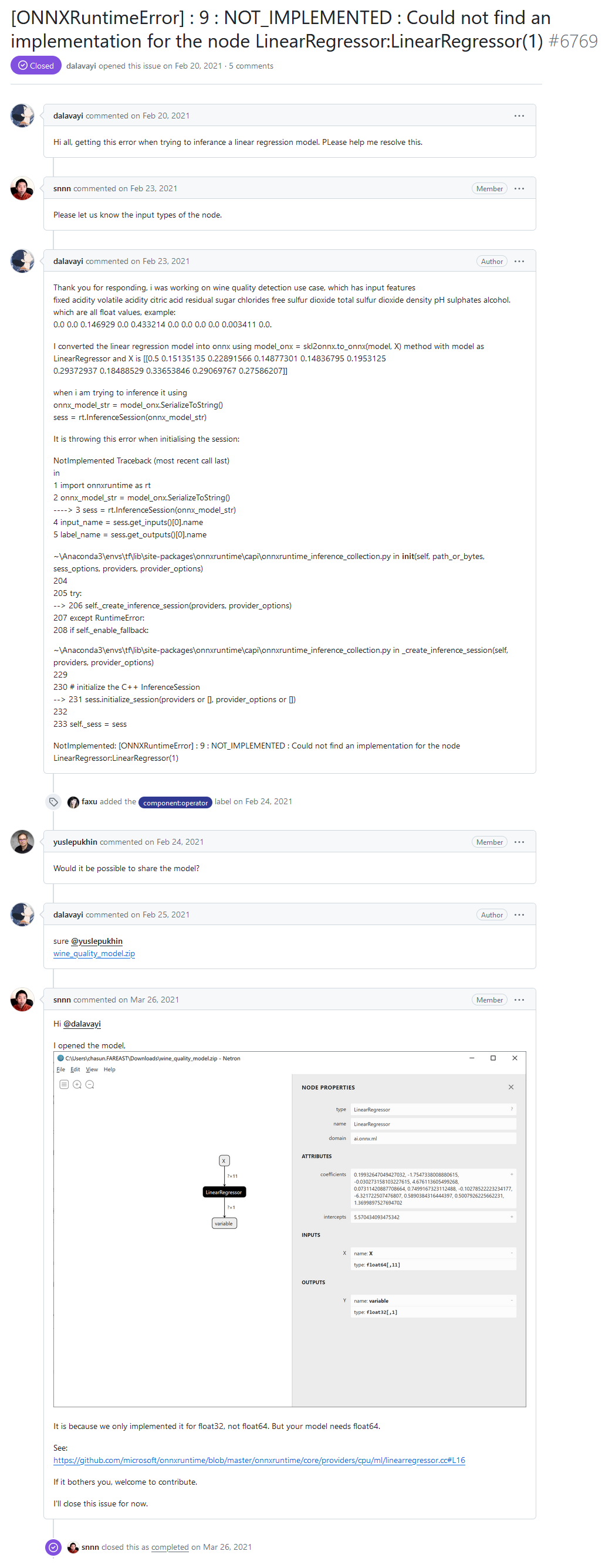
"NOT_IMPLEMENTED : Impossibile trovare un'implementazione per il nodo LinearRegressor:LinearRegressor(1)" errore dal forum degli sviluppatori di ONNX Runtime
Risposta dello sviluppatore:
È perché l'abbiamo implementato solo per float32 e non per float64. Ma il tuo modello ha bisogno di float64.
Vedi:
https://github.com/microsoft/onnxruntime/blob/master/onnxruntime/core/providers/cpu/ml/linearregressor.cc#L16
Se ti dà fastidio, ben venga il tuo contributo.
Nel modello ONNX dell'utente, l'operatore ai.onnx.ml.LinearRegressor è chiamato con il tipo di dati double (float64) e il messaggio di errore si verifica perché il Runtime ONNX non supporta l'operatore LinearRegressor() con precisione double.
Secondo le specifiche dell'operatore ai.onnx.ml.LinearRegressor, il tipo di dati di ingresso double è possibile (T: tensor(float), tensor(double), tensor(int64), tensor(int32)); tuttavia, gli sviluppatori hanno scelto intenzionalmente di non implementarlo.
Il motivo è che l'uscita restituisce sempre il valore Y: tensor(float). Inoltre, i parametri di calcolo sono numeri float (coefficienti: lista di float, intercette: lista di float).
Di conseguenza, quando i calcoli vengono eseguiti in precisione double, questo operatore riduce la precisione a float e la sua implementazione nei calcoli in precisione double ha un valore discutibile.
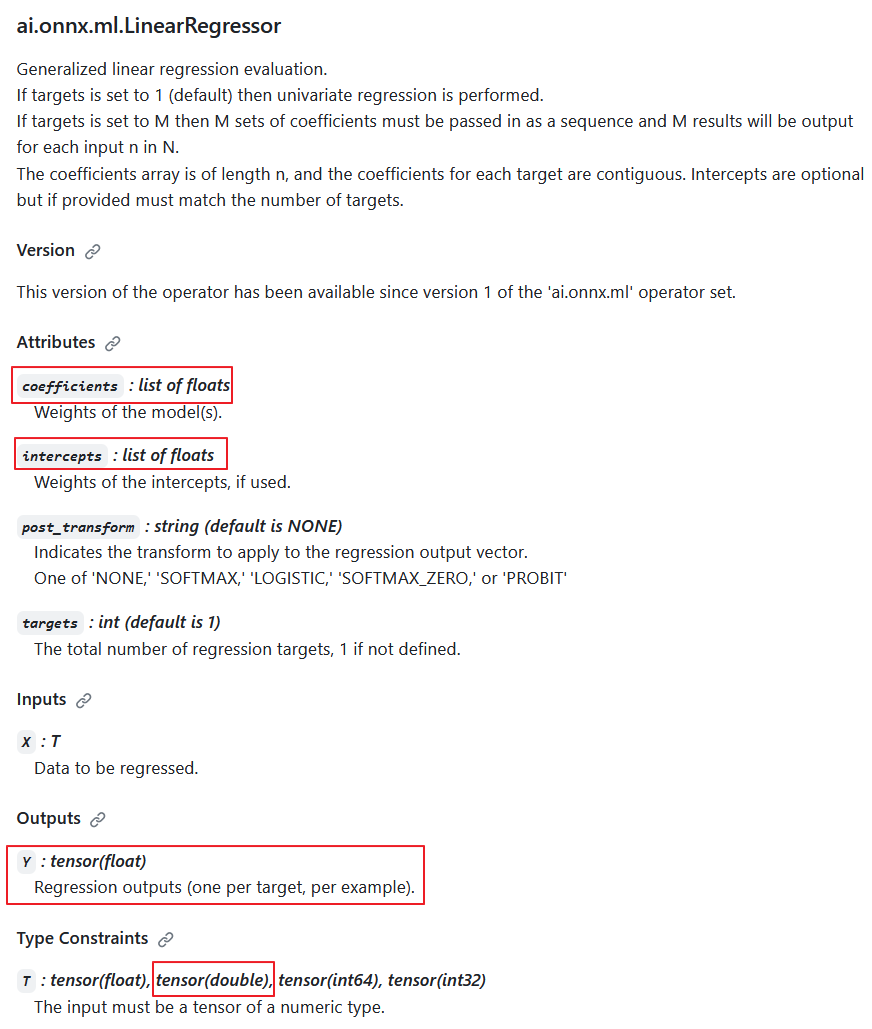
Descrizione dell'operatore ai.onnx.ml.LinearRegressor
Pertanto, la riduzione della precisione a float nei parametri e nel valore di uscita rende impossibile il pieno funzionamento di ai.onnx.ml.LinearRegressor con numeri double (float64). Presumibilmente, per questo motivo, gli sviluppatori del Runtime ONNX hanno deciso di non implementarlo per il tipo double
Il metodo di "aggiunta del supporto double" è stato dimostrato dagli sviluppatori nei commenti al codice (evidenziati in giallo).
In ONNX Runtime, il suo calcolo viene eseguito utilizzando la classe LinearRegressor (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.h).
I parametri dell'operatore, coefficienti_ e intercette_, sono memorizzati come std::vector<float>:
#pragma once #include "core/common/common.h" #include "core/framework/op_kernel.h" #include "core/util/math_cpuonly.h" #include "ml_common.h" namespace onnxruntime { namespace ml { class LinearRegressor final : public OpKernel { public: LinearRegressor(const OpKernelInfo& info); Status Compute(OpKernelContext* context) const override; private: int64_t num_targets_; std::vector<float> coefficients_; std::vector<float> intercepts_; bool use_intercepts_; POST_EVAL_TRANSFORM post_transform_; }; } // namespace ml } // namespace onnxruntimeL'implementazione dell'operatore LinearRegressor (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.cc)
// Copyright (c) Microsoft Corporation. All rights reserved. // Licensed under the MIT License. #include "core/providers/cpu/ml/linearregressor.h" #include "core/common/narrow.h" #include "core/providers/cpu/math/gemm.h" namespace onnxruntime { namespace ml { ONNX_CPU_OPERATOR_ML_KERNEL( LinearRegressor, 1, // KernelDefBuilder().TypeConstraint("T", std::vector<MLDataType>{ // DataTypeImpl::GetTensorType<float>(), // DataTypeImpl::GetTensorType<double>()}), KernelDefBuilder().TypeConstraint("T", DataTypeImpl::GetTensorType<float>()), LinearRegressor); LinearRegressor::LinearRegressor(const OpKernelInfo& info) : OpKernel(info), intercepts_(info.GetAttrsOrDefault<float>("intercepts")), post_transform_(MakeTransform(info.GetAttrOrDefault<std::string>("post_transform", "NONE"))) { ORT_ENFORCE(info.GetAttr<int64_t>("targets", &num_targets_).IsOK()); ORT_ENFORCE(info.GetAttrs<float>("coefficients", coefficients_).IsOK()); // use the intercepts_ if they're valid use_intercepts_ = intercepts_.size() == static_cast<size_t>(num_targets_); } // Use GEMM for the calculations, with broadcasting of intercepts // https://github.com/onnx/onnx/blob/main/docs/Operators.md#Gemm // // X: [num_batches, num_features] // coefficients_: [num_targets, num_features] // intercepts_: optional [num_targets]. // Output: X * coefficients_^T + intercepts_: [num_batches, num_targets] template <typename T> static Status ComputeImpl(const Tensor& input, ptrdiff_t num_batches, ptrdiff_t num_features, ptrdiff_t num_targets, const std::vector<float>& coefficients, const std::vector<float>* intercepts, Tensor& output, POST_EVAL_TRANSFORM post_transform, concurrency::ThreadPool* threadpool) { const T* input_data = input.Data<T>(); T* output_data = output.MutableData<T>(); if (intercepts != nullptr) { TensorShape intercepts_shape({num_targets}); onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans, num_batches, num_targets, num_features, 1.f, input_data, coefficients.data(), 1.f, intercepts->data(), &intercepts_shape, output_data, threadpool); } else { onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans, num_batches, num_targets, num_features, 1.f, input_data, coefficients.data(), 1.f, nullptr, nullptr, output_data, threadpool); } if (post_transform != POST_EVAL_TRANSFORM::NONE) { ml::batched_update_scores_inplace(gsl::make_span(output_data, SafeInt<size_t>(num_batches) * num_targets), num_batches, num_targets, post_transform, -1, false, threadpool); } return Status::OK(); } Status LinearRegressor::Compute(OpKernelContext* ctx) const { Status status = Status::OK(); const auto& X = *ctx->Input<Tensor>(0); const auto& input_shape = X.Shape(); if (input_shape.NumDimensions() > 2) { return ORT_MAKE_STATUS(ONNXRUNTIME, INVALID_ARGUMENT, "Input shape had more than 2 dimension. Dims=", input_shape.NumDimensions()); } ptrdiff_t num_batches = input_shape.NumDimensions() <= 1 ? 1 : narrow<ptrdiff_t>(input_shape[0]); ptrdiff_t num_features = input_shape.NumDimensions() <= 1 ? narrow<ptrdiff_t>(input_shape.Size()) : narrow<ptrdiff_t>(input_shape[1]); Tensor& Y = *ctx->Output(0, {num_batches, num_targets_}); concurrency::ThreadPool* tp = ctx->GetOperatorThreadPool(); auto element_type = X.GetElementType(); switch (element_type) { case ONNX_NAMESPACE::TensorProto_DataType_FLOAT: { status = ComputeImpl<float>(X, num_batches, num_features, narrow<ptrdiff_t>(num_targets_), coefficients_, use_intercepts_ ? &intercepts_ : nullptr, Y, post_transform_, tp); break; } case ONNX_NAMESPACE::TensorProto_DataType_DOUBLE: { // TODO: Add support for 'double' to the scoring functions in ml_common.h // once that is done we can just call ComputeImpl<double>... // Alternatively we could cast the input to float. } default: status = ORT_MAKE_STATUS(ONNXRUNTIME, FAIL, "Unsupported data type of ", element_type); } return status; } } // namespace ml } // namespace onnxruntime
Si è scoperto che esiste un'opzione per utilizzare i numeri double come valori di ingresso ed eseguire il calcolo dell'operatore con parametri float. Un'altra possibilità potrebbe essere quella di ridurre la precisione dei dati di ingresso a float. Tuttavia, nessuna di queste opzioni può essere considerata una soluzione adeguata.
La specifica dell'operatore ai.onnx.ml.LinearRegressor limita la possibilità di operare completamente con i numeri double, poiché i parametri e il valore di uscita sono limitati al tipo float.
Una situazione simile si verifica con altri operatori ONNX ML, come ai.onnx.ml.SVMRegressor e ai.onnx.ml.TreeEnsembleRegressor.
Di conseguenza, tutti gli sviluppatori che utilizzano l'esecuzione di modelli ONNX in doppia precisione devono affrontare questa limitazione delle specifiche. Una soluzione potrebbe comportare l'estensione delle specifiche ONNX (o l'aggiunta di operatori simili come LinearRegressor64, SVMRegressor64 e TreeEnsembleRegressor64 con parametri e valori di uscita double). Tuttavia, al momento la questione rimane irrisolta.
Molto dipende dal convertitore ONNX. Per i modelli calcolati in double, potrebbe essere preferibile evitare l'uso di questi operatori (anche se ciò non è sempre possibile). In questo caso particolare, il convertitore ONNX non ha funzionato in modo ottimale con il modello dell'utente.
Come vedremo in seguito, il convertitore sklearn-onnx riesce ad aggirare la limitazione di LinearRegressor: per i modelli ONNX double, utilizza invece gli operatori ONNX MatMul() e Add(). Grazie a questo metodo, numerosi modelli di regressione della libreria Scikit-learn vengono convertiti con successo in modelli ONNX calcolati in double, conservando l'accuratezza dei modelli double originali.
1. Set dei dati di prova
Per eseguire gli esempi, è necessario installare Python (noi abbiamo usato la versione 3.10.8), le librerie aggiuntive (pip install -U scikit-learn numpy matplotlib onnx onnxruntime skl2onnx) e specificare il percorso di Python nel MetaEditor (nel menu Strumenti->Opzioni->Compilatori->Python).
Come set di dati di prova, utilizzeremo i valori generati della funzione y = 4X + 10sin(X*0,5).
Per visualizzare il grafico di una funzione di questo tipo, aprire MetaEditor, creare un file chiamato RegressionData.py, copiare il testo dello script ed eseguirlo facendo clic sul pulsante "Compilare".
Lo script per la visualizzazione del set di dati di prova
# RegressionData.py # The code plots the synthetic data, used for all regression models # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # import necessary libraries import numpy as np import matplotlib.pyplot as plt # generate synthetic data for regression X = np.arange(0,100,1).reshape(-1,1) y = 4*X + 10*np.sin(X*0.5) # set the figure size plt.figure(figsize=(8,5)) # plot the initial data for regression plt.scatter(X, y, label='Regression Data', marker='o') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.title('Regression data') plt.show()
Di conseguenza, verrà visualizzato un grafico della funzione, che verrà utilizzato per testare i metodi di regressione.
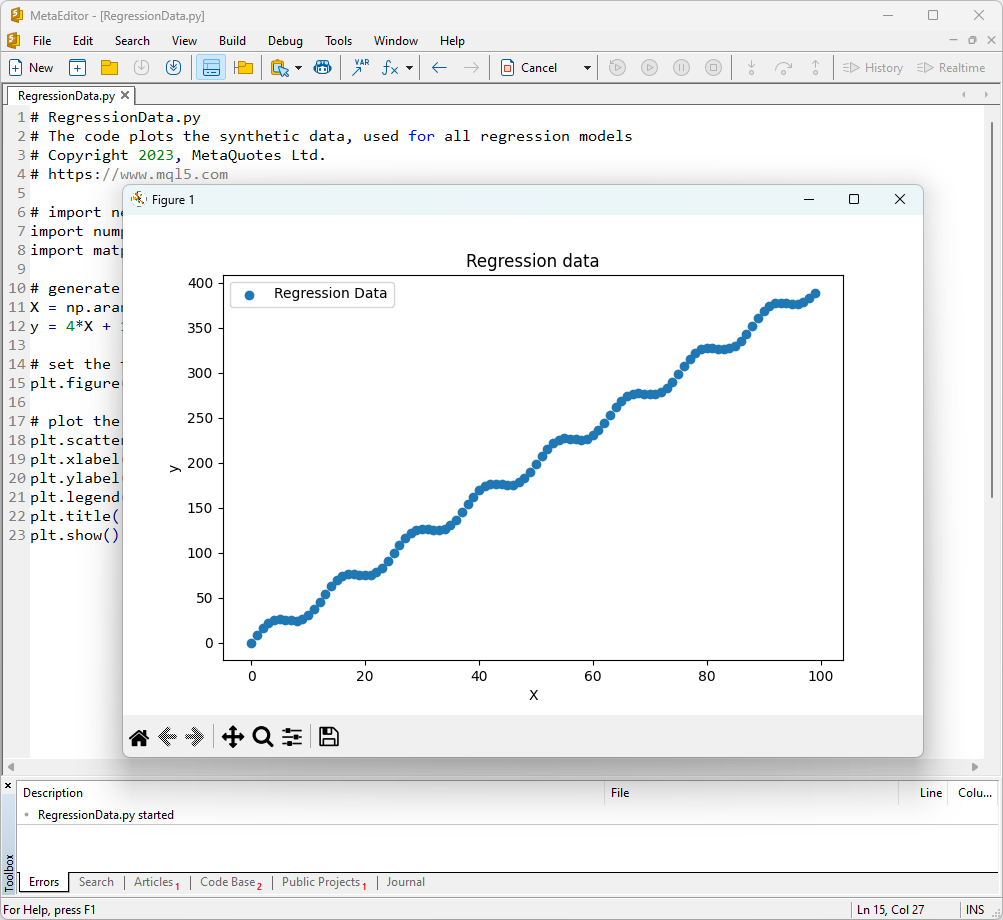
Fig.1. Funzione per testare i modelli di regressione
2. Modelli di regressione
L'obiettivo di un compito di regressione è trovare una funzione matematica o un modello che descriva al meglio la relazione tra le caratteristiche e la variabile target per prevedere i valori numerici di nuovi dati. Ciò consente di fare previsioni, ottimizzare soluzioni e prendere decisioni informate sulla base dei dati.
Consideriamo i principali modelli di regressione del pacchetto scikit-learn.
2.0. Elenco dei Modelli di Regressione di Scikit-learn
Per visualizzare un elenco dei modelli di regressione scikit-learn disponibili, è possibile utilizzare lo script:
# ScikitLearnRegressors.py # The script lists all the regression algorithms available inb scikit-learn # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # print Python version from platform import python_version print("The Python version is ", python_version()) # print scikit-learn version import sklearn print('The scikit-learn version is {}.'.format(sklearn.__version__)) # print scikit-learn regression models from sklearn.utils import all_estimators regressors = all_estimators(type_filter='regressor') for index, (name, RegressorClass) in enumerate(regressors, start=1): print(f"Regressor {index}: {name}")
Output:
La versione di Python è la 3.10.8
La versione di scikit-learn è la 1.3.2.
Regressore 1: ARDRegression
Regressore 2: AdaBoostRegressor
Regressore 3: BaggingRegressor
Regressore 4: BayesianRidge
Regressore 5: CCA
Regressore 6: DecisionTreeRegressor
Regressore 7: DummyRegressor
Regressore 8: ElasticNet
Regressore 9: ElasticNetCV
Regressore 10: ExtraTreeRegressor
Regressore 11: ExtraTreesRegressor
Regressore 12: GammaRegressor
Regressore 13: GaussianProcessRegressor
Regressore 14: GradientBoostingRegressor
Regressore 15: HistGradientBoostingRegressor
Regressore 16: HuberRegressor
Regressore 17: IsotonicRegression
Regressore 18: KNeighborsRegressor
Regressore 19: KernelRidge
Regressore 20: Lars
Regressore 21: LarsCV
Regressore 22: Lasso
Regressore 23: LassoCV
Regressore 24: LassoLars
Regressore 25: LassoLarsCV
Regressore 26: LassoLarsIC
Regressore 27: LinearRegression
Regressore 28: LinearSVR
Regressore 29: MLPRegressor
Regressore 30: MultiOutputRegressor
Regressore 31: MultiTaskElasticNet
Regressore 32: MultiTaskElasticNetCV
Regressore 33: MultiTaskLasso
Regressore 34: MultiTaskLassoCV
Regressore 35: NuSVR
Regressore 36: OrthogonalMatchingPursuit
Regressore 37: OrthogonalMatchingPursuitCV
Regressore 38: PLSCanonical
Regressore 39: PLSRegression
Regressore 40: PassiveAggressiveRegressor
Regressore 41: PoissonRegressor
Regressore 42: QuantileRegressor
Regressore 43: RANSACRegressor
Regressore 44: RadiusNeighborsRegressor
Regressore 45: RandomForestRegressor
Regressore 46: RegressorChain
Regressore 47: Ridge
Regressore 48: RidgeCV
Regressore 49: SGDRegressor
Regressore 50: SVR
Regressore 51: StackingRegressor
Regressore 52: TeilSenRegressor
Regressore 53: TransformedTargetRegressor
Regressore 54: TweedieRegressor
Regressore 55: VotingRegressor
La versione di scikit-learn è la 1.3.2.
Regressore 1: ARDRegression
Regressore 2: AdaBoostRegressor
Regressore 3: BaggingRegressor
Regressore 4: BayesianRidge
Regressore 5: CCA
Regressore 6: DecisionTreeRegressor
Regressore 7: DummyRegressor
Regressore 8: ElasticNet
Regressore 9: ElasticNetCV
Regressore 10: ExtraTreeRegressor
Regressore 11: ExtraTreesRegressor
Regressore 12: GammaRegressor
Regressore 13: GaussianProcessRegressor
Regressore 14: GradientBoostingRegressor
Regressore 15: HistGradientBoostingRegressor
Regressore 16: HuberRegressor
Regressore 17: IsotonicRegression
Regressore 18: KNeighborsRegressor
Regressore 19: KernelRidge
Regressore 20: Lars
Regressore 21: LarsCV
Regressore 22: Lasso
Regressore 23: LassoCV
Regressore 24: LassoLars
Regressore 25: LassoLarsCV
Regressore 26: LassoLarsIC
Regressore 27: LinearRegression
Regressore 28: LinearSVR
Regressore 29: MLPRegressor
Regressore 30: MultiOutputRegressor
Regressore 31: MultiTaskElasticNet
Regressore 32: MultiTaskElasticNetCV
Regressore 33: MultiTaskLasso
Regressore 34: MultiTaskLassoCV
Regressore 35: NuSVR
Regressore 36: OrthogonalMatchingPursuit
Regressore 37: OrthogonalMatchingPursuitCV
Regressore 38: PLSCanonical
Regressore 39: PLSRegression
Regressore 40: PassiveAggressiveRegressor
Regressore 41: PoissonRegressor
Regressore 42: QuantileRegressor
Regressore 43: RANSACRegressor
Regressore 44: RadiusNeighborsRegressor
Regressore 45: RandomForestRegressor
Regressore 46: RegressorChain
Regressore 47: Ridge
Regressore 48: RidgeCV
Regressore 49: SGDRegressor
Regressore 50: SVR
Regressore 51: StackingRegressor
Regressore 52: TeilSenRegressor
Regressore 53: TransformedTargetRegressor
Regressore 54: TweedieRegressor
Regressore 55: VotingRegressor
Per comodità, in questo elenco i regressori sono evidenziati con colori diversi. I modelli che richiedono un modello di regressione base sono evidenziati in grigio, mentre gli altri modelli possono essere utilizzati indipendentemente. Notare che i modelli esportati con successo nel formato ONNX sono contrassegnati in verde, mentre i modelli che incontrano errori durante la conversione nella versione corrente di scikit-learn 1.2.2 sono contrassegnati in rosso. I metodi non adatti al compito del test considerato sono evidenziati in blu.
L'analisi della qualità della regressione utilizza metriche di regressione, che sono funzioni dei valori veri e previsti. Nel linguaggio MQL5 sono disponibili diverse metriche, descritte nell'articolo "Valutazione dei modelli ONNX utilizzando metriche di regressione".
In questo articolo verranno utilizzate tre metriche per confrontare la qualità dei diversi modelli:
- Coefficiente di determinazione R-quadro (R2);
- Errore Assoluto Medio (MAE);
- Errore Quadratico Medio (MSE).
2.1. I Modelli di Regressione Scikit-learn che convertono in modelli ONNX float e double
In questa sezione vengono presentati i modelli di regressione convertiti con successo nei formati ONNX sia con precisione float che double.
Tutti i modelli di regressione discussi in seguito sono presentati nel seguente formato:
- Descrizione del modello, principio di funzionamento, vantaggi e limitazioni
- Script Python per la creazione del modello, esportazione nel file ONNX nei formati float e double ed esecuzione dei modelli ottenuti utilizzando ONNX Runtime in Python. Metriche come R^2, MAE, MSE, calcolate con sklearn.metrics, sono utilizzate per valutare la qualità dei modelli originali e ONNX.
- Script MQL5 per l'esecuzione dei modelli ONNX (float e double) tramite ONNX Runtime, con metriche calcolate tramite RegressionMetric().
- Rappresentazione del modello ONNX in Netron per i modelli con precisione float e double.
2.1.1. sklearn.linear_model.ARDRegression
ARDRegression (Automatic Relevance Determination Regression) è un metodo di regressione progettato per risolvere i problemi di regressione determinando automaticamente l'importanza (rilevanza) delle caratteristiche e stabilendo i loro pesi durante il processo di addestramento del modello.
ARDRegression consente di individuare e utilizzare solo le caratteristiche più importanti per costruire un modello di regressione, il che può essere vantaggioso quando si ha a che fare con un ampio numero di caratteristiche.
Principio di funzionamento di ARDRegression:
- Regressione lineare: ARDRegression si basa sulla regressione lineare, ipotizzando una relazione lineare tra le variabili indipendenti (caratteristiche) e la variabile target.
- Determinazione Automatica delle Caratteristiche Importanti: La principale caratteristica di ARDRegression è la determinazione automatica di quali caratteristiche sono più importanti per la previsione della variabile target. Ciò si ottiene introducendo distribuzioni prioritarie (regolarizzazione) sui pesi, consentendo al modello di impostare automaticamente i pesi su zero per le caratteristiche meno significative.
- Stima delle Probabilità Posteriori: ARDRegression calcola le probabilità posteriori per ogni caratteristica, consentendo di determinarne l'importanza. Le caratteristiche con alte probabilità posteriori sono considerate rilevanti e ricevono pesi diversi da zero, mentre le caratteristiche con basse probabilità posteriori ricevono pesi pari a zero.
- Riduzione della Dimensionalità: Pertanto, ARDRegression può portare alla riduzione della dimensionalità dei dati eliminando le caratteristiche non significative.
Vantaggi di ARDRegression:
- Determinazione Automatica delle Caratteristiche Importanti: Il metodo identifica e utilizza automaticamente solo le caratteristiche più importanti, potenzialmente migliorando le prestazioni del modello e riducendo il rischio di overfitting.
- Resilienza alla Multicollinearità: ARDRegression gestisce bene la multicollinearità, anche quando le caratteristiche sono altamente correlate.
Limitazioni di ARDRegression:
- Richiede la Selezione delle Distribuzioni Prioritarie: La scelta di distribuzioni prioritarie adeguate potrebbe richiedere una sperimentazione.
- Complessità Computazionale: L'addestramento di ARDRegression può essere computazionalmente costoso, in particolare per i dataset di grandi dimensioni.
ARDRegression è un metodo di regressione che determina automaticamente l'importanza delle caratteristiche e stabilisce i loro pesi in base alle probabilità posteriori. Questo metodo è utile quando si considerano solo le caratteristiche significative per costruire un modello di regressione ed è necessario ridurre la dimensionalità dei dati.
2.1.1.1. Codice per la creazione del modello ARDRegression ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.ARDRegression, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di ingresso sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# ARDRegression.py
# Il codice dimostra il processo di addestramento del modello ARDRegressor, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegressione
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"
# creare un modello ARDRegression
regression_model = ARDRegression()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# predire i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# predire i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello ARDRegressor, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegressione
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"
# creare un modello ARDRegression
regression_model = ARDRegression()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# predire i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# predire i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Lo script crea e addestra il modello sklearn.linear_model.ARDRegression (il modello originale è considerato double), quindi esporta il modello in ONNX per float e double (ard_regression_float.onnx e ard_regression_double.onnx) e confronta l'accuratezza del suo funzionamento.
Genera anche i file ARDRegression_plot_float.png e ARDRegression_plot_double.png, che consentono una valutazione visiva dei risultati dei modelli ONNX per float e double (Fig. 2-3).
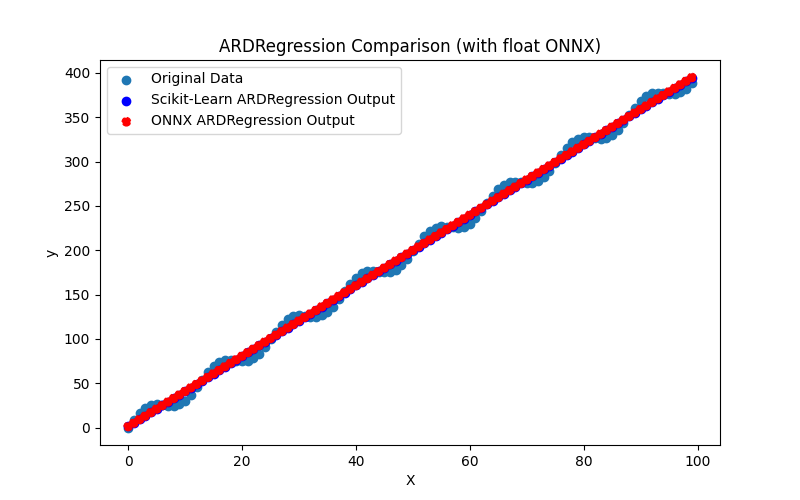
Fig.2. Risultati di ARDRegression.py (float)
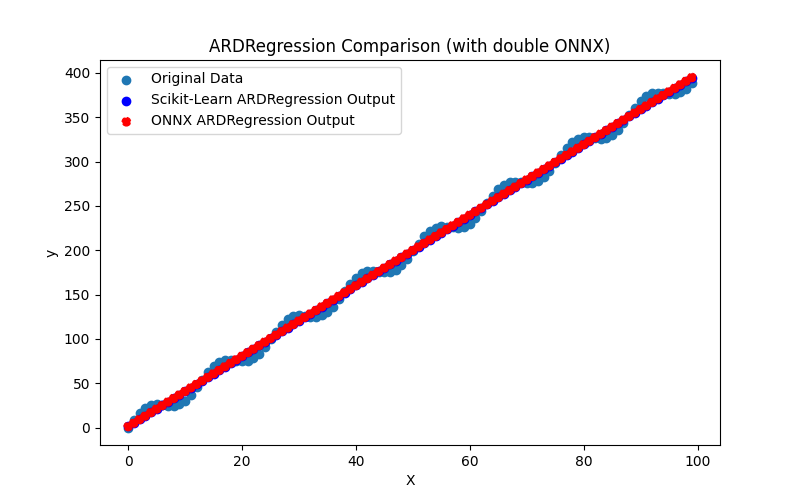
Fig.3. Risultati di ARDRegression.py (double)
Visivamente, i modelli ONNX per float e double sembrano uguali (Fig. 2-3); informazioni dettagliate sono disponibili nella scheda Journal:
Python ARDRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891289 Python Python ARDRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382627587808 Python Mean Absolute Error: 6.347568283744705 Python Mean Squared Error: 49.778160054267204 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python ARDRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891289 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
In questo esempio, il modello originale è stato considerato double, quindi è stato esportato nei modelli ONNX ard_regression_float.onnx e ard_regression_double.onnx rispettivamente per float e double.
Se l'accuratezza del modello viene valutata in base al Mean Absolute Error (MAE), l'accuratezza del modello ONNX per float è fino a 6 cifre decimali, mentre il modello ONNX che utilizza double ha mostrato un mantenimento di precisione fino a 15 cifre decimali, in linea con la precisione del modello originale.
Le proprietà dei modelli ONNX possono essere visualizzate in MetaEditor (Fig. 4-5).
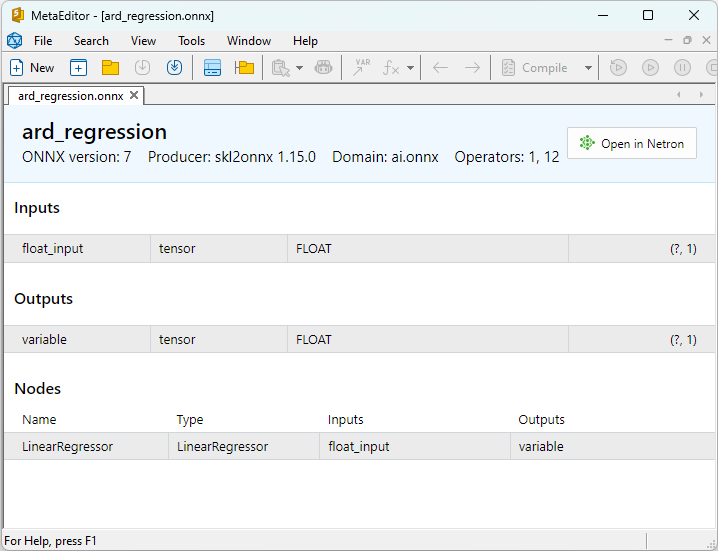
Fig.4. modello ONNX ard_regression_float.onnx in MetaEditor
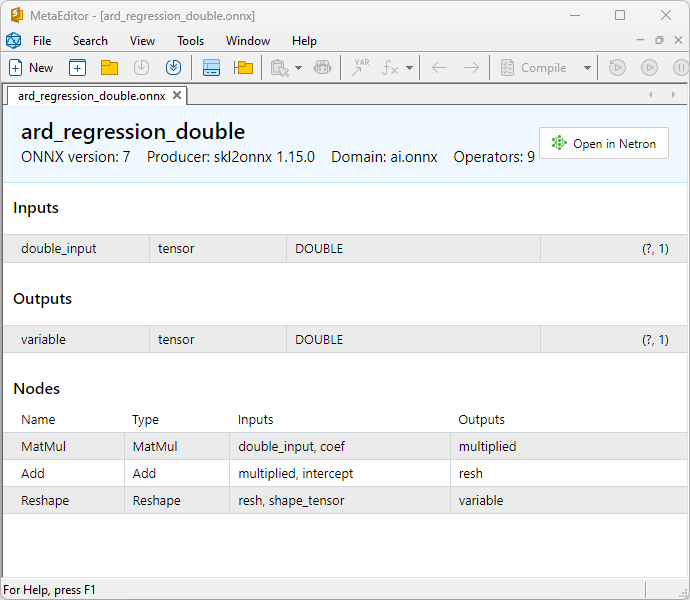
Fig.5. modello ONNX ard_regression_double.onnx in MetaEditor
Un confronto tra modelli ONNX float e double mostra che in questo caso il calcolo dei modelli ONNX per ARDRegression avviene in modo diverso: per i numeri float si utilizza l'operatore LinearRegressor() da ONNX-ML, mentre per i numeri double si utilizzano gli operatori ONNX MatMul(), Add() e Reshape().
L'implementazione del modello in ONNX dipende dal convertitore; negli esempi per l'esportazione in ONNX, verrà utilizzata la funzione skl2onnx.convert_sklearn() della libreria skl2onnx.
2.1.1.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati ONNX ard_regression_float.onnx e ard_regression_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| ARDRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ARDRegression" #define ONNXFilenameFloat "ard_regression_float.onnx" #define ONNXFilenameDouble "ard_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
ARDRegression (EURUSD,H1) Testing ONNX float: ARDRegression (ard_regression_float.onnx) ARDRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382627587808 ARDRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475682837447049 ARDRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781600542671896 ARDRegression (EURUSD,H1) ARDRegression (EURUSD,H1) Testing ONNX double: ARDRegression (ard_regression_double.onnx) ARDRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382628120845 ARDRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475680128537597 ARDRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781593489128795
Confronto con il modello double originale in Python:
Testing ONNX float: ARDRegression (ard_regression_float.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475682837447049 Testing ONNX double: ARDRegression (ard_regression_double.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475680128537597
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.1.3. Le rappresentazioni ONNX dei modelli ard_regression_float.onnx e ard_regression_double.onnx
Netron (versione web) è uno strumento per la visualizzazione dei modelli e l'analisi dei grafici di calcolo, che può essere utilizzato per i modelli in formato ONNX (Open Neural Network Exchange).
Netron presenta i grafici dei modelli e la loro architettura in forma chiara e interattiva, consentendo l'esplorazione della struttura e dei parametri dei modelli di deep learning, compresi quelli creati con ONNX.
Le caratteristiche principali di Netron includono:
- Visualizzazione dei Grafici: Netron visualizza l'architettura del modello come grafico, consentendo di vedere gli strati, le operazioni e le connessioni tra loro. È possibile comprendere facilmente la struttura e il flusso di dati all'interno del modello.
- Esplorazione Interattiva: È possibile selezionare i nodi del grafico per ottenere ulteriori informazioni su ciascun operatore e sui suoi parametri.
- Supporto per Diversi Formati: Netron supporta diversi formati di modelli di deep learning, tra cui ONNX, TensorFlow, PyTorch, CoreML e altri.
- Capacità di Analisi dei Parametri: È possibile visualizzare i parametri e i pesi del modello, utili per comprendere i valori utilizzati nelle diverse parti del modello.
Netron è comodo per gli sviluppatori e i ricercatori nel campo dell'apprendimento automatico e del deep learning, in quanto semplifica la visualizzazione e l'analisi dei modelli, favorendo la comprensione e il debug di reti neurali complesse.
Questo strumento consente una rapida ispezione del modello, esplorandone la struttura e i parametri, facilitando il lavoro con le reti neurali profonde.
Per ulteriori dettagli su Netron, consultare gli articoli: Visualizzazione della rete neurale con Netron e Visualizzare Le Reti Neurali Keras con Netron.
Video su Netron::
Il modello ard_regression_float.onnx è mostrato nella Fig.6:
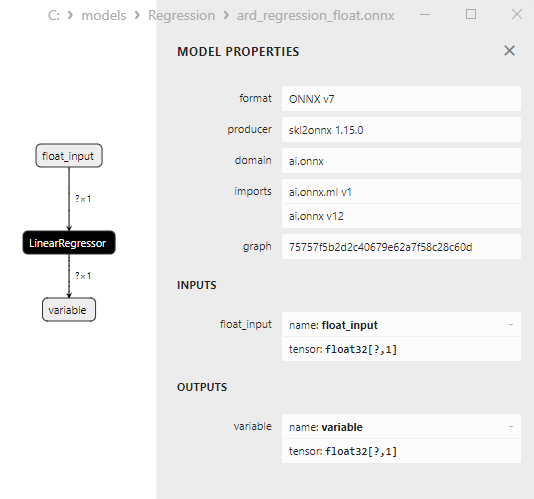
Fig.6. Rappresentazione ONNX del modello ard_regression_float.onnx in Netron
L'operatore ONNX ai.onnx.ml LinearRegressor() fa parte dello standard ONNX e descrive un modello per compiti di regressione. Questo operatore viene utilizzato per la regressione, che prevede la previsione di valori numerici (continua) sulla base delle caratteristiche di input.
Prende in input i parametri del modello, come i pesi e il bias, insieme alle caratteristiche in ingresso, ed esegue una regressione lineare. La regressione lineare stima i parametri (pesi) per ogni caratteristica in ingresso e poi esegue una combinazione lineare di queste caratteristiche con i pesi per generare una previsione.
Questo operatore esegue le seguenti operazioni:
- Prende i pesi e i bias del modello, insieme alle caratteristiche di input.
- Per ogni esempio di dati di input, esegue una combinazione lineare dei pesi con le caratteristiche corrispondenti.
- Aggiunge il bias al valore risultante.
Il risultato è la previsione della variabile target nel compito di regressione.
I parametri di LinearRegressor() sono mostrati nella Fig.7.
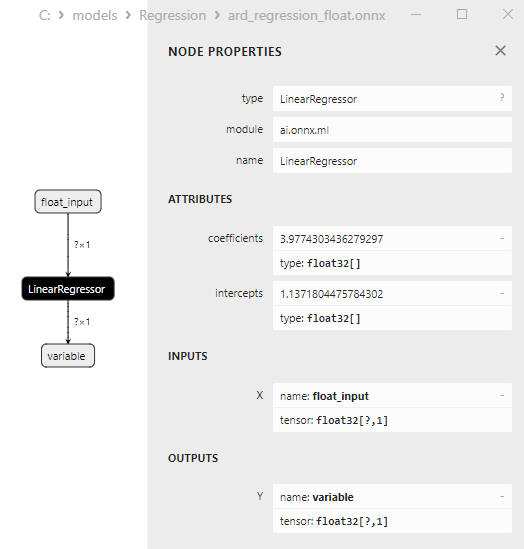
Fig.7. Le proprietà dell'operatore LinearRegressor() del modello ard_regression_float.onnx in Netron
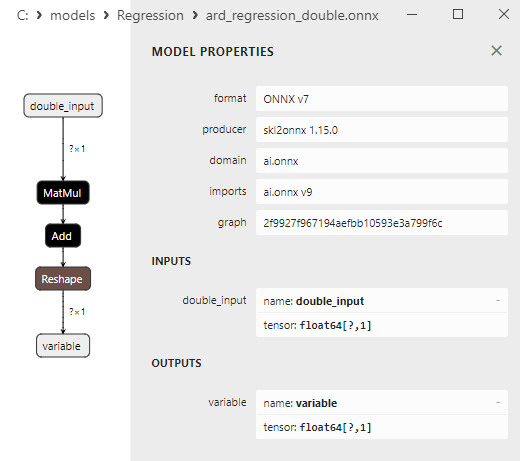
Fig.8. Rappresentazione ONNX del modello ard_regression_double.onnx in Netron
I parametri degli operatori ONNX MatMul(), Add() e Reshape() sono illustrati nella Fig.9-11.
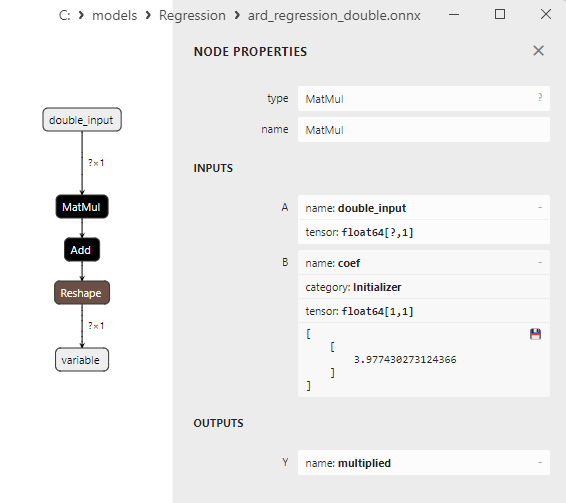
Fig.9. Proprietà dell'operatore MatMul nel modello ard_regression_double.onnx in Netron
L’operatore ONNX MatMul (moltiplicazione matriciale) esegue la moltiplicazione di due matrici.
Richiede due input: due matrici e restituisce il loro prodotto matriciale.
Se si hanno due matrici, A e B, il risultato di Matmul(A, B) è una matrice C, in cui ogni elemento C[i][j] è calcolato come la somma dei prodotti degli elementi della riga i della matrice A per gli elementi della colonna j della matrice B.
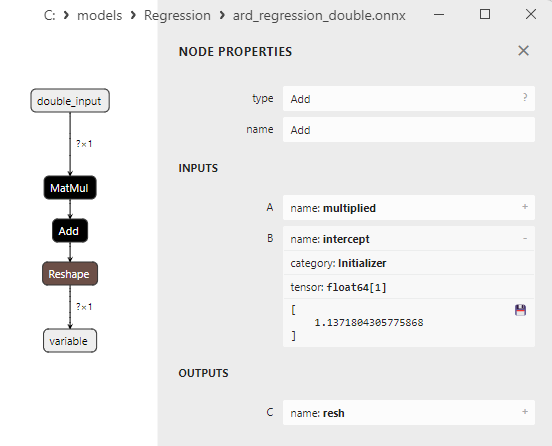
Fig.10. Proprietà dell'operatore Add nel modello ard_regression_double.onnx in Netron
L'operatore ONNX Add() esegue l'addizione elementare di due tensori o matrici della stessa forma.
Prende due input e restituisce il risultato, dove ogni elemento del tensore risultante è uguale alla somma degli elementi corrispondenti dei tensori di input.
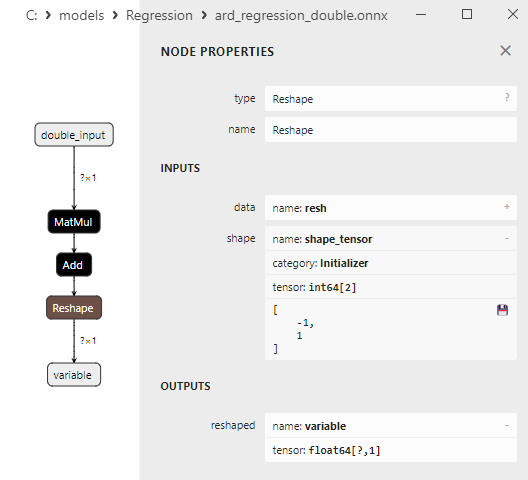
Fig.11. Proprietà dell'operatore Reshape nel modello ard_regression_double.onnx in Netron
L’operatore ONNX Reshape(-1,1) viene utilizzato per modificare la forma (o dimensione) dei dati di input. In questo operatore, il valore -1 per la dimensione indica che la grandezza di quella dimensione deve essere calcolata automaticamente in base alle altre dimensioni per garantire la coerenza dei dati.
Il valore 1 nella seconda dimensione specifica che, dopo la trasformazione della forma, ogni elemento avrà una singola sottodimensione.
2.1.2. sklearn.linear_model.BayesianRidge
BayesianRidge è un metodo di regressione che utilizza un approccio Bayesiano per stimare i parametri del modello. Questo metodo consente di modellare la distribuzione precedente dei parametri e di aggiornarla in base ai dati per ottenere la distribuzione posteriore dei parametri.
BayesianRidge è un metodo di regressione Bayesiano progettato per prevedere la variabile dipendente in base a una o più variabili indipendenti.
Principio di Funzionamento di BayesianRidge:
- Distribuzione prioritaria dei parametri: Si inizia con la definizione della distribuzione prioritaria dei parametri del modello. Questa distribuzione rappresenta la conoscenza preliminare o le ipotesi sui parametri del modello prima di considerare i dati. Nel caso di BayesianRidge, si utilizzano distribuzioni prioritarie di forma Gaussiana.
- Aggiornamento della distribuzione dei parametri: Una volta impostata la distribuzione prioritaria dei parametri, questa viene aggiornata in base ai dati. Questo viene fatto utilizzando la teoria Bayesiana, dove la distribuzione posteriore dei parametri viene calcolata considerando i dati. Un aspetto essenziale è la stima degli iperparametri, che influenzano la forma della distribuzione posteriore.
- Previsione: Dopo aver stimato la distribuzione posteriore dei parametri, è possibile fare previsioni per nuove osservazioni. In questo modo si ottiene una distribuzione delle previsioni piuttosto che un singolo valore puntuale, tenendo conto dell'incertezza nelle previsioni.
Vantaggi di BayesianRidge:
- Considerazione dell'incertezza: BayesianRidge tiene conto dell'incertezza dei parametri del modello e delle previsioni. Invece di previsioni puntuali, vengono forniti intervalli di affidabilità.
- Regolarizzazione: Il metodo di regressione Bayesiano può essere utile per la regolarizzazione del modello, aiutando a prevenire l'overfitting.
- Selezione automatica delle caratteristiche: BayesianRidge può determinare automaticamente le caratteristiche importanti riducendo i pesi delle caratteristiche non significative.
Limitazioni di BayesianRidge:
- Complessità computazionale: Il metodo richiede risorse computazionali per stimare i parametri e calcolare la distribuzione posteriore.
- Livello di astrazione elevato: Per comprendere e utilizzare BayesianRidge potrebbe essere necessaria una conoscenza più approfondita della statistica bayesiana.
- Non sempre è la scelta migliore: Il metodo BayesianRidge può non essere il più adatto in alcuni compiti di regressione, in particolare quando si tratta di dati limitati.
BayesianRidge è utile nei compiti di regressione in cui l'incertezza dei parametri e delle previsioni è importante e nei casi in cui è necessaria la regolarizzazione del modello.
2.1.2.1. Codice per la creazione del modello BayesianRidge ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.BayesianRidge, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# BayesianRidge.py
# Il codice dimostra il processo di addestramento del modello BayesianRidge, l'esportazione in formato ONNX (sia float che double) e l'elaborazione di previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"
# creare un modello di regressione Bayesian Ridge
regression_model = BayesianRidge()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello BayesianRidge, l'esportazione in formato ONNX (sia float che double) e l'elaborazione di previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"
# creare un modello di regressione Bayesian Ridge
regression_model = BayesianRidge()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python BayesianRidge Original model (double) Python R-squared (Coefficient of determination): 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891288 Python Python BayesianRidge ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382627587808 Python Mean Absolute Error: 6.347568283744705 Python Mean Squared Error: 49.778160054267204 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python BayesianRidge ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891288 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
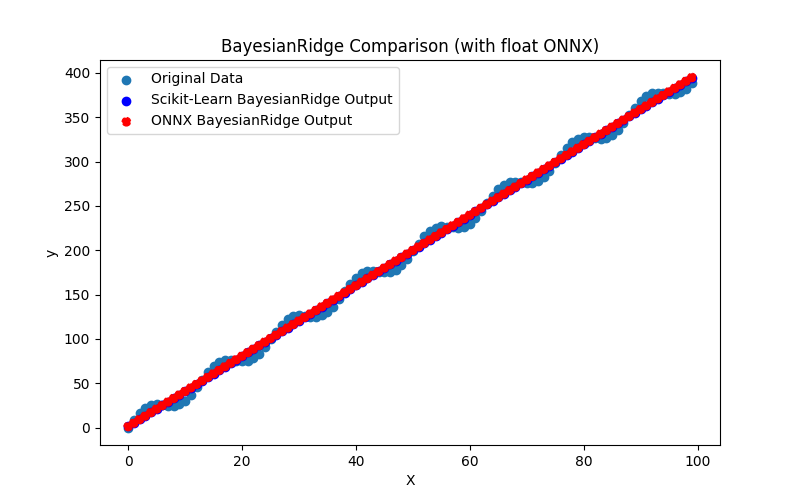
Fig.12. Risultati di BayesianRidge.py (float ONNX)
2.1.2.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli ONNX bayesian_ridge_float.onnx e bayesian_ridge_double.onnx salvati e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| BayesianRidge.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "BayesianRidge" #define ONNXFilenameFloat "bayesian_ridge_float.onnx" #define ONNXFilenameDouble "bayesian_ridge_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
BayesianRidge (EURUSD,H1) Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx) BayesianRidge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382627587808 BayesianRidge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475682837447049 BayesianRidge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781600542671896 BayesianRidge (EURUSD,H1) BayesianRidge (EURUSD,H1) Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx) BayesianRidge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382628120845 BayesianRidge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475680128537624 BayesianRidge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781593489128866
Confronto con il modello double originale in Python:
Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475682837447049 Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475680128537624
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.2.3. Rappresentazione ONNX di bayesian_ridge_float.onnx e bayesian_ridge_double.onnx
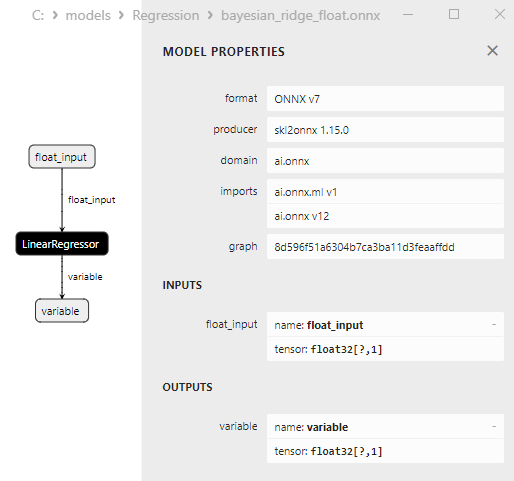
Fig.13. Rappresentazione ONNX di bayesian_ridge_float.onnx in Netron
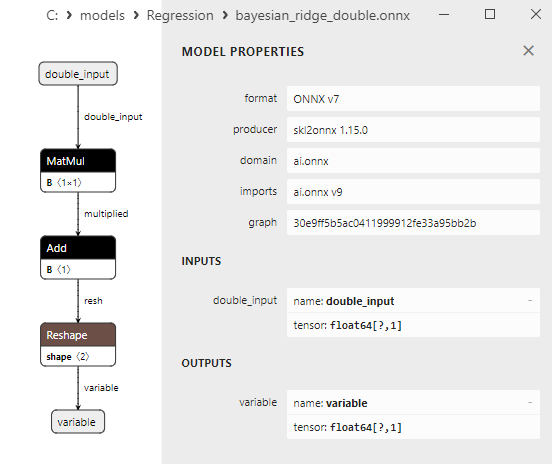
Fig.14. Rappresentazione ONNX di bayesian_ridge_double.onnx in Netron
Nota sui Metodi ElasticNet ed ElasticNetCV
ElasticNet ed ElasticNetCV sono due metodi di apprendimento automatico correlati utilizzati per regolarizzare i modelli di regressione, in particolare la regressione lineare. Condividono funzionalità comuni, ma si differenziano per le modalità di utilizzo e applicazione.
ElasticNet (Elastic Net Regression):
- Principio di funzionamento: ElasticNet è un metodo di regressione che combina Lasso (regolarizzazione L1) e Ridge (regolarizzazione L2). Aggiunge due componenti di regolarizzazione alla funzione di perdita: una penalizza il modello per i grandi valori assoluti dei coefficienti (come Lasso) e l'altra penalizza il modello per i grandi quadrati dei coefficienti (come Ridge).
- ElasticNet viene comunemente utilizzato in presenza di multicollinearità nei dati (quando le caratteristiche sono altamente correlate) e quando è necessaria la riduzione della dimensionalità, nonché il controllo dei valori dei coefficienti.
ElasticNetCV (Elastic Net Cross-Validation):
- Principio di funzionamento: ElasticNetCV è un'estensione di ElasticNet che prevede la selezione automatica degli iperparametri ottimali alfa (il coefficiente di miscelazione tra la regolarizzazione L1 e L2) e lambda (la forza di regolarizzazione) utilizzando la convalida incrociata. Esegue un'analisi dei vari valori alfa e lambda, scegliendo la combinazione che si comporta meglio nella convalida incrociata.
- Vantaggi: ElasticNetCV regola automaticamente i parametri del modello in base alla convalida incrociata, consentendo di selezionare i valori ottimali degli iperparametri senza doverli regolare manualmente. Questo rende più comodo l'utilizzo e aiuta a prevenire l'overfitting del modello.
Pertanto, la differenza principale tra ElasticNet ed ElasticNetCV è che ElasticNet è il metodo di regressione applicato ai dati, mentre ElasticNetCV è uno strumento che trova automaticamente i valori ottimali degli iperparametri per il modello ElasticNet utilizzando la convalida incrociata. ElasticNetCV è utile quando è necessario trovare i migliori parametri del modello e rendere il processo di messa a punto automatizzato.
2.1.3. sklearn.linear_model.ElasticNet
ElasticNet è un metodo di regressione che rappresenta una combinazione di regolarizzazione L1 (Lasso) e L2 (Ridge).
Questo metodo viene utilizzato per la regressione, che significa prevedere i valori numerici di una variabile target sulla base di un insieme di caratteristiche. ElasticNet aiuta a controllare l'overfitting e considera le penalizzazioni L1 e L2 sui coefficienti del modello.
Principio di funzionamento di ElasticNet:
- Dati di input: Si parte dal set di dati originale in cui sono presenti le caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target.
- Funzione Obiettivo: ElasticNet minimizza la funzione di perdita che comprende due componenti - l’errore quadratico medio (mean squared error MSE) e due regolarizzazioni: L1 (Lasso) e L2 (Ridge). Ciò significa che la funzione obiettivo appare così:
Funzione obiettivo = MSE + α * L1 + β * L2
Dove α e β sono rispettivamente gli iperparametri che controllano i pesi della regolarizzazione L1 e L2. - Trovare i valori ottimali di α e β: Il metodo della convalida incrociata viene solitamente utilizzato per trovare i valori migliori di α e β. In questo modo è possibile selezionare valori che raggiungono un equilibrio tra la riduzione dell'overfitting e la conservazione delle caratteristiche essenziali.
- Addestramento dei Modelli: ElasticNet addestra il modello considerando i valori ottimali di α e β, minimizzando la funzione obiettivo.
- Previsione: Dopo l'addestramento del modello, ElasticNet può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di ElasticNet:
- Capacità di Selezione delle Caratteristiche: ElasticNet è in grado di selezionare automaticamente le caratteristiche più importanti, impostando i pesi a zero per le caratteristiche non significative (in modo simile a Lasso).
- Controllo dell'Overfitting: ElasticNet consente di controllare l'overfitting grazie alla regolarizzazione L1 e L2.
- Gestire la Multicollinearità: Questo metodo è utile quando esiste la multicollinearità (elevata correlazione tra le caratteristiche), poiché la regolarizzazione L2 può ridurre l'influenza delle caratteristiche multicollineari.
Limitazioni di ElasticNet:
- Richiede la regolazione degli iperparametri α e β, che può essere un compito non banale.
- A seconda della scelta dei parametri, ElasticNet può conservare un numero insufficiente o eccessivo di caratteristiche, con ripercussioni sulla qualità del modello.
ElasticNet è un potente metodo di regressione che può essere utile in compiti in cui la selezione delle caratteristiche e il controllo dell'overfitting sono cruciali.
2.1.3.1. Codice per la creazione del modello ElasticNet ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.ElasticNet, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# ElasticNet.py
# Il codice dimostra il processo di addestramento del modello ElasticNet, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"
# creare un modello ElasticNet
regression_model = ElasticNet()
# Adattare il modello ai dati
regression_model.fit(X,y)
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello ElasticNet, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"
# creare un modello ElasticNet
regression_model = ElasticNet()
# Adattare il modello ai dati
regression_model.fit(X,y)
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python ElasticNet Original model (double) Python R-squared (Coefficient of determination): 0.9962377031744798 Python Mean Absolute Error: 6.344394662876524 Python Mean Squared Error: 49.78556489812415 Python Python ElasticNet ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962377032416807 Python Mean Absolute Error: 6.344395027824294 Python Mean Squared Error: 49.78556400887057 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 5 Python MSE matching decimal places: 6 Python float ONNX model precision: 5 Python Python ElasticNet ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962377031744798 Python Mean Absolute Error: 6.344394662876524 Python Mean Squared Error: 49.78556489812415 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
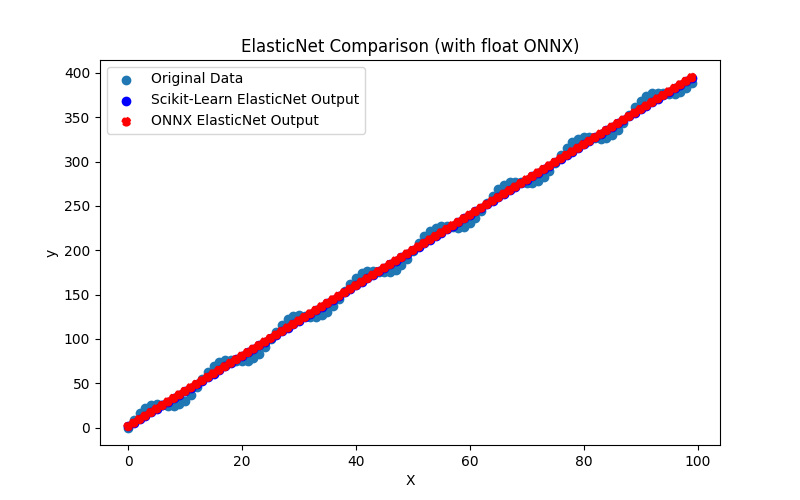
Fig.15. Risultati di ElasticNet.py (float ONNX)
2.1.3.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati elastic_net_double.onnx ed elastic_net_float.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| ElasticNet.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ElasticNet" #define ONNXFilenameFloat "elastic_net_float.onnx" #define ONNXFilenameDouble "elastic_net_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
ElasticNet (EURUSD,H1) Testing ONNX float: ElasticNet (elastic_net_float.onnx) ElasticNet (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962377032416807 ElasticNet (EURUSD,H1) MQL5: Mean Absolute Error: 6.3443950278242944 ElasticNet (EURUSD,H1) MQL5: Mean Squared Error: 49.7855640088705869 ElasticNet (EURUSD,H1) ElasticNet (EURUSD,H1) Testing ONNX double: ElasticNet (elastic_net_double.onnx) ElasticNet (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962377031744798 ElasticNet (EURUSD,H1) MQL5: Mean Absolute Error: 6.3443946628765220 ElasticNet (EURUSD,H1) MQL5: Mean Squared Error: 49.7855648981241217
Confronto con il modello double originale in Python:
Testing ONNX float: ElasticNet (elastic_net_float.onnx) Python Mean Absolute Error: 6.344394662876524 MQL5: Mean Absolute Error: 6.3443950278242944 Testing ONNX double: ElasticNet (elastic_net_double.onnx) Python Mean Absolute Error: 6.344394662876524 MQL5: Mean Absolute Error: 6.3443946628765220
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.3.3. Rappresentazione ONNX di elastic_net_float.onnx e elastic_net_double.onnx
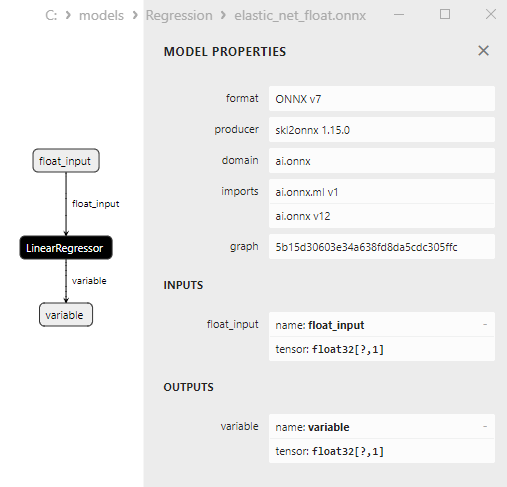
Fig.16. Rappresentazione ONNX di elastic_net_float.onnx in Netron
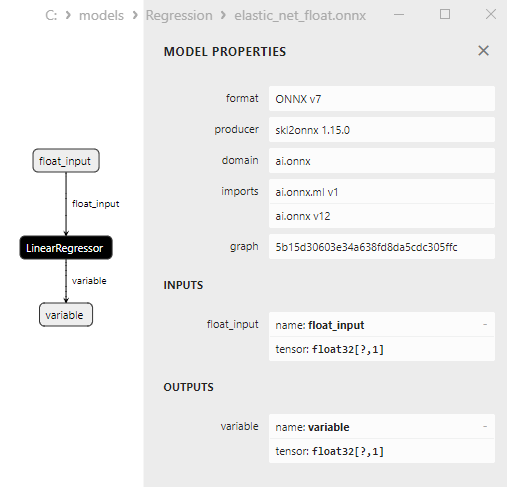
Fig.17. Rappresentazione ONNX di elastic_net_double.onnx in Netron
2.1.4. sklearn.linear_model.ElasticNetCV
ElasticNetCV è un'estensione del metodo ElasticNet progettato per selezionare automaticamente i valori ottimali degli iperparametri α e β (regolarizzazione L1 e L2) utilizzando la convalida incrociata.
Ciò consente di trovare la migliore combinazione di regolarizzazioni per il modello ElasticNet senza la necessità di regolare manualmente i parametri.
Principio di Funzionamento di ElasticNetCV:
- Dati di input: Si parte dal dataset originale contenente le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Definizione dell'Intervallo α e β: L'utente specifica l'intervallo di valori di α e β da considerare durante l'ottimizzazione. Questi valori sono tipicamente scelti su una scala logaritmica.
- Suddivisione dei Dati: Il set di dati viene suddiviso in più passaggi per la convalida incrociata. Ciascun passaggio viene utilizzato come dataset di prova, mentre le altre vengono utilizzate per l'addestramento.
- Convalida Incrociata: Per ogni combinazione di α e β all'interno dell'intervallo specificato, viene eseguita una convalida incrociata. Il modello ElasticNet viene addestrato sui dati di addestramento e poi valutato sui dati di test.
- Valutazione delle Prestazioni: L'errore medio sui set di dati di prova nella convalida incrociata viene calcolato per ogni combinazione α e β.
- Selezione dei Parametri Ottimali: Vengono determinati i valori di α e β corrispondenti all'errore medio minimo ottenuto durante la convalida incrociata.
- Addestramento del modello con i Parametri Ottimali: Il modello ElasticNetCV viene addestrato utilizzando i valori ottimali trovati di α e β.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di ElasticNetCV:
- Selezione Automatica degli Iperparametri: ElasticNetCV trova automaticamente i valori ottimali di α e β, semplificando la messa a punto del modello.
- Prevenzione dell'Overfitting: La convalida incrociata aiuta a selezionare un modello con una buona capacità di generalizzazione.
- Robustezza al Rumore: Questo metodo è robusto contro il rumore dei dati e può identificare la migliore combinazione di regolarizzazione tenendo conto del rumore.
Limitazioni di ElasticNetCV:
- Complessità Computazionale: L'esecuzione della convalida incrociata su un ampio intervallo di parametri può richiedere molto tempo.
- I Parametri Ottimali Dipendono dalla Scelta dell'Intervallo: I risultati possono dipendere dalla scelta dell'intervallo di α e β, quindi è importante regolare attentamente questo intervallo.
ElasticNetCV è un potente strumento per regolare automaticamente la regolarizzazione del modello ElasticNet e migliorarne le prestazioni.
2.1.4.1. Codice per la creazione del modello ElasticNetCV ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.ElasticNetCV, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# ElasticNetCV.py
# Il codice dimostra il processo di addestramento del modello ElasticNetCV, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNetCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNetCV"
onnx_model_filename = data_path + "elastic_net_cv"
# creare un modello ElasticNetCV
regression_model = ElasticNetCV()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python ElasticNetCV Original model (double) Python R-squared (Coefficient of determination): 0.9962137763338385 Python Mean Absolute Error: 6.334487104423225 Python Mean Squared Error: 50.10218299945999 Python Python ElasticNetCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962137770260989 Python Mean Absolute Error: 6.334486542922601 Python Mean Squared Error: 50.10217383894468 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python ElasticNetCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962137763338385 Python Mean Absolute Error: 6.334487104423225 Python Mean Squared Error: 50.10218299945999 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
< 
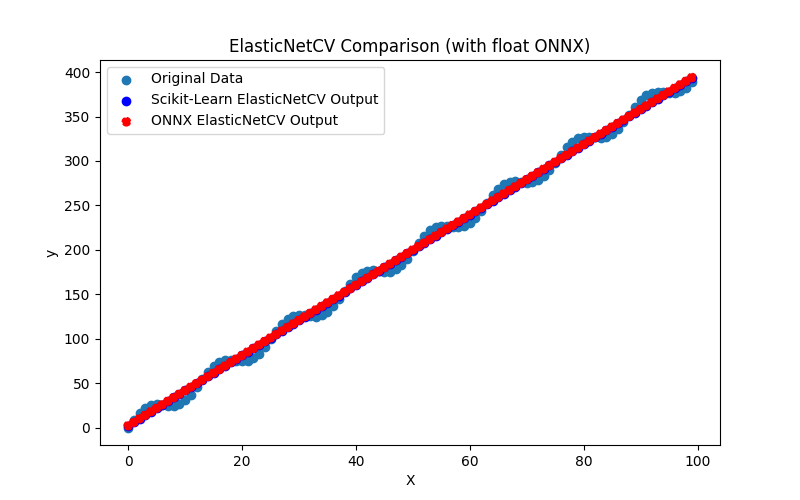
Fig.18. Risultati di ElasticNetCV.py (float ONNX)
2.1.4.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli ONNX salvati elastic_net_cv_float.onnx e elastic_net_cv_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| ElasticNetCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ElasticNetCV" #define ONNXFilenameFloat "elastic_net_cv_float.onnx" #define ONNXFilenameDouble "elastic_net_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
ElasticNetCV (EURUSD,H1) Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx) ElasticNetCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962137770260989 ElasticNetCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3344865429226038 ElasticNetCV (EURUSD,H1) MQL5: Mean Squared Error: 50.1021738389446938 ElasticNetCV (EURUSD,H1) ElasticNetCV (EURUSD,H1) Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx) ElasticNetCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962137763338385 ElasticNetCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3344871044232205 ElasticNetCV (EURUSD,H1) MQL5: Mean Squared Error: 50.1021829994599983
Confronto con il modello double originale in Python:
Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx) Python Mean Absolute Error: 6.334487104423225 MQL5: Mean Absolute Error: 6.3344865429226038 Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx) Python Mean Absolute Error: 6.334487104423225 MQL5: Mean Absolute Error: 6.3344871044232205
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.4.3. Rappresentazione ONNX di elastic_net_cv_float.onnx e elastic_net_cv_double.onnx
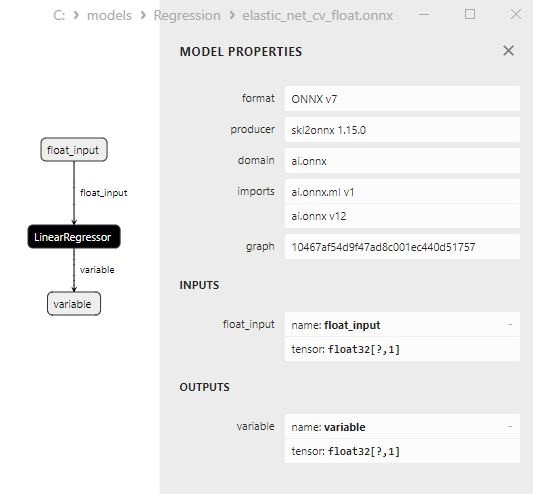
Fig.19. Rappresentazione ONNX di elastic_net_cv_float.onnx in Netron
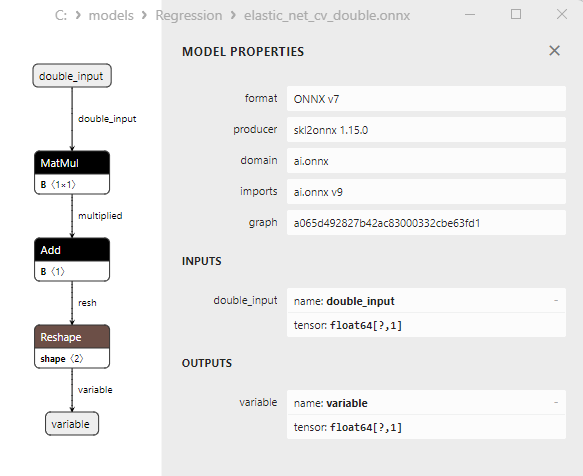
Fig.20. Rappresentazione ONNX di elastic_net_cv_double.onnx in Netron
2.1.5. sklearn.linear_model.HuberRegressor
HuberRegressor - è un metodo di apprendimento automatico utilizzato per compiti di regressione, che è una modifica del metodo dei Minimi Quadrati Ordinari (Ordinary Least Squares OLS) ed è progettato per essere robusto ai valori anomali nei dati.
A differenza di OLS, che minimizza i quadrati degli errori, HuberRegressor minimizza una combinazione di errori quadrati ed errori assoluti. Ciò consente al metodo di funzionare in modo più robusto in presenza di valori anomali nei dati.
Principio di funzionamento di HuberRegressor:
- Dati di input: Si parte dal set di dati originale, dove sono presenti le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Funzione di Perdita di Huber: HuberRegressor utilizza la funzione di perdita di Huber, che combina una funzione di perdita quadratica per errori piccoli e una funzione di perdita lineare per errori grandi. Questo rende il metodo più resistente ai valori anomali.
- Addestramento dei Modelli: Il modello viene addestrato sui dati utilizzando la funzione di perdita di Huber. Durante l'addestramento, regola i pesi (coefficienti) per ogni caratteristica e il bias.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di HuberRegressor:
- Robustezza ai Valori Anomali: Rispetto a OLS, HuberRegressor è più robusto nei confronti dei valori anomali nei dati, il che lo rende utile nelle attività in cui i dati potrebbero contenere valori anomali.
- Stima degli Errori: La funzione di perdita di Huber contribuisce alla stima degli errori di previsione, che può essere utile per analizzare i risultati del modello.
- Livello di Regolarizzazione: HuberRegressor può anche incorporare un livello di regolarizzazione, che può ridurre l'overfitting.
Limitazioni di HuberRegressor:
- Non così Accurata come OLS in Assenza di Valori Anomali: Nei casi in cui non vi siano valori anomali nei dati, OLS potrebbe fornire risultati più accurati.
- Regolazione dei Parametri: HuberRegressor ha un parametro che definisce la soglia di ciò che è considerato "grande" per passare alla funzione di perdita lineare. Questo parametro richiede una messa a punto.
HuberRegressor è utile nelle attività di regressione in cui i dati possono contenere valori anomali ed è necessario un modello robusto a tali anomalie.
2.1.5.1. Codice per creare il modello HuberRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.HuberRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza sia del modello originale che dei modelli esportati in ONNX.
# HuberRegressor.py
# Il codice dimostra il processo di addestramento del modello HuberRegressor, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"
# creare un modello Huber Regressor
huber_regressor_model = HuberRegressor()
# Adattare il modello ai dati
huber_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = huber_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello HuberRegressor, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"
# creare un modello Huber Regressor
huber_regressor_model = HuberRegressor()
# Adattare il modello ai dati
huber_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = huber_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python HuberRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962363935647066 Python Mean Absolute Error: 6.341633708569641 Python Mean Squared Error: 49.80289464784336 Python Python HuberRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962363944236795 Python Mean Absolute Error: 6.341633300252807 Python Mean Squared Error: 49.80288328126165 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python HuberRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962363935647066 Python Mean Absolute Error: 6.341633708569641 Python Mean Squared Error: 49.80289464784336 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
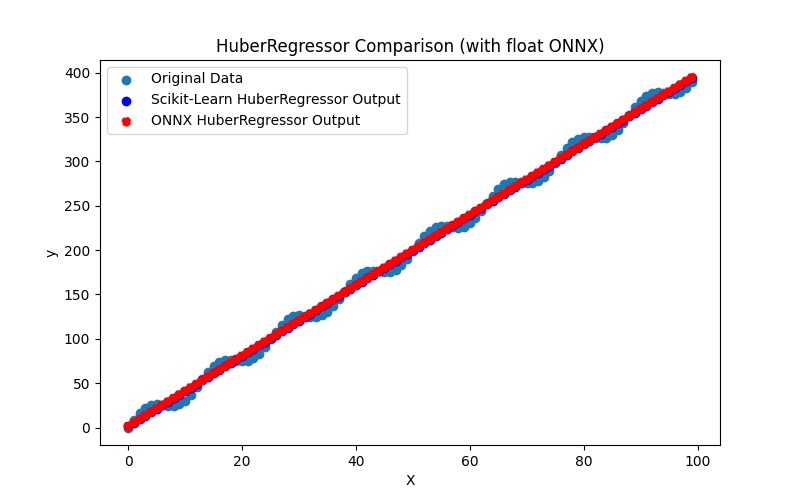
Fig.21. Risultati di HuberRegressor.py (float ONNX)
2.1.5.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli ONNX salvati huber_regressor_float.onnx e huber_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| HuberRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "HuberRegressor" #define ONNXFilenameFloat "huber_regressor_float.onnx" #define ONNXFilenameDouble "huber_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
HuberRegressor (EURUSD,H1) Testing ONNX float: HuberRegressor (huber_regressor_float.onnx) HuberRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962363944236795 HuberRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3416333002528074 HuberRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8028832812616571 HuberRegressor (EURUSD,H1) HuberRegressor (EURUSD,H1) Testing ONNX double: HuberRegressor (huber_regressor_double.onnx) HuberRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962363935647066 HuberRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3416337085696410 HuberRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8028946478433525
Confronto con il modello double originale in Python:
Testing ONNX float: HuberRegressor (huber_regressor_float.onnx) Python Mean Absolute Error: 6.341633708569641 MQL5: Mean Absolute Error: 6.3416333002528074 Testing ONNX double: HuberRegressor (huber_regressor_double.onnx) Python Mean Absolute Error: 6.341633708569641 MQL5: Mean Absolute Error: 6.3416337085696410
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.5.3. Rappresentazione ONNX di huber_regressor_float.onnx e huber_regressor_double.onnx
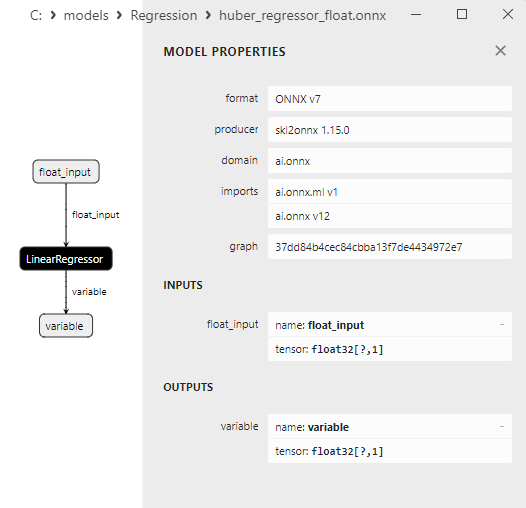
Fig.22. Rappresentazione ONNX di huber_regressor_float.onnx in Netron
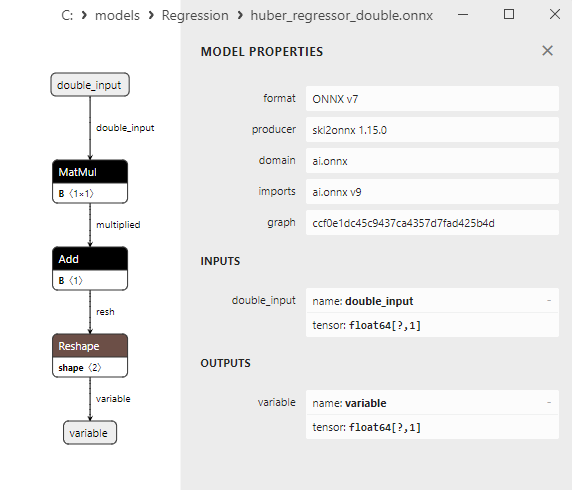
Fig.23. Rappresentazione ONNX di huber_regressor_double.onnx in Netron
2.1.6. sklearn.linear_model.Lars
LARS (Least Angle Regression) è un metodo di apprendimento automatico utilizzato per compiti di regressione. È un algoritmo che costruisce un modello di regressione lineare selezionando le caratteristiche attive (variabili) durante il processo di apprendimento.
LARS cerca di trovare il minor numero di caratteristiche che forniscono la migliore approssimazione alla variabile target.
Principio di Funzionamento di LARS:
- Dati di input: Si parte dal dataset originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Inizializzazione: Si inizia con un modello nullo, cioè senza caratteristiche attive. Tutti i coefficienti sono impostati a zero.
- Selezione delle Caratteristiche: Ad ogni passo, LARS seleziona la caratteristica più correlata con i residui del modello. Questa caratteristica viene quindi aggiunta al modello e il suo coefficiente corrispondente viene regolato con il metodo dei minimi quadrati.
- Regressione Lungo le Caratteristiche Attive: Dopo aver aggiunto la caratteristica al modello, LARS aggiorna i coefficienti di tutte le caratteristiche attive per adattarli alle modifiche del nuovo modello.
- Passi Ripetitivi: Questo processo continua finché non vengono selezionate tutte le caratteristiche o finché non viene soddisfatto un criterio di arresto specificato.
- Previsione: Dopo l'addestramento del modello, può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di LARS:
- Efficienza: LARS può essere un metodo efficiente, soprattutto quando ci sono molte caratteristiche, ma solo alcune influenzano significativamente la variabile target.
- Interpretabilità: Poiché LARS mira a selezionare solo le caratteristiche più informative, il modello rimane relativamente interpretabile.
Limitazioni di LARS:
- Modello Lineare: LARS costruisce un modello lineare, che potrebbe essere insufficiente per modellare relazioni complesse e non lineari.
- Sensibilità al Rumore: Il metodo può essere sensibile ai valori anomali dei dati.
- Incapacità di Gestire la Multicollinearità: Se le caratteristiche sono altamente correlate, LARS potrebbe avere problemi di multicollinearità.
LARS è utile nei compiti di regressione in cui è essenziale selezionare le caratteristiche più informative e costruire un modello lineare con un numero minimo di caratteristiche.
2.1.6.1. Codice per creare il modello Lars ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.Lars, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# Lars.py
# Il codice dimostra il processo di addestramento del modello Lars, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lars"
onnx_model_filename = data_path + "lars"
# creare un modello Lars Regressor
lars_regressor_model = Lars()
# Adattare il modello ai dati
lars_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lars_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello Lars, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lars"
onnx_model_filename = data_path + "lars"
# creare un modello Lars Regressor
lars_regressor_model = Lars()
# Adattare il modello ai dati
lars_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lars_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python Lars Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python Python Lars ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python Lars ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 15 Python double ONNX model precision: 15
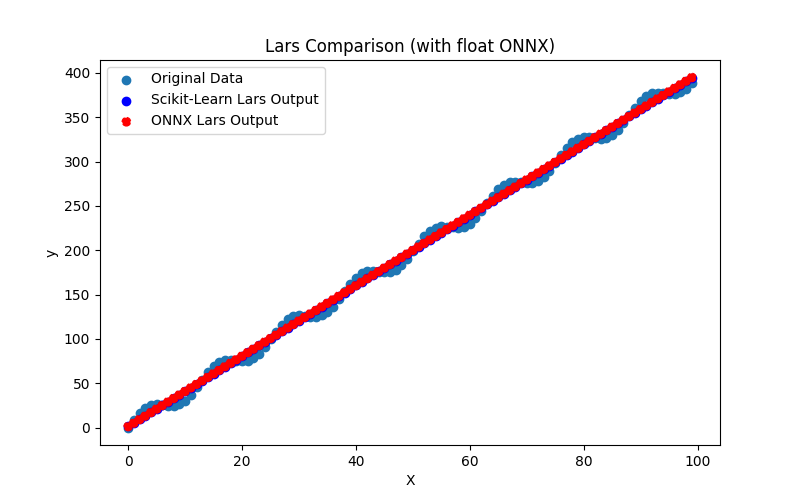
Fig.24. Risultati di Lars.py (float ONNX)
2.1.6.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati lars_cv_float.onnx e lars_cv_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| Lars.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Lars" #define ONNXFilenameFloat "lars_float.onnx" #define ONNXFilenameDouble "lars_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
Lars (EURUSD,H1) Testing ONNX float: Lars (lars_float.onnx) Lars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 Lars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 Lars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 Lars (EURUSD,H1) Lars (EURUSD,H1) Testing ONNX double: Lars (lars_double.onnx) Lars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 Lars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364302 Lars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Confronto con il modello double originale in Python:
Testing ONNX float: Lars (lars_float.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: Lars (lars_double.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477379263364302
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.6.3. Rappresentazione ONNX di lars_float.onnx e lars_double.onnx
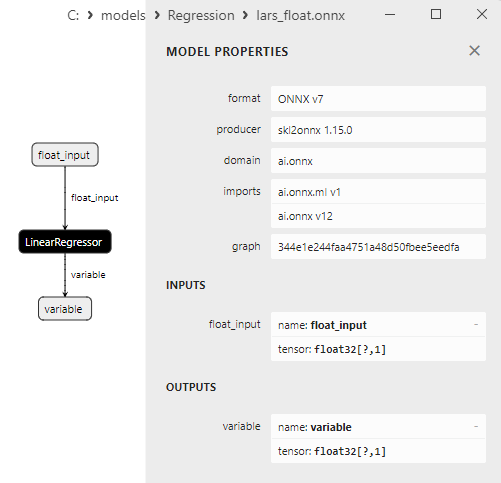
Fig.25. Rappresentazione ONNX di lars_float.onnx in Netron
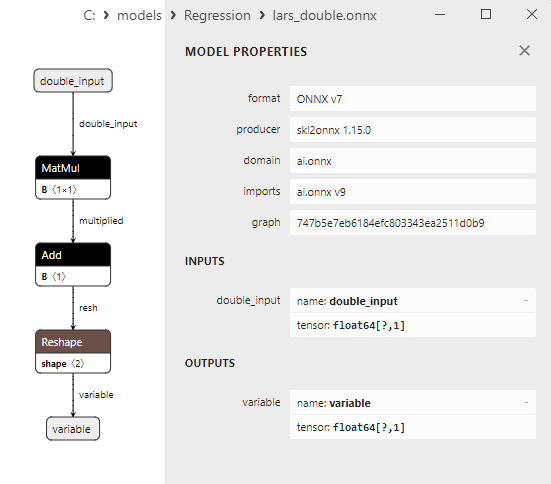
Fig.26. Rappresentazione ONNX di lars_double.onnx in Netron
2.1.7. sklearn.linear_model.LarsCV
LarsCV è una variante del metodo LARS (Least Angle Regression) che seleziona automaticamente il numero ottimale di caratteristiche da includere nel modello utilizzando la convalida incrociata.
Questo metodo aiuta a trovare un equilibrio tra un modello che generalizza i dati in modo efficace e uno che utilizza un numero minimo di caratteristiche.
Principio di Funzionamento di LarsCV:
- Dati di input: Si parte dal dataset originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Inizializzazione: Si inizia con un modello nullo, cioè senza caratteristiche attive. Tutti i coefficienti sono impostati a zero.
- Convalida Incrociata: LarsCV esegue una convalida incrociata per diverse quantità di caratteristiche incluse. In questo modo si valutano le prestazioni del modello con diversi set di caratteristiche.
- Selezione del Numero Ottimale di Caratteristiche: LarsCV sceglie il numero di caratteristiche che produce le migliori prestazioni del modello, determinate attraverso la convalida incrociata.
- Addestramento dei Modelli: Il modello viene addestrato utilizzando il numero scelto di caratteristiche e i rispettivi coefficienti.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di LarsCV:
- Selezione Automatica delle Caratteristiche: LarsCV sceglie automaticamente il numero ottimale di caratteristiche, semplificando il processo di impostazione del modello.
- Interpretabilità: Come il normale LARS, LarsCV mantiene un'interpretabilità del modello relativamente alta.
- Efficienza: Il metodo può essere efficiente, soprattutto quando i set di dati hanno molte caratteristiche, ma solo alcune sono significative.
Limitazioni di LarsCV:
- Modello Lineare: LarsCV costruisce un modello lineare, che potrebbe essere insufficiente per modellare relazioni non lineari complesse.
- Sensibilità al Rumore: Il metodo può essere sensibile ai valori anomali dei dati.
- Incapacità di Gestire la Multicollinearità: Se le caratteristiche sono altamente correlate, LarsCV potrebbe avere problemi di multicollinearità.
LarsCV è utile nelle attività di regressione in cui è importante scegliere automaticamente il miglior set di caratteristiche utilizzate nel modello e mantenere l'interpretabilità del modello.
2.1.7.1. Codice per creare il modello LarsCV ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LarsCV, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LarsCV.py
# Il codice dimostra il processo di addestramento del modello LarsCV, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"
# creare un modello LarsCV Regressor
larscv_regressor_model = LarsCV()
# Adattare il modello ai dati
larscv_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = larscv_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello LarsCV, la sua esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_valore1[dot_position1 + i] == str_valore2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"
# creare un modello LarsCV Regressor
larscv_regressor_model = LarsCV()
# Adattare il modello ai dati
larscv_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = larscv_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LarsCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python Python LarsCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382640824089 Python Mean Absolute Error: 6.347737845846069 Python Mean Squared Error: 49.778142539016564 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LarsCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 14 Python double ONNX model precision: 16
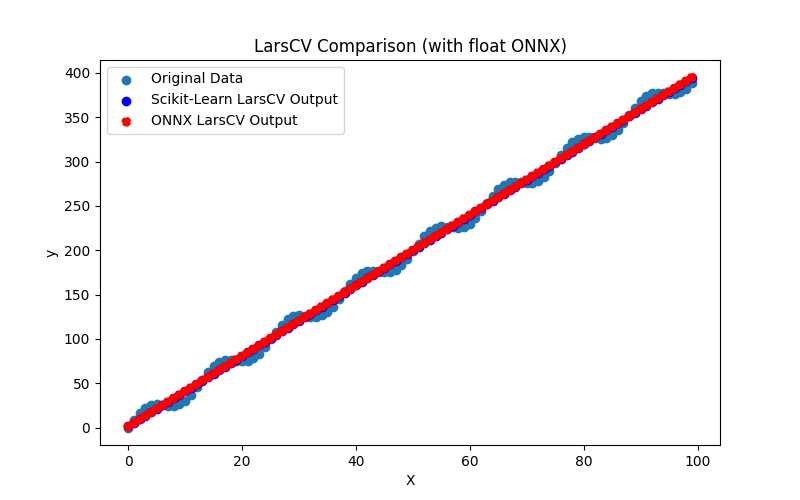
Fig.27. Risultati di LarsCV.py (float ONNX)
2.1.7.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati lars_cv_float.onnx e lars_cv_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LarsCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LarsCV" #define ONNXFilenameFloat "lars_cv_float.onnx" #define ONNXFilenameDouble "lars_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
LarsCV (EURUSD,H1) Testing ONNX float: LarsCV (lars_cv_float.onnx) LarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382640824089 LarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477378458460691 LarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781425390165566 LarsCV (EURUSD,H1) LarsCV (EURUSD,H1) Testing ONNX double: LarsCV (lars_cv_double.onnx) LarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642612767 LarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 LarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401721031642
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: LarsCV (lars_cv_float.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477378458460691 Testing ONNX double: LarsCV (lars_cv_double.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477379221400145
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 16 cifre decimali.
2.1.7.3. Rappresentazione ONNX di lars_cv_float.onnx e lars_cv_double.onnx
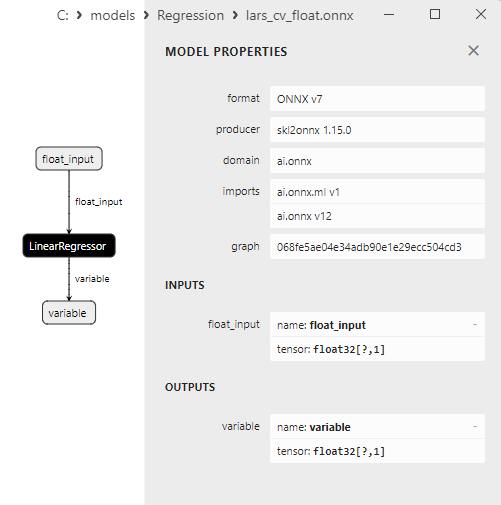
Fig.28. Rappresentazione ONNX di lars_cv_float.onnx in Netron
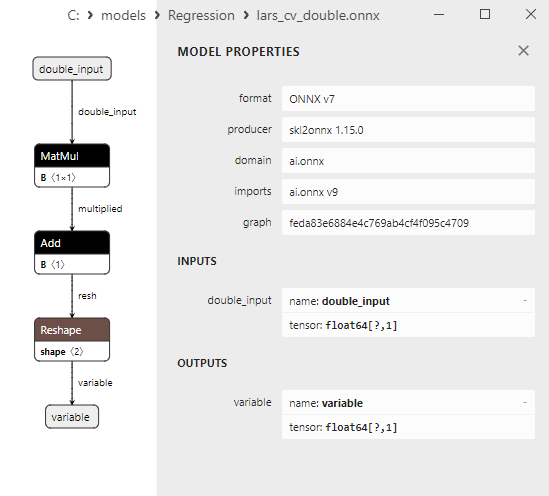
Fig.29. Rappresentazione ONNX di lars_cv_double.onnx in Netron
2.1.8. sklearn.linear_model.Lasso
Lasso (Least Absolute Shrinkage and Selection Operator) è un metodo di regressione utilizzato per selezionare le caratteristiche più importanti e ridurre la dimensionalità del modello.
Ciò si ottiene aggiungendo una penalità per la somma dei valori assoluti dei coefficienti (regolarizzazione L1) nel problema di ottimizzazione della regressione lineare.
Principio di Funzionamento di Lasso:
- Dati di input: Si parte dal set di dati originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Funzione Obiettivo: La funzione obiettivo di Lasso comprende la somma degli errori di regressione al quadrato e una penalità sulla somma dei valori assoluti dei coefficienti associati alle caratteristiche.
- Ottimizzazione: Il modello Lasso viene addestrato minimizzando la funzione obiettivo, con il risultato che alcuni coefficienti diventano nulli, escludendo di fatto le caratteristiche corrispondenti dal modello.
- Selezione del Valore Ottimale della Penalità: Lasso include un iperparametro che determina la forza della regolarizzazione. La scelta del valore ottimale di questo iperparametro può richiedere una convalida incrociata.
- Generazione di Previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di Lasso:
- Selezione delle Caratteristiche: Lasso seleziona automaticamente le caratteristiche più importanti, escludendo dal modello quelle meno significative. Questo riduce la dimensionalità dei dati e semplifica il modello.
- Regolarizzazione: La penalità sulla somma dei valori assoluti dei coefficienti aiuta a prevenire l'overfitting del modello e ne migliora la generalizzazione.
- Interpretabilità: Poiché Lasso esclude alcune caratteristiche, il modello rimane relativamente interpretabile.
Limitazioni di Lasso:
- Modello Lineare: Lasso costruisce un modello lineare, che potrebbe essere insufficiente per modellare relazioni non lineari complesse.
- Sensibilità al Rumore: Il metodo può essere sensibile ai valori anomali dei dati.
- Incapacità di Gestire la Multicollinearità: Se le caratteristiche sono altamente correlate, Lasso potrebbe incontrare problemi di multicollinearità.
Lasso è utile nelle attività di regressione in cui è essenziale selezionare le caratteristiche più importanti e ridurre la dimensionalità del modello mantenendo l'interpretabilità.
2.1.8.1. Codice per creare il modello Lasso ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.Lasso, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza sia del modello originale che dei modelli esportati in ONNX.
# Lasso.py
# Il codice dimostra il processo di addestramento del modello Lasso, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lasso"
onnx_model_filename = data_path + "lasso"
# creare un modello Lasso
lasso_model = Lasso()
# Adattare il modello ai dati
lasso_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = lasso_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello Lasso, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(valore1, valore2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lasso"
onnx_model_filename = data_path + "lasso"
# creare un modello Lasso
lasso_model = Lasso()
# Adattare il modello ai dati
lasso_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = lasso_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python Lasso Original model (double) Python R-squared (Coefficient of determination): 0.9962381735682287 Python Mean Absolute Error: 6.346393791922984 Python Mean Squared Error: 49.77934029129379 Python Python Lasso ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962381720269486 Python Mean Absolute Error: 6.346395056911361 Python Mean Squared Error: 49.77936068668213 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python Lasso ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962381735682287 Python Mean Absolute Error: 6.346393791922984 Python Mean Squared Error: 49.77934029129379 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
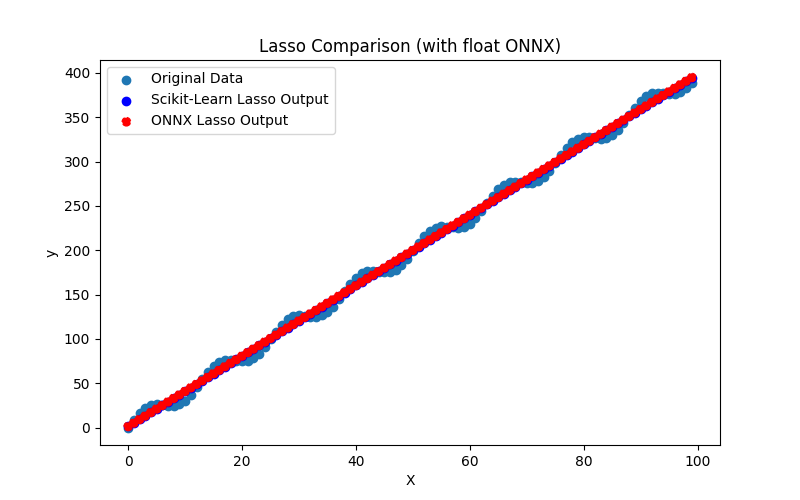
Fig.30. Risultati di Lasso.py (float ONNX)
2.1.8.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati lasso_float.onnx e lasso_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| Lasso.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Lasso" #define ONNXFilenameFloat "lasso_float.onnx" #define ONNXFilenameDouble "lasso_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
Lasso (EURUSD,H1) Testing ONNX float: Lasso (lasso_float.onnx) Lasso (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962381720269486 Lasso (EURUSD,H1) MQL5: Mean Absolute Error: 6.3463950569113612 Lasso (EURUSD,H1) MQL5: Mean Squared Error: 49.7793606866821037 Lasso (EURUSD,H1) Lasso (EURUSD,H1) Testing ONNX double: Lasso (lasso_double.onnx) Lasso (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962381735682287 Lasso (EURUSD,H1) MQL5: Mean Absolute Error: 6.3463937919229840 Lasso (EURUSD,H1) MQL5: Mean Squared Error: 49.7793402912937850
Confronto con il modello double originale in Python:
Testing ONNX float: Lasso (lasso_float.onnx) Python Mean Absolute Error: 6.346393791922984 MQL5: Mean Absolute Error: 6.3463950569113612 Testing ONNX double: Lasso (lasso_double.onnx) Python Mean Absolute Error: 6.346393791922984 MQL5: Mean Absolute Error: 6.3463937919229840
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 15 cifre decimali.
2.1.8.3. Rappresentazione ONNX di lasso_float.onnx e lasso_double.onnx
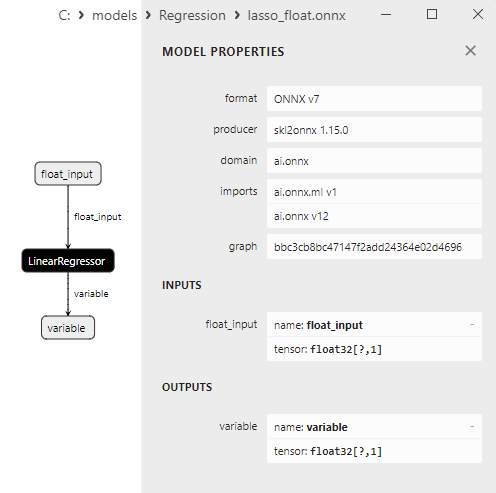
Fig.31. Rappresentazione ONNX di lasso_float.onnx in Netron
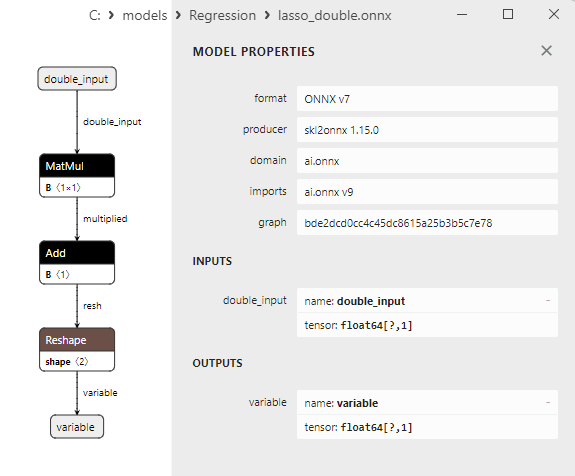
Fig.32. Rappresentazione ONNX di lasso_double.onnx in Netron
2.1.9. sklearn.linear_model.LassoCV
LassoCV è una variante del metodo Lasso (Least Absolute Shrinkage and Selection Operator) che seleziona automaticamente il valore ottimale dell'iperparametro di regolarizzazione (alfa) utilizzando la convalida incrociata.
Questo metodo consente di trovare un bilanciamento tra la riduzione della dimensionalità del modello (selezionando le caratteristiche importanti) e la prevenzione dell'overfitting, rendendolo utile per i compiti di regressione.
Principio di Funzionamento di LassoCV:
- Dati di input: Si parte dal set di dati originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Inizializzazione: LassoCV inizializza differenti valori dell'iperparametro di regolarizzazione (alfa) che coprono un intervallo da basso ad alto.
- Convalida Incrociata: Per ogni valore alfa, LassoCV esegue una convalida incrociata per valutare le prestazioni del modello. Vengono comunemente utilizzate metriche come l'errore quadratico medio (MSE) o il coefficiente di determinazione (R^2).
- Selezione dell'Alfa Ottimale: LassoCV seleziona il valore di alfa in cui il modello ottiene le migliori prestazioni determinate dalla convalida incrociata.
- Addestramento dei Modelli: Il modello Lasso viene addestrato utilizzando il valore alfa scelto, escludendo le caratteristiche meno importanti e applicando la regolarizzazione L1.
- Generazione di Previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di LassoCV:
- Selezione Automatica dell'Alfa: LassoCV seleziona automaticamente il valore alfa ottimale utilizzando la convalida incrociata, semplificando la messa a punto del modello.
- Selezione delle Caratteristiche: LassoCV sceglie automaticamente le caratteristiche più importanti, riducendo la dimensionalità del modello e semplificandone l'interpretazione.
- Regolarizzazione: Il metodo previene l'overfitting del modello attraverso la regolarizzazione L1.
Limitazioni di LassoCV:
- Modello Lineare: LassoCV costruisce un modello lineare, che potrebbe essere insufficiente per modellare relazioni non lineari complesse.
- Sensibilità al Rumore: Il metodo può essere sensibile ai valori anomali dei dati.
- Incapacità di Gestire la Multicollinearità: Quando le caratteristiche sono altamente correlate, LassoCV potrebbe avere problemi di multicollinearità.
LassoCV è utile nei compiti di regressione in cui è importante selezionare le caratteristiche più importanti e ridurre la dimensionalità del modello mantenendo l'interpretabilità e prevenendo l'overfitting.
2.1.9.1. Codice per creare il modello LassoCV ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LassoCV, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LassoCV.py
# Il codice dimostra il processo di addestramento del modello LassoCV, l'esportazione in formato ONNX (sia float che double) e l'esecuzione di previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"
# creare un modello LassoCV Regressor
lassocv_regressor_model = LassoCV()
# Adattare il modello ai dati
lassocv_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lassocv_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello LassoCV, l'esportazione in formato ONNX (sia float che double) e l'esecuzione di previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"
# creare un modello LassoCV Regressor
lassocv_regressor_model = LassoCV()
# Adattare il modello ai dati
lassocv_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lassocv_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LassoCV Original model (double) Python R-squared (Coefficient of determination): 0.9962241428413416 Python Mean Absolute Error: 6.33567334453819 Python Mean Squared Error: 49.96500551028169 Python Python LassoCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.996224142876629 Python Mean Absolute Error: 6.335673221332177 Python Mean Squared Error: 49.96500504333324 Python R^2 matching decimal places: 10 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 6 Python float ONNX model precision: 6 Python Python LassoCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962241428413416 Python Mean Absolute Error: 6.33567334453819 Python Mean Squared Error: 49.96500551028169 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
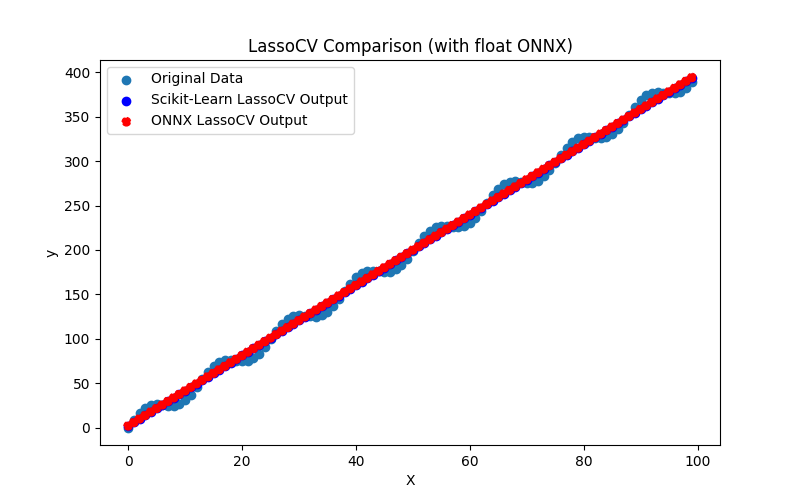
Fig.33. Risultati di LassoCV.py (float ONNX)
2.1.9.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati lasso_cv_float.onnx e lasso_cv_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LassoCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoCV" #define ONNXFilenameFloat "lasso_cv_float.onnx" #define ONNXFilenameDouble "lasso_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
2023.10.26 22:14:00.736 LassoCV (EURUSD,H1) Testing ONNX float: LassoCV (lasso_cv_float.onnx) 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962241428766290 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3356732213321800 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: Mean Squared Error: 49.9650050433332211 2023.10.26 22:14:00.748 LassoCV (EURUSD,H1) 2023.10.26 22:14:00.748 LassoCV (EURUSD,H1) Testing ONNX double: LassoCV (lasso_cv_double.onnx) 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962241428413416 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3356733445381899 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: Mean Squared Error: 49.9650055102816992
Confronto con il modello double originale in Python:
Testing ONNX float: LassoCV (lasso_cv_float.onnx) Python Mean Absolute Error: 6.33567334453819 MQL5: Mean Absolute Error: 6.3356732213321800 Testing ONNX double: LassoCV (lasso_cv_double.onnx) Python Mean Absolute Error: 6.33567334453819 MQL5: Mean Absolute Error: 6.3356733445381899
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.9.3. Rappresentazione ONNX di lasso_cv_float.onnx e lasso_cv_double.onnx
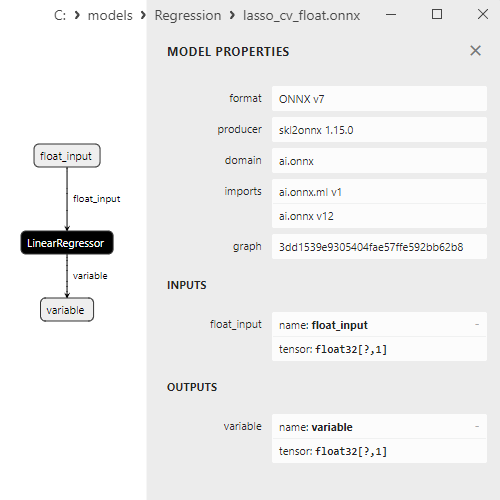
Fig.34. Rappresentazione ONNX di lasso_cv_float.onnx in Netron
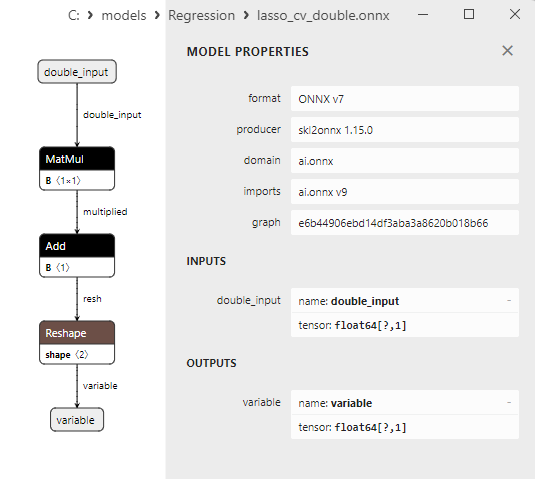
Fig.35. Rappresentazione ONNX di lasso_cv_double.onnx in Netron
2.1.10. sklearn.linear_model.LassoLars
LassoLars è una combinazione di due metodi: Lasso (Least Absolute Shrinkage and Selection Operator) e LARS (Least Angle Regression).
Questo metodo viene utilizzato per compiti di regressione e combina i vantaggi di entrambi gli algoritmi, consentendo la selezione simultanea delle caratteristiche e la riduzione della dimensionalità del modello.
Principio di Funzionamento di LassoLars:
- Dati di input: Si parte dal set di dati originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Inizializzazione: LassoLars inizia con un modello nullo, cioè senza caratteristiche attive. Tutti i coefficienti sono impostati a zero.
- Selezione Graduale delle Caratteristiche: Simile al metodo LARS, LassoLars seleziona, ad ogni passaggio, la caratteristica più correlata con i residui del modello e la aggiunge al modello. Quindi, il coefficiente di questa caratteristica viene regolato con il metodo dei minimi quadrati.
- Applicazione della Regolarizzazione L1: Contemporaneamente alla selezione graduale delle caratteristiche, LassoLars applica la regolarizzazione L1, aggiungendo una penalità per la somma dei valori assoluti dei coefficienti. Ciò consente di modellare relazioni complesse e di scegliere le caratteristiche più importanti.
- Effettuare Previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di LassoLars:
- Selezione delle Caratteristiche: LassoLars seleziona automaticamente le caratteristiche più importanti e riduce la dimensionalità del modello, aiutando ad evitare l'overfitting e semplificando l'interpretazione.
- Interpretabilità: Il metodo mantiene l'interpretabilità del modello, rendendo facile determinare quali caratteristiche sono incluse e come influenzano la variabile target.
- Regolarizzazione: LassoLars applica la regolarizzazione L1, evitando l'overfitting e migliorando la generalizzazione del modello.
Limitazioni di LassoLars:
- Modello Lineare: LassoLars costruisce un modello lineare, che potrebbe essere insufficiente per modellare relazioni non lineari complesse.
- Sensibilità al Rumore: Il metodo potrebbe essere sensibile ai valori anomali dei dati.
- Complessità Computazionale: La selezione delle caratteristiche in ogni fase e l'applicazione della regolarizzazione potrebbero richiedere maggiori risorse computazionali rispetto alla semplice regressione lineare.
LassoLars è utile nei compiti di regressione in cui è importante scegliere le caratteristiche più importanti, ridurre la dimensionalità del modello e mantenere l'interpretabilità.
2.1.10.1. Codice per la creazione del modello LassoLars ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LassoLars, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LassoLars.py
# Il codice dimostra il processo di addestramento del modello LassoLars, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"
# creare un modello LassoLars Regressor
lassolars_regressor_model = LassoLars(alpha=0.1)
# Adattare il modello ai dati
lassolars_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lassolars_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la retta di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello LassoLars, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"
# creare un modello LassoLars Regressor
lassolars_regressor_model = LassoLars(alpha=0.1)
# Adattare il modello ai dati
lassolars_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lassolars_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la retta di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LassoLars Original model (double) Python R-squared (Coefficient of determination): 0.9962382633544077 Python Mean Absolute Error: 6.3476035128950805 Python Mean Squared Error: 49.778152172481896 Python Python LassoLars ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382635045889 Python Mean Absolute Error: 6.3476034814795375 Python Mean Squared Error: 49.77815018516975 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLars ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382633544077 Python Mean Absolute Error: 6.3476035128950805 Python Mean Squared Error: 49.778152172481896 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
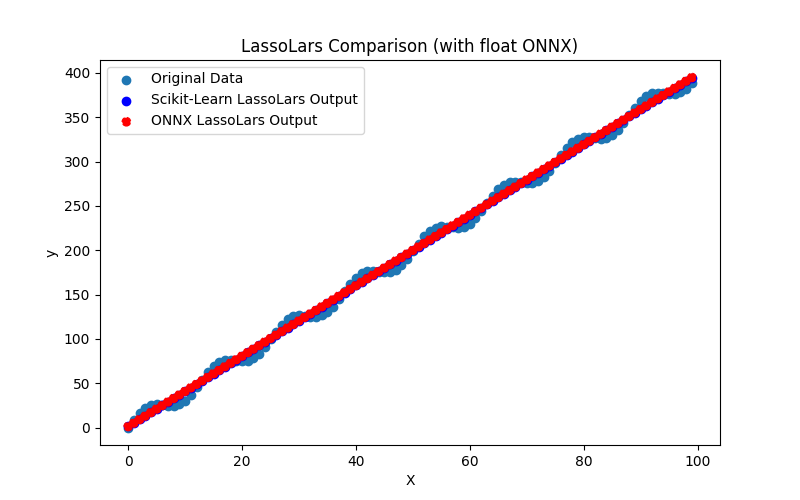
Fig.36. Risultato di LassoLars.py (float)
2.1.10.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i file salvati lasso_lars_float.onnx e lasso_lars_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LassoLars.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLars" #define ONNXFilenameFloat "lasso_lars_float.onnx" #define ONNXFilenameDouble "lasso_lars_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
LassoLars (EURUSD,H1) Testing ONNX float: LassoLars (lasso_lars_float.onnx) LassoLars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382635045889 LassoLars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476034814795375 LassoLars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781501851697357 LassoLars (EURUSD,H1) LassoLars (EURUSD,H1) Testing ONNX double: LassoLars (lasso_lars_double.onnx) LassoLars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382633544077 LassoLars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476035128950858 LassoLars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781521724819029
Confronto con il modello double originale in Python:
Testing ONNX float: LassoLars (lasso_lars_float.onnx) Python Mean Absolute Error: 6.3476035128950805 MQL5: Mean Absolute Error: 6.3476034814795375 Testing ONNX double: LassoLars (lasso_lars_double.onnx) Python Mean Absolute Error: 6.3476035128950805 MQL5: Mean Absolute Error: 6.3476035128950858
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.10.3. Rappresentazione ONNX di lasso_lars_float.onnx e lasso_lars_double.onnx
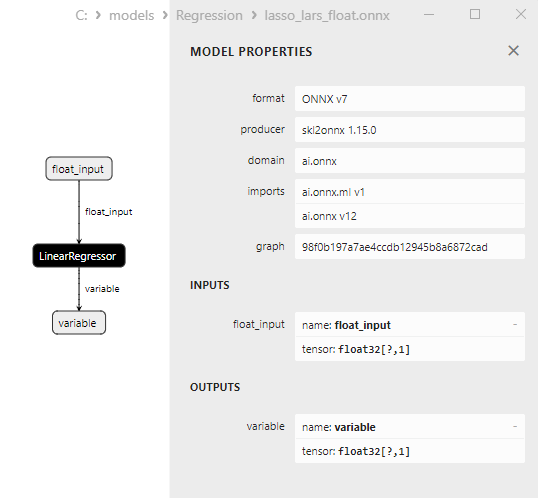
Fig.37. Rappresentazione ONNX di lasso_lars_float.onnx in Netron
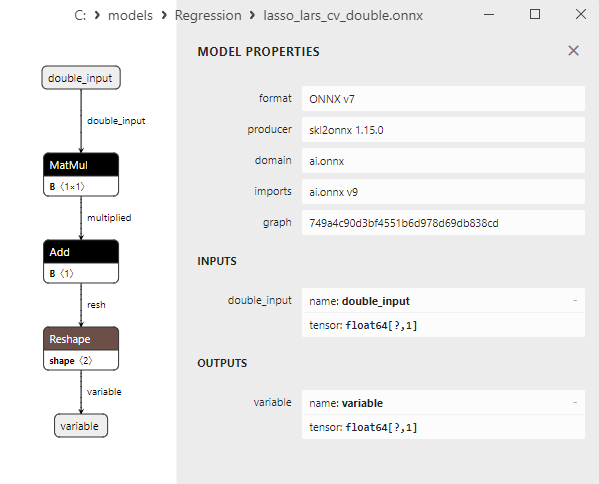
Fig.38. Rappresentazione ONNX di lasso_lars_double.onnx in Netron
2.1.11. sklearn.linear_model.LassoLarsCV
LassoLarsCV è un metodo che combina Lasso (Least Absolute Shrinkage and Selection Operator) e LARS (Least Angle Regression) con la selezione automatica dell'iperparametro di regolarizzazione ottimale (alfa) mediante convalida incrociata.
Questo metodo combina i vantaggi di entrambi gli algoritmi e consente di determinare il valore alfa ottimale per il modello, considerando la selezione delle caratteristiche e la regolarizzazione.
Principio di Funzionamento di LassoLarsCV:
- Dati di input: Si parte dal set di dati originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Inizializzazione: LassoLarsCV inizia con un modello nullo, in cui tutti i coefficienti sono impostati a zero.
- Definizione dell’Intervallo Alfa: Viene determinato un intervallo di valori per l'iperparametro alfa, che verrà considerato durante il processo di selezione. Di solito si utilizza una scala logaritmica dei valori alfa.
- Convalida Incrociata: Per ogni valore alfa dell'intervallo scelto, LassoLarsCV esegue una convalida incrociata per valutare le prestazioni del modello con questo valore alfa. In genere si utilizzano metriche come l'errore quadratico medio (MSE) o il coefficiente di determinazione (R^2).
- Selezione dell'Alfa Ottimale: LassoLarsCV sceglie il valore alfa in cui il modello ottiene le migliori prestazioni in base ai risultati della convalida incrociata.
- Addestramento dei Modelli: Il modello LassoLars viene addestrato utilizzando il valore alfa selezionato, escludendo le caratteristiche meno importanti e applicando la regolarizzazione L1.
- Effettuare Previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di LassoLarsCV:
- Selezione Automatica dell'Alfa: LassoLarsCV seleziona automaticamente l'iperparametro alfa ottimale utilizzando la convalida incrociata, semplificando la messa a punto del modello.
- Selezione delle Caratteristiche: LassoLarsCV sceglie automaticamente le caratteristiche più importanti e riduce la dimensionalità del modello.
- Regolarizzazione: Il metodo applica la regolarizzazione L1, evitando l'overfitting e migliorando la generalizzazione del modello.
Limitazioni di LassoLarsCV:
- Modello Lineare: LassoLarsCV costruisce un modello lineare, che potrebbe essere insufficiente per modellare relazioni non lineari complesse.
- Sensibilità al Rumore: Il metodo potrebbe essere sensibile ai valori anomali dei dati.
- Complessità Computazionale: La selezione delle caratteristiche in ogni fase e l'applicazione della regolarizzazione potrebbero richiedere maggiori risorse computazionali rispetto alla semplice regressione lineare.
LassoLarsCV è utile nei compiti di regressione in cui è essenziale scegliere le caratteristiche più importanti, ridurre la dimensionalità del modello, evitare l'overfitting e regolare automaticamente gli iperparametri del modello.
2.1.11.1. Codice per la creazione del modello LassoLarsCV ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LassoLarsCV, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LassoLarsCV.py
# Il codice dimostra il processo di addestramento del modello LassoLars, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"
# creare un modello LassoLarsCV Regressor
lassolars_cv_regressor_model = LassoLarsCV(cv=5)
# Adattare il modello ai dati
lassolars_cv_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lassolars_cv_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello LassoLars, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"
# creare un modello LassoLarsCV Regressor
lassolars_cv_regressor_model = LassoLarsCV(cv=5)
# Adattare il modello ai dati
lassolars_cv_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lassolars_cv_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LassoLarsCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python Python LassoLarsCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382640824089 Python Mean Absolute Error: 6.347737845846069 Python Mean Squared Error: 49.778142539016564 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLarsCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 14 Python double ONNX model precision: 16
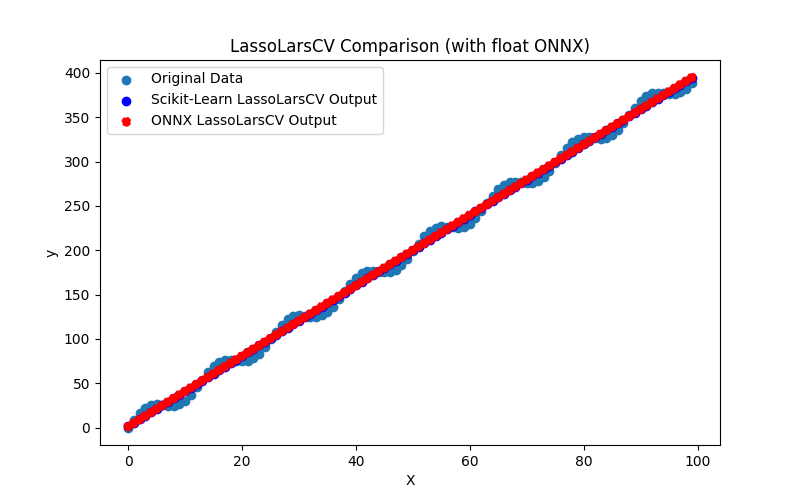
Fig.39. Risultati di LassoLarsCV.py (float ONNX)
2.1.11.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati lasso_lars_cv_float.onnx e lasso_lars_cv_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LassoLarsCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLarsCV" #define ONNXFilenameFloat "lasso_lars_cv_float.onnx" #define ONNXFilenameDouble "lasso_lars_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
LassoLarsCV (EURUSD,H1) Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx) LassoLarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382640824089 LassoLarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477378458460691 LassoLarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781425390165566 LassoLarsCV (EURUSD,H1) LassoLarsCV (EURUSD,H1) Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx) LassoLarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642612767 LassoLarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 LassoLarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401721031642
Confronto con il modello double originale in Python:
Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477378458460691 Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477379221400145
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 16 cifre decimali.
2.1.11.3. Rappresentazione ONNX di lasso_lars_cv_float.onnx e lasso_lars_cv_double.onnx
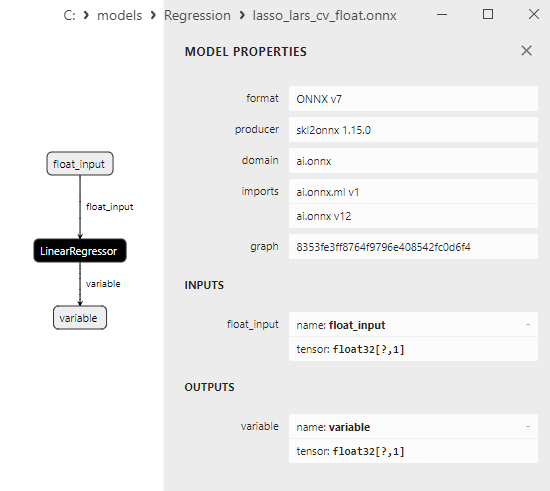
Fig.40. Rappresentazione ONNX di lasso_lars_cv_float.onnx in Netron
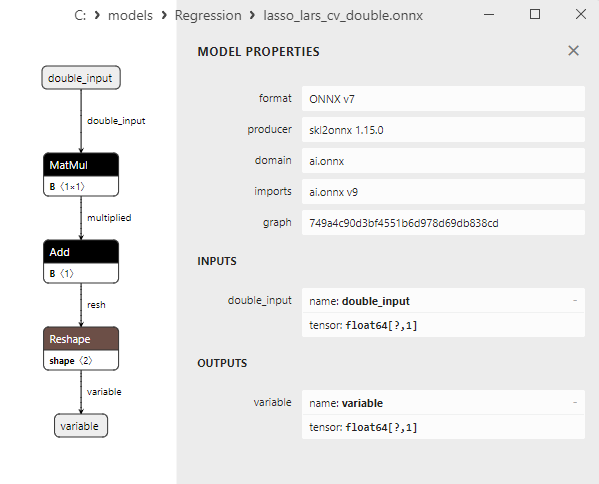
Fig.41. Rappresentazione ONNX di lasso_lars_cv_double.onnx in Netron
2.1.12. sklearn.linear_model.LassoLarsIC
LassoLarsIC è un metodo di regressione che combina Lasso (Least Absolute Shrinkage and Selection Operator) e Information Criterion (IC) per selezionare automaticamente l'insieme ottimale di caratteristiche.
Utilizza criteri informativi come AIC (Akaike Information Criterion) e BIC (Bayesian Information Criterion) per determinare quali caratteristiche includere nel modello e applica la regolarizzazione L1 per stimare i coefficienti del modello.
Principio di Funzionamento di LassoLarsIC:
- Dati di input: Si parte dal set di dati originale, che comprende le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Inizializzazione: LassoLarsIC inizia con un modello nullo, cioè senza caratteristiche attive. Tutti i coefficienti sono impostati a zero.
- Selezione delle Caratteristiche mediante Information Criterion: Il metodo valuta il criterio di informazione (ad esempio, AIC o BIC) per diversi set di caratteristiche, partendo da un modello vuoto e incorporando gradualmente le caratteristiche nel modello. Il criterio di informazione valuta la qualità del modello, considerando il compromesso tra adattamento ai dati e complessità del modello.
- Selezione dell'Insieme Ottimale di Caratteristiche: LassoLarsIC sceglie l'insieme di caratteristiche per il quale il criterio di informazione ottiene il valore migliore. Questo insieme di caratteristiche sarà incluso nel modello.
- Applicazione della Regolarizzazione L1: La regolarizzazione L1 viene applicata alle caratteristiche selezionate, aiutando nella stima dei coefficienti del modello.
- Effettuare Previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di LassoLarsIC:
- Selezione Automatica delle Caratteristiche: LassoLarsIC sceglie automaticamente il set di caratteristiche ottimale, riducendo la dimensionalità del modello ed evitando l'overfitting.
- Criteri di Informazione: L'uso di criteri informativi consente di bilanciare la qualità e la complessità del modello.
- Regolarizzazione: Il metodo applica la regolarizzazione L1, evitando l'overfitting e migliorando la generalizzazione del modello.
Limitazioni di LassoLarsIC:
- Modello Lineare: LassoLarsIC costruisce un modello lineare, che può essere insufficiente per modellare complesse relazioni non lineari.
- Sensibilità al Rumore: Il metodo potrebbe essere sensibile ai valori anomali dei dati.
- Complessità Computazionale: La valutazione dei criteri informativi per diversi set di caratteristiche potrebbe richiedere ulteriori risorse computazionali.
LassoLarsIC è utile nei compiti di regressione in cui è fondamentale selezionare automaticamente il miglior set di caratteristiche e ridurre la dimensionalità del modello in base a criteri informativi.
2.1.12.1. Codice per creare il modello LassoLarsIC ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LassoLarsIC, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LassoLarsIC.py
# Il codice dimostra il processo di addestramento del modello LassoLarsIC, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"
# creare un modello LassoLarsIC Regressor
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')
# Adattare il modello ai dati
lasso_lars_ic_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lasso_lars_ic_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello LassoLarsIC, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"
# creare un modello LassoLarsIC Regressor
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')
# Adattare il modello ai dati
lasso_lars_ic_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = lasso_lars_ic_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LassoLarsIC Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python Python LassoLarsIC ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLarsIC ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 15 Python double ONNX model precision: 15
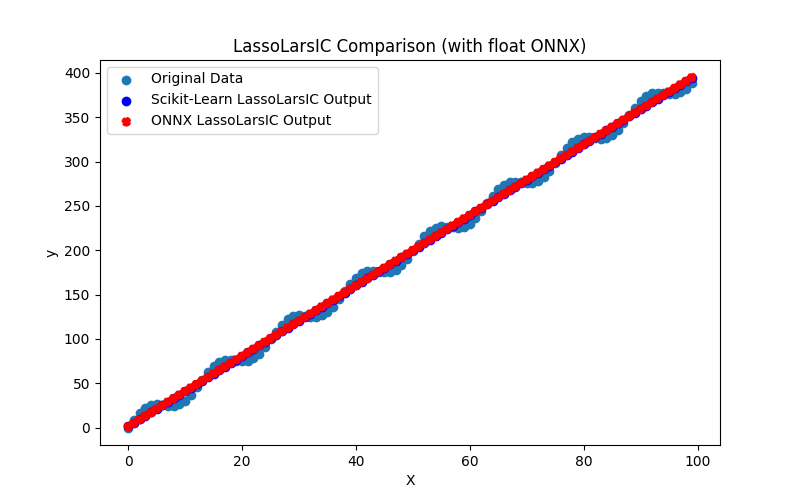
Fig.42. Risultati di LassoLarsIC.py (float ONNX)
2.1.12.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati lasso_lars_ic_float.onnx e lasso_lars_ic_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LassoLarsIC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLarsIC" #define ONNXFilenameFloat "lasso_lars_ic_float.onnx" #define ONNXFilenameDouble "lasso_lars_ic_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
LassoLarsIC (EURUSD,H1) Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx) LassoLarsIC (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 LassoLarsIC (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 LassoLarsIC (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 LassoLarsIC (EURUSD,H1) LassoLarsIC (EURUSD,H1) Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx) LassoLarsIC (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 LassoLarsIC (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364302 LassoLarsIC (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477379263364302
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.12.3. Rappresentazione ONNX di lasso_lars_ic_float.onnx e lasso_lars_ic_double.onnx
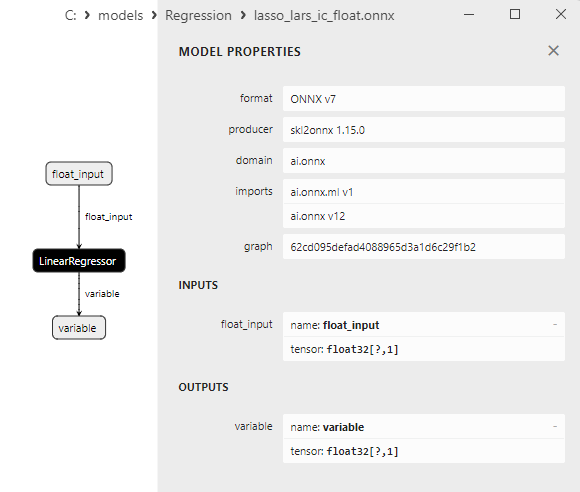
Fig.43. Rappresentazione ONNX di lasso_lars_ic_float.onnx in Netron
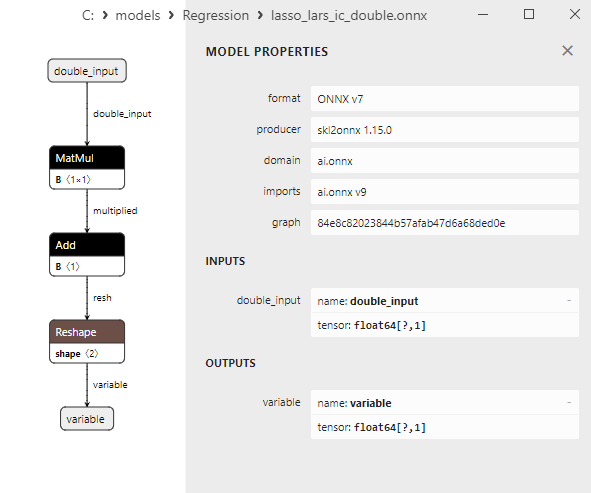
Fig.44. Rappresentazione ONNX di lasso_lars_ic_double.onnx in Netron
2.1.13. sklearn.linear_model.LinearRegression
LinearRegression è uno dei metodi più semplici e più utilizzati nell'apprendimento automatico per i compiti di regressione.
Viene utilizzato per costruire modelli lineari che prevedono valori numerici (continua) della variabile target sulla base di una combinazione lineare di caratteristiche di input.
Principio di Funzionamento di LinearRegression:
- Modello Lineare: Il modello LinearRegression presuppone l'esistenza di una relazione lineare tra le variabili indipendenti (caratteristiche) e la variabile target. Questa relazione può essere espressa dall'equazione di regressione lineare: y = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ, dove y è la variabile target, β₀ - è il coefficiente di intercetta, β₁, β₂, ... βₚ - sono i coefficienti delle caratteristiche, x₁, x₂, ... xₚ sono i valori delle caratteristiche.
- Stima dei Parametri: L'obiettivo di LinearRegression è stimare i coefficienti β₀, β₁, β₂, ... βₚ, che meglio si adattano ai dati. Questo si ottiene in genere con il metodo dei Minimi Quadrati Ordinari (Ordinary Least Squares OLS), minimizzando la somma delle differenze al quadrato tra i valori effettivi e quelli previsti.
- Valutazione del Modello: Per valutare la qualità del modello LinearRegression vengono utilizzate diverse metriche, come l'Errore Quadratico Medio (Mean Squared Error MSE), il Coefficiente di Determinazione (R²) e altre ancora.
Vantaggi di LinearRegression:
- Semplicità e Interpretabilità: LinearRegression è un metodo semplice e di facile interpretazione, che consente di analizzare l'influenza di ogni caratteristica sulla variabile target.
- Alta Velocità di Addestramento e Previsione: Il modello di regressione lineare ha un'elevata velocità di addestramento e di previsione, che lo rende una buona scelta per i grandi set di dati.
- Applicabilità: LinearRegression può essere applicata con successo a diversi compiti di regressione.
Limiti di LinearRegression:
- Linearità: Questo metodo presuppone la linearità della relazione tra le caratteristiche e la variabile target, che potrebbe essere insufficiente per modellare complesse dipendenze non lineari.
- Sensibilità ai Valori Anomali: LinearRegression è sensibile ai valori anomali nei dati, che possono influire sulla qualità del modello.
LinearRegression è un metodo di regressione semplice e ampiamente utilizzato che costruisce un modello lineare per prevedere i valori numerici della variabile target in base a una combinazione lineare di caratteristiche di input. È adatto a problemi con una relazione lineare e quando l'interpretabilità del modello è importante.
2.1.13.1. Codice per creare il modello LinearRegression ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LinearRegression, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LinearRegression.py
# Il codice dimostra il processo di addestramento del modello LinearRegression, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"
# creare un modello Linear Regression
linear_model = LinearRegression()
# Adattare il modello ai dati
linear_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = linear_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello LinearRegression, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"
# creare un modello Linear Regression
linear_model = LinearRegression()
# Adattare il modello ai dati
linear_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = linear_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LinearRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python Python LinearRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LinearRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
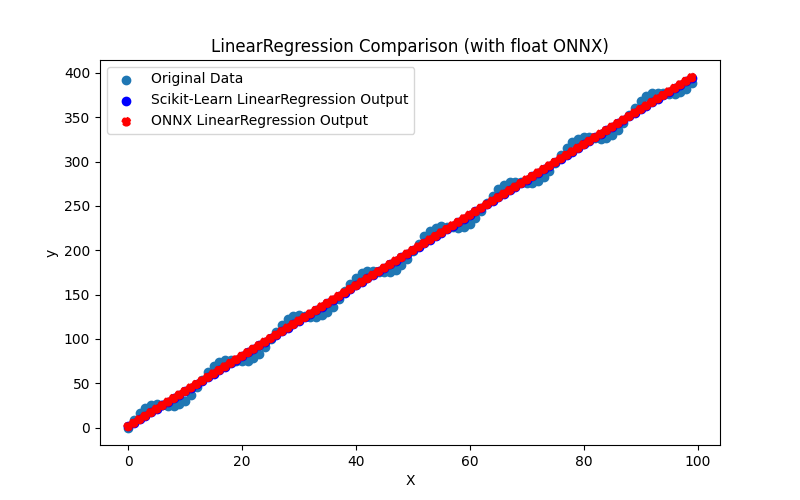
Fig.45.Risultati di LinearRegression.py (float ONNX)
2.1.13.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i file salvati linear_regression_float.onnx e linear_regression_double.onnx, dimostrando l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LinearRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LinearRegression" #define ONNXFilenameFloat "linear_regression_float.onnx" #define ONNXFilenameDouble "linear_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
LinearRegression (EURUSD,H1) Testing ONNX float: LinearRegression (linear_regression_float.onnx) LinearRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 LinearRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 LinearRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 LinearRegression (EURUSD,H1) LinearRegression (EURUSD,H1) Testing ONNX double: LinearRegression (linear_regression_double.onnx) LinearRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 LinearRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364266 LinearRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: LinearRegression (linear_regression_float.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: LinearRegression (linear_regression_double.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477379263364266
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.13.3. Rappresentazione ONNX di linear_regression_float.onnx e linear_regression_double.onnx
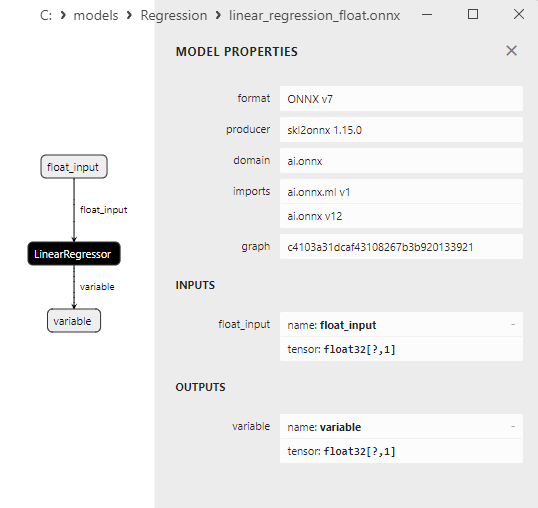
Fig.46. Rappresentazione ONNX di linear_regression_float.onnx in Netron
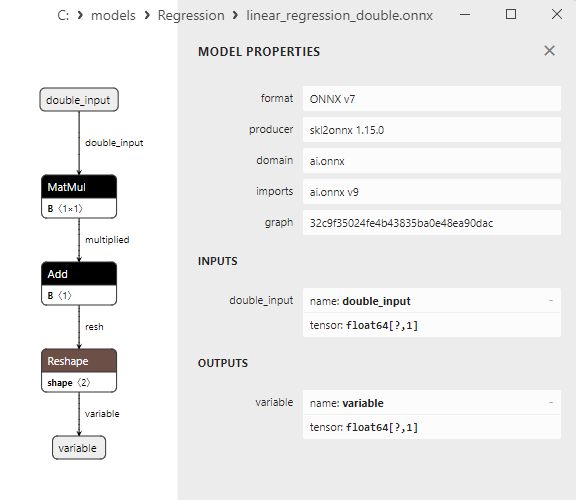
Fig.47. Rappresentazione ONNX di linear_regression_double.onnx in Netron
Nota sui Metodi Ridge e RidgeCV
Ridge e RidgeCV sono due metodi correlati nell'apprendimento automatico utilizzati per la regolarizzazione nella regressione Ridge. Condividono funzionalità simili, ma si differenziano per l'uso e la regolazione dei parametri.
Principio di Funzionamento di Ridge (Ridge Regression):
- Ridge è un metodo di regressione che prevede la regolarizzazione L2. Significa che aggiunge la somma dei coefficienti al quadrato (norma L2) alla funzione di perdita minimizzata dal modello. Questo termine di regolarizzazione aggiuntivo aiuta a ridurre l'entità dei coefficienti del modello, evitando così l'overfitting.
- Uso del parametro alfa: Nel metodo Ridge, il parametro alfa (noto anche come forza di regolarizzazione) è preimpostato e non viene modificato automaticamente. Gli utenti devono selezionare un valore alfa adeguato in base alla loro conoscenza dei dati e degli esperimenti.
Principio di Funzionamento di RidgeCV (Ridge Cross-Validation):
- RidgeCV è un'estensione del metodo Ridge, che prevede la selezione automatica del valore ottimale per il parametro alfa utilizzando la convalida incrociata. Invece di impostare manualmente alfa, RidgeCV itera tra diversi valori alfa e sceglie quello che fornisce le migliori prestazioni nella convalida incrociata.
- Vantaggi della regolazione automatica: Il vantaggio principale di RidgeCV è la determinazione automatica del valore alfa ottimale, senza bisogno di regolazioni manuali. Ciò rende più comodo il processo di regolazione e previene potenziali errori nella selezione di alfa.
La differenza principale tra Ridge e RidgeCV è che Ridge richiede agli utenti di specificare esplicitamente il valore del parametro alfa, mentre RidgeCV trova automaticamente il valore alfa ottimale utilizzando la convalida incrociata. RidgeCV è in genere una scelta preferibile quando si ha a che fare con una grande quantità di dati e si vuole evitare la regolazione manuale dei parametri.
2.1.14. sklearn.linear_model.Ridge
Ridge è un metodo di regressione utilizzato nell'apprendimento automatico per risolvere problemi di regressione. Fa parte della famiglia dei modelli lineari e rappresenta una regressione lineare regolarizzata.
La caratteristica principale della regressione Ridge è l'aggiunta della regolarizzazione L2 al metodo dei minimi quadrati ordinari (OLS) standard.
Come funziona la regressione Ridge:
- Regressione lineare: Simile alla regressione lineare normale, la regressione Ridge mira a trovare una relazione lineare tra le variabili indipendenti (caratteristiche) e la variabile target.
- Regolarizzazione L2: La distinzione principale della regressione Ridge è l'aggiunta della regolarizzazione L2 alla funzione di perdita. Ciò significa che alla somma delle differenze al quadrato tra i valori effettivi e quelli previsti viene aggiunta una penalizzazione per i grandi valori dei coefficienti di regressione.
- Coefficienti di penalizzazione: La regolarizzazione L2 impone una penalizzazione sui valori dei coefficienti di regressione. Di conseguenza, alcuni coefficienti tendono ad avvicinarsi a zero, riducendo l'overfitting e migliorando la stabilità del modello.
- Iperparametro α: Uno dei parametri essenziali della regressione Ridge è l'iperparametro α (alfa), che determina il grado di regolarizzazione. Valori α più alti portano a una regolarizzazione più forte, con conseguenti modelli più semplici e valori di coefficiente più bassi.
Vantaggi della regressione Ridge:
- Riduzione dell'overfitting: La regolarizzazione L2 in Ridge aiuta a ridurre l'overfitting, rendendo il modello più robusto contro il rumore dei dati.
- Gestione della multicollinearità: La regressione Ridge è in grado di gestire bene i problemi di multicollinearità, in particolare quando le caratteristiche sono altamente correlate.
- Affrontare la maledizione della dimensionalità: Ridge è utile in scenari con molte caratteristiche, in cui OLS potrebbe essere instabile.
Limiti della regressione Ridge:
- Non elimina le caratteristiche: La regressione Ridge non azzera i coefficienti delle caratteristiche, ma si limita a ridurli, il che significa che alcune caratteristiche potrebbero ancora rimanere nel modello.
- Scelta dell'α ottimale: La selezione del valore corretto dell'iperparametro α può richiedere una convalida incrociata.
La regressione Ridge è un metodo di regressione che introduce la regolarizzazione L2 alla regressione lineare standard per ridurre l'overfitting, migliorare la stabilità e risolvere i problemi di multicollinearità. Questo metodo è utile quando è necessario bilanciare precisione e stabilità del modello.
2.1.14.1. Codice per creare il modello Ridge ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.Ridge, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza sia del modello originale che dei modelli esportati in ONNX.
# Ridge.py
# Il codice dimostra il processo di addestramento del modello Ridge, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Ridge"
onnx_model_filename = data_path + "ridge"
# creare un modello Ridge
regression_model = Ridge()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello Ridge, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Ridge"
onnx_model_filename = data_path + "ridge"
# creare un modello Ridge
regression_model = Ridge()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python Ridge Original model (double) Python R-squared (Coefficient of determination): 0.9962382641178552 Python Mean Absolute Error: 6.347684462929819 Python Mean Squared Error: 49.77814206996523 Python Python Ridge ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382634837793 Python Mean Absolute Error: 6.347684915729416 Python Mean Squared Error: 49.77815046053819 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python Ridge ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641178552 Python Mean Absolute Error: 6.347684462929819 Python Mean Squared Error: 49.77814206996523 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
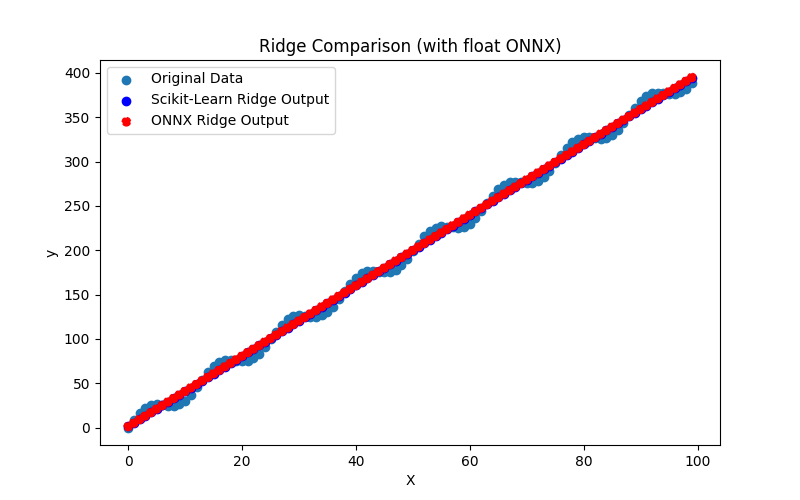
Fig.49. Risultati di Ridge.py (float ONNX)
2.1.14.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvatiridge_float.onnx e ridge_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| Ridge.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Ridge" #define ONNXFilenameFloat "ridge_float.onnx" #define ONNXFilenameDouble "ridge_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
Ridge (EURUSD,H1) Testing ONNX float: Ridge (ridge_float.onnx) Ridge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382634837793 Ridge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476849157294160 Ridge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781504605381784 Ridge (EURUSD,H1) Ridge (EURUSD,H1) Testing ONNX double: Ridge (ridge_double.onnx) Ridge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641178552 Ridge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476844629298235 Ridge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781420699652131
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: Ridge (ridge_float.onnx) Python Mean Absolute Error: 6.347684462929819 MQL5: Mean Absolute Error: 6.3476849157294160 Testing ONNX double: Ridge (ridge_double.onnx) Python Mean Absolute Error: 6.347684462929819 MQL5: Mean Absolute Error: 6.3476844629298235
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.14.3. Rappresentazione ONNX di ridge_float.onnx e ridge_double.onnx
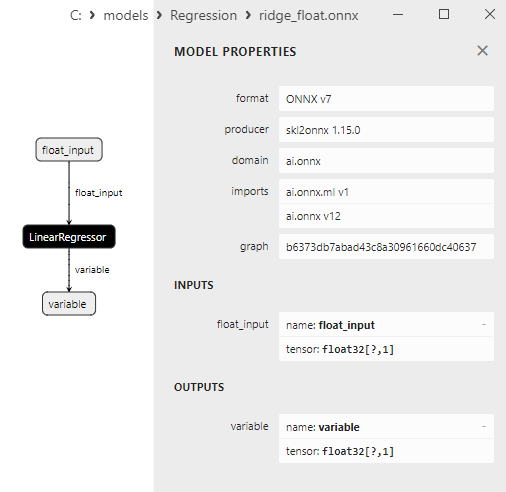
Fig.50. Rappresentazione ONNX di ridge_float.onnx in Netron
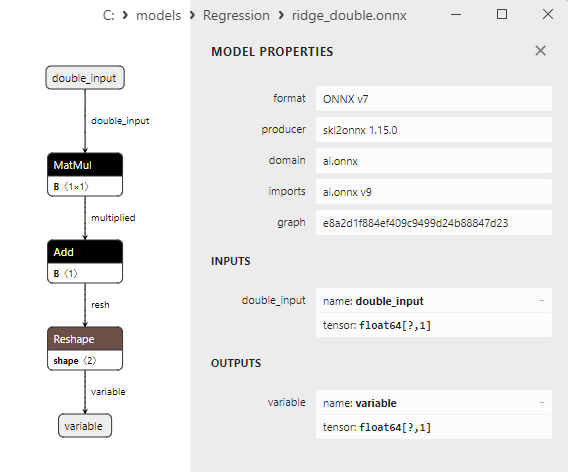
Fig.51. Rappresentazione ONNX di ridge_double.onnx in Netron
2.1.15. sklearn.linear_model.RidgeCV
RidgeCV - è un'estensione della regressione Ridge che include la selezione automatica del miglior iperparametro α (alfa), che determina il grado di regolarizzazione nella regressione Ridge. L'iperparametro α controlla l'equilibrio tra la minimizzazione della somma degli errori al quadrato (come nella regressione lineare ordinaria) e la minimizzazione del valore dei coefficienti di regressione (regolarizzazione). RidgeCV seleziona automaticamente il valore ottimale di α in base ai parametri e ai criteri specificati.
Come funziona RidgeCV:
- Dati di input: RidgeCV prende in input dati costituiti da caratteristiche (variabili indipendenti) e dalla variabile target (continua).
- Scelta di α: La regressione Ridge richiede la selezione dell'iperparametro α, che determina il grado di regolarizzazione. RidgeCV seleziona automaticamente il valore ottimale di α dall'intervallo indicato.
- Convalida incrociata: RidgeCV utilizza la convalida incrociata, come la convalida incrociata k-fold, per valutare quale valore di α fornisce la migliore generalizzazione del modello su dati indipendenti.
- α ottimale: Al termine del processo di addestramento, RidgeCV sceglie il valore α che offre le migliori prestazioni nella convalida incrociata e lo utilizza per addestrare il modello finale di regressione Ridge.
Vantaggi di RidgeCV:
- Selezione automatica di α: RidgeCV consente di selezionare automaticamente il valore ottimale dell'iperparametro α, semplificando il processo di regolazione del modello.
- Equilibrio tra regolarizzazione e prestazioni: Questo metodo aiuta a trovare l'equilibrio ottimale tra regolarizzazione (riduzione dell'overfitting) e prestazioni del modello.
Limitazioni di RidgeCV:
- Complessità computazionale: La convalida incrociata può richiedere notevoli risorse computazionali, soprattutto quando si utilizza un'ampia gamma di valori α.
RidgeCV è un metodo di regressione Ridge con selezione automatica dell'iperparametro ottimale α mediante convalida incrociata. Questo metodo semplifica il processo di selezione degli iperparametri e consente di trovare il miglior equilibrio tra regolarizzazione e prestazioni del modello.
2.1.15.1. Codice per la creazione del modello RidgeCV ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.RidgeCV, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# RidgeCV.py
# Il codice dimostra il processo di addestramento del modello RidgeCV, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"
# creare un modello RidgeCV
regression_model = RidgeCV()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello RidgeCV, l'esportazione in formato ONNX (sia float che double) ed effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"
# creare un modello RidgeCV
regression_model = RidgeCV()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python RidgeCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382499160807 Python Mean Absolute Error: 6.34720334999352 Python Mean Squared Error: 49.77832999861571 Python Python RidgeCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382499108485 Python Mean Absolute Error: 6.3472036427935485 Python Mean Squared Error: 49.77833006785168 Python R^2 matching decimal places: 11 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python RidgeCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382499160807 Python Mean Absolute Error: 6.34720334999352 Python Mean Squared Error: 49.77832999861571 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
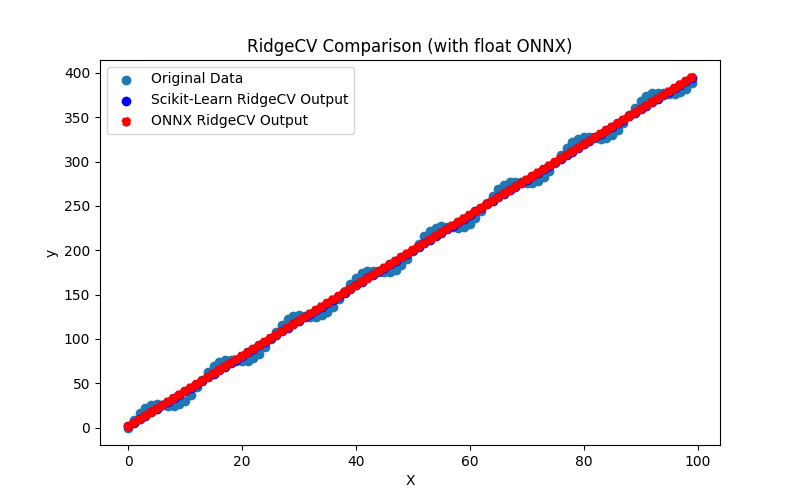
Fig.52. Risultati di RidgeCV.py (float ONNX)
2.1.15.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati ridge_cv_float.onnx e ridge_cv_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| RidgeCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RidgeCV" #define ONNXFilenameFloat "ridge_cv_float.onnx" #define ONNXFilenameDouble "ridge_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
RidgeCV (EURUSD,H1) Testing ONNX float: RidgeCV (ridge_cv_float.onnx) RidgeCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382499108485 RidgeCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3472036427935485 RidgeCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7783300678516909 RidgeCV (EURUSD,H1) RidgeCV (EURUSD,H1) Testing ONNX double: RidgeCV (ridge_cv_double.onnx) RidgeCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382499160807 RidgeCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3472033499935216 RidgeCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7783299986157246
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: RidgeCV (ridge_cv_float.onnx) Python Mean Absolute Error: 6.34720334999352 MQL5: Mean Absolute Error: 6.3472036427935485 Testing ONNX double: RidgeCV (ridge_cv_double.onnx) Python Mean Absolute Error: 6.34720334999352 MQL5: Mean Absolute Error: 6.3472033499935216
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.15.3. Rappresentazione ONNX di ridge_cv_float.onnx e ridge_cv_double.onnx
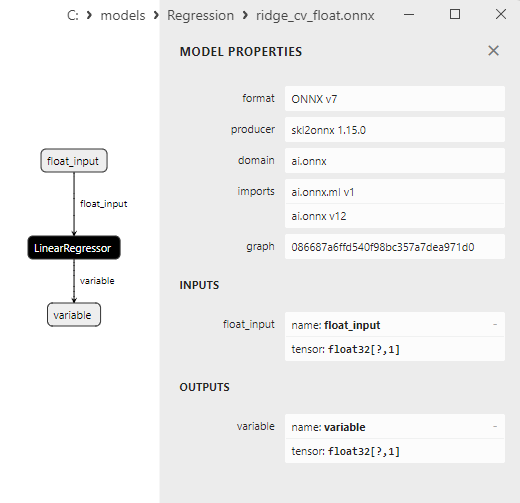
Fig.53. Rappresentazione ONNX di ridge_cv_float.onnx in Netron
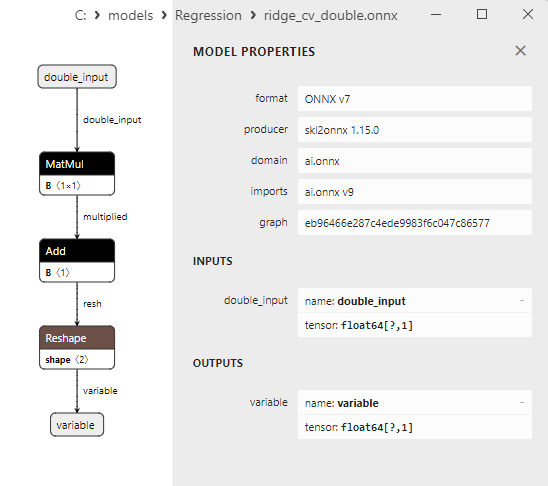
Fig.54. Rappresentazione ONNX di ridge_cv_double.onnx in Netron
2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
OrthogonalMatchingPursuit (OMP) è un algoritmo utilizzato per risolvere problemi di selezione delle caratteristiche e di regressione lineare.
È uno dei metodi per selezionare le caratteristiche più significative, che possono essere utili a ridurre la dimensionalità dei dati e migliorare la capacità di generalizzazione del modello.
Come funziona OrthogonalMatchingPursuit:
- Dati di input: Si parte da un set di dati contenente caratteristiche (variabili indipendenti) e valori della variabile target (continua).
- Selezione del numero di caratteristiche: Una delle fasi iniziali dell'utilizzo di OrthogonalMatchingPursuit consiste nel determinare il numero di caratteristiche da includere nel modello. Questo numero può essere predefinito o scelto con criteri quali Akaike Information Criterion (AIC) o il criterio dell'errore minimo.
- Aggiunta iterativa delle caratteristiche: L'algoritmo inizia con un modello vuoto e aggiunge iterativamente le caratteristiche che meglio spiegano i residui del modello. Ad ogni iterazione, viene scelta una nuova caratteristica ortogonale alle caratteristiche selezionate in precedenza. La caratteristica ottimale viene selezionata in base alla sua correlazione con i residui del modello.
- Addestramento del modello: Dopo aver aggiunto il numero specificato di caratteristiche, il modello viene addestrato sui dati considerando solo le caratteristiche selezionate.
- Effettuare previsioni: Dopo l'addestramento, il modello può prevedere i valori della variabile target su nuovi dati.
Vantaggi di OrthogonalMatchingPursuit:
- Riduzione della dimensionalità: OMP può ridurre la dimensionalità dei dati selezionando solo le caratteristiche più informative.
- Interpretabilità: Poiché OMP seleziona solo un numero ridotto di caratteristiche, i modelli creati con questo metodo possono essere più interpretabili.
Limitazioni di OrthogonalMatchingPursuit:
- Sensibilità al numero di caratteristiche selezionate: Il numero di caratteristiche selezionate deve essere regolato in modo appropriato e scelte errate possono portare ad un overfitting o ad un underfitting.
- Non considera la multicollinearità: L'OMP potrebbe non tenere conto della multicollinearità tra le caratteristiche, che potrebbe influire sulla selezione delle caratteristiche ottimali.
- Complessità computazionale: OMP è computazionalmente costoso, soprattutto per i grandi set di dati.
OrthogonalMatchingPursuit è un algoritmo per la selezione delle caratteristiche e la regressione lineare, che consente di selezionare le caratteristiche più informative per il modello. Questo metodo può essere utile per ridurre la dimensionalità dei dati e migliorare l'interpretabilità dei modelli.
2.1.16.1. Codice per creare il modello OrthogonalMatchingPursuit ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.OrthogonalMatchingPursuit, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# OrthogonalMatchingPursuit.py
# Il codice dimostra il processo di addestramento del modello OrthogonalMatchingPursuit, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"
# creare un modello OrthogonalMatchingPursuit
regression_model = OrthogonalMatchingPursuit()
# Adattare il modello ai dati
regression_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello OrthogonalMatchingPursuit, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"
# creare un modello OrthogonalMatchingPursuit
regression_model = OrthogonalMatchingPursuit()
# Adattare il modello ai dati
regression_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python OrthogonalMatchingPursuit Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281784 Python Python OrthogonalMatchingPursuit ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python OrthogonalMatchingPursuit ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
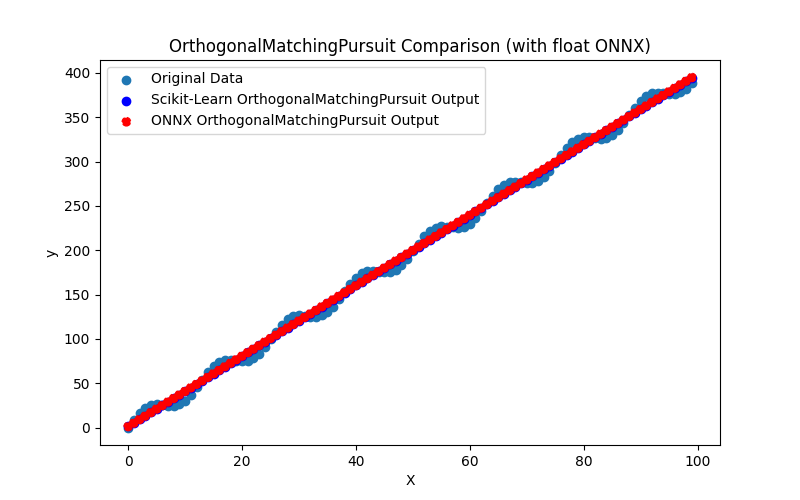
Fig.55. Risultati di OrthogonalMatchingPursuit.py (float ONNX)
2.1.16.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati orthogonal_matching_pursuit_float.onnx e orthogonal_matching_pursuit_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| OrthogonalMatchingPursuit.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "OrthogonalMatchingPursuit" #define ONNXFilenameFloat "orthogonal_matching_pursuit_float.onnx" #define ONNXFilenameDouble "orthogonal_matching_pursuit_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
OrthogonalMatchingPursuit (EURUSD,H1) Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx) OrthogonalMatchingPursuit (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 OrthogonalMatchingPursuit (EURUSD,H1) OrthogonalMatchingPursuit (EURUSD,H1) Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx) OrthogonalMatchingPursuit (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364275 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379263364275
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 16 cifre decimali.
2.1.16.3. Rappresentazione ONNX di orthogonal_matching_pursuit_float.onnx e orthogonal_matching_pursuit_double.onnx
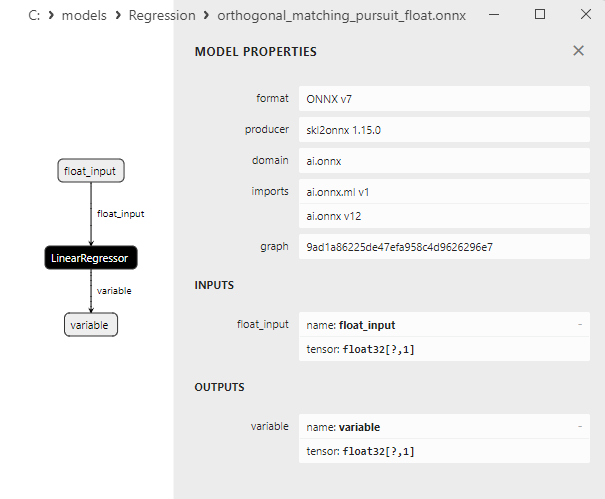
Fig.56. Rappresentazione ONNX del file orthogonal_matching_pursuit_float.onnx in Netron
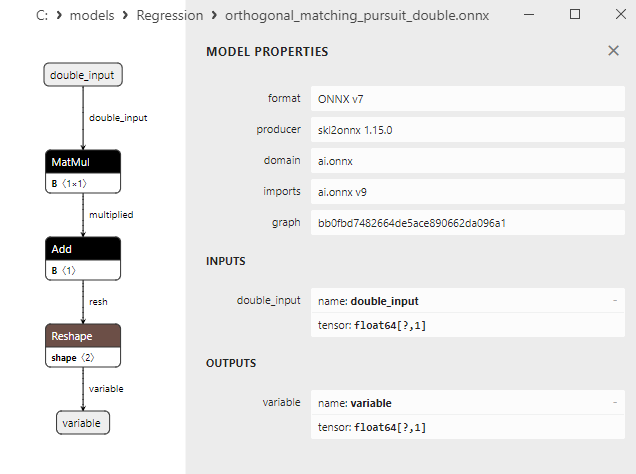
Fig.57. Rappresentazione ONNX di orthogonal_matching_pursuit_double.onnx in Netron
2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
PassiveAggressiveRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione.
Questo metodo è una variante dell'algoritmo Passive-Aggressive (PA) che può essere impiegato per addestrare un modello in grado di prevedere i valori continui della variabile target.
Come funziona PassiveAggressiveRegressor:
- Dati di input: Si parte da un set di dati che comprende le caratteristiche (variabili indipendenti) e i valori della variabile target (continua).
- Apprendimento supervisionato: PassiveAggressiveRegressor è un metodo di apprendimento supervisionato addestrato su coppie (X, y), dove X rappresenta le caratteristiche e y corrisponde ai valori delle variabili target.
- Apprendimento adattivo: L'idea principale dietro il metodo passivo-aggressivo è l'approccio di apprendimento adattivo. Il modello apprende minimizzando l'errore di previsione ad ogni esempio di addestramento. Si aggiorna correggendo i pesi per ridurre l'errore di previsione.
- Parametro C: PassiveAggressiveRegressor ha un iperparametro C, che controlla quanto fortemente il modello si adatta agli errori. Un valore C più alto significa aggiornamenti del peso più aggressivi, mentre un valore C più basso rende il modello meno aggressivo.
- Previsione: Una volta addestrato, il modello può prevedere i valori della variabile target per i nuovi dati.
Vantaggi di PassiveAggressiveRegressor:
- Adattabilità: Il metodo può adattarsi alle variazioni dei dati e aggiornare il modello per ridurre al minimo gli errori di previsione.
- Efficienza per grandi set di dati: PassiveAggressiveRegressor può essere un metodo efficace per la regressione, in particolare quando addestrato su volumi consistenti di dati.
Limitazioni di PassiveAggressiveRegressor:
- Sensibilità alla scelta del parametro C: La scelta del valore di C può richiedere una messa a punto e una sperimentazione.
- Potrebbero essere necessarie altre caratteristiche: In alcuni casi, per un buon addestramento del modello, potrebbero essere necessarie ulteriori caratteristiche ingegnerizzate.
PassiveAggressiveRegressor è un metodo di apprendimento automatico per compiti di regressione che apprende in modo adattivo minimizzando gli errori di previsione sui dati di addestramento. Questo metodo può essere utile per gestire grandi set di dati e richiede la regolazione del parametro C per ottenere prestazioni ottimali.
2.1.17.1. Codice per la creazione del modello PassiveAggressiveRegressor e per la sua esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.PassiveAggressiveRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# PassiveAggressiveRegressor.py
# Il codice dimostra il processo di addestramento del modello PassiveAggressiveRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni con i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"
# creare un modello PassiveAggressiveRegressor
regression_model = PassiveAggressiveRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello PassiveAggressiveRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni con i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"
# creare un modello PassiveAggressiveRegressor
regression_model = PassiveAggressiveRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python PassiveAggressiveRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9894376841493092 Python Mean Absolute Error: 9.64524669506544 Python Mean Squared Error: 139.76857373191007 Python Python PassiveAggressiveRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9894376801868329 Python Mean Absolute Error: 9.645248834431873 Python Mean Squared Error: 139.76862616640122 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python PassiveAggressiveRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9894376841493092 Python Mean Absolute Error: 9.64524669506544 Python Mean Squared Error: 139.76857373191007 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
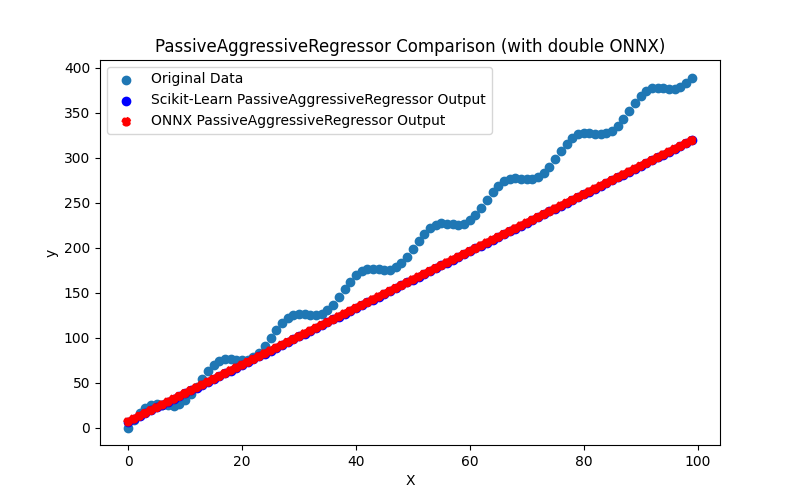
Fig.58. Risultati del file PassiveAggressiveRegressor.py (double ONNX)
2.1.17.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati passive_aggressive_regressor_float.onnx e passive_aggressive_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| PassiveAggressiveRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PassiveAggressiveRegressor" #define ONNXFilenameFloat "passive_aggressive_regressor_float.onnx" #define ONNXFilenameDouble "passive_aggressive_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
PassiveAggressiveRegressor (EURUSD,H1) Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx) PassiveAggressiveRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9894376801868329 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.6452488344318716 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Squared Error: 139.7686261664012761 PassiveAggressiveRegressor (EURUSD,H1) PassiveAggressiveRegressor (EURUSD,H1) Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx) PassiveAggressiveRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9894376841493092 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.6452466950654419 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Squared Error: 139.7685737319100667
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx) Python Mean Absolute Error: 9.64524669506544 MQL5: Mean Absolute Error: 9.6452488344318716 Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx) Python Mean Absolute Error: 9.64524669506544 MQL5: Mean Absolute Error: 9.6452466950654419
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.17.3. Rappresentazione ONNX di passive_aggressive_regressor_float.onnx e passive_aggressive_regressor_double.onnx
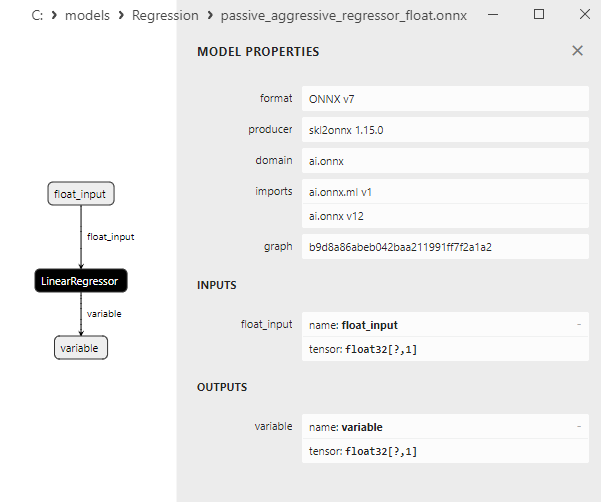
Fig.59. Rappresentazione ONNX di passive_aggressive_regressor_float.onnx in Netron
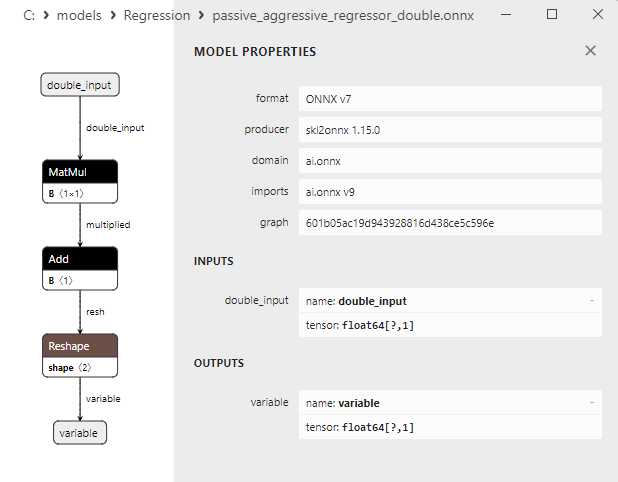
Fig.60. Rappresentazione ONNX di passive_aggressive_regressor_double.onnx in Netron
2.1.18. sklearn.linear_model.QuantileRegressor
QuantileRegressor è un metodo di apprendimento automatico utilizzato per stimare i quantili (percentili specifici) della variabile target nei compiti di regressione.
Invece di prevedere il valore medio della variabile target, come avviene tipicamente nei compiti di regressione, QuantileRegressor prevede i valori corrispondenti ai quantili specificati, come la mediana (50° percentile) o il 25° e 75° percentile.
Come funziona QuantileRegressor:
- Dati di input: Si inizia con un set di dati contenente le caratteristiche (variabili indipendenti) e la variabile target (continua).
- Focus sui quantili: Invece di prevedere i valori esatti della variabile target, QuantileRegressor modella la distribuzione condizionale della variabile target e prevede i valori per determinati quantili di questa distribuzione.
- Addestramento per differenti quantili: L'addestramento di un modello QuantileRegressor comporta l'addestramento di modelli separati per ciascun quantile desiderato. Ciascuno di questi modelli prevede un valore corrispondente al suo quantile.
- Parametro quantile: Il parametro principale di questo metodo è la scelta dei quantili desiderati per i quali si vogliono ottenere le previsioni. Ad esempio, se avete bisogno di previsioni per la mediana, dovrete addestrare il modello sul 50° percentile.
- Previsione quantile: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori corrispondenti ai quantili specificati su nuovi dati.
Vantaggi di QuantileRegressor:
- Flessibilità: QuantileRegressor offre flessibilità nella previsione di vari quantili, che può essere utile in compiti in cui sono importanti diversi percentili della distribuzione.
- Robustezza ai valori anomali: Un approccio orientato ai quantili può essere robusto contro i valori anomali, poiché non considera la media, che può essere fortemente influenzata dai valori estremi.
Limitazioni di QuantileRegressor:
- Necessità di selezione dei quantili: La scelta dei quantili ottimali potrebbe richiedere una certa conoscenza del lavoro.
- Aumento della complessità computazionale: L'addestramento di modelli separati per i diversi quantili può aumentare la complessità computazionale del compito.
QuantileRegressor è un metodo di apprendimento automatico progettato per prevedere i valori corrispondenti ai quantili specificati della variabile target. Questo metodo può essere utile nelle attività che interessano i vari percentili della distribuzione e nei casi in cui i dati possono contenere valori anomali.
2.1.18.1. Codice per creare il modello QuantileRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.QuantileRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# QuantileRegressor.py
# Il codice dimostra il processo di addestramento del modello QuantileRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"
# creare un modello QuantileRegressor
regression_model = QuantileRegressor(solver='highs')
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello QuantileRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"
# creare un modello QuantileRegressor
regression_model = QuantileRegressor(solver='highs')
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python QuantileRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9959915738839231 Python Mean Absolute Error: 6.3693091850025185 Python Mean Squared Error: 53.0425343337143 Python Python QuantileRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9959915739158818 Python Mean Absolute Error: 6.3693091422201125 Python Mean Squared Error: 53.042533910812814 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 7 Python MSE matching decimal places: 5 Python float ONNX model precision: 7 Python Python QuantileRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9959915738839231 Python Mean Absolute Error: 6.3693091850025185 Python Mean Squared Error: 53.0425343337143 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 13 Python double ONNX model precision: 16
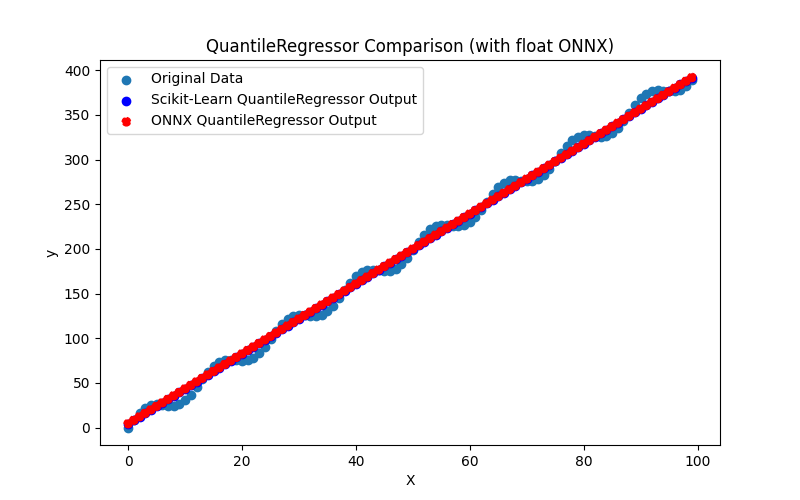
Fig.61. Risultati di QuantileRegressor.py (float ONNX)
2.1.18.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati quantile_regressor_float.onnx e quantile_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| QuantileRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "QuantileRegressor" #define ONNXFilenameFloat "quantile_regressor_float.onnx" #define ONNXFilenameDouble "quantile_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
QuantileRegressor (EURUSD,H1) Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx) QuantileRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9959915739158818 QuantileRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3693091422201169 QuantileRegressor (EURUSD,H1) MQL5: Mean Squared Error: 53.0425339108128071 QuantileRegressor (EURUSD,H1) QuantileRegressor (EURUSD,H1) Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx) QuantileRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9959915738839231 QuantileRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3693091850025185 QuantileRegressor (EURUSD,H1) MQL5: Mean Squared Error: 53.0425343337142721
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx) Python Mean Absolute Error: 6.3693091850025185 MQL5: Mean Absolute Error: 6.3693091422201169 Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx) Python Mean Absolute Error: 6.3693091850025185 MQL5: Mean Absolute Error: 6.3693091850025185
Precisione di ONNX float MAE: 7 cifre decimali, Precisione di ONNX double MAE: 16 cifre decimali.
2.1.18.3. Rappresentazione ONNX di quantile_regressor_float.onnx e di quantile_regressor_double.onnx
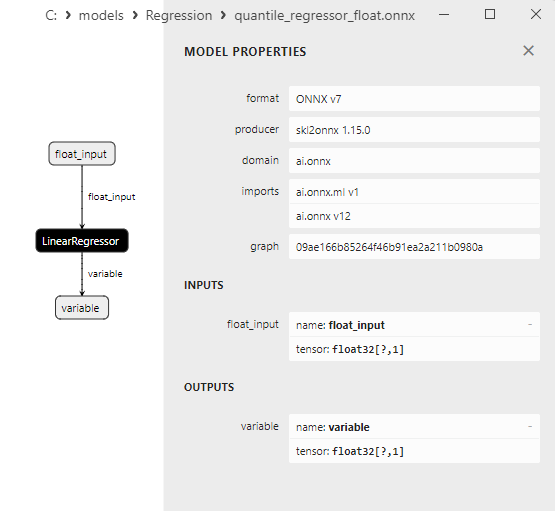
Fig.62. Rappresentazione ONNX di quantile_regressor_float.onnx in Netron
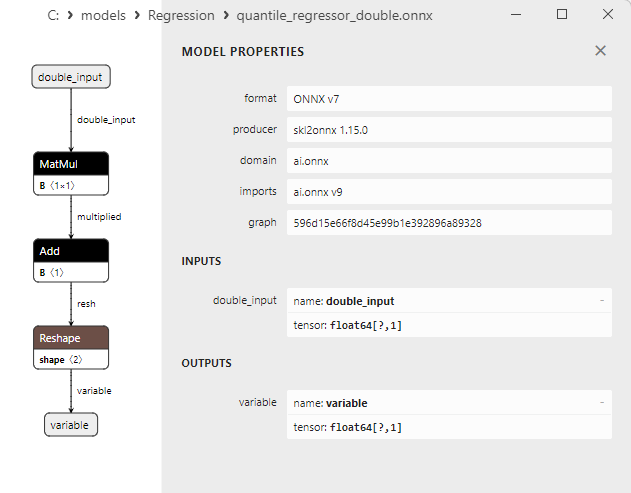
Fig.63. Rappresentazione ONNX di quantile_regressor_double.onnx in Netron
2.1.19. sklearn.linear_model.RANSACRegressor
RANSACRegressor è un metodo di apprendimento automatico utilizzato per risolvere problemi di regressione con il metodo RANSAC (Random Sample Consensus).
Il metodo RANSAC è progettato per gestire i dati contenenti valori anomali o imperfezioni, consentendo di ottenere un modello di regressione più robusto escludendo l'influenza dei valori anomali.
Come funziona RANSACRegressor:
- Dati di input: Si inizia con un set di dati contenente le caratteristiche (variabili indipendenti) e la variabile target (continua).
- Selezione di sottogruppi casuali: RANSAC inizia scegliendo sottogruppi casuali di dati utilizzati per addestrare il modello di regressione. Questi sottogruppi sono chiamati "ipotesi".
- Adattamento del modello alle ipotesi: Per ogni ipotesi scelta, viene addestrato un modello di regressione. Nel caso di RANSACRegressor, di solito si utilizza la regressione lineare e il modello viene adattato al sottogruppo di dati.
- Valutazione dei valori anomali: Dopo l'addestramento del modello, viene valutato il suo adattamento a tutti i dati. Per ogni punto dati viene calcolato l'errore tra i valori previsti e quelli effettivi.
- Identificazione dei valori anomali: I punti dati con errori superiori a una determinata soglia sono considerati anomali. Questi valori anomali possono influenzare l'addestramento del modello e distorcere i risultati.
- Aggiornamento del modello: Tutti i punti dati non considerati anomali vengono utilizzati per aggiornare il modello di regressione. Questo processo può essere ripetuto più volte con diverse ipotesi casuali.
- Modello finale: Dopo diverse iterazioni, RANSACRegressor seleziona il miglior modello addestrato sul sottogruppo di dati e lo restituisce come modello di regressione finale.
Vantaggi di RANSACRegressor:
- Robustezza ai valori anomali: RANSACRegressor è un metodo robusto contro i valori anomali, in quanto li esclude dall’addestramento.
- Regressione robusta: Questo metodo consente di creare un modello di regressione più affidabile quando i dati contengono valori anomali o imperfezioni.
Limitazioni di RANSACRegressor:
- Sensibilità alla soglia di errore: La scelta di una soglia di errore per determinare quali punti sono considerati anomali potrebbe richiedere una sperimentazione.
- Complessità della selezione delle ipotesi: La scelta di buone ipotesi nella fase iniziale potrebbe non essere un compito semplice.
RANSACRegressor è un metodo di apprendimento automatico utilizzato per problemi di regressione basato sul metodo RANSAC. Questo metodo consente di creare un modello di regressione più robusto quando i dati contengono valori anomali o imperfezioni, escludendo la loro influenza sul modello.
2.1.19.1. Codice per la creazione del modello RANSACRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.RANSACRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# RANSACRegressor.py
# Il codice dimostra il processo di addestramento del modello RANSACRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"
# creare un modello RANSACRegressor
regression_model = RANSACRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello RANSACRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"
# creare un modello RANSACRegressor
regression_model = RANSACRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python RANSACRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python Python RANSACRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python RANSACRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
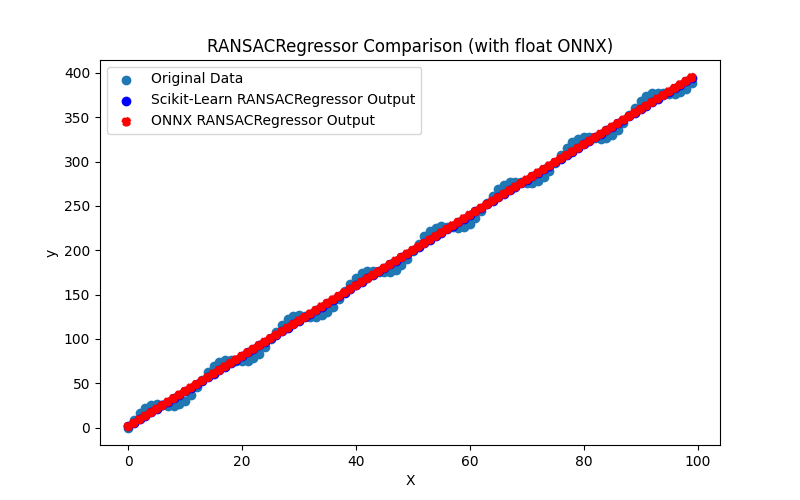
Fig.64. Risultati di RANSACRegressor.py (float ONNX)
2.1.19.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati ransac_regressor_float.onnx e ransac_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| RANSACRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RANSACRegressor" #define ONNXFilenameFloat "ransac_regressor_float.onnx" #define ONNXFilenameDouble "ransac_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
RANSACRegressor (EURUSD,H1) Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx) RANSACRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 RANSACRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 RANSACRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 RANSACRegressor (EURUSD,H1) RANSACRegressor (EURUSD,H1) Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx) RANSACRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 RANSACRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364266 RANSACRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477379263364266
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.19.3. Rappresentazione ONNX di ransac_regressor_float.onnx e ransac_regressor_double.onnx
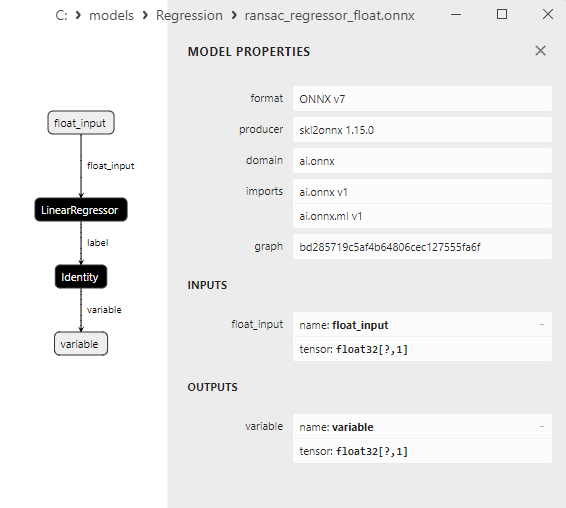
Fig.65. Rappresentazione ONNX di ransac_regressor_float.onnx in Netron
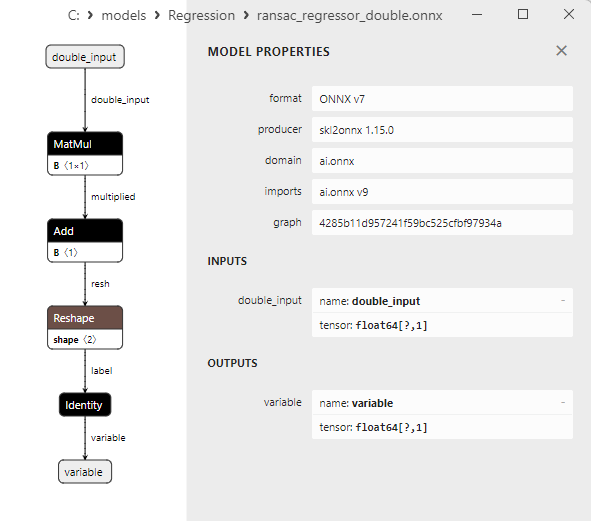
Fig.66. Rappresentazione ONNX di ransac_regressor_double.onnx in Netron
2.1.20. sklearn.linear_model.TheilSenRegressor
La regressioneTheil-Sen (stimatore Theil-Sen) è un metodo di stima della regressione utilizzato per approssimare le relazioni lineari tra le variabili indipendenti e la variabile target.
Offre una stima più robusta rispetto alla regressione lineare ordinaria in presenza di valori anomali e rumore nei dati.
Come funziona la regressione Theil-Sen:
- Selezione dei punti: Inizialmente, Theil-Sen seleziona coppie casuali di punti nei dati del dataset di addestramento.
- Calcolo della pendenza: Per ogni coppia di punti di dati, il metodo calcola la pendenza della retta che passa per questi punti, creando un insieme di pendenze.
- Pendenza media: Quindi, il metodo trova la pendenza media dall'insieme delle pendenze. Questa pendenza media viene utilizzata come stima della pendenza della regressione lineare.
- Deviazioni medie: Per ogni punto di dati, il metodo calcola la deviazione (differenza tra il valore effettivo e il valore previsto in base alla pendenza media) e trova la media di queste deviazioni. In questo modo si ottiene una stima del coefficiente dell'intercetta della regressione lineare.
- Stima finale: Le stime finali dei coefficienti di pendenza e di intercetta vengono utilizzate per costruire il modello di regressione lineare.
Vantaggi della regressione Theil-Sen:
- Resilienza dei valori anomali: La regressione Theil-Sen è più robusta contro i valori anomali e il rumore dei dati rispetto alla normale regressione lineare.
- Assunzioni meno rigide: Il metodo non richiede ipotesi rigorose sulla distribuzione dei dati o sulla forma di dipendenza, rendendolo più versatile.
- Adatto a dati multicollineari: La regressione Theil-Sen funziona bene con dati in cui le variabili indipendenti sono altamente correlate (problema di multicollinearità).
Limiti della regressione Theil-Sen:
- Complessità computazionale: Il calcolo delle pendenze medie per tutte le coppie di punti di dati potrebbe richiedere molto tempo, soprattutto per i set di dati di grandi dimensioni.
- Stima del coefficiente dell'intercetta: Le deviazioni medie sono utilizzate per stimare il coefficiente di intercetta, che può portare a distorsioni in presenza di valori anomali.
La regressione Theil-Sen è un metodo di stima per la regressione che fornisce una valutazione stabile della relazione lineare tra le variabili indipendenti e la variabile target, in particolare in presenza di valori anomali e rumore dei dati. Questo metodo è utile quando è necessaria una stima stabile in condizioni di dati reali.
2.1.20.1. Codice per la creazione di TheilSenRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.TheilSenRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza sia del modello originale che dei modelli esportati in ONNX.
# TheilSenRegressor.py
# Il codice dimostra il processo di addestramento del modello TheilSenRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"
# creare un modello TheilSen Regressor
regression_model = TheilSenRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello TheilSenRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"
# creare un modello TheilSen Regressor
regression_model = TheilSenRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python TheilSenRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962329196940459 Python Mean Absolute Error: 6.338686004537594 Python Mean Squared Error: 49.84886353898735 Python Python TheilSenRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.996232919516505 Python Mean Absolute Error: 6.338686370832071 Python Mean Squared Error: 49.84886588834327 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python TheilSenRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962329196940459 Python Mean Absolute Error: 6.338686004537594 Python Mean Squared Error: 49.84886353898735 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
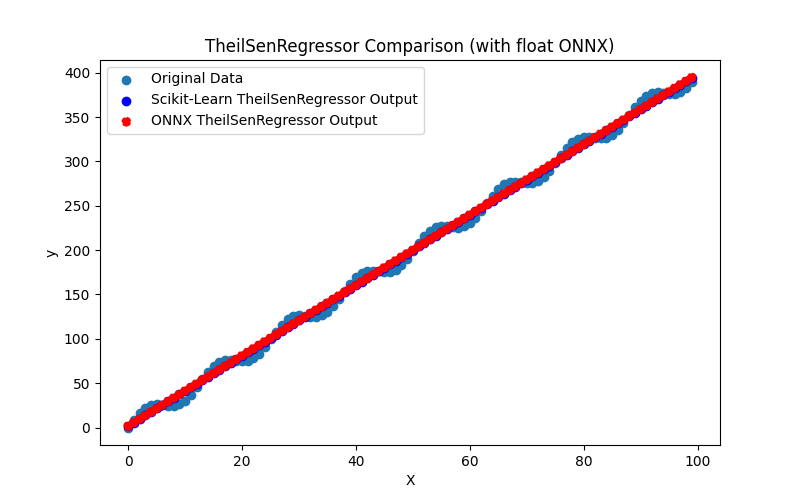
Fig.67. Risultati di TheilSenRegressor.py (float ONNX)
2.1.20.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati theil_sen_regressor_float.onnx e theil_sen_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| TheilSenRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "TheilSenRegressor" #define ONNXFilenameFloat "theil_sen_regressor_float.onnx" #define ONNXFilenameDouble "theil_sen_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
TheilSenRegressor (EURUSD,H1) Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx) TheilSenRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962329195165051 TheilSenRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3386863708320735 TheilSenRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8488658883432691 TheilSenRegressor (EURUSD,H1) TheilSenRegressor (EURUSD,H1) Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx) TheilSenRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962329196940459 TheilSenRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3386860045375943 TheilSenRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8488635389873735
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx) Python Mean Absolute Error: 6.338686004537594 MQL5: Mean Absolute Error: 6.3386863708320735 Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx) Python Mean Absolute Error: 6.338686004537594 MQL5: Mean Absolute Error: 6.3386860045375943
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 15 cifre decimali.
2.1.20.3. Rappresentazione ONNX di theil_sen_regressor_float.onnx e theil_sen_regressor_double.onnx
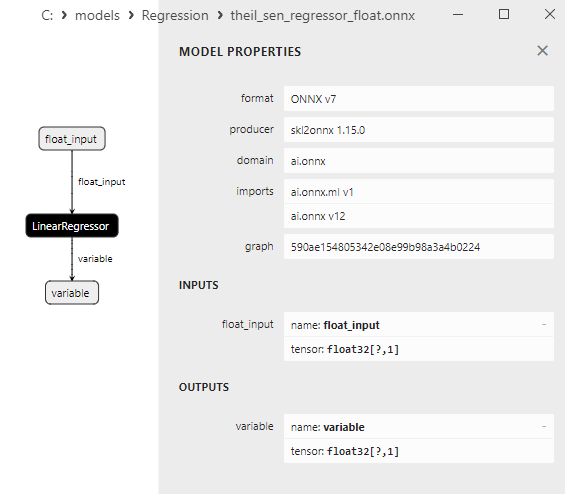
Fig.68. Rappresentazione ONNX di theil_sen_regressor_float.onnx in Netron
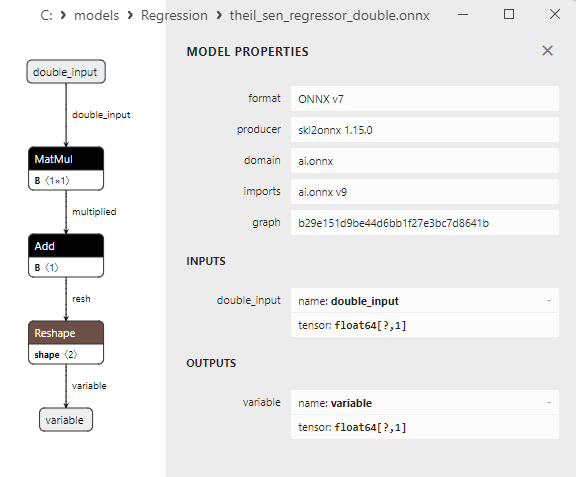
Fig.69. Rappresentazione ONNX di theil_sen_regressor_double.onnx in Netron
2.1.21. sklearn.linear_model.LinearSVR
LinearSVR (Linear Support Vector Regression) è un modello di apprendimento automatico per compiti di regressione basato sul metodo Support Vector Machines (SVM).
Questo metodo viene utilizzato per trovare relazioni lineari tra le caratteristiche e la variabile target utilizzando un kernel lineare.
Come funziona LinearSVR:
- Dati di input: LinearSVR inizia con un set di dati che include le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Selezione di un modello lineare: Il modello presuppone una relazione lineare tra le caratteristiche e la variabile target, descritta da un'equazione di regressione lineare.
- Addestramento del modello: LinearSVR trova i valori ottimali per i coefficienti del modello minimizzando una funzione di perdita che considera l'errore di previsione e un errore accettabile (epsilon).
- Generazione di previsioni: Dopo l'addestramento, il modello può prevedere i valori della variabile target per i nuovi dati sulla base dei coefficienti scoperti.
Vantaggi di LinearSVR:
- Supporto Regressione Vettoriale: LinearSVR impiega il metodo Support Vector Machines, che consente di trovare la separazione ottimale tra i dati tenendo conto di un errore accettabile.
- Supporto per caratteristiche multiple: Il modello è in grado di gestire più caratteristiche e di elaborare dati in dimensioni elevate.
- Regolarizzazione: LinearSVR prevede la regolarizzazione, che aiuta a combattere l'overfitting e a garantire previsioni più stabili.
Limitazioni di LinearSVR:
- Linearità: LinearSVR è vincolato dall'utilizzo di relazioni lineari tra le caratteristiche e la variabile target. Nel caso di relazioni complesse e non lineari, il modello potrebbe non essere sufficientemente flessibile.
- Sensibilità ai valori anomali: Il modello può essere sensibile ai valori anomali dei dati e all'errore accettabile (epsilon).
- Incapacità di cogliere relazioni complesse: LinearSVR, come altri modelli lineari, non è in grado di cogliere relazioni non lineari complesse tra le caratteristiche e la variabile target.
LinearSVR è un modello di apprendimento automatico a regressione che utilizza il metodo Support Vector Machines per trovare relazioni lineari tra le caratteristiche e la variabile target. Supporta la regolarizzazione e può essere utilizzato in compiti in cui è essenziale controllare l'errore accettabile. Tuttavia, il modello è limitato dalla sua dipendenza lineare e potrebbe essere sensibile ai valori anomali.
2.1.21.1. Codice per creare il modello LinearSVR ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.LinearSVR, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# LinearSVR.py
# Il codice dimostra il processo di addestramento del modello LinearSVR, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearSVR"
onnx_model_filename = data_path + "linear_svr"
# creare un modello Linear SVR
linear_svr_model = LinearSVR()
# Adattare il modello ai dati
linear_svr_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = linear_svr_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(linear_svr_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(linear_svr_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python LinearSVR Original model (double) Python R-squared (Coefficient of determination): 0.9944935515149387 Python Mean Absolute Error: 7.026852359381935 Python Mean Squared Error: 72.86550241109444 Python Python LinearSVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9944935580726729 Python Mean Absolute Error: 7.026849848037511 Python Mean Squared Error: 72.86541563418206 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 4 Python MSE matching decimal places: 3 Python float ONNX model precision: 4 Python Python LinearSVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9944935515149387 Python Mean Absolute Error: 7.026852359381935 Python Mean Squared Error: 72.86550241109444 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
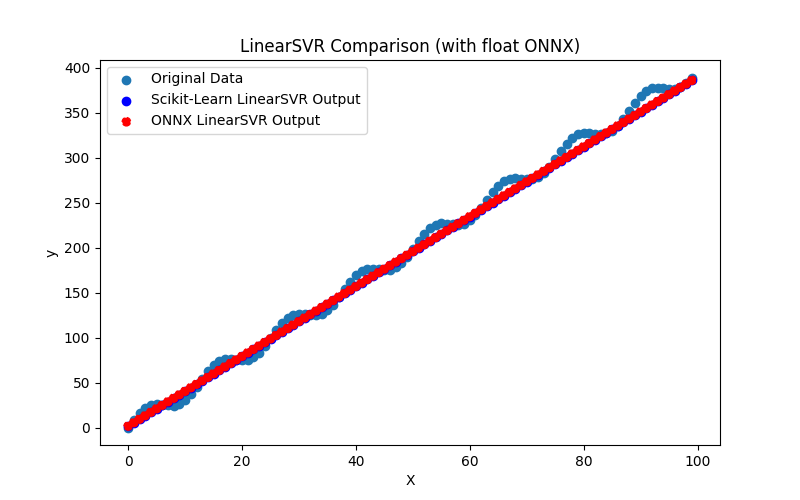
Fig.70. Risultati di LinearSVR.py (float ONNX)
2.1.21.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i file salvati linear_svr_float.onnx e linear_svr_double.onnx, dimostrando l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| LinearSVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LinearSVR" #define ONNXFilenameFloat "linear_svr_float.onnx" #define ONNXFilenameDouble "linear_svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
LinearSVR (EURUSD,H1) Testing ONNX float: LinearSVR (linear_svr_float.onnx) LinearSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9944935580726729 LinearSVR (EURUSD,H1) MQL5: Mean Absolute Error: 7.0268498480375108 LinearSVR (EURUSD,H1) MQL5: Mean Squared Error: 72.8654156341820567 LinearSVR (EURUSD,H1) LinearSVR (EURUSD,H1) Testing ONNX double: LinearSVR (linear_svr_double.onnx) LinearSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9944935515149387 LinearSVR (EURUSD,H1) MQL5: Mean Absolute Error: 7.0268523593819374 LinearSVR (EURUSD,H1) MQL5: Mean Squared Error: 72.8655024110944680
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: LinearSVR (linear_svr_float.onnx) Python Mean Absolute Error: 7.026852359381935 MQL5: Mean Absolute Error: 7.0268498480375108 Testing ONNX double: LinearSVR (linear_svr_double.onnx) Python Mean Absolute Error: 7.026852359381935 MQL5: Mean Absolute Error: 7.0268523593819374
Precisione di ONNX float MAE: 4 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.21.3. Rappresentazione ONNX di linear_svr_float.onnx e linear_svr_double.onnx
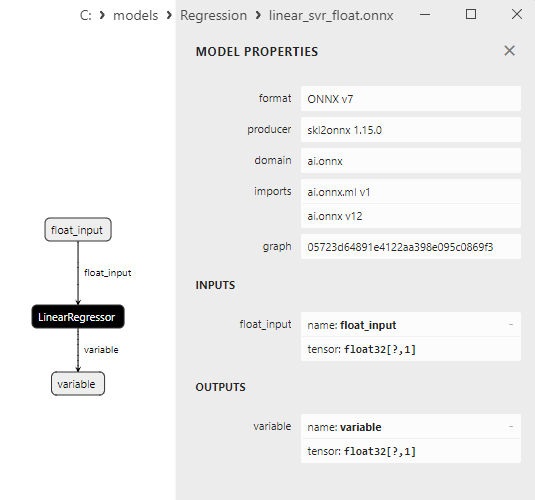
Fig.71. Rappresentazione ONNX di linear_svr_float.onnx in Netron
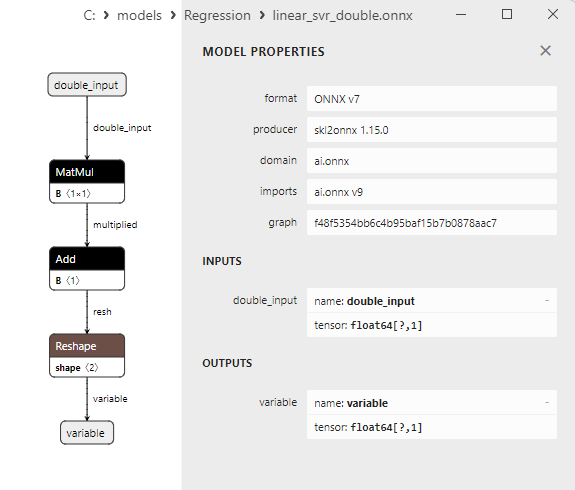
Fig.72. Rappresentazione ONNX di linear_svr_double.onnx in Netron
2.1.22. sklearn.neural_network.MLPRegressor
MLPRegressor (Multi-Layer Perceptron Regressor) è un modello di apprendimento automatico che utilizza reti neurali artificiali per compiti di regressione.
Si tratta di una rete neurale multistrato che comprende diversi strati di neuroni (compresi gli strati di input, nascosti e di uscita) addestrati per prevedere i valori continui della variabile target.
Come funziona MLPRegressor:
- Dati di input: Si parte da un set di dati contenente le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Creazione di una rete neurale multistrato: MLPRegressor impiega una rete neurale multistrato con più strati nascosti di neuroni. Questi neuroni sono collegati tramite connessioni ponderate e funzioni di attivazione.
- Addestramento del modello: MLPRegressor addestra la rete neurale regolando i pesi e il bias per minimizzare una funzione di perdita che misura la disparità tra le previsioni della rete e i valori effettivi della variabile target. Ciò si ottiene attraverso algoritmi di retropropagazione.
- Generazione di previsioni: Dopo l'addestramento, il modello può prevedere i valori delle variabili target per i nuovi dati.
Vantaggi di MLPRegressor:
- Flessibilità: Le reti neurali multistrato possono modellare complesse relazioni non lineari tra le caratteristiche e la variabile target.
- Versatilità: MLPRegressor può essere utilizzato per diversi compiti di regressione, tra cui problemi di serie temporali, approssimazione di funzioni e altro ancora.
- Capacità di generalizzazione: Le reti neurali imparano dai dati e possono generalizzare le dipendenze trovate nei dati di addestramento ai nuovi dati.
Limitazioni di MLPRegressor:
- Complessità del modello di base: Le reti neurali di grandi dimensioni possono essere costose dal punto di vista computazionale e richiedono un'ampia quantità di dati per l'addestramento.
- Regolazione dell'iperparametro: La scelta degli iperparametri ottimali (numero di strati, numero di neuroni in ogni strato, tasso di apprendimento, ecc.) potrebbe richiedere la sperimentazione.
- Suscettibilità all'overfitting: Le reti neurali di grandi dimensioni possono essere soggette a overfitting se i dati sono insufficienti o la regolarizzazione è insufficiente.
MLPRegressor rappresenta un potente modello di apprendimento automatico basato su reti neurali multistrato e può essere utilizzato per un ampio numero di compiti di regressione. Questo modello è flessibile, ma richiede una messa a punto e un addestramento meticoloso su grandi volumi di dati per ottenere risultati ottimali.
2.1.22.1. Codice per creare il modello MLPRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.neural_network.MLPRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# MLPRegressor.py
# Il codice dimostra il processo di addestramento del modello MLPRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"
# creare un modello MLP Regressor
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)
# Adattare il modello ai dati
mlp_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = mlp_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello MLPRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"
# creare un modello MLP Regressor
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)
# Adattare il modello ai dati
mlp_regressor_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = mlp_regressor_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python MLPRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9874070836467945 Python Mean Absolute Error: 10.62249788982753 Python Mean Squared Error: 166.63901957615224 Python Python MLPRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9874070821340352 Python Mean Absolute Error: 10.62249972216809 Python Mean Squared Error: 166.63903959413219 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python MLPRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9874070836467945 Python Mean Absolute Error: 10.622497889827532 Python Mean Squared Error: 166.63901957615244 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 12 Python double ONNX model precision: 14
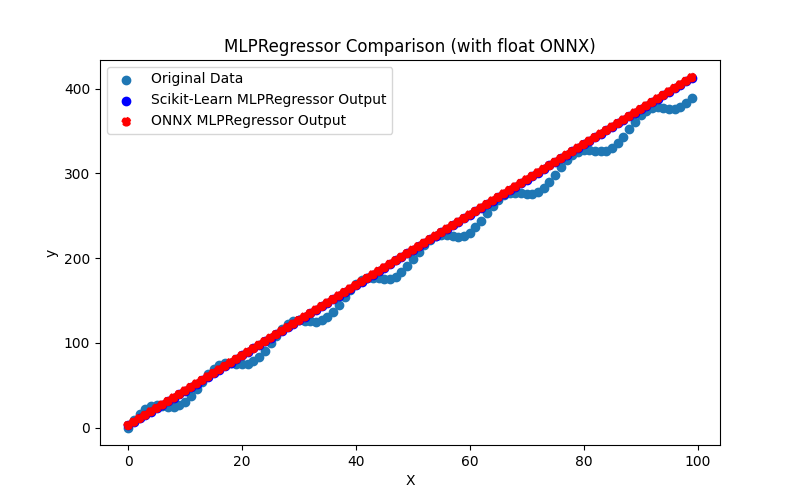
Fig.73. Risultati di MLPRegressor.py (float ONNX)
2.1.22.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati mlp_regressor_float.onnx e mlp_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| MLPRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "MLPRegressor" #define ONNXFilenameFloat "mlp_regressor_float.onnx" #define ONNXFilenameDouble "mlp_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
MLPRegressor (EURUSD,H1) Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx) MLPRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9875198695654352 MLPRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 10.5596681685341309 MLPRegressor (EURUSD,H1) MQL5: Mean Squared Error: 165.1465507645494597 MLPRegressor (EURUSD,H1) MLPRegressor (EURUSD,H1) Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx) MLPRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9875198617341387 MLPRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 10.5596715833884609 MLPRegressor (EURUSD,H1) MQL5: Mean Squared Error: 165.1466543942046599
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx) Python Mean Absolute Error: 10.62249788982753 MQL5: Mean Absolute Error: 10.6224997221680901 Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx) Python Mean Absolute Error: 10.62249788982753 MQL5: Mean Absolute Error: 10.6224978898275282
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.22.3. Rappresentazione ONNX di mlp_regressor_float.onnx e mlp_regressor_double.onnx
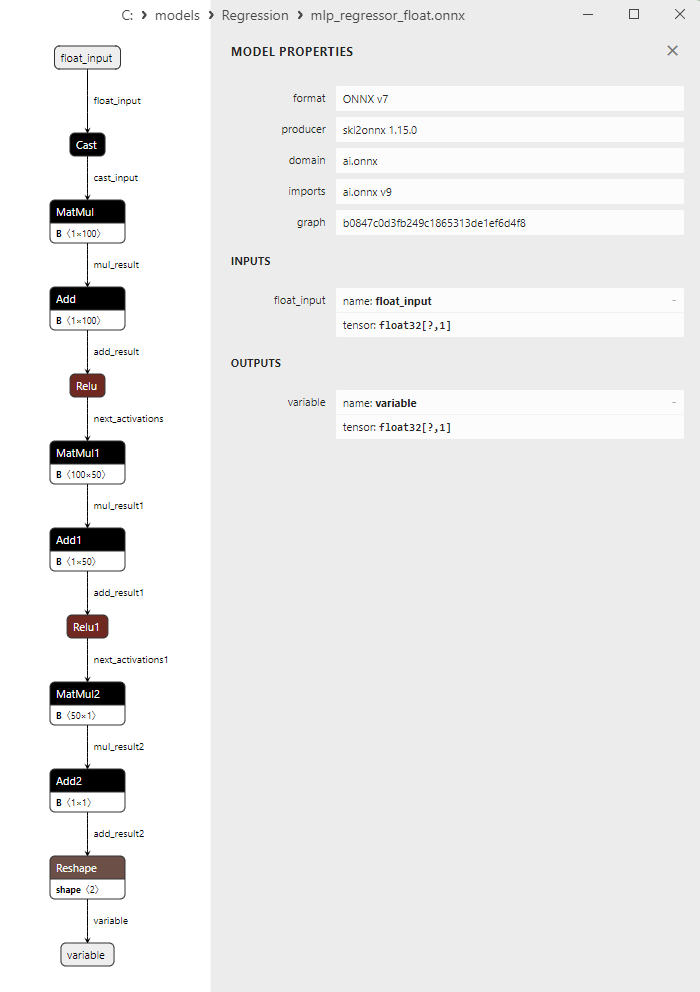
Fig.74. Rappresentazione ONNX di mlp_regressor_float.onnx in Netron
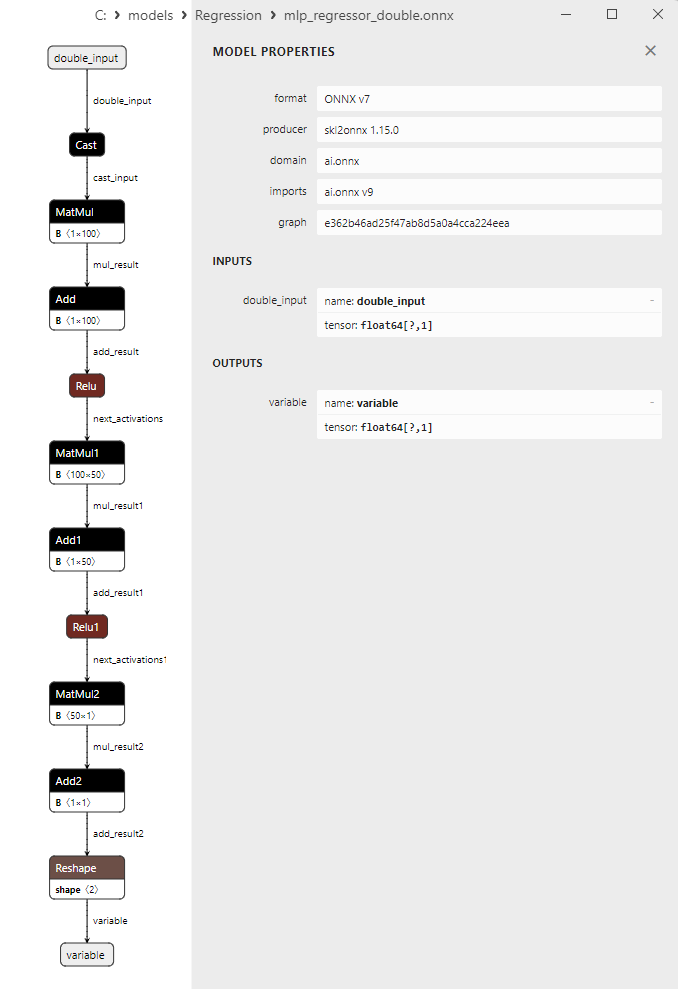
Fig.75. Rappresentazione ONNX di mlp_regressor_double.onnx in Netron
2.1.23. sklearn.cross_decomposition.PLSRegression
PLSRegression (Partial Least Squares Regression) è un metodo di apprendimento automatico utilizzato per risolvere problemi di regressione.
Fa parte della famiglia dei metodi PLS e si applica per analizzare e modellare le relazioni tra due insiemi di variabili, dove un insieme serve come predittori e l'altro insieme è costituito dalle variabili target.
Come funziona la PLSRegression:
- Dati di input: Si parte da due set di dati, etichettati come X e Y. L'insieme X contiene variabili indipendenti (predittori) e l'insieme Y contiene variabili target (dipendenti).
- Selezione di combinazioni lineari: PLSRegression identifica combinazioni lineari (componenti) negli insiemi X e Y che massimizzano la covarianza tra loro. Questi componenti sono menzionati come componenti PLS.
- Massimizzazione della covarianza: L'obiettivo primario della PLSRegression è trovare le componenti PLS che massimizzano la covarianza tra X e Y. Ciò consente di estrarre le relazioni più informative tra predittori e variabili target.
- Addestramento del modello: Una volta trovate le componenti PLS, queste possono essere utilizzate per creare un modello che prevede i valori Y in base a X.
- Generazione di previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori Y per i nuovi dati utilizzando i valori X corrispondenti.
Vantaggi della PLSRegression:
- Analisi di correlazione: PLSRegression consente di analizzare e modellare le correlazioni tra due gruppi di variabili, che possono essere utili per comprendere le relazioni tra predittori e variabili target.
- Riduzione della dimensionalità: Il metodo può essere utilizzato anche per ridurre la dimensionalità dei dati, identificando i componenti PLS più importanti.
Limitazioni della PLSRegression:
- Sensibilità alla scelta del numero di componenti: La selezione del numero ottimale di componenti PLS può richiedere una certa sperimentazione.
- Dipendenza dalla struttura dei dati: I risultati della PLSRegression possono dipendere fortemente dalla struttura dei dati e dalle correlazioni tra loro.
La PLSRegression è un metodo di apprendimento automatico utilizzato per analizzare e modellare le correlazioni tra due insiemi di variabili, dove un insieme funge da predittori e l'altro da variabili target. Questo metodo consente di studiare le relazioni all'interno dei dati e può essere utile per ridurre la dimensionalità dei dati e prevedere i valori delle variabili target in base ai predittori.
2.1.23.1. Codice per la creazione del modello PLSRegression ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.cross_decomposition.PLSRegression, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# PLSRegression.py
# Il codice dimostra il processo di addestramento del modello PLSRegression, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"
# creare un modello PLSRegression
pls_model = PLSRegression(n_components=1)
# Adattare il modello ai dati
pls_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = pls_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello PLSRegression, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"
# creare un modello PLSRegression
pls_model = PLSRegression(n_components=1)
# Adattare il modello ai dati
pls_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = pls_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python PLSRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281805 Python Python PLSRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382638567003 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.778145525764096 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 8 Python MSE matching decimal places: 5 Python float ONNX model precision: 8 Python Python PLSRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281805 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
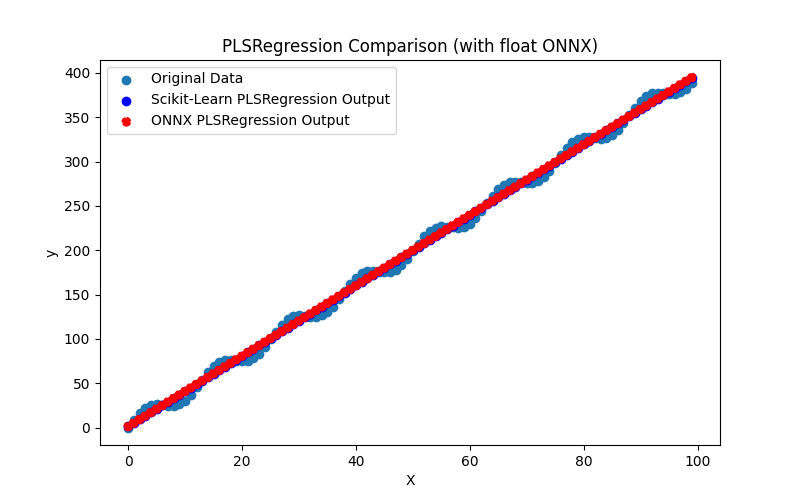
Fig.76. Risultati di PLSRegression.py (float ONNX)
2.1.23.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati pls_regression_float.onnx e pls_regression_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| PLSRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PLSRegression" #define ONNXFilenameFloat "pls_regression_float.onnx" #define ONNXFilenameDouble "pls_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
PLSRegression (EURUSD,H1) Testing ONNX float: PLSRegression (pls_regression_float.onnx) PLSRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382638567003 PLSRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 PLSRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781455257640815 PLSRegression (EURUSD,H1) PLSRegression (EURUSD,H1) Testing ONNX double: PLSRegression (pls_regression_double.onnx) PLSRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 PLSRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364275 PLSRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817839
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: PLSRegression (pls_regression_float.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379221400145 Testing ONNX double: PLSRegression (pls_regression_double.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379263364275
Precisione di ONNX float MAE: 8 cifre decimali, Precisione di ONNX double MAE: 16 cifre decimali.
2.1.23.3. Rappresentazione ONNX di pls_regression_float.onnx e pls_regression_double.onnx
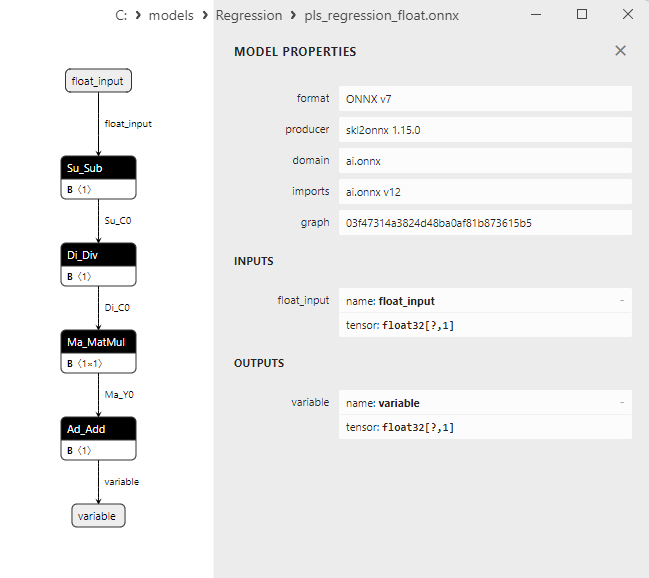
Fig.77. Rappresentazione ONNX di pls_regression_float.onnx in Netron
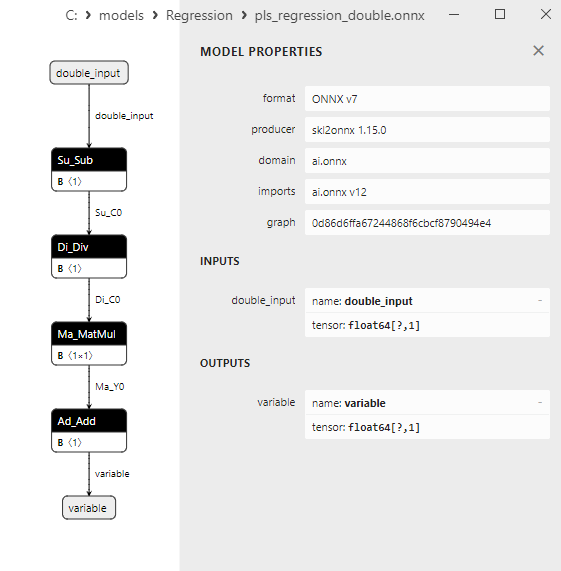
Fig.78. Rappresentazione ONNX di pls_regression_double.onnx in Netron
2.1.24. sklearn.linear_model.TweedieRegressor
TweedieRegressor è un metodo di regressione progettato per risolvere problemi di regressione utilizzando la distribuzione Tweedie. La distribuzione Tweedie è una distribuzione di probabilità che può descrivere un'ampia gamma di dati, compresi quelli con una struttura della varianza variabile. TweedieRegressor si applica nei compiti di regressione in cui la variabile target possiede caratteristiche che si allineano alla distribuzione Tweedie.
Come funziona TweedieRegressor:
- Variabile target e distribuzione Tweedie: TweedieRegressor presuppone che la variabile target segua una distribuzione Tweedie. La distribuzione Tweedie dipende dal parametro "p", che determina la forma della distribuzione e il grado di varianza.
- Addestramento del modello: TweedieRegressor addestra un modello di regressione per prevedere la variabile target in base alle variabili indipendenti (caratteristiche). Il modello massimizza la probabilità per i dati corrispondenti alla distribuzione Tweedie.
- Scelta del parametro "p": La selezione del parametro 'p' è un aspetto cruciale nell'utilizzo di TweedieRegressor. Questo parametro definisce la forma e la varianza della distribuzione. Valori di "p" diversi corrispondono a tipi di dati diversi; ad esempio, p=1 corrisponde alla distribuzione di Poisson, mentre p=2 corrisponde alla distribuzione normale.
- Trasformare le risposte: A volte il modello può richiedere trasformazioni delle risposte (variabili target) prima dell'addestramento. Questa trasformazione si riferisce al parametro "p" e può comportare funzioni logaritmiche o altre trasformazioni per conformarsi alla distribuzione Tweedie.
Vantaggi di TweedieRegressor:
- Capacità di modellare dati con varianza variabile: La distribuzione Tweedie può adattarsi a dati con strutture di varianza differenti, il che è prezioso per i dati del mondo reale in cui la varianza può variare.
- Varietà di parametri 'p': La possibilità di scegliere diversi valori di "p" consente di modellare vari tipi di dati.
Limitazioni di TweedieRegressor:
- Complessità nella scelta del parametro "p": La selezione del valore "p" corretto può richiedere la conoscenza dei dati e la sperimentazione.
- Conformità alla distribuzione Tweedie: Per applicare con successo TweedieRegressor, la variabile target deve corrispondere alla distribuzione Tweedie. L'inosservanza può portare a scarse prestazioni del modello.
TweedieRegressor è un metodo di regressione che utilizza la distribuzione Tweedie per modellare dati con strutture di varianza differenti. Questo metodo è utile nei compiti di regressione in cui la variabile target è conforme alla distribuzione Tweedie e può essere regolato con diversi valori del parametro 'p' per un migliore adattamento ai dati.
2.1.24.1. Codice per creare il modello TweedieRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.TweedieRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# TweedieRegressor.py
# Il codice dimostra il processo di addestramento del modello TweedieRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"
# creare un modello Tweedie Regressor
regression_model = TweedieRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello TweedieRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"
# creare un modello Tweedie Regressor
regression_model = TweedieRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
2023.10.31 11:39:36.223 Python TweedieRegressor Original model (double) 2023.10.31 11:39:36.223 Python R-squared (Coefficient of determination): 0.9962368328117072 2023.10.31 11:39:36.223 Python Mean Absolute Error: 6.342397897667562 2023.10.31 11:39:36.223 Python Mean Squared Error: 49.797082198408745 2023.10.31 11:39:36.223 Python 2023.10.31 11:39:36.223 Python TweedieRegressor ONNX model (float) 2023.10.31 11:39:36.223 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_float.onnx 2023.10.31 11:39:36.253 Python Information about input tensors in ONNX: 2023.10.31 11:39:36.253 Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] 2023.10.31 11:39:36.253 Python Information about output tensors in ONNX: 2023.10.31 11:39:36.253 Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] 2023.10.31 11:39:36.253 Python R-squared (Coefficient of determination) 0.9962368338709323 2023.10.31 11:39:36.253 Python Mean Absolute Error: 6.342397072978867 2023.10.31 11:39:36.253 Python Mean Squared Error: 49.797068181938165 2023.10.31 11:39:36.253 Python R^2 matching decimal places: 8 2023.10.31 11:39:36.253 Python MAE matching decimal places: 6 2023.10.31 11:39:36.253 Python MSE matching decimal places: 4 2023.10.31 11:39:36.253 Python float ONNX model precision: 6 2023.10.31 11:39:36.613 Python 2023.10.31 11:39:36.613 Python TweedieRegressor ONNX model (double) 2023.10.31 11:39:36.613 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_double.onnx 2023.10.31 11:39:36.613 Python Information about input tensors in ONNX: 2023.10.31 11:39:36.613 Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] 2023.10.31 11:39:36.613 Python Information about output tensors in ONNX: 2023.10.31 11:39:36.628 Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] 2023.10.31 11:39:36.628 Python R-squared (Coefficient of determination) 0.9962368328117072 2023.10.31 11:39:36.628 Python Mean Absolute Error: 6.342397897667562 2023.10.31 11:39:36.628 Python Mean Squared Error: 49.797082198408745 2023.10.31 11:39:36.628 Python R^2 matching decimal places: 16 2023.10.31 11:39:36.628 Python MAE matching decimal places: 15 2023.10.31 11:39:36.628 Python MSE matching decimal places: 15 2023.10.31 11:39:36.628 Python double ONNX model precision: 15
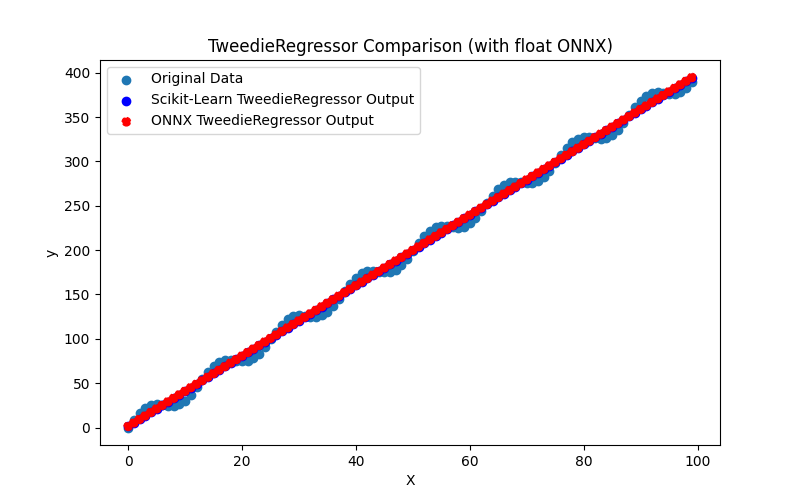
Fig.79. Risultati di TweedieRegressor.py (float ONNX)
2.1.24.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati tweedie_regressor_float.onnx e tweedie_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| TweedieRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "TweedieRegressor" #define ONNXFilenameFloat "tweedie_regressor_float.onnx" #define ONNXFilenameDouble "tweedie_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
2023.10.31 11:42:20.113 TweedieRegressor (EURUSD,H1) Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx) 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962368338709323 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3423970729788666 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7970681819381653 2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1) 2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1) Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx) 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962368328117072 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3423978976675608 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7970821984087593
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx) Python Mean Absolute Error: 6.342397897667562 MQL5: Mean Absolute Error: 6.3423970729788666 Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx) Python Mean Absolute Error: 6.342397897667562 MQL5: Mean Absolute Error: 6.3423978976675608
Precisione di ONNX float MAE: 6 cifre decimali, Precisione di ONNX double MAE: 14 cifre decimali.
2.1.24.3. Rappresentazione ONNX di tweedie_regressor_float.onnx e tweedie_regressor_double.onnx
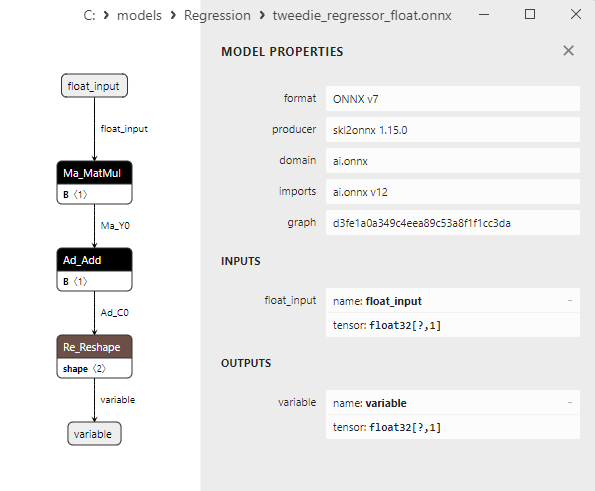
Fig.80. Rappresentazione ONNX di tweedie_regressor_float.onnx in Netron
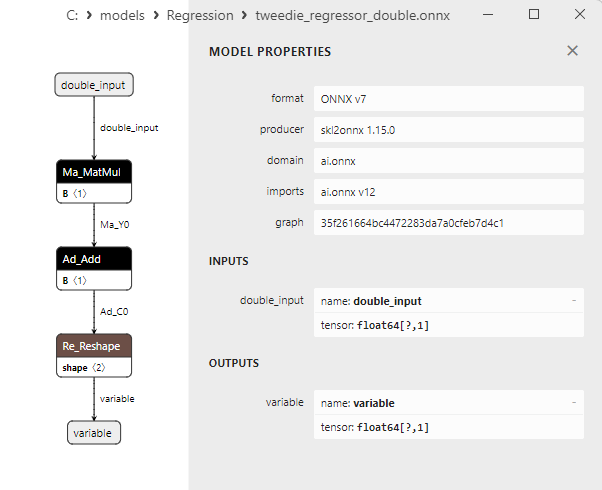
Fig.81. Rappresentazione ONNX di tweedie_regressor_double.onnx in Netron
2.1.25. sklearn.linear_model.PoissonRegressor
PoissonRegressor è un metodo di apprendimento automatico applicato per risolvere compiti di regressione basati sulla distribuzione di Poisson...
Questo metodo è adatto quando la variabile dipendente (variabile target) è un conteggio dati, che rappresentano il numero di eventi verificatisi in un determinato periodo di tempo o in un intervallo di spazio fisso. PoissonRegressor modella la relazione tra i predittori (variabili indipendenti) e la variabile target assumendo che tale relazione sia conforme alla distribuzione di Poisson.
Come funziona PoissonRegressor:
- Dati di input: Si parte da un set di dati che include le caratteristiche (variabili indipendenti) e la variabile target, che rappresenta il conteggio degli eventi.
- Distribuzione di Poisson: Il metodo PoissonRegressor modella la variabile target assumendo che segua la distribuzione di Poisson. La distribuzione di Poisson è adatta a modellare eventi che si verificano con un'intensità media fissa in un determinato intervallo di tempo o in un intervallo di spazio.
- Addestramento del modello: PoissonRegressor addestra un modello che stima i parametri della distribuzione di Poisson, considerando i predittori. Il modello cerca di trovare il miglior adattamento ai dati osservati utilizzando la funzione di probabilità che corrisponde alla distribuzione di Poisson.
- Previsione dei valori di conteggio: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori di conteggio (il numero di eventi) su nuovi dati, e anche queste previsioni seguono la distribuzione di Poisson.
Vantaggi di PoissonRegressor:
- Adatto per i dati di conteggio: PoissonRegressor è adatto a compiti in cui la variabile target rappresenta dati di conteggio, come il numero di ordini, di chiamate, ecc.
- Specificità della distribuzione: Poiché il modello aderisce alla distribuzione di Poisson, può essere più accurato per i dati che sono ben descritti da questa distribuzione.
Limitazioni di PoissonRegressor:
- Adatto solo per i dati di conteggio: PoissonRegressor non è adatto per regressioni in cui la variabile target è continua e non numerica.
- Dipendenza dalla selezione delle caratteristiche: La qualità del modello può dipendere fortemente dalla selezione e dalla progettazione delle caratteristiche.
PoissonRegressor è un metodo di apprendimento automatico utilizzato per risolvere compiti di regressione quando la variabile target rappresenta dati di conteggio ed è modellata utilizzando la distribuzione di Poisson. Questo metodo è vantaggioso per compiti legati a eventi che si verificano con un'intensità fissa entro intervalli temporali o di spazio specifici.
2.1.25.1. Codice per creare il modello PoissonRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.PoissonRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# PoissonRegressor.py
# Il codice dimostra il processo di addestramento del modello PoissonRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"
# creare un modello PoissonRegressor
regression_model = PoissonRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello PoissonRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"
# creare un modello PoissonRegressor
regression_model = PoissonRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python PoissonRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9204304782362495 Python Mean Absolute Error: 27.59790466048524 Python Mean Squared Error: 1052.9242570153044 Python Python PoissonRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9204305082536851 Python Mean Absolute Error: 27.59790825165078 Python Mean Squared Error: 1052.9238598018305 Python R^2 matching decimal places: 6 Python MAE matching decimal places: 5 Python MSE matching decimal places: 2 Python float ONNX model precision: 5 Python Python PoissonRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9204304782362495 Python Mean Absolute Error: 27.59790466048524 Python Mean Squared Error: 1052.9242570153044 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 13 Python double ONNX model precision: 14
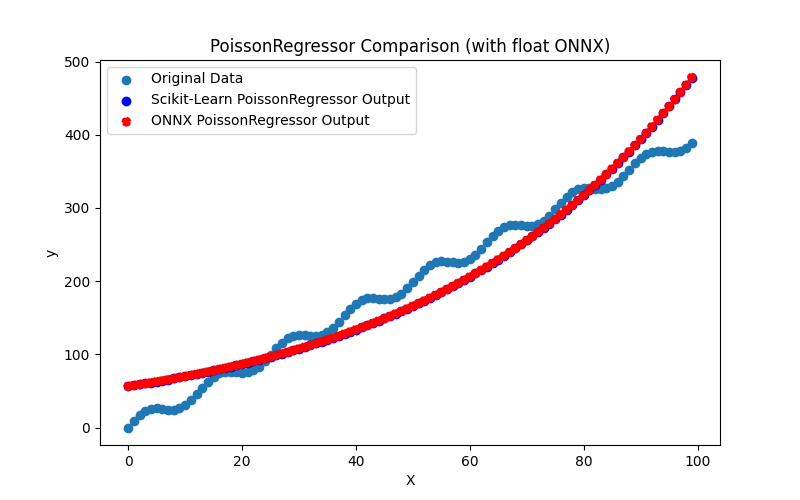
Fig.82. Risultati di PoissonRegressor.py (float ONNX)
2.1.25.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati poisson_regressor_float.onnx e poisson_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| PoissonRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PoissonRegressor" #define ONNXFilenameFloat "poisson_regressor_float.onnx" #define ONNXFilenameDouble "poisson_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
PoissonRegressor (EURUSD,H1) Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx) PoissonRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9204305082536851 PoissonRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 27.5979082516507788 PoissonRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1052.9238598018305311 PoissonRegressor (EURUSD,H1) PoissonRegressor (EURUSD,H1) Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx) PoissonRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9204304782362493 PoissonRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 27.5979046604852343 PoissonRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1052.9242570153051020
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx) Python Mean Absolute Error: 27.59790466048524 MQL5: Mean Absolute Error: 27.5979082516507788 Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx) Python Mean Absolute Error: 27.59790466048524 MQL5: Mean Absolute Error: 27.5979046604852343
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.25.3. Rappresentazione ONNX di poisson_regressor_float.onnx e poisson_regressor_double.onnx
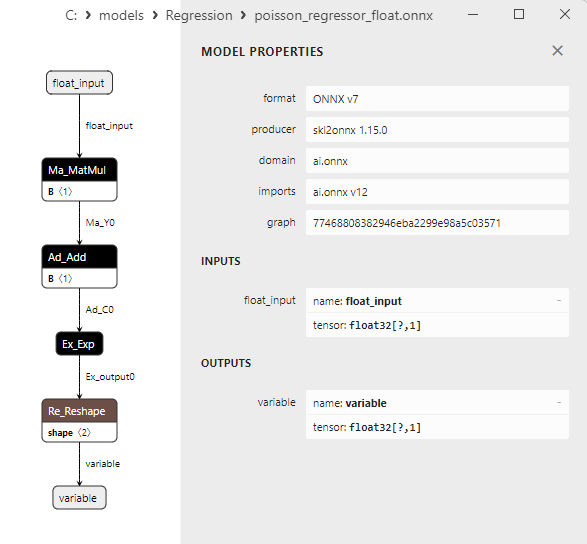
Fig.83. Rappresentazione ONNX di poisson_regressor_float.onnx in Netron
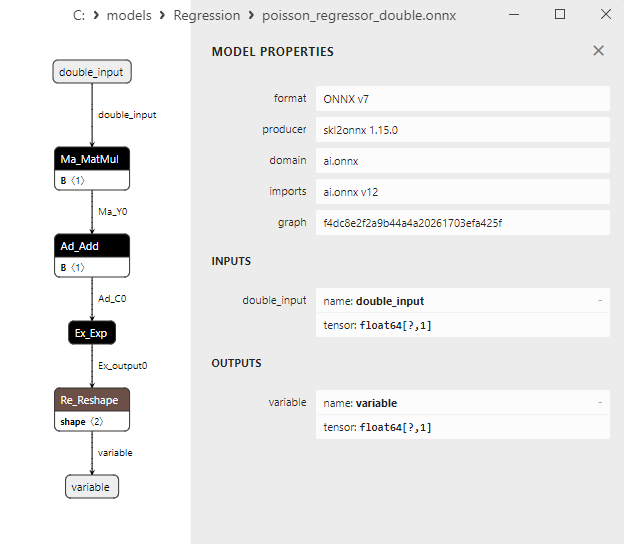
Fig.84. Rappresentazione ONNX di poisson_regressor_double.onnx in Netron
2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
RadiusNeighborsRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione. È una variante del metodo k-Nearest Neighbors (k-NN), progettato per prevedere i valori della variabile target in base ai vicini più prossimi nello spazio delle caratteristiche. Tuttavia, invece di un numero fisso di vicini (come nel metodo k-NN), RadiusNeighborsRegressor utilizza un raggio fisso per determinare i vicini per ogni campione.Come funziona RadiusNeighborsRegressor:
- Dati di input: Si parte da un set di dati che include le caratteristiche (variabili indipendenti) e la variabile target (continua).
- Impostazione del raggio: RadiusNeighborsRegressor richiede l'impostazione di un raggio fisso per determinare i vicini più prossimi per ogni campione nello spazio delle caratteristiche.
- Definizione di vicino: Per ogni campione, vengono determinati tutti i punti dei dati all'interno del raggio specificato, che diventano vicini di quel campione.
- Media ponderata: Per prevedere il valore della variabile target per ogni campione, si utilizzano i valori delle variabili target dei suoi vicini. Spesso si ricorre alla media ponderata, in cui i pesi dipendono dalla distanza tra i campioni.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori della variabile target su nuovi dati basandosi sui vicini più prossimi nello spazio delle caratteristiche.
- Versatilità: RadiusNeighborsRegressor può essere utilizzato per compiti di regressione, in particolare quando il numero di vicini può variare significativamente in base al raggio.
- Resilienza ai valori anomali: Un approccio basato sui vicini può essere resistente ai valori anomali perché il modello considera solo i punti dei dati vicini.
- Dipendenza dalla selezione del raggio: La scelta del raggio giusto può richiedere una messa a punto e una sperimentazione.
- Complessità computazionale: La gestione di grandi set di dati può richiedere notevoli risorse computazionali.
2.1.26.1. Codice per creare RadiusNeighborsRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.neighbors.RadiusNeighborsRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# RadiusNeighborsRegressor.py
# Il codice dimostra il processo di addestramento del modello RadiusNeighborsRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"
# creare un modello RadiusNeighborsRegressor
regression_model = RadiusNeighborsRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello RadiusNeighborsRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"
# creare un modello RadiusNeighborsRegressor
regression_model = RadiusNeighborsRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python RadiusNeighborsRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9999521132921395 Python Mean Absolute Error: 0.591458244376554 Python Mean Squared Error: 0.6336732353950723 Python Python RadiusNeighborsRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999971 Python Mean Absolute Error: 4.393654615473253e-06 Python Mean Squared Error: 3.829042036424747e-11 Python R^2 matching decimal places: 4 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python RadiusNeighborsRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 1.0 Python Mean Absolute Error: 0.0 Python Mean Squared Error: 0.0 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python double ONNX model precision: 0
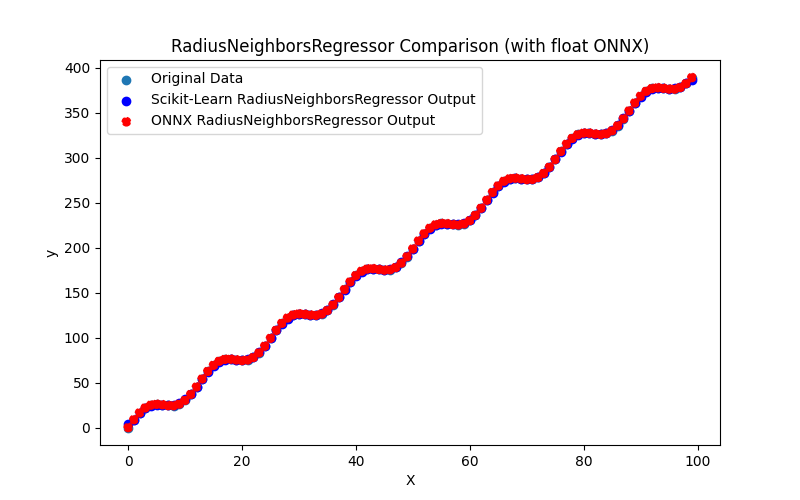
Fig.85. Risultati di RadiusNeighborsRegressor.py (float ONNX)
2.1.26.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati radius_neighbors_regressor_float.onnx e radius_neighbors_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| RadiusNeighborsRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RadiusNeighborsRegressor" #define ONNXFilenameFloat "radius_neighbors_regressor_float.onnx" #define ONNXFilenameDouble "radius_neighbors_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
RadiusNeighborsRegressor (EURUSD,H1) Testing ONNX float: RadiusNeighborsRegressor (radius_neighbors_regressor_float.onnx) RadiusNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 RadiusNeighborsRegressor (EURUSD,H1) RadiusNeighborsRegressor (EURUSD,H1) Testing ONNX double: RadiusNeighborsRegressor (radius_neighbors_regressor_double.onnx) RadiusNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 1.0000000000000000 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000000000000000 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000000000
2.1.26.3. Rappresentazione ONNX di radius_neighbors_regressor_float.onnx e radius_neighbors_regressor_double.onnx
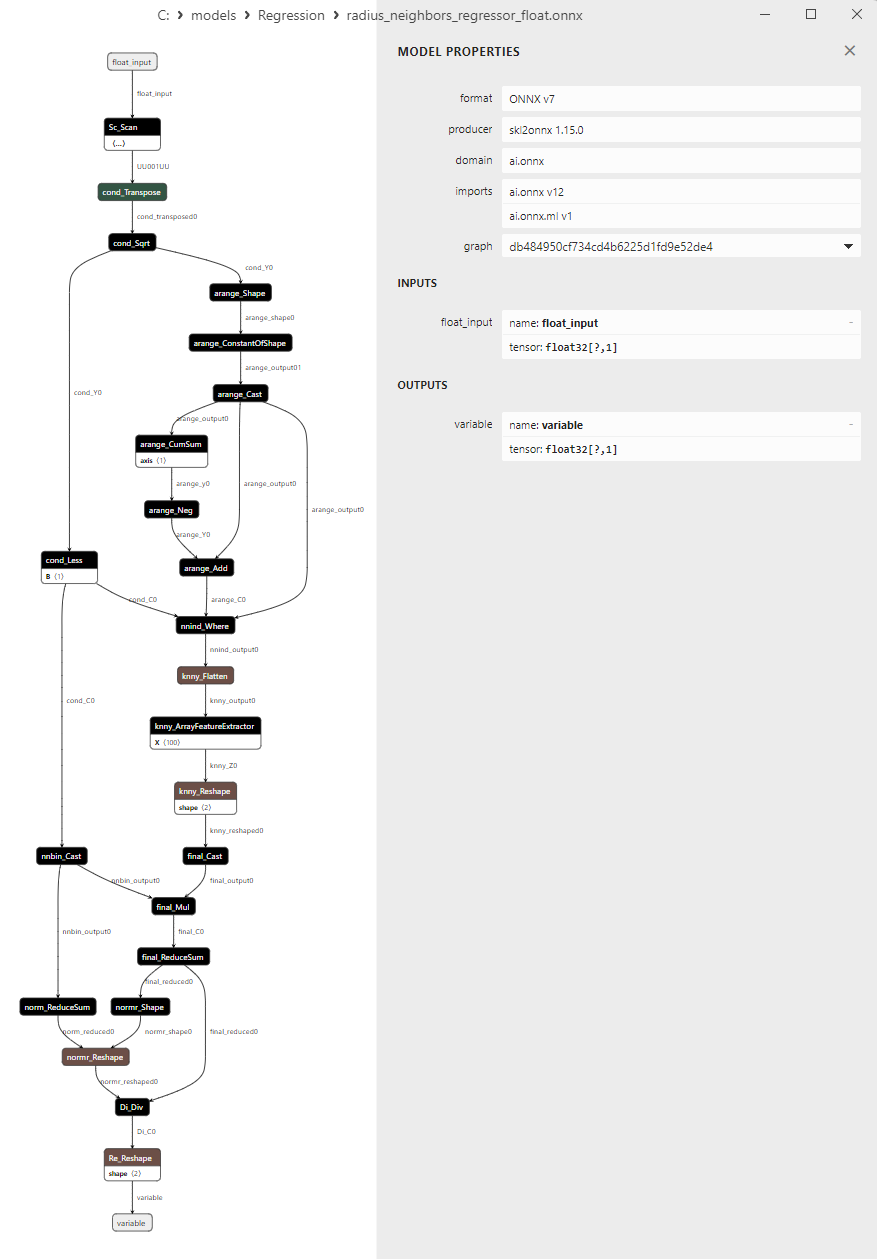
Fig.86. Rappresentazione ONNX di radius_neighbors_regressor_float.onnx in Netron
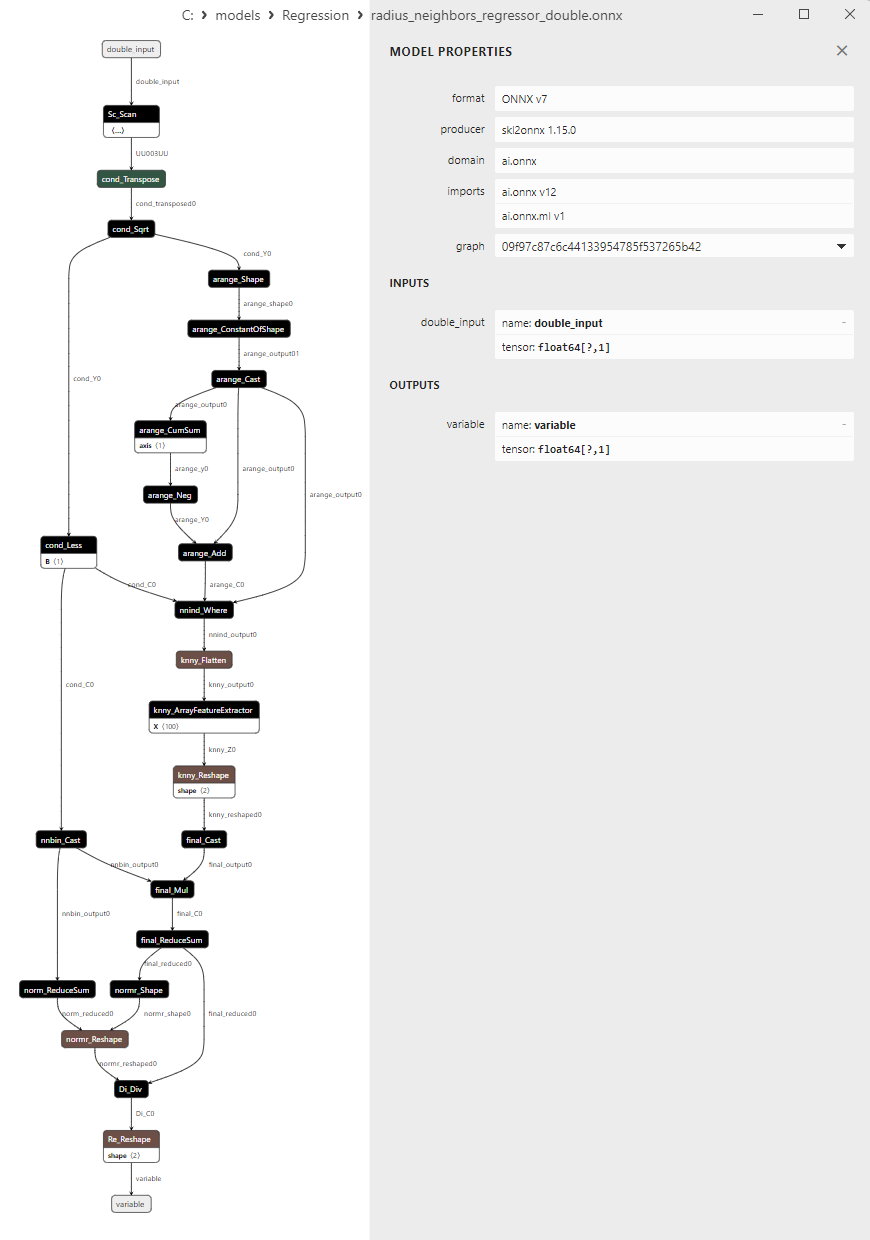
Fig.87. ONNX-ripresentazione di radius_neighbors_regressor_double.onnx in Netron
2.1.27. sklearn.neighbors.KNeighborsRegressor
KNeighborsRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione.
Appartiene alla categoria degli algoritmi k-Nearest Neighbors (k-NN) e viene utilizzato per prevedere i valori numerici della variabile target in base alla prossimità (similarità) tra gli oggetti nel set di dati di addestramento.
Come funziona KNeighborsRegressor:
- Dati di input: Si inizia con il set di dati iniziale, che comprende le caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target.
- Selezione del numero di vicini (k): È necessario scegliere il numero di vicini (k) da considerare durante la previsione. Questo numero è uno degli iperparametri del modello.
- Calcolo della prossimità: Per i nuovi dati (punti per i quali è necessaria una previsione), viene calcolata la distanza o la similarità tra questi dati e tutti gli oggetti del set di dati di addestramento.
- Scelta di k vicini: vengono selezionati i k oggetti del set di dati di addestramento più vicini ai nuovi dati.
- Previsione: Per i compiti di regressione, la previsione del valore della variabile target per i nuovi dati viene calcolata come il valore medio delle variabili target dei k vicini più prossimi.
Vantaggi di KNeighborsRegressor:
- Facilità d'uso: KNeighborsRegressor è un algoritmo semplice che non richiede una complessa pre elaborazione dei dati.
- Natura non parametrica: Il metodo non presuppone una specifica forma funzionale di dipendenza tra le caratteristiche e la variabile target, consentendo la modellazione di relazioni diverse.
- Riproducibilità: I risultati di KNeighborsRegressor possono essere riprodotti poiché le previsioni si basano sulla prossimità dei dati.
Limitazioni di KNeighborsRegressor:
- Complessità computazionale: Il calcolo delle distanze da tutti i punti del set di dati di addestramento può essere computazionalmente costoso per grandi volumi di dati.
- Sensibilità alla scelta del numero di vicini: La selezione del valore ottimale di k richiede una messa a punto e può influire significativamente sulle prestazioni del modello.
- Sensibilità al rumore: Il metodo può essere sensibile al rumore dei dati e ai valori anomali.
KNeighborsRegressor è utile nei compiti di regressione in cui è essenziale considerare i vicini degli oggetti per prevedere la variabile target. Può essere particolarmente utile in situazioni in cui la relazione tra le caratteristiche e la variabile target è non lineare e complessa.
2.1.27.1. Codice per la creazione del modello KNeighborsRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.neighbors.KNeighborsRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# KNeighborsRegressor.py
# Il codice dimostra il processo di addestramento del modello KNeighborsRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"
# creare un modello KNeighbors Regressor
kneighbors_model = KNeighborsRegressor(n_neighbors=5)
# Adattare il modello ai dati
kneighbors_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = kneighbors_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello KNeighborsRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"
# creare un modello KNeighbors Regressor
kneighbors_model = KNeighborsRegressor(n_neighbors=5)
# Adattare il modello ai dati
kneighbors_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = kneighbors_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python KNeighborsRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9995599863346534 Python Mean Absolute Error: 1.7414210057117578 Python Mean Squared Error: 5.822594523532273 Python Python KNeighborsRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9995599867417418 Python Mean Absolute Error: 1.7414195457976402 Python Mean Squared Error: 5.8225891366283875 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 4 Python MSE matching decimal places: 4 Python float ONNX model precision: 4 Python Python KNeighborsRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9995599863346534 Python Mean Absolute Error: 1.7414210057117583 Python Mean Squared Error: 5.822594523532269 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 13 Python double ONNX model precision: 14
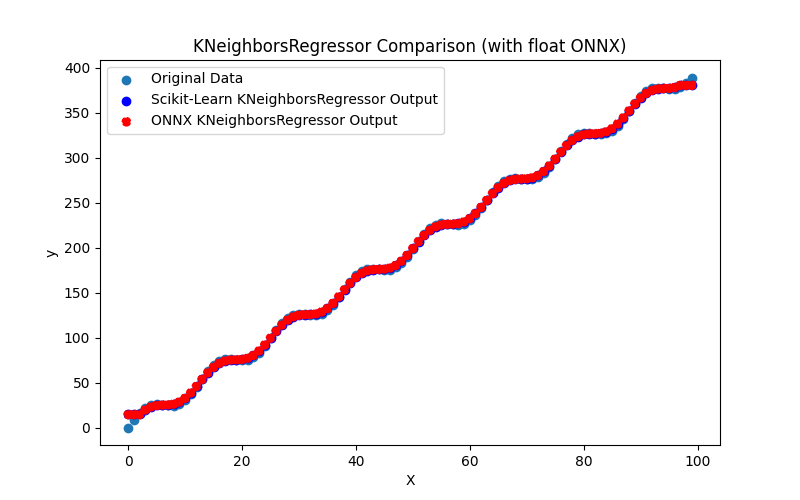
Fig.88. Risultati di KNeighborsRegressor.py (float ONNX)
2.1.27.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati kneighbors_regressor_float.onnx e kneighbors_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| KNeighborsRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "KNeighborsRegressor" #define ONNXFilenameFloat "kneighbors_regressor_float.onnx" #define ONNXFilenameDouble "kneighbors_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
KNeighborsRegressor (EURUSD,H1) Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx) KNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9995599860116634 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.7414200607817711 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 5.8225987975798184 KNeighborsRegressor (EURUSD,H1) KNeighborsRegressor (EURUSD,H1) Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx) KNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9995599863346534 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.7414210057117601 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 5.8225945235322705
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx) Python Mean Absolute Error: 1.7414210057117578 MQL5: Mean Absolute Error: 1.7414200607817711 Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx) Python Mean Absolute Error: 1.7414210057117578 MQL5: Mean Absolute Error: 1.7414210057117601
Precisione di ONNX float MAE: 5 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.27.3. Rappresentazione ONNX di kneighbors_regressor_float.onnx e kneighbors_regressor_double.onnx
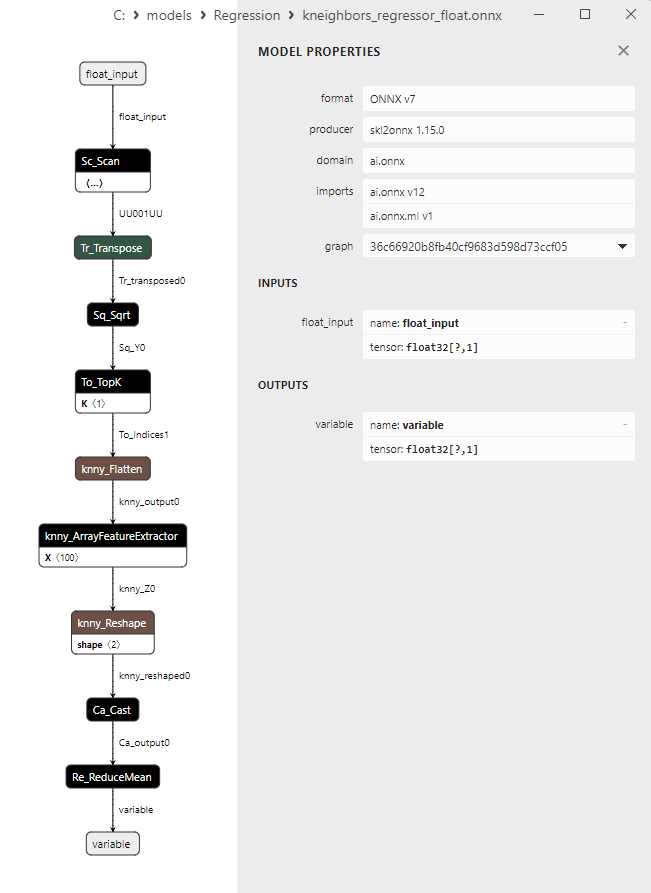
Fig.89. Rappresentazione ONNX di kneighbors_regressor_float.onnx in Netron
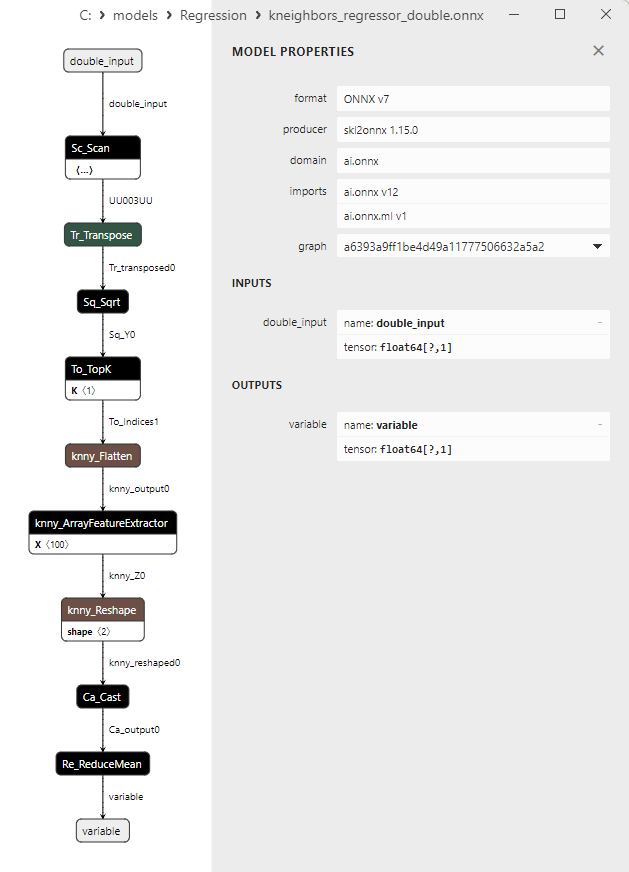
Fig.90. Rappresentazione ONNX di kneighbors_regressor_double.onnx in Netron
2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
GaussianProcessRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione che consente di modellare l'incertezza nelle previsioni.
Gaussian Process (GP) è un potente strumento dell'apprendimento automatico Bayesiano ed è utilizzato per modellare funzioni complesse e prevedere i valori delle variabili target tenendo conto dell'incertezza.
Come funziona GaussianProcessRegressor:
- Dati di input: Si inizia con il set di dati iniziale, che comprende le caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target.
- Modellazione del processo Gaussiano: Gaussian Process impiega un processo Gaussiano, ovvero un insieme di variabili casuali descritte da una distribuzione Gaussiana (normale). La GP modella non solo i valori medi di ciascun punto di dati, ma anche la covarianza (o similarità) tra questi punti.
- Scelta della funzione di covarianza: Un aspetto cruciale della GP è la selezione della funzione di covarianza (o kernel) che determina l'interconnessione e la forza tra i punti dei dati. È possibile utilizzare diverse funzioni di covarianza in base alla natura dei dati e al compito da svolgere.
- Addestramento del modello: GaussianProcessRegressor addestra il GP utilizzando i dati di addestramento. Durante l'addestramento, il modello regola i parametri della funzione di covarianza e valuta l'incertezza delle previsioni.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati. Una caratteristica importante di GP è che prevede non solo il valore medio, ma anche un intervallo di affidabilità che stima il livello di certezza nelle previsioni.
Vantaggi di GaussianProcessRegressor:
- Modellare l'incertezza: GP consente di tenere conto dell'incertezza nelle previsioni, il che è vantaggioso nei compiti in cui è fondamentale conoscere l’affidabilità nei valori previsti.
- Flessibilità: GP può modellare diverse funzioni e le sue funzioni di covarianza possono essere adattate a diversi tipi di dati.
- Pochi iperparametri: GP ha un numero relativamente ridotto di iperparametri, semplificando la messa a punto del modello.
Limitazioni di GaussianProcessRegressor:
- Complessità computazionale: GP può essere costosa dal punto di vista computazionale, soprattutto con un grande volume di dati.
- Inefficienza negli spazi ad alta dimensione: GP potrebbe perdere efficienza in compiti con numerose caratteristiche a causa della maledizione della dimensionalità.
GaussianProcessRegressor è utile nelle attività di regressione in cui è fondamentale modellare l'incertezza e fornire previsioni affidabili. Questo metodo è spesso utilizzato nell'apprendimento automatico Bayesiano e nella meta-analisi.
2.1.28.1. Codice per la creazione del modello GaussianProcessRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.gaussian_process.GaussianProcessRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# GaussianProcessRegressor.py
# Il codice dimostra il processo di addestramento del modello GaussianProcessRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"
# creare un modello GaussianProcessRegressor
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
# Adattare il modello ai dati
gp_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = gp_model.predict(X, return_std=False)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello GaussianProcessRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"
# creare un modello GaussianProcessRegressor
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
# Adattare il modello ai dati
gp_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = gp_model.predict(X, return_std=False)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python GaussianProcessRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 3.504041501400934e-13 Python Mean Squared Error: 1.6396606443650807e-25 Python Python GaussianProcessRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: GPmean, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999936 Python Mean Absolute Error: 6.454076974495848e-06 Python Mean Squared Error: 8.493606782250733e-11 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python GaussianProcessRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: GPmean, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 1.0 Python Mean Absolute Error: 3.504041501400934e-13 Python Mean Squared Error: 1.6396606443650807e-25 Python R^2 matching decimal places: 1 Python MAE matching decimal places: 19 Python MSE matching decimal places: 20 Python double ONNX model precision: 19
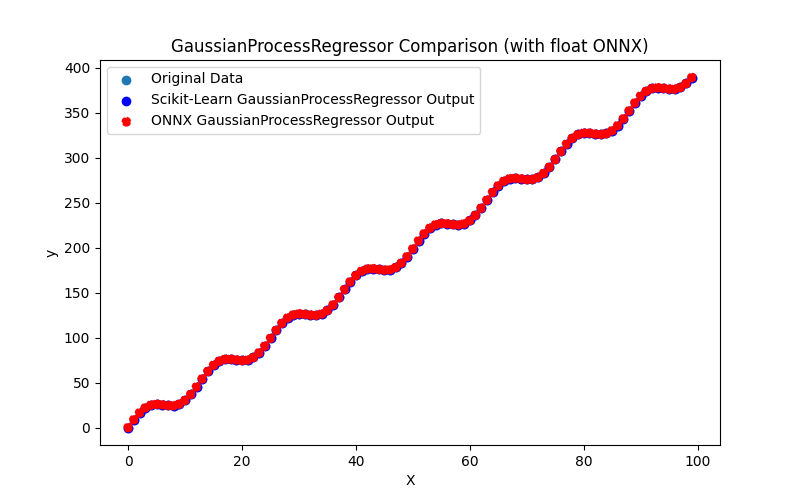
Fig.91. Risultati di GaussianProcessRegressor.py (float ONNX)
2.1.28.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati gaussian_process_regressor_float.onnx e gaussian_process_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| GaussianProcessRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GaussianProcessRegressor" #define ONNXFilenameFloat "gaussian_process_regressor_float.onnx" #define ONNXFilenameDouble "gaussian_process_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
GaussianProcessRegressor (EURUSD,H1) Testing ONNX float: GaussianProcessRegressor (gaussian_process_regressor_float.onnx) GaussianProcessRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999936 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000064540769745 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000849361 GaussianProcessRegressor (EURUSD,H1) GaussianProcessRegressor (EURUSD,H1) Testing ONNX double: GaussianProcessRegressor (gaussian_process_regressor_double.onnx) GaussianProcessRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 1.0000000000000000 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000000000003504 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000000000
2.1.28.3. Rappresentazione ONNX di gaussian_process_regressor_float.onnx e gaussian_process_regressor_double.onnx
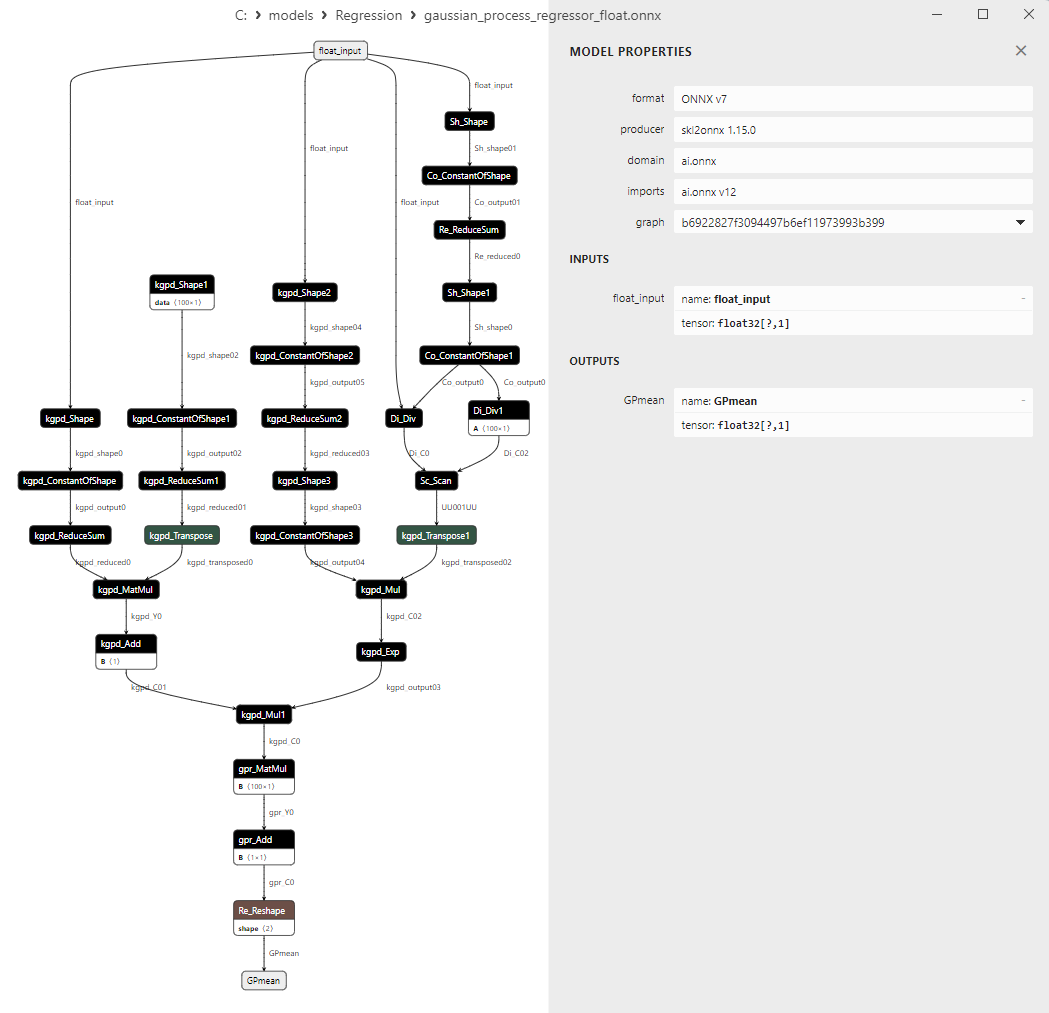
Fig.92. Rappresentazione ONNX di gaussian_process_regressor_float.onnx in Netron
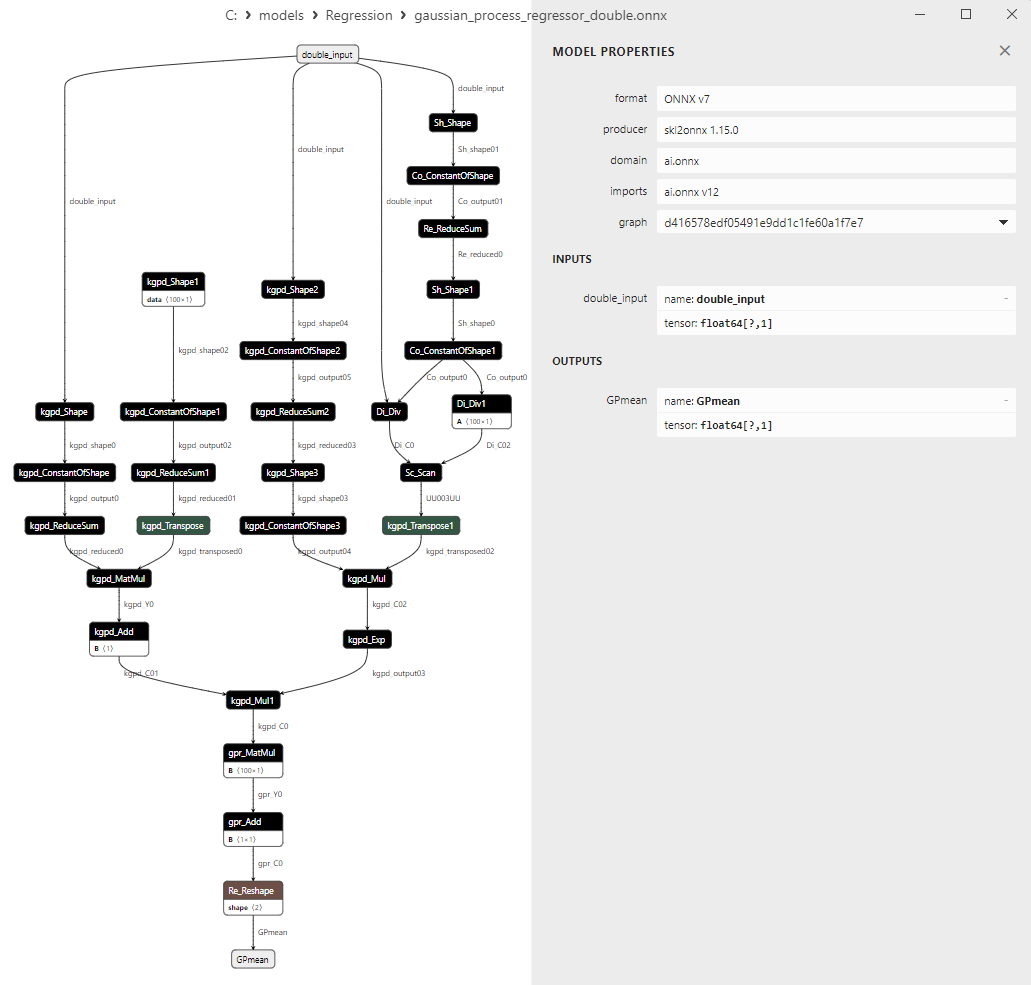
Fig.93. Rappresentazione ONNX di gaussian_process_regressor_double.onnx in Netron
2.1.29. sklearn.linear_model.GammaRegressor
GammaRegressor è un metodo di apprendimento automatico progettato per compiti di regressione in cui la variabile target segue una distribuzione gamma.
La distribuzione gamma è una distribuzione di probabilità utilizzata per modellare variabili casuali positive e continue. Questo metodo consente di modellare e prevedere valori numerici positivi, come costi, tempi o proporzioni.
Come funziona GammaRegressor:
- Dati di input: Si parte dal set di dati iniziale, in cui sono presenti caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target che seguono la distribuzione gamma.
- Selezione della funzione di perdita: GammaRegressor utilizza una funzione di perdita che corrisponde alla distribuzione gamma e considera le peculiarità di questa distribuzione. Ciò consente di modellare i dati tenendo conto della non negatività e della giusta inclinazione della distribuzione gamma.
- Addestramento del modello: Il modello viene addestrato sui dati utilizzando la funzione di perdita scelta. Durante l'addestramento, regola i parametri del modello per minimizzare la funzione di perdita.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori della variabile target per i nuovi dati.
Vantaggi di GammaRegressor:
- Modellare i valori positivi: Questo metodo è stato progettato specificamente per la modellazione di valori numerici positivi, il che può essere utile in compiti in cui la variabile target ha un limite inferiore.
- Considerare la forma della distribuzione gamma: GammaRegressor tiene conto delle caratteristiche della distribuzione gamma, consentendo una modellazione più accurata dei dati che seguono questa distribuzione.
- Utilità nell'econometria e nella ricerca medica: La distribuzione gamma è spesso utilizzata per modellare i costi, i tempi di attesa e altre variabili casuali positive in econometria e nella ricerca medica.
Limitazioni di GammaRegressor:
- Limitazione del tipo di dati: Questo metodo è adatto solo per compiti di regressione in cui la variabile target segue la distribuzione gamma o distribuzioni simili. Per i dati non conformi a tale distribuzione, questo metodo potrebbe non essere efficace.
- Richiede la scelta di una funzione di perdita: La scelta di una funzione di perdita appropriata potrebbe richiedere la conoscenza della distribuzione della variabile target e delle sue caratteristiche.
GammaRegressor è utile nei compiti che richiedono la modellazione e la previsione di valori numerici positivi che si allineano alla distribuzione gamma.
2.1.29.1. Codice per creare il modello GammaRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.GammaRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# GammaRegressor.py
# Il codice dimostra il processo di addestramento del modello GammaRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)
model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"
# creare un modello Gamma Regressor
regression_model = GammaRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello GammaRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)
model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"
# creare un modello Gamma Regressor
regression_model = GammaRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python GammaRegressor Original model (double) Python R-squared (Coefficient of determination): 0.7963797339354436 Python Mean Absolute Error: 37.266200319422815 Python Mean Squared Error: 2694.457784927322 Python Python GammaRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.7963795030042045 Python Mean Absolute Error: 37.266211754095956 Python Mean Squared Error: 2694.4608407846144 Python R^2 matching decimal places: 6 Python MAE matching decimal places: 4 Python MSE matching decimal places: 1 Python float ONNX model precision: 4 Python Python GammaRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.7963797339354436 Python Mean Absolute Error: 37.266200319422815 Python Mean Squared Error: 2694.457784927322 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 12 Python double ONNX model precision: 15
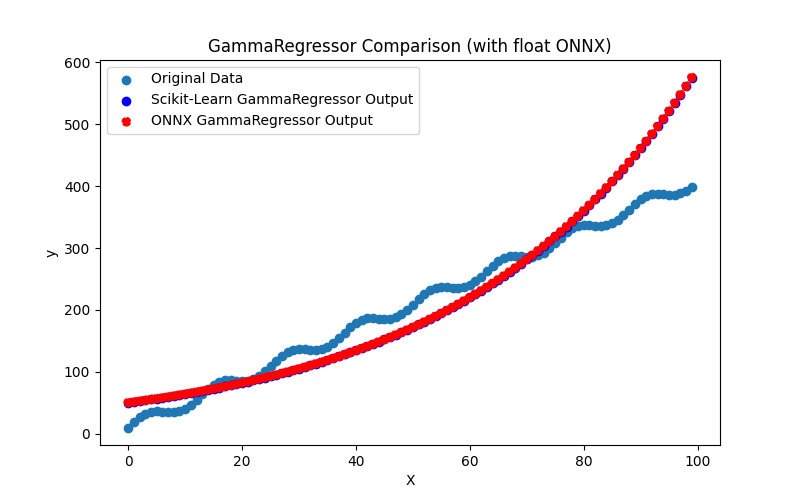
Fig.94. Risultati di GammaRegressor.py (float ONNX)
2.1.29.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati gamma_regressor_float.onnx e gamma_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| GammaRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GammaRegressor" #define ONNXFilenameFloat "gamma_regressor_float.onnx" #define ONNXFilenameDouble "gamma_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(10+4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
GammaRegressor (EURUSD,H1) Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx) GammaRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.7963795030042045 GammaRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 37.2662117540959628 GammaRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2694.4608407846144473 GammaRegressor (EURUSD,H1) GammaRegressor (EURUSD,H1) Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx) GammaRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.7963797339354435 GammaRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 37.2662003194228220 GammaRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2694.4577849273218817
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx) Python Mean Absolute Error: 37.266200319422815 MQL5: Mean Absolute Error: 37.2662117540959628 Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx) Python Mean Absolute Error: 37.266200319422815 MQL5: Mean Absolute Error: 37.2662003194228220
Precisione di ONNX float MAE: 4 cifre decimali, Precisione di ONNX double MAE: 13 cifre decimali.
2.1.29.3. Rappresentazione ONNX di gamma_regressor_float.onnx e gamma_regressor_double.onnx
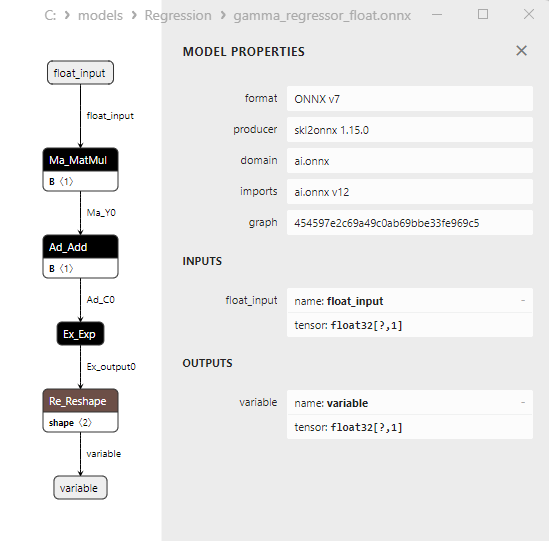
Fig.95. Rappresentazione ONNX di gamma_regressor_float.onnx in Netron
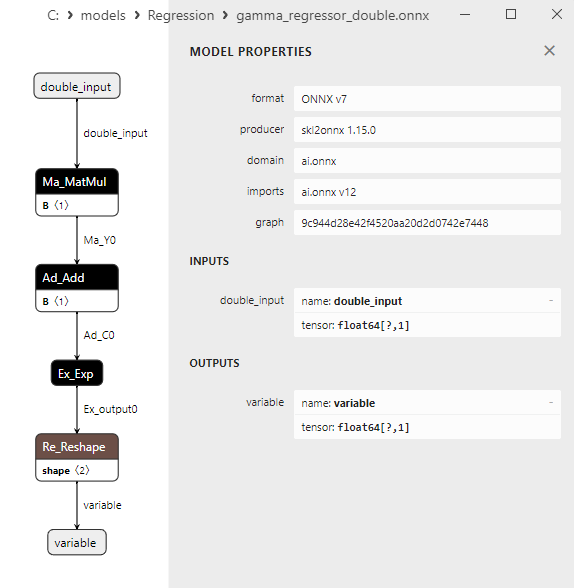
Fig.96. Rappresentazione ONNX di gamma_regressor_double.onnx in Netron
2.1.30. sklearn.linear_model.SGDRegressor
SGDRegressor è un metodo di regressione che utilizza la Stochastic Gradient Descent (SGD) per addestrare un modello di regressione. Fa parte della famiglia dei modelli lineari e può essere utilizzato per compiti di regressione. Le caratteristiche principali di SGDRegressor sono l'efficienza e la capacità di gestire grandi volumi di dati.
Come funziona SGDRegressor:
- Regressione lineare: Simile a Ridge e Lasso, SGDRegressor mira a trovare una relazione lineare tra le variabili indipendenti (caratteristiche) e la variabile target in un problema di regressione.
- Stochastic Gradient Descent: La base di SGDRegressor è la discesa stocastica del gradiente. Invece di calcolare i gradienti sull'intero set di dati di addestramento, aggiorna il modello sulla base di piccole quantità di dati selezionati casualmente. Ciò consente di addestrare in modo efficiente i modelli e di lavorare con set di dati consistenti.
- Regolarizzazione: SGDRegressor supporta la regolarizzazione L1 e L2 (Lasso e Ridge). Questo aiuta a controllare l'overfitting e a migliorare la stabilità del modello.
- Iperparametri: Come Ridge e Lasso, SGDRegressor consente di regolare gli iperparametri come il parametro di regolarizzazione (α, alfa) e il tipo di regolarizzazione.
Vantaggi di SGDRegressor:
- Efficienza: SGDRegressor si comporta bene con grandi set di dati e addestra in modo efficiente i modelli su dati estesi.
- Possibilità di regolarizzazione: La possibilità di applicare la regolarizzazione L1 e L2 rende questo metodo adatto a gestire i problemi di overfitting.
- Discesa adattativa del gradiente: La discesa stocastica del gradiente consente di adattarsi al cambiamento dei dati e di addestrare i modelli al volo.
Limitazioni di SGDRegressor:
- Sensibilità alla scelta dell'iperparametro: La regolazione di iperparametri come il tasso di apprendimento e il coefficiente di regolarizzazione può richiedere una sperimentazione.
- Non sempre converge al minimo globale: A causa della natura stocastica della discesa del gradiente, SGDRegressor non sempre converge al minimo globale della funzione di perdita.
SGDRegressor è un metodo di regressione che utilizza la discesa stocastica del gradiente per addestrare un modello di regressione. È efficiente, in grado di gestire grandi set di dati e supporta la regolarizzazione per gestire l'overfitting.
2.1.30.1. Codice per la creazione del modello SGDRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.SGDRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# SGDRegressor2.py
# Il codice dimostra il processo di addestramento del modello SGDRegressor, la sua esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)
model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"
# creare un modello SGDRegressor
regression_model = SGDRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello SGDRegressor, la sua esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)
model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"
# creare un modello SGDRegressor
regression_model = SGDRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python SGDRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9961197872743282 Python Mean Absolute Error: 0.6405924406136998 Python Mean Squared Error: 0.5169867345998348 Python Python SGDRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9961197876338647 Python Mean Absolute Error: 0.6405924014799271 Python Mean Squared Error: 0.5169866866963753 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 7 Python MSE matching decimal places: 6 Python float ONNX model precision: 7 Python Python SGDRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9961197872743282 Python Mean Absolute Error: 0.6405924406136998 Python Mean Squared Error: 0.5169867345998348 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 16 Python double ONNX model precision: 16
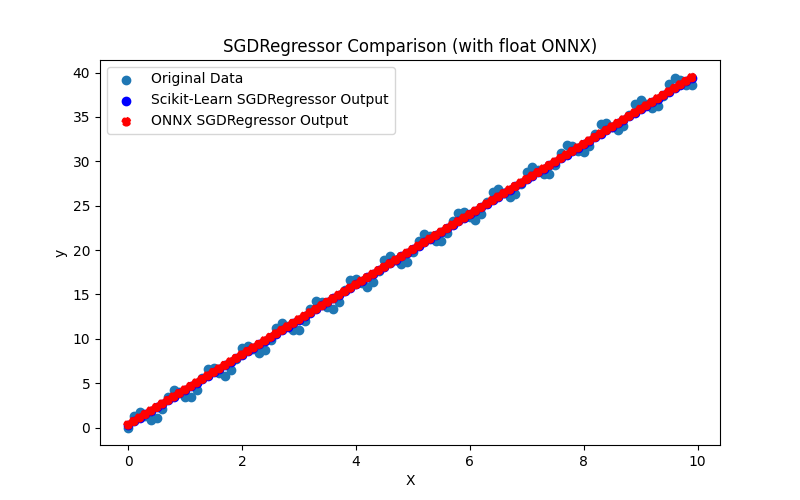
Fig.97. Risultati di SGDRegressor.py (float ONNX)
2.1.30.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati sgd_regressor_float.onnx e sgd_rgressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| SGDRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "SGDRegressor" #define ONNXFilenameFloat "sgd_regressor_float.onnx" #define ONNXFilenameDouble "sgd_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i*0.1; y[i]=(double)(4*x[i] + sin(x[i]*10)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
SGDRegressor (EURUSD,H1) Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx) SGDRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9961197876338647 SGDRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.6405924014799272 SGDRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.5169866866963754 SGDRegressor (EURUSD,H1) SGDRegressor (EURUSD,H1) Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx) SGDRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9961197872743282 SGDRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.6405924406136998 SGDRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.5169867345998348
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx) Python Mean Absolute Error: 0.6405924406136998 MQL5: Mean Absolute Error: 0.6405924014799272 Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx) Python Mean Absolute Error: 0.6405924406136998 MQL5: Mean Absolute Error: 0.6405924406136998
Precisione di ONNX float MAE: 7 cifre decimali, Precisione di ONNX double MAE: 16 cifre decimali.
2.1.30.3. Rappresentazione ONNX di sgd_regressor_float.onnx e sgd_regressor_double.onnx
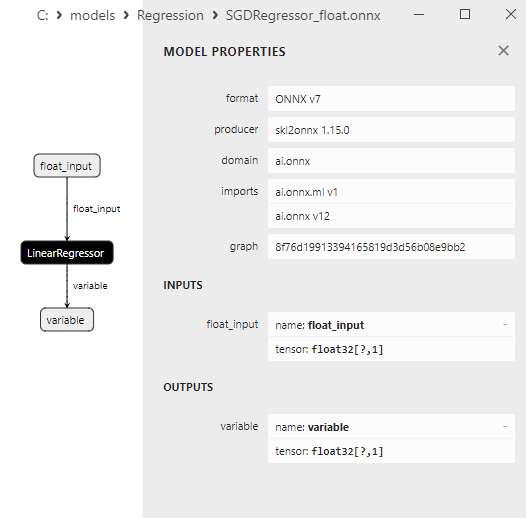
Fig.98. Rappresentazione ONNX del sgd_regressor_float.onnx in Netron
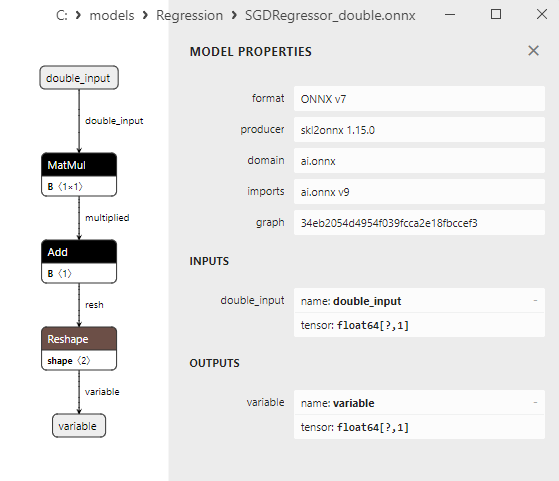
Fig.99. Rappresentazione ONNX di sgd_rgressor_double.onnx in Netron
2.2. Modelli di regressione dalla libreria Scikit-learn che vengono convertiti solo in modelli ONNX con precisione float
Questa sezione riguarda i modelli che possono funzionare solo con precisione float. La conversione in ONNX con precisione double porta a errori legati alle limitazioni degli operatori ONNX ai.onnx.ml.
2.2.1. sklearn.linear_model.AdaBoostRegressor
AdaBoostRegressor - è un metodo di apprendimento automatico utilizzato per la regressione, che implica la previsione di valori numerici (ad esempio, prezzi degli immobili, volumi di vendita, ecc.).
Questo metodo è una variante dell'algoritmo AdaBoost (Adaptive Boosting), sviluppato inizialmente per compiti di classificazione.
Come funziona AdaBoostRegressor:
- Set di dati originali: Si parte dal set di dati originale contenente le caratteristiche (variabili indipendenti) e le corrispondenti variabili target (variabili dipendenti che si vogliono prevedere).
- Inizializzazione del peso: Inizialmente, ogni punto di dati (osservazione) ha pesi uguali e il modello viene costruito sulla base di questo set di dati ponderati.
- Addestramento degli apprendisti deboli: AdaBoostRegressor costruisce diversi modelli di regressione deboli (ad esempio, alberi decisionali) che cercano di prevedere la variabile target. Questi modelli sono definiti "apprendisti deboli". Ogni apprendista debole viene addestrato sui dati tenendo conto dei pesi di ogni osservazione.
- Selezione dei pesi dell’apprendista debole: AdaBoostRegressor calcola i pesi per ciascun apprendista debole in base al suo rendimento nelle previsioni. Gli apprendisti che fanno previsioni più accurate ricevono pesi maggiori e viceversa.
- Aggiornamento dei pesi delle osservazioni: I pesi delle osservazioni vengono aggiornati in modo che le osservazioni precedentemente previste in modo errato ricevano pesi maggiori, aumentando così la loro importanza per il modello successivo.
- Previsione finale: AdaBoostRegressor combina le previsioni di tutti gli apprendisti deboli, assegnando pesi in base alle loro prestazioni. In questo modo si ottiene la previsione finale del modello.
Vantaggi di AdaBoostRegressor:
- Adattabilità: AdaBoostRegressor si adatta a funzioni complesse e tratta meglio le relazioni non lineari.
- Riduzione dell'overfitting: AdaBoostRegressor utilizza la regolarizzazione attraverso l'aggiornamento dei pesi di osservazione, aiutando a prevenire l'overfitting.
- Un gruppo potente: Combinando più modelli deboli, AdaBoostRegressor può creare modelli forti in grado di prevedere la variabile target in modo abbastanza accurato.
Limitazioni di AdaBoostRegressor:
- Sensibilità ai valori anomali: AdaBoostRegressor è sensibile ai valori anomali dei dati, che influiscono sulla qualità della previsione.
- Costi computazionali elevati: La costruzione di più apprendisti deboli potrebbe richiedere più risorse computazionali e tempo.
- Non sempre è la scelta migliore: AdaBoostRegressor non è sempre la scelta ottimale e, in alcuni casi, altri metodi di regressione potrebbero dare risultati migliori.
AdaBoostRegressor è un utile metodo di apprendimento automatico applicabile a vari compiti di regressione, soprattutto in situazioni in cui i dati contengono dipendenze complesse.
2.2.1.1. Codice per creare il modello AdaBoostRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.AdaBoostRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# AdaBoostRegressor.py
# Il codice dimostra il processo di addestramento del modello AdaBoostRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"
# creare un modello AdaBoostRegressor
regression_model = AdaBoostRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello AdaBoostRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"
# creare un modello AdaBoostRegressor
regression_model = AdaBoostRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python AdaBoostRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9991257208809748 Python Mean Absolute Error: 2.3678022748065457 Python Mean Squared Error: 11.569124350863143 Python Python AdaBoostRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9991257199849699 Python Mean Absolute Error: 2.36780399225718 Python Mean Squared Error: 11.569136207480646 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python AdaBoostRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx
Qui il modello è stato esportato in modelli ONNX per float e double. Il modello ONNX float è stato eseguito correttamente, mentre si è verificato un errore di esecuzione con il modello double (errori nella scheda Errori):
AdaBoostRegressor.py started AdaBoostRegressor.py 1 1 Traceback (most recent call last): AdaBoostRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) AdaBoostRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx failed:Type Error: onnxruntime_inference_collection.py 424 1 AdaBoostRegressor.py finished in 3207 ms 5 1
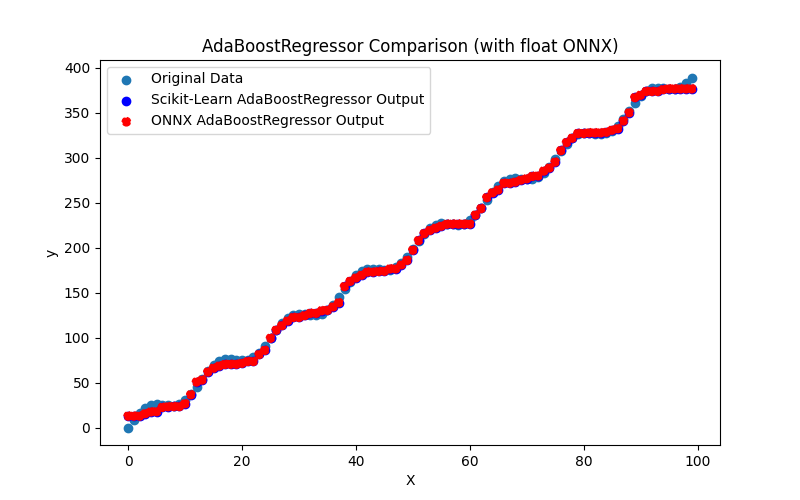
Fig.100. Risultati di AdaBoostRegressor.py (float ONNX)
2.2.1.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati adaboost_regressor_float.onnx e adaboost_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| AdaBoostRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "AdaBoostRegressor" #define ONNXFilenameFloat "adaboost_regressor_float.onnx" #define ONNXFilenameDouble "adaboost_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
AdaBoostRegressor (EURUSD,H1) AdaBoostRegressor (EURUSD,H1) Testing ONNX float: AdaBoostRegressor (adaboost_regressor_float.onnx) AdaBoostRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9991257199849699 AdaBoostRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 2.3678039922571803 AdaBoostRegressor (EURUSD,H1) MQL5: Mean Squared Error: 11.5691362074806463 AdaBoostRegressor (EURUSD,H1) AdaBoostRegressor (EURUSD,H1) Testing ONNX double: AdaBoostRegressor (adaboost_regressor_double.onnx) AdaBoostRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type parameter (T) of Optype (Mul) bound to different types (tensor(float) and tensor(double) in node (Mul).'), inspect code 'Scripts\Regression\AdaBoostRegressor.mq5' (133:16) AdaBoostRegressor (EURUSD,H1) model_name=AdaBoostRegressor OnnxCreate error 5800Il modello ONNX float è stato eseguito correttamente, mentre si è verificato un errore di esecuzione con il modello double.
2.2.1.3. Rappresentazione ONNX di adaboost_regressor_float.onnx e adaboost_regressor_double.onnx
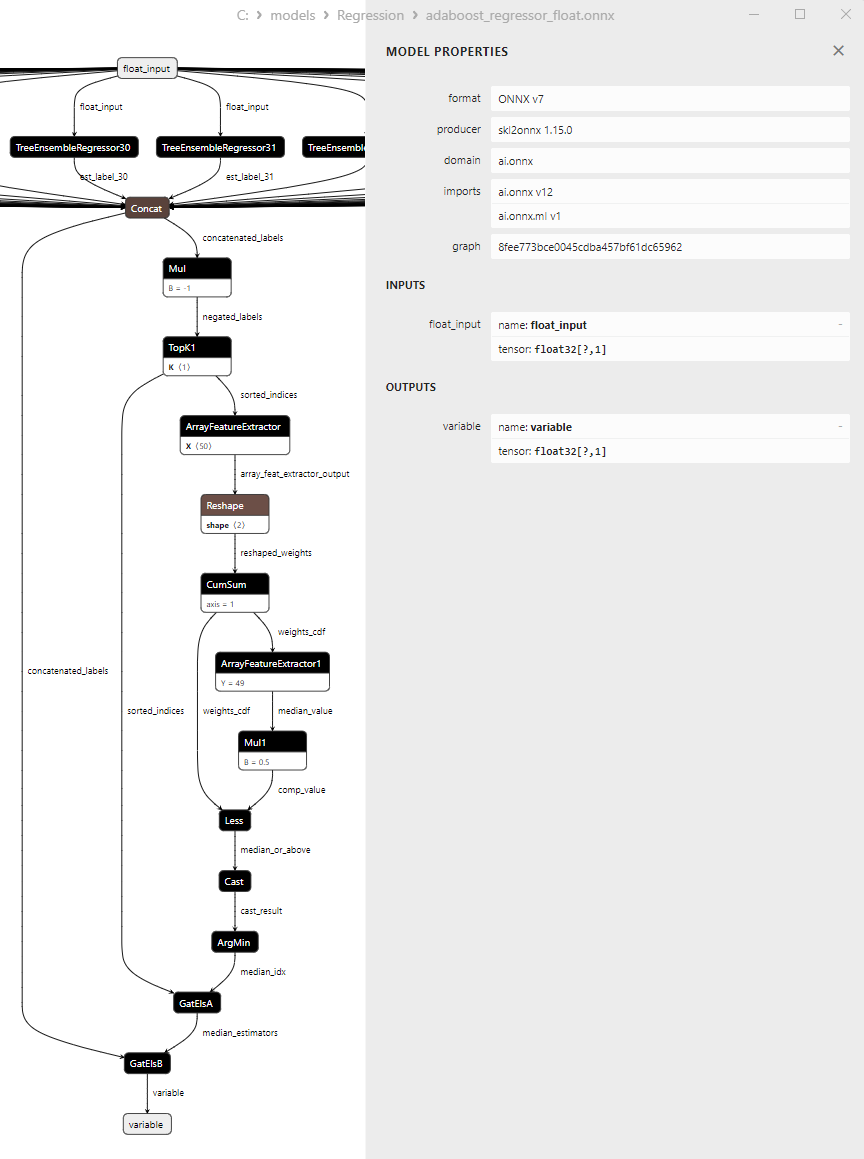
Fig.101. Rappresentazione ONNX di adaboost_regressor_float.onnx in Netron
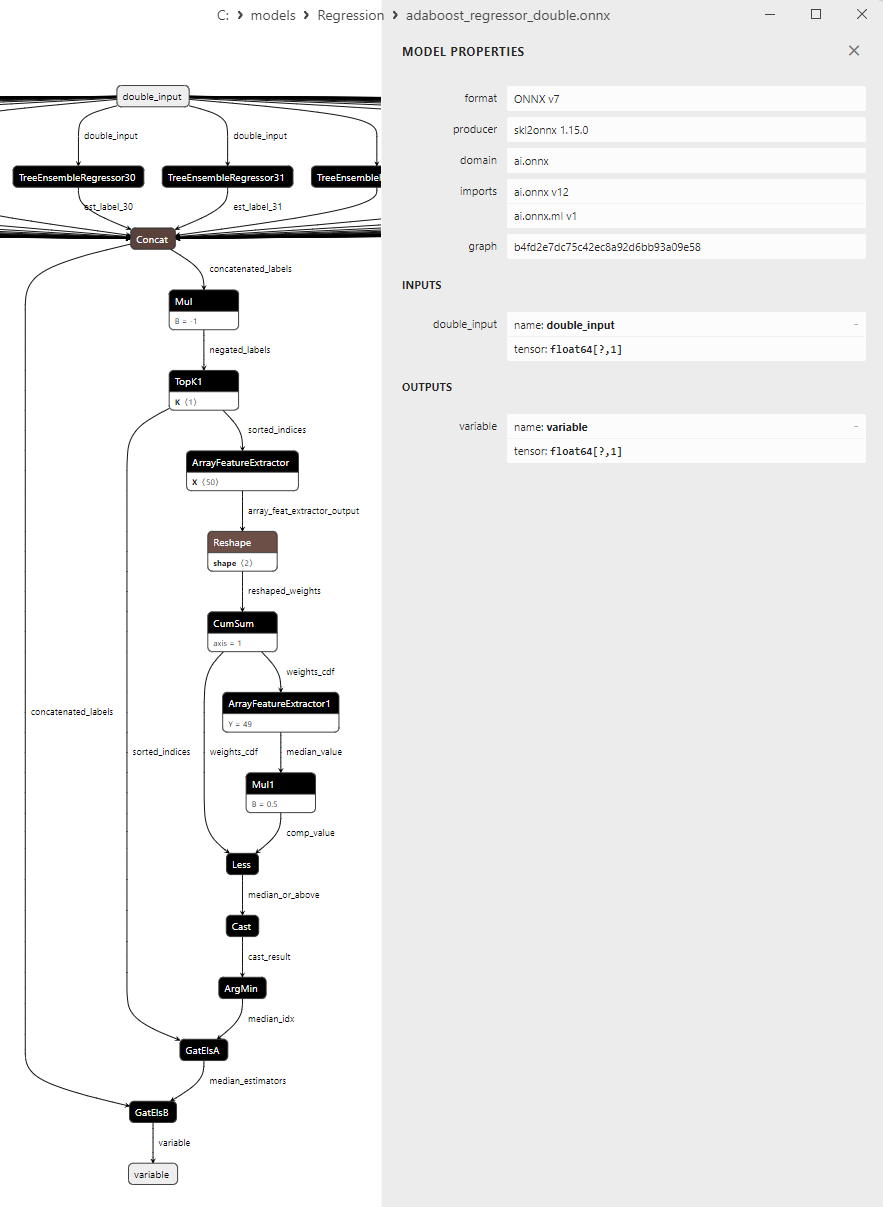
Fig.102. Rappresentazione ONNX di adaboost_regressor_double.onnx in Netron
2.2.2. sklearn.linear_model.BaggingRegressor
BaggingRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione.
Rappresenta un metodo di gruppo basato sull'idea di "bagging" (Bootstrap Aggregating), che prevede la costruzione di più modelli di regressione di base e la combinazione delle loro previsioni per ottenere un risultato più stabile e accurato.
Come funziona BaggingRegressor:
- Set di dati originali: Si parte dal set di dati originale contenente le caratteristiche (variabili indipendenti) e le corrispondenti variabili target (variabili dipendenti che si vogliono prevedere).
- Generazione di sottoinsiemi: BaggingRegressor crea casualmente diversi sottoinsiemi (campioni con sostituzione) dai dati originali. Ogni sottoinsieme contiene un insieme casuale di osservazioni dei dati originali.
- Addestramento di modelli di regressione di base: Per ogni sottoinsieme, BaggingRegressor costruisce un modello di regressione di base separato (ad esempio, albero decisionale, foresta casuale, modello di regressione lineare, ecc.)
- Previsioni dai modelli di base: Ogni modello di base viene utilizzato per prevedere la variabile target sulla base del sottoinsieme corrispondente.
- Media o combinazione: BaggingRegressor media o combina le previsioni di tutti i modelli di base per ottenere la previsione finale della regressione.
Vantaggi di BaggingRegressor:
- Riduzione della varianza: BaggingRegressor riduce la varianza del modello, rendendolo più robusto alle fluttuazioni dei dati.
- Riduzione dell'overfitting: Poiché il modello viene addestrato su diversi sottoinsiemi di dati, BaggingRegressor di solito riduce il rischio di overfitting.
- Miglioramento della generalizzazione: Combinando le previsioni di più modelli, BaggingRegressor fornisce in genere previsioni più accurate e stabili.
- Ampia gamma di modelli base: BaggingRegressor può utilizzare diversi tipi di modelli di regressione di base, rendendolo un metodo flessibile.
Limitazioni di BaggingRegressor:
- Non sempre è in grado di migliorare le prestazioni quando il modello di base ha già un buon rendimento sui dati.
- BaggingRegressor potrebbe richiedere più risorse computazionali e tempo rispetto all'addestramento di un singolo modello.
BaggingRegressor è un potente metodo di apprendimento automatico che può essere utile nelle attività di regressione, soprattutto in presenza di rumore nei dati e nella necessità di migliorare la stabilità della previsione.
2.2.2.1. Codice per la creazione del modello BaggingRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.BaggingRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# BaggingRegressor.py
# Il codice dimostra il processo di addestramento del modello BaggingRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"
# creare un modello Bagging Regressor
regression_model = BaggingRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello BaggingRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"
# creare un modello Bagging Regressor
regression_model = BaggingRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python Python BaggingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9998128324923137 Python Mean Absolute Error: 1.0257279210387649 Python Mean Squared Error: 2.4767424083953005 Python Python BaggingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9998128317934672 Python Mean Absolute Error: 1.0257282792130034 Python Mean Squared Error: 2.4767516560614187 Python R^2 matching decimal laces: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python BaggingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx
Scheda Errori:
BaggingRegressor.py started BaggingRegressor.py 1 1 Traceback (most recent call last): BaggingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) BaggingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx failed:Type Error: T onnxruntime_inference_collection.py 424 1 BaggingRegressor.py finished in 3173 ms 5 1
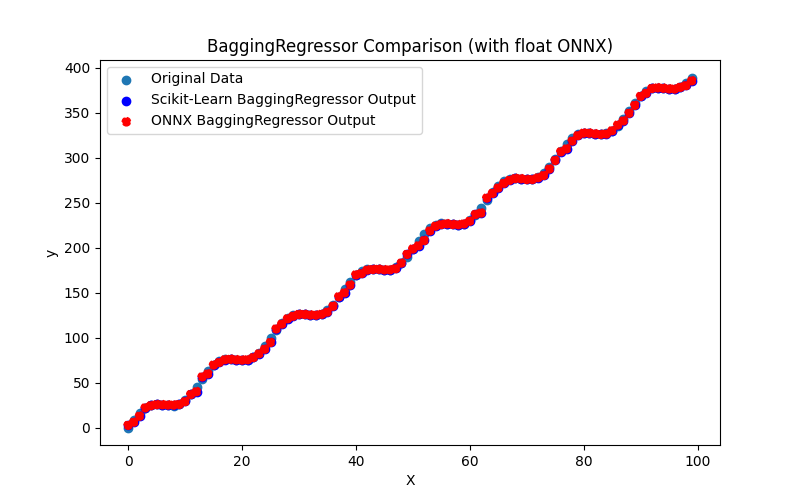
Fig.103. Risultati di BaggingRegressor.py (float ONNX)
2.2.2.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati bagging_regressor_float.onnx e bagging_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| BaggingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "BaggingRegressor" #define ONNXFilenameFloat "bagging_regressor_float.onnx" #define ONNXFilenameDouble "bagging_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
BaggingRegressor (EURUSD,H1) Testing ONNX float: BaggingRegressor (bagging_regressor_float.onnx) BaggingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9998128317934672 BaggingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.0257282792130034 BaggingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2.4767516560614196 BaggingRegressor (EURUSD,H1) BaggingRegressor (EURUSD,H1) Testing ONNX double: BaggingRegressor (bagging_regressor_double.onnx) BaggingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (ReduceMean) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\BaggingRegressor.mq5' (133:16) BaggingRegressor (EURUSD,H1) model_name=BaggingRegressor OnnxCreate error 5800
Il modello ONNX calcolato in float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello double.
2.2.2.3. Rappresentazione ONNX di bagging_regressor_float.onnx e bagging_regressor_double.onnx
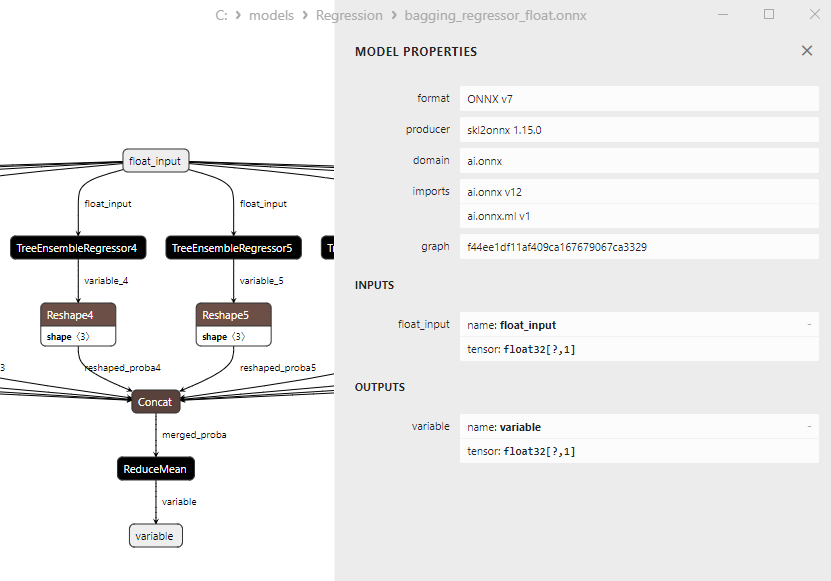
Fig.104. Rappresentazione ONNX di bagging_regressor_float.onnx in Netron
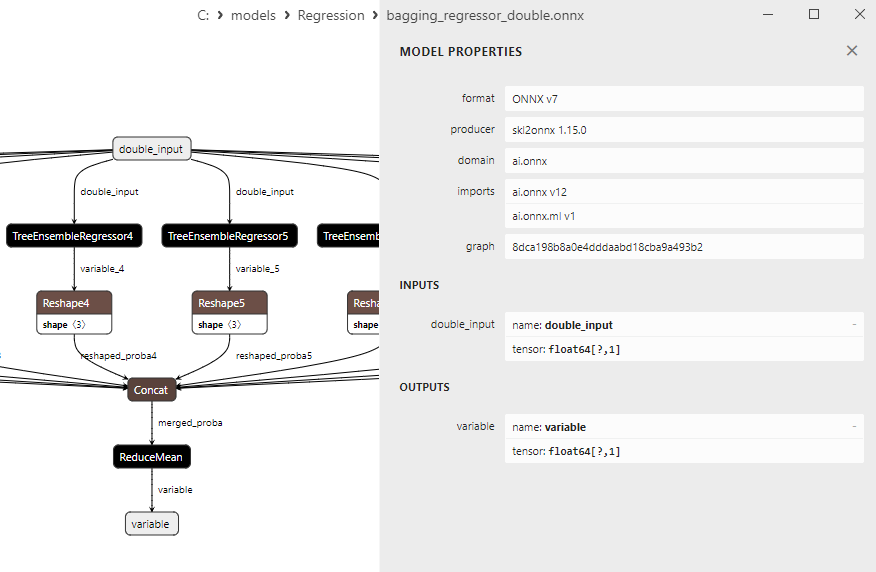
Fig.105. Rappresentazione ONNX di bagging_regressor_double.onnx in Netron
2.2.3. sklearn.linear_model.DecisionTreeRegressor
DecisionTreeRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione, prevedendo i valori numerici della variabile target sulla base di un set di caratteristiche (variabili indipendenti).
Questo metodo si basa sulla costruzione di alberi decisionali che suddividono lo spazio delle caratteristiche in intervalli e prevedono il valore della variabile target per ogni intervallo.
Principio di funzionamento di DecisionTreeRegressor:
- Inizio della struttura: Si parte dal set di dati iniziale contenente le caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target.
- Selezione e suddivisione delle caratteristiche: L'albero decisionale seleziona una caratteristica e un valore soglia che divide i dati in due o più sottogruppi. Questa suddivisione viene eseguita per minimizzare l'errore quadratico medio (la deviazione quadratica media tra i valori previsti e quelli effettivi della variabile target) all'interno di ciascun sottogruppo.
- Costruzione ricorsiva: Il processo di selezione e suddivisione delle caratteristiche viene ripetuto per ogni sottogruppo, creando sotto-alberi. Questo processo viene eseguito in modo ricorsivo fino a quando non vengono soddisfatti alcuni criteri di arresto, come la massima profondità dell'albero o il minimo di campioni in un nodo.
- Nodi foglia: Quando vengono soddisfatti i criteri di arresto, vengono creati i nodi foglia, prevedendo i valori numerici della variabile target per i campioni che rientrano in un determinato nodo foglia.
- Previsione: Per i nuovi dati, viene applicato l'albero decisionale e le nuove osservazioni attraversano l'albero fino a raggiungere un nodo foglia che prevede il valore numerico della variabile target.
Vantaggi di DecisionTreeRegressor:
- Interpretabilità: Gli alberi decisionali sono facili da comprendere e da visualizzare, rendendoli utili per spiegare il processo decisionale dei modelli.
- Robustezza ai valori anomali: Gli alberi decisionali possono essere resistenti ai valori anomali nei dati.
- Gestione di dati numerici e categorici: Gli alberi decisionali sono in grado di elaborare caratteristiche sia numeriche che categoriche senza ulteriori pre elaborazioni.
- Selezione automatica delle caratteristiche: Gli alberi possono selezionare automaticamente le caratteristiche importanti, ignorando quelle meno rilevanti.
Limitazioni di DecisionTreeRegressor:
- Vulnerabilità da overfitting: Gli alberi decisionali possono essere soggetti a overfitting, soprattutto se sono troppo profondi.
- Problemi di generalizzazione: Gli alberi decisionali possono non generalizzare bene ai dati non inclusi nel set di addestramento.
- Non sempre è una scelta ottimale: In alcuni casi, altri metodi di regressione come la regressione lineare o k-nearest neighbors potrebbero dare risultati migliori.
DecisionTreeRegressor è un metodo prezioso per le attività di regressione, soprattutto quando è fondamentale comprendere la logica decisionale del modello e visualizzare il processo.
2.2.3.1. Codice per creare il modello DecisionTreeRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.linear_model.DecisionTreeRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# DecisionTreeRegressor.py
# Il codice dimostra il processo di addestramento del modello DecisionTreeRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"
# creare un modello Decision Tree Regressor
regression_model = DecisionTreeRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello DecisionTreeRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"
# creare un modello Decision Tree Regressor
regression_model = DecisionTreeRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y)
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python DecisionTreeRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 0.0 Python Mean Squared Error: 0.0 Python Python DecisionTreeRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999971 Python Mean Absolute Error: 4.393654615473253e-06 Python Mean Squared Error: 3.829042036424747e-11 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python DecisionTreeRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx
Scheda Errori:
DecisionTreeRegressor.py started DecisionTreeRegressor.py 1 1 Traceback (most recent call last): DecisionTreeRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) DecisionTreeRegressor.py 160 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx failed:Type Er onnxruntime_inference_collection.py 424 1 DecisionTreeRegressor.py finished in 2957 ms 5 1
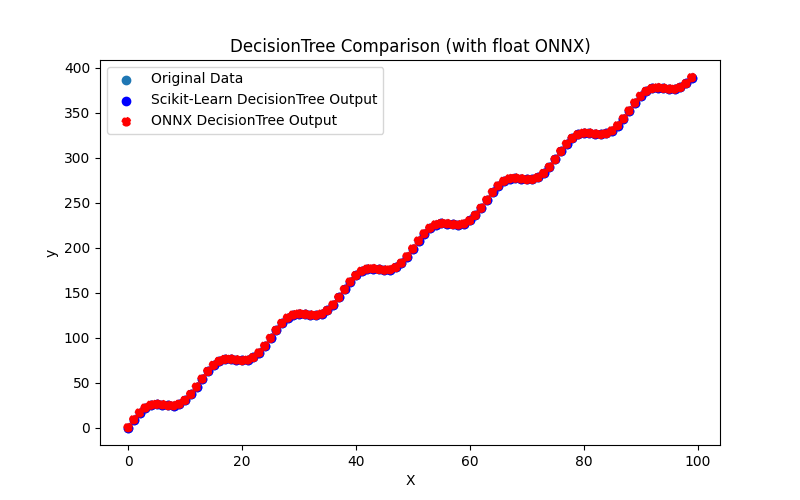
Fig.106. Risultati di DecisionTreeRegressor.py (float ONNX)
2.2.3.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati decision_tree_regressor_float.onnx e decision_tree_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| DecisionTreeRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "DecisionTreeRegressor" #define ONNXFilenameFloat "decision_tree_regressor_float.onnx" #define ONNXFilenameDouble "decision_tree_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
DecisionTreeRegressor (EURUSD,H1) Testing ONNX float: DecisionTreeRegressor (decision_tree_regressor_float.onnx) DecisionTreeRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 DecisionTreeRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 DecisionTreeRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 DecisionTreeRegressor (EURUSD,H1) DecisionTreeRegressor (EURUSD,H1) Testing ONNX double: DecisionTreeRegressor (decision_tree_regressor_double.onnx) DecisionTreeRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\DecisionTreeRegressor.mq5' (133:16) DecisionTreeRegressor (EURUSD,H1) model_name=DecisionTreeRegressor OnnxCreate error 5800
Il modello ONNX calcolato in float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello double.
2.2.3.3. Rappresentazione ONNX di decision_tree_regressor_float.onnx e decision_tree_regressor_double.onnx
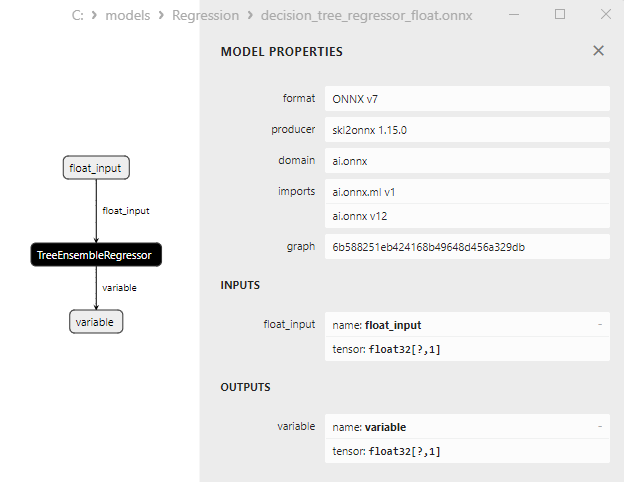
Fig.107. Rappresentazione ONNX di decision_tree_regressor_float.onnx in Netron
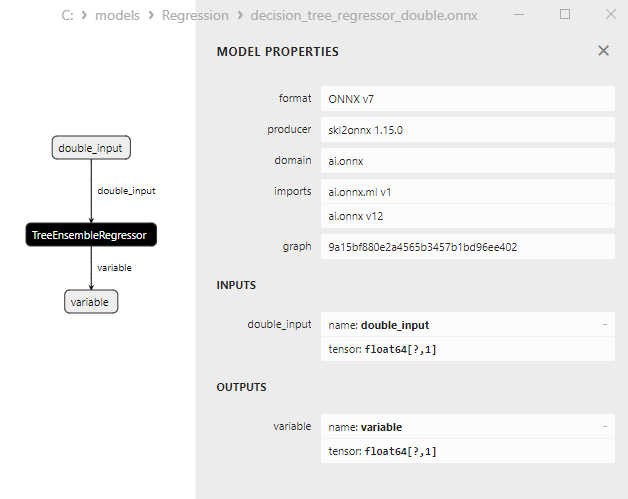
Fig.108. Rappresentazione ONNX di decision_tree_regressor_double.onnx in Netron
2.2.4. sklearn.tree.ExtraTreeRegressor
ExtraTreeRegressor o Extremely Randomized Trees Regressor, è un metodo di regressione di gruppo basato su alberi decisionali.
Questo metodo è una variante delle foreste casuali e si differenzia per il fatto che invece di scegliere la migliore suddivisione per ogni nodo dell'albero, utilizza suddivisioni casuali per ogni nodo. Questo rende più casuale e più veloce, il che può essere vantaggioso in certe situazioni.
Principio di funzionamento di ExtraTreeRegressor:
- Inizio della struttura: Si parte dal set di dati iniziale contenente le caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target.
- Casualità nelle suddivisioni: A differenza dei normali alberi decisionali, in cui viene scelta la suddivisione migliore, ExtraTreeRegressor utilizza valori di soglia casuali per dividere i nodi dell'albero. Questo rende il processo di suddivisione più casuale e meno incline all'overfitting.
- Costruzione dell’albero: L'albero viene costruito dividendo i nodi in base a caratteristiche casuali e valori di soglia. Questo processo continua fino a quando non vengono soddisfatti alcuni criteri di arresto, come la profondità massima dell'albero o il numero minimo di campioni in un nodo.
- Gruppi di alberi: ExtraTreeRegressor costruisce più alberi casuali simili, il cui numero è controllato dall'iperparametro "n_estimators".
- Previsione: Per prevedere la variabile target per i nuovi dati, ExtraTreeRegressor fa semplicemente una media delle previsioni di tutti gli alberi del gruppo.
Vantaggi di ExtraTreeRegressor:
- Riduzione dell'overfitting: L'utilizzo di suddivisioni casuali dei nodi rende il metodo meno incline all'overfitting rispetto ai normali alberi decisionali.
- Alta parallelizzazione: Poiché gli alberi sono costruiti in modo indipendente, ExtraTreeRegressor può essere facilmente parallelizzato per l'addestramento su più processori.
- Addestramento rapido: Rispetto ad altri metodi come il gradient boosting, ExtraTreeRegressor può essere addestrato più velocemente.
Limitazioni di ExtraTreeRegressor:
- Può essere meno preciso: In alcuni casi, soprattutto con piccoli set di dati ExtraTreeRegressor può essere meno accurato rispetto a metodi più complessi.
- Meno interpretabile: Rispetto ai modelli lineari, agli alberi decisionali e ad altri metodi più semplici, ExtraTreeRegressor è tipicamente meno interpretabile.
ExtraTreeRegressor può essere un metodo utile per la regressione in situazioni che richiedono una riduzione dell'overfitting e un addestramento rapido.
2.2.4.1. Codice per la creazione del modello ExtraTreeRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.tree.ExtraTreeRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# ExtraTreeRegressor.py
# Il codice dimostra il processo di addestramento del modello ExtraTreeRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni con i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"
# creare un modello ExtraTreeRegressor
regression_model = ExtraTreeRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello ExtraTreeRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni con i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"
# creare un modello ExtraTreeRegressor
regression_model = ExtraTreeRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e i dati della regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
2023.10.30 14:40:57.665 Python ExtraTreeRegressor Original model (double) 2023.10.30 14:40:57.665 Python R-squared (Coefficient of determination): 1.0 2023.10.30 14:40:57.665 Python Mean Absolute Error: 0.0 2023.10.30 14:40:57.665 Python Mean Squared Error: 0.0 2023.10.30 14:40:57.681 Python 2023.10.30 14:40:57.681 Python ExtraTreeRegressor ONNX model (float) 2023.10.30 14:40:57.681 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_float.onnx 2023.10.30 14:40:57.681 Python Information about input tensors in ONNX: 2023.10.30 14:40:57.681 Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] 2023.10.30 14:40:57.681 Python Information about output tensors in ONNX: 2023.10.30 14:40:57.681 Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] 2023.10.30 14:40:57.681 Python R-squared (Coefficient of determination) 0.9999999999999971 2023.10.30 14:40:57.681 Python Mean Absolute Error: 4.393654615473253e-06 2023.10.30 14:40:57.681 Python Mean Squared Error: 3.829042036424747e-11 2023.10.30 14:40:57.681 Python R^2 matching decimal places: 0 2023.10.30 14:40:57.681 Python MAE matching decimal places: 0 2023.10.30 14:40:57.681 Python MSE matching decimal places: 0 2023.10.30 14:40:57.681 Python float ONNX model precision: 0 2023.10.30 14:40:58.011 Python 2023.10.30 14:40:58.011 Python ExtraTreeRegressor ONNX model (double) 2023.10.30 14:40:58.011 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx
Scheda Errori:
ExtraTreeRegressor.py started ExtraTreeRegressor.py 1 1 Traceback (most recent call last): ExtraTreeRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) ExtraTreeRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx failed:Type Error onnxruntime_inference_collection.py 424 1 ExtraTreeRegressor.py finished in 2980 ms 5 1
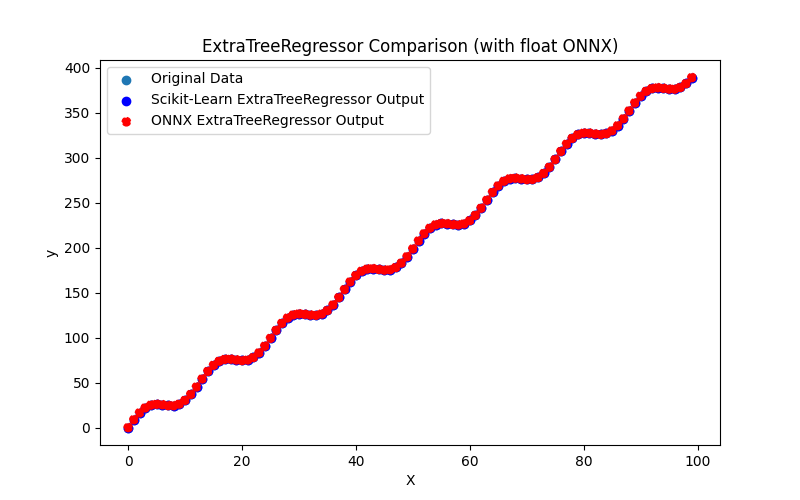
Fig.109. Risultati di ExtraTreeRegressor.py (float ONNX)
2.2.4.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati extra_tree_regressor_float.onnx e extra_tree_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| ExtraTreeRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ExtraTreeRegressor" #define ONNXFilenameFloat "extra_tree_regressor_float.onnx" #define ONNXFilenameDouble "extra_tree_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
ExtraTreeRegressor (EURUSD,H1) Testing ONNX float: ExtraTreeRegressor (extra_tree_regressor_float.onnx) ExtraTreeRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 ExtraTreeRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 ExtraTreeRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 ExtraTreeRegressor (EURUSD,H1) ExtraTreeRegressor (EURUSD,H1) Testing ONNX double: ExtraTreeRegressor (extra_tree_regressor_double.onnx) ExtraTreeRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreeRegressor.mq5' (133:16) ExtraTreeRegressor (EURUSD,H1) model_name=ExtraTreeRegressor OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double.
2.2.4.3. Rappresentazione ONNX extra_tree_regressor_float.onnx e extra_tree_regressor_double.onnx
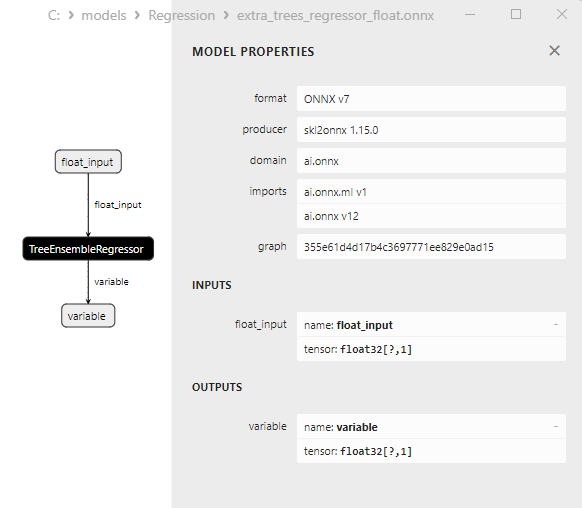
Fig.110. Rappresentazione ONNX di extra_tree_regressor_float.onnx in Netron
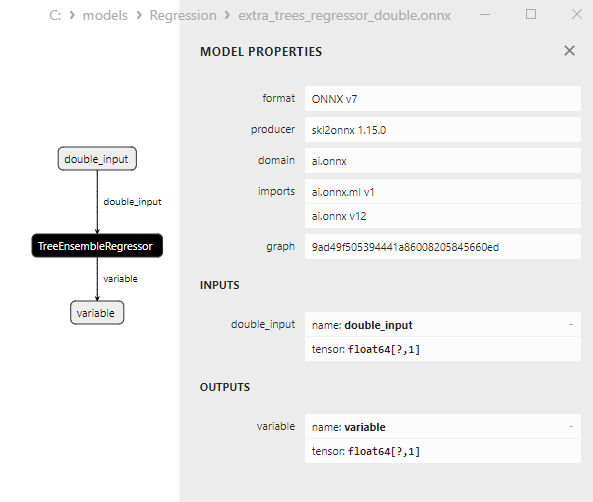
Fig.111. Rappresentazione ONNX di extra_tree_regressor_double.onnx in Netron
2.2.5. sklearn.ensemble.ExtraTreesRegressor
ExtraTreesRegressor(Extremely Randomized Trees Regressor) è un metodo di apprendimento automatico che rappresenta una variante di Random Forests per compiti di regressione.
Questo metodo impiega un gruppo di alberi decisionali per prevedere i valori numerici della variabile target sulla base di un insieme di caratteristiche.
Come funziona ExtraTreesRegressor:
- Inizio della struttura: Si parte dal set di dati originale, che comprende le caratteristiche (variabili indipendenti) e i valori corrispondenti della variabile target.
- Casualità nelle Suddivisioni: A differenza dei normali alberi decisionali, in cui viene selezionata la divisione migliore per dividere i nodi, ExtraTreesRegressor utilizza valori di soglia casuali per dividere i nodi dell'albero. Questa casualità rende il processo di suddivisione più arbitrario e meno incline all'overfitting.
- Costruzione degli Alberi: ExtraTreesRegressor costruisce più alberi decisionali nel gruppo. Il numero di alberi è controllato dall'iperparametro "n_estimators". Ogni albero viene addestrato su un sottocampione casuale di dati (con sostituzione) e su sottoinsiemi casuali di caratteristiche.
- Previsione: Per prevedere la variabile target per i nuovi dati, ExtraTreesRegressor aggrega le previsioni di tutti gli alberi del gruppo (solitamente facendo una media).
Vantaggi di ExtraTreesRegressor:
- Riduzione dell'overfitting: L'utilizzo di suddivisioni casuali dei nodi e del sottocampionamento dei dati rende il metodo meno incline all'overfitting rispetto agli alberi decisionali convenzionali.
- Alta Parallelizzazione: Poiché gli alberi sono costruiti in modo indipendente, ExtraTreesRegressor può essere facilmente parallelizzato per l'addestramento su più processori.
- Robustezza ai Valori Anomali: Il metodo mostra tipicamente una certa resistenza ai valori anomali nei dati.
- Gestione di Dati Numerici e Categorici: ExtraTreesRegressor è in grado di gestire caratteristiche sia numeriche che categoriche senza ulteriori pre elaborazioni.
Limitazioni di ExtraTreesRegressor:
- Può Richiedere un’Ottimizzazione degli Iperparametri: Sebbene ExtraTreesRegressor funzioni solitamente bene con i parametri predefiniti, per ottenere le massime prestazioni potrebbe essere necessaria una ottimizzazione degli iperparametri.
- Minore Interpretabilità: Come altri metodi di gruppo, ExtraTreesRegressor è meno interpretabile rispetto a modelli più semplici come la regressione lineare.
ExtraTreesRegressor può essere un metodo vantaggioso per la regressione in diversi compiti, in particolare quando è necessario ridurre l'overfitting e migliorare la generalizzazione del modello.
2.2.5.1. Codice per creare il modello ExtraTreesRegressor ed esportarlo in ONNX per float e double
Questo codice crea il modello sklearn.ensemble.ExtraTreesRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# ExtraTreesRegressor.py
# Il codice dimostra il processo di addestramento del modello ExtraTreesRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"
# creare un modello Extra Trees Regressor
regression_model = ExtraTreesRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello ExtraTreesRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"
# creare un modello Extra Trees Regressor
regression_model = ExtraTreesRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python ExtraTreesRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 2.2302160118670144e-13 Python Mean Squared Error: 8.41048471722451e-26 Python Python ExtraTreesRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999998015 Python Mean Absolute Error: 3.795239380975701e-05 Python Mean Squared Error: 2.627067474763585e-09 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python ExtraTreesRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx
Scheda Errori:
ExtraTreesRegressor.py started ExtraTreesRegressor.py 1 1 Traceback (most recent call last): ExtraTreesRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) ExtraTreesRegressor.py 160 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx failed:Type Erro onnxruntime_inference_collection.py 424 1 ExtraTreesRegressor.py finished in 4654 ms 5 1
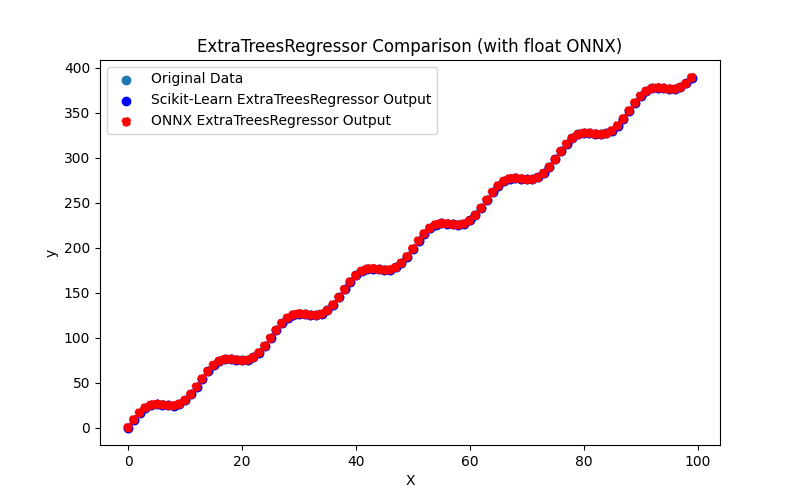
Fig.112. Risultati di ExtraTreesRegressor.py (float ONNX)
2.2.5.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice crea i modelli extra_trees_regressor_float.onnx e extra_trees_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| ExtraTreesRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ExtraTreesRegressor" #define ONNXFilenameFloat "extra_trees_regressor_float.onnx" #define ONNXFilenameDouble "extra_trees_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
ExtraTreesRegressor (EURUSD,H1) Testing ONNX float: ExtraTreesRegressor (extra_trees_regressor_float.onnx) ExtraTreesRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999998015 ExtraTreesRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000379523938098 ExtraTreesRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000026270675 ExtraTreesRegressor (EURUSD,H1) ExtraTreesRegressor (EURUSD,H1) Testing ONNX double: ExtraTreesRegressor (extra_trees_regressor_double.onnx) ExtraTreesRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreesRegressor.mq5' (133:16) ExtraTreesRegressor (EURUSD,H1) model_name=ExtraTreesRegressor OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double.
2.2.5.3. Rappresentazione ONNX di extra_trees_regressor_float.onnx e extra_trees_regressor_double.onnx
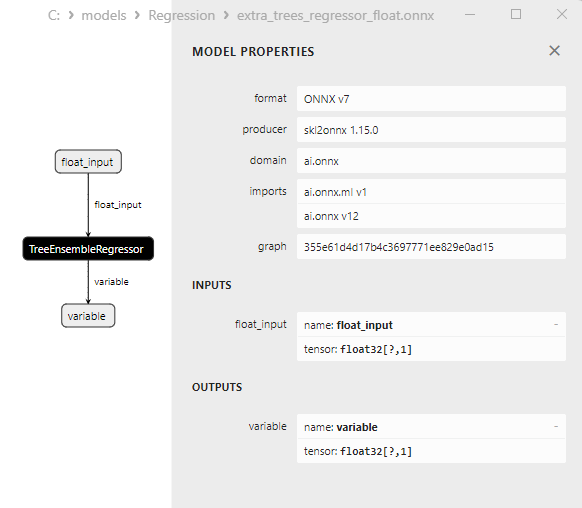
Fig.113. Rappresentazione ONNX di extra_trees_regressor_float.onnx in Netron
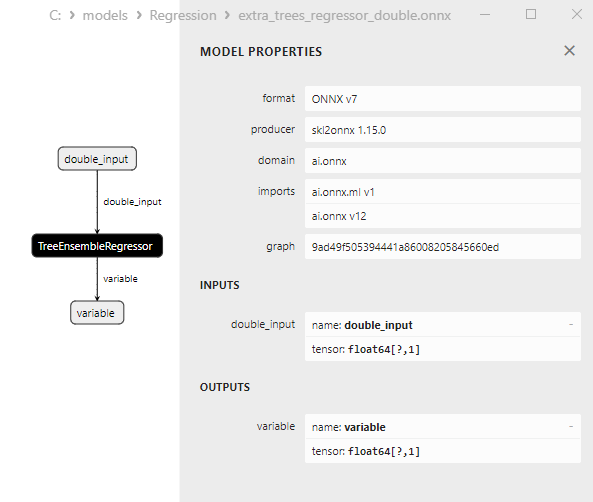
Fig.114. Rappresentazione ONNX di extra_trees_regressor_double.onnx in Netron
2.2.6. sklearn.svm.NuSVR
NuSVR è un metodo di apprendimento automatico utilizzato per compiti di regressione. Questo metodo si basa sulla Support Vector Machine (SVM), ma viene applicato a compiti di regressione anziché di classificazione.
NuSVR è una variante di SVM progettata per risolvere compiti di regressione prevedendo valori continui della variabile target.
Come funziona NuSVR:
- Dati di Input: Si parte da un set di dati che include caratteristiche (variabili indipendenti) e valori della variabile target (continua).
- Selezione del kernel: NuSVR utilizza kernel come quelli lineari, polinomiali o con funzione di base radiale (RBF) per trasformare i dati in uno spazio di dimensioni superiori, dove è possibile trovare un iperpiano di separazione lineare.
- Definizione del parametro Nu: Il parametro Nu controlla la complessità del modello e definisce quanti esempi di addestramento saranno considerati come valori anomali. Il valore Nu deve essere compreso tra 0 e 1, influenzando il numero di vettori di supporto.
- Costruzione del Vettore di Supporto: NuSVR mira a trovare un iperpiano di separazione ottimale che massimizzi lo scarto tra questo iperpiano e i punti campione più vicini.
- Addestramento dei Modelli: Il modello viene addestrato per minimizzare l'errore di regressione e soddisfare i vincoli associati al parametro Nu.
- Effettuare Previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori della variabile target su nuovi dati.
Vantaggi di NuSVR:
- Gestione dei Valori Anomali: NuSVR consente di controllare i valori anomali utilizzando il parametro Nu, che regola il numero di esempi di addestramento considerati come valori anomali.
- Kernel Multipli: Il metodo supporta diversi tipi di kernel, consentendo la modellazione di relazioni non lineari complesse.
Limitazioni di NuSVR:
- Selezione dei Parametri Nu: La scelta del valore corretto per il parametro Nu può richiedere una certa sperimentazione.
- Sensibilità alla Scala dei Dati: Gli SVM, compreso NuSVR, possono essere sensibili alla scala dei dati, quindi potrebbe essere necessaria una standardizzazione o normalizzazione delle caratteristiche.
- Complessità Computazionale: Per grandi set di dati e kernel complessi, NuSVR può essere computazionalmente costoso.
NuSVR è un metodo di apprendimento automatico per compiti di regressione basato sul metodo Support Vector Machine (SVM). Consente la previsione di valori continui della variabile target e offre la possibilità di gestire i valori anomali utilizzando il parametro Nu.
2.2.6.1. Codice per la creazione del modello NuSVR ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.svm.NuSVR, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# NuSVR.py
# Il codice dimostra il processo di addestramento del modello NuSVR, la sua esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"
# creare un modello NuSVR
nusvr_model = NuSVR()
# Adattare il modello ai dati
nusvr_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = nusvr_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello NuSVR, la sua esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"
# creare un modello NuSVR
nusvr_model = NuSVR()
# Adattare il modello ai dati
nusvr_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = nusvr_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python NuSVR Original model (double) Python R-squared (Coefficient of determination): 0.2771437770527445 Python Mean Absolute Error: 83.76666411704255 Python Mean Squared Error: 9565.381751764757 Python Python NuSVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_float.onnx Python Information about input tensors in ONNX: 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.27714379657935495 Python Mean Absolute Error: 83.766663385322 Python Mean Squared Error: 9565.381493373838 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python NuSVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_double.onnx
Scheda Errori:
NuSVR.py started NuSVR.py 1 1 Traceback (most recent call last): NuSVR.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) NuSVR.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess.initialize_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 435 1 onnxruntime.capi.onnxruntime_pybind11_state.NotImplemented: [ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for SVMRegressor(1) node with name 'SVM' onnxruntime_inference_collection.py 435 1 NuSVR.py finished in 2925 ms 5 1
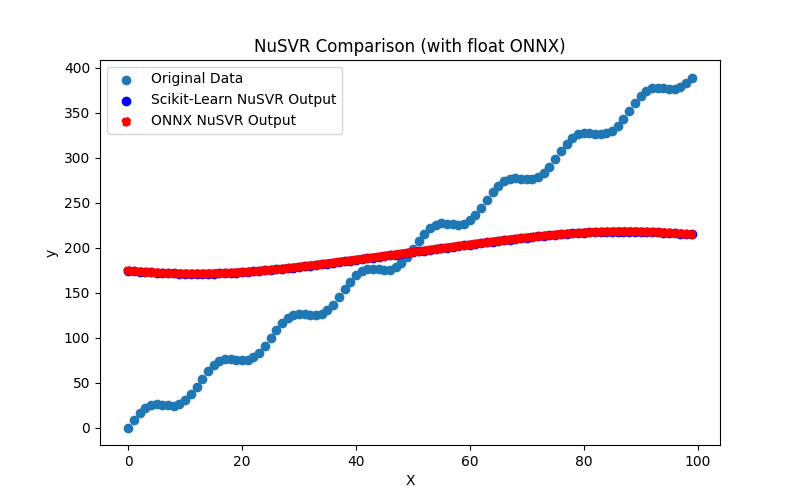
Fig.115. Risultati di NuSVR.py (float ONNX)
2.2.6.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati nu_svr_float.onnx e nu_svr_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| NuSVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "NuSVR" #define ONNXFilenameFloat "nu_svr_float.onnx" #define ONNXFilenameDouble "nu_svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
NuSVR (EURUSD,H1) Testing ONNX float: NuSVR (nu_svr_float.onnx) NuSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.2771437965793548 NuSVR (EURUSD,H1) MQL5: Mean Absolute Error: 83.7666633853219906 NuSVR (EURUSD,H1) MQL5: Mean Squared Error: 9565.3814933738358377 NuSVR (EURUSD,H1) NuSVR (EURUSD,H1) Testing ONNX double: NuSVR (nu_svr_double.onnx) NuSVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\Regression\NuSVR.mq5' (133:16) NuSVR (EURUSD,H1) model_name=NuSVR OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double.
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: NuSVR (nu_svr_float.onnx) Python Mean Absolute Error: 83.76666411704255 MQL5: Mean Absolute Error: 83.7666633853219906
2.2.6.3. Rappresentazione ONNX di nu_svr_float.onnx e nu_svr_double.onnx
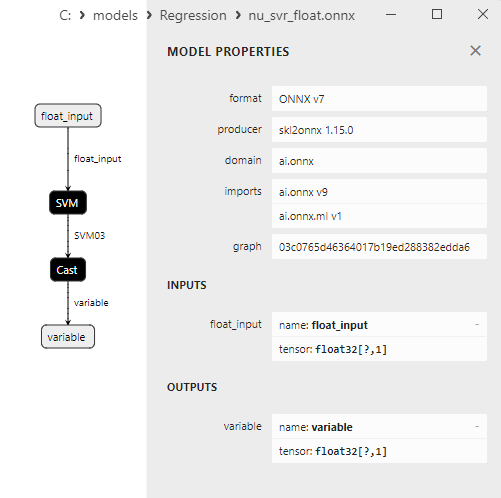
Fig.116. Rappresentazione ONNX di nu_svr_float.onnx in Netron
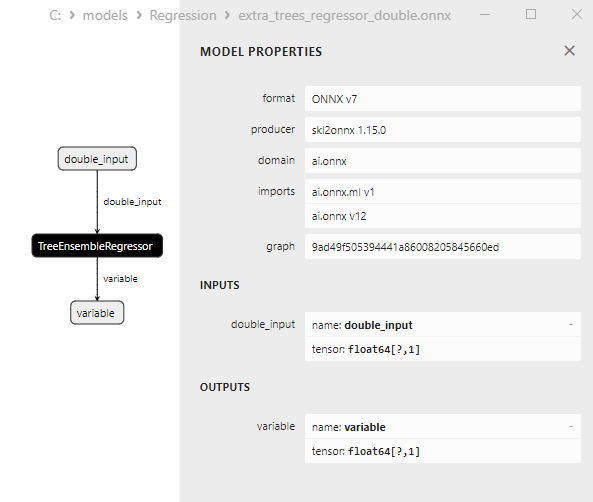
Fig.117. Rappresentazione ONNX di nu_svr_double.onnx in Netron
2.2.7. sklearn.ensemble.RandomForestRegressor
RandomForestRegressor è un metodo di apprendimento automatico utilizzato per risolvere compiti di regressione.
È uno dei metodi più popolari basati sull'apprendimento di gruppo e impiega l'algoritmo Random Forest per creare modelli di regressione potenti e robusti.
Ecco come funziona RandomForestRegressor:
- Dati di Input: Si parte da un set di dati che comprende le caratteristiche (variabili indipendenti) e una variabile target (continua).
- Foresta Casuale: RandomForestRegressor utilizza un gruppo di alberi decisionali per risolvere il compito di regressione. Ogni albero della foresta lavora per prevedere i valori della variabile target.
- Campionamento Bootstrap: Ogni albero viene addestrato utilizzando campioni bootstrap, ossia un campionamento casuale con sostituzione dal set di dati di addestramento. Questo permette di diversificare i dati da cui ogni albero apprende.
- Selezione Casuale delle Caratteristiche: Durante la costruzione di ogni albero, viene selezionato anche un sottogruppo casuale di caratteristiche, rendendo il modello più robusto e riducendo le correlazioni tra gli alberi.
- Media delle Previsioni: Una volta costruiti tutti gli alberi, RandomForestRegressor media o combina le loro previsioni per ottenere la previsione finale della regressione.
Vantaggi di RandomForestRegressor:
- Potenza e Robustezza: RandomForestRegressor è un potente metodo di regressione che spesso offre buone prestazioni.
- Gestione di Dati di Grandi Dimensioni: Gestisce bene grandi set di dati e può gestire una moltitudine di caratteristiche.
- Resilienza all'Overfitting: Grazie al campionamento bootstrap e alla selezione casuale delle caratteristiche, la foresta casuale è in genere robusta contro l'Overfitting.
- Stima dell'Importanza delle Caratteristiche: Random Forest può fornire informazioni sull'importanza di ciascuna caratteristica nel compito di regressione.
Limitazioni di RandomForestRegressor:
- Mancanza di Interpretabilità: Il modello potrebbe essere meno interpretabile rispetto ai modelli lineari.
- Non Sempre è il Modello Più Accurato: In alcuni compiti, gruppi più complessi potrebbero essere superflui e i modelli lineari potrebbero essere più adatti.
RandomForestRegressor è un potente metodo di apprendimento automatico per compiti di regressione che utilizza un gruppo di alberi decisionali casuali per creare un modello di regressione stabile e altamente performante. Questo metodo è particolarmente utile per compiti con grandi set di dati e per valutare l'importanza delle caratteristiche.
2.2.7.1. Codice per la creazione del modello RandomForestRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.ensemble.RandomForestRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# RandomForestRegressor.py
# Il codice dimostra il processo di addestramento del modello RandomForestRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"
# creare un modello RandomForestRegressor
regression_model = RandomForestRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello RandomForestRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"
# creare un modello RandomForestRegressor
regression_model = RandomForestRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python RandomForestRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9998854509605539 Python Mean Absolute Error: 0.9186485980852603 Python Mean Squared Error: 1.5157997632401086 Python Python RandomForestRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9998854516013125 Python Mean Absolute Error: 0.9186420704511761 Python Mean Squared Error: 1.515791284236419 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 5 Python float ONNX model precision: 5 Python Python RandomForestRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx
Scheda Errori:
RandomForestRegressor.py started RandomForestRegressor.py 1 1 Traceback (most recent call last): RandomForestRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) RandomForestRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx failed:Type Er onnxruntime_inference_collection.py 424 1 RandomForestRegressor.py finished in 4392 ms 5 1
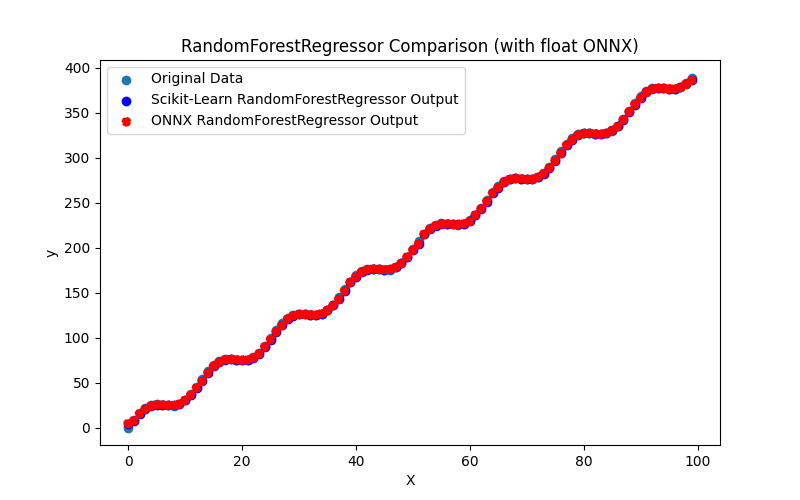
Fig.118. Risultati di RandomForestRegressor.py (float ONNX)
2.2.7.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati random_forest_regressor_float.onnx e random_forest_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| RandomForestRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RandomForestRegressor" #define ONNXFilenameFloat "random_forest_regressor_float.onnx" #define ONNXFilenameDouble "random_forest_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
RandomForestRegressor (EURUSD,H1) RandomForestRegressor (EURUSD,H1) Testing ONNX float: RandomForestRegressor (random_forest_regressor_float.onnx) RandomForestRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9998854516013125 RandomForestRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.9186420704511761 RandomForestRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1.5157912842364190 RandomForestRegressor (EURUSD,H1) RandomForestRegressor (EURUSD,H1) Testing ONNX double: RandomForestRegressor (random_forest_regressor_double.onnx) RandomForestRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\RandomForestRegressor.mq5' (133:16) RandomForestRegressor (EURUSD,H1) model_name=RandomForestRegressor OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double....
2.2.7.3. Rappresentazione ONNX di random_forest_regressor_float.onnx e random_forest_regressor_double.onnx
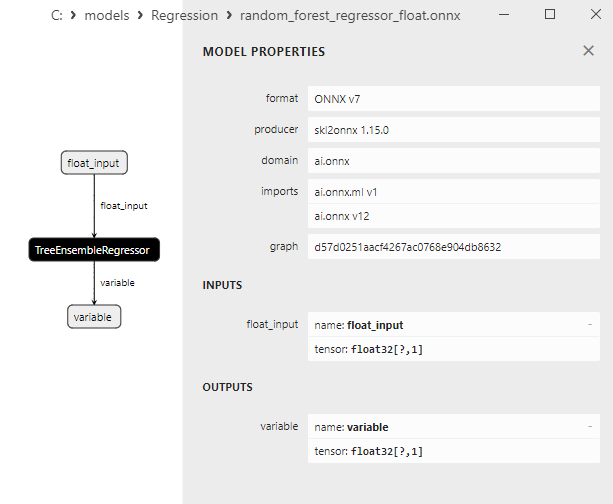
Fig.119. Rappresentazione ONNX di random_forest_regressor_float.onnx in Netron
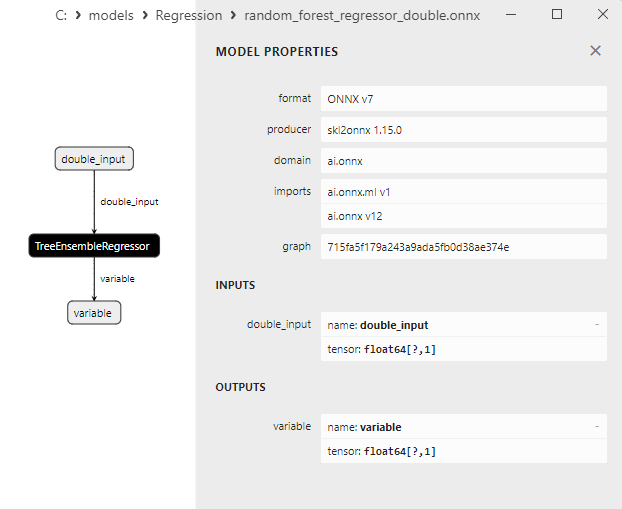
Fig.120. Rappresentazione ONNX di random_forest_regressor_double.onnx in Netron
2.2.8. sklearn.ensemble.GradientBoostingRegressor
GradientBoostingRegressor è un metodo di apprendimento automatico utilizzato per compiti di regressione. Fa parte della famiglia dei metodi di gruppo e si basa sull'idea di costruire modelli deboli e combinarli in un modello forte utilizzando il gradient boosting.
Il Gradient Boosting è una tecnica per migliorare i modelli aggiungendo iterativamente modelli deboli e correggendo gli errori dei modelli precedenti.
Ecco come funziona GradientBoostingRegressor:
- Inizializzazione: Si parte dal dataset originale contenente le caratteristiche (variabili indipendenti) e i corrispondenti valori target.
- Primo Modello: Si inizia con l'addestramento del primo modello, spesso scelto come modello di regressione semplice (ad esempio, albero decisionale) sui dati originali.
- Residui e Discesa del Gradiente: Vengono calcolati i residui, ovvero la differenza tra i valori previsti dal primo modello e i valori effettivi della variabile target. Quindi, viene calcolata la discesa del gradiente di questa funzione di perdita, che indica la direzione da seguire per migliorare il modello.
- Costruire il Modello Successivo: Il modello successivo viene costruito, concentrandosi sulla previsione della discesa del gradiente (errori del primo modello). Questo modello viene addestrato sui residui e aggiunto al primo modello.
- Iterazioni: Il processo di costruzione di nuovi modelli e di correzione dei residui viene ripetuto più volte. Ogni nuovo modello tiene conto dei residui dei modelli precedenti e mira a migliorare le previsioni.
- Combinazione di Modelli: Le previsioni di tutti i modelli vengono combinate nella previsione finale attraverso una media o una ponderazione in base alla loro importanza.
Vantaggi di GradientBoostingRegressor:
- Prestazioni Elevate: Il Gradient Boosting è un metodo potente in grado di ottenere prestazioni elevate nei compiti di regressione.
- Robustezza ai Valori Anomali: Gestisce i valori anomali nei dati e costruisce modelli tenendo conto di questa incertezza.
- Selezione Automatica delle Caratteristiche: Seleziona automaticamente le caratteristiche più importanti per la previsione della variabile target.
- Gestione di Varie Funzioni di Perdita: Il metodo consente di utilizzare diverse funzioni di perdita a seconda del compito.
Limitazioni di GradientBoostingRegressor:
- Regolazione dell'Iperparametro Necessaria: Per ottenere le massime prestazioni è necessario regolare gli iperparametri come il tasso di apprendimento, la profondità dell'albero e il numero di modelli.
- Computazionalmente Dispendioso: Il Gradient Boosting può essere computazionalmente costoso, soprattutto con grandi volumi di dati ed un numero elevato di alberi.
GradientBoostingRegressor è un potente metodo di regressione spesso utilizzato in attività pratiche per ottenere prestazioni elevate con la corretta regolazione degli iperparametri.
2.2.8.1. Codice per la creazione del modello GradientBoostingRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.ensemble.GradientBoostingRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# GradientBoostingRegressor.py
# Il codice dimostra il processo di addestramento del modello GradientBoostingRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"
# creare un modello Gradient Boosting Regressor
regression_model = GradientBoostingRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello GradientBoostingRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"
# creare un modello Gradient Boosting Regressor
regression_model = GradientBoostingRegressor()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python GradientBoostingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9999959514652565 Python Mean Absolute Error: 0.15069342754017417 Python Mean Squared Error: 0.053573282108575676 Python Python GradientBoostingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999959514739537 Python Mean Absolute Error: 0.15069457426101718 Python Mean Squared Error: 0.05357316702127665 Python R^2 matching decimal places: 10 Python MAE matching decimal places: 5 Python MSE matching decimal places: 6 Python float ONNX model precision: 5 Python Python GradientBoostingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx
Scheda Errori:
GradientBoostingRegressor.py started GradientBoostingRegressor.py 1 1 Traceback (most recent call last): GradientBoostingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) GradientBoostingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 419 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 452 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx failed:Typ onnxruntime_inference_collection.py 452 1 GradientBoostingRegressor.py finished in 3073 ms 5 1
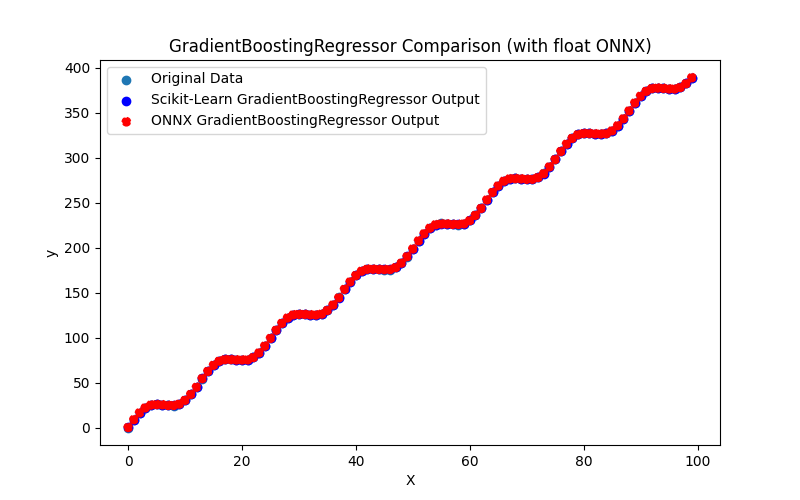
Fig.121. Risultati di GradientBoostingRegressor.py (float ONNX)
2.2.8.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli gradient_boosting_regressor_float.onnx e gradient_boosting_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| GradientBoostingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GradientBoostingRegressor" #define ONNXFilenameFloat "gradient_boosting_regressor_float.onnx" #define ONNXFilenameDouble "gradient_boosting_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
GradientBoostingRegressor (EURUSD,H1) Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx) GradientBoostingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999959514739537 GradientBoostingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.1506945742610172 GradientBoostingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0535731670212767 GradientBoostingRegressor (EURUSD,H1) GradientBoostingRegressor (EURUSD,H1) Testing ONNX double: GradientBoostingRegressor (gradient_boosting_regressor_double.onnx) GradientBoostingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\GradientBoostingRegressor.mq5' (133:16) GradientBoostingRegressor (EURUSD,H1) model_name=GradientBoostingRegressor OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double.
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx) Python Mean Absolute Error: 0.15069342754017417 MQL5: Mean Absolute Error: 0.1506945742610172
Precisione di ONNX float MAE: 5 cifre decimali.
2.2.8.3. Rappresentazione ONNX di gradient_boosting_regressor_float.onnx e gradient_boosting_regressor_double.onnx
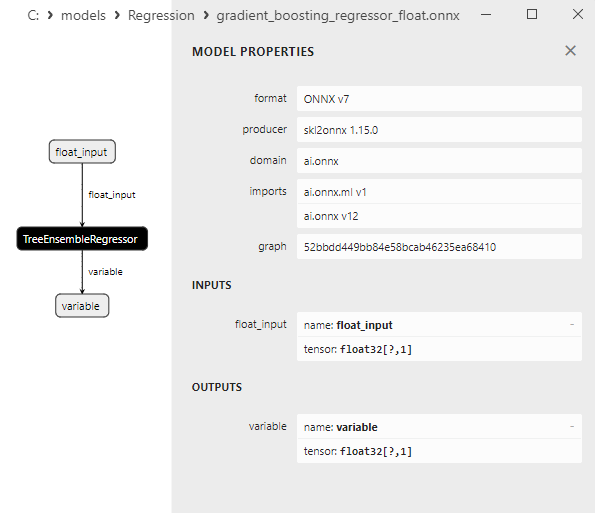
Fig.122. Rappresentazione ONNX di gradient_boosting_regressor_float.onnx in Netron
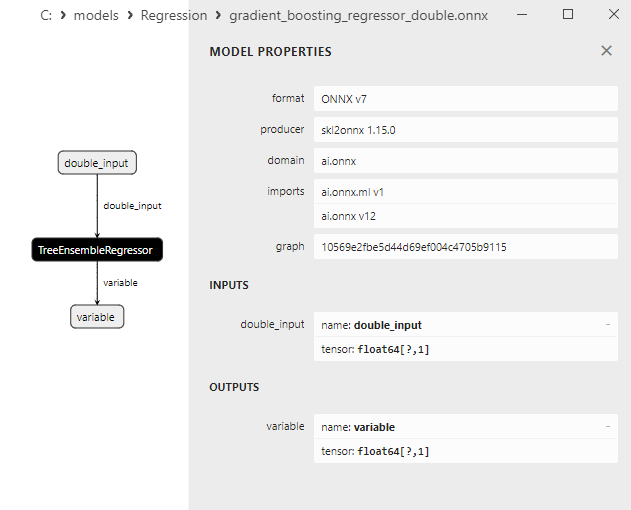
Fig.123. Rappresentazione ONNX di gradient_boosting_regressor_double.onnx in Netron
2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
HistGradientBoostingRegressor è un metodo di apprendimento automatico che rappresenta una variante di gradient boosting ottimizzata per lavorare con grandi set di dati.
Questo metodo viene utilizzato per compiti di regressione e il suo nome "Hist" indica che impiega metodi basati sugli istogrammi per accelerare il processo di addestramento.
Come Funziona HistGradientBoostingRegressor:
- Inizializzazione: Si parte dal dataset originale contenente le caratteristiche (variabili indipendenti) e i corrispondenti valori target.
- Metodi Basati sugli Istogrammi: Invece di dividere esattamente i dati nei nodi dell'albero, HistGradientBoostingRegressor utilizza metodi basati sugli istogrammi per rappresentare in modo efficiente i dati sotto forma di istogrammi. Questo accelera notevolmente il processo di addestramento, soprattutto su grandi set di dati.
- Costruire Alberi di Base: Il metodo costruisce una serie di alberi decisionali di base, denominati "alberi decisionali a istogramma", utilizzando le rappresentazioni a istogramma dei dati. Questi alberi sono costruiti sulla base del gradient boosting e adattati ai residui del modello precedente.
- Addestramento Graduale: HistGradientBoostingRegressor aggiunge in modo incrementale nuovi alberi al gruppo, con ogni albero che corregge i residui degli alberi precedenti.
- Combinazione di Modelli: Dopo aver costruito gli alberi di base, le previsioni di tutti gli alberi vengono combinate per ottenere la previsione finale.
Vantaggi di HistGradientBoostingRegressor:
- Prestazioni Elevate: Questo metodo è ottimizzato per gestire grandi volumi di dati e può raggiungere prestazioni elevate.
- Robustezza al Rumore: HistGradientBoostingRegressor ha generalmente buone prestazioni anche in presenza di rumore nei dati.
- Efficienza ad Alta Dimensionalità: Il metodo è in grado di gestire compiti con un numero elevato di caratteristiche (dati ad alta dimensionalità).
- Eccellente Parallelizzazione: È in grado di parallelizzare in modo efficiente l’addestramento su più processori.
Limitazioni di HistGradientBoostingRegressor:
- Regolazione dell'Iperparametro Richiesta: Per ottenere le massime prestazioni è necessario regolare gli iperparametri come la profondità dell'albero e il numero di modelli.
- Minore Interpretabilità Rispetto ai Modelli Lineari: Come altri metodi di gruppo, HistGradientBoostingRegressor è meno interpretabile di modelli più semplici come la regressione lineare.
HistGradientBoostingRegressor può essere un metodo di regressione utile per compiti che coinvolgono set di dati di grandi dimensioni, dove sono essenziali prestazioni elevate ed efficienza dei dati ad alta dimensionalità.
2.2.9.1. Codice per la creazione del modello HistGradientBoostingRegressor ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.ensemble.HistGradientBoostingRegressor, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# HistGradientBoostingRegressor.py
# Il codice dimostra il processo di addestramento del modello HistGradientBoostingRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"
# creare un modello Histogram-Based Gradient Boosting Regressor
hist_gradient_boosting_model = HistGradientBoostingRegressor()
# Adattare il modello ai dati
hist_gradient_boosting_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = hist_gradient_boosting_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello HistGradientBoostingRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"
# creare un modello Histogram-Based Gradient Boosting Regressor
hist_gradient_boosting_model = HistGradientBoostingRegressor()
# Adattare il modello ai dati
hist_gradient_boosting_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = hist_gradient_boosting_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python HistGradientBoostingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9833421349506157 Python Mean Absolute Error: 9.070567104488434 Python Mean Squared Error: 220.4295035561544 Python Python HistGradientBoostingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9833421351962779 Python Mean Absolute Error: 9.07056497799043 Python Mean Squared Error: 220.42950030536645 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 5 Python float ONNX model precision: 5 Python Python HistGradientBoostingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx
Scheda Errori:
HistGradientBoostingRegressor.py started HistGradientBoostingRegressor.py 1 1 Traceback (most recent call last): HistGradientBoostingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) HistGradientBoostingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 419 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 452 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx faile onnxruntime_inference_collection.py 452 1 HistGradientBoostingRegressor.py finished in 3100 ms 5 1
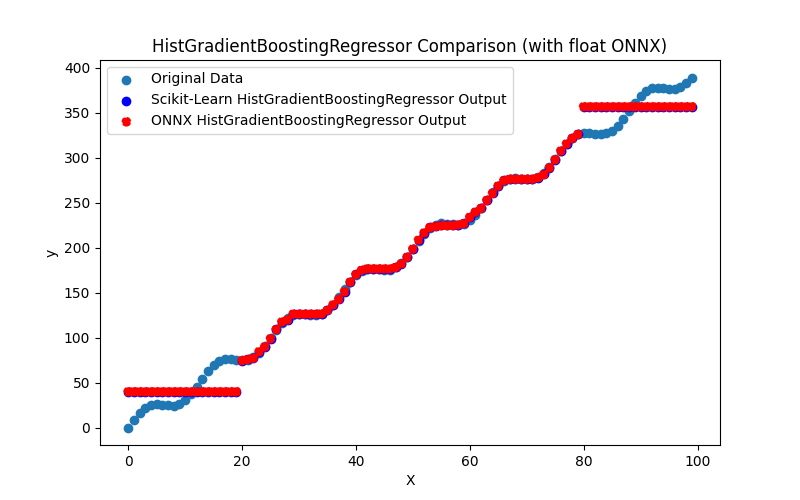
Fig.124. Risultati di HistGradientBoostingRegressor.py (float ONNX)
2.2.9.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati hist_gradient_boosting_regressor_float.onnx e hist_gradient_boosting_regressor_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| HistGradientBoostingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "HistGradientBoostingRegressor" #define ONNXFilenameFloat "hist_gradient_boosting_regressor_float.onnx" #define ONNXFilenameDouble "hist_gradient_boosting_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
HistGradientBoostingRegressor (EURUSD,H1) Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx) HistGradientBoostingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9833421351962779 HistGradientBoostingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.0705649779904292 HistGradientBoostingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 220.4295003053665312 HistGradientBoostingRegressor (EURUSD,H1) HistGradientBoostingRegressor (EURUSD,H1) Testing ONNX double: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_double.onnx) HistGradientBoostingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\HistGradientBoostingRegressor.mq5' (133:16) HistGradientBoostingRegressor (EURUSD,H1) model_name=HistGradientBoostingRegressor OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double.
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx) Python Mean Absolute Error: 9.070567104488434 MQL5: Mean Absolute Error: 9.0705649779904292
Precisione di ONNX float MAE: 5 cifre decimali
2.2.9.3. Rappresentazione ONNX di hist_gradient_boosting_regressor_float.onnx e hist_gradient_boosting_regressor_double.onnx
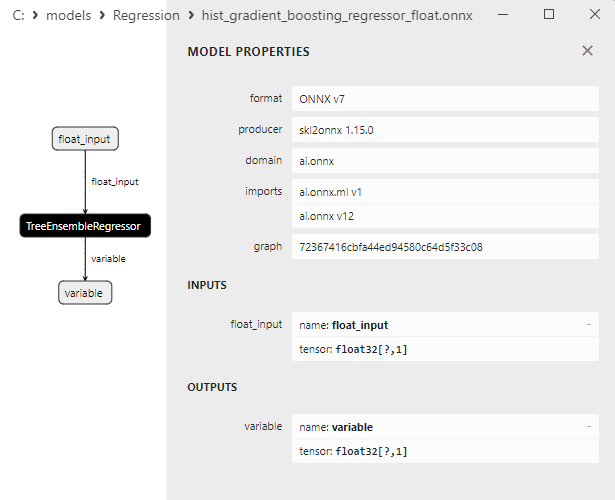
Fig.125. Rappresentazione ONNX di hist_gradient_boosting_regressor_float.onnx in Netron
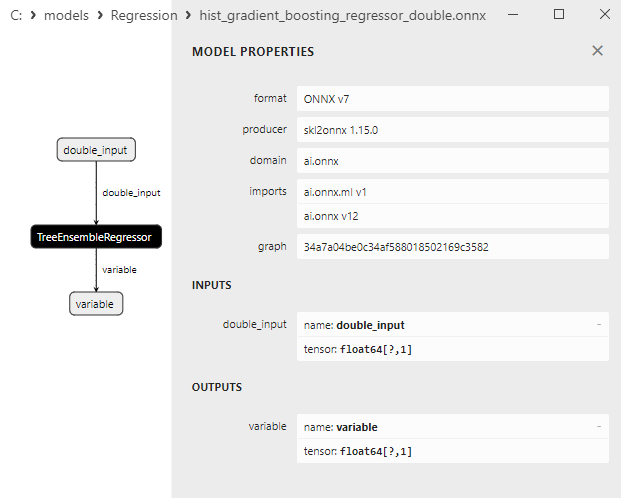
Fig.126. Rappresentazione ONNX di hist_gradient_boosting_regressor_double.onnx in Netron
2.2.10. sklearn.svm.SVR
SVR (Support Vector Regression) è un metodo di apprendimento automatico utilizzato per compiti di regressione. Si basa sullo stesso concetto della Support Vector Machine (SVM) per la classificazione, ma è adattata alla regressione. L'obiettivo principale di SVR è quello di prevedere i valori continui della variabile target basandosi sulla distanza media massima tra i punti dei dati e la retta di regressione.
Come Funziona SVR:
- Definizione dei Confini: Analogamente a SVM, SVR costruisce dei confini che separano le diverse classi di punti dei dati. Invece di separare le classi, SVR mira a costruire un "tubo" attorno ai punti dei dati, la cui larghezza è controllata da un iperparametro.
- Variabile Target e Funzione di Perdita: Invece di utilizzare le classi come nella classificazione, SVR tratta i valori continui della variabile target. Minimizza l'errore di previsione, misurato con una funzione di perdita, come la differenza al quadrato tra i valori previsti e quelli effettivi.
- Regolarizzazione: SVR supporta anche la regolarizzazione, che aiuta a controllare la complessità del modello e a prevenire l'overfitting.
- Funzioni del Kernel: L'SVR impiega tipicamente funzioni kernel che consentono di gestire le dipendenze non lineari tra le caratteristiche e la variabile target. Le funzioni kernel più diffuse sono la funzione di base radiale (RBF), le funzioni polinomiali e le funzioni lineari.
Vantaggi di SVR:
- Robustezza ai Valori Anomali: SVR è in grado di gestire i valori anomali nei dati, poiché mira a minimizzare l'errore di previsione.
- Supporto per le Dipendenze Non Lineari: L'uso di funzioni kernel consente a SVR di modellare dipendenze complesse e non lineari tra le caratteristiche e la variabile target.
- Alta Qualità di Previsione: Nei compiti di regressione che richiedono previsioni precise, SVR può fornire risultati di alta qualità.
Limiti di SVR:
- Sensibilità agli Iperparametri: La scelta della funzione kernel e dei parametri del modello, come l'ampiezza del tubo (iperparametri), può richiedere un'attenta messa a punto e ottimizzazione.
- Complessità Computazionale: L'addestramento del modello SVR, soprattutto quando si utilizzano funzioni kernel complesse e grandi set di dati, può essere computazionalmente intenso.
SVR è un metodo di apprendimento automatico per compiti di regressione basato sull'idea di costruire un "tubo" intorno ai punti di dati per minimizzare gli errori di previsione. Presenta una certa robustezza nei confronti dei valori anomali e la capacità di gestire le dipendenze non lineari, che lo rendono utile in diversi compiti di regressione.
2.2.10.1. Codice per la creazione del modello SVR ed esportazione in ONNX per float e double
Questo codice crea il modello sklearn.svm.SVR, lo addestra su dati sintetici, salva il modello nel formato ONNX ed esegue previsioni utilizzando dati di input sia float che double. Inoltre, valuta l'accuratezza del modello originale e dei modelli esportati in ONNX.
# SVR.py
# Il codice dimostra il processo di addestramento del modello SVR, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "SVR"
onnx_model_filename = data_path + "svr"
# creare un modello SVR
regression_model = SVR()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello SVR, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "SVR"
onnx_model_filename = data_path + "svr"
# creare un modello SVR
regression_model = SVR()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python SVR Original model (double) Python R-squared (Coefficient of determination): 0.398243655775797 Python Mean Absolute Error: 73.63683696034649 Python Mean Squared Error: 7962.89631509593 Python Python SVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.3982436352100983 Python Mean Absolute Error: 73.63683840363255 Python Mean Squared Error: 7962.896587236852 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python SVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_double.onnx
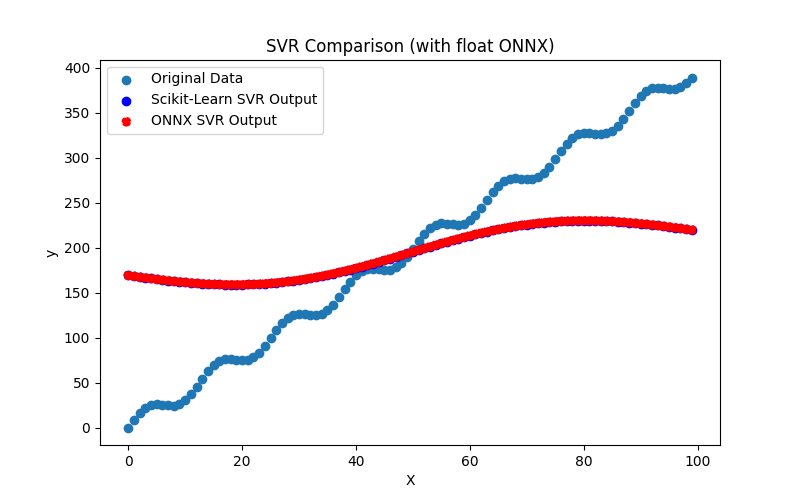
Fig.127. Risultati di SVR.py (float ONNX)
2.2.10.2. Codice MQL5 per l'esecuzione dei Modelli ONNX
Questo codice esegue i modelli salvati svr_float.onnx e svr_double.onnx e dimostra l'uso delle metriche di regressione in MQL5.
//+------------------------------------------------------------------+ //| SVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "SVR" #define ONNXFilenameFloat "svr_float.onnx" #define ONNXFilenameDouble "svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Output:
SVR (EURUSD,H1) Testing ONNX float: SVR (svr_float.onnx) SVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.3982436352100981 SVR (EURUSD,H1) MQL5: Mean Absolute Error: 73.6368384036325523 SVR (EURUSD,H1) MQL5: Mean Squared Error: 7962.8965872368517012 SVR (EURUSD,H1) SVR (EURUSD,H1) Testing ONNX double: SVR (svr_double.onnx) SVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\R\SVR.mq5' (133:16) SVR (EURUSD,H1) model_name=SVR OnnxCreate error 5800
Il modello ONNX float è stato eseguito normalmente, ma si è verificato un errore durante l'esecuzione del modello ONNX double.
Confronto con il modello originale a doppia precisione in Python:
Testing ONNX float: SVR (svr_float.onnx) Python Mean Absolute Error: 73.63683696034649 MQL5: Mean Absolute Error: 73.6368384036325523
Precisione di ONNX float MAE: 5 cifre decimali
2.2.10.3. Rappresentazione ONNX di svr_float.onnx e svr_double.onnx
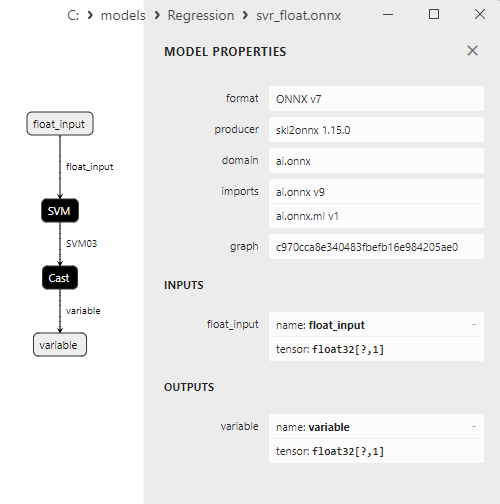
Fig.128. Rappresentazione ONNX di svr_float.onnx in Netron
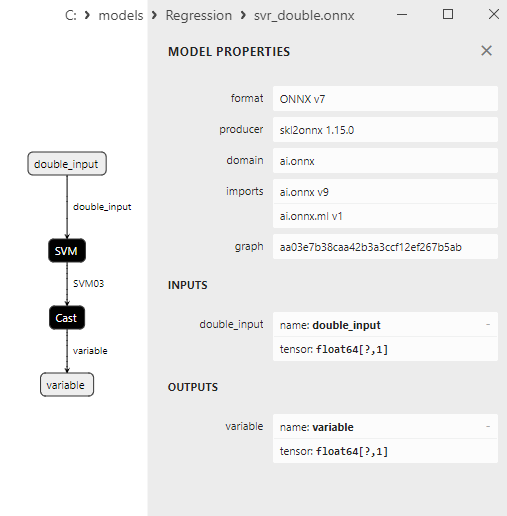
Fig.129. Rappresentazione ONNX di svr_double.onnx in Netron
2.3. Modelli di Regressione che hanno Incontrato Problemi Durante la Conversione in ONNX
Alcuni modelli di regressione non potevano essere convertiti nel formato ONNX dal convertitore sklearn-onnx.
2.3.1. sklearn.dummy.DummyRegressor
DummyRegressor è un metodo di apprendimento automatico utilizzato nelle attività di regressione per creare un modello di base che prevede la variabile target utilizzando semplici regole. È utile per il confronto con altri modelli più complessi e per valutarne le prestazioni. Questo metodo viene spesso utilizzato nel contesto della valutazione della qualità di altri modelli di regressione.
Il DummyRegressor offre diverse strategie di previsione:
- "mean" (predefinito): DummyRegressor prevede il valore medio della variabile target dal set di dati di addestramento. Questa strategia è utile per determinare quanto sia migliore un altro modello rispetto alla semplice previsione della media.
- "median": DummyRegressor prevede il valore mediano della variabile target dal set di dati di addestramento.
- "quantile": DummyRegressor prevede il valore quantile della variabile target (specificata dal parametro quantile) dal set di dati di addestramento.
- "costante": DummyRegressor prevede un valore costante impostato dall'utente (utilizzando il parametro strategy).
Vantaggi di DummyRegressor:
- Valutazione delle Prestazioni: DummyRegressor è utile per valutare le prestazioni di altri modelli più complessi. Se il vostro modello non riesce a superare le previsioni fatte da DummyRegressor, ciò potrebbe indicare problemi nel modello.
- Confronto con i Modelli di Base: DummyRegressor consente di confrontare le prestazioni di modelli più complessi rispetto ad uno di base (ad esempio, un valore medio o mediano).
- Facile da Usare: DummyRegressor è facile da implementare e da utilizzare per l'analisi comparativa.
Limitazioni di DummyRegressor:
- Non è per una Previsione Accurata: DummyRegressor fornisce solo previsioni di base e non è destinato a previsioni accurate.
- Ignora le Dipendenze Complesse: DummyRegressor non tiene conto delle strutture di dati complesse e delle dipendenze dalle caratteristiche.
- Non è Adatto a Compiti che Richiedono una Previsione Accurata: Nei compiti di previsione del mondo reale, l'uso di DummyRegressor per prevedere la variabile target è insufficiente.
DummyRegressor è uno strumento prezioso per una rapida valutazione e un confronto delle prestazioni di altri modelli di regressione, ma non è un modello di regressione serio e indipendente.
2.3.1.1. Codice per la creazione del modello DummyRegressor
# DummyRegressor.py
# Il codice dimostra il processo di addestramento del modello DummyRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"
# creare un modello Dummy Regressor
regression_model = DummyRegressor(strategy="mean")
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello DummyRegressor, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"
# creare un modello Dummy Regressor
regression_model = DummyRegressor(strategy="mean")
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python DummyRegressor Original model (double) Python R-squared (Coefficient of determination): 0.0 Python Mean Absolute Error: 100.00329851715793 Python Mean Squared Error: 13232.758393867645
Scheda Errori:
DummyRegressor.py started DummyRegressor.py 1 1 Traceback (most recent call last): DummyRegressor.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) DummyRegressor.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyRegressor'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 DummyRegressor.py finished in 2565 ms 19 1
2.3.2. sklearn.kernel_ridge.KernelRidge
KernelRidge è un metodo di apprendimento automatico utilizzato per compiti di regressione. Combina il metodo kernel di Support Vector Machines (Kernel SVM) e la regressione. KernelRidge consente di modellare relazioni complesse e non lineari tra le caratteristiche e la variabile target utilizzando le funzioni kernel.
Principio di funzionamento di KernelRidge:
- Dati di input: Si parte dal set di dati originale contenente le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Funzioni del kernel: KernelRidge utilizza funzioni kernel (come quelle polinomiali, RBF - radial basis function e altre) che trasformano i dati in uno spazio ad alta dimensionalità, consentendo la modellazione di relazioni non lineari più complesse.
- Addestramento del modello: Il modello viene addestrato sui dati minimizzando l'errore quadratico medio tra i valori previsti e i valori effettivi della variabile target. Le funzioni del kernel sono utilizzate per tenere conto di dipendenze complesse.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per nuovi dati, utilizzando le stesse funzioni kernel.
Vantaggi di KernelRidge:
- Modellazione di relazioni complesse e non lineari: KernelRidge consente di modellare dipendenze complesse e non lineari tra le caratteristiche e la variabile target.
- Selezione di differenti kernel: È possibile scegliere kernel diversi a seconda della natura dei dati e del compito da svolgere.
- Regolarizzazione: Il metodo include la regolarizzazione, che aiuta a prevenire l'overfitting del modello.
Limitazioni di KernelRidge:
- Mancanza di interpretabilità: Come molti metodi non lineari, KernelRidge è meno interpretabile dei modelli lineari.
- Complessità computazionale: L'uso di funzioni kernel può essere computazionalmente costoso in presenza di grandi volumi di dati e/o di elevata dimensionalità.
- Requisiti per la messa a punto dei parametri: La scelta appropriata del kernel e dei parametri del modello richiede una messa a punto e un'esperienza.
KernelRidge è utile nelle attività di regressione in cui i dati presentano dipendenze complesse e non lineari ed è necessario un modello in grado di considerare queste relazioni. È utile anche nei compiti in cui si possono utilizzare le funzioni kernel per trasformare i dati in una rappresentazione più informativa.
2.3.2.1. Codice per la creazione del modello KernelRidge
# KernelRidge.py
# Il codice dimostra il processo di addestramento del modello KernelRidge, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"
# creare un modello KernelRidge
regression_model = KernelRidge(alpha=1.0, kernel='linear')
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello KernelRidge, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"
# creare un modello KernelRidge
regression_model = KernelRidge(alpha=1.0, kernel='linear')
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python KernelRidge Original model (double) Python R-squared (Coefficient of determination): 0.9962137909675411 Python Mean Absolute Error: 6.36977985227399 Python Mean Squared Error: 50.10198935520715
Scheda Errori:
KernelRidge.py started KernelRidge.py 1 1 Traceback (most recent call last): KernelRidge.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) KernelRidge.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.kernel_ridge.KernelRidge'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 KernelRidge.py finished in 2516 ms 19 1
2.3.3. sklearn.isotonic.IsotonicRegression
IsotonicRegression - è un metodo di apprendimento automatico utilizzato per compiti di regressione che modella una relazione monotona tra le caratteristiche e la variabile target. In questo contesto, "monotonicità" significa che un aumento del valore di una delle caratteristiche porta a un aumento o a una diminuzione del valore della variabile target, preservando la direzione del cambiamento.
Principio di funzionamento di IsotonicRegression:
- Dati di input: Si parte dal set di dati originale contenente le caratteristiche (variabili indipendenti) e i corrispondenti valori delle variabili target.
- Regressione monotona: IsotonicRegression mira a trovare la migliore funzione monotona che descrive la relazione tra le caratteristiche e la variabile target. Questa funzione può essere lineare o non lineare, ma deve mantenere la monotonicità.
- Addestramento del modello: Il modello viene addestrato sui dati per determinare i parametri della funzione monotona. Durante l'addestramento, il modello cerca di minimizzare la somma degli errori al quadrato tra le previsioni e i valori effettivi della variabile target.
- Previsione: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori delle variabili target per i nuovi dati, mantenendo la relazione monotona.
Vantaggi di IsotonicRegression:
- Modellazione di relazioni monotone: Questo metodo è la scelta ideale quando i dati mostrano dipendenze monotone ed è importante mantenere questa caratteristica nel modello.
- Interpretabilità: I modelli monotoni possono essere più interpretabili in quanto consentono di definire chiaramente la direzione dell'influenza di ciascuna caratteristica sulla variabile target.
Limiti di IsotonicRegression:
- Non è adatto a relazioni complesse e non lineari: Questo metodo è limitato alla modellazione di relazioni monotone e, pertanto, non è adatto alla modellazione di complesse dipendenze non lineari.
- Messa a punto dei parametri: Alcune implementazioni di IsotonicRegression potrebbero avere parametri che richiedono una messa a punto per ottenere prestazioni ottimali.
IsotonicRegression è utile nei compiti in cui la monotonicità della relazione tra le caratteristiche e la variabile target è considerata un fattore importante e vi è la necessità di costruire un modello che preservi questa caratteristica.
2.3.3.1. Codice per la creazione dei modelli IsotonicRegression
# IsotonicRegression.py
# Il codice dimostra il processo di addestramento del modello IsotonicRegression, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"
# creare un modello IsotonicRegression
regression_model = IsotonicRegression()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello IsotonicRegression, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"
# creare un modello IsotonicRegression
regression_model = IsotonicRegression()
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python IsotonicRegression Original model (double) Python R-squared (Coefficient of determination): 0.9999898125037958 Python Mean Absolute Error: 0.20093409873424467 Python Mean Squared Error: 0.13480867590911208
Scheda Errori:
IsotonicRegression.py started IsotonicRegression.py 1 1 Traceback (most recent call last): IsotonicRegression.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) IsotonicRegression.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.isotonic.IsotonicRegression'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 IsotonicRegression.py finished in 2499 ms 19 1
2.3.4. sklearn.cross_decomposition.PLSCanonical
PLSCanonical (Partial Least Squares Canonical) è un metodo di apprendimento automatico utilizzato per risolvere problemi di correlazione canonica. È un'estensione del metodo Partial Least Squares (PLS) e si applica per analizzare e modellare le relazioni tra due gruppi di variabili.
Principio di funzionamento di PLSCanonical:
- Dati di input: Si parte da due set di dati (X e Y), dove ogni set rappresenta un insieme di variabili (caratteristiche). Di solito, X e Y contengono dati correlati e il compito è trovare combinazioni lineari di caratteristiche che massimizzino la correlazione tra loro.
- Selezione di combinazioni lineari: PLSCanonical trova combinazioni lineari (componenti) sia in X che in Y per massimizzare la correlazione tra i componenti dei due set di dati. Queste componenti sono chiamate variabili canoniche.
- Ricerca della massima correlazione: L'obiettivo principale di PLSCanonical è trovare le variabili canoniche che massimizzano la correlazione tra X e Y, evidenziando le relazioni più informative tra i due set di dati.
- Addestramento del modello: Una volta trovate le variabili canoniche, queste possono essere utilizzate per creare un modello che preveda i valori di Y in base a X.
- Generazione di previsioni: Dopo l'addestramento, il modello può essere utilizzato per prevedere i valori Y nei nuovi dati utilizzando i valori X corrispondenti.
Vantaggi di PLSCanonical:
- Analisi di correlazione: PLSCanonical consente di analizzare e modellare le correlazioni tra due set di dati, che possono essere utili per comprendere le relazioni tra le variabili.
- Riduzione della dimensionalità: Il metodo può essere utilizzato anche per ridurre la dimensionalità dei dati, evidenziando i componenti più importanti.
Limitazioni di PLSCanonical:
- Sensibilità alla scelta del numero di componenti: La selezione del numero ottimale di variabili canoniche può richiedere una certa sperimentazione.
- Dipendenza dalla struttura dei dati: I risultati di PLSCanonical possono dipendere fortemente dalla struttura dei dati e dalle correlazioni tra loro.
PLSCanonical è un metodo di apprendimento automatico utilizzato per analizzare e modellare le correlazioni tra due serie di variabili. Questo metodo consente di studiare le relazioni tra i dati e può essere utile per ridurre la dimensionalità dei dati e prevedere i valori in base ai componenti correlati.
2.3.4.1. Codice per la creazione di PLSCanonical
# PLSCanonical.py
# Il codice dimostra il processo di addestramento del modello PLSCanonical, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"
# creare un modello PLSCanonical
regression_model = PLSCanonical(n_components=1)
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello PLSCanonical, l'esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"
# creare un modello PLSCanonical
regression_model = PLSCanonical(n_components=1)
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8, 5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python Python PLSCanonical Original model (double) Python R-squared (Coefficient of determination): 0.9962347199278333 Python Mean Absolute Error: 6.3561407034365995 Python Mean Squared Error: 49.82504148022689
Scheda Errori:
PLSCanonical.py started PLSCanonical.py 1 1 Traceback (most recent call last): PLSCanonical.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) PLSCanonical.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.PLSCanonical'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 PLSCanonical.py finished in 2513 ms 19 1
2.3.5. sklearn.cross_decomposition.CCA
Canonical Correlation Analysis (CCA) è un metodo di analisi statistica multivariata utilizzato per studiare le relazioni tra due gruppi di variabili (gruppo X e gruppo Y). L'obiettivo principale di CCA è trovare combinazioni lineari di variabili X e Y che massimizzino la correlazione tra loro. Queste combinazioni lineari sono chiamate variabili canoniche.
Principio di funzionamento di CCA:
- Dati di input: Si parte da due gruppi di variabili X e Y. Può esserci un numero qualsiasi di variabili in questi gruppi e CCA cerca di trovare combinazioni lineari che massimizzino la correlazione tra loro.
- Costruzione di variabili canoniche: CCA identifica le variabili canoniche in X e Y che massimizzano la loro correlazione. Queste variabili canoniche sono combinazioni lineari delle variabili originali, una per ogni indicatore canonico.
- Valutazione della correlazione: CCA valuta la correlazione tra coppie di variabili canoniche. Le variabili canoniche sono solitamente ordinate per correlazione decrescente, per cui la prima coppia ha la correlazione più alta, la seconda quella successiva più alta e così via.
- Interpretazione: Le variabili canoniche possono essere interpretate considerando la loro correlazione e i pesi delle variabili. Questo permette di capire quali variabili dal gruppo X e Y sono più fortemente correlate.
Vantaggi di CCA:
- Rivela le connessioni nascoste: CCA può aiutare a scoprire correlazioni nascoste tra due gruppi di variabili che potrebbero non essere evidenti durante l'analisi iniziale.
- Robustezza al rumore: CCA può tenere conto del rumore nei dati e concentrarsi sulle correlazioni più significative.
- Applicazioni multiple: CCA può essere utilizzata in vari campi, tra cui la statistica, la bioinformatica, la finanza, per studiare le relazioni tra gruppi di variabili.
Limiti di CCA:
- Richiede più dati: CCA potrebbe richiedere una quantità di dati maggiore rispetto ad altri metodi di analisi per stimare in modo affidabile le correlazioni.
- Relazioni lineari: CCA presuppone relazioni lineari tra le variabili, che in alcuni casi potrebbe essere insufficiente.
- Complessità di interpretazione: L'interpretazione delle variabili canoniche può essere complessa, soprattutto quando ci sono molte variabili nei gruppi X e Y.
CCA è utile nelle attività in cui è necessario studiare la relazione tra due gruppi di variabili e scoprire correlazioni nascoste.
2.3.5.1. Codice per la creazione del modello CCA
# CCA.py
# Il codice dimostra il processo di addestramento del modello CCA, la sua esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="CCA"
onnx_model_filename = data_path + "cca"
# creare un modello CCA
regression_model = CCA(n_components=1)
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Il codice dimostra il processo di addestramento del modello CCA, la sua esportazione in formato ONNX (sia float che double) e di effettuare previsioni utilizzando i modelli ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# funzione per confrontare le cifre decimali corrispondenti
def compare_decimal_places(value1, value2):
# Convertire entrambi i valori in stringhe
str_value1 = str(value1)
str_value2 = str(value2)
# trovare le posizioni dei punti decimali nelle stringhe
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# se uno dei valori non ha un punto decimale, restituire 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calcolare il numero di cifre decimali
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# Trovare il minimo delle due cifre decimali contate
min_decimal_places = min(decimal_places1, decimal_places2)
# inizializzare un conteggio per le cifre decimali corrispondenti
matching_count = 0
# confrontare i caratteri dopo il punto decimale
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# importare le librerie necessarie
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# definire il percorso per il salvataggio del modello
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generare dati sintetici per la regressione
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="CCA"
onnx_model_filename = data_path + "cca"
# creare un modello CCA
regression_model = CCA(n_components=1)
# Adattare il modello ai dati
regression_model.fit(X, y.ravel())
# Prevedere i valori per l'intero set di dati
y_pred = regression_model.predict(X)
# valutare le prestazioni del modello
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# Convertire in modello ONNX (float)
# definire il tipo di dati di input come FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come FloatTensorType
initial_type_float = X.astype(np.float32)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convertire in modello ONNX (double)
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# esportare il modello in formato ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# salvare il modello in un file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# stampare il percorso del modello
print(f"ONNX model saved to {onnx_filename}")
# caricare il modello ONNX e fare previsioni
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# visualizzare le informazioni sui tensori di input in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# visualizzare le informazioni sui tensori di output in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# definire il tipo di dati di input come DoubleTensorType
initial_type_double = X.astype(np.float64)
# prevedere i valori per l'intero set di dati usando ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calcolare e visualizzare gli errori per i modelli originale e ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# impostare le dimensioni della figura
plt.figure(figsize=(8,5))
# tracciare i dati originali e la linea di regressione
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Output:
Python CCA Original model (double) Python R-squared (Coefficient of determination): 0.9962347199278333 Python Mean Absolute Error: 6.3561407034365995 Python Mean Squared Error: 49.82504148022689
Scheda Errori:
CCA.py started CCA.py 1 1 Traceback (most recent call last): CCA.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) CCA.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.CCA'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 CCA.py finished in 2543 ms 19 1
Conclusioni
L'articolo ha esaminato 45 modelli di regressione disponibili nella versione 1.3.2 della libreria Scikit-learn.
1. Di questo gruppo, 5 modelli hanno incontrato difficoltà nella conversione al formato ONNX:
- DummyRegressor (Dummy regressor);
- KernelRidge (Kernel Ridge Regression);
- IsotonicRegression (Isotonic Regression);
- PLSCanonical (Partial Least Squares Canonical Analysis);
- CCA (Canonical Correlation Analysis).
Questi modelli potrebbero essere troppo complessi nella loro struttura o logica e potrebbero utilizzare strutture di dati o algoritmi specifici che non sono pienamente compatibili con il formato ONNX.
2. I restanti 40 modelli sono stati convertiti con successo in ONNX con calcoli in precisione float.
- ARDRegression: Automatic Relevance Determination Regression (ARD);
- BayesianRidge: Bayesian Ridge Regression con regolarizzazione;
- ElasticNet: Combinazione di regolarizzazione L1 e L2 per attenuare l'overfitting;
- ElasticNetCV: Elastic Net con selezione automatica dei parametri di regolarizzazione;
- HuberRegressor: Regressione con sensibilità ridotta ai valori anomali;
- Lars: Least Angle Regression;
- LarsCV: Least Angle Regression con convalida incrociata;
- Lasso: Regressione L1-regolarizzata per la selezione delle caratteristiche;
- LassoCV: Regressione Lasso con convalida incrociata;
- LassoLars: Combinazione di Lasso e LARS per la regressione;
- LassoLarsCV: Regressione LassoLars con convalida incrociata;
- LassoLarsIC: Criteri informativi per la selezione dei parametri di LassoLars;
- LinearRegression: Regressione lineare semplice;
- Ridge: Regressione lineare con regolarizzazione L2;
- RidgeCV: Regressione Ridge con convalida incrociata;
- OrthogonalMatchingPursuit: Regressione con selezione ortogonale delle caratteristiche;
- PassiveAggressiveRegressor: Regressione con un approccio di apprendimento passivo-aggressivo;
- QuantileRegressor: Regressione quantile;
- RANSACRegressor: Regressione con il metodo RANdom SAmple Consensus;
- TheilSenRegressor: Regressione non lineare basata sul metodo Theil-Sen.
- LinearSVR: Regressione vettoriale di supporto lineare;
- MLPRegressor: Regressione con l’utilizzo di un percettrone multistrato;
- PLSRegression: Regressione Parziale ai Minimi Quadrati (Partial Least Squares Regression);
- TweedieRegressor: Regressione basata sulla distribuzione Tweedie;
- PoissonRegressor: Regressione per la modellazione di dati secondo la distribuzione di Poisson;
- RadiusNeighborsRegressor: Regressione basata sul raggio dei vicini;
- KNeighborsRegressor: Regressione basata su k-nearest neighbors;
- GaussianProcessRegressor: Regressione basata su processi gaussiani;
- GammaRegressor: Regressione per la modellazione di dati distribuiti in modo gamma;
- SGDRegressor: Regressione basata sulla discesa stocastica del gradiente;
- AdaBoostRegressor: Regressione con l'algoritmo AdaBoost;
- BaggingRegressor: Regressione con il metodo Bagging;
- DecisionTreeRegressor: Regressione basata su alberi decisionali;
- ExtraTreeRegressor: Regressione supplementare basata su alberi decisionali;
- ExtraTreesRegressor: Regressione con alberi decisionali aggiuntivi;
- NuSVR: Regressione vettoriale di supporto lineare continua (SVR);
- RandomForestRegressor: Regressione con un gruppo di alberi decisionali (Random Forest);
- GradientBoostingRegressor: Regressione con gradient boosting;
- HistGradientBoostingRegressor: Regressione con gradiente di istogramma boosting;
- SVR: Metodo di regressione vettoriale di supporto.
3. È stata inoltre esplorata la possibilità di convertire i modelli di regressione in ONNX con calcoli in doppia precisione (double).
Un problema serio riscontrato durante la conversione dei modelli double in ONNX è la limitazione degli operatori ML ai.onnx.ml.LinearRegressor, ai.onnx.ml.SVMRegressor, ai.onnx.ml.TreeEnsembleRegressor: i loro parametri e valori di uscita sono di tipo float. In sostanza, si tratta di componenti di riduzione della precisione e la loro esecuzione nei calcoli a doppia precisione è dubbia. Per questo motivo, la libreria ONNXRuntime non ha implementato alcuni operatori per i modelli ONNX in doppia precisione (potrebbero verificarsi errori di natura NOT_IMPLEMENTED: 'Impossibile trovare un'implementazione per il nodo LinearRegressor:LinearRegressor(1)', 'Impossibile trovare un'implementazione per il nodo SVMRegressor(1) con nome 'SVM', e così via). Pertanto, nell'ambito delle attuali specifiche ONNX, il funzionamento completo in doppia precisione per questi operatori ML è impossibile.
Per i modelli di regressione lineare, il convertitore sklearn-onnx è riuscito ad aggirare la limitazione di LinearRegressor: Si utilizzano gli operatori ONNX MatMul() e Add(). Grazie a questo approccio, i primi 30 modelli dell'elenco precedente sono stati convertiti con successo in modelli ONNX con calcoli in doppia precisione e questi modelli hanno mantenuto l'accuratezza dei modelli originali in doppia precisione.
Tuttavia, per gli operatori ML più complessi, come SVMRegressor e TreeEnsembleRegressor, questo non è stato raggiunto. Perciò, modelli come AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor e SVR sono attualmente disponibili solo in modelli ONNX con calcoli float.
Riepilogo
L'articolo riguardava 45 modelli di regressione della libreria Scikit-learn versione 1.3.2 e i loro risultati di conversione in formato ONNX per calcoli sia float che double.
Di tutti i modelli esaminati, 5 si sono rivelati complessi per la conversione ONNX. Questi modelli includono DummyRegressor, KernelRidge, IsotonicRegression, PLSCanonical e CCA. La loro complessa struttura o logica può richiedere ulteriori adattamenti per il successo della conversione in ONNX.
I restanti 40 modelli di regressione sono stati trasformati con successo in formato ONNX per float. Tra questi, 30 modelli sono stati convertiti con successo in formato ONNX a doppia precisione, mantenendo la loro accuratezza.
A causa della limitazione degli operatori ML per SVMRegressor e TreeEnsembleRegressor, i moduli AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor e SVR sono attualmente disponibili solo nei modelli ONNX con calcoli float.
Tutti gli script dell'articolo sono disponibili anche nel progetto pubblico MQL5\Shared Projects\Scikit.Regression.ONNX.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/13538
File allegati |
Scikit.Regression.ONNX.zip
(563.48 KB)
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.
Vai alla discussione
Come gestire le linee utilizzando MQL5
In questo articolo, troverete il modo di gestire le linee più importanti come le trend line, supporto e resistenza con MQL5.
Modelli di classificazione nella libreria Scikit-Learn e la loro esportazione in ONNX
In questo articolo esploreremo l'applicazione di tutti i modelli di classificazione disponibili nella libreria Scikit-Learn per risolvere il compito di classificazione del set di dati Iris di Fisher. Cercheremo di convertire questi modelli in formato ONNX e di utilizzare i modelli risultanti nei programmi MQL5. Inoltre, confronteremo l'accuratezza dei modelli originali con le loro versioni ONNX sull'intero set di dati Iris.
Impara come progettare un sistema di trading tramite Gator Oscillator
Un nuovo articolo della nostra serie su come progettare un sistema di trading basato sugli indicatori tecnici popolari riguarderà l'indicatore tecnico Gator Oscillator e come creare un sistema di trading attraverso semplici strategie.
Come guadagnare denaro eseguendo gli ordini dei trader nel servizio Freelance
MQL5 Freelance è un servizio online in cui gli sviluppatori vengono pagati per creare applicazioni di trading per i clienti trader. Il servizio è attivo con successo sin dal 2010, con oltre 100.000 progetti completati fino ad oggi, per un valore complessivo di 7 milioni di dollari. Come si può notare, si tratta di una somma di denaro considerevole.
Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati