
Experiments with neural networks (Part 5): Normalizing inputs for passing to a neural network
Introduction
After a little reflection on the results of our previous experiments, I started thinking on how to improve the training performance and profitability of the Expert Advisors we developed earlier.
Today I will highlight the importance of a signal, namely, transmitting data to a neural network for analyzing and forecasting future results. Probably, this is the most important component of the neural network. I want to convey the importance of understanding signals to my readers so that you avoid annoying misunderstandings, like "I used the most advanced library, and it did not work". In previous articles, we applied some interesting methods. Now we will try to transfer the indicator data by normalizing its values.
As usual, I will try to explain everything in detail but without excessive complexity. I think, everyone will be able to figure it out.
The importance of normalizing inputs for passing to a neural network
Normalization of inputs is an important step in preparing data for training neural networks. This process allows us to bring the inputs to a certain range of values, which helps to improve the stability and speed of training convergence.
In this article, we will look at why normalization is an important step in neural network training and what normalization methods can be used.
What is normalization of inputs?
Normalization of inputs consists in transforming the input data so that it has a certain range of values. Two main methods of normalization are normalization by mean and standard deviation (z-normalization) and normalization by minimum and maximum (min-max normalization).
Z-normalization uses the mean and standard deviation to center and scale the data. To achieve this, each value is subtracted from the mean and divided by the standard deviation. Min-max normalization uses the minimum and maximum values to scale the data to a given range.
Why is normalization of inputs important?
Normalization of inputs is important to improve the stability and rate of training convergence. If the input data is not normalized, then some parameters may have a large range of values, which can lead to problems in training the neural network. For example, gradients can become too large or small, leading to optimization issues and poor prediction accuracy.
Normalization also allows speeding up the training process, since the convergence of the optimization algorithm can be improved. Properly normalized data can also help avoid the overfitting problem that can occur if the input data is not representative enough.
What normalization methods can be used?
Normalization methods may vary depending on the type of data and the problem we are trying to solve. For example, the most common normalization methods for images are Z-normalization and min-max normalization. However, for other types of data, such as audio signals or text data, it may be more efficient to use other normalization methods.
For example, in case of audio signals, the maximum amplitude normalization is often used, where all signal values are scaled between -1 and 1. For text data, it can be useful to normalize by the number of words or characters in a sentence.
In addition, in some cases it can be useful to normalize not only the input data, but also the target variables. For example, in regression problems where the target variable has a large range of values, it can be useful to normalize the target variable to improve training stability and prediction accuracy.
Normalization of inputs is an important step in preparing data for training neural networks. This process allows us to bring the inputs to a certain range of values, which helps to improve the stability and speed of training convergence. Depending on the type of data and the problem we are trying to solve, different normalization methods can be used. In addition, in some cases it can be useful to normalize not only the input data, but also the target variables.
Normalization methods
Min-Max normalization
In machine learning, normalization is an important data preprocessing step that improves the stability and training convergence rate. One of the most common normalization methods is Min-Max normalization, which allows you to bring data values into the range from 0 to 1. In this article, we will look at how you can use Min-Max normalization for time series.
Time series are a sequence of values measured at different points in time. Examples of time series are data on temperature, stock prices, or the number of goods sales. Time series can be used to predict future values, analyze trends and patterns, or detect anomalies.
Time series may have a different range of values and changes over time may not be uniform. For example, stock prices can range widely and fluctuate based on seasonality, news, and other factors. For effective analysis and forecasting of time series, it is necessary to bring the values to a certain range.
The Min-Max normalization method normalizes values to a range of 0 to 1 by scaling the values according to the minimum and maximum values. The Min-Max normalization equation looks as follows:
x_norm = (x - x_min) / (x_max - x_min)
where x is the data value, x_min is the minimum value in the entire dataset, x_max is the maximum value in the entire dataset, x_norm is the normalized value.
Applying the Min-Max normalization method to time series can help bring data into a common range of values and simplify analysis. For example, if we have temperature data that ranges from -30 to +30 degrees, we can apply Min-Max normalization to bring the values into the range from 0 to 1. This will allow us to compare values over different time periods and identify trends and anomalies.
However, when applying Min-Max normalization to time series, it is necessary to take into account the features of this method and its impact on the data. First, the use of Min-Max normalization can lead to loss of information about the distribution of values within the range. For example, if there are outliers or extreme values in the dataset, they will be cast to 0 or 1 and lost in the analysis. In this case, alternative normalization methods can be used, such as Z-score normalization.
Secondly, when using Min-Max normalization, it is necessary to take into account the dynamics of data changes. If the data has an uneven dynamics of change, then normalization can cause a distortion of time patterns and anomalies. In this case, we can apply local normalization, where the minimum and maximum values are determined for each data group within a certain period of time.
Thirdly, when using Min-Max normalization, it is necessary to consider the influence of the sample on the analysis results. If the sample of observations is not balanced or contains spikes, then normalization can lead to erroneous conclusions. In this case, alternative data processing methods can be used, such as spikes removal or data smoothing.
In conclusion, the Min-Max normalization method is one of the most common normalization methods in machine learning and can be effectively applied to time series to bring values to a common range. However, when using this method, it is necessary to take into account the features of the data and apply additional processing methods in order to avoid distortions in the analysis and forecasting of time series.
Example:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // find the minimum and maximum value in the array double min_value = ArrayMinimum(data_array, 0, ArraySize(data_array)-1); double max_value = ArrayMaximum(data_array, 0, ArraySize(data_array)-1); // create an array to store the normalization result double norm_array[ArraySize(data_array)]; // normalize the array for(int i = 0; i < ArraySize(data_array); i++) { norm_array[i] = (data_array[i] - min_value) / (max_value - min_value); } // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Min-Max normalization result: ", norm_array[i]); } return(INIT_SUCCEEDED); }
The code creates the data_array array containing five floating point numbers. It then finds the minimum and maximum values in the array using the ArrayMinimum() and ArrayMaximum() functions, creates the new array called norm_array to store the normalization result and populates it by calculating (data_array[i] - min_value) / (max_value - min_value) for each element. Finally, the result is displayed on the screen using the Print() function.
Result:
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 0.39999999999999997 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 0.7666666666666666 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 1.1333333333333333 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 1.5
Z-normalization
Time series are an important tool in data analysis, especially in economics, finance, meteorology, materials science and other fields. One of the main time series preprocessing methods is Z-normalization, which can help improve the quality of data analysis.
Z-normalization is a method for centering and scaling time series. It consists in transforming the time series in such a way that the mean value of the time series is equal to zero and the standard deviation is equal to one. This can be useful for comparing time series with each other, as well as for removing the influence of seasonality and trends.
The process of Z-normalization of time series includes the following steps:
- Calculating the mean of the time series.
- Calculating the standard deviation of the time series.
- For each element of the time series, calculate the difference between its value and the average value of the time series.
- Divide each difference by the standard deviation.
The resulting values will have a mean of zero and a standard deviation of one.
Benefits of Z-normalization:
- Improving the quality of data analysis. Z-normalization can help remove the effects of seasonality and trends, which can improve the quality of your data analysis.
- Ease of use. Z-normalization is easy to use and can be applied to different types of time series.
- Useful for comparing time series. Z-normalization allows comparing time series with each other, as it eliminates the influence of different scales and units of measurement.
However, Z-normalization also has some limitations:
- It is not suitable for time series with extreme values. If the time series contains extreme values, Z-normalization can lead to skewed results.
- It is not suitable for non-stationary time series. If the time series is non-stationary (i.e. has a trend or seasonality), then Z-normalization can eliminate these characteristics, which can lead to incorrect data analysis.
- No guarantee of normal distribution. Z-normalization can help normalize the distribution of the time series, but it does not guarantee that the distribution will be exactly normal.
Despite these limitations, Z-normalization is an important time series preprocessing technique that can help improve the quality of data analysis. It can be used in various fields including economics, finance, meteorology, and materials science.
For example, in economics and finance, Z-normalization can be used to compare the performance of different assets or portfolios, and to analyze risk and volatility.
In meteorology, Z-normalization can help remove seasonality and trends from the analysis of weather data such as temperature or precipitation.
In materials science, Z-normalization can be used to analyze time series of material properties such as thermal expansion or magnetic properties.
In conclusion, Z-normalization is an important time series preprocessing technique that can help improve the quality of data analysis in various areas. Despite some limitations, Z-normalization is easy to use and can be applied to different types of time series.
Example:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // find the mean and standard deviation in the array double mean_value = ArrayAverage(data_array, 0, ArraySize(data_array)-1); double std_value = ArrayStdDev(data_array, 0, ArraySize(data_array)-1); // create an array to store the normalization result double norm_array[ArraySize(data_array)]; // normalize the array for(int i = 0; i < ArraySize(data_array); i++) { norm_array[i] = (data_array[i] - mean_value) / std_value; } // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Z-normalization result: ", norm_array[i]); } return(INIT_SUCCEEDED); } double ArrayAverage(double &array[], int start_pos=0, int count=-1) { double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of elements for(int i = start_pos; i <= end_pos; i++) { sum += array[i]; } // Calculate the average value double avg = sum / (end_pos - start_pos + 1); return (avg); } double ArrayStdDev(double &array[], int start_pos=0, int count=-1) { double mean = ArrayAverage(array, start_pos, count); double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of squared deviations from the mean for(int i = start_pos; i <= end_pos; i++) { sum += MathPow(array[i] - mean, 2); } // Calculation of standard deviation double std_dev = MathSqrt(sum / (end_pos - start_pos + 1)); return (std_dev); }
The code creates the data_array array containing five floating point numbers. It then finds the mean and standard deviation in the array using the ArrayAverage() and ArrayStdDev() functions, creates the new array called norm_array to store the normalization result and populates it by calculating (data_array[i] - mean_value) / std_value for each element. Finally, the result is displayed on the screen using the Print() function.
Result:
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: -1.3416407864998738 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: -0.4472135954999581 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: 0.44721359549995776 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: 1.3416407864998736
Differentiation
Differentiation of time series is an important method of data analysis, which allows removing a trend and/or seasonality from the series, making it more stationary. In this article, we will look at what differentiation is, how to apply it, and what benefits it can provide.
What is time series differentiation?
Differentiation is the process of finding differences between successive values in a time series. The number of differences you need to find depends on the degree of stationarity you want to achieve. Usually one or two differences are enough to eliminate a trend or seasonality. One difference step looks like this:
y'(t) = y(t) - y(t-1)
where y'(t) is the difference between the current value of the series and the previous value.
If the series is non-stationary, then after differentiation, its values become more random, with no visible trends or seasonality. This can help highlight more obvious features of the time series, such as cycles or volatility.
How to apply time series differentiation?
To differentiate a time series, follow these steps:
- Determine if the series is non-stationary. If there is a trend or seasonality in the series, then it is non-stationary.
- Determine how many differences you need to get stationarity. If you want to remove only the trend, then one difference is enough. If you want to remove seasonality, then two or more differences may be required.
- Apply a difference transformation to the series. Use the y'(t) = y(t) - y(t-1) equation to find the first difference. If you need to find the second difference, apply the equation to y'(t).
- Check if the series is stationary. To do this, you can use statistical tests for stationarity, such as the Dickey-Fuller test.
- If the series is non-stationary, repeat the differentiation process until the series becomes stationary.
What are the benefits of differentiating time series?
Differentiating time series can provide several benefits:
- Forecasting improvement: When a time series is stationary, forecasting becomes easier because the statistical properties of the series do not change over time.
- Detrending: Differentiating a series removes the linear trend, making the series more stationary and improving its analysis.
- Seasonality removal: By using multiple difference steps, you can remove seasonality from a time series, making it more stationary.
- Noise removal: Differentiating a series removes low-frequency components (trend and seasonality), which can help remove the noise introduced by these components.
- Improving interpretation: When a series is stationary, it can be analyzed using classical statistical methods, making data interpretation easier and more understandable.
However, differentiation can also have disadvantages. For example, if you differentiate a series too many times, it may lose important signals, leading to incorrect conclusions. In addition, differentiation can introduce additional noise into the series.
Time series differentiation is a useful data analysis technique that removes trend and/or seasonality from a series, making it more stationary. This improves prediction, removes noise, and improves data interpretation. However, differentiation can also have disadvantages, so it should be used with caution and in combination with other data analysis methods.
Example:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // create an array to store the result of differentiation double diff_array[ArraySize(data_array)]; // differentiate the array for(int i = 0; i < ArraySize(data_array)-1; i++) { diff_array[i] = data_array[i+1] - data_array[i]; } // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Differentiation result: ", diff_array[i]); } return(INIT_SUCCEEDED); }
The code creates the data_array array containing five floating point numbers. It then creates a new array diff_array to store the result of the differentiation and fill it in subtracting each element i+1 from i in data_array . Finally, the result is displayed on the screen using the Print() function.
Result:
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.0999999999999999 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.1 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.1 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.0999999999999996
Logarithmic transformation
Time series logarithmic transformation is a data transformation technique that is used to improve the properties of a series before analysis and modeling. This method is especially useful when the data has a high variability or the original values are in a wide range.
What is a logarithmic transformation?
Logarithmic transformation is the process of applying a logarithmic function to each value in a time series. The logarithmic function is used to compress the values of a series, especially if they are in a wide range. The use of the logarithm reduces the variability of the series, as it smooths out peaks and dips in the data, making them less pronounced.
When is the logarithmic transformation useful?
The logarithmic transformation can be useful in the following situations:
- If the data has high variability, then a logarithmic transformation can smooth it out and make it more predictable.
- If the data is in a wide range, then a logarithmic transformation can compress it and improve its interpretation.
- If the data has an exponential trend, then the logarithmic transformation can make it linear, which makes it easier to analyze and model.
- If the data is not normally distributed, then a logarithmic transformation can make it more normal.
An example of applying the logarithmic transformation:
Suppose that we have a time series that represents the daily sales of a store over several years. Since sales can be very variable and patchy, we can apply a logarithmic transformation to smooth the data and make it more predictable.
Continuing with our example, we can apply a logarithmic transformation to our sales time series. To do this, we will apply a logarithmic function to each value in our series.
For example, if we have a series of sales {100, 200, 300, 400}, we can apply a logarithmic transformation to get {log(100), log(200), log(300), log(400)} or just {2 , 2.3, 2.5, 2.6} using the natural logarithm.
As we can see from the example, the logarithmic transformation compressed the values of the series making it more convenient for analysis and modeling. This allows us to better understand sales trends and make more accurate forecasts.
However, do not forget that the logarithmic transformation is not a universal method and is not always suitable for all data types. Also, when applying the logarithmic transformation, you should be careful not to forget to revert to the original data scale if necessary.
In conclusion, the logarithmic transformation is a useful method for transforming time series to improve their properties before analysis and modeling. It can be especially useful for data with high variability or a wide range. However, when using it, one must be aware of its limitations and correctly interpret the results.
Example:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // create an array to store the normalization result double norm_array[ArraySize(data_array)]; // normalize the array LogTransform(data_array, norm_array); // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Logarithmic transformation result: ", norm_array[i]); } return(INIT_SUCCEEDED); } void LogTransform(double& array1[], double& array2[]) { int size = ArraySize(array1); for(int i = 0; i < size; i++) { array2[i] = MathLog10(array1[i]); } }
The LogTransform() function is used to logarithmically transform array1 and store the result in array2.
The algorithm works as follows: the MathLog10() function is used to convert each element of array1 to a base 10 logarithm, and the result is stored in the corresponding element of array2.
Note that the LogTransform() function accepts data arrays by reference (via & ), which means that the changes made to array2 inside the function will be reflected in the original array passed as an argument when the function is called.
Result:
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.07918124604762482 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.36172783601759284 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.5314789170422551 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.6532125137753437
Additional processing methods to avoid distortions in the analysis and forecasting of time series
Time series are widely used for analysis and forecasting in various fields such as economics, finance, climate science, etc. However, real-world data often contains distortions such as spikes, missing values, or noise that can affect the accuracy of time series analysis and forecasting. Let's consider additional processing methods that will help to avoid distortions in the analysis and forecasting of time series.
Removing spikes
Spikes are values that are very different from the rest of the values in the series. They can be caused by measurement errors, data entry errors or unforeseen events such as crises or accidents. Removing spikes from the time series can improve the quality of analysis and forecasting.
MQL5 language provides several functions for removing spikes. For example, the iqr() function can be used to determine the interquartile range and calculate spike bounds. The MODE_OUTLIERS function can be used to determine spikes based on a decision layer value. These functions can be used in combination with other spike-removing functions.
Example:
void RemoveOutliers(double& array[]) { int size = ArraySize(array); double mean = ArrayAverage(array); double stddev = ArrayStdDev(array, mean); for(int i = 0; i < size; i++) { if(MathAbs(array[i] - mean) > 2 * stddev) { array[i] = mean; } } } double ArrayAverage(double &array[], int start_pos=0, int count=-1) { double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of elements for(int i = start_pos; i <= end_pos; i++) { sum += array[i]; } // Calculate the average value double avg = sum / (end_pos - start_pos + 1); return (avg); } double ArrayStdDev(double &array[], int start_pos=0, int count=-1) { double mean = ArrayAverage(array, start_pos, count); double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of squared deviations from the mean for(int i = start_pos; i <= end_pos; i++) { sum += MathPow(array[i] - mean, 2); } // Calculation of standard deviation double std_dev = MathSqrt(sum / (end_pos - start_pos + 1)); return (std_dev); }
The RemoveOutliers() function uses the mean and standard deviation to determine the spikes in 'array'. If the array element is outside the range of two standard deviations from the mean, it is considered a spike and is replaced by the mean.
Note that the RemoveOutliers() function also accepts a data array by reference (via & ), which means that changes made to the array inside the function will be reflected in the original array passed as an argument when the function is called.
Data smoothing
Data smoothing is removing noise from a time series. Noise can be caused by random fluctuations or unforeseen events. Data smoothing allows you to reduce the impact of noise on the analysis and forecasting of time series.
The MQL5 language provides several functions for data smoothing. For example, the iMA() function can be used to calculate a moving average. This allows us to smooth the data, reduce noise and detect trends. The iRSI() function can be used to calculate the relative strength of the index, which can also be used to smooth data and identify trends.
Example:
void SmoothData(double& array[], int period) { int size = ArraySize(array); double smoothed[size]; double weight = 1.0 / period; for(int i = 0; i < size; i++) { double sum = 0.0; for(int j = i - period + 1; j <= i; j++) { if(j >= 0 && j < size) { sum += array[j]; } } smoothed[i] = sum * weight; } ArrayCopy(smoothed, array, 0, 0, size); }
This function uses a simple moving average to smooth the data in 'array'. 'Period' specifies the number of elements used to calculate the average value at each point.
Inside the function, the new 'smoothed' array is created to store the smoothed data. Then iterate over each element of 'array' and calculate the average value for the period specified by 'period'.
Finally, the 'smoothed' array is copied back to array using the ArrayCopy() function. Note that the SmoothData() function also accepts a data array by reference (via & ), which means that changes made to the array inside the function will be reflected in the original array passed as an argument when the function is called.
Missing values
Missing values are values that are missing from the time series. This can be caused by data entry errors or data collection issues. Missing values can have a significant impact on time series analysis and forecasting. When handling missing values, we need to decide how to fill them. The MQL5 language provides several functions for handling missing values.
The iBarShift() function can be used to find the bar index corresponding to a specific date. If a time series value is missing for a certain date, we can use the value from the previous bar or fill it with the average value of the time series for a certain period of time.
Example:
void FillMissingValues(double& array[]) { int size = ArraySize(array); double last_valid = 0.0; for(int i = 0; i < size; i++) { if(IsNaN(array[i])) { array[i] = last_valid; } else { last_valid = array[i]; } } }
This function uses the "filling" method - it replaces any missing values with the previous valid value in 'array'. To do this, we create the last_valid variable that stores the last valid value in the array, and loop through each element of the array. If the current value is missing ( NaN ), replace it with last_valid. If the value is not missing, we store it in last_valid and keep iterating.
Note that the FillMissingValues() function also accepts a data array by reference (via & ), which means that changes made to the array inside the function will be reflected in the original array passed as an argument when the function is called.
Interpolation
Interpolation is a method of filling in missing values which assumes that the missing values between two known values can be calculated using some function. In MQL5, we can use the MathSpline() function to interpolate values.
Of course, there are other data processing techniques that can help improve time series analysis and forecasting. For example, time series decomposition can help highlight trends, cycles and seasonal components. Cluster analysis and factor analysis can help identify factors that influence time series.
In conclusion, the use of additional data processing methods can significantly improve the analysis and forecasting of time series. The MQL5 language provides various data processing functions that can be used to remove spikes, smooth data and handle missing values. In addition, there are other data processing methods that can be applied to improve the analysis and forecasting of time series.
Example:
double Interpolate(double& array[], double x) { int size = ArraySize(array); int i = 0; // Find the two closest elements in the array while(i < size && array[i] < x) { i++; } if(i == 0 || i == size) { // x is out of the array range return 0.0; } // Calculate weights for interpolation double x0 = array[i-1]; double x1 = array[i]; double w1 = (x - x0) / (x1 - x0); double w0 = 1.0 - w1; // Interpolate value return w0 * array[i-1] + w1 * array[i]; }
The Interpolate function takes two arguments: a reference to an array of floating point numbers, and an x value to be interpolated. The interpolation algorithm is to find the two closest elements in the array, calculate the weights for the interpolation and then calculate the interpolated value. If the x value is outside the range of the array, the function returns 0.
Note that the Interpolate function also accepts a data array by reference (via & ), which means that changes made to the array inside the function will be reflected in the original array passed as an argument when the function is called.
Types of signals that are most suitable for being transmitted to the neural network
Signals are a key element for the operation of neural networks. They represent data passed to the neural network for processing and analysis. Choosing the right type of signal to transmit to a neural network can greatly affect its efficiency and accuracy. Here we will consider the most preferred types of signals for transmission to a neural network.
Numerical signals
Numerical signals are the most common type of signals used in neural networks. These are numerical values that can be processed and analyzed by a neural network. Numerical signals can be either discrete or continuous. Discrete signals have a finite number of values, while continuous signals have an infinite number of values.
Images
Images are also a popular type of signal used in neural networks. These are graphic images that can be processed by a neural network. Images can be either black and white or color. To transfer images to the neural network, they must be converted to a numerical format.
Text signals
Text signals can also be used to send data to a neural network. These are text strings that can be processed and analyzed by a neural network. Text signals can be in both natural languages and special programming languages.
Audio signals
Audio signals can also be used to send data to a neural network. These are audio signals that can be processed and analyzed by a neural network. Audio signals can be both voice and music.
Video signals
Video signals are a sequence of images that can be processed and analyzed by a neural network.
Sensory signals
Sensory signals are an important type of signals for transmission to a neural network in machine vision and robotics problems. They may include data from sensors such as gyroscopes, accelerometers, distance sensors and others. This data can be used to train the neural network so that it can analyze and respond to the environment.
Graphic signals
Graphic signals are vector or bitmap images that can be processed and analyzed by a neural network. They can be used for graphics and design related tasks such as character and shape recognition, automatic drawing creation, etc.
Time series
Time series are a sequence of numbers that are measured over time. They can be used for tasks related to forecasting, trend prediction and analysis of temporal data. Neural networks can be used to process time series to reveal hidden patterns and predict future values.
How to choose the appropriate type of signal to transmit to the neural network?
The choice of the appropriate type of signal to transmit to the neural network depends on the specific task and available data. Some tasks may require the use of several signal types at the same time. For example, a speech recognition task may involve using audio signals and text signals at the same time.
When choosing the type of signal to be transmitted to the neural network, it is necessary to take into account its characteristics, such as size, resolution, format, etc. In addition, it is necessary to provide appropriate data pre-processing, such as normalization, filtering, etc., to ensure optimal quality and accuracy of data processing by the neural network.
In conclusion, choosing the appropriate type of signal to send to the neural network is an important step to achieve optimal results in machine learning tasks. Different types of signals can be used to train neural networks depending on the specific task and available data. The right choice of signal type and appropriate data preprocessing can help ensure optimal accuracy and performance of the neural network.
However, the limitations of computing power and data availability should also be considered. Some types of signals may be more difficult for the neural network to process, which may require more processing power and more training data. Therefore, it is necessary to balance between the quality and availability of data when choosing the type of signal for neural network training.
In general, choosing the right type of signal to send to a neural network is an important step to achieve optimal results in machine learning tasks. Neural networks can process various types of signals such as audio, video, text, sensory data, graphical data and time series. The right choice of signal type and appropriate data preprocessing can help ensure optimal accuracy and performance of the neural network in a particular task.
Practice
Let's consider several EAs based on our favorite perceptron. We will pass Accelerator Oscillator indicator values. Let's pass the indicator value on four candles and apply the normalization methods described above. For more detail, let's compare the results of EAs with and without transformation. In the EA without transformation, we will pass the indicator values directly.
Here I will provide all the parameters for optimization and forward testing, so as not to repeat myself in the text:
- Forex;
- EURUSD;
- Timeframe: H1;
- StopLoss 300 and TakeProfit 600;
- "Open prices only" and "Complex Criterion max" optimization and testing modes. It is very important to use the "Maximum complex criterion" mode, it showed more stable and profitable results compared to "Maximum profitability";
- Optimization range 3 years. From 2019.04.06 to 2022.04.06 . 3 years is not a reliable criterion. You can experiment with this parameter on your own;
- Forward test range is 1 year. From 2022.04.06 to 2023.04.06 . Check everything based on the algorithm described in my article (Experiments with neural networks (Part 3): Practical application). This means simultaneous trading of several best optimization results;
- We will now perform the optimization 40 times. Let's increase it by 2 times compared to the previous tests and look at the results.
- In all forward tests, 40 optimization results were used simultaneously. The value is increased 2 times in comparison with the previous tests;
- Optimization of EAs with the "Fast (genetic based algorithm)" perceptron;
- Initial deposit 10,000 units;
- Leverage 1:500.
For optimization, I use a small auto clicker program I developed in Delphi. I cannot post it here, but I will send it to anyone who needs it in a private message. It works as follows:
- Enter the required number of optimizations.
- Hover the mouse cursor over the Start button in the strategy optimizer.
- Wait.
Optimization ends after the specified cycles and the program closes. The autoclicker responds to the change in the color of the Start button. The program is displayed in the screenshot below.
EA perceptron AC 4 SL TP:
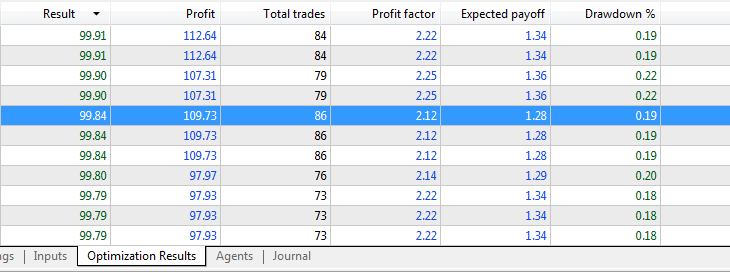
Indicator data is passed directly without using normalization.
Optimization results:

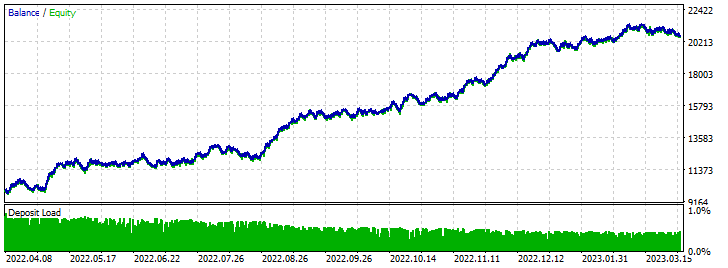
Forward test results:
EA perceptron AC 4 (Differentiation) SL TP:
Indicator data is passed using Min-Max normalization.
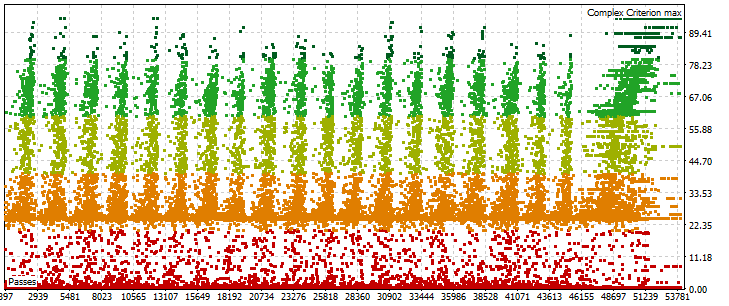
Optimization results:
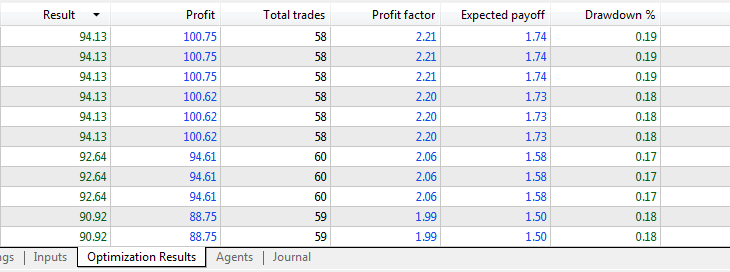
Forward test results:
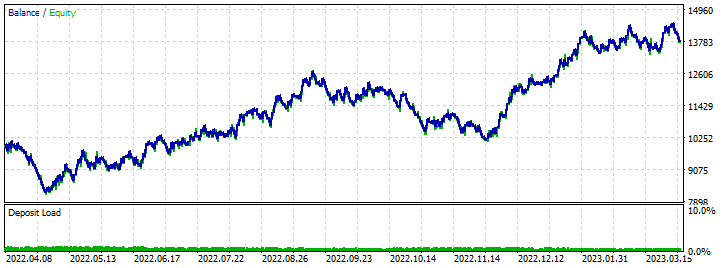
Conclusion
The list of attached files:
- perceptron AC 4 SL TP - opt - perceptron-based EA for optimization on AC indicator without normalization;
- perceptron AC 4 SL TP - trade - optimized perceptron-based EA on AC indicator without normalization;
- perceptron AC 4 (Differentiation) SL TP - opt - perceptron-based EA for optimization on AC indicator using differentiation for normalization;
- perceptron AC 4 (Differentiation) SL TP - trade - optimized perceptron-based EA on AC indicator using differentiation for normalization;
Normalization reduces the impact of spikes in the data, which can help prevent model overfitting. Properly normalized data allows the network to better "understand" relationships between parameters, leading to more accurate predictions and improved model quality.
In the article, we looked at several normalization methods, but these are not the only ways to process data to improve the training of neural networks. Each specific case requires an individual approach, and the normalization method should be chosen depending on the characteristics of the data and the specific task.
In general, normalization of input parameters is an important step in training neural networks. Incorrectly processed data can lead to poor results and adversely affect the performance of the model. Properly normalized data can improve the stability and convergence rate of training, as well as lead to more accurate predictions and improved model quality.
Thank you for your attention!
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/12459
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use