
Experimente mit neuronalen Netzen (Teil 5): Normalisierung der Eingaben zur Weitergabe an ein neuronales Netz
Einführung
Nach einer kurzen Reflexion über die Ergebnisse unserer früheren Experimente begann ich darüber nachzudenken, wie wir die Trainingsleistung und Rentabilität der von uns entwickelten Expert Advisors verbessern können.
Heute möchte ich die Bedeutung eines Signals hervorheben, nämlich die Übermittlung von Daten an ein neuronales Netz zur Analyse und Vorhersage künftiger Ergebnisse. Wahrscheinlich ist dies die wichtigste Komponente des neuronalen Netzes. Ich möchte meinen Lesern vermitteln, wie wichtig es ist, Signale zu verstehen, damit Sie ärgerliche Missverständnisse vermeiden können, wie z. B. „Ich habe die fortschrittlichste Bibliothek verwendet, und es hat nicht funktioniert“. In früheren Artikeln haben wir einige interessante Methoden angewandt. Nun werden wir versuchen, die Indikatordaten zu übertragen, indem wir ihre Werte normalisieren.
Wie üblich werde ich versuchen, alles ausführlich, aber nicht zu kompliziert zu erklären. Ich denke, dass jeder in der Lage sein wird, es herauszufinden.
Die Bedeutung der Normalisierung von Eingaben für die Weitergabe an ein neuronales Netz
Die Normalisierung der Eingaben ist ein wichtiger Schritt bei der Vorbereitung der Daten für das Training neuronaler Netze. Dieses Verfahren ermöglicht es uns, die Eingaben in einen bestimmten Wertebereich zu bringen, was die Stabilität und die Konvergenzgeschwindigkeit des Trainings verbessert.
In diesem Artikel wird untersucht, warum die Normalisierung ein wichtiger Schritt beim Training neuronaler Netze ist und welche Normalisierungsmethoden verwendet werden können.
Was bedeutet Normalisierung der Eingaben?
Die Normalisierung der Eingaben besteht darin, die Eingabedaten so zu transformieren, dass sie einen bestimmten Wertebereich aufweisen. Zwei Hauptmethoden der Normalisierung sind die Normalisierung nach Mittelwert und Standardabweichung (z-Normalisierung) und die Normalisierung nach Minimum und Maximum (min-max-Normalisierung).
Bei der Z-Normalisierung werden der Mittelwert und die Standardabweichung zur Zentrierung und Skalierung der Daten verwendet. Dazu wird jeder Wert vom Mittelwert subtrahiert und durch die Standardabweichung geteilt. Die Min-Max-Normalisierung verwendet die Minimal- und Maximalwerte, um die Daten auf einen bestimmten Bereich zu skalieren.
Warum ist die Normalisierung der Eingaben wichtig?
Die Normalisierung der Eingaben ist wichtig, um die Stabilität und die Konvergenzrate des Trainings zu verbessern. Wenn die Eingabedaten nicht normalisiert sind, können einige Parameter einen großen Wertebereich aufweisen, was zu Problemen beim Training des neuronalen Netzes führen kann. Beispielsweise können die Gradienten zu groß oder zu klein werden, was zu Optimierungsproblemen und schlechter Vorhersagegenauigkeit führt.
Die Normalisierung ermöglicht auch eine Beschleunigung des Trainingsprozesses, da die Konvergenz des Optimierungsalgorithmus verbessert werden kann. Richtig normalisierte Daten können auch dazu beitragen, das Problem der Überanpassung zu vermeiden, das auftreten kann, wenn die Eingabedaten nicht repräsentativ genug sind.
Welche Normalisierungsmethoden können verwendet werden?
Die Normalisierungsmethoden können je nach Art der Daten und des zu lösenden Problems variieren. Die gebräuchlichsten Normalisierungsmethoden für Bilder sind zum Beispiel die Z-Normalisierung und die Min-Max-Normalisierung. Für andere Datentypen, wie z. B. Audiosignale oder Textdaten, kann es jedoch effizienter sein, andere Normalisierungsmethoden zu verwenden.
Bei Audiosignalen wird zum Beispiel häufig die Maximalamplitudennormierung verwendet, bei der alle Signalwerte zwischen -1 und 1 skaliert werden. Bei Textdaten kann es sinnvoll sein, nach der Anzahl der Wörter oder Zeichen in einem Satz zu normalisieren.
Darüber hinaus kann es in einigen Fällen sinnvoll sein, nicht nur die Eingabedaten, sondern auch die Zielvariablen zu normalisieren. Bei Regressionsproblemen, bei denen die Zielvariable einen großen Wertebereich aufweist, kann es beispielsweise sinnvoll sein, die Zielvariable zu normalisieren, um die Trainingsstabilität und die Vorhersagegenauigkeit zu verbessern.
Die Normalisierung der Eingaben ist ein wichtiger Schritt bei der Vorbereitung der Daten für das Training neuronaler Netze. Dieses Verfahren ermöglicht es uns, die Eingaben in einen bestimmten Wertebereich zu bringen, was die Stabilität und die Konvergenzgeschwindigkeit des Trainings verbessert. Je nach Art der Daten und des zu lösenden Problems können verschiedene Normalisierungsmethoden verwendet werden. Darüber hinaus kann es in einigen Fällen sinnvoll sein, nicht nur die Eingabedaten, sondern auch die Zielvariablen zu normalisieren.
Normalisierungsmethoden
Min-Max-Normalisierung
Beim maschinellen Lernen ist die Normalisierung ein wichtiger Schritt der Datenvorverarbeitung, der die Stabilität und die Konvergenzrate beim Training verbessert. Eine der gebräuchlichsten Normalisierungsmethoden ist die Min-Max-Normalisierung, mit der Sie Datenwerte in den Bereich von 0 bis 1 bringen können. In diesem Artikel werden wir uns ansehen, wie Sie die Min-Max-Normalisierung für Zeitreihen verwenden können.
Zeitreihen sind eine Folge von Werten, die zu verschiedenen Zeitpunkten gemessen werden. Beispiele für Zeitreihen sind Daten zur Temperatur, zu Aktienkursen oder zur Anzahl der verkauften Waren. Zeitreihen können zur Vorhersage zukünftiger Werte, zur Analyse von Trends und Mustern oder zur Erkennung von Anomalien verwendet werden.
Zeitreihen können einen unterschiedlichen Wertebereich aufweisen, und die Veränderungen im Laufe der Zeit sind möglicherweise nicht einheitlich. So können die Aktienkurse beispielsweise stark schwanken und je nach Saisonalität, Nachrichten und anderen Faktoren variieren. Für eine wirksame Analyse und Vorhersage von Zeitreihen ist es notwendig, die Werte in einen bestimmten Bereich zu bringen.
Die Min-Max-Normalisierungsmethode normalisiert die Werte auf einen Bereich von 0 bis 1, indem sie die Werte entsprechend den Werten für Tief und Hoch skaliert. Die Min-Max-Normalisierungsgleichung sieht wie folgt aus:
x_norm = (x - x_min) / (x_max - x_min)
wobei x der Datenwert, x_min der Mindestwert im gesamten Datensatz, x_max der Höchstwert im gesamten Datensatz und x_norm der normierte Wert ist.
Die Anwendung der Min-Max-Normalisierungsmethode auf Zeitreihen kann dazu beitragen, Daten in einen gemeinsamen Wertebereich zu bringen und die Analyse zu vereinfachen. Wenn wir beispielsweise Temperaturdaten haben, die von -30 bis +30 Grad reichen, können wir die Min-Max-Normalisierung anwenden, um die Werte in den Bereich von 0 bis 1 zu bringen. So können wir die Werte über verschiedene Zeiträume hinweg vergleichen und Trends und Anomalien erkennen.
Bei der Anwendung der Min-Max-Normalisierung auf Zeitreihen müssen jedoch die Merkmale dieser Methode und ihre Auswirkungen auf die Daten berücksichtigt werden. Erstens kann die Verwendung der Min-Max-Normalisierung zu einem Verlust von Informationen über die Verteilung der Werte innerhalb des Bereichs führen. Gibt es beispielsweise Ausreißer oder Extremwerte im Datensatz, so werden diese auf 0 oder 1 gesetzt und gehen in der Analyse verloren. In diesem Fall können alternative Normalisierungsmethoden verwendet werden, z. B. die Z-Score-Normalisierung.
Zweitens muss bei der Verwendung der Min-Max-Normalisierung die Dynamik der Datenänderungen berücksichtigt werden. Wenn die Daten eine ungleichmäßige Veränderungsdynamik aufweisen, kann die Normalisierung zu einer Verzerrung der Zeitmuster und Anomalien führen. In diesem Fall können wir eine lokale Normalisierung anwenden, bei der die Tiefst- und Höchstwerte für jede Datengruppe innerhalb eines bestimmten Zeitraums bestimmt werden.
Drittens muss bei der Verwendung der Min-Max-Normalisierung der Einfluss der Stichprobe auf die Analyseergebnisse berücksichtigt werden. Wenn die Stichprobe der Beobachtungen nicht ausgewogen ist oder Spitzen enthält, kann die Normalisierung zu falschen Schlussfolgerungen führen. In diesem Fall können alternative Datenverarbeitungsmethoden verwendet werden, wie z. B. die Entfernung von Ausreißern (spikes) oder die Glättung der Daten.
Zusammenfassend lässt sich sagen, dass die Min-Max-Normalisierungsmethode eine der gebräuchlichsten Normalisierungsmethoden beim maschinellen Lernen ist und effektiv auf Zeitreihen angewandt werden kann, um Werte in einen gemeinsamen Bereich zu bringen. Bei der Anwendung dieser Methode müssen jedoch die Merkmale der Daten berücksichtigt und zusätzliche Verarbeitungsmethoden angewandt werden, um Verzerrungen bei der Analyse und Vorhersage von Zeitreihen zu vermeiden.
Beispiel:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // find the minimum and maximum value in the array double min_value = ArrayMinimum(data_array, 0, ArraySize(data_array)-1); double max_value = ArrayMaximum(data_array, 0, ArraySize(data_array)-1); // create an array to store the normalization result double norm_array[ArraySize(data_array)]; // normalize the array for(int i = 0; i < ArraySize(data_array); i++) { norm_array[i] = (data_array[i] - min_value) / (max_value - min_value); } // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Min-Max normalization result: ", norm_array[i]); } return(INIT_SUCCEEDED); }
Der Code erstellt das Array data_array mit fünf Gleitkommazahlen. Anschließend werden die Minimal- und Maximalwerte im Array mit den Funktionen ArrayMinimum() und ArrayMaximum() ermittelt, ein neues Array mit dem Namen norm_array erstellt, um das Ergebnis der Normalisierung zu speichern, und es durch Berechnung von (data_array[i] - min_value) / (max_value - min_value) für jedes Element aufgefüllt. Schließlich wird das Ergebnis mit der Funktion Print() auf dem Bildschirm angezeigt.
Ergebnis:
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 0.39999999999999997 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 0.7666666666666666 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 1.1333333333333333 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1) Min-Max normalization result: 1.5
Z-Normierung
Zeitreihen sind ein wichtiges Instrument der Datenanalyse, insbesondere in den Bereichen Wirtschaft, Finanzen, Meteorologie, Materialwissenschaft und anderen Bereichen. Eine der wichtigsten Methoden zur Vorverarbeitung von Zeitreihen ist die Z-Normalisierung, mit der die Qualität der Datenanalyse verbessert werden kann.
Die Z-Normalisierung ist eine Methode zur Zentrierung und Skalierung von Zeitreihen. Sie besteht darin, die Zeitreihe so zu transformieren, dass der Mittelwert der Zeitreihe gleich Null und die Standardabweichung gleich Eins ist. Dies kann nützlich sein, um Zeitreihen miteinander zu vergleichen und um den Einfluss von Saisonalität und Trends zu beseitigen.
Der Prozess der Z-Normalisierung von Zeitreihen umfasst die folgenden Schritte:
- Berechnen des Mittelwerts der Zeitreihe.
- Berechnen der Standardabweichung der Zeitreihe.
- Berechnen der Differenz zwischen seinem Wert und dem Durchschnittswert der Zeitreihe für jedes Element der Zeitreihe.
- Teilen jeder Differenz durch die Standardabweichung.
Die resultierenden Werte haben einen Mittelwert von Null und eine Standardabweichung von Eins.
Vorteile der Z-Normalisierung:
- Verbesserung der Qualität der Datenanalyse. Die Z-Normalisierung kann dazu beitragen, die Auswirkungen von Saisonalität und Trends zu beseitigen, was die Qualität Ihrer Datenanalyse verbessern kann.
- Einfache Nutzung. Die Z-Normalisierung ist einfach zu handhaben und kann auf verschiedene Arten von Zeitreihen angewendet werden.
- Hilfreich für den Vergleich von Zeitreihen. Die Z-Normierung ermöglicht den Vergleich von Zeitreihen untereinander, da sie den Einfluss unterschiedlicher Skalen und Maßeinheiten eliminiert.
Allerdings hat die Z-Normalisierung auch einige Einschränkungen:
- Sie ist nicht für Zeitreihen mit Extremwerten geeignet. Wenn die Zeitreihe Extremwerte enthält, kann die Z-Normalisierung zu verzerrten Ergebnissen führen.
- Sie ist für nicht-stationäre Zeitreihen nicht geeignet. Wenn die Zeitreihe nicht stationär ist (d. h. einen Trend oder eine Saisonalität aufweist), kann die Z-Normalisierung diese Merkmale eliminieren, was zu einer falschen Datenanalyse führen kann.
- Keine Garantie für Normalverteilung. Die Z-Normalisierung kann dazu beitragen, die Verteilung der Zeitreihe zu normalisieren, aber sie garantiert nicht, dass die Verteilung dann exakt normalverteilt ist.
Trotz dieser Einschränkungen ist die Z-Normalisierung ein wichtiges Verfahren zur Vorverarbeitung von Zeitreihen, das zur Verbesserung der Qualität der Datenanalyse beitragen kann. Sie kann in verschiedenen Bereichen wie Wirtschaft, Finanzen, Meteorologie und Materialwissenschaft eingesetzt werden.
In den Wirtschafts- und Finanzwissenschaften kann die Z-Normalisierung beispielsweise zum Vergleich der Leistung verschiedener Vermögenswerte oder Portfolios sowie zur Analyse von Risiko und Volatilität verwendet werden.
In der Meteorologie kann die Z-Normalisierung dazu beitragen, saisonale Schwankungen und Trends aus der Analyse von Wetterdaten wie Temperatur oder Niederschlag zu entfernen.
In der Materialwissenschaft kann die Z-Normierung zur Analyse von Zeitreihen von Materialeigenschaften wie Wärmeausdehnung oder magnetischen Eigenschaften verwendet werden.
Zusammenfassend lässt sich sagen, dass die Z-Normalisierung ein wichtiges Verfahren zur Vorverarbeitung von Zeitreihen ist, das die Qualität der Datenanalyse in verschiedenen Bereichen verbessern kann. Trotz einiger Einschränkungen ist die Z-Normalisierung einfach zu handhaben und kann auf verschiedene Arten von Zeitreihen angewendet werden.
Beispiel:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // find the mean and standard deviation in the array double mean_value = ArrayAverage(data_array, 0, ArraySize(data_array)-1); double std_value = ArrayStdDev(data_array, 0, ArraySize(data_array)-1); // create an array to store the normalization result double norm_array[ArraySize(data_array)]; // normalize the array for(int i = 0; i < ArraySize(data_array); i++) { norm_array[i] = (data_array[i] - mean_value) / std_value; } // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Z-normalization result: ", norm_array[i]); } return(INIT_SUCCEEDED); } double ArrayAverage(double &array[], int start_pos=0, int count=-1) { double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of elements for(int i = start_pos; i <= end_pos; i++) { sum += array[i]; } // Calculate the average value double avg = sum / (end_pos - start_pos + 1); return (avg); } double ArrayStdDev(double &array[], int start_pos=0, int count=-1) { double mean = ArrayAverage(array, start_pos, count); double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of squared deviations from the mean for(int i = start_pos; i <= end_pos; i++) { sum += MathPow(array[i] - mean, 2); } // Calculation of standard deviation double std_dev = MathSqrt(sum / (end_pos - start_pos + 1)); return (std_dev); }
Der Code erstellt das Array data_array mit fünf Gleitkommazahlen. Anschließend werden der Mittelwert und die Standardabweichung im Array mit den Funktionen ArrayAverage() und ArrayStdDev() ermittelt, ein neues Array mit dem Namen norm_array erstellt, um das Ergebnis der Normalisierung zu speichern, und es durch Berechnung von (data_array[i] - mean_value) / std_value für jedes Element aufgefüllt. Schließlich wird das Ergebnis mit der Funktion Print() auf dem Bildschirm angezeigt.
Ergebnis:
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: -1.3416407864998738 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: -0.4472135954999581 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: 0.44721359549995776 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1) Z-normalization result: 1.3416407864998736
Differenzierung
Die Differenzierung von Zeitreihen ist eine wichtige Methode der Datenanalyse, die es ermöglicht, einen Trend und/oder eine Saisonalität aus der Reihe zu entfernen und sie dadurch stationärer zu machen. In diesem Artikel werden wir uns ansehen, was Differenzierung ist, wie man sie anwendet und welche Vorteile sie bringen kann.
Was bedeutet eine Differenzierung von Zeitreihen?
Unter Differenzierung versteht man die Ermittlung von Unterschieden zwischen aufeinanderfolgenden Werten in einer Zeitreihe. Die Anzahl der Unterschiede, die Sie finden müssen, hängt von dem Grad der gewünschten Stationarität ab. Normalerweise reichen ein oder zwei Unterschiede aus, um einen Trend oder eine Saisonalität auszuschließen. Ein Differenzierungsschritt sieht folgendermaßen aus:
y'(t) = y(t) - y(t-1)
wobei y'(t) die Differenz zwischen dem aktuellen Wert der Reihe und dem vorherigen Wert ist.
Wenn die Reihe nicht stationär ist, werden ihre Werte nach der Differenzierung zufälliger, ohne sichtbare Trends oder Saisonalität. Dies kann dazu beitragen, offensichtlichere Merkmale der Zeitreihe, wie Zyklen oder Volatilität, hervorzuheben.
Wie wendet man die Differenzierung von Zeitreihen an?
Um eine Zeitreihe zu differenzieren, gehen Sie folgendermaßen vor:
- Bestimmen, ob die Reihe nicht stationär ist. Gibt es einen Trend oder eine Saisonalität in der Reihe, dann ist sie nichtstationär.
- Bestimmen, wie viele Differenzen Sie benötigen, um Stationarität zu erreichen. Wenn Sie nur den Trend entfernen wollen, reicht ein Unterschied aus. Wenn Sie die Saisonabhängigkeit beseitigen wollen, können zwei oder mehr Unterschiede erforderlich sein.
- Anwenden einer Differenztransformation auf die Zeitreihe. Verwenden Sie die Gleichung y'(t) = y(t) - y(t-1), um die erste Differenz zu ermitteln. Wenn Sie die zweite Differenz finden müssen, wenden Sie die Gleichung auf y'(t) an.
- Prüfen, ob die Serie stationär ist. Zu diesem Zweck können Sie statistische Tests auf Stationarität, wie den Dickey-Fuller-Test, verwenden.
- Wenn die Reihe nicht stationär ist, wird der Differenzierungsprozess wiederholt, bis die Reihe stationär wird.
Welche Vorteile bietet die Differenzierung von Zeitreihen?
Die Differenzierung von Zeitreihen kann mehrere Vorteile bieten:
- Verbesserung der Vorhersage: Wenn eine Zeitreihe stationär ist, wird die Vorhersage einfacher, weil sich die statistischen Eigenschaften der Reihe im Laufe der Zeit nicht ändern.
- Detrending: Durch die Differenzierung einer Reihe wird der lineare Trend entfernt, wodurch die Reihe stationärer wird und ihre Analyse verbessert wird.
- Beseitigung der Saisonabhängigkeit: Durch die Verwendung mehrerer Differenzschritte können Sie die Saisonalität aus einer Zeitreihe entfernen und sie so stationärer machen.
- Entfernen des Rauschens: Durch die Differenzierung einer Reihe werden niederfrequente Komponenten (Trend und Saisonalität) entfernt, was dazu beitragen kann, das durch diese Komponenten verursachte Rauschen zu beseitigen.
- Verbesserung der Interpretation: Wenn eine Reihe stationär ist, kann sie mit klassischen statistischen Methoden analysiert werden, was die Interpretation der Daten erleichtert und verständlicher macht.
Die Differenzierung kann aber auch Nachteile haben. Wenn Sie zum Beispiel eine Reihe zu oft differenzieren, können wichtige Signale verloren gehen, was zu falschen Schlussfolgerungen führt. Darüber hinaus kann die Differenzierung zusätzliches Rauschen in die Reihe bringen.
Die Zeitreihendifferenzierung ist eine nützliche Datenanalysetechnik, die den Trend und/oder die Saisonalität aus einer Reihe entfernt und sie damit stationärer macht. Dies verbessert die Vorhersage, beseitigt Rauschen und verbessert die Interpretation der Daten. Die Differenzierung kann jedoch auch Nachteile haben, weshalb sie mit Vorsicht und in Kombination mit anderen Datenanalysemethoden eingesetzt werden sollte.
Beispiel:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // create an array to store the result of differentiation double diff_array[ArraySize(data_array)]; // differentiate the array for(int i = 0; i < ArraySize(data_array)-1; i++) { diff_array[i] = data_array[i+1] - data_array[i]; } // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Differentiation result: ", diff_array[i]); } return(INIT_SUCCEEDED); }
Der Code erstellt das Array data_array mit fünf Gleitkommazahlen. Dann wird ein neues Array diff_array erstellt , um das Ergebnis der Differenzierung zu speichern, und es wird gefüllt, indem jedes Element i+1 von i in data_array subtrahiert wird. Schließlich wird das Ergebnis mit der Funktion Print() auf dem Bildschirm angezeigt.
Ergebnis:
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.0999999999999999 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.1 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.1 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1) Differentiation result: 1.0999999999999996
Logarithmische Transformation
Die logarithmische Transformation von Zeitreihen ist eine Datentransformationstechnik, die zur Verbesserung der Eigenschaften einer Reihe vor der Analyse und Modellierung verwendet wird. Diese Methode ist besonders nützlich, wenn die Daten eine hohe Variabilität aufweisen oder die ursprünglichen Werte in einem großen Bereich liegen.
Was ist eine logarithmische Transformation?
Unter logarithmischer Transformation versteht man die Anwendung einer logarithmischen Funktion auf jeden Wert einer Zeitreihe. Die logarithmische Funktion wird verwendet, um die Werte einer Reihe zu komprimieren, insbesondere wenn sie in einem großen Bereich liegen. Durch die Verwendung des Logarithmus wird die Variabilität der Reihen verringert, da Spitzen und Einbrüche in den Daten geglättet werden, sodass sie weniger ausgeprägt sind.
Wann ist die logarithmische Transformation sinnvoll?
Die logarithmische Transformation kann in den folgenden Situationen nützlich sein:
- Wenn die Daten eine hohe Variabilität aufweisen, kann eine logarithmische Transformation sie glätten und berechenbarer machen.
- Liegen die Daten in einem breiten Bereich, kann eine logarithmische Transformation die Daten komprimieren und ihre Interpretation verbessern.
- Wenn die Daten einen exponentiellen Trend aufweisen, kann die logarithmische Transformation sie linear machen, was die Analyse und Modellierung erleichtert.
- Wenn die Daten nicht normal verteilt sind, kann eine logarithmische Transformation sie normaler machen.
Ein Beispiel für die Anwendung der logarithmischen Transformation:
Angenommen, wir haben eine Zeitreihe, die den täglichen Umsatz eines Geschäfts über mehrere Jahre hinweg darstellt. Da die Verkäufe sehr variabel und uneinheitlich sein können, können wir eine logarithmische Transformation anwenden, um die Daten zu glätten und sie berechenbarer zu machen.
Um mit unserem Beispiel fortzufahren, können wir eine logarithmische Transformation auf unsere Umsatzzeitreihe anwenden. Zu diesem Zweck wenden wir auf jeden Wert unserer Reihe eine logarithmische Funktion an.
Wenn wir zum Beispiel eine Reihe von Verkäufen {100, 200, 300, 400} haben, können wir eine logarithmische Transformation anwenden, um {log(100), log(200), log(300), log(400)} oder einfach {2 , 2.3, 2.5, 2.6} unter Verwendung des natürlichen Logarithmus zu erhalten.
Wie aus dem Beispiel hervorgeht, wurden die Werte der Reihe durch die logarithmische Transformation komprimiert, was die Analyse und Modellierung erleichtert. So können wir Verkaufstrends besser verstehen und genauere Prognosen erstellen.
Vergessen Sie jedoch nicht, dass die logarithmische Transformation keine universelle Methode ist und nicht immer für alle Datentypen geeignet ist. Außerdem sollten Sie bei der Anwendung der logarithmischen Transformation darauf achten, dass Sie nicht vergessen, gegebenenfalls zur ursprünglichen Datenskala zurückzukehren.
Zusammenfassend lässt sich sagen, dass die logarithmische Transformation eine nützliche Methode zur Umwandlung von Zeitreihen ist, um deren Eigenschaften vor der Analyse und Modellierung zu verbessern. Sie kann besonders nützlich sein für Daten mit hoher Variabilität oder einer großen Bandbreite. Allerdings muss man sich bei der Verwendung dieser Methode ihrer Grenzen bewusst sein und die Ergebnisse richtig interpretieren.
Beispiel:
int OnInit() { // declare and initialize the array double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6}; // create an array to store the normalization result double norm_array[ArraySize(data_array)]; // normalize the array LogTransform(data_array, norm_array); // display the result for(int i = 0; i < ArraySize(data_array)-1; i++) { Print("Source array: ", data_array[i]); Print("Logarithmic transformation result: ", norm_array[i]); } return(INIT_SUCCEEDED); } void LogTransform(double& array1[], double& array2[]) { int size = ArraySize(array1); for(int i = 0; i < size; i++) { array2[i] = MathLog10(array1[i]); } }
Die Funktion LogTransform() wird verwendet, um array1 logarithmisch zu transformieren und das Ergebnis in array2 zu speichern.
Der Algorithmus funktioniert folgendermaßen: Die Funktion MathLog10() wird verwendet, um jedes Element von array1 in einen Logarithmus zur Basis 10 umzuwandeln, und das Ergebnis wird in dem entsprechenden Element von array2 gespeichert.
Beachten Sie, dass die Funktion LogTransform() Datenarrays per Verweis (über & ) akzeptiert, was bedeutet, dass die Änderungen, die innerhalb der Funktion an array2 vorgenommen werden, sich in dem ursprünglichen Array widerspiegeln, das als Argument übergeben wird, wenn die Funktion aufgerufen wird.
Ergebnis:
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 1.2 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.07918124604762482 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 2.3 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.36172783601759284 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 3.4 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.5314789170422551 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Source array: 4.5 2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1) Logarithmic transformation result: 0.6532125137753437
Zusätzliche Verarbeitungsmethoden zur Vermeidung von Verzerrungen bei der Analyse und Vorhersage von Zeitreihen
Zeitreihen werden häufig für Analysen und Prognosen in verschiedenen Bereichen wie Wirtschaft, Finanzen, Klimawissenschaften usw. verwendet. Daten aus der realen Welt enthalten jedoch häufig Verzerrungen wie Spitzen, fehlende Werte oder Rauschen, die die Genauigkeit von Zeitreihenanalysen und Prognosen beeinträchtigen können. Betrachten wir weitere Verarbeitungsmethoden, die dazu beitragen, Verzerrungen bei der Analyse und Vorhersage von Zeitreihen zu vermeiden.
Entfernen von Ausreißern
Ausreißer (spikes) sind Werte, die sich stark vom Rest der Werte in der Reihe unterscheiden. Sie können durch Messfehler, Dateneingabefehler oder unvorhergesehene Ereignisse wie Krisen oder Unfälle verursacht werden. Das Entfernen von Spitzen aus den Zeitreihen kann die Qualität von Analysen und Prognosen verbessern.
Die Sprache MQL5 bietet mehrere Funktionen zum Entfernen von Ausreißern. Die Funktion iqr() kann zum Beispiel zur Bestimmung des Interquartilsbereichs und zur Berechnung der Grenzen der Ausreißer verwendet werden. Die Funktion MODE_OUTLIERS kann verwendet werden, um Ausreißer auf der Grundlage eines Entscheidungsschichtwertes zu bestimmen. Diese Funktionen können in Kombination mit anderen Spike-Entfernungsfunktionen verwendet werden.
Beispiel:
void RemoveOutliers(double& array[]) { int size = ArraySize(array); double mean = ArrayAverage(array); double stddev = ArrayStdDev(array, mean); for(int i = 0; i < size; i++) { if(MathAbs(array[i] - mean) > 2 * stddev) { array[i] = mean; } } } double ArrayAverage(double &array[], int start_pos=0, int count=-1) { double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of elements for(int i = start_pos; i <= end_pos; i++) { sum += array[i]; } // Calculate the average value double avg = sum / (end_pos - start_pos + 1); return (avg); } double ArrayStdDev(double &array[], int start_pos=0, int count=-1) { double mean = ArrayAverage(array, start_pos, count); double sum = 0.0; int size = ArraySize(array); // Determine the last element index int end_pos = count < 0 ? size - 1 : start_pos + count - 1; end_pos = end_pos >= size ? size - 1 : end_pos; // Calculate the sum of squared deviations from the mean for(int i = start_pos; i <= end_pos; i++) { sum += MathPow(array[i] - mean, 2); } // Calculation of standard deviation double std_dev = MathSqrt(sum / (end_pos - start_pos + 1)); return (std_dev); }
Die Funktion RemoveOutliers() verwendet den Mittelwert und die Standardabweichung, um die Ausreißer in 'array' zu bestimmen. Wenn das Array-Element außerhalb des Bereichs von zwei Standardabweichungen vom Mittelwert liegt, wird es als Ausreißer betrachtet und durch den Mittelwert ersetzt.
Beachten Sie, dass die Funktion RemoveOutliers() auch ein Datenarray als Referenz akzeptiert (über & ), was bedeutet, dass Änderungen am Array innerhalb der Funktion in dem ursprünglichen Array, das als Argument übergeben wird, wenn die Funktion aufgerufen wird, wiedergegeben werden.
Datenglättung
Datenglättung ist das Entfernen des Rauschens aus einer Zeitreihe. Rauschen kann durch zufällige Schwankungen oder unvorhergesehene Ereignisse verursacht werden. Mit der Datenglättung können Sie die Auswirkungen von Rauschen auf die Analyse und Prognose von Zeitreihen verringern.
Die Sprache MQL5 bietet mehrere Funktionen zur Datenglättung. Die Funktion iMA() kann zum Beispiel zur Berechnung eines gleitenden Durchschnitts verwendet werden. So können wir die Daten glätten, Rauschen reduzieren und Trends erkennen. Die Funktion iRSI() kann zur Berechnung der relativen Stärke des Index verwendet werden, die auch zur Glättung von Daten und zur Ermittlung von Trends genutzt werden kann.
Beispiel:
void SmoothData(double& array[], int period) { int size = ArraySize(array); double smoothed[size]; double weight = 1.0 / period; for(int i = 0; i < size; i++) { double sum = 0.0; for(int j = i - period + 1; j <= i; j++) { if(j >= 0 && j < size) { sum += array[j]; } } smoothed[i] = sum * weight; } ArrayCopy(smoothed, array, 0, 0, size); }
Diese Funktion verwendet einen einfachen gleitenden Durchschnitt, um die Daten in 'array' zu glätten. „Period' gibt die Anzahl der Elemente an, die zur Berechnung des Durchschnittswerts an jedem Punkt verwendet werden.
Innerhalb der Funktion wird das neue Array „geglättet“ (smoothed) erstellt, um die geglätteten Daten zu speichern. Dann wird über jedes Element von „array“ iteriert und der Durchschnittswert für den durch „period“ angegebenen Zeitraum berechnet.
Schließlich wird das „geglättete“ Array mit der Funktion ArrayCopy() zurück in das Array kopiert. Beachten Sie, dass die Funktion SmoothData() auch ein Datenarray als Referenz akzeptiert (über & ), was bedeutet, dass Änderungen am Array innerhalb der Funktion in dem ursprünglichen Array, das als Argument übergeben wird, wenn die Funktion aufgerufen wird, wiedergegeben werden.
Fehlende Werte
Fehlende Werte sind Werte, die in der Zeitreihe fehlen. Dies kann durch Fehler bei der Dateneingabe oder bei der Datenerfassung verursacht werden. Fehlende Werte können erhebliche Auswirkungen auf die Zeitreihenanalyse und -prognose haben. Beim Umgang mit fehlenden Werten müssen wir entscheiden, wie wir sie auffüllen. Die Sprache MQL5 bietet mehrere Funktionen zur Behandlung fehlender Werte.
Die Funktion iBarShift() kann verwendet werden, um den einem bestimmten Datum entsprechenden Balkenindex zu ermitteln. Wenn ein Zeitreihenwert für ein bestimmtes Datum fehlt, können wir den Wert des vorherigen Balkens verwenden oder ihn mit dem Durchschnittswert der Zeitreihe für einen bestimmten Zeitraum füllen.
Beispiel:
void FillMissingValues(double& array[]) { int size = ArraySize(array); double last_valid = 0.0; for(int i = 0; i < size; i++) { if(IsNaN(array[i])) { array[i] = last_valid; } else { last_valid = array[i]; } } }
Diese Funktion verwendet die „Füllmethode“ - sie ersetzt alle fehlenden Werte durch den letzten gültigen Wert in „array“. Zu diesem Zweck erstellen wir die Variable last_valid, die den letzten gültigen Wert im Array speichert, und durchlaufen jedes Element des Arrays in einer Schleife. Wenn der aktuelle Wert fehlt (NaN), wird er durch last_valid ersetzt. Wenn der Wert nicht fehlt, speichern wir ihn in last_valid und setzen die Iteration fort.
Beachten Sie, dass die Funktion FillMissingValues() auch ein Datenarray per Referenz (über & ) akzeptiert, was bedeutet, dass Änderungen am Array, die innerhalb der Funktion vorgenommen werden, im ursprünglichen Array, das als Argument übergeben wird, wenn die Funktion aufgerufen wird, wiedergegeben werden.
Interpolation
Interpolation ist eine Methode zum Auffüllen fehlender Werte, die davon ausgeht, dass die fehlenden Werte zwischen zwei bekannten Werten mit Hilfe einer Funktion berechnet werden können. In MQL5 können wir die Funktion MathSpline() verwenden, um Werte zu interpolieren.
Natürlich gibt es auch andere Datenverarbeitungstechniken, die zur Verbesserung der Zeitreihenanalyse und -prognose beitragen können. So kann beispielsweise die Zerlegung von Zeitreihen dazu beitragen, Trends, Zyklen und saisonale Komponenten hervorzuheben. Mit Hilfe der Clusteranalyse und der Faktorenanalyse können Faktoren ermittelt werden, die Zeitreihen beeinflussen.
Zusammenfassend lässt sich sagen, dass der Einsatz zusätzlicher Datenverarbeitungsmethoden die Analyse und Vorhersage von Zeitreihen erheblich verbessern kann. Die Sprache MQL5 bietet verschiedene Datenverarbeitungsfunktionen, mit denen sich Spitzen entfernen, Daten glätten und fehlende Werte verarbeiten lassen. Darüber hinaus gibt es weitere Datenverarbeitungsmethoden, die zur Verbesserung der Analyse und Vorhersage von Zeitreihen eingesetzt werden können.
Beispiel:
double Interpolate(double& array[], double x) { int size = ArraySize(array); int i = 0; // Find the two closest elements in the array while(i < size && array[i] < x) { i++; } if(i == 0 || i == size) { // x is out of the array range return 0.0; } // Calculate weights for interpolation double x0 = array[i-1]; double x1 = array[i]; double w1 = (x - x0) / (x1 - x0); double w0 = 1.0 - w1; // Interpolate value return w0 * array[i-1] + w1 * array[i]; }
Die Funktion Interpolate benötigt zwei Argumente: einen Verweis auf ein Array von Fließkommazahlen und einen zu interpolierenden x-Wert. Der Interpolationsalgorithmus besteht darin, die beiden nächstgelegenen Elemente in der Matrix zu finden, die Gewichte für die Interpolation zu berechnen und dann den interpolierten Wert zu ermitteln. Wenn der x-Wert außerhalb des Bereichs des Arrays liegt, gibt die Funktion 0 zurück.
Beachten Sie, dass die Funktion Interpolate auch ein Datenarray als Referenz akzeptiert (über & ), was bedeutet, dass Änderungen am Array innerhalb der Funktion in dem ursprünglichen Array, das als Argument beim Funktionsaufruf übergeben wird, wiedergegeben werden.
Arten von Signalen, die sich am besten für die Übertragung an das neuronale Netz eignen
Signale sind ein Schlüsselelement für den Betrieb von neuronalen Netzen. Sie stellen Daten dar, die an das neuronale Netz zur Verarbeitung und Analyse weitergeleitet werden. Die Wahl der richtigen Signalart für die Übertragung an ein neuronales Netz kann dessen Effizienz und Genauigkeit stark beeinflussen. Hier werden wir die bevorzugten Signaltypen für die Übertragung an ein neuronales Netz betrachten.
Numerische Signale
Numerische Signale sind die häufigste Art von Signalen, die in neuronalen Netzen verwendet werden. Dies sind numerische Werte, die von einem neuronalen Netz verarbeitet und analysiert werden können. Numerische Signale können entweder diskret oder kontinuierlich sein. Diskrete Signale haben eine endliche Anzahl von Werten, während kontinuierliche Signale eine unendliche Anzahl von Werten haben.
Bilder
Bilder sind auch eine beliebte Signalart, die in neuronalen Netzen verwendet wird. Dies sind grafische Bilder, die von einem neuronalen Netz verarbeitet werden können. Die Bilder können entweder schwarz-weiß oder farbig sein. Um Bilder an das neuronale Netz zu übertragen, müssen sie in ein numerisches Format umgewandelt werden.
Text-Signale
Textsignale können auch verwendet werden, um Daten an ein neuronales Netz zu senden. Dabei handelt es sich um Textstrings, die von einem neuronalen Netz verarbeitet und analysiert werden können. Textsignale können sowohl in natürlichen Sprachen als auch in speziellen Programmiersprachen vorliegen.
Audio-Signale
Auch Audiosignale können verwendet werden, um Daten an ein neuronales Netz zu senden. Dabei handelt es sich um Audiosignale, die von einem neuronalen Netz verarbeitet und analysiert werden können. Audiosignale können sowohl Sprache als auch Musik sein.
Video-Signale
Videosignale sind eine Folge von Bildern, die von einem neuronalen Netz verarbeitet und analysiert werden können.
Sensorische Signale
Sensorische Signale sind eine wichtige Art von Signalen für die Übertragung an ein neuronales Netz bei Problemen des maschinellen Sehens und der Robotik. Sie können Daten von Sensoren wie Gyroskopen, Beschleunigungsmessern, Abstandssensoren und anderen enthalten. Mit diesen Daten kann das neuronale Netz trainiert werden, damit es die Umgebung analysieren und darauf reagieren kann.
Grafische Signale
Grafiksignale sind Vektor- oder Bitmap-Bilder, die von einem neuronalen Netz verarbeitet und analysiert werden können. Sie können für grafik- und designbezogene Aufgaben wie die Erkennung von Zeichen und Formen, die automatische Erstellung von Zeichnungen usw. verwendet werden.
Zeitreihen
Zeitreihen sind eine Folge von Zahlen, die im Laufe der Zeit gemessen werden. Sie können für Aufgaben im Zusammenhang mit Prognosen, Trendvorhersagen und der Analyse zeitlicher Daten verwendet werden. Neuronale Netze können zur Verarbeitung von Zeitreihen verwendet werden, um verborgene Muster aufzudecken und zukünftige Werte vorherzusagen.
Wie wählt man die geeignete Signalart für die Übertragung an das neuronale Netz aus?
Die Wahl des geeigneten Signaltyps für die Übertragung an das neuronale Netz hängt von der jeweiligen Aufgabe und den verfügbaren Daten ab. Einige Aufgaben können die gleichzeitige Verwendung mehrerer Signaltypen erfordern. Eine Spracherkennungsaufgabe kann zum Beispiel die gleichzeitige Verwendung von Audio- und Textsignalen beinhalten.
Bei der Wahl des Signals, das an das neuronale Netz übertragen werden soll, müssen seine Eigenschaften wie Größe, Auflösung, Format usw. berücksichtigt werden. Darüber hinaus ist eine geeignete Datenvorverarbeitung wie Normalisierung, Filterung usw. erforderlich, um eine optimale Qualität und Genauigkeit der Datenverarbeitung durch das neuronale Netz zu gewährleisten.
Zusammenfassend lässt sich sagen, dass die Wahl des geeigneten Signaltyps, der an das neuronale Netz gesendet werden soll, ein wichtiger Schritt ist, um optimale Ergebnisse bei maschinellen Lernaufgaben zu erzielen. Für das Training neuronaler Netze können je nach Aufgabenstellung und verfügbaren Daten unterschiedliche Signaltypen verwendet werden. Die richtige Wahl des Signaltyps und eine angemessene Datenvorverarbeitung können zu einer optimalen Genauigkeit und Leistung des neuronalen Netzes beitragen.
Allerdings sollten auch die Grenzen der Rechenleistung und der Datenverfügbarkeit berücksichtigt werden. Einige Signaltypen können für das neuronale Netz schwieriger zu verarbeiten sein, sodass mehr Verarbeitungsleistung und mehr Trainingsdaten erforderlich sein können. Daher muss bei der Wahl der Signalart für das Training des neuronalen Netzes ein Gleichgewicht zwischen der Qualität und der Verfügbarkeit der Daten gefunden werden.
Im Allgemeinen ist die Wahl des richtigen Signaltyps, der an ein neuronales Netz gesendet werden soll, ein wichtiger Schritt, um optimale Ergebnisse bei maschinellen Lernaufgaben zu erzielen. Neuronale Netze können verschiedene Arten von Signalen verarbeiten, z. B. Audio, Video, Text, sensorische Daten, grafische Daten und Zeitreihen. Die richtige Wahl des Signaltyps und eine angemessene Datenvorverarbeitung können dazu beitragen, eine optimale Genauigkeit und Leistung des neuronalen Netzes bei einer bestimmten Aufgabe zu gewährleisten.
Praxis
Betrachten wir mehrere EAs, die auf unserem bevorzugten Perceptron basieren. Wir werden die Werte des Accelerator Oscillator Indikators weitergeben. Übertragen wir den Indikatorwert auf vier Kerzen und wenden wir die oben beschriebenen Normalisierungsmethoden an. Vergleichen wir die Ergebnisse der EAs mit und ohne Umwandlung, um mehr zu erfahren. Im EA ohne Transformation werden wir die Indikatorwerte direkt übergeben.
Hier werde ich alle Parameter für die Optimierung und die Vorwärtsprüfung angeben, um mich im Text nicht zu wiederholen:
- Forex;
- EURUSD;
- Zeitrahmen: H1;
- StopLoss 300 und TakeProfit 600;
- Optimierungs- und Testmodi „Nur Eröffnungspreise“ und „Komplexes Kriterium, Maximum“. Es ist sehr wichtig, den Modus „Maximales komplexes Kriterium“ zu verwenden, da er im Vergleich zu „Maximale Rentabilität“ stabilere und rentablere Ergebnisse zeigt;
- Optimierungsbereich 3 Jahre. Von 2019.04.06 bis 2022.04.06. 3 Jahre sind kein zuverlässiges Kriterium. Sie können mit diesem Parameter selbst experimentieren;
- Die Dauer des Vorwärtstest beträgt 1 Jahr. Von 2022.04.06 bis 2023.04.06. Wir überprüfen alles anhand des in meinem Artikel (Experimente mit Neuronalen Netzen (Teil 3) beschriebenen Algorithmus: Praktische Anwendung). Das bedeutet, dass gleichzeitig mehrere beste Optimierungsergebnisse gehandelt werden;
- Wir werden die Optimierung nun 40 Mal durchführen. Erhöhen wir sie im Vergleich zu den vorherigen Tests um das Zweifache und sehen wir uns die Ergebnisse an.
- Bei allen Vorwärtstests wurden 40 Optimierungsergebnisse gleichzeitig verwendet. Der Wert ist im Vergleich zu den vorherigen Tests um das Zweifache erhöht;
- Optimierung des Expert Advisors mit Perceptron „Schneller genetischer Algorithmus“;
- Anfangssaldo 10.000 Einheiten;
- Hebel 1:500.
Zur Optimierung verwende ich ein kleines Autoklicker-Programm, das ich in Delphi entwickelt habe. Ich kann sie hier nicht veröffentlichen, aber ich werde sie jedem, der sie braucht, in einer privaten Nachricht schicken. Es funktioniert folgendermaßen:
- Geben Sie die gewünschte Anzahl von Optimierungen ein.
- Bewegen Sie den Mauszeiger über die Schaltfläche Start im Strategieoptimierer.
- Warten Sie.
Die Optimierung endet nach den angegebenen Zyklen und das Programm wird geschlossen. Der Autoclicker reagiert auf die Änderung der Farbe der Schaltfläche Start. Das Programm ist in der nachstehenden Abbildung dargestellt.
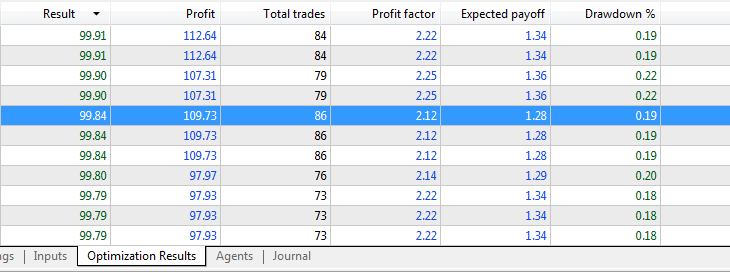
EA perceptron AC 4 SL TP:
Indikatordaten werden direkt ohne Normalisierung übergeben.
Optimierungsergebnisse:

Vorwärts-Test-Ergebnisse:
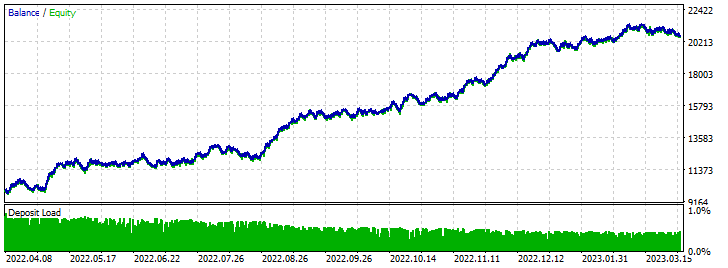
EA perceptron AC 4 (Differenzierung) SL TP:
Die Indikatordaten werden unter Verwendung der Min-Max-Normalisierung übergeben.
Optimierungsergebnisse:
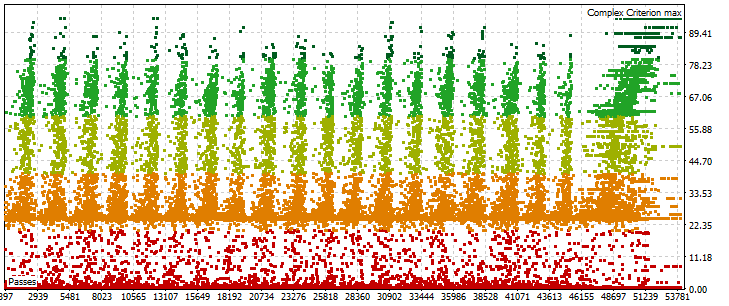
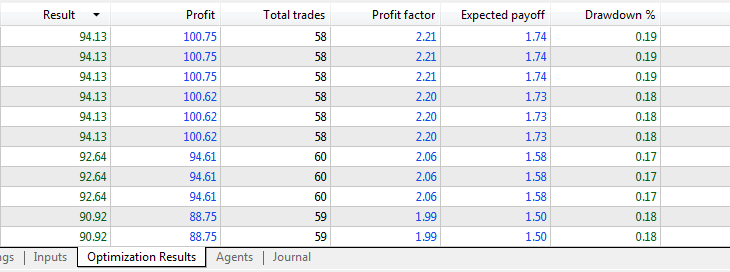
Vorwärts-Test-Ergebnisse:
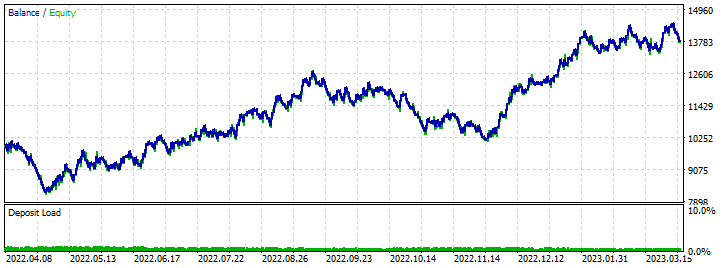
Schlussfolgerung
Die Liste der angehängten Dateien:
- perceptron AC 4 SL TP - opt - Perceptron-basierter EA für die Optimierung von AC-Indikatoren ohne Normalisierung;
- perceptron AC 4 SL TP - trade - optimierter Perceptron-basierter EA auf AC-Indikator ohne Normalisierung;
- perceptron AC 4 (Differenzierung) SL TP - opt - Perceptron-basierter EA zur Optimierung von AC-Indikatoren unter Verwendung von Differenzierung zur Normalisierung;
- perceptron AC 4 (Differenzierung) SL TP - trade - optimierter Perceptron-basierter EA auf AC-Indikator mit Differenzierung für Normalisierung;
Durch die Normalisierung werden die Auswirkungen von Spitzen in den Daten verringert, was eine Überanpassung des Modells verhindern kann. Richtig normalisierte Daten ermöglichen es dem Netz, die Beziehungen zwischen den Parametern besser zu „verstehen“, was zu genaueren Vorhersagen und einer besseren Modellqualität führt.
In diesem Artikel haben wir uns verschiedene Normalisierungsmethoden angesehen, aber das sind nicht die einzigen Möglichkeiten, Daten zu verarbeiten, um das Training neuronaler Netze zu verbessern. Jeder spezifische Fall erfordert einen individuellen Ansatz, und die Normalisierungsmethode sollte in Abhängigkeit von den Merkmalen der Daten und der spezifischen Aufgabe gewählt werden.
Im Allgemeinen ist die Normalisierung der Eingabeparameter ein wichtiger Schritt beim Training neuronaler Netze. Falsch verarbeitete Daten können zu schlechten Ergebnissen führen und die Leistung des Modells beeinträchtigen. Richtig normalisierte Daten können die Stabilität und Konvergenzrate des Trainings verbessern und zu genaueren Vorhersagen und einer besseren Modellqualität führen.
Vielen Dank für Ihre Aufmerksamkeit!
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/12459
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.