神经网络实验（第 5 部分）：常规化传输到神经网络的输入参数

MetaTrader 5 — 交易系统 | 25 九月 2023, 08:49

866

Roman Poshtar

概述

在对之前实验的结果进行了一些反思之后，我开始思考如何提高我们之前开发的智能系统的训练性成效和盈利能力。

今天我将强调信号的重要性，即传输数据到神经网络进行分析，和预测未来结果。这可能是神经网络中最重要的组成部分。我想向我的读者传达理解信号的重要性，这样您就可以避免恼人的误解，例如“我使用了最先进的函数库，但它却不起作用”。在之前的文章中，我们应用了一些有趣的方法。现在，我们将尝试把指标值规范化之后再传输数据。

如往常一样，我将尝试详细解释所有内容，但不会过度复杂。我认为，每个人都能弄清楚。

规范化输入再传递给神经网络的重要性

输入的规范化是为训练神经网络准备数据阶段的重要步骤。这个过程允许我们将数据输入纳入一定范围内，这有助于提高训练收敛的稳定性和速度。

在本文中，我们将研究为什么规范化是神经网络训练中的重要步骤，以及可以使用哪些规范化方法。

什么是输入的规范化？

输入的规范化包括转换输入数据，如此其具有一定的数值范围。归一化的两种主要方法是通过平均值和标准差进行（z-归一化），以及通过最小值和最大值归一化（最小-最大归一化）。

Z-归一化使用平均值和标准差来居中和缩放数据。为此，从平均值中减去每个值，并除以标准差。最小-最大归一化采用最小值和最大值将数据缩放到给定范围。

为什么输入的规范化很重要？

输入的规范化对于提高训练收敛的稳定性和速率非常重要。如果输入数据未规范化，则某些参数可能具有较大的数值范围，这可能会导致神经网络训练出现问题。例如，梯度可能会变得太大或太小，从而导致优化问题和预测精度差。

规范化还允许加快训练过程，因为可以改进优化算法的收敛性。正确规范化的数据还有助于避免在输入数据缺乏代表性时可能发生的过度拟合问题。

哪些规范化方法可以使用？

规范化方法可能会因数据类型和我们尝试解决的问题而异。例如，图像最常见的规范化方法是 Z-归一化和最小-最大归一化。然而，对于其它类型的数据，例如音频信号或文本数据，采用其它规范化方法可能更有效。

例如，对于音频信号，通常采用最大幅度归一化，其中所有信号值都在 -1 和 1 之间缩放。对于文本数据，按句子中的单词或字符数量进行规范化可能很有用。

此外，在某些情况下，不仅规范化输入数据，而且规范化目标变量也很有用。例如，在回归问题中，若目标变量具有较大数值范围，规范化目标变量以提升训练稳定性和预测准确性可能很有用。

输入的规范化是为训练神经网络准备数据阶段的重要步骤。这个过程允许我们将数据输入纳入一定范围内，这有助于提高训练收敛的稳定性和速度。取决于数据类型和我们尝试解决的问题，可以采用不同的常规化方法。此外，在某些情况下，不仅规范化输入数据，而且规范化目标变量也很有用。

规范化方法

最小-最大归一化

在机器学习中，常规化是提升稳定性和训练收敛率的重要数据预处理步骤。最常见的常规化方法之一是最小-最大归一化，它允许您将数据值纳入 0 到 1 的范围之内。在本文中，我们将查看如何针对时间序列运用最小-最大归一化。

时间序列是在不同时间点测量的数值序列。时间序列的示例包括有关热度、股票价格或商品销售数量的数据。时间序列可用于预测未来值、分析趋势和形态、或检测异常。

时间序列可能拥有不同的数值范围，且随时间变化很可能不均匀。例如，股票价格可能范围很广，并根据季节性、新闻和其它因素而波动。为了有效地分析和预测时间序，有必要把数纳入一定的范围。

最小-最大归一化方法根据最小值和最大值缩放值，将数值归一化到 0 至 1 的范围。最小-最大归一化方程如下所示：

x_norm = (x - x_min) / (x_max - x_min)

其中 x 是数据值，x_min 是整个数据集中的最小值，x_max 是整个数据集中的最大值，x_norm 是归一化值。

将 Min-Max 归一化方法应用于时间序列有助于将数据纳入正常数值范围，并简化分析。例如，如果我们有 -30 到 +30 度的热度数据，我们可以应用最小-最大归一化将数值纳入 0 到 1 的范围内。这将令我们能够比较不同时间段的数值，并识别趋势和异常。

然而，在针对时间序列应用最小-最大归一化时，有必要考虑该方法的特征，及其对数据的影响。首先，运用最小-最大归一化可能会导致有关范围内数值分布的信息丢失。例如，如果数据集合当中存在异常值或极值，则它们将被强制变换为 0 或 1，并在分析中丢失。在这种情况下，可以采用其它归一化方法，例如 Z-分数常规化。

其次，在运用最小-最大归一化时，需要考虑数据变化的动态。如果数据的变化动态不均匀，则归一化可能会导致时间形态和异常的失真。在这种情况下，我们可以应用局部规范化，其中判定特定时间区间内每个数据组的最小值和最大值。

第三，在运用最小-最大归一化时，需要考虑样本对分析结果的影响。如果观测值样本不平衡，或包含峰值，则归一化可能会导致错误的结论。在这种情况下，可以使用替代数据处理方法，例如峰值消除，或数据平滑。

综上所述，最小-最大归一化方法是机器学习中最常见的归一化方法之一，可以有效地应用于时间序列，令数值达到正常范围。不过，在运用此方法时，有必要考虑数据的特征，并应用其它处理方法，从而避免基于时间序列的分析和预测失真。

示例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// find the minimum and maximum value in the array
double min_value = ArrayMinimum(data_array, 0, ArraySize(data_array)-1);
double max_value = ArrayMaximum(data_array, 0, ArraySize(data_array)-1);

// create an array to store the normalization result
double norm_array[ArraySize(data_array)];

// normalize the array
for(int i = 0; i < ArraySize(data_array); i++) {
    norm_array[i] = (data_array[i] - min_value) / (max_value - min_value);
}

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Min-Max normalization result: ", norm_array[i]);
}

return(INIT_SUCCEEDED);
}

该代码创建包含五个浮点数的 data_array 数组。然后，它调用 ArrayMinimum() 和 ArrayMaximum() 函数查找数组中的最小值和最大值，创建名为 norm_array 的新数组来存储归一化结果，并计算每个元素 (data_array[i] - min_value) / (max_value - min_value) 填充它。最后，调用 Print() 函数将结果显示在屏幕上。

结果：

2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 0.39999999999999997
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 0.7666666666666666
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 1.1333333333333333
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 1.5

Z-常规化

时间序列是数据分析的重要工具，特别是在经济、金融、气象、材料科学、等等领域。主要的时间序列预处理方法之一是 Z-常规化，它有助于提高数据分析的品质。

Z-常规化是一种居中和缩放时间序列的方法。它的构成会按这样的方式转换时间序列，即时间序列的平均值等于零，标准差等于一。这对于比较时间序列，以及消除季节性和趋势的影响非常有用。

时间序列的 Z-常规化过程包括以下步骤：

计算时间序列的平均值。
计算时间序列的标准偏差。
针对时间序列的每个元素，计算其值与时间序列平均值之间的差值。
将每个差值除以标准偏差。

结果值的平均值为 0，标准差为 1。

Z-常规化的益处：

提升数据分析的品质。 Z-常规化有助于消除季节性和趋势的影响，从而提高数据分析的质量。
易于使用。 Z-常规化易于使用，可应用于不同类型的时间序列。
可用于比较时间序列。 Z-常规化允许相互比较时间序列，因为它消除了不同尺度和测量单位的影响。

然而，Z-常规化也有一些限制：

它不适用于含有极值的时间序列。如果时间序列包含极值，则 Z-常规化可能会导致结果偏斜。
它不适用于非稳态时间序列。如果时间序列是非稳态的（即具有趋势或季节性），则 Z-常规化可以消除这些特征，这可能导致不正确的数据分析。
不能保证呈正态分布。 Z-常规化能有助于针对时间序列的分布进行常规化，但不能保证分布呈完全正态化。

尽管存在这些限制，但 Z-常规化是一种重要的时间序列预处理技术，可以帮助提高数据分析的品质。它可用于各个领域，包括经济、金融、气象、和材料科学。

例如，在经济和金融中，Z-常规化可用于比较不同资产或投资组合的表现，并分析风险和波动性。

在气象学中，Z-常规化有助于从天气数据（如温度或降水）分析中消除季节性和趋势。

在材料科学中，Z-常规化可用于分析材料属性的时间序列，例如热膨胀或磁性。

综上所述，Z-常规化是一种重要的时间序列预处理技术，有助于提升各个领域的数据分析品质。尽管存在诸多限制，但 Z-常规化易于使用，可应用于不同类型的时间序列。

示例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// find the mean and standard deviation in the array
double mean_value = ArrayAverage(data_array, 0, ArraySize(data_array)-1);
double std_value = ArrayStdDev(data_array, 0, ArraySize(data_array)-1);

// create an array to store the normalization result
double norm_array[ArraySize(data_array)];

// normalize the array
for(int i = 0; i < ArraySize(data_array); i++) {
    norm_array[i] = (data_array[i] - mean_value) / std_value;
}

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Z-normalization result: ", norm_array[i]);
}

return(INIT_SUCCEEDED);
}

double ArrayAverage(double &array[], int start_pos=0, int count=-1)
{
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of elements
    for(int i = start_pos; i <= end_pos; i++) {
        sum += array[i];
    }

    // Calculate the average value
    double avg = sum / (end_pos - start_pos + 1);
    return (avg);
}

double ArrayStdDev(double &array[], int start_pos=0, int count=-1)
{
    double mean = ArrayAverage(array, start_pos, count);
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of squared deviations from the mean
    for(int i = start_pos; i <= end_pos; i++) {
        sum += MathPow(array[i] - mean, 2);
    }

    // Calculation of standard deviation
    double std_dev = MathSqrt(sum / (end_pos - start_pos + 1));
    return (std_dev);
}

该代码创建包含五个浮点数的 data_array 数组。然后，它调用 ArrayAverage() 和 ArrayStdDev() 函数查找数组中的平均值和标准偏差，创建名为 norm_array 的新数组来存储归一化结果，并计算每个元素 (data_array[i] - mean_value) / std_value 填充它。最后，调用 Print() 函数将结果显示在屏幕上。

结果：

2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: -1.3416407864998738
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: -0.4472135954999581
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: 0.44721359549995776
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: 1.3416407864998736

差分

时间序列的差分是数据分析的重要方法，它允许从序列中删除趋势和/或季节性，令其更加平稳。在本文中，我们将看看什么是差分，如何应用它，以及它可以提供什么好处。

什么是时间序列差分？

差分是查找时间序列中连续值之间的差值的过程。您需要查找的差值数量取决于要实现的平稳程度。通常一两个差值足以消除趋势或季节性。差分的步骤如下所示：

y'(t) = y(t) - y(t-1)

其中 y'(t) 是序列的当前值与前一个值之间的差值。

如果序列是非稳态的，则在差分后，其值变得更加随机，没有可见的趋势或季节性。这有助于突显时间序列中更可观的特征，例如周期或波动性。

如何应用时间序列差分？

若要差分时序，执行以下步骤：

判别序列是否非稳态。如果序列中存在趋势或季节性，则它是非稳态。
判别获得稳态需要多少差分。如果您只想删除趋势，那么一次差分就足够了。如果要删除季节性，则可能需要两次或多次差。
针对序列应用差分变换。使用 y'(t) = y(t) - y(t-1) 方程求解第一个差分。如果需要求解第二个差分，将方程应用于 y'(t)。
检查序列是否稳态。为此，您可以使用稳态的统计测试，例如 Dickey-Fuller 测试。
如果序列是非稳态的，则重复差分过程，直到序列变为稳态。

差分时间序列有什么益处？

差分时间序列可以提供以下几个益处：

预测改进：当时间序列是稳态时，预测变得更加容易，因为序列的统计性质不会随时间变化。
去趋势：对序列进行差分可消除线性趋势，令序列更加平稳，并改进其分析。
季节性删除：通过使用多个差分步骤，您可以从时间序列中删除季节性，令其更加平稳。
噪声消除：差分一个序列可消除低频成分（趋势和季节性），这有助于消除这些成分引入的噪声。
改进解释：当序列是稳态时，可以使用经典的统计方法对其进行分析，令数据解释更容易、更易于理解。

不过，差分也有缺点。例如，如果针对一个序列进行过多的差分，它可能会丢失重要的信号，从而导致错误的结论。此外，差分会给序列带来额外的噪声。

时间序列差分是一种有用的数据分析技术，它从序列中删除趋势和/或季节性，令其更加平稳。这改进了预测，消除了噪音，并改进了数据解释。不过，差分也可能有缺点，因此应谨慎使用，并与其它数据分析方法结合使用。

示例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// create an array to store the result of differentiation
double diff_array[ArraySize(data_array)];

// differentiate the array
for(int i = 0; i < ArraySize(data_array)-1; i++) {
    diff_array[i] = data_array[i+1] - data_array[i];
}

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Differentiation result: ", diff_array[i]);
}

return(INIT_SUCCEEDED);
}

该代码创建包含五个浮点数的 data_array 数组。然后，它创建一个新的数组 diff_array 来存储差分的结果，即填充从每个 data_array 的 i 元素减去 i+1 元素。最后，调用 Print() 函数将结果显示在屏幕上。

结果：

2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.0999999999999999
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.1
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.1
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.0999999999999996

对数变换

时间序列对数变换是一种数据转换技术，用于在分析和建模之前改善序列的性质。当数据含有高可变性或原始数值的范围较大时，此方法特别有用。

什么是对数变换？

对数变换是对时间序列中的每个数值应用对数函数的过程。对数函数用于压缩序列的值，特别是当它们在很宽泛的范围之内时。使用对数减少了序列的可变性，因为它可以把数据中的峰值和低谷进行平滑，令它们不那么明显。

对数变换何时有用？

对数变换在以下情况下很有用：

如果数据具有高度可变性，则对数变换可以将其平滑化，并令其更具可预测性。
如果数据范围很宽广，那么对数变换可将其压缩，并改进其解释。
如果数据具有指数趋势，则对数变换可以令其线性化，从而更易于分析和建模。
如果数据并不呈正态分布，则对数变换可以令其更加正态。

应用对数变换的示例：

假设我们有一个时间序列，代表商店在几年内的每日销售额。由于销售额可能非常可变，且不完整，因此我们可以应用对数变换来平滑数据，并令其更具可预测性。

继续我们的示例，我们可以针对销售时间序列应用对数变换。为此，我们针对序列中的每个值应用对数函数。

例如，如果我们有一序列销售 {100, 200, 300, 400}，我们可以应用对数变换来得到 {log(100), log(200), log(300), log(400)} 或仅针对 {2 , 2.3, 2.5, 2.6} 使用自然对数。

从示例中可以看出，对数变换压缩了序列的数值，令其更便于分析和建模。这令我们能够更好地理解销售趋势，并做出更准确的预测。

然而，不要忘记对数变换并非一种通用方法，并不总是适用于所有数据类型。此外，在应用对数变换时，您应注意不要忘记在必要时恢复到原始数据尺度。

综上所述，对数变换是一种有用的方法，在分析和建模之前将时间序列进行变换，从而改善其性质。它对于含有高可变性或宽广范围的数据特别有用。不过，在使用它时，必须意识到它的局限性，并正确解释结果。

示例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// create an array to store the normalization result
double norm_array[ArraySize(data_array)];

// normalize the array
LogTransform(data_array, norm_array);

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Logarithmic transformation result: ", norm_array[i]);
}

return(INIT_SUCCEEDED);
}

void LogTransform(double& array1[], double& array2[])
{
    int size = ArraySize(array1);

    for(int i = 0; i < size; i++) {
        array2[i] = MathLog10(array1[i]);
    }
}

LogTransform() 函数针对 array1 进行对数变换，并将结果存储在 array2 之中。

该算法的工作原理如下：MathLog10() 函数将 array1 的每个元素转换为以 10 为底的对数，结果存储在 array2 的相应元素之中。

请注意，LogTransform() 函数通过引用 (via &) 接受数据数组，这意味着在函数内部对 array2 所做的更改将反映在调用函数时作为参数传递的原始数组中。

结果：

2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.07918124604762482
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.36172783601759284
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.5314789170422551
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.6532125137753437

避免时间序列分析和预测失真的其它处理方法

时间序列广泛用于经济、金融、气候科学、等各个领域的分析和预测。不过，现实世界的数据通常包含可能影响时间序列分析和预测准确性的失真，例如峰值、缺失值、或噪声。我们考虑其它有助于避免时间序列分析和预测失真的处理方法。

去除尖刺

尖刺是与序列中的其它数值差别极大的数值。它们可能是由测量误差、数据输入错误、或不可预见的事件（如危机或事故）引起的。从时间序列中删除峰值可以提高分析和预测的品质。

MQL5 语言提供了多个消除尖刺的函数。例如，iqr() 函数可判定四分位数间距和计算尖刺边界。 MODE_OUTLIERS 函数可基于决策层值检测尖刺。这些函数可与其它去除尖刺的函数结合使用。

示例：

void RemoveOutliers(double& array[])
{
    int size = ArraySize(array);
    double mean = ArrayAverage(array);
    double stddev = ArrayStdDev(array, mean);

    for(int i = 0; i < size; i++) {
        if(MathAbs(array[i] - mean) > 2 * stddev) {
            array[i] = mean;
        }
    }
}

double ArrayAverage(double &array[], int start_pos=0, int count=-1)
{
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of elements
    for(int i = start_pos; i <= end_pos; i++) {
        sum += array[i];
    }

    // Calculate the average value
    double avg = sum / (end_pos - start_pos + 1);
    return (avg);
}

double ArrayStdDev(double &array[], int start_pos=0, int count=-1)
{
    double mean = ArrayAverage(array, start_pos, count);
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of squared deviations from the mean
    for(int i = start_pos; i <= end_pos; i++) {
        sum += MathPow(array[i] - mean, 2);
    }

    // Calculation of standard deviation
    double std_dev = MathSqrt(sum / (end_pos - start_pos + 1));
    return (std_dev);
}

RemoveOutliers() 函数使用平均值和标准偏差来判定 “array” 中的尖刺。如果数组元素超出平均值的两个标准差范围，则将其视为尖刺，并替换为平均值。

请注意，RemoveOutliers() 函数还通过引用（via &）接受数据数组，这意味着对函数内部数组所做的更改将反映在调用函数时作为参数传递的原始数组之中。

数据平滑

数据平滑正在从时间序列中消除噪声。噪声可能是由随机波动，或不可预见的事件引起的。数据平滑允许您减少噪声对时间序列分析和预测的影响。

MQL5 语言提供了多个数据平滑函数。例如，iMA() 函数可用于计算移动平均线。这令我们能够平滑数据，减少噪音，并检测趋势。 iRSI() 函数可计算指数的相对强度，也可平滑数据和识别趋势。

示例：

void SmoothData(double& array[], int period)
{
    int size = ArraySize(array);
    double smoothed[size];
    double weight = 1.0 / period;

    for(int i = 0; i < size; i++) {
        double sum = 0.0;
        for(int j = i - period + 1; j <= i; j++) {
            if(j >= 0 && j < size) {
                sum += array[j];
            }
        }
        smoothed[i] = sum * weight;
    }

    ArrayCopy(smoothed, array, 0, 0, size);
}

此函数使用简单的移动平均线来平滑 “array” 中的数据。 “Period” 指定计算每个点处平均值的元素数量。

在函数内部，创建新的 “smoothed” 数组来存储平滑后的数据。然后遍历 “array” 内的每个元素，并按 “period” 指定的周期计算平均值。

最后，调用 ArrayCopy() 函数将 “smoothed” 数组复制回数组。请注意，SmoothData() 函数还通过引用（via &）接受数据数组，这意味着对函数内部数组所做的更改将反映在调用函数时作为参数传递的原始数组之中。

缺失数值

缺失数值是时间序列中缺少的数值。这可能是由数据输入错误，或数据收集问题引起的。缺失值会对时序分析和预测产生重大影响。当处理缺失值时，我们需要决定如何填充它们。 MQL5 语言提供了多个函数来处理缺失值。

iBarShift() 函数可查找与特定日期对应的柱线索引。如果某个日期缺少时间序列值，我们可以取前一根柱线的数值，或者用特定时间段内的时间序列平均值来填充它。

示例：

void FillMissingValues(double& array[])
{
    int size = ArraySize(array);
    double last_valid = 0.0;

    for(int i = 0; i < size; i++) {
        if(IsNaN(array[i])) {
            array[i] = last_valid;
        }
        else {
            last_valid = array[i];
        }
    }
}

此函数使用 “filling” 方法 - 它将任何缺失值替换为 “array” 中先前的有效值。为此，我们创建 last_valid 变量，用于将最后一个有效值存储在数组中，并循环遍历数组的每个元素。如果缺少当前值（ NaN），则取 last_valid 将其替换。如果该值未缺失，我们则将其存储在 last_valid 中，并继续迭代。

请注意，FillMissingValues() 函数还通过引用（via &）接受数据数组，这意味着对函数内部数组所做的更改将反映在调用函数时作为参数传递的原始数组之中。

插值

插值是一种填充缺失值的方法，它假设可以调用某个函数计算两个已知值之间的缺失值。在 MQL5 中，我们可以调用 MathSpline() 函数进行插值。

当然，还有其它数据处理技术可以帮助改进时间序列分析和预测。例如，时间序列分解可以帮助突显趋势、周期和季节性成分。聚类分析和因子分析有助于识别影响时间序列的因素。

总之，使用额外的数据处理方法可以显著改善时间序列的分析和预测。 MQL5 语言提供各种数据处理函数，可消除尖刺、平滑数据、和处理缺失值。此外，还有其它数据处理方法可改进时间序列的分析和预测。

示例：

double Interpolate(double& array[], double x)
{
    int size = ArraySize(array);
    int i = 0;

    // Find the two closest elements in the array
    while(i < size && array[i] < x) {
        i++;
    }

    if(i == 0 || i == size) {
        // x is out of the array range
        return 0.0;
    }

    // Calculate weights for interpolation
    double x0 = array[i-1];
    double x1 = array[i];
    double w1 = (x - x0) / (x1 - x0);
    double w0 = 1.0 - w1;

    // Interpolate value
    return w0 * array[i-1] + w1 * array[i];
}

Interpolate 函数接受两个参数：指向浮点数数组的引用，和要内插的 x 值。插值算法是查找数组中两个最接近的元素，计算插值的权重，然后计算插值。如果 x 值超出数组的范围，则该函数返回 0。

请注意，Interpolate 函数还通过引用（via &）接受数据数组，这意味着对函数内部数组所做的更改将反映在调用函数时作为参数传递的原始数组之中。

最适合传输到神经网络的信号类型

信号是神经网络运行的关键要素。它们代表传递给神经网络进行处理和分析的数据。选择正确的信号类型传输到神经网络会极大地影响其效率和准确性。在此，我们将考虑传输到神经网络的最优选信号类型。

数字信号

数字信号是神经网络中最常用的信号类型。这些是可经神经网络处理和分析的数值。数字信号可以是离散的，也可以是连续的。离散信号具有有限数量的值，而连续信号具有无限数量的值。

图像

图像也是神经网络中使用的一种流行信号类型。这些是可经神经网络处理的图形图像。图像可以是黑白或彩色。为了将图像传输到神经网络，必须将其转换为数字格式。

文本信号

文本信号也可将数据发送到神经网络。这些是可经神经网络处理和分析的文本字符串。文本信号既可以是自然语言，也可以是特殊的编程语言。

音频信号

音频信号也可将数据发送到神经网络。这些是可经神经网络处理和分析的音频信号。音频信号既可以是语音也可以是音乐。

视频信号

视频信号是可经神经网络处理和分析的图像序列。

感官信号

感观信号是重要信号类型，把机器视觉和机器人感知传输到神经网络。它们可能包括来自陀螺仪、加速度计、距离传感器等传感器的数据。这些数据可用于训练神经网络，以便它可以分析和响应环境。

图形信号

图形信号是可经神经网络处理和分析的矢量或位图图像。它们可用于图形和设计相关任务，例如字符和形状识别、自动绘图创建、等等。

时间序列

时间序列是随时间测量的数字序列。它们可用于与预测、趋势预测、和时态数据分析相关的任务。神经网络可处理时间序列，从而揭示隐藏的形态，并预测未来值。

如何选择适合传输到神经网络的信号类型？

取决于特定任务和可用数据，选择传输到神经网络的相应类型信号。某些任务可能需要同时用到多种信号类型。例如，语音识别任务可能涉及同时使用音频信号和文本信号。

当选择要传输到神经网络的信号类型时，有必要考虑其特性，例如大小、分辨率、格式、等等。此外，还需要提供相应的数据预处理，如常规化、过滤、等等，从而确保神经网络数据处理的最佳品质和准确性。

总之，选择要发送到神经网络的适当类型的信号是重要步骤，以便在机器学习任务中达成最优结果。不同类型的信号可用于训练神经网络，具体取决于特定任务和可用数据。正确选择信号类型和相应的数据预处理，有助于确保神经网络的最优精度和性能。

不过，还应考虑计算能力和数据可用性的限制。某些类型的信号对于神经网络来说可能更难处理，这可能需要更多的处理能力和更多的训练数据。因此，在选择神经网络训练的信号类型时，有必要在数据的品质和可用性之间取得平衡。

通常，选择要发送到神经网络的正确类型的信号是重要步骤，以便在机器学习任务中达成最优结果。神经网络可以处理各种类型的信号，如音频、视频、文本、感官数据、图形数据和时间序列。正确选择信号类型和相应的数据预处理有助于确保神经网络在特定任务中的最优精度和性能。

实践

我们基于我们最喜欢的感知器考虑几个 EA。我们将传递加速器振荡器指标值。我们传递四根蜡烛上的指标值，并应用上述常规化方法。有关更多详细信息，我们比较有和没有转换的 EA 结果。在没有转换的 EA 中，我们将直接传递指标值。

在此，我将提供优化和前向验证测试的所有参数，以免在文本中重复：

外汇；
EURUSD;
时间帧：H1；
止损 300 和止盈 600;
“仅开盘价”和“最复杂准则”优化和测试模式。常重要的是使用“最大复杂准则”模式，与“最大盈利能力”相比，它展示出更稳定和有利可图的结果；
优化范围 3 年。 2019.04.06 至 2022.04.06。 3 年并非是一个可靠的准则。您可以自行试验此参数;
前向验证测试范围为 1 年。从 2022.04.06 至 2023.04.06。根据我的文章（神经网络实验（第 3 部分）：实际应用）中讲述的算法检查所有内容。这意味着若干个最佳优化同时交易结果；
我们现在将执行 40 次优化。与之前的测试相比，我们将其增加 2 倍并查看结果。
在所有前向验证测试中，同时使用了 40 个优化结果。与之前的测试相比，该值增加了 2 倍；
EA 优化采用“快速（基于遗传算法）”感知器；
初始本金 10000 单位；
杠杆 1:500。

为了优化，我用 Delphi 开发了一个小型自动点击器程序。我不能在这里发布它，但我会在私人消息中将其发送给任何需要它的人。它的工作原理如下：

输入所需的优化次数。
将鼠标光标悬停在策略优化器中的“开始”按钮上。
等待。

优化在指定的循环后结束，且程序关闭。自动点击器响应“开始”按钮颜色的变化。该程序显示在下面的屏幕截图中。

Autoclicker

EA 感知器 AC 4 SL TP：

指标数据直接传递，未经常规化。

优化结果：

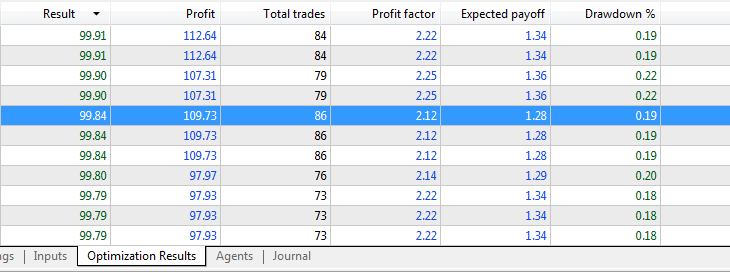
前向验证测试结果：

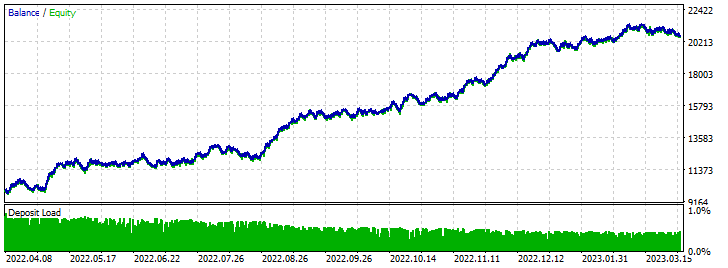
EA 感知器 AC 4 （差分）SL TP：

指标数据经最小-最大归一化后传递。

优化结果：

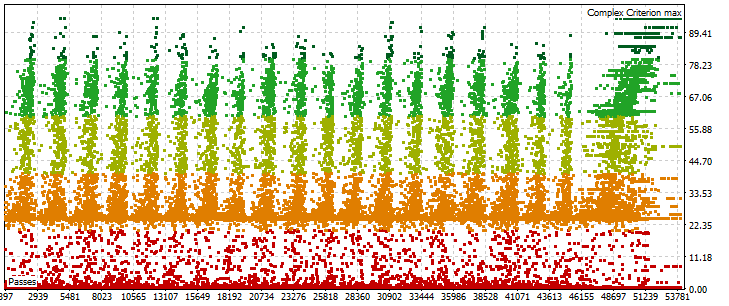
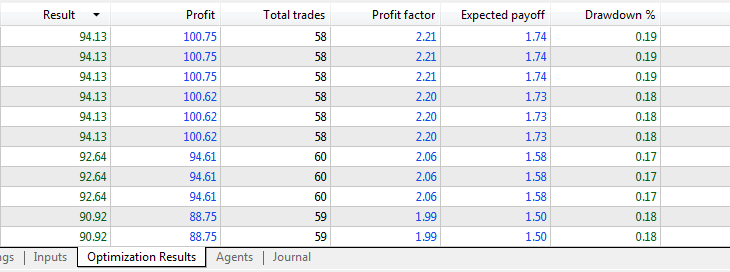
前向验证测试结果：

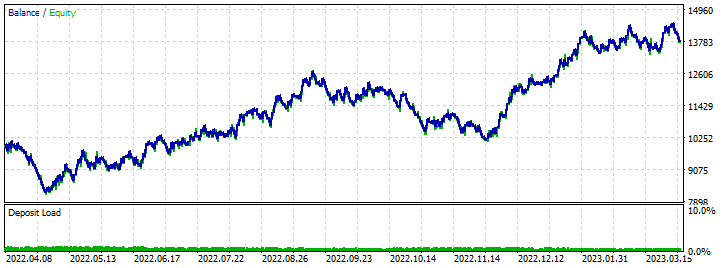
结束语

附件清单：

perceptron AC 4 SL TP - opt - 进行优化的感知器 EA，基于 AC 指标，未经常规化;
perceptron AC 4 SL TP - trade - 优化的感知器 EA，基于 AC 指标，未经常规化;
perceptron AC 4 (Differentiation) SL TP - opt - 进行欧化的感知器 EA，基于 AC 指标并经差分常规化;
perceptron AC 4 (Differentiation) SL TP - trade - 优化的感知器 EA，基于 AC 指标，并经差分常规化;

常规化可减少数据尖刺的影响，这有助于防止模型过度拟合。正确常规化的数据令网络能够更好地“理解”参数之间的关系，从而实现更准确的预测和更高的模型品质。

在本文中，我们研究了几种常规化方法，但这些并不是处理数据，从而改进神经网络训练的唯一方法。每个特定案例都需要单独的方法，应根据数据的特征和特定任务选择常规化方法。

通常，输入参数的常规化是训练神经网络的重要步骤。未正确处理的数据可能会导致结果不佳，并对模型的性能产生不利影响。正确常规化的数据可以提高训练的稳定性和收敛率，并导致更准确的预测和更高的模型品质。

感谢您的关注！

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/12459

附加的文件 |

下载ZIP

EA.zip (199.53 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论

从自营公司那里吸取一些教训（第 1 部分）— 简介

在这篇介绍性文章中，我将讨论从自营交易公司实施的挑战规则中吸取的一些教训。这对于初学者和那些努力在这个交易世界中站稳脚跟的人来说尤其重要。后续文章会介绍代码实现。

MQL5 中的范畴论 (第 6 部分)：单态回拉和满态外推

范畴论是数学的一个多样化和不断扩展的分支，直到最近才在 MQL5 社区中得到一些报道。这些系列文章旨在探索和验证一些概念和公理，其总体目标是建立一个开放的函数库，提供洞察力，同时也希望进一步在交易者的策略开发中运用这个非凡的领域。

神经网络实验（第 6 部分）：自给自足的价格预测工具 — 感知器

本文提供了一个的示例，运用感知器作为自给自足的价格预测工具，展示其一般概念和最简单的已制备智能系统，然后是其优化结果。

如何将 MetaTrader 5 与 PostgreSQL 连接

本文讲述了将 MQL5 代码与 Postgres 数据库连接的四种方法，并提供了一个分步教程，指导如何使用 Windows 子系统 Linux （WSL）为 REST API 设置一个开发环境。所提供 API 的演示应用程序，配以插入数据并查询相应数据表的 MQL5 代码，以及消化此数据的演示智能系统。