Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Ich weiß es nicht, ich habe die Formel aufgeschrieben und alle Variablen sind definiert. Ich möchte auch klarstellen, dass es sich um den Betrag des monatlich entnommenen Gewinns handelt (nicht um den Gesamtgewinn für m Monate).
Es bleibt die Formel für die Summe der Reihen abzuleiten, du hast geschrieben, dass du es einfach machst - mach es. Dann nimmt man die Ableitung, setzt sie mit Null gleich...
In meinen Notizen sieht Ihre Formel für die Entnahme des laufenden Monats wie folgt aus:
Dementsprechend ist die Zerlegung der tierähnlichen Ableitung dieser Funktion genauso schwierig wie die obige.
Ich denke, man kann versuchen, f vorzuprologarithmieren und dann sein Maximum zu suchen... Vielleicht ist es auf diese Weise einfacher.
avtomat:
Im zweiten Schritt öffnen Sie dann das Ventil, das den Durchfluss in zwei Teile teilt. Dadurch wird der Eingabefluss geändert.
Sie sehen die Lösung noch nicht?
Nein, ich weiß nicht, was Sie denken. Sagen Sie es mir.
Es gibt einige, die sogar den Satz des Pythagoras, wie er von ihnen interpretiert wird, nicht verstehen können.
OFFTOP:
In der Schule gaben sie den prägnantesten Beweis für den Satz des Pythagoras.
Man beachte, dass die einfachste (nicht standardisierte) Idee p.2 ist. Es werden keine Kenntnisse über die Eigenschaften ähnlicher Dreiecke verwendet, und es sind auch keine Kenntnisse der Trigonometrie erforderlich, um die Existenz der Funktion f zu verstehen. D.h. ein solcher Nachweis kann in Grundschulen erbracht werden, nachdem den Kindern (nicht wie üblich) erklärt wurde, was eine Fläche ist.
OFFTOP:
In der Schule gaben sie den prägnantesten Beweis für den Satz des Pythagoras.
In welcher Klasse?
Die Formel S = c^2 * f(alpha) ist für einen Siebtklässler nicht offensichtlich. Es ist eine Selbstverständlichkeit, dass es so ist.
Dementsprechend ist es genauso schwierig, die tierähnliche Ableitung dieser Funktion zu brechen wie die obige.
Bleibt der gesamte Prozess am Derivat hängen?
Ist diese Funktion x0*k*(1-(1+q-k)^2)/(k-q)?
Wenn ja, dann ist das kein Problem, ich habe sie leicht gelöst, ich muss mich nur ein bisschen erinnern. Die Variable q?
in welcher Klasse?
Die Formel S = c^2 * f(alpha) ist für einen Siebtklässler nicht offensichtlich. Es ist eine Selbstverständlichkeit, dass es so ist.
Fast jedes Kind, das den Begriff des Flächeninhalts einer Figur gut genug kennengelernt hat, um ihn zu verstehen, wird kaum Schwierigkeiten haben, den obigen Beweis zu verstehen.
Wenn ein Kind wirklich versteht, was eine Fläche ist, versteht es auch, wie sie gemessen wird, und es versteht auch, dass die Fläche jeder Figur durch ihre Merkmale (in diesem Fall die Hypotenuse und der Winkel) ausgedrückt werden kann, die die Figur eindeutig definieren.
Es sind keine Kenntnisse über die Eigenschaften ähnlicher Dreiecke und Trigonometrie erforderlich.
Ich war kürzlich zu Besuch und sah zwei Steinpyramiden (ähnlich den ägyptischen Pyramiden). Ich nahm sie in die Hand und legte sie an ihre Basis (sie sind etwas unterschiedlich groß):
Und er hat einen weiteren Beweis für den Satz des Pythagoras gefunden (aus der Konstruktion ersichtlich).
Integer:
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
Nein, das Problem ist die Ableitung von k aus: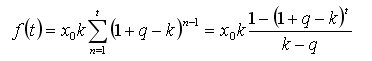
Sie muss mit Null gleichgesetzt und in Bezug auf k gelöst werden.
Ich kann es nicht auf die intelligente Art machen, also mache ich es einfach:
Nehmen wir an, die Einlage beträgt zu Beginn des Zeitraums 10.000. In jeder Periode erhöhen wir die Einlage um 5% und legen sie wieder an. In jeder Periode dürfen wir nur 3 % abheben.
Wenn Sie alle 3% Ihres Geldes jede Periode abheben, bekommen wir alle mehr als 4k$ (und geben einen Scheiß auf die Einzahlung), sonst bekommen wir nur 0,5k$ (aber mit viel auf die Einzahlung).
Fast jedes Kind, das den Begriff des Flächeninhalts einer Figur gut genug kennengelernt hat, um ihn zu verstehen, wird kaum Schwierigkeiten haben, den obigen Beweis zu verstehen.
Wenn ein Kind wirklich versteht, was eine Fläche ist, versteht es auch das Maß der Fläche und weiß, dass die Fläche jeder Figur durch ihre Merkmale (in diesem Fall die Hypotenuse und der Winkel) ausgedrückt werden kann, die die Figur eindeutig definieren.
Aber es ist kein strenger Beweis.
Ich kann es nicht auf die intelligente Art machen, also mache ich es einfach:
Deshalb brauchen wir eine allgemeine analytische Lösung, bei der wir nicht solche Tabellen zeichnen, sondern zwei Eingabewerte in eine einfache Formel einsetzen und die Antwort erhalten.
Das ist der Punkt, alles oben genannte ist "es fühlt sich so an, als ob es so sein wird". Dass "es irgendwie durch etwas ausgedrückt werden kann".
Aber es ist kein strenger Beweis.
Was ist das für ein harter Beweis?! Das liegt auf der Hand: