Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Es liegt auf der Hand, dass q entnommen werden sollte, und zwar erst am Ende der Periode t. In allen anderen Fällen beträgt der abgezogene Betrag weniger als
Der Igel hat beschlossen, analytische Berechnungen durchzuführen))))
Das Problem hat keine Extrema, denn wir haben eine monoton ansteigende Zahlenreihe - eine Funktion mit einem Argument in Form der Größe der Einlage. Das heißt, es gibt nichts zu optimieren. Je größer das Argument und t, desto größer der Wert der Funktion. In jedem anderen Fall wird der Wert der Funktion sinken.
Es ist schwer, eine schwarze Katze in einem dunklen Raum zu suchen, besonders wenn sie nicht da ist (c) Konfuzius
Es bleibt nur noch, die zeitliche Ableitung zu nehmen und sie mit Null gleichzusetzen... Ja, ja.
Übrigens, wenn überhaupt, sollte die Ableitung über k genommen werden
Pardon! Wirklich auf dem K .
Reschetow:
Es liegt auf der Hand, dass Sie q abheben müssen, und zwar erst am Ende der Periode t. In allen anderen Fällen ist der abgezogene Betrag geringer.
Jura, du bist so selbstbewusst, dass es lustig ist, wenn du dich irrst.
Auf der ersten Seite hat avtomat ein Bild gezeigt, auf dem das Optimum für den Parameter k deutlich zu erkennen ist . Vielleicht haben Sie es nur nicht bemerkt. Ich zeige Ihnen eine andere:
Sehen Sie das Maximum? Nein? Aber sie ist da!
Mach eine Pause, du Igel.
Niemals!...
Können Sie das genauer erläutern? Ich meine, in Form einer Formel.
Mit anderen Worten: Das Optimum in Bezug auf den Rücknahmeprozentsatz ist tatsächlich sichtbar!
Ich habe kürzlich ein ähnliches Problem gelöst...
Und dann kombinieren wir all dies und erhalten die resultierende Funktion von zwei Variablen.
Es sollte auch erwähnt werden, dass das Ergebnis vom Optimierungszeitraum abhängt, d.h.
das Optimum für 12 Monate ist nicht gleich den vier Optima für 3-Monats-Zeiträume.
Ich habe kürzlich ein ähnliches Problem gelöst...
Das ist richtig, Avtomat. Genau so verhält es sich auch. Ich brauche aber unbedingt eine analytische Lösung für den optimalen Anteil von k. Wenn man die Ableitung von k von f(k) nimmt, erhält man die folgende Gleichung: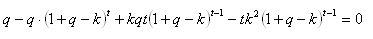
Die folgende Abbildung zeigt deutlich, dass die Abszisse, auf der df/dk Null ist, mit dem Maximum von f(k) zusammenfällt.
Aber wie löst man sie in Bezug auf k?
Nun, das Problem hat ohnehin nichts mit dem Handel zu tun. Es handelt sich um ein Problem des Rentiers. Sie wäre für diese Branche gut geeignet.
P.S. Ich frage mich, was Jura in dieser Situation tun wird? Wird er so tun, als hätte er nichts bemerkt (kein Höchstwert für den Parameter k ), und keine Kommentare zu diesem Thema hinterlassen, oder wird er seine Grundannahmen für das Leben überdenken müssen...
P.S. Ich frage mich, was Jura in dieser Situation tun wird? Wird er so tun, als ob er nichts bemerkt (kein Höchstwert für den Parameter k ), und keine weiteren Kommentare zu diesem Thema hinterlassen, oder wird er seine wichtigsten Einstellungen für das Leben überdenken müssen...
Ich habe eine Kaution von X0 Rubel für t Monate verwenden dürfen. Jeden Monat erhält die Einlage einen festen Prozentsatz q vom aktuellen Wert der Einlage X. Ich darf jeden Monat einen bestimmten Prozentsatz k vom Konto abheben, der den Wert von q nicht übersteigt.
Ich darf Geschäfte mit der Losgröße HO eröffnen. Jeder offene positive Handel hat eine u%ige Chance, w Pips zu akkumulieren, während q natürlich vom aktuellen Wert der XO-Einlage verdient wird. Ich kann einen Auftrag um einen bestimmten Prozentsatz k so oft schließen, wie ich möchte (bis zu 100 %), und zwar mit einer Häufigkeit von n Pips, die w nicht überschreitet.
Frage: Finden Sie relativ zu u% optimale Werte für k, n.
Das ist richtig, Avtomat. Genau so verhält es sich auch. Aber ich brauche eine analytische Lösung für den optimalen Anteil der Entfernung k. Wenn man die Ableitung von k von f(k) nimmt, erhält man die folgende Gleichung:
Die folgende Abbildung zeigt deutlich, dass die Abszisse, auf der df/dk Null ist, mit dem Maximum von f(k) zusammenfällt.
Aber wie löst man sie in Bezug auf k?
wenn die obige Gleichung wahr ist, dann können wir das tun:
Aber noch einmal: Was sind die Anforderungen, was sind die Bedingungen?
q und t - gegebene konstante Größen oder ...