Unter TA-Indikatoren gibt es 5 Indikatoren, die mit Volumina verbunden sind: A/D (Accumulation Distribution), MFI (Money Flow Index), OBV (On Balance Volume), PVT (Price and Volume Trend ), VROC (Volume Rate of Change). Jede von ihnen soll es einem Händler ermöglichen, einige Schlussfolgerungen über die Preisentwicklung zu ziehen. Mit Ausnahme von MFI haben jedoch alle diese Indikatoren keine eindeutige Bedeutung. Das heißt, sie können eigentlich nur für die Analyse der Muster dieser Indikatoren verwendet werden. Und diese Muster wiederholen aufgrund ihrer Berechnungsalgorithmen im Allgemeinen die Kursbewegungen. Das wichtigste Gegenargument ist jedoch die Tatsache, dass der Preis nicht willkürlich von einem Makler geändert werden kann, und das Volumen elementar verändert werden kann. Es genügt, die Parameter für die Tick-Flow-Filterung zu ändern, die jeder Broker unabhängig voneinander festlegt.
Ein weiterer Aspekt in Bezug auf die Lautstärke ist, dass sie stark von der Tageszeit und der Sitzung abhängt. Jeder weiß das, aber es macht auch die Verwendung von Volumina über Standardindikatoren recht fragwürdig. Um diese Periodizität zu kompensieren, sollte man die Volumina zumindest nicht mit früheren Werten vergleichen, sondern mit einem Standard, der für die Tageszeit, den Wochentag und die Sitzung typisch ist.
Die einfachste Formulierung des Problems lautet wie folgt.
Im Devisenhandel gibt es nur 5 Arbeitstage, sagen wir von Montag bis Freitag. Natürlich kann sich dieses Intervall für jeden Makler je nach Zeitzone nach vorne oder nach hinten verschieben. Da der Devisenmarkt jedoch ein weltweiter Markt ist, ist der Prozess für alle gleich und seine Dauer ist überall gleich.
Gehen wir davon aus, dass der Handel am Montag um 00:00 Uhr beginnt und am Freitag um 23:59 Uhr nach der letzten Handelsminute endet. Das heißt, wir haben insgesamt 5x24 = 120 Stunden pro Woche.
Addieren wir nun das Volumen der Geschäfte der ersten Stunde aller Montagsgeschäfte und teilen das Ergebnis durch ihre Anzahl. Wir erhalten das durchschnittliche Volumen der ersten Stunde am Montag. Auf ähnliche Weise erhalten wir das durchschnittliche Volumen der zweiten Stunde des Montags und so weiter, das durchschnittliche Volumen für jede der 120 Stunden der Arbeitswoche. Die Darstellung dieser Daten in einem Diagramm zeigt die zyklischen Veränderungen des durchschnittlichen Volumens im Laufe der Woche. Wenn Sie dieses Diagramm mit ähnlichen Diagrammen aus den Vorjahren vergleichen, können Sie erkennen, wie sich dieser Aspekt des Marktes im Laufe der Jahre verändert.
Dies war die einfachste Version. Wenn wir 10 Minuten statt 1 Stunde als Mindestintervall nehmen, können wir ein etwas intensiveres, aber ähnlich einfaches Diagramm verwenden. Dies würde zu einer 6-fachen Anzahl von Punkten in der Grafik führen, d. h. zu 720 Punkten. Und die größte, wenn Sie ein 1-Minuten-Intervall nehmen. In diesem Fall sind es 7200 Punkte. Diese letzte Option ist nur sinnvoll, wenn es genügend Ticks pro Minute gibt.
Und wozu? Der Markt hat bekanntlich eine fraktale Struktur. Auf jeder Ebene dieser Struktur kann es eigene Auswirkungen geben. Um sie zu finden, sollte jede Ebene separat untersucht werden. Genau das wurde auch getan.
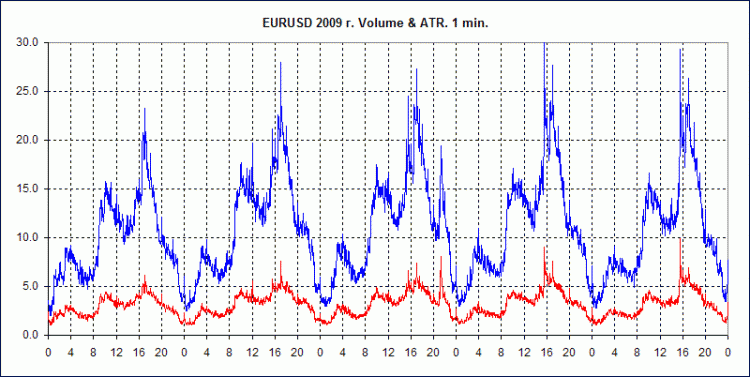
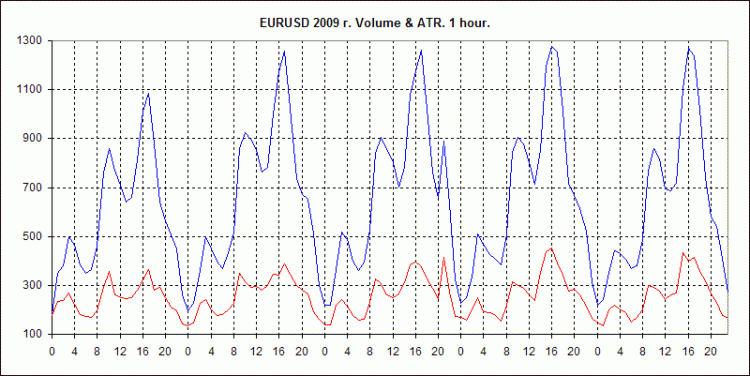
Unten sehen Sie 3 Charts für EURUSD, 2009. GainCapital-Daten.
Sie zeigen das durchschnittliche wöchentliche Volumenverhalten für die Intervalle H1, M10 und M1 sowie ähnlich berechnete durchschnittliche ATR-Werte für diese Zeitrahmen.
AvrVOL - durchschnittliches Volumen, blaue Linie.
AvrATR - durchschnittliche ATR-Werte, rote Linie.
Auf der Ordinatenachse - Volumen in Ticks (für AvrVOL) und High-Low in Punkten (für AvrATR).
Die Abszissenachse zeigt die Stundenzahlen des Tages von 0 bis 23. Die Markierung befindet sich am Anfang der Stunde.
Um die Visualisierung beizubehalten, werden die AvrATR-Werte mit dem Verhältnis k=8(für H1), k=3(für M10), k=1(für M1) multipliziert. Das heißt, um den tatsächlichen Wert von AvrATR zu schätzen, müssen Sie den Wert in der Grafik durch diesen Koeffizienten teilen.
Ich sollte auch erwähnen, dass für H1 und M10 die AvrVOL-Werte direkt für die Darstellung verwendet werden. Und für M1 habe ich die Berechnungsergebnisse über 5 Punkte gemittelt. Ich möchte gleich anmerken, dass dies nicht ganz dasselbe ist wie die Berechnung der Mengen für M5. Sie ermöglicht es, die Streuung der Werte ein wenig zu verringern, wobei jedoch alle feinen Details des Diagramms erhalten bleiben. Die Mittelwertbildungsformel unterscheidet sich geringfügig von der eines einfachen SMA. Hier ist es : AvrVOL[i] = ( AV[i-2] + AV[i-1] + AV[i] + AV[i+1] + AV[i+2] )/5.
AV[i] sind hier die Ergebnisse der Berechnungen des durchschnittlichen Volumens für die i-te Minute der Woche.
Was ist für mich persönlich an diesen Diagrammen interessant?
1) Das Verhalten der Volumina stimmt vollständig mit dem Verhalten der ATR überein. Diese Korrespondenz betrifft sowohl das lokale Kurvenverhalten als auch die zeitlichen Veränderungen. Das Verhalten der Volumina ist jedoch ausgeprägter und ihre Werte steigen bei höheren TF proportional an, was man von den ATR-Werten nicht sagen kann, bei denen die Abhängigkeit von der TF komplexer ist.
2. Die ATR wird zusammen mit dem RMS als Maß für die Marktvolatilität verwendet. Die obigen Diagramme sehen imho überzeugend genug aus, um zu dem Schluss zu kommen, dass die Volumina auch als Maß für die Volatilität dienen können und nicht schlechter sind als die traditionellen Maßstäbe.
Die gleiche Schlussfolgerung führt jedoch dazu, dass sich die Volumina nicht für eine Bewertung der Preisrichtung eignen. Die Volatilität gibt einen Hinweis auf die Art der Preisbewegung, aber nicht auf ihre Richtung.
3. Eine niedrige Volatilität wird eher als Renditecharakter des Marktes interpretiert, während eine hohe Volatilität eher als Trendcharakter interpretiert wird. Ein ähnliches Maß ist der Hearst-Index. In diesem Sinne wird es interessant sein, die obigen Diagramme mit dem entsprechenden Hearst-Index-Diagramm zu vergleichen. Aber das wird später kommen.
4. Die Charts zeigen deutlich die Aufteilung eines jeden Devisenhandelstages in drei Wellen - drei Sitzungen: asiatisch, europäisch und amerikanisch. Bei jedem von ihnen ist der Beginn der Sitzung mit einer erhöhten Volatilität verbunden, die zum Ende hin allmählich abnimmt. Jede Sitzung ist durch ihre eigene Volatilitätsspanne gekennzeichnet. Die asiatische Sitzung ist durch ein Minimum gekennzeichnet, während die amerikanische Sitzung durch ein Maximum gekennzeichnet ist. Die Volatilität brach vor der amerikanischen Sitzung aufgrund der Veröffentlichung von Nachrichten ein, und ein noch größerer Ausbruch zu Beginn der Sitzung ist deutlich zu erkennen. Für die beiden vorangegangenen Sitzungen ergibt sich ein ähnliches Muster, das jedoch nicht so auffällig ist.
5. Ein interessantes Phänomen ist in der amerikanischen Sitzung am Mittwoch zu beobachten. Zwischen 21 und 22 Uhr ist erneut ein deutlicher Anstieg der Volatilität zu verzeichnen. An anderen Tagen oder in anderen Sitzungen gibt es so etwas nicht. Soweit ich weiß, gibt es abgesehen von der FED-Erklärung, die 8 Mal im Jahr stattfindet (und der Durchschnitt liegt bei 52 Dingen), keine weiteren Ereignisse in dieser Zeit. Es ist schwer zu glauben, dass diese 8 Male einen solchen Einfluss auf den Gesamtdurchschnitt haben. Für die Volatilität ist die Erklärung der FED jedoch wahrscheinlich das einflussreichste Ereignis. Es ist also alles möglich.
6. Wie Sie sehen können, sind die 3 obigen Diagramme sehr eng aufeinander abgestimmt. Das heißt, es gibt bei keinem von ihnen Auswirkungen, die bei den anderen nicht vorhanden sind. Einerseits ist es vielleicht nicht sehr schön (es konnten keine Goldadern gefunden werden :-), aber andererseits ist es sehr optimistisch. Dies bestätigt die Fraktalität des Marktes - jedes Niveau ähnelt den anderen - und ermöglicht es, die Volumina als angemessenes Maß für die Volatilität selbst bei den kleinsten TFs zu verwenden.
Soweit ich weiß, werden Volumina von Händlern in ihrem TS nicht oft verwendet.
Indikatoren sind ein Marketing-Trick - eine hübsche Tarnung. Für diejenigen, die eher an Bildern als an statistischen Indikatoren und mathematischen Modellen interessiert sind.
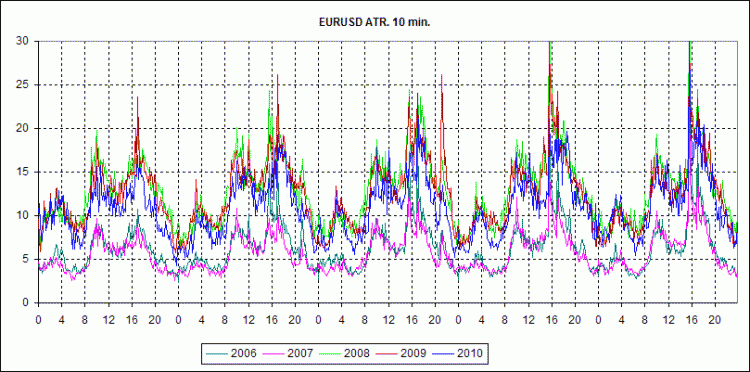
Um die Dynamik der Volumina und der ATR nach Jahren zu sehen, habe ich die folgenden 2 Diagramme erstellt.
Sie zeigen im Allgemeinen, dass sich die Art des Marktes insofern geändert hat, als er viel schneller geworden ist. Nach den Tageshöchstständen zu urteilen, hat sich das Volumen ungefähr verdoppelt. Das Gleiche gilt für die ATR. Die Kurven in den Diagrammen sind in zwei Gruppen unterteilt: 2006-2007 und 2008-2009-2010. Das heißt, die Krise hat die Maschine seit Mitte 2008 auf Hochtouren laufen lassen. Ich denke, dass die Makler einfach die Hard- und Software aufrüsten mussten, um mit der Zeit Schritt zu halten. Und jetzt gibt es kein Zurück mehr.
Aber auch ohne diese Diagramme weiß jeder über den Anstieg des Volumens Bescheid. Aber nicht alle haben darauf geachtet, dass die ATR in etwa demselben Verhältnis gestiegen ist. Und das ist eine interessante Tatsache.
Eine weitere wichtige Tatsache ist meines Erachtens, dass sich die Art der täglichen Zyklizität der Märkte nicht geändert hat. Die Krise und alles, was darauf folgte, hat das Verhalten der Volatilität des Devisenmarktes weder innerhalb der Sitzungen noch in Bezug auf die Sitzungen untereinander noch in Bezug auf die Wochentage verändert. Selbst die Volatilitätsspitzen nach 20 Uhr am Mittwoch blieben unverändert. Und kleine Details seines Verhaltens spielen keine Rolle. Jedenfalls standen sie nicht auf meiner Liste der Ziele. Dieser zufällige Prozess hat also eine Menge stabiler Aspekte, und das bedeutet, dass die Suche nach Regelmäßigkeiten in ihm kein aussichtsloses Unterfangen ist.
Die Frage ist nur, wie man sie nutzt. Hier ist ein einfaches Bild: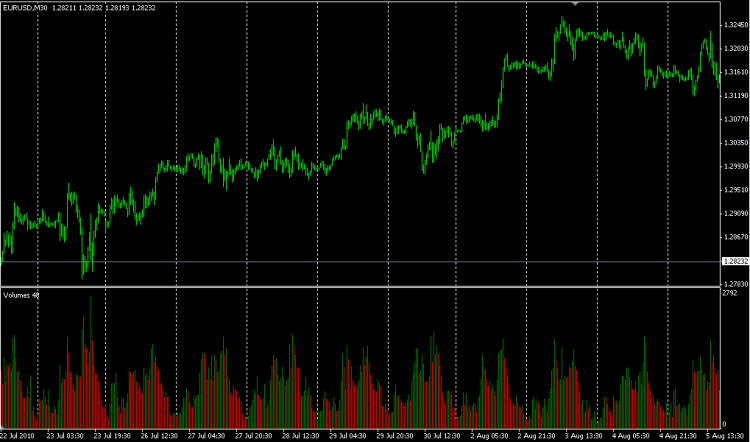
Es ist leicht zu erkennen, dass die Handelsaktivität zur Mittagszeit zunimmt und der Kurs steigt, in der Nacht sinkt er, und so ist das Bild jeden Tag ungefähr dasselbe. Ich will damit sagen, dass es keinen Sinn macht, wenn man sich das Thema genau ansieht. Es ist sinnvoll, sich die realen Volumina anzusehen, die von vielen Brokern als reale ECN-Werte bereitgestellt werden, und zu sehen, was passiert. Was Ataers und dergleichen angeht, so ist das meiner Meinung nach Blödsinn und nutzlos.
Nun zurück zu Volumen und ATR als Maß für die Volatilität. Grafisch spiegeln sie sein Verhalten recht gut wider. Es gibt jedoch auch einen Nachteil. Beide Werte haben Dimensionen, ihre Durchschnittswerte ändern sich mit der Verbesserung der Markttechnologien. Dies erschwert ihre Verwendung als Maß für die Volatilität erheblich, da sich das Ausmaß dieser Größenordnungen ständig ändert. Und sie nur als qualitative Merkmale zu verwenden, ist uninteressant. Sie ist nicht viel besser als die Verwendung der Standard-TA-Indikatoren für die Volumina, die wir bereits aufgegeben haben.
Die Ähnlichkeit der Veränderungen bei den Volumina und der ATR im Laufe der Jahre (beide Spitzenwerte haben sich ungefähr verdoppelt) legt nahe, dass ein quantitatives Maß für die Volatilität das Verhältnis dieser beiden Werte sein könnte. Einige werden sich an dieser Stelle sicherlich an den Hearst-Index erinnern. Und das zu Recht. :-)
Ein paar Worte zum Hearst-Verhältnis.
Ohne auf die Geschichte einzugehen, sei nur erwähnt, dass die Streuung einer Zufallsreihe nach der Annahme von Hearst durch das Verhältnis R/S = c * (T)^h bestimmt wird. Dabei ist R die Streuung einer Zufallsreihe, S ihr RMS, T die seit dem Startpunkt verstrichene Zeit, c die durch den gegebenen Prozess definierte Konstante und h der Hurst-Exponent. Wenn sich der RMS eines Prozesses nicht ändert, kann er ebenfalls in der Konstante c versteckt werden.
Für die Brownsche Bewegung, deren Inkremente durch eine Normalverteilung beschrieben werden, erhielt Einstein diese Formel explizit. Für diesen besonderen Fall ist h = 1/2. Bei anderen Verteilungen wird h natürlich mehr oder weniger von 1/2 abweichen. Ich persönlich bin der Meinung, dass die Formel von Hurst überhaupt nicht korrekt ist. Ich meine für den Fall einer willkürlichen Verteilung. Ja, ein Glück für die Normalverteilung, dass sie sich zu einer so einfachen Form zusammenrollt. Aber für den willkürlichen Fall kann es unverhältnismäßig komplizierter sein. Als erste Näherung ist diese Formel jedoch gut geeignet (jede Funktion T kann durch ihr Argument in eine Potenzreihe zerlegt werden).
Um diese Formel auf unseren Fall anwenden zu können, müssen wir ein paar Dinge bestimmen. Erstens: Was ist T? Imho ist die optimale Zeit die intrinsische oder, wie man sagt, die operative Marktzeit, gemessen in Ticks. Er ist ein sehr wichtiger - dimensionsloser - Zähler für reale Prozessereignisse - Preisänderungen. Es handelt sich also um einen Zähler einer Reihe von SV. Zweitens: Was ist das Maß für den R-Wert? Sein natürliches Maß ist der Punkt. Diese Maßeinheit ist jedoch nicht für jede Serie geeignet. Glücklicherweise treten etwa 99% der Preisänderungen im Datafeed an einem Punkt auf (4 Ziffern!!!). Dies ist ein Grund, 1 Tick => 1 Punkt zu berücksichtigen (es ist kein "größer oder gleich "-Zeichen ). Unter solchen Bedingungen kann der Proportionalitätskoeffizient in der Hurst-Formel mit eins gleichgesetzt werden. Wir haben also R = (T)^h. Daraus lässt sich leicht h = Log(R)/Log(T) ableiten. Die Basis des Logarithmus spielt keine Rolle.
Die endgültige Form für den Hurst-Exponenten lautet also: h = Log(Hoch-Tief)/Log(N). Dabei ist N die Anzahl der einzelnen Ticks im Zeitintervall, High und Low sind die maximalen und minimalen Kurswerte, die in diesem Intervall erreicht werden. Ihre Differenz wird in 4-stelligen Punkten ausgedrückt.
Wie wir sehen können, ist das Zeitintervall, für das der Hurst-Index bestimmt wird, noch vorhanden. Für die in diesem Thema vorgestellten Diagramme waren dies H1, M10 und M1. Und das ist kein Nachteil, sondern ein absolut notwendiger Parameter. Sie bestimmt, auf welche Fraktalebene sich der berechnete Hearst-Index bezieht.
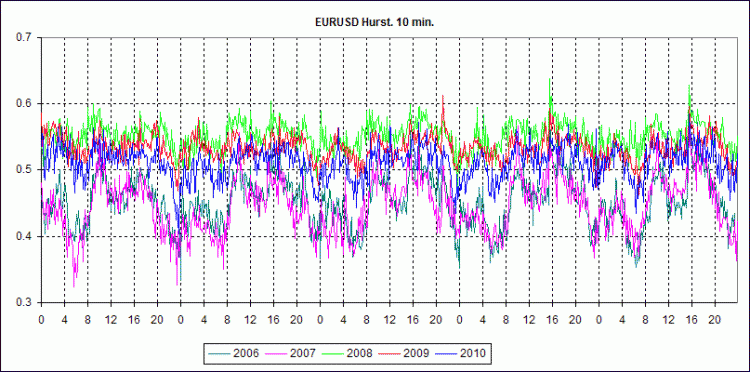
Nachfolgend finden Sie die Diagramme des wöchentlichen Verhaltens des Hearst-Indikators, berechnet für M10 im Zeitraum 2006-2010.
Wie Sie sehen, zeigt das Verhalten in den Jahren 2006 und 2007, dass der Euro-Markt während des größten Teils der Handelswoche eine Umkehrung vollzog. Im Jahr 2008 und in geringerem Maße auch 2009 war der Euro-Markt relativ trendy. In diesem Jahr bewegte er sich um die 0,5-Marke, was typisch für einen Wiener Random Walk ist.
Dies ist jedoch nur eine Veranschaulichung dessen, was Sie erhalten, wenn Sie die obige Formel verwenden.
Ich habe mich einmal sehr für den Algorithmus zur Berechnung des Hurst-Index interessiert. Ehrlich gesagt, gefielen mir mehrere in der Literatur zu findende Berechnungsmethoden nicht. Dies gilt auch für die von Peters in seinem Buch Fractal Analysis of Financial Markets beschriebene Methode, die als grundlegend angesehen wird. Dort ist Hearst definiert als der Grenztangens des Steigungswinkels des Graphen R an T in logarithmischen Koordinaten. Als Ergebnis erhält man Hurst als eine Zahl, die die gesamte Reihe charakterisiert. Das ist natürlich richtig, aber wenig hilfreich. Ich habe nach einem Algorithmus gesucht, der die Berechnung von Hurst lokal und in Echtzeit ermöglicht. Und jetzt, nachdem ich mir die Marktstatistiken eines Jahres angesehen habe, habe ich einen solchen Algorithmus entwickelt.
Ich beanspruche weder Originalität noch Urheberschaft. Die Tatsache, dass ich es noch nicht gesehen habe, beweist nur, dass ich nicht genug gesehen habe.
Ich weiß nicht, ob dieser Algorithmus zur Berechnung des Hurst-Index nützlich sein wird. Auf jeden Fall lassen sich daraus Rückschlüsse auf die Stabilität des Marktes (wichtig für die Anwendung einer bestimmten Strategie) und seinen Charakter (wichtig für die Wahl der Strategie) ziehen, nachdem man seine Dynamik über einen langen Zeitraum verfolgt hat. Als wir den Hearst-Index für die gesamte Serie auf einmal ermittelten (eigentlich nur den Durchschnitt), hatten wir diese Möglichkeit nicht.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.


Soweit ich weiß, werden Volumina von Händlern in ihrem TS nicht oft verwendet. Dennoch kommen sie vor. Deshalb stellte sich die Frage, ob sie geeignet sind und wenn ja, in welcher Form sie eingesetzt werden können. Zumal sich in den letzten Jahren auf dem Devisenmarkt viel verändert hat: fünfstellige Vorzeichen tauchten auf, die Volumina stiegen erheblich, die Krise begann, was sich auch auf die Art des Marktes auswirkte.
Dies ist ein Vorwort zu den Untersuchungen, die ich durchgeführt habe und deren Ergebnisse ich hier veröffentliche. Ich warne Sie gleich vor: Es gibt keine Grals, keine TSs, keine fertigen Rezepte. Nur die Ergebnisse der Marktforschung der letzten Jahre, die mir ein besseres Verständnis dafür vermitteln, was vor sich geht und wie einige der Parameter genutzt werden können. Es wird auch keine Mathematik geben, alles ist sehr einfach und anschaulich.