Kategorientheorie in MQL5 (Teil 20): Ein Abstecher über die Selbstaufmerksamkeit (Self-Attention) und den Transformer

Einführung

Ich denke, es wäre nachlässig, mit den Artikeln dieser Reihe fortzufahren, solange es um Kategorientheorie und natürliche Transformationen geht, ohne auf den Elefanten im Raum, chatGPT, einzugehen. Inzwischen ist jeder in irgendeiner Form mit chatGPT und einer Vielzahl anderer KI-Plattformen vertraut und hat den möglichen Transformer (Maschinelles Lernen) von neuronalen Netzen gesehen und hoffentlich auch zu schätzen gelernt, das nicht nur unsere Forschung erleichtert, sondern auch dringend benötigte Zeit von niederen Aufgaben abzieht. Deshalb mache ich in dieser Serie einen Abstecher und versuche, die Frage zu beantworten, ob natürliche Transformationen der Kategorientheorie in irgendeiner Weise der Schlüssel zu den Algorithmen der generativen vortrainierten Transformer sind, die von Open AI eingesetzt werden.

Neben der Suche nach Synonymen mit der Formulierung „transform“ wäre es meiner Meinung nach auch interessant, Teile des Codes des GPT-Algorithmus in MQL5 zu sehen und sie an einer vorläufigen Klassifizierung einer Wertpapierkursreihe zu testen.

Der Transformer, der in der Veröffentlichung „Attention Is All You Need“ vorgestellt wurde, war eine Innovation im Bereich der neuronalen Netze, die für Übersetzungen zwischen gesprochenen Sprachen (z. B. Italienisch-Französisch) verwendet werden und die Rekurrenten neuronale Netze und Convolutional Neural Network abschaffen sollten. Ihr Vorschlag? Self-Attention. Es wird davon ausgegangen, dass viele der heute genutzten KI-Plattformen aus diesen frühen Bemühungen hervorgegangen sind.

Der tatsächliche Algorithmus, der von Open AI verwendet wird, ist sicherlich geheim, aber nichtsdestotrotz wurde davon ausgegangen, dass er Worteinbettungen Positional Encoding, Selbstaufmerksamkeit und ein Feedforward Neural Networks als Teil eines Stapels in einem Decode-only Transformer verwendet. Nichts davon ist bestätigt, also sollten Sie mich nicht beim Wort nehmen. Und um das klarzustellen, diese Referenz bezieht sich auf den Wort-/Sprachübersetzungsteil des Algorithmus. Ja, da die meisten Eingaben in chatGPT Text sind, spielt dieser eine wichtige, fast grundlegende Rolle im Algorithmus, aber wir wissen jetzt, dass chatGPT viel mehr kann als nur Text zu interpretieren. Wenn Sie z. B. eine Excel-Datei hochgeladen haben, kann es diese nicht nur öffnen und ihren Inhalt lesen, sondern auch Diagramme erstellen und sogar eine Stellungnahme zu den dargestellten Statistiken abgeben. Der Punkt hier ist, dass der chatGPT-Algorithmus hier nicht vollständig dargestellt wird, sondern nur Teile von dem, was verstanden wird.

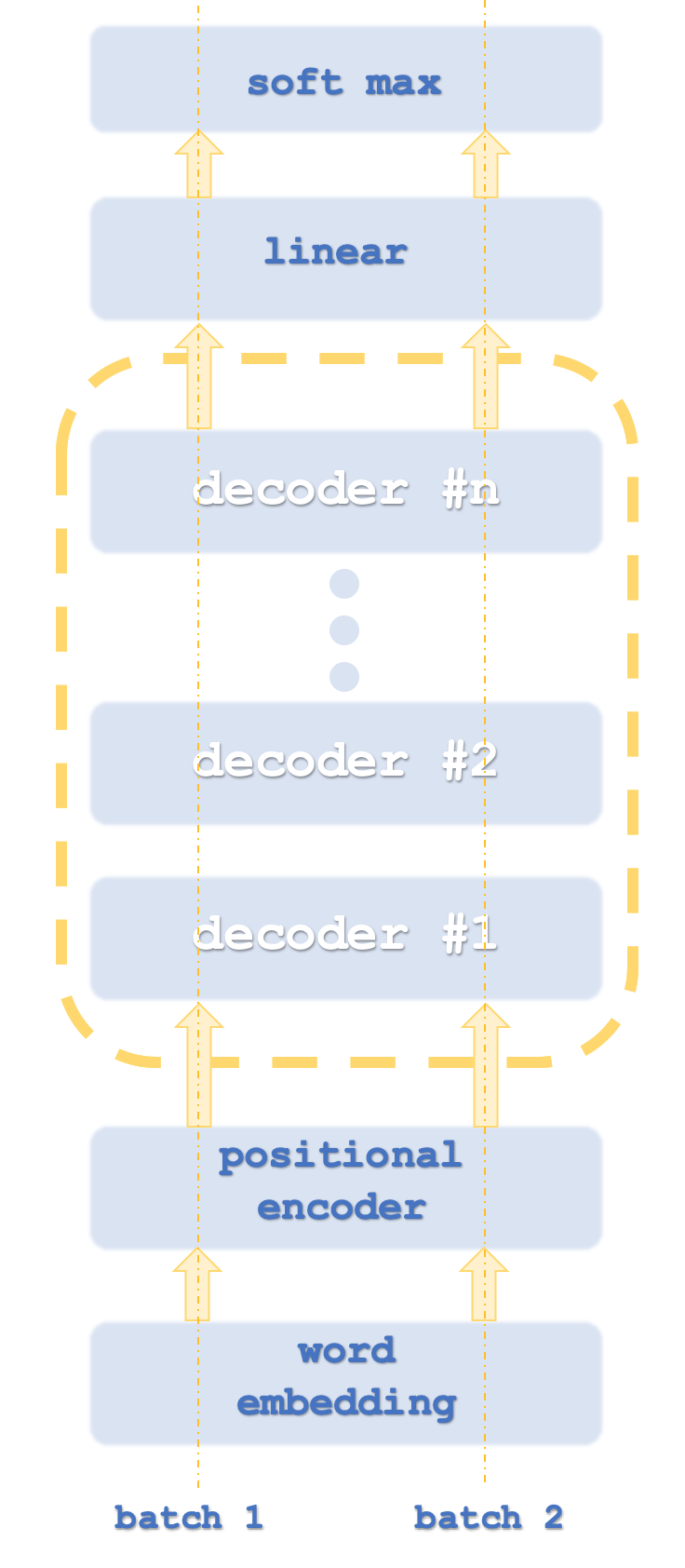
Batch 1 und 2 sind mit Computer-Threads vergleichbar, da Transformer in der Regel Netzinstanzen parallel ausführen.

Da wir Zahlen klassifizieren, entfällt die Notwendigkeit der Wort-Einbettung. Die Positionskodierung soll die absolute Bedeutung jedes Wortes in einem Satz aufgrund seiner Position erfassen. Der Algorithmus dafür ist einfach: Jedem Wort (auch Token genannt) wird ein Wert auf einer Sinuswelle aus einer Reihe von Sinuswellen mit unterschiedlichen Frequenzen zugeordnet. Die Werte der einzelnen Wellen werden addiert, um die Positionskodierung für das jeweilige Token zu erhalten. Dieser Wert kann ein Vektor sein, was bedeutet, dass Sie die Werte von mehr als einem Array von Frequenzen summieren.

Dies führt dann zur Selbstaufmerksamkeit. Dabei wird die relative Bedeutung jedes Wortes in einem Satz im Vergleich zu den Wörtern, die vor ihm in diesem Satz erscheinen, berechnet. Dieses scheinbar triviale Unterfangen ist in Sätzen wichtig, in denen unter anderem das Wort „es“ vorkommt. Zum Beispiel im folgenden Satz:

„Der Geschirrspüler hat das Glas teilweise gereinigt und es ist gesprungen.“

Wofür stehen die „es“? Für einen Menschen ist das ganz einfach, für eine Lernmaschine jedoch nicht. So banal dieses Problem auf den ersten Blick auch erscheinen mag, so war es doch die Fähigkeit, die relative Bedeutung dieses Wortes zu quantifizieren, die wohl entscheidend für die Einführung neuronaler Netze war, die sich als parallelisierbarer erwiesen und deutlich weniger Zeit zum Trainieren benötigten als rekurrente und faltige Netze, ihre Vorgänger.

In diesem Artikel wird daher die Selbstaufmerksamkeit den Kernpunkt unserer Testsignalklasse bilden. Interessanterweise hat der Self-Attention-Algorithmus jedoch eine gewisse Ähnlichkeit mit einer Kategorie in der Art und Weise, wie sich Wörter zueinander verhalten. Die Wortbeziehungen, die zur Quantifizierung der relativen Bedeutung (Ähnlichkeit) verwendet werden, können als Morphismen betrachtet werden, wobei die Wörter selbst Objekte bilden. In der Tat ist diese Beziehung ein wenig unheimlich, da jedes Wort seine Ähnlichkeit oder Wichtigkeit mit sich selbst berechnen muss. Dies ist dem Identitätsmorphismus sehr ähnlich! Darüber hinaus können wir nicht nur Morphismen und Objekte ableiten, sondern auch Funktoren und Kategorien in Beziehung setzen, wie wir in den späteren Artikeln gesehen haben.

Verstehen des Transformer-Decoders

Typischerweise enthält ein Transformer-Netzwerk sowohl Kodier- als auch Dekodier-Stapel (stacks), wobei jeder Stapel eine Wiederholung im Selbstbeobachtungs- und Feed-Forward-Netzwerk darstellt. Sie könnte in etwa so aussehen wie unten:

Darüber hinaus wird jeder Schritt mit parallelen „Threads“ ausgeführt, d. h. wenn beispielsweise der Schritt der Selbstbeobachtung und der Feed-Forward-Analyse durch ein mehrschichtiges Perzeptron dargestellt werden könnte, dann gäbe es bei einem Transformer mit 8 Threads 8 mehrschichtige Perzeptrons in jeder Stufe. Das ist natürlich ressourcenintensiv, aber genau das macht den Vorteil dieses Konzepts aus, denn trotz dieses Ressourcenverbrauchs ist es immer noch effizienter als das Vorgängersystem, die gefalteten Netze.

Der von Open AI verwendete Ansatz ist als eine Variante davon zu verstehen, da er nur dekodiert. Die Schritte wurden in unserem ersten Diagramm grob dargestellt. Die Tatsache, dass das Modell nur dekodiert wird, beeinträchtigt offensichtlich nicht die Genauigkeit des Modells, während es sicherlich mehr Leistung bringt, da nur die „Hälfte“ des Transformers verarbeitet wird. Es könnte hilfreich sein, an dieser Stelle darauf hinzuweisen, dass sich die Zuordnung der Selbstaufmerksamkeit beim Enkodieren von der beim Dekodieren insofern unterscheidet, als beim Enkodieren die relative Bedeutung aller Wörter unabhängig von ihrer relativen Position im Satz berechnet wird. Dies ist eindeutig noch ressourcenintensiver, da, wie auf der Decoderseite erwähnt, die Selbstbeobachtung (auch Ähnlichkeitsberechnungen genannt) nur für jedes einzelne Wort und nur für die Wörter durchgeführt wird, die in einem Satz vor ihm stehen. Man könnte argumentieren, dass dies sogar die Notwendigkeit einer Positionskodierung negiert, aber für unsere Zwecke werden wir sie in die Quelle aufnehmen. Dieser reine Dekodierungsansatz ist daher unser Schwerpunkt.

Die Rolle der Selbstaufmerksamkeit und der Feed-Forward-Netzwerke innerhalb eines Transformerschritts besteht darin, Positionscodierung oder vorherige Stack-Ausgänge zu nehmen und Eingänge für den Linear-SoftMax-Schritt oder Eingänge für den nächsten Decoderschritt zu erzeugen, je nach Stack.

Die Positionskodierung, die manche für unsere Signalklasse und unseren Artikel als übertrieben empfinden mögen, ist hier zu Informationszwecken enthalten. Die absolute Reihenfolge der eingegebenen Preisbalkeninformationen könnte ebenso wichtig sein wie die Wortfolge innerhalb eines Satzes. Wir verwenden einen einfachen Algorithmus, der einen 4-kardinalen Vektor von reellen Werten liefert, die als „Koordinaten“ für jeden Eingabepreispunkt dienen.

Manche mögen einwenden, warum nicht eine einfache Indizierung für jede Eingabe verwenden. Es hat sich herausgestellt, dass dies beim Training von Netzen zu verschwindenden und explodierenden Gradienten führt und daher ein weniger flüchtiges und normalisiertes Format erforderlich ist. Man könnte dies mit einem Verschlüsselungsschlüssel vergleichen, der eine Standardlänge hat, z. B. 128, unabhängig davon, was verschlüsselt wird. Ja, es macht das Knacken des versteckten Schlüssels schwieriger, aber es bietet auch eine effizientere Methode zur Erzeugung und Speicherung der Schlüssel.

Wir werden also 4 Sinuswellen mit unterschiedlichen Frequenzen verwenden. Gelegentlich kann es vorkommen, dass trotz dieser 4 Frequenzen zwei Wörter die gleichen „Koordinaten“ haben, aber das sollte kein Problem sein, da in diesem Fall viele Wörter (oder in unserem Fall Preispunkte) verwendet werden, um diese kleine Anomalie zu neutralisieren. Diese Koordinatenwerte werden zu den 4 Preispunkten unseres Eingabevektors addiert, der dem entspricht, was wir durch die Einbettung von Wörtern erhalten hätten, aber nicht erhalten haben, da wir bereits mit Zahlen in Form von Wertpapierpreisen arbeiten. Unsere Signalklasse wird Preisänderungen verwenden. Und um unsere Positionskodierung zu „normalisieren“, werden die Positionskodierungswerte, die zwischen +5,0 und -5,0 und manchmal sogar darüber hinaus schwanken können, mit der Punktgröße des betreffenden Wertpapiers multipliziert, bevor sie zur Preisänderung addiert werden.

Der Mechanismus der Selbstbeobachtung ist, wie Sie dem/den gemeinsamen Hyperlink(s) oben entnehmen können, mit der Bestimmung von 3 Vektoren beauftragt, nämlich dem Abfragevektor, dem Schlüsselvektor und dem Wertevektor. Diese Vektoren ergeben sich aus der Multiplikation des positionskodierten Ausgangsvektors mit einer Matrix von Gewichten. Wie werden diese Gewichte ermittelt? Von der Rückvermehrung. Für unsere Zwecke werden wir jedoch Instanzen der Klasse der mehrschichtigen Perceptrons verwenden, um diese Gewichte zu initialisieren und zu trainieren. Nur eine Schicht. Eine schematische Darstellung des Prozesses für diese kritische Phase könnte wie folgt aussehen:

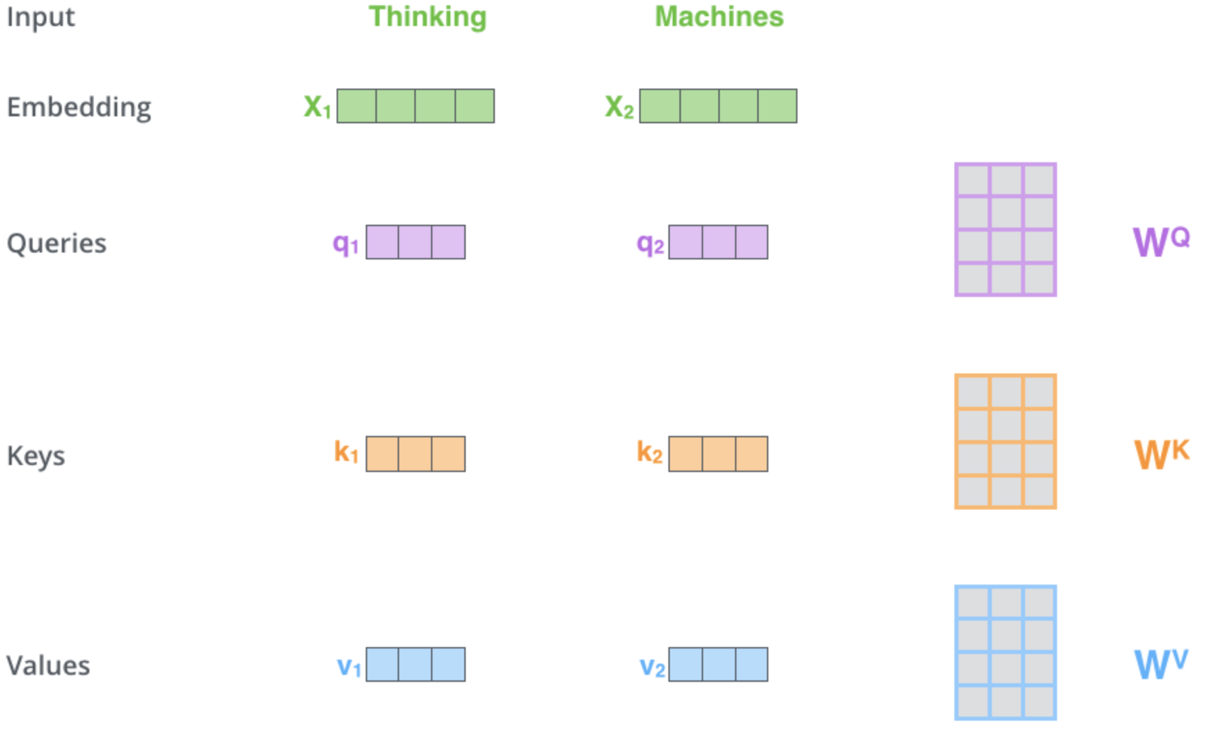
Diese Illustration und einige Punkte in diesem Artikel stammen von dieser Website Web-Seite. Das obige Bild stellt 2 Wörter als Eingaben dar („Thinking“ und „Machines“). Beim Einbetten (Umwandlung in numerische Vektoren) werden sie in Vektoren in grüner Farbe umgewandelt. Die Matrizen auf der rechten Seite stellen die Gewichte dar, die wir, wie oben erwähnt, mit Hilfe von Multi-Layer-Perceptrons erhalten werden.

Sobald unsere Netzwerke also einen Vorwärtsdurchlauf durchführen und dabei die Abfrage-, Schlüssel- und Wertvektoren erhalten, bilden wir ein Punktprodukt aus der Abfrage und dem Schlüssel, teilen dieses Ergebnis durch die Quadratwurzel der Kardinalzahl des Schlüsselvektors und das Ergebnis ist die Ähnlichkeit zwischen dem Preispunkt mit dem Abfragevektor und dem Preispunkt mit dem Schlüsselvektor. Diese Multiplikationen werden über alle Preispunkte hinweg durchgeführt, wobei die Abbildung der Selbstbeobachtung beibehalten wird, bei der wir die Preispunkte nur mit sich selbst und den vorherigen vergleichen. Da die Ergebnisse sehr weit auseinander liegen, werden sie mit Hilfe der SoftMax-Funktion zu einer Wahrscheinlichkeitsverteilung normiert. Die Summe all dieser Wahrscheinlichkeitsgewichte ergibt erwartungsgemäß eins. Sie werden effektiv gewichtet. Im letzten Schritt wird jedes Gewicht mit seinem jeweiligen Vektorwert multipliziert, und alle diese Produkte werden zu einem einzigen Vektor summiert, der den Ausgang der Selbstbeobachtungsschicht bildet.

Das Feed-Forward-Netz nimmt den Ausgangsvektor der Selbstbeobachtung, verarbeitet ihn durch ein mehrschichtiges Perzeptron und gibt einen anderen Vektor aus, der in seiner Größe dem Eingangsvektor der Selbstbeobachtung entspricht.

Der theoretische Rahmen für die Implementierung des Transformer-Decoders in MQL5 wird über eine einfache Signalklasse und nicht über einen Expertenratgeber erfolgen. Dieses Thema ist im Moment noch etwas komplex, da einige dieser Ideen erst seit weniger als einem Jahrzehnt existieren, sodass man der Meinung ist, dass Tests und Vertrautheit im Moment wichtiger sind als Ausführung und Ergebnisse. Es steht dem Leser natürlich frei, diese Ideen weiterzuentwickeln und zu übernehmen, wenn er sich damit wohlfühlt.

Die Signalklasse MQL5: Ein Einblick in Selbstaufmerksamkeit und Feed-Forward-Netzwerke

Die Signalklasse, die diesem Artikel beigefügt ist, versucht, Preisänderungen mit einem Transformer-Decoder vorherzusagen, der nur einen Stapel und einen einzigen Thread!! Mit dem beigefügten Code kann die Anzahl der Stapel erhöht werden, indem der Definitionsparameter '__DECODERS' angepasst wird. Wie bereits erwähnt, gibt es in der Regel mehrere Stapel, und zwar meistens in einer Umgebung mit mehreren Threads. In der Regel werden in einem Decoder mehrere Stapel verwendet, sodass ein Residual Neural Network erforderlich ist. Dies wiederum dient dazu, das Problem der verschwindenden und explodierenden Gradienten zu vermeiden. Wir arbeiten also mit einem reinen, einfachen Transformer und sehen, was er kann. Der Leser kann von hier aus weitere Anpassungen vornehmen, um seinen Implementierungsbedürfnissen gerecht zu werden.

Die Positionskodierung ist wahrscheinlich die einfachste aller aufgeführten Funktionen, da sie einfach einen Vektor von Koordinaten bei einer bestimmten Anzahl von Eingaben zurückgibt. Dieser Code ist wie folgt:

//+------------------------------------------------------------------+
//| Positional Encoding vector given length.                         |
//+------------------------------------------------------------------+
vector CSignalCT::PositionalEncoding(int Positions)
   {
      vector _positions;
      _positions.Init(Positions);_positions.Fill(0.0);
      
      for(int i=0;i<Positions;i++)
      {
         for(int ii=0;ii<Positions;ii++)
         {
            _positions[i]+=MathSin((((ii+1)/Positions)*(i+1))*__PI);
         }
      }
      
      return(_positions);
   }

Unsere Signalklasse verweist also auf eine Reihe von Funktionen, aber die wichtigste von ihnen ist die Decode-Funktion, deren Quelle im Folgenden aufgeführt ist:

//+------------------------------------------------------------------+
//| Decode Function.                                                 |
//+------------------------------------------------------------------+
void CSignalCT::Decode(int &DecoderIndex,matrix &Input,matrix &Sum,matrix &Output)
   {
      Input.ReplaceNan(0.0);
      //
      //output matrices
      Sum.Init(1,int(Input.Cols()));Sum.Fill(0.0);
      
      Ssimilarity _s[];
      ArrayResize(_s,int(Input.Cols()));
      
      for(int i=int(Input.Rows())-1;i>=0;i--)
      {
         matrix _i;_i.Init(1,int(Input.Cols()));
         for(int ii=0;ii<int(Input.Cols());ii++)
         {
            _i[0][ii]=Input[i][ii];
         }
         //
         SelfAttention(DecoderIndex,_i,_s[i].queries,_s[i].keys,_s[i].values);
      }
      
      for(int i=int(Input.Cols())-1;i>=0;i--)
      {
         for(int ii=i;ii>=0;ii--)
         {
            matrix _similarity=DotProduct(_s[i].queries,_s[ii].keys);
            Sum+=DotProduct(_similarity,_s[i].values);
         }
      }
      //
      Sum.ReplaceNan(0.0);
      //
      FeedForward(DecoderIndex,Sum,Output);
   }

Wie Sie sehen können, ruft sie sowohl die Selbstaufmerksamkeitsfunktion als auch die Feed-Forward-Funktion auf und bereitet auch die für diese beiden Schichtfunktionen erforderlichen Eingabedaten vor.

Die Selbstbeobachtungsfunktion führt die eigentlichen Matrixgewichtsberechnungen durch, um die Vektoren für Abfragen, Schlüssel und Werte zu erhalten. Wir haben diese „Vektoren“ als Matrizen dargestellt, obwohl wir für die Zwecke unserer Signalklasse einzeilige Matrizen verwenden werden, weil in der Praxis oft mehrere Vektoren durch ein Netzwerk geleitet oder mit einem Matrixsystem von Gewichten multipliziert werden, um eine Matrix von Abfragen, Schlüsseln und Werten zu erhalten. Den Quellcode hierfür ist wie folgt:

//+------------------------------------------------------------------+
//| Self Attention Function.                                         |
//+------------------------------------------------------------------+
void CSignalCT::SelfAttention(int &DecoderIndex,matrix &Input,matrix &Queries,matrix &Keys,matrix &Values)
   {
      Input.ReplaceNan(0.0);
      //
      Queries.Init(int(Input.Rows()),int(Input.Cols()));Queries.Fill(0.0);
      Keys.Init(int(Input.Rows()),int(Input.Cols()));Keys.Fill(0.0);
      Values.Init(int(Input.Rows()),int(Input.Cols()));Values.Fill(0.0);
      
      for(int i=0;i<int(Input.Rows());i++)
      {
         double _x_inputs[],_q_outputs[],_k_outputs[],_v_outputs[];
         vector _i=Input.Row(i);ArrayResize(_x_inputs,int(_i.Size()));
         for(int ii=0;ii<int(_i.Size());ii++){ _x_inputs[ii]=_i[ii]; }
         
         m_base_q[DecoderIndex].MLPProcess(m_mlp_q[DecoderIndex],_x_inputs,_q_outputs);
         m_base_k[DecoderIndex].MLPProcess(m_mlp_k[DecoderIndex],_x_inputs,_k_outputs);
         m_base_v[DecoderIndex].MLPProcess(m_mlp_v[DecoderIndex],_x_inputs,_v_outputs);
         
         for(int ii=0;ii<int(_q_outputs.Size());ii++){ if(!MathIsValidNumber(_q_outputs[ii])){ _q_outputs[ii]=0.0; }}
         for(int ii=0;ii<int(_k_outputs.Size());ii++){ if(!MathIsValidNumber(_k_outputs[ii])){ _k_outputs[ii]=0.0; }}
         for(int ii=0;ii<int(_v_outputs.Size());ii++){ if(!MathIsValidNumber(_v_outputs[ii])){ _v_outputs[ii]=0.0; }}
         
         for(int ii=0;ii<int(Queries.Cols());ii++){ Queries[i][ii]=_q_outputs[ii]; }   Queries.ReplaceNan(0.0);
         for(int ii=0;ii<int(Keys.Cols());ii++){ Keys[i][ii]=_k_outputs[ii]; }         Keys.ReplaceNan(0.0);
         for(int ii=0;ii<int(Values.Cols());ii++){ Values[i][ii]=_v_outputs[ii]; }     Values.ReplaceNan(0.0);
      }
   }

Die Feed-Forward-Funktion ist eine einfache Verarbeitung eines mehrschichtigen Perzeptrons, und es gibt hier nichts, was aus unserer Sicht spezifisch für den Dekodier-Transformer ist. Natürlich könnten andere Implementierungen hier nutzerdefinierte Einstellungen haben, wie z. B. mehrere verborgene Schichten oder sogar andere Arten von Netzen wie Boltzmann-Maschinen, aber für unsere Zwecke ist dies ein einfaches Netz mit einer verborgenen Schicht.

Die Funktion Punktprodukt ist insofern interessant, als es sich um eine eigene Implementierung der Multiplikation zweier Matrizen handelt. Wir verwenden es hauptsächlich zum Multiplizieren von einzeiligen Matrizen (auch Vektoren genannt), aber es ist skalierbar und könnte einfallsreich sein, da vorläufige Tests der eingebauten Matrixmultiplikationsfunktion ergeben haben, dass sie im Moment fehlerhaft ist.

SoftMax ist eine Implementierung dessen, was bei Wikipedia aufgeführt ist. Alles, was wir tun, ist die Rückgabe eines Vektors von Wahrscheinlichkeiten angesichts eines Eingabefeldes von Werten. Der Ausgangsvektor hat alle positiven Werte und summiert sich zu eins.

Zusammengefasst lädt unsere Signalklasse also Kursdaten vom 01.01.2020 bis zum 01.08.2023 für das Devisenpaar USDJPY. Beim täglichen Zeitrahmen geben wir einen Vektor von 4 Preispunkten, die einfach die letzten 4 Änderungen des Schlusskurses darstellen, in die Positionskodierungsfunktion ein. Wie bereits erwähnt, ermittelt diese Funktion die Koordinaten jeder Kursänderung, normalisiert sie durch Multiplikation mit der USDJPY-Punktgröße und addiert sie zu den eingegebenen Kursänderungen.

Der Ausgangsvektor wird in die Decode-Funktion eingespeist, um den Abfrage-, Schlüssel- und Wertvektor für jeden der 4 Eingänge im Vektor zu berechnen. Da bei der Selbstzuordnung die Ähnlichkeit nur für jeden Preispunkt mit sich selbst und den vorangegangenen Preisänderungen geprüft wird, kommen wir bei 4 Vektorwerten auf 10 Vektorwerte, die mit SoftMax normalisiert werden müssen.

Wenn wir dies durch SoftMax laufen lassen, haben wir eine Reihe von zehn Gewichten, von denen nur eines zum ersten Preispunkt gehört, zwei zum zweiten, drei zum dritten und vier zum vierten. Da wir also mit jedem Preispunkt auch einen Wertvektor haben, den wir während der Selbstbeobachtungsfunktion erhalten haben, multiplizieren wir diesen Vektor mit seinem jeweiligen Gewicht, das wir von SoftMax erhalten haben, und summieren dann alle diese Vektoren zu einem einzigen Ausgangsvektor. Da die Transformerstapel hintereinander geschaltet sind, sollte ihr Betrag mit dem Betrag des Eingangsvektors übereinstimmen. Da wir mehrschichtige Perceptrons verwenden, ist es wichtig zu erwähnen, dass die Gewichte, die mit jedem der Netze initialisiert werden, zufällig sind und mit jedem aufeinanderfolgenden Balken trainiert (und somit verbessert) werden.

Unsere Signalklasse, wenn sie zu einem Expert Advisor kompiliert und für die ersten 5 Monate des Jahres 2023 optimiert wird und einen Walk-Forward-Test vom 2023.06.01 bis 2023.08.01 durchführt, liefert uns die folgenden Berichte:

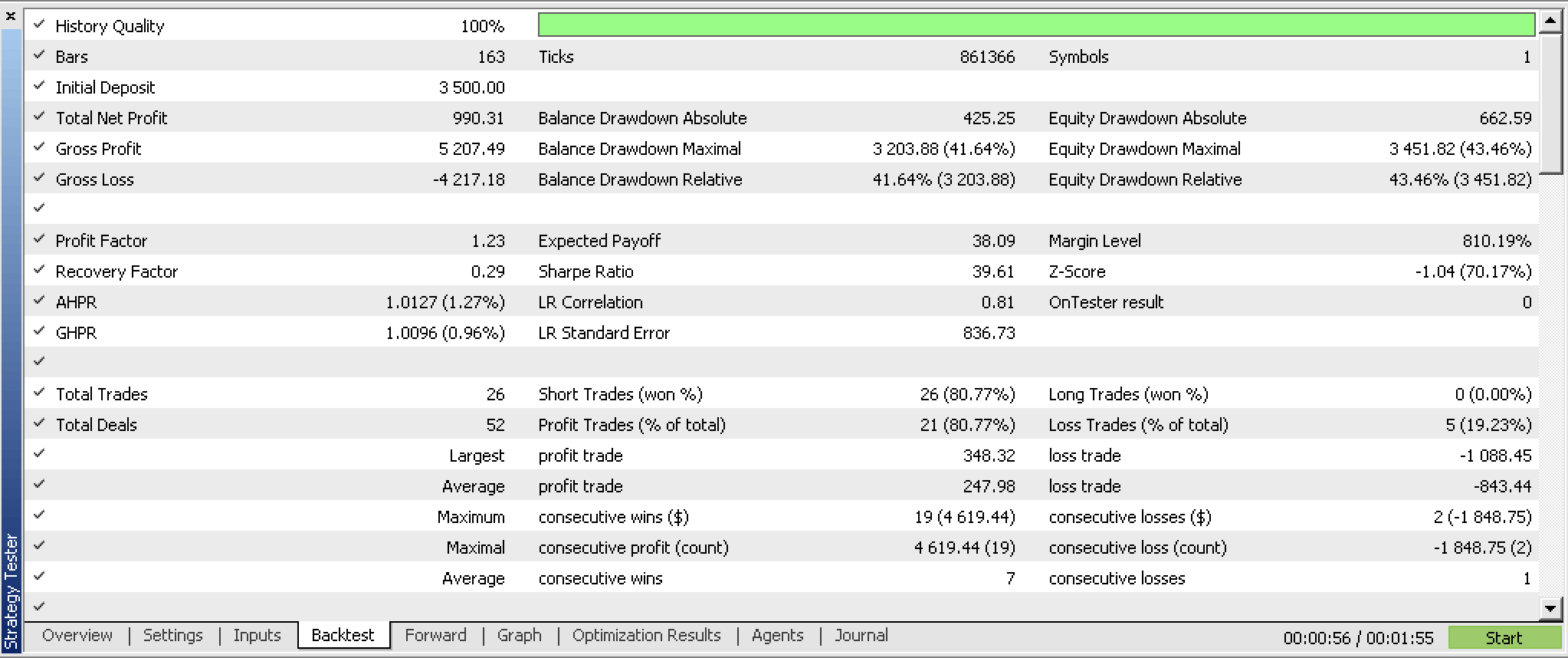
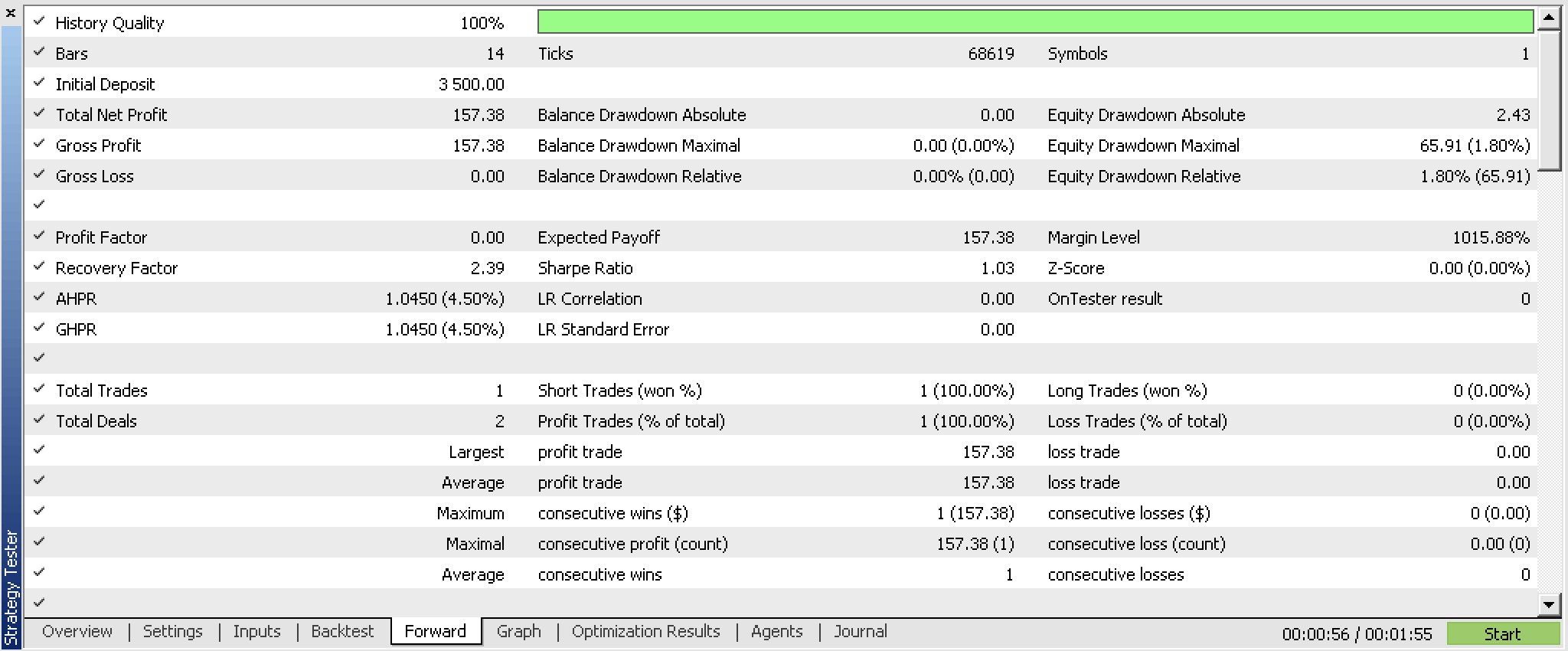
Diese Berichte wurden mit einem Experten erstellt, der über Funktionen zum Lesen und Schreiben von Netzwerkgewichten verfügt, die im beigefügten Code nicht enthalten sind, da die Implementierung dem Leser überlassen bleibt. Da die Gewichte bei der Initialisierung nicht aus einer eindeutigen Quelle gelesen werden, sind die Ergebnisse bei jedem Durchlauf zwangsläufig unterschiedlich.

Anwendungen in der realen Welt

Die potenziellen Anwendungen dieser Signalklasse und nicht des Transformer-Decoders könnten in der Suche nach potenziellen Wertpapieren liegen, die mit dem Transformer-Decoder gehandelt werden können. Wenn wir Tests mit mehreren Handelspapieren über einen Zeitraum von Jahrzehnten durchführen, erhalten wir vielleicht ein Gefühl dafür, was durch zusätzliche Tests und Systementwicklung weiter untersucht werden sollte und was vermieden werden sollte.

Innerhalb eines Stapels des Decoder-Transformers ist die Selbstaufmerksamkeitsschicht entscheidend und wird uns einen Vorteil verschaffen, da das hier verwendete Feed-Forward-Netzwerk ziemlich einfach ist. So wird die relative Bedeutung jeder früheren Preisänderung in einer Weise erfasst, die Korrelationsfunktionen leicht übersehen, da sie sich auf Durchschnittswerte konzentrieren. Die Verwendung von mehrschichtigen Perceptrons bei der Erfassung der Gewichtsmatrizen für die Abfrage-, Schlüssel- und Wertvektoren ist ein möglicher Ansatz, für den es eine Fülle von anderen zwischengeschalteten Optionen des maschinellen Lernens gibt, um dies zu erreichen. Im Großen und Ganzen wäre das Verständnis der Empfindlichkeit der Selbstaufmerksamkeit gegenüber der Vorhersagbarkeit des Netzes der Schlüssel.

Beschränkungen und Nachteile

Das Netzwerktraining für unsere Signalklasse erfolgt inkrementell für jeden neuen Balken, und es gibt keine Möglichkeit, vortrainierte Gewichte zu laden, was bedeutet, dass wir häufig zufällige Ergebnisse erhalten werden. Aus diesem Grund sollte der Leser jedes Mal, wenn die Signalklasse ausgeführt wird, andere Ergebnisse erwarten.

Darüber hinaus gibt es keine Möglichkeit, die trainierten Gewichte am Ende der Signalklasse zu speichern, sodass wir nicht auf dem Gelernten aufbauen können.

Diese Einschränkungen sind meiner Meinung nach kritisch und müssen behoben werden, bevor man mit der Weiterentwicklung unseres Transformer-Decoders zu einem Handelssystem fortfährt. Wir sollten nicht nur trainierte Gewichte verwenden und auch in der Lage sein, Trainingsgewichte zu speichern, sondern auch Tests mit Daten aus der Stichprobe mit trainierten Gewichten durchführen, bevor das System eingesetzt werden kann.

Schlussfolgerung

Also, um die Frage zu beantworten, ist der Algorithmus von chatGP mit natürlichen Transformationen verbunden? Das könnte sein. Denn wenn wir die Stapel des Decoder-Transformers als Kategorien betrachten, dann sind die Threads (parallele Operationen, die den Transformer durchlaufen) Funktoren. Bei dieser Analogie entspräche die Differenz zwischen den Endergebnissen der einzelnen Operationen einer Natürliche Transformation.

Unser Decoder-Transformer hat auch ohne richtige Gewichtserfassung und -auslesung einiges an Potenzial gezeigt. Es ist sicherlich ein interessantes System, das man weiterentwickeln und sogar zu seinem Werkzeugkasten hinzufügen könnte, wenn man sich einen Vorteil verschafft.

Zusammenfassend lässt sich sagen, dass der Algorithmus der Selbstaufmerksamkeit in der Lage ist, die relative Ähnlichkeit zwischen Token (den Eingaben in einem Transformer) zu quantifizieren. In unserem Fall handelte es sich bei diesen Token um Preisänderungen zu verschiedenen, aber aufeinander folgenden Zeitpunkten. In anderen Modellen könnte es sich dabei um mehrere Wirtschaftsindikatoren, Nachrichtenereignisse oder Stimmungswerte von Anlegern usw. handeln, aber der Prozess wäre derselbe. Das Ergebnis mit diesen verschiedenen Eingaben wird jedoch zwangsläufig die komplexen und dynamischen Beziehungen dieser Eingabewerte enthüllen und somit modellieren, was dem Entwickler hilft, sie besser zu verstehen. Auf diese Weise kann der Transformer bei jedem neuen Trainingsdurchgang adaptiv relevante Merkmale aus den eingegebenen Token extrahieren. Selbst in volatilen Situationen, in denen es viele Nachrichten gibt, sollte das Modell das weiße Rauschen herausfiltern und widerstandsfähiger sein.

Außerdem hilft der Selbstbeobachtungsalgorithmus, wenn er mit verzögerten oder Eingangsdaten zu verschiedenen Zeitpunkten konfrontiert wird, wie wir es mit der beigefügten Signalklasse untersucht haben, bei der Quantifizierung der relativen Bedeutung dieser verschiedenen Zeiträume und erfasst somit langfristige Abhängigkeiten. Dies führt dazu, dass Prognosen über verschiedene Zeithorizonte erstellt werden können, ein weiterer Vorteil für Händler. Zusammenfassend lässt sich also sagen, dass die relative Gewichtung der Token-Inputs den Händlern nicht nur Aufschluss über die verschiedenen Wirtschaftsindikatoren geben sollte, die als Inputs dienen können, sondern auch über die verschiedenen Zeitrahmen, wenn verzögerte Zeitindikatoren (oder Preise) verwendet werden.

Zusätzliche Ressourcen

Die Referenzen sind größtenteils Wikipedia, wie in den Links angegeben, mit dem Zusatz von Cornell University Computer Science Publications Stack Exchange, und dieser Website.

Anmerkung des Autors

Der in diesem Artikel geteilte Quellcode ist NICHT der von chatGPT verwendete Code. Es handelt sich einfach um die Implementierung eines reinen Dekodier-Transformers. Es liegt in einem Signalklassenformat vor, was bedeutet, dass der Nutzer es mit dem MQL5-Assistenten kompilieren muss, um einen testbaren Experten zu erstellen. Einen Leitfaden dazu gibt es hier. Außerdem sollte er Lese- und Schreibmechanismen zum Lesen und Speichern der gelernten Netzgewichte implementieren.