Prognose mit ARIMA-Modellen in MQL5

MetaTrader 5 — Handelssysteme | 2 August 2023, 09:54

254

Francis Dube

Einführung

Der Artikel Implementierung eines ARIMA-Trainingsalgorithmus in MQL5 beschreibt die CArima-Klasse zur Erstellung von ARIMA-Modellen. Obwohl es technisch möglich ist, die Klasse so zu verwenden, wie sie ist, um ein Modell anzuwenden und Vorhersagen zu treffen, erschließt sich einem nicht intuitiv. In diesem Artikel werden wir dieses Manko beheben und die Klasse erweitern, um einfachere Methoden für die Anwendung von Modellen zur Erstellung von Vorhersagen zu ermöglichen. Wir werden einige der Komplikationen im Zusammenhang mit der Implementierung von Vorhersagen sowie einige neue Funktionen, die der Klasse hinzugefügt wurden, diskutieren. Abschließend werden wir die gesamte Klasse verwenden, um ein Modell zu erstellen und es zur Vorhersage von Devisenkursen einzusetzen, indem wir es auf einen Expert Advisor und einen Indikator anwenden.

Die Reihe der Eingänge

Es ist allgemein bekannt, dass ARIMA-Modelle auf zeitlichen Abhängigkeiten in einem Datensatz beruhen. Um eine oder mehrere Vorhersagen zu treffen, müssen wir das Modell mit einer Reihe von Eingabedaten füttern. Die Spezifikation des Modells bestimmt die Mindestgröße der Eingangsreihen. Wenn man dies weiß, wird klar, dass bei unzureichenden Eingangsreihen keine Vorhersagen möglich sind oder zumindest die Vorhersagen das angewandte Modell nicht widerspiegeln werden. Die verschiedenen Arten von ARIMA-Modellen stellen unterschiedliche Anforderungen an die Größe der Eingangsreihen, die über die Ordnung des Modells hinausgehen.

Die Implementierung von Vorhersagen für reine autoregressive Modelle ist trivial, da nur Eingaben erforderlich sind, die der größten Verzögerung des Modells entsprechen. Gemischte Modelle, die gleitende Durchschnittswerte verwenden, verursachen Probleme bei der Erstellung von Prognosen. Wir haben noch keine aktuellen Fehler- oder Innovationsreihen. Um dieses Problem zu lösen, müssen wir zunächst entscheiden, wie die Anfangswerte der Fehler berechnet werden sollen.

Bei diesem Verfahren werden zunächst alle verfügbaren Modellparameter verwendet, um den Anfangszustand des Modells zu erhalten, bei dem alle Terme des gleitenden Durchschnitts ausgeschlossen sind, da sie in diesem Stadium als 0 angenommen werden. Anschließend werden die bekannten Zeitreihen zur Berechnung der anfänglichen Fehlerwerte verwendet, indem eine Reihe redundanter Vorhersagen durchlaufen werden, die nichts mit den endgültigen Vorhersagen zu tun haben, an denen wir letztendlich interessiert sind. Dies stellt natürlich höhere Anforderungen an die Anzahl der für die Vorhersage benötigten Eingaben. Entscheidend ist hier, wie viele redundante Vorhersagezyklen durchgeführt werden müssen, um geeignete Fehlerserienwerte für gültige Vorhersagen zu erhalten.

Es gibt noch mehr zu bedenken, was die Anzahl der Modelleingaben angeht. Die Klasse CArima ermöglicht es, Modelle mit nicht zusammenhängenden Verzögerungen anzugeben. Dadurch wird die Zahl der erforderlichen Eingaben noch größer. In diesem Fall wird die größte Verzögerung der beiden Typen (AR/MA) die Anforderungen an die Eingabegröße erhöhen. Betrachten Sie ein Modell, das durch die Funktion

Preis(t) = constant_term + AR*Preis(t-4)

Diese Funktion spezifiziert ein Modell mit einem einzigen AR-Term mit einer Verzögerung von vier. Das bedeutet, dass der aktuelle Preis teilweise durch den Wert vor 4 Zeiteinheiten bestimmt wird. Auch wenn wir nur einen solchen Wert benötigen, müssen wir darauf achten, dass die zeitlichen Beziehungen der Eingaben erhalten bleiben. Anstelle einer einzigen Eingabeanforderung benötigen wir also vier, zusätzlich zu den anderen Modellanforderungen. Die letzte Determinante für den Umfang der Inputreihen hängt davon ab, ob eine Differenzierung erforderlich ist.

Berechnung bei Differenzierung

Die Anforderungen der Differenzenbildung erhöhen die Anzahl der erforderlichen Eingaben nicht wegen der Berechnung des/der vorhergesagten Werte(s), sondern aufgrund der Tatsache, dass die Differenzenbildung zu einem Informationsverlust führt. Wenn eine Differenzenreihe erstellt wird, ist sie im Vergleich zur ursprünglichen Reihe immer um eins kürzer. Diese kürzere Reihe wird schließlich als Input für das Modell verwendet. Daher sind im Allgemeinen zusätzliche Eingaben zum Ausgleich erforderlich, die der vom Modell vorgegebenen Differenzenreihe entsprechen.

Die Differenzenbildung wirkt sich nicht nur auf die Größe der Eingaben aus, sondern auch auf die endgültigen Vorhersagen, da diese im Bereich der Differenzen liegen. Die Vorhersagen müssen zusammen mit den gelieferten Eingangsreihen kombiniert und integriert werden, um die kombinierten Werte in den ursprünglichen Bereich zurückzuführen.

Weit in die Zukunft voraussagen

In manchen Fällen sind die Nutzer daran interessiert, auf der Grundlage eines einzigen Satzes von Eingaben mehrere Zeitfenster in die Zukunft zu prognostizieren. Obwohl dies nicht empfohlen wird, ist es eine Möglichkeit, die es wert ist, erforscht und ausgepackt zu werden. Bei Vorhersagen, die weit in die Zukunft reichen, müssen wir bestimmte Wahrheiten berücksichtigen. Erstens müssen wir, je weiter wir gehen, schließlich Vorhersagen aus früheren Zeitabschnitten als Eingaben für alle autoregressiven Terme verwenden. Sobald wir die bekannten Reihen, die als Ausgangswerte verwendet werden, überschreiten, haben wir keine Möglichkeit mehr, Fehlerwerte zu berechnen, da die wirklichen, zukünftigen Werte unbekannt sind. Daher kann für solche Zeitfenster nur angenommen werden, dass der gleitende Durchschnitt Null ist. Dies führt dazu, dass die vorhergesagte Reihe entweder zu einem reinen autoregressiven Prozess degeneriert, wenn er spezifiziert ist, oder zu einem Prozess, der nur durch den konstanten Term definiert ist. Bei der Erstellung von Mehrfachprognosen, die weit in die Zukunft reichen, sollte man sich der damit verbundenen Einschränkungen bewusst sein.

Ergänzungen zur Klasse CArima

Die erste Änderung, die an der Klasse vorgenommen wurde, bezieht sich auf die übergeordnete CPowellsMethod. Die Methode Optimize() hat jetzt den Zugriffsmodifikator protected und kann nicht von außerhalb der Klasse aufgerufen werden. Natürlich gilt diese Änderung auch für CArima. Aufgrund dieser Änderung wird der Name der Include-Datei, die die Klasse CPowellsMethod enthält, einfach in Powells.mqh geändert.

//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
   double            P[],Xi[];
   double            Pcom[],Xicom[],Xt[];
   double            Pt[],Ptt[],Xit[];
   int               N;
   double            Fret;
   int               Iter;
   int               ItMaxPowell;
   double            FtolPowell;
   int               ItMaxBrent;
   double            FtolBrent;
   int               MaxIterFlag;
   int               Optimize(double &p[],int n=0);
public:
   void              PowellsMethod(void);
   void              SetItMaxPowell(int n)           { ItMaxPowell=n; }
   void              SetFtolPowell(double er)        { FtolPowell=er; }
   void              SetItMaxBrent(int n)            { ItMaxBrent=n;  }
   void              SetFtolBrent(double er)         { FtolBrent=er;  }
   double            GetFret(void)                   { return(Fret);  }
   int               GetIter(void)                   { return(Iter);  }
private:
   void              powell(void);
   void              linmin(void);
   void              mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
   double            brent(double ax,double bx,double cx,double &xmin);
   double            f1dim(double x);
   virtual double    func(const double &p[]) { return(0); }
  };

Eine wichtige Funktion, die der Klasse hinzugefügt wurde, ist die Möglichkeit, Modelle zu speichern und zu laden. Dies ermöglicht es, ein Modell zu trainieren und zu speichern, um es später zu verwenden oder in ein anderes Mql5-Programm zu übernehmen.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::SaveModel(const string model_name)
  {
   uint model_order[]= {m_const,m_ar_order,m_diff_order,m_ma_order};

   CFileBin file;
   ResetLastError();
   if(!file.Open("models\\"+model_name+".model",FILE_WRITE|FILE_COMMON))
     {
      Print("Failed to save model.Error: ",GetLastError());
      return false;
     }

   m_modelname=(m_modelname=="")?model_name:m_modelname;

   long written=0;

   written = file.WriteIntegerArray(model_order);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(m_ar_order)
     {
      written = file.WriteIntegerArray(m_arlags);

      if(!written)
        {
         Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
         return false;
        }
     }

   if(m_ma_order)
     {
      written = file.WriteIntegerArray(m_malags);

      if(!written)
        {
         Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
         return false;
        }
     }

   written = file.WriteDoubleArray(m_model);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   written = file.WriteDouble(m_sse);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }


   file.Close();

   return true;

  }

Die Methode SaveModel ermöglicht das Speichern von Modellen, sie erfordert eine Text-Eingabe, die den neuen Namen des Modells darstellt, die Methode selbst schreibt in eine binäre Datei .model, die im Verzeichnis models des Ordners „common files“ ( Terminal\Common\Files\models ) gespeichert ist. Die gespeicherte Datei enthält die Modellreihenfolge sowie die Parameter des Modells, falls es trainiert wurde, einschließlich der Summe der quadratischen Fehler (sse).

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::LoadModel(const string model_name)
  {
   int found=StringFind(model_name,".model");

   if(found>=0)
      m_modelname=StringSubstr(model_name,0,found);
   else
      m_modelname=model_name;

   if(StringFind(m_modelname,"\\")>=0)
      return false;

   string filename="models\\"+m_modelname+".model";

   if(!FileIsExist(filename,FILE_COMMON))
     {
      Print("Failed to find model, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   CFileBin file;
   ResetLastError();
   if(file.Open(filename,FILE_READ|FILE_COMMON)<0)
     {
      Print("Failed open operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   uint model_order[];


   file.Seek(0,SEEK_SET);

   if(!file.ReadIntegerArray(model_order,0,4))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   m_const=bool(model_order[0]);
   m_ar_order=model_order[1];
   m_diff_order=model_order[2];
   m_ma_order=model_order[3];

   file.Seek(sizeof(uint)*4,SEEK_SET);

   if(m_ar_order && !file.ReadIntegerArray(m_arlags,0,m_ar_order))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(!m_ar_order)
      ArrayFree(m_arlags);



   if(m_ar_order)
      file.Seek(sizeof(uint)*(4+m_ar_order),SEEK_SET);


   if(m_ma_order && !file.ReadIntegerArray(m_malags,0,m_ma_order))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   ArrayPrint(m_malags);

   if(!m_ma_order)
      ArrayFree(m_malags);


   if(m_ar_order || m_ma_order)
      file.Seek(sizeof(uint)*(4+m_ar_order+m_ma_order),SEEK_SET);



   if(!file.ReadDoubleArray(m_model,0,m_ma_order+m_ar_order+1))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   file.Seek(sizeof(uint)*(4+m_ar_order+m_ma_order) + sizeof(double)*ArraySize(m_model),SEEK_SET);

   if(!file.ReadDouble(m_sse))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(m_model[1])
      m_istrained=true;
   else
      m_istrained=false;

   ZeroMemory(m_differenced);
   ZeroMemory(m_leads);
   ZeroMemory(m_innovation);

   m_insize=0;

   return true;
  }

Die Methode LoadModel benötigt den Modellnamen und liest alle Attribute eines zuvor gespeicherten Modells ein. Beide Methoden geben entweder true oder false zurück und nützliche Fehlermeldungen werden in das Journal des Terminals geschrieben.

string            GetModelName(void)                      { return m_modelname;}

Die Methode GetModelName() gibt den Namen eines Modells zurück. Sie gibt eine leere Zeichenkette zurück, wenn das Modell noch nie gespeichert wurde, andernfalls gibt sie den Namen zurück, der beim Speichern des Modells festgelegt wurde.

//+------------------------------------------------------------------+
//| calculate the bayesian information criterion                     |
//+------------------------------------------------------------------+
double CArima::BIC(void)
  {
   if(!m_istrained||!m_sse)
     {
      Print(m_modelname," Model not trained. Train the model first to calculate the BIC.");
      return 0;
     }

   if(!m_differenced.Size())
     {
      Print("To calculate the BIC, supply a training data set");
      return 0;
     }
   uint n = m_differenced.Size();
   uint k = m_ar_order+m_ma_order+m_diff_order+uint(m_const);

   return((n*MathLog(m_sse/n)) + (k*MathLog(n)));

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CArima::AIC(void)
  {
   if(!m_istrained||!m_sse)
     {
      Print(m_modelname," Model not trained. Train the model first to calculate the AIC.");
      return 0;
     }

   if(!m_differenced.Size())
     {
      Print("To calculate the AIC, supply a training data set");
      return 0;
     }

   uint n = m_differenced.Size();
   uint k = m_ar_order+m_ma_order+m_diff_order+uint(m_const);

   return((2.0*k)+(double(n)*MathLog(m_sse/double(n))));
  }
//+------------------------------------------------------------------+

Ebenfalls neu sind die Methoden BIC und AIC . Die AIC-Methode berechnet das Akaike-Informationskriterium und funktioniert ähnlich wie die BIC-Funktion. Die AIC-Methode berechnet das Akiake-Informationskriterium und funktioniert ähnlich wie die BIC-Funktion. Das Bayessche Informationskriterium (BIC) und das Akaike-Informationskriterium (AIC) sind statistische Maße, die für die Modellauswahl verwendet werden. Beide Kriterien zielen darauf ab, ein Gleichgewicht zwischen der Anpassungsgüte eines Modells und seiner Komplexität herzustellen, sodass einfachere Modelle bevorzugt werden, wenn sie die Daten fast genauso gut abbilden wie komplexere Modelle.

BIC und AIC unterscheiden sich darin, wie sie Anpassungsgüte und Komplexität ausbalancieren. Der BIC legt mehr Gewicht auf die Einfachheit des Modells als der AIC, d. h. er bevorzugt noch einfachere Modelle als der AIC. Andererseits wählt der AIC mit größerer Wahrscheinlichkeit komplexere Modelle aus als der BIC. Einfach ausgedrückt: BIC und AIC ermöglichen es uns, verschiedene Modelle zu vergleichen und dasjenige auszuwählen, das unseren Daten am besten entspricht, wobei die Komplexität des Modells berücksichtigt wird. Durch die Wahl eines einfacheren Modells können wir eine Überanpassung vermeiden, die auftritt, wenn ein Modell zu komplex ist und die Daten zu genau abbildet, wodurch es für die Vorhersage neuer Beobachtungen weniger nützlich ist.

Beide geben im Fehlerfall 0 zurück und sollten direkt nach dem Training eines Modells aufgerufen werden, während die Trainingsdaten noch geladen sind. Bei der Initialisierung eines trainierten Modells sind die zum Training verwendeten Daten nicht verfügbar, sodass weder der BIC noch der AIC berechnet werden können.

uint              GetMinModelInputs(void)                 { return(m_diff_order + GetMaxArLag() + (GetMaxMaLag()*m_infactor));}

Es ist jetzt auch möglich, die Mindestanzahl der für ein Modell erforderlichen Eingaben abzufragen. Dies wird mit der Methode GetMinModelInputs() durchgeführt.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CArima::Summary(void)
  {

   string print = m_modelname+" Arima("+IntegerToString(m_ar_order)+","+IntegerToString(m_diff_order)+","+IntegerToString(m_ma_order)+")\n";
   print+= "SSE : "+string(m_sse);

   int k=0;
   if(m_const)
      print+="\nConstant: "+string(m_model[k++]);
   else
      k++;
   for(uint i=0; i<m_ar_order; i++)
      print+="\nAR coefficient at lag "+IntegerToString(m_arlags[i])+": "+string(m_model[k++]);
   for(uint j=0; j<m_ma_order; j++)
      print+="\nMA coefficient at lag "+IntegerToString(m_malags[j])+": "+string(m_model[k++]);

   Print(print);

   return;

  }

Schließlich werden durch den Aufruf von Summary() die Attribute des Modells in das Terminal geschrieben, und es wird keine Zeichenkette mehr zurückgegeben.

Umsetzen der Prognostik

   bool              Predict(const uint num_pred,double &predictions[]);
   bool              Predict(const uint num_pred,double &in_raw[], double &predictions[]);
   bool              SaveModel(const string model_name);
   bool              LoadModel(const string model_name);
   double            BIC(void);
   double            AIC(void);

Die Anwendung eines Modells zur Erstellung von Vorhersagen wird durch zwei überladene Methoden namens Predict() implementiert. Beide nehmen als Input zwei ähnliche Inputs:

num_pred - Dieser ganzzahlige Wert gibt die Anzahl der gewünschten Vorhersagen an.

predictions - Ist ein Array vom Typ double, in dem die vorhergesagten Werte ausgegeben werden.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::Predict(const uint num_pred,double &predictions[])
  {
   if(!num_pred)
     {
      Print("Invalid number of predictions");
      return false;
     }

   if(!m_istrained || !m_insize)
     {
      ZeroMemory(predictions);
      if(m_istrained)
         Print("Model not trained");
      else
         Print("No input data available to make predictions");
      return false;
     }

   ArrayResize(m_differenced,ArraySize(m_differenced)+num_pred,num_pred);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   evaluate(num_pred);

   if(m_diff_order)
     {
      double raw[];
      integrate(m_differenced,m_leads,raw);
      ArrayPrint(raw,_Digits,NULL,m_insize-5);
      ArrayCopy(predictions,raw,0,m_insize+m_diff_order);
      ArrayFree(raw);
     }
   else
      ArrayCopy(predictions,m_differenced,0,m_insize);

   return true;
  }

Die Methoden zur Vorhersage unterscheiden sich in der Anzahl der Funktionsparameter: Die erste Methode, die zwei Parameter benötigt, wird verwendet, um Vorhersagen auf der Grundlage der Trainingsdaten zu treffen, die zur Ableitung der optimalen Koeffizienten des Modells verwendet werden.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::Predict(const uint num_pred,double &in_raw[],double &predictions[])
  {
   if(!num_pred)
     {
      Print("Invalid number of predictions");
      return false;
     }

   if(!m_istrained)
     {
      ZeroMemory(predictions);
      Print("Model not trained");
      return false;
     }

   int numofinputs=0;

   if(m_ar_order)
      numofinputs+=(int)GetMaxArLag();
   if(m_ma_order)
      numofinputs+=int(GetMaxMaLag()*m_infactor);
   if(m_diff_order)
      numofinputs+=(int)m_diff_order;

   if(in_raw.Size()<(uint)numofinputs)
     {
      ZeroMemory(predictions);
      Print("Input dataset size inadequate. Size required: ",numofinputs);
      return false;
     }

   ZeroMemory(m_differenced);

   if(m_diff_order)
     {
      difference(m_diff_order,in_raw,m_differenced,m_leads);
      m_insize=m_differenced.Size();
     }
   else
     {
      m_insize=in_raw.Size();
      ArrayCopy(m_differenced,in_raw);
     }


   if(m_differenced.Size()!=(m_insize+num_pred))
      ArrayResize(m_differenced,m_insize+num_pred,num_pred);

   ArrayFill(m_differenced,m_insize,num_pred,0.0);

   if(m_innovation.Size()!=m_insize+num_pred)
      ArrayResize(m_innovation,ArraySize(m_differenced));

   ArrayInitialize(m_innovation,0.0);

   evaluate(num_pred);

   if(m_diff_order)
     {
      double raw[];
      integrate(m_differenced,m_leads,raw);
      ArrayCopy(predictions,raw,0,m_insize+m_diff_order);
      ArrayFree(raw);
     }
   else
      ArrayCopy(predictions,m_differenced,0,m_insize);

   return true;

  }

Die zweite Vorhersagemethode erfordert ein drittes Eingabeparameter-Array, das die Reihe von Eingaben enthalten sollte, die zur Berechnung der Vorhersagen verwendet werden sollen. Beide Methoden geben einen booleschen Wert zurück und verwenden auch die private Evaluierungsfunktion.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CArima::evaluate(const uint num_p)
  {

   double pred=0;
   uint start_shift=(m_ma_order)?((!m_innovation[m_insize-1])?m_insize-(GetMaxMaLag()*m_infactor):m_insize):m_insize;
   uint d_size=(uint)ArraySize(m_differenced);

   int p_shift;

   for(uint i=start_shift; i<d_size; i++)
     {
      p_shift=0;
      pred=0;
      if(i>=m_insize)
         m_innovation[i]=0.0;
      if(m_const)
         pred+=m_model[p_shift++];
      for(uint j=0; j<m_ar_order; j++)
         pred+=m_model[p_shift++]*m_differenced[i-m_arlags[j]];
      for(uint k=0; i>=GetMaxMaLag() && k<m_ma_order; k++)
         pred+=m_model[p_shift++]*m_innovation[i-m_malags[k]];
      if(i>=m_insize)
         m_differenced[i]=pred;
      if(i<m_insize)
         m_innovation[i]=pred-m_differenced[i];
     }

   return;
  }

Die Methode evaluate() ähnelt der Methode func() mit einigen kleinen Unterschieden. Es nimmt die gewünschte Anzahl von Vorhersagen als einziges Argument und durchläuft je nach Modellspezifikation bis zu fünf Arrays. Es berechnet neue Vorhersagen und fügt bei Bedarf neue Werte zu den Fehlerreihen (Innovationen) hinzu. Anschließend werden die vorhergesagten Werte extrahiert und in das der Methode Predict() übergebene Zielfeld kopiert. Die Vorhersagemethoden geben bei Erfolg true zurück und false, wenn ein Fehler auftritt.

Verwendung der Klasse

Um die Verwendung der modifizierten Klasse CArima zu demonstrieren, werden wir ein Skript erstellen, das einige Modelle trainiert und das beste Modell durch eine Brute-Force-Suche speichert. Dann werden wir zeigen, wie dieses gespeicherte Modell in einem Indikator verwendet werden kann, indem wir es nutzen, um Vorhersagen einen Schritt voraus zu machen. Zum Schluss werden wir dasselbe Modell verwenden, um einen einfachen Expertenberater zu erstellen.

//+------------------------------------------------------------------+
//|                                                 TrainARModel.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Arima.mqh>

enum ENUM_QUOTES
  {
   closeprices,//Close price
   medianprices//Mid price
  };

input uint MaximumSearchLag=5;
input bool DifferenceQuotes=true;
input datetime TrainingDataStartDate=D'2020.01.01 00:01';
input datetime TrainingDataStopDate=D'2021.01.01 23:59';
input string Sy="AUDUSD";//Set The Symbol
input ENUM_TIMEFRAMES SetTimeFrame=PERIOD_M1;
input ENUM_QUOTES quotestypes = closeprices;
input string SetModelName = "ModelName";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CArima *arima[];
   uint max_it=MaximumSearchLag;
   double sse[],quotes[],mid_prices[];


   if(!max_it)
      ++max_it;


   MqlRates prices[];

   int a_size=CopyRates(Sy,SetTimeFrame,TrainingDataStartDate,TrainingDataStopDate,prices);

   if(a_size<=0)
     {
      Print("downloaded size is ", a_size," error ",GetLastError());
      return;
     }

   ArrayResize(arima,max_it);
   ArrayResize(sse,max_it);
   ArrayResize(quotes,a_size);

   for(uint i=0; i<prices.Size(); i++)
     {

      switch(quotestypes)
        {
         case medianprices:
            quotes[i]=(prices[i].high+prices[i].low)/2;
            break;
         case closeprices:
            quotes[i]=prices[i].close;
            break;
        }
     }

   uint u=0;
   for(uint i=0; i<max_it; i++)
     {
      u=uint(DifferenceQuotes);
      arima[i]=new CArima(i+1,u,0,true);
      if(arima[i].Fit(quotes))
        {
         sse[i]=arima[i].GetSSE()*1.e14;
         Print("Fitting model ",i+1," completed successfully.");
        }
      else
        {
         sse[i]=DBL_MAX;
         Print("Fitting model ",i+1, " failed.");
        }


     }

   int index = ArrayMinimum(sse);
   Print("**** Saved model *****");
   arima[index].Summary();
//save the best model for later use.
   arima[index].SaveModel(SetModelName);

   for(int i=0; i<(int)arima.Size(); i++)
      if(CheckPointer(arima[i])==POINTER_DYNAMIC)
         delete arima[i];

  }
//+------------------------------------------------------------------+

Das Skript erleichtert die Suche nach einem optimalen reinen autoregressiven Modell, das zu einer Stichprobe von Schlusskursen passt, mit Brachialgewalt. Es sollte betont werden, dass dies nur eine einfache Demonstration ist. Es ist möglich, komplexere Modelle mit Variationen in der Anzahl und Art der (AR/MA)-Terme zu implementieren, nicht zu vergessen die Möglichkeit, nicht zusammenhängende Lags für diese Terme anzugeben. Die Möglichkeiten sind also vielfältig. Im Moment beschränken wir uns auf die Anpassung eines reinen autoregressiven Modells.

Modellschulung

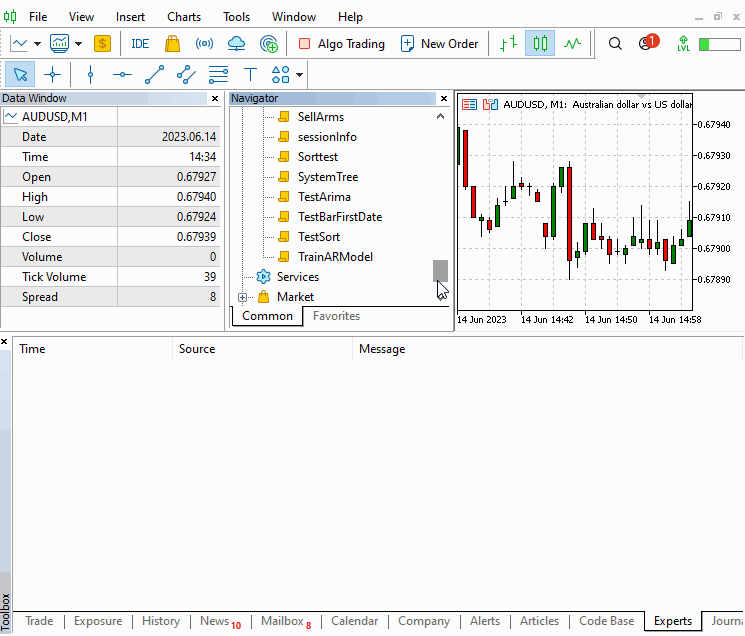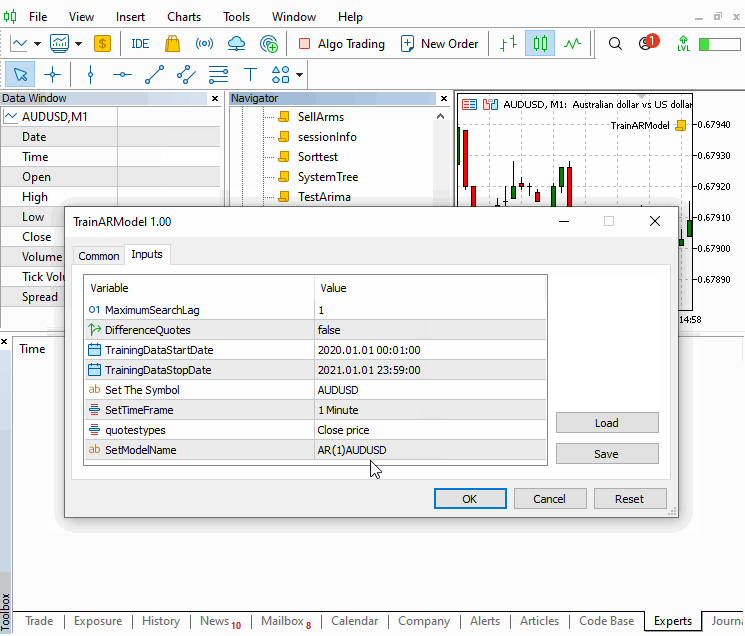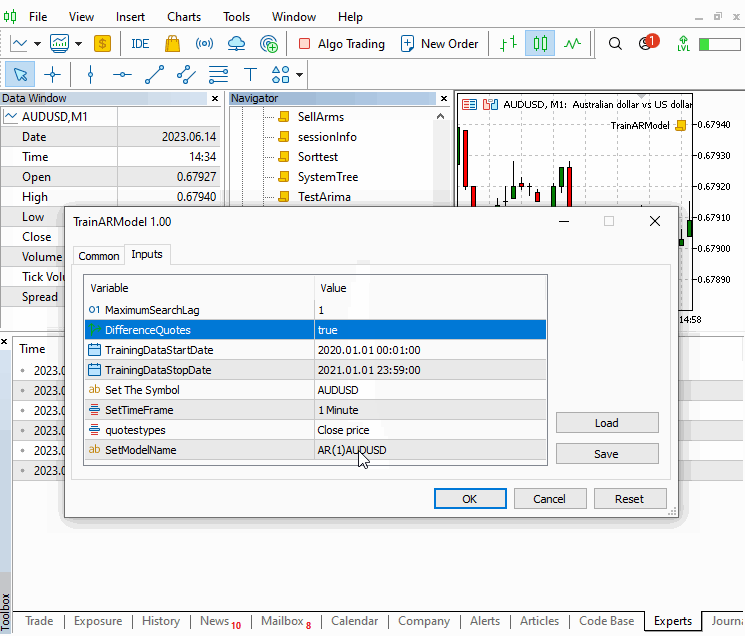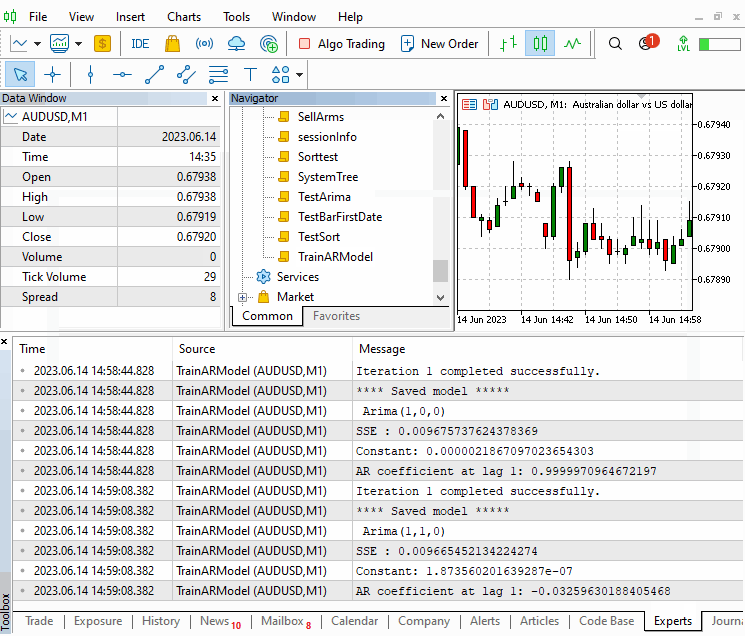
Das Skript ermöglicht die Einstellung der maximalen AR-Order, um die Suche zu beenden, sowie das Symbol, den Zeitrahmen und den Zeitraum der Preisstichproben-Daten. Es ist wichtig, eine Stichprobe aus Preisen zu verwenden, die für die Bedingungen repräsentativ ist, die bei der Anwendung des Modells zur Erstellung von Vorhersagen wahrscheinlich anzutreffen sind.

Gespeicherte Modellparameter angezeigt

Das Skript ermittelt das optimale Modell, indem es aus der Menge der trainierten Modelle dasjenige mit dem geringsten sse-Wert auswählt, das ausgewählte Modell speichert und seine Attribute auf dem Terminal ausgibt.

//+------------------------------------------------------------------+
//|                                         ArimaOneStepForecast.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_plots   1
#include<Arima.mqh>
//--- plot PredictedPrice
#property indicator_label1  "PredictedPrice"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input string   ModelName = "Model name";

//--- indicator buffers
uint     NumberOfPredictions=1;
double         PredictedPriceBuffer[];
double         forecast[];
double         pricebuffer[];
uint         modelinputs;

CArima arima;
double mj[];

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,PredictedPriceBuffer,INDICATOR_DATA);


   ArraySetAsSeries(PredictedPriceBuffer,true);

   if(!arima.LoadModel(ModelName))
      return(INIT_FAILED);
//---
   modelinputs=arima.GetMinModelInputs();

   ArrayResize(pricebuffer,modelinputs);

   ArrayResize(forecast,NumberOfPredictions);

   if(modelinputs<=0)
      return(INIT_FAILED);

   arima.Summary();

   arima.GetModelParameters(mj);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   int limit = (prev_calculated<=0)?1000-(int)modelinputs-1:rates_total-prev_calculated+1;

   if(NewBar(time[0]))
     {
      for(int i = limit; i>=0; i--)
        {
         if(CopyClose(_Symbol,_Period,i+1,modelinputs,pricebuffer)==modelinputs)
            if(arima.Predict(NumberOfPredictions,pricebuffer,forecast))
               PredictedPriceBuffer[i]=forecast[NumberOfPredictions-1];
        }
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool NewBar(datetime c_time)
  {
   static datetime prev_time;

   if(c_time>prev_time)
     {
      prev_time=c_time;
      return true;
     }

   return false;
  }
//+------------------------------------------------------------------+

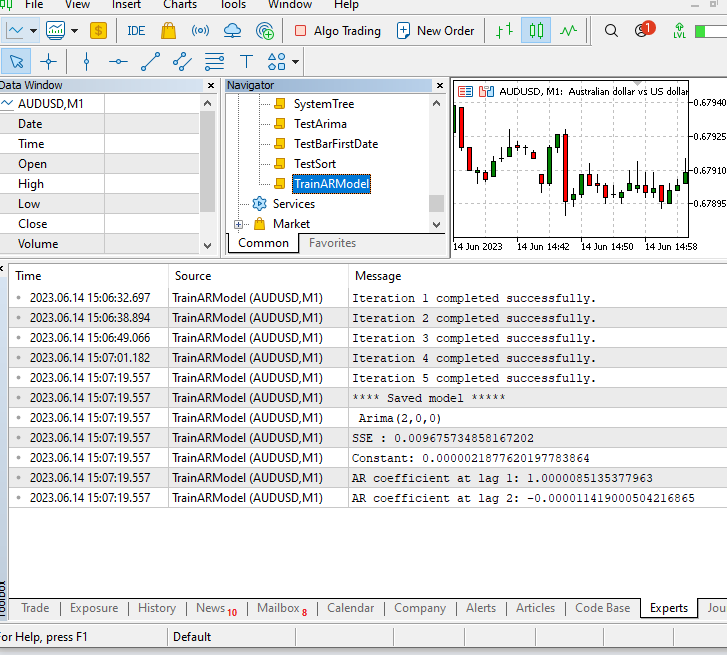
Der Indikator verwendet das ausgewählte Modell, um eine Vorhersage für den nächsten Schritt zu machen.

Indikator

Das angegebene Modell wird bei der Initialisierung des Indikators geladen. Die Predict-Methode wird dann in der Hauptindikatorschleife verwendet, um Vorhersagen auf der Grundlage der gelieferten Schlusskurseingaben zu treffen.

//+------------------------------------------------------------------+
//|                                               ArForecasterEA.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include <Arima.mqh>
//---
input string ModelName   ="model name"; // Saved Arima model name
input long   InpMagicNumber = 87383;
input double InpLots          =0.1; // Lots
input int    InpTakeProfit    =40;  // Take Profit (in pips)
input int    InpTrailingStop  =30;  // Trailing Stop Level (in pips)

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int    InpOpenThreshold =1; // Differential to trigger trade (in points)
int    InpStopLoss     = 0;//   Stoploss (in pips)

//---
//+------------------------------------------------------------------+
//| ARIMA Sample expert class                                         |
//+------------------------------------------------------------------+
class CArExpert
  {
protected:
   double            m_adjusted_point;             // point value adjusted for 3 or 5 points
   CTrade            m_trade;                      // trading object
   CSymbolInfo       m_symbol;                     // symbol info object
   CPositionInfo     m_position;                   // trade position object
   CAccountInfo      m_account;                    // account info wrapper
   CArima            *m_arima;                      // Arma object pointer
   uint              m_inputs;                     // Minimum number of inputs for Arma model
   //--- indicator buffers
   double            m_buffer[];                   // close prices buffer
   double            m_pbuffer[1];                 // predicted close prices go here


   //---
   double            m_open_level;


   double            m_traling_stop;
   double            m_take_profit;
   double            m_stop_loss;

public:
                     CArExpert(void);
                    ~CArExpert(void);
   bool              Init(void);
   void              Deinit(void);
   void              OnTick(void);

protected:
   bool              InitCheckParameters(const int digits_adjust);
   bool              InitModel(void);
   bool              CheckForOpen(void);
   bool              LongModified(void);
   bool              ShortModified(void);
   bool              LongOpened(void);
   bool              ShortOpened(void);
  };

Der Expert Advisor wendet wiederum das gespeicherte Modell an, um eine einfache Strategie umzusetzen. Auf der Grundlage der Vorhersage des nächsten Balkens kaufen wir, wenn der prognostizierte Schlusskurs größer ist als der letzte bekannte Schlusskurs. Und verkaufen, wenn die Prognose nach unten zeigt.

Ergebnisse des Backtests

Dies ist nur eine einfache Demonstration, die nicht für den Handel mit einem Live-Konto verwendet werden sollte.

Der Code für die komplette CArima-Klasse und ihre Abhängigkeiten sind in der Zip-Datei enthalten, die am Ende des Artikels angehängt ist, zusammen mit dem Skript, dem Indikator und dem EA, die im Artikel beschrieben werden.

Schlussfolgerung

Autoregressive Modelle lassen sich mit dem MT5-Terminal leicht trainieren und in allen möglichen Programmen anwenden. Der schwierige Teil ist die Modellspezifikation und -auswahl. Um diese Herausforderungen zu meistern und effektive autoregressive Modelle für die Forex-Analyse zu erstellen, sollten Händler einige bewährte Verfahren befolgen. Dazu gehören:

Beginnen Sie mit einer klaren Forschungsfrage: Vor der Erstellung eines autoregressiven Modells sollten die Händler eine klare Forschungsfrage und eine Hypothese definieren, die sie testen wollen. Dies trägt dazu bei, dass der Modellierungsprozess zielgerichtet und relevant für die Ziele des Händlers bleibt.

Sammeln Sie hochwertige Daten: Die Genauigkeit des Modells hängt weitgehend von der Qualität der verwendeten Daten ab. Die Händler sollten zuverlässige Datenquellen verwenden und sicherstellen, dass die Daten sauber, vollständig und für ihre Forschungsfrage relevant sind.

Testen Sie mehrere Modelle: Händler sollten mehrere Modelle mit unterschiedlichen Verzögerungen (lag) und Parametern testen, um das genaueste und effektivste Modell für ihre Daten zu ermitteln.

Validieren Sie das Modell: Sobald ein Modell erstellt wurde, sollten die Händler dessen Genauigkeit mit Hilfe statistischer Verfahren validieren.

Überwachung und Anpassung des Modells: Da sich die Marktbedingungen im Laufe der Zeit ändern, kann sich auch die Wirksamkeit des Modells ändern. Händler sollten die Leistung ihres Modells im Laufe der Zeit überwachen und bei Bedarf Anpassungen vornehmen, um sicherzustellen, dass es weiterhin genaue Erkenntnisse über künftige Kursbewegungen liefert.

Wenn Händler diese bewährten Verfahren befolgen, können sie effektive autoregressive Modelle für die Forex-Analyse erstellen und wertvolle Einblicke in zukünftige Markttrends gewinnen. Ich hoffe, dass der Code andere Nutzer weiter bringt und sie vielleicht dazu inspiriert, die Bibliothek weiter auszubauen. Viel Glück.

Datei	Beschreibung
Mql5/include/Powells.mqh	Include-Datei mit Erklärung und Definition der Klasse CPowellsMethod
Mql5/include/Arima.mqh	Include-Datei für die CArima-Klasse
Mql5/indicator/ArimaOneStepForecast.mql5	Indikator-Quellcode, der zeigt, wie man ein Modell in einen Indikator lädt und anwendet
Mql5/scripts/TrainARModel.mql5	Skript, das zeigt, wie man ein Modell trainiert und zur späteren Verwendung speichert
Mql5/experts/ArForecasterEA.mql5	Expert Advisor, der die Verwendung eines gespeicherten Modells in einem EA zeigt.

Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/12798

Beigefügte Dateien |

ZIP herunterladen

Arima.mqh (22.87 KB)

Powells.mqh (17.57 KB)

ArForecasterEA.mq5 (14.83 KB)

ArimaOneStepForecast.mq5 (3.48 KB)

TrainARModel.mq5 (2.77 KB)

Mql5.zip (12.64 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Zyklusanalyse mit dem Goertzel-Algorithmus

In diesem Artikel stellen wir Code-Utilities vor, die den Goertzel-Algorithmus in Mql5 implementieren, und untersuchen zwei Möglichkeiten, wie die Technik bei der Analyse von Kursen für die Entwicklung möglicher Strategien eingesetzt werden kann.

Wie man ein erfolgreicher Signalanbieter auf MQL5.com wird

Mein Hauptziel in diesem Artikel ist es, Ihnen eine einfache und genaue Beschreibung der Schritte zu geben, die Ihnen helfen werden, ein Top-Signalanbieter auf MQL5.com zu werden. Auf der Grundlage meines Wissens und meiner Erfahrung werde ich erklären, was nötig ist, um ein erfolgreicher Signalanbieter zu werden, und wie man eine gute Strategie findet, testet und optimiert. Darüber hinaus gebe ich Tipps zur Veröffentlichung Ihres Signals, zum Verfassen einer überzeugenden Beschreibung und zur effektiven Werbung und Verwaltung des Signals.

Die Wiederaufnahme einer alten Trendhandelsstrategie: Zwei Stochastik-Oszillatoren, ein MA und Fibonacci

Eine alte Handelsstrategie. In diesem Artikel wird eine der Strategien vorgestellt, mit denen sich der Trend auf rein technische Weise verfolgen lässt. Die Strategie ist rein technisch und verwendet einige technische Indikatoren und Werkzeuge, um Signale und Ziele zu liefern. Die Komponenten der Strategie sind wie folgt: Ein stochastischer Oszillator mit 14 Perioden. Ein 5-Perioden-Stochastik-Oszillator. Ein gleitender 200-Perioden-Durchschnitt. Ein Werkzeug zur Fibonacci-Projektion (für die Festlegung von Zielen).

Verbessern Sie Ihre Handelscharts mit interaktiven GUIs in MQL5 (Teil I): Bewegliche GUsI (I)

Entfesseln Sie die Macht der dynamischen Datendarstellung in Ihren Handelsstrategien oder Dienstprogrammen mit unserem umfassenden Leitfaden zur Erstellung beweglicher GUIs in MQL5. Tauchen Sie ein in das Kernkonzept von Chartereignissen und lernen Sie, wie Sie einfache und mehrfach bewegliche GUI auf demselben Chart entwerfen und implementieren. Dieser Artikel befasst sich auch mit dem Hinzufügen von Elementen zu Ihrer grafischen Nutzeroberfläche, um deren Funktionsweise und Ästhetik zu verbessern.