Zyklusanalyse mit dem Goertzel-Algorithmus
451
0
Einführung
Der Goertzel-Algorithmus ist eine digitale Signalverarbeitungstechnik, die für ihre Effizienz bei der Erkennung bestimmter Frequenzkomponenten bekannt ist. Dank seiner Präzision, Echtzeitfähigkeit und Recheneffizienz eignet es sich für die Analyse von Finanzzeitreihen. In diesem Artikel werden wir praktische Möglichkeiten untersuchen und aufzeigen, wie die Methode zur Analyse der vorherrschenden Zyklen für eine mögliche Strategieentwicklung eingesetzt werden kann. Wir werden einen Blick auf die Implementierung des Algorithmus in MQL5 werfen und ein Beispiel für die Verwendung des Codes zur Identifizierung von Zyklen in Preisnotierungen vorstellen.
Der Goertzel-Algorithmus
Der Goertzel-Algorithmus, der seinen Namen von Gerald Goertzel hat, wird verwendet, um einzelne Terme der Diskreten Fourier-Transformation (DFT) effizient zu berechnen. Der Goertzel-Algorithmus wird in erster Linie zur Identifizierung spezifischer Frequenzkomponenten innerhalb eines digitalen Signals eingesetzt, was ihn in Szenarien, in denen nur wenige Frequenzkomponenten wichtig sind, sehr wertvoll macht. Im Vergleich zur schnellen Fourier-Transformation (FFT) erfordert sie weniger Berechnungen bei der Erkennung einer begrenzten Anzahl von Frequenzkomponenten, was sie recheneffizient macht.
Sie wird durch die folgende Formel dargestellt:
Wobei:
- X ist die akkumulierte Größe bei der Frequenz k
- cos() ist die Kosinusfunktion
- π ist die mathematische Konstante pi (ungefähr 3,14159)
- k ist der Index des interessierenden Frequenzbereichs (von 0 bis N - 1, wobei N die Gesamtzahl der Stichproben ist)
- N ist die Länge des Eingangssignals
- X[k-1] und X[k-2] sind die zuvor berechneten Werte von X für die Frequenz bei k
- x[n] ist der n-te Abtastwert des Eingangssignals
Um die Real- und Imaginärkomponenten mit dem Goertzel-Algorithmus zu berechnen, müssen wir die Stichprobe der Eingangssignale durchlaufen und die folgenden Berechnungen durchführen:
- N : Anzahl der Samples im Eingangssignal.
- k : Index des interessierenden Frequenzbereichs (0 <= k < N).
- omega : Frequenz, die dem gewünschten Frequenzbereich entspricht (2 * pi * k / N).
- coeff : In der Berechnung verwendeter Koeffizient (2 * cos(omega)).
- s_prev : Vorheriger Wert der Variablen „state“.
- s_prev2 : vorvorheriger Wert der Variablen „state“.
- s : Aktueller Wert der Variablen „state“.
-
Aktualisieren des aktuellen Werts der Variablen „state“ ( s ) anhand der Formel:
wobei x[n] die aktuelle Eingabeprobe ist.
Aktualisieren der vorherigen Werte der Variablen „state“:
Nach der Iteration durch alle Stichproben stellen die endgültigen Werte der Variablen „state“ (S, Sprev, Sprev2) die realen und imaginären Komponenten der DFT im gewünschten Frequenzbereich (k) dar.
Die reale Komponente ist gegeben durch:
Die imaginäre Komponente ist gegeben durch:
Die Frequenzen, die mit der DFT ermittelt werden können, reichen von 1/N bis (N/2)/N, wobei N die Anzahl der Datenpunkte in der Reihe oder in unserem Fall die Anzahl der analysierten Kursbalken darstellt. Bei der Analyse von Kursen kann es einschränkend sein, nur Frequenzbänder zu beobachten, die auf den 1/N-Abstand beschränkt sind. Aus diesem Grund hat J. Ehlers die Maximum-Entropie-Spektralanalyse (MESA) vorgeschlagen, um diese Einschränkung zu überwinden.
Der Goertzel-Algorithmus kann als Alternative zu Ehlers MESA verwendet werden, der laut einer von D. Meyers verfassten Forschungsarbeit unter bestimmten Bedingungen bessere Ergebnisse (in Bezug auf die spektrale Auflösung) erzielen kann. Eine dieser Bedingungen bezieht sich zufällig auf den Rauschanteil im Signal. Laut Meyers ist der Goertzel-Algorithmus in der Lage, die MESA-Technik zu übertreffen, insbesondere wenn es um verrauschte Signale geht, was ein häufiges Problem bei finanziellen Zeitreihen ist. Interessierte Leser können das Whitepaper im pdf-Format lesen.
Die Klasse CGoertzel
Die Klasse CGoertzel ist eine einfache Implementierung des Goertzel-Algorithmus, die es ermöglicht, einen Bereich von Frequenzen in einem Datensatz abzutasten.
//+------------------------------------------------------------------+ //| CGoertze class implementing Goertzel algorithm | //+------------------------------------------------------------------+ class CGoertzel { private: uint m_minPeriod; uint m_maxPeriod; public: //constructor CGoertzel(void) { m_minPeriod=m_maxPeriod=0; } //destructor ~CGoertzel(void) { } //get methods uint GetMinPeriodLength(void) { return m_minPeriod;} uint GetMaxPerodLength(void) { return m_maxPeriod;} //set methods bool SetMinMaxPeriodLength(const uint min_wavePeriod, const uint max_wavePeriod); // goertzel dft transform methods bool Dft(const double &in_data[],complex &out[]); bool Dft(const double &in_data[], double &out_real[], double &out_imaginary[]); bool Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]); bool Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]); };
Da der Goertzel nur eine begrenzte Anzahl von Frequenzen auf einmal abtastet, müssen wir das Frequenzband festlegen, an dem wir interessiert sind. In der Klasse wird das Frequenzband in Form der minimalen und maximalen Periode der Frequenzen festgelegt.
Es gibt zwei Möglichkeiten, diese Werte einzustellen: Mit der Funktion SetMinMaxPeriodLength() können die Mindest- und Höchstzeiträume festgelegt werden.
//+------------------------------------------------------------------+ //| Set the Minimum and maximum periods of selected frequency band | //+------------------------------------------------------------------+ bool CGoertzel::SetMinMaxPeriodLength(const uint min_wavePeriod,const uint max_wavePeriod) { if(min_wavePeriod<2 || min_wavePeriod>=max_wavePeriod) { Print("Critical error min_wavePeriod cannot be less than max_wavePeriod or less than 2"); return false; } m_minPeriod=min_wavePeriod; m_maxPeriod=max_wavePeriod; return true; }
Auch das Frequenzband kann beim Aufruf einer der beiden Überladungen der Methode Dft festgelegt werden.
//+-----------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as complex array | //+-----------------------------------------------------------------------------------+ bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]) { if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod)) return(false); return Dft(in_data,out); } //+------------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as two separate arrays| //+------------------------------------------------------------------------------------+ bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]) { if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod)) return(false); return Dft(in_data,out_real,out_imaginary); }
Je nach der verwendeten Version der Dft-Methode werden die realen und imaginären Komponenten des Dft entweder in getrennten Arrays oder in einem einzigen Array vom Typ komplex ausgegeben.
//+-----------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as complex array | //+-----------------------------------------------------------------------------------+ bool CGoertzel::Dft(const double &in_data[],complex &out[]) { uint minsize=(3*m_maxPeriod); uint fullsize=in_data.Size(); if(fullsize<minsize) { Print("Sample size too small in relation to the largest period cycle parameter"); return false; } if(m_minPeriod>=m_maxPeriod || m_minPeriod<2) { Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2"); return false; } if(out.Size()!=m_maxPeriod) ArrayResize(out,m_maxPeriod); double v0,v1,v2,freq,coeff,real,imag; for(uint i=0; i<m_maxPeriod; i++) { if(i<m_minPeriod) { out[i].imag=out[i].real=0.0; continue; } v0=v1=v2=0.0; freq=MathPow(i,-1); coeff=2.0*MathCos(2.0*M_PI*freq); for(uint k=minsize-1; k>0; k--) { v0=coeff*v1-v2+in_data[k]; v2=v1; v1=v0; } real=v1-v2*0.5*coeff; imag=v2*MathSin(2*M_PI*freq); out[i].real=real; out[i].imag=imag; } return true; } //+------------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as two separate arrays| //+------------------------------------------------------------------------------------+ bool CGoertzel::Dft(const double &in_data[],double &out_real[],double &out_imaginary[]) { uint minsize=(3*m_maxPeriod); uint fullsize=in_data.Size(); if(fullsize<minsize) { Print("Sample size too small in relation to the largest period cycle parameter"); return false; } if(m_minPeriod>=m_maxPeriod || m_minPeriod<2) { Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2"); return false; } if(out_real.Size()!=m_maxPeriod) ArrayResize(out_real,m_maxPeriod); if(out_imaginary.Size()!=m_maxPeriod) ArrayResize(out_imaginary,m_maxPeriod); double v0,v1,v2,freq,coeff,real,imag; for(uint i=0; i<m_maxPeriod; i++) { if(i<m_minPeriod) { out_real[i]=out_imaginary[i]=0.0; continue; } v0=v1=v2=0.0; freq=MathPow(i,-1); coeff=2.0*MathCos(2.0*M_PI*freq); for(uint k=minsize-1; k>0; k--) { v0=coeff*v1-v2+in_data[k]; v2=v1; v1=v0; } real=v1-v2*0.5*coeff; imag=v2*MathSin(2*M_PI*freq); out_real[i]=real; out_imaginary[i]=imag; } return true; }
Vorverarbeitung
Daten lassen sich nicht immer einfach in den Goertzel-Algorithmus einfügen und in den Frequenzbereich transformieren. Je nach Art der Datenprobe können einige Vorverarbeitungsschritte erforderlich sein. Der Goertzel-Algorithmus ist eine Teilmenge des dft und daher gelten die vor der Durchführung einer schnellen Fourier-Transformation erforderlichen Transformationen auch hier. Dies gilt insbesondere für Daten, die nicht periodisch sind. Solche Reihen müssen mit einer geeigneten Fensterfunktion behandelt werden. Dadurch werden die Enden der Reihe angemessen verkleinert, was die Möglichkeit eines spektralen Lecks minimiert. Die meisten Anwendungen des Goertzels in der Literatur verwenden einen Algorithmus zur Abflachung der Endpunkte. Die Umsetzung dieser Technik ist durch die Formel gegeben:
wobei a der erste Preiswert in der zu analysierenden Reihe ist , b der letzte, flat(i) ist die Reihe, die an den Goertzel-Algorithmus übergeben wird.
Vor der Fensterung der Daten empfiehlt es sich, alle offensichtlichen Trends und Ausreißer zu entfernen. Die Rohdaten sollten nur dann vom Trend bereinigt werden, wenn dies notwendig ist, denn eine ungerechtfertigte Trendbereinigung kann zu Verzerrungen führen, die sich auf die Darstellung der Probe im Frequenzbereich auswirken. Trendbereinigung ist ein umfangreiches Thema, und es gibt zahlreiche Arten von Trendbereinigungen, die angewendet werden können. Jede hat ihre eigenen Vor- und Nachteile. Die Praktiker sollten sich die Mühe machen, die am besten geeignete Methode gründlich zu untersuchen. Für die Zwecke dieses Artikels werden wir eine einfache Anpassung nach der Methode der kleinsten Quadrate verwenden, um die Kursnotierungen zu entzerren. Der Code ist unten abgebildet.
//+------------------------------------------------------------------+ //| helper method for detrending data | //+------------------------------------------------------------------+ void CGoertzelCycle::detrend(const double &in_data[], double &out_data[]) { uint i ; double xmean, ymean, x, y, xy, xx ; xmean=ymean=x=y=xx=xy=0.0; xmean=0.5*double(in_data.Size()-1); if(out_data.Size()!=in_data.Size()) ArrayResize(out_data,in_data.Size()); for(i=0; i<out_data.Size(); i++) { x = double(i) - xmean ; y = in_data[i] - ymean ; xx += x * x ; xy += x * y ; } m_slope=xy/xx; m_pivot=xmean; for(i=0; i<out_data.Size(); i++) out_data[i]=in_data[i]-(double(i)-xmean)*m_slope; }
Die Klasse CGoertzelCycle
Die Include-Datei GoertzelCycle.mqh enthält die Klasse CGoertzelCycle, die zur Durchführung von Zyklusanalysen von Datensätzen mit dem Goertzel-Algorithmus verwendet wird.
//+------------------------------------------------------------------+ //| CGoertzelCycle class for cycle using the Goertzel Algorithm | //+------------------------------------------------------------------+ class CGoertzelCycle { private: CGoertzel*m_ga; double m_pivot; double m_slope; bool m_detrend; bool m_squaredamp; bool m_flatten; uint m_cycles; uint m_maxper,m_minper; double m_amplitude[]; double m_peaks[]; double m_cycle[]; double m_phase[]; uint m_peaks_index[]; double m_detrended[]; double m_flattened[]; double m_raw[]; void detrend(const double &in_data[], double &out_data[]); double wavepoint(bool use_cycle_strength,uint max_cycles); bool spectrum(const double &in_data[],int shift=-1); uint cyclepeaks(bool use_cycle_strength); public : CGoertzelCycle(void); CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period); ~CGoertzelCycle(void); bool GetSpectrum(const double &in_data[],double &out_amplitude[]); bool GetSpectrum(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]); uint GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]); uint GetDominantCycles(bool use_cycle_strenght,bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_cycles[]); void CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]); void CalculateWave(uint prev,uint total,uint max_cycles, bool use_cycle_strength,const double &in_data[], double &out_signal[]); };
Sie hat zwei Konstruktoren. Der parametrisierte Konstruktor ermöglicht die Initialisierung einer Instanz mit benutzerdefinierten Einstellungen.
//+------------------------------------------------------------------+ //| Default Constructor | //+------------------------------------------------------------------+ CGoertzelCycle::CGoertzelCycle(void) { m_pivot=m_slope=0.0; m_maxper=m_minper=m_cycles=0; m_detrend=m_squaredamp=m_flatten=false; m_ga=new CGoertzel(); } //+------------------------------------------------------------------+ //| Parametric Constructor | //+------------------------------------------------------------------+ CGoertzelCycle::CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period) { m_pivot=m_slope=0.0; m_cycles=0; m_maxper=max_period; m_minper=min_period; m_detrend=detrend; m_squaredamp=squared_amp; m_flatten=apply_window; m_ga=new CGoertzel(); if(m_maxper) { ArrayResize(m_amplitude,m_maxper); ArrayResize(m_phase,m_maxper); ArrayResize(m_cycle,m_maxper); ArrayResize(m_peaks,m_maxper); ArrayResize(m_peaks_index,m_maxper); } }
Die Eingabeparameter sind unten angegeben:
- detrend - eine boolesche Eingabe, die angibt, dass der Trend entfernt werden muss.
- apply_window - ein weiterer boolescher Parameter, der angibt, ob eine Funktion zur Fensterbildung angewendet werden soll oder nicht.
- min_period - dieser Parameter legt die kürzeste Periode oder die höchste Frequenz fest, die vom Goertzel-Algorithmus aufgelöst wird; bitte beachten Sie, dass dieser Wert nicht unter 2 gesetzt werden kann.
- max_period - die längste Periode, die bei der Analyse berücksichtigt wird; dieser Wert stellt die Häufigkeit mit der längsten Periode dar, er kann nicht kleiner oder gleich min_period sein.
- squard_amp - gibt an, wie der Amplitudenwert dargestellt werden soll. Wenn Sie false wählen, wird die Amplitude als Quadratwurzel berechnet.
Die Klasse hat 6 verfügbare Methoden, die für die Nutzer von Interesse sein dürften.
//+-------------------------------------------------------------------+ //| public method to access the amplitude values | //+-------------------------------------------------------------------+ bool CGoertzelCycle::GetSpectrum(const double &in_data[],double &out_amplitude[]) { if(spectrum(in_data)) { ArrayCopy(out_amplitude,m_amplitude); return true; } return false; }
GetSpectrum() benötigt 2 Eingabe-Arrays, von denen das erste in_data die zu analysierende Rohreihe ist. Das zweite Array enthält die Amplitudenwerte, die ausgegeben werden. Die für die Transformation verwendeten Parameter sollten durch Initialisierung einer Instanz mit dem parametrisierten Konstruktor angegeben werden.
//+------------------------------------------------------------------+ //| public method to access the amplitude values | //+------------------------------------------------------------------+ bool CGoertzelCycle::GetSpectrum(bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]) { m_pivot=m_slope=0.0; m_cycles=0; m_maxper=max_period; m_minper=min_period; m_detrend=detrend; m_squaredamp=squared_amp; m_flatten=apply_window; if(m_maxper) { ArrayResize(m_amplitude,m_maxper); ArrayResize(m_phase,m_maxper); ArrayResize(m_cycle,m_maxper); ArrayResize(m_peaks,m_maxper); ArrayResize(m_peaks_index,m_maxper); } if(spectrum(in_data)) { ArrayCopy(out_amplitude,m_amplitude); return true; } return false; }
Die andere überladene Methode GetSpectrum() nimmt zusätzliche Parameter entgegen, die mit denen des parametrisierten Konstruktors identisch sind. Beide geben bei Erfolg true und bei einem Fehler false zurück, wobei alle Fehlerdaten in das Journal des Terminals geschrieben werden.
//+----------------------------------------------------------------------------+ //|public method to get the dominant cycle periods arranged in descending order| //+----------------------------------------------------------------------------+ uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]) { if(!spectrum(in_data)) { ArrayInitialize(out_cycles,0.0); return(0); } cyclepeaks(use_cycle_strength); if(out_cycles.Size()!=m_cycles) ArrayResize(out_cycles,m_cycles); for(uint i=0; i<m_cycles; i++) out_cycles[i]=m_cycle[m_peaks_index[i]]; return m_cycles; } //+----------------------------------------------------------------------------+ //|public method to get the dominant cycle periods arranged in descending order| //+----------------------------------------------------------------------------+ uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_cycles[]) { m_pivot=m_slope=0.0; m_cycles=0; m_maxper=max_period; m_minper=min_period; m_detrend=detrend; m_squaredamp=squared_amp; m_flatten=apply_window; if(m_maxper) { ArrayResize(m_amplitude,m_maxper); ArrayResize(m_phase,m_maxper); ArrayResize(m_cycle,m_maxper); ArrayResize(m_peaks,m_maxper); ArrayResize(m_peaks_index,m_maxper); } return(GetDominantCycles(use_cycle_strength,in_data,out_cycles)); }
Die Methode GetDominantCycle() wird in ähnlicher Weise überladen wie GetSpectrum(). Neben den 2 Arrays muss ein boolescher Parameter use_cycle_strength angegeben werden. Die Einstellung false bedeutet, dass die Frequenzen mit den größten Amplituden verwendet werden, während die Alternative den dominanten Zyklus durch Berechnung der Zyklusstärke nach der Formel bestimmt:
Die vorherrschenden Zyklen werden in das letzte der Eingabefelder ausgegeben, wobei die Werte in absteigender Reihenfolge angeordnet sind.
//+-----------------------------------------------------------------------+ //|method used to access calculated dominant cycles , for use in indcators| //+-----------------------------------------------------------------------+ void CGoertzelCycle::CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]) { uint limit =0; bool indexOut=ArrayGetAsSeries(out_signal); bool indexIn=ArrayGetAsSeries(in_data); if(prev<=0) { uint firstindex=0; if(indexOut) { limit=total-(m_maxper*3); firstindex=limit+1; } else { limit=m_maxper*3; firstindex=limit-1; } out_signal[firstindex]=0; } else { limit=(indexOut)?total-prev:prev; } uint found_cycles=0; if(indexOut) { for(int ibar=(int)limit; ibar>=0; ibar--) { spectrum(in_data,(indexIn)?ibar:total-ibar-1); out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0; } } else { for(int ibar=(int)limit; ibar<(int)total; ibar++) { spectrum(in_data,(indexIn)?total-ibar-1:ibar); out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0; } } }
Die Methoden mit dem Präfix Calculate sollten idealerweise in Indikatoren verwendet werden. CalculateDominantCycles() gibt die dominanten Zyklen für einen entsprechenden Balken aus, prev sollte auf die Anzahl der zuvor berechneten Indikatorwerte gesetzt werden, total sollte die Anzahl der verfügbaren Balken auf dem Chart sein, in_data ist der Ort, an dem man die Kursnotierungen übergeben würde und out_signal sollte einer der Indikatorpuffer sein.
//+-----------------------------------------------------------------------+ //|method used to access newly formed wave form, for use in indcators | //+-----------------------------------------------------------------------+ void CGoertzelCycle::CalculateWave(uint prev,uint total,uint max_cycles,bool use_cycle_strength,const double &in_data[], double &out_signal[]) { uint limit =0; bool indexOut=ArrayGetAsSeries(out_signal); bool indexIn=ArrayGetAsSeries(in_data); if(prev<=0) { uint firstindex=0; if(indexOut) { limit=total-(m_maxper*3); firstindex=limit+1; } else { limit=m_maxper*3; firstindex=limit-1; } out_signal[firstindex]=0; } else { limit=(indexOut)?total-prev:prev; } uint found_cycles=0; if(indexOut) { for(int ibar=(int)limit; ibar>=0; ibar--) { spectrum(in_data,(indexIn)?ibar:total-ibar-1); out_signal[ibar]=out_signal[ibar+1]+wavepoint(use_cycle_strength,max_cycles); } } else { for(int ibar=(int)limit; ibar<(int)total; ibar++) { spectrum(in_data,(indexIn)?total-ibar-1:ibar); out_signal[ibar]=out_signal[ibar-1]+wavepoint(use_cycle_strength,max_cycles); } } } //+------------------------------------------------------------------+
CalculateWave() hat die meisten seiner Parameter mit CalculateDominantCycles() gemeinsam. Er gibt einen gefilterten Wert aus, der aus den vom Goertzel-Algorithmus ermittelten dominanten Frequenzkomponenten berechnet wird. Die maximale Anzahl der Frequenzkomponenten wird durch den Parameter max_cycles festgelegt.
Konstruktion der Wellenform
Demonstration sowohl der Verwendung der Klasse als auch der möglichen Anwendungen des Goertzels in der Strategieentwicklung. Wir werden zwei Indikatoren vorstellen. Bei der ersten handelt es sich um die Umsetzung einer Strategie, die in dem von Dennis Meyers verfassten Artikel The Adaptive 10 Cycle Goertzel DFT System vorgestellt wurde. Er nennt diese Strategie das adaptive 10-Zyklen-Goertzel-DFT-System. Genaue Einzelheiten über die Strategie sind in dem Dokument zu finden. Kurz gesagt verwendet die Strategie den Goertzel, um die zehn wichtigsten Zyklen aus einem gleitenden Fenster von Preisdaten zu extrahieren, und verwendet dann diese Zyklen, um eine neue Preiskurve zu konstruieren. Dieser stellt angeblich das Verhalten des Preises dar, wenn das Rauschen herausgefiltert wird. Die wichtigsten Parameter dieser Strategie sind die Mindest- und Höchstdauer der abzutastenden Frequenzen. Zusammen mit der maximalen Anzahl von Frequenzkomponenten, die für die Konstruktion des gefilterten Signals verwendet werden sollen.
//--- input parameters input bool Detrend=true; input bool EndFlatten=true; input bool SquaredAmp=true; input bool UseCycleStrength=false; input uint Maxper=72; input uint Minper=5; input uint MaxCycles=10; input double pntup=0.5;//Percent increase threshold input double pntdn=0.5;//Percent decrease threshold //--- indicator buffers
Der Indikator verwendet zwei Schwellenwerte, um Kauf- und Verkaufssignale auszulösen, die von der Größe einer Bewegung im Verhältnis zu einem kürzlichen Höchst- oder Tiefststand abhängen. Im Code stellen die Eingabevariablen pntup und pntdn Prozentsätze dar.
//+------------------------------------------------------------------+ //| NCycleGoertzelDft.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<GoertzelCycle.mqh> #property indicator_separate_window #property indicator_buffers 5 #property indicator_plots 5 //--- plot Wave #property indicator_label1 "Wave" #property indicator_type1 DRAW_LINE #property indicator_color1 clrBlack #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- plot Up #property indicator_label2 "Peak" #property indicator_type2 DRAW_NONE //--- plot Dwn #property indicator_label3 "Trough" #property indicator_type3 DRAW_NONE //--- plot Up #property indicator_label4 "Long" #property indicator_type4 DRAW_LINE #property indicator_color4 clrBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 2 //--- plot Dwn #property indicator_label5 "Short" #property indicator_type5 DRAW_LINE #property indicator_color5 clrRed #property indicator_style5 STYLE_SOLID #property indicator_width5 2 //--- input parameters input bool Detrend=true; input bool EndFlatten=true; input bool SquaredAmp=true; input bool UseCycleStrength=false; input uint Maxper=72; input uint Minper=5; input uint MaxCycles=10; input double pntup=0.5;//Percent increase threshold input double pntdn=0.5;//Percent decrease threshold //--- indicator buffers double Wave[],Peak[],Trough[],Long[],Short[]; CGoertzelCycle *Gc; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,Wave,INDICATOR_DATA); SetIndexBuffer(1,Peak,INDICATOR_DATA); SetIndexBuffer(2,Trough,INDICATOR_DATA); SetIndexBuffer(3,Long,INDICATOR_DATA); SetIndexBuffer(4,Short,INDICATOR_DATA); //--- IndicatorSetInteger(INDICATOR_DIGITS,5); //--- PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(2,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(3,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(4,PLOT_EMPTY_VALUE,0.0); //--- Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper); if(Gc==NULL) { Print("Invalid Goertzel object"); return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Indicator DeInitialization function | //+------------------------------------------------------------------+ void OnDeinit (const int reason) { if(CheckPointer(Gc)==POINTER_DYNAMIC) delete Gc; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { int lim=0; if(prev_calculated<=0) lim=(int)(Maxper*3)+2; else lim=prev_calculated; //--- Gc.CalculateWave(prev_calculated,rates_total,MaxCycles,UseCycleStrength,price,Wave); //--- for(int i=lim;i<rates_total-1;i++) { Peak[i]=Trough[i]=0.0; if(Wave[i]>Wave[i+1] && Wave[i]>Wave[i-1]) Peak[i]=Wave[i]; else if(Wave[i]<Wave[i+1] && Wave[i]<Wave[i-1]) Trough[i]=Wave[i]; if(i<int(Maxper*3*2)) { continue; } double lp,lt; lp=lt=0; if(i==int(Maxper*3*2)) { lp=getlastPeakTrough(i,Peak); lt=getlastPeakTrough(i,Trough); if(Wave[i]>Wave[i-1] && lt) { Long[i]=Wave[i]; Short[i]=0.0; } else if(Wave[i]<Wave[i-1] && lp) { Short[i]=Wave[i]; Long[i]=0.0; } } else { Long[i]=(Long[i-1]!=0)?Wave[i]:Long[i-1]; Short[i]=(Short[i-1]!=0)?Wave[i]:Short[i-1]; if(Short[i-1]!=0 && Wave[i]>Wave[i-1]) { lt=getlastPeakTrough(i,Trough); if(lt && (Wave[i]-lt)/lt > pntup/100 ) { Long[i]=Wave[i]; Short[i]=0.0; } else { Short[i]=Wave[i]; Long[i]=0.0; } } else if(Long[i-1]!=0 && Wave[i]<Wave[i-1]) { lp=getlastPeakTrough(i,Peak); if(lp && (lp-Wave[i])/lp > pntdn/100 ) { Short[i]=Wave[i]; Long[i]=0.0; } else { Long[i]=Wave[i]; Short[i]=0.0; } } } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+ //| helper function that returns either last peak or trough | //+------------------------------------------------------------------+ double getlastPeakTrough(int shift, double &buffer[]) { uint j; double value=0.0; for(j=shift-1;j>(Maxper*3)+2;j--) { if(buffer[j]==0.0) continue; else return(buffer[j]); } return(value); } //+-----------------------------------------------------------------------------------------------++
Das Signal wird nach der folgenden Formel berechnet:
wobei a die Amplitude ist, phi die Phase, f die Frequenz, B die Anzahl der in der Vergangenheit abgetasteten Balken, die die Daten darstellen, aus denen die Frequenzkomponenten extrahiert werden, was der Größe des beweglichen Fensters entspricht. Dieser Wert ist gleich dem Dreifachen des betrachteten maximalen Periodendauerzyklus. Der Code für den Indikator ist oben abgebildet. Der Wellenpunkt ist der Wert der Kurve beim entsprechenden Index.
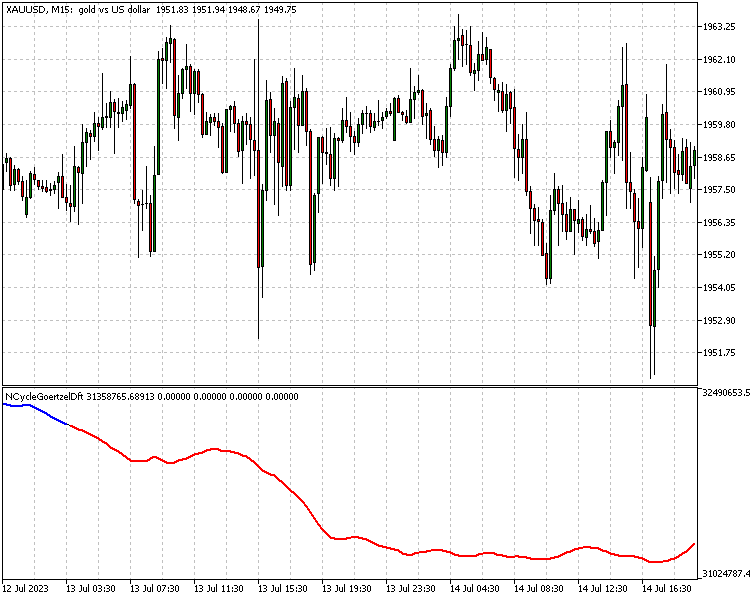
Mehr Einzelheiten zu den Handelsregeln finden Sie in dem Artikel, falls Sie daran interessiert sind.
Adaptive Indikatoren
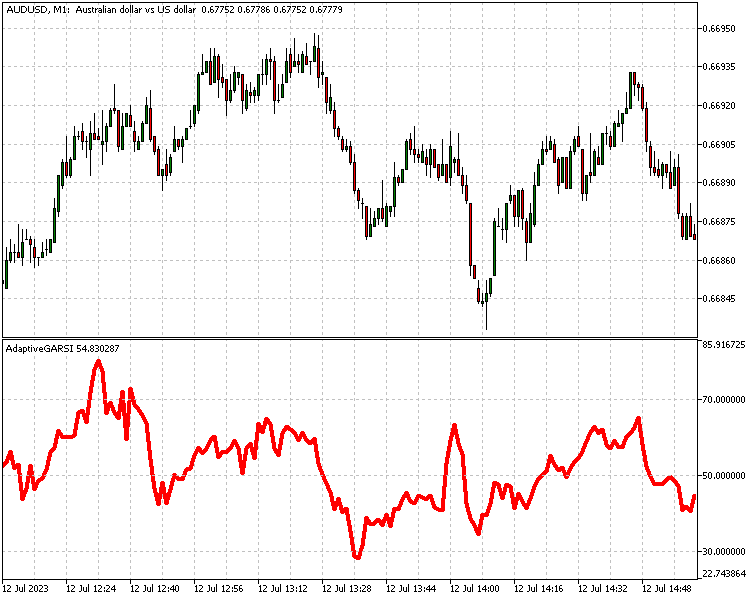
Eine weitere Möglichkeit, den Goertzel für die Strategieentwicklung zu nutzen, besteht darin, die Indikatoren anpassungsfähig zu machen. Der Artikel Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5 beschreibt diese Methode anhand der berühmten Techniken von J. Ehlers. Das Gleiche können wir mit dem Goertzel machen. Nachfolgend finden Sie eine Implementierung einer adaptiven Version des Relative-Stärke-Indikators.
//+------------------------------------------------------------------+ //| AdaptiveGARSI.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #include<GoertzelCycle.mqh> #property indicator_buffers 2 #property indicator_plots 1 //--- plot RSi #property indicator_label1 "RSi" #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- #property indicator_level1 70 #property indicator_level2 50 #property indicator_level3 30 //--- input bool Detrend=true; input bool EndFlatten=true; input bool SquaredAmp=true; input bool UseCycleStrength=false; input uint Maxper=72; input uint Minper=5; //--- indicator buffers double RSiBuffer[]; double DomPeriodBuffer[]; CGoertzelCycle *Gc; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,RSiBuffer,INDICATOR_DATA); SetIndexBuffer(1,DomPeriodBuffer,INDICATOR_CALCULATIONS); //--- Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper); //--- if(Gc==NULL) { Print("Invalid Goertzel object"); return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Indicator DeInitialization function | //+------------------------------------------------------------------+ void OnDeinit (const int reason) { if(CheckPointer(Gc)==POINTER_DYNAMIC) delete Gc; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- uint lim=0; //--- Gc.CalculateDominantCycles(prev_calculated,rates_total,UseCycleStrength,close,DomPeriodBuffer); //--- if(prev_calculated<=0) lim=int(Maxper*3)+int(DomPeriodBuffer[(Maxper*3)-1]) - 1; else lim=prev_calculated; //--- double cu,cd; for(int i =int(lim);i<rates_total;i++) { cd=0.0; cu=0.0; double p=DomPeriodBuffer[i]; int j=0; for(j=0;j<int(p);j++) { if(close[i-j]-close[i-j-1]>0)cu=cu+(close[i-j]-close[i-j-1]); if(close[i-j]-close[i-j-1]<0)cd=cd+(close[i-j-1]-close[i-j]); } if(cu+cd!=0) RSiBuffer[i]=100*cu/(cu+cd); else RSiBuffer[i]=0.0; } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Schlussfolgerung
Die Fähigkeiten des Goertzel-Algorithmus wurden zusammen mit nützlichen Code-Utilities für seine Anwendung deutlich demonstriert. Die Herausforderung besteht darin, diese Technik effektiv auf Finanzdaten anzuwenden und aussagekräftige Signale zu gewinnen. Die GA ist gegenüber der MESA-Technik eindeutig im Nachteil, da sie nur eine Frequenz auf einmal auflösen kann. Seine praktische Anwendung zeigt auch die Schwäche der Zykluserkennung auf den Finanzmärkten auf, da es schwierig ist, einen vorherrschenden Zyklus zu messen und genau zu bestimmen, wann er endet. Die Bewältigung dieser Schwierigkeiten erfordert eine Kombination aus Fachwissen, robusten Datenvorverarbeitungstechniken, Risikomanagementstrategien sowie eine kontinuierliche Überwachung und Anpassung an die sich verändernde Marktdynamik.
Die angehängte Zip-Datei enthält den gesamten im Artikel beschriebenen Quellcode.
| Dateiname | Beschreibung |
|---|---|
| Mql5/include/Goertzel.mqh | Include-Datei für die CGoertzel-Klasse, die den Goertzel-Algorithmus implementiert |
| Mql5/include/ GoertzelCycle.mqh | Include-Datei für die Klasse CGoertzelCycle zur Analyse von Zyklen mit dem Goertzel-Algorithmus |
| Mql5/indicators/ NCycleGoertzelDft.mq5 | Indikator, der teilweise eine von D. Meyers entwickelte Strategie umsetzt, die den Goertzel-Algorithmus verwendet |
| Mql5/indicators/ AdaptiveGARSI.mq5 | Implementierung einer adaptiven Version des Relative-Stärke-Indikators mit dynamischem Lookback, berechnet durch den Goertzel-Algorithmus |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/975
Die Wiederaufnahme einer alten Trendhandelsstrategie: Zwei Stochastik-Oszillatoren, ein MA und Fibonacci
Prognose mit ARIMA-Modellen in MQL5
Kann Heiken-Ashi in Kombination mit gleitenden Durchschnitten gute Signale liefern?
Wie man ein erfolgreicher Signalanbieter auf MQL5.com wird
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.