Experimente mit Neuronalen Netzen (Teil 4): Schablonen (Templates)

Ich würde meine Erfahrungen gerne öfter mit Ihnen teilen, aber wie Sie verstehen, erfordert eine solche Tätigkeit Zeit und Computerressourcen, die im Vergleich zu den gestellten Aufgaben leider sehr knapp bemessen sind.

In den vorangegangenen Artikeln (Teil 1, Teil 2, Teil 3) haben wir mit Formen und Winkeln experimentiert, deren Werte an das Perceptron und das auf der Grundlage der Bibliothek DeepNeuralNetwork.mqh aufgebaute Neuronale Netz übergeben wurden. Wir haben auch Experimente zu Optimierungsmethoden im Strategietester durchgeführt. Ich war nicht ganz zufrieden mit den Ergebnissen der Arbeit Neuronaler Netze, die auf der Bibliothek DeepNeuralNetwork.mqh basieren, sowie mit der langsamen Arbeit des in Teil 3 beschriebenen intelligenten Optimierungsalgorithmus. Die Ergebnisse eines einfachen Perceptrons erwiesen sich als besser als die eines Neuronalen Netzes. Vielleicht übergeben wir dem Neuronalen Netz für solche Aufgaben ungeeignete Daten, und sein Streubereich kann kein stabiles Ergebnis liefern. Darüber hinaus enthielten die Rückmeldungen zu früheren Artikeln Kritik am Verhältnis von TakeProfit zu StopLoss. All dies wurde bei den folgenden Experimenten berücksichtigt.

Bei meinen Recherchen stieß ich in unserem beliebten MQL5-Forum auf einen interessanten Algorithmus zur Musterverfolgung. Sein Wesen bestand darin, den Preis auf ein bestimmtes Muster zu bringen, um den Einstieg in eine Position zu bestimmen, wobei es nicht um seine Verwendung in Neuronalen Netzen ging.

Ich habe diese Schablonen „technology“ genannt. Ich weiß nicht, ob es richtig ist oder nicht, aber es schien mir das passendste Wort zu sein.

Eine wichtige Aufgabe in den aktuellen Experimenten war es, den Einfluss der Menge der übertragenen Daten und der Tiefe der Geschichte, aus der wir diese Daten nehmen, zu verfolgen. Außerdem mussten wir Muster aufdecken, ob kurze oder lange Schablonen besser sind und ob wir weniger oder mehr Parameter zur Übergabe verwenden sollten.

Jetzt schreibe ich diese Einleitung, und ehrlich gesagt, weiß ich nicht, zu welchem Ergebnis ich am Ende kommen werde. Wie immer werde ich nur MetaTrader 5-Tools ohne jegliche Software von Drittanbietern verwenden. Dieser Artikel wird höchstwahrscheinlich einer Schritt-für-Schritt-Anleitung ähneln. Ich werde versuchen, alles so klar und einfach wie möglich zu erklären.

1. Währungspaar, Optimierung und Vorwärtstestbereich, Einstellungen

Hier werde ich alle Parameter für die Optimierung und die Vorwärtsprüfung angeben, um mich im Text nicht zu wiederholen:

• Forex;
• EURUSD;
• Zeitrahmen: H1;
• Templates: Fächer, Parallelogramm, Dreieck;
• Stop-Loss und Take-Profit für die entsprechenden Modifikationen von 600 und 60, 200 und 230 für den Saldo, unter Berücksichtigung des Spreads, fügen wir 30 Punkte für fünf Dezimalstellen zu TakeProfit, 200 und 430 Take-Profit ist 2 mal mehr als Stop-Loss, 30 Punkte für fünf Dezimalstellen zu Take-Profit für den Saldo;
• Optimierungs- und Testmodi „Nur Eröffnungspreise“ und „Komplexes Kriterium, Maximum“. Es ist sehr wichtig, den Modus „Maximales komplexes Kriterium“ zu verwenden, da er im Vergleich zu „Maximale Rentabilität“ stabilere und rentablere Ergebnisse zeigt;
• Optimierungsbereich 3 Jahre. 2019.02.18 - 2022.02.18. 3 Jahre sind kein zuverlässiges Kriterium. Sie können mit diesem Parameter selbst experimentieren;
• Die Dauer des Vorwärtstest beträgt 1 Jahr. 2022.02.18 - 2023.02.18. Wir überprüfen alles anhand des in meinem Artikel (Experimente mit Neuronalen Netzen (Teil 3) beschriebenen Algorithmus: Praktische Anwendung). Das bedeutet, dass gleichzeitig mehrere beste Optimierungsergebnisse gehandelt werden;
• Wir werden die Optimierung nun 20 Mal durchführen. Erhöhen wir sie im Vergleich zu den vorherigen Tests um das Zweifache und sehen wir uns die Ergebnisse an. 
• Bei allen Vorwärtstests wurden 40 Optimierungsergebnisse gleichzeitig verwendet. Der Wert ist im Vergleich zu den vorherigen Tests um das Zweifache erhöht;
• Optimierung des Expert Advisors mit Perceptron „Schneller genetischer Algorithmus“;
• EA-Optimierung mit der Bibliothek DeepNeuralNetwork.mqh „Schneller genetischer Algorithmus“. Aufgrund der langsamen Optimierung des in Teil 2 betrachteten Algorithmus wurde beschlossen, direkt mit MetaTrader 5 zu optimieren;
• Ersteinlage 10.000 Einheiten;
• Hebel 1:500.

Ich hätte fast vergessen, Ihnen zu erzählen, wie ich 20, 40 oder mehr Mal im Modus „Schneller genetischer Algorithmus“ optimiere. Dazu verwende ich ein kleines Autoclicker-Programm, das ich in Delphi geschrieben habe. Ich kann sie hier nicht veröffentlichen, aber ich werde sie jedem, der sie braucht, in einer privaten Nachricht schicken. Es funktioniert folgendermaßen:

1. Geben Sie die gewünschte Anzahl von Optimierungen ein.
2. Bewegen Sie den Mauszeiger über die Schaltfläche Start im Strategieoptimierer.
3. Warten Sie.

Die Optimierung endet nach den angegebenen Zyklen und das Programm wird geschlossen. Der Autoclicker reagiert auf die Änderung der Farbe der Schaltfläche Start. Das Programm ist in der nachstehenden Abbildung dargestellt. 

2. Schablonen (Templates)

Eine Schablone, engl. Template, ist eine Art Konstruktion, die einem „schwebenden Muster“ ähnelt. Seine Werte ändern sich ständig je nach Marktlage, aber jeder Wert liegt in einem bestimmten Bereich, den wir für unsere Experimente benötigen. Da wir bereits wissen, dass die Daten, die wir an das Neuronale Netz übermitteln, in einem bestimmten Bereich liegen sollten, wird der Wert in der Schablone der Einfachheit halber und zum besseren Verständnis durch das Perceptron und das Neuronale Netz auf eine ganze Zahl aufgerundet. Dadurch ergeben sich mehr Situationen für Auslösebedingungen und eine geringere Belastung für das Perceptron und das Neuronale Netz. Unten sehen Sie die erste der Schablone, die mir in den Sinn kam. Ich nannte sie Fächer (fan). Ich denke, die Ähnlichkeit ist offensichtlich. In diesem Artikel werden wir keine Indikatoren verwenden, sondern mit Kerzen arbeiten.

Nachfolgend finden Sie Beispiele, bei denen der Verlauf gezoomt wird, sodass wir einen kürzeren oder tieferen Verlauf analysieren können.

Die Verwendung einer gleichen Anzahl von Kerzen in den Schablonen ist keine Voraussetzung, was ein zusätzliches Feld für Überlegungen zur Relevanz früherer Preiswerte eröffnet. In unserem Fall sind dies die Schlusskurse der Kerzen.

Es ist wichtig zu verstehen, dass wir in den Beispielen, die die Bibliothek DeepNeuralNetwork.mqh für 24 Kerzen verwenden, verschiedene Bibliotheken verwenden, die ich in den vorherigen Artikeln beschrieben habe. Sie haben unterschiedliche Eingangseinstellungen. Nämlich 4 und 8 Parameter für den Eingang des Neuronalen Netzes. Sie brauchen sich keine Sorgen zu machen. Ich habe bereits EAs und notwendige Bibliotheken im Anhang hinzugefügt.

2.1 Die Schablone eines Fächers mit vier Werten, die sich über 24 Kerzen erstrecken. Sie entspricht einem Tag auf H1. 

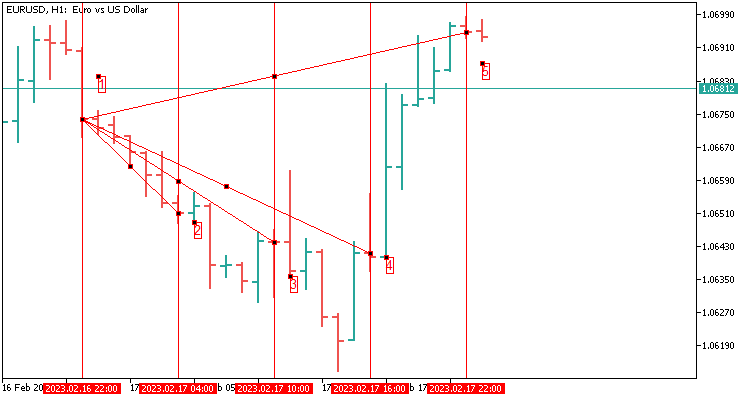
Lassen Sie uns zum besseren Verständnis beschreiben, was wir auf das Perceptron und das Neuronale Netz übertragen werden:

1. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 2;
2. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 3;
3. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 4;
4. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 5;

So wird es im Code für Perceptron EAs aussehen:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

So wird es im Code für EAs aussehen, die auf der Bibliothek DeepNeuralNetwork.mqh basieren:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   xInputs[3] = (int)(a4/100)*100;  
   
   return(1);

  }

2.2 Schablone des Fächers mit acht Werten, die sich über 24 Kerzen erstrecken. Sie entspricht einem Tag auf H1.

 

 

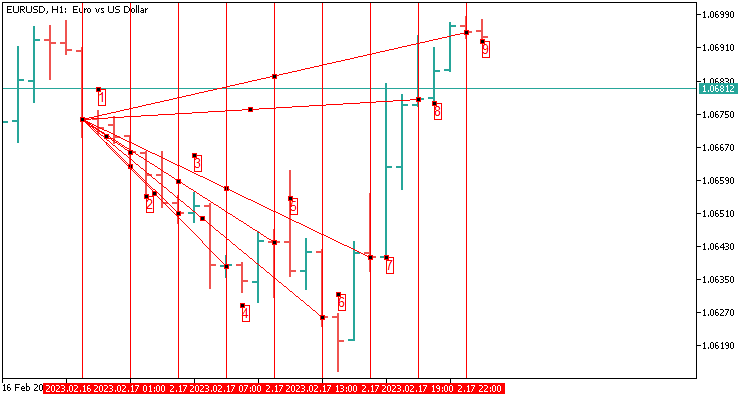
Schauen wir uns an, was wir zum besseren Verständnis an das Perceptron und das Neuronale Netz weitergeben:

1. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 2;
2. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 3;
3. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 4;
4. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 5;
5. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 6;
6. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 7;
7. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 8;
8. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 9;

So wird es im Code für Perceptron EAs aussehen:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point()));
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point()));
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   b3 = (int)(b3/100)*100;
   int b4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point()));
   b4 = (int)(b4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

So wird es im Code für EAs aussehen, die auf der Bibliothek DeepNeuralNetwork.mqh basieren:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point()));
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point()));
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point()));
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.3 Schablone des Fächers mit vier Werten, die sich über 48 Kerzen erstrecken. Entspricht zwei Tagen auf H1.

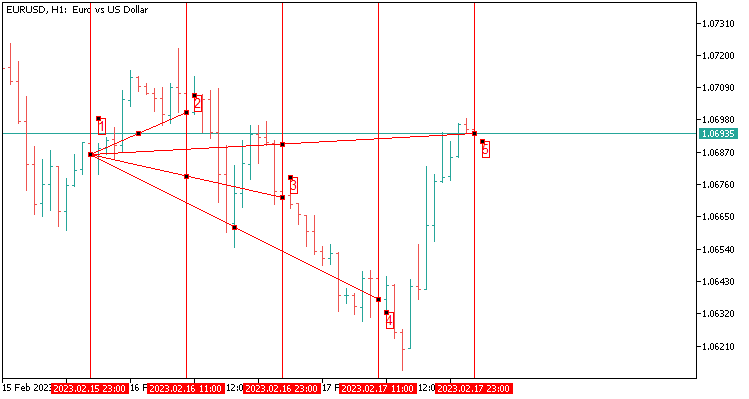
Zum besseren Verständnis ist hier die Beschreibung:

1. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 2;
2. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 3;
3. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 4;
4. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 5;

So wird es im Code für Perceptron EAs aussehen. Das vorherige Beispiel wurde um 2 Tage verlängert:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

So sieht es im Code in DeepNeuralNetwork.mqh aus. Das vorherige Beispiel wurde um 2 Tage verlängert:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   xInputs[3] = (int)(a4/100)*100;  
   
   return(1);

  }

2.4 Die Schablone des Fächers mit acht Werten, die sich über 48 Kerzen erstrecken. Entspricht zwei Tagen auf H1.

Die Bezugspunkte haben sich um die gleiche Anzahl von Kerzen verschoben:

1. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 2;
2. Gerundeter Abstand in Punkten von Punkt 1 zu Punkt 3;
3. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 4;
4. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 5;
5. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 6;
6. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 7;
7. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 8;
8. Gerundeter Abstand in Punkten von Punkt 1 bis Punkt 9;

Der Code in Perceptron-EAs:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point()));
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   b3 = (int)(b3/100)*100;
   int b4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point()));
   b4 = (int)(b4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

Der Code in den EAs basiert auf DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point()));
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point()));
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.5 Die Schablone des Parallelogramm mit vier Werten, die sich über 24 Kerzen erstrecken. Eine komplexere Konstruktion zur Übergabe von Parametern. Entspricht einem Tag auf H1.

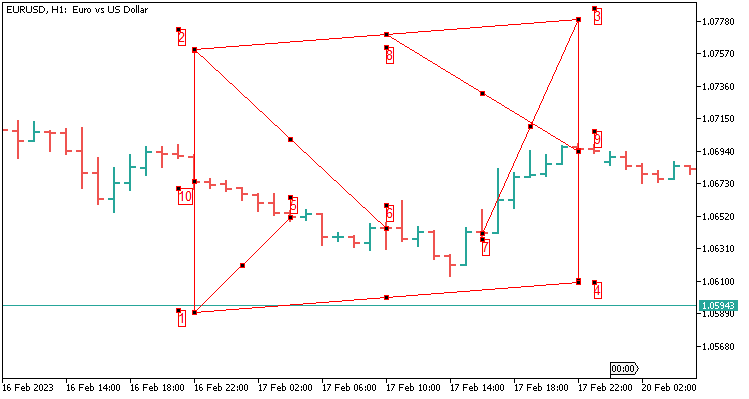
Im Folgenden wird beschrieben, welche Werte wir übergeben:

1. In meinem Fall sind 800 Punkte für fünf Dezimalstellen von Punkt 10 bis Punkt 2 zu addieren;
2. Wir ziehen 800 Punkte von Punkt 10 zu Punkt 1 ab,
3. addieren 800 Punkte von Punkt 9 zu Punkt 3,
4. ziehen 800 Punkte von Punkt 9 bis Punkt 4 ab.
5. Gerundeter Wert von Punkt 8 bis Punkt 9 (Punkt 8 ergibt sich aus der Differenz der Punkte 2 und 3);
6. Gerundeter Wert von Punkt 3 bis Punkt 7;
7. Gerundeter Wert von Punkt 2 bis Punkt 6;
   
8. Gerundeter Wert von Punkt 1 bis Punkt 5;
   

Der Code in Perceptron-EAs:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,7)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

Der Code in den EAs basiert auf DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,7)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.6 Die Schablone des Parallelogramms mit vier Werten, die sich über 48 Kerzen erstrecken. Größere Reichweite im Laufe der Zeit. Entspricht zwei Tagen auf H1.

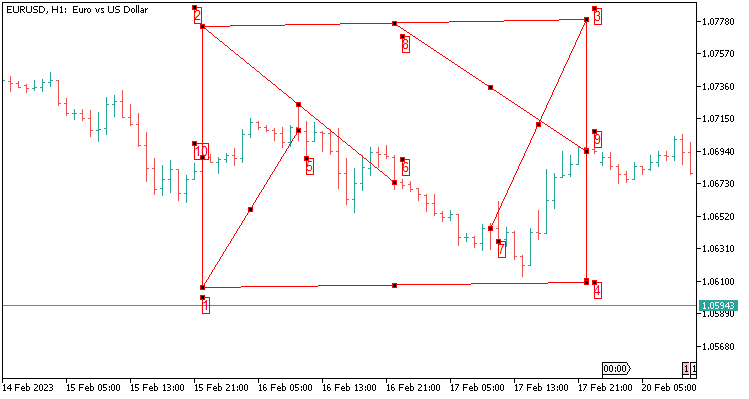
Im Folgenden wird beschrieben, welche Werte wir übergeben:

1. In meinem Fall addieren wir 1200 Punkte für fünf Dezimalstellen von Punkt 10 bis Punkt 2; ich habe den Wert in Punkten erhöht, da der Preis innerhalb von zwei Tagen stark schwanken kann. Auf diese Weise bleibt unsere Konstruktion intakt;
2. Wir ziehen 1200 Punkte von Punkt 10 zu Punkt 1 ab,
3. addieren 1200 Punkte von Punkt 9 bis Punkt 3,
4. ziehen 1200 Punkte von Punkt 9 bis Punkt 4 ab.
5. Gerundeter Wert von Punkt 8 bis Punkt 9 (Punkt 8 ergibt sich aus der Differenz der Punkte 2 und 3);
6. Gerundeter Wert von Punkt 3 bis Punkt 7;
7. Gerundeter Wert von Punkt 2 bis Punkt 6;
   
8. Gerundeter Wert von Punkt 1 bis Punkt 5;

Der Code in Perceptron-EAs:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

Der Code in den EAs basiert auf DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.7 Schablone des Parallelogramms mit acht Werten, die sich über 24 Kerzen erstrecken. Sie entspricht einem Tag auf H1.

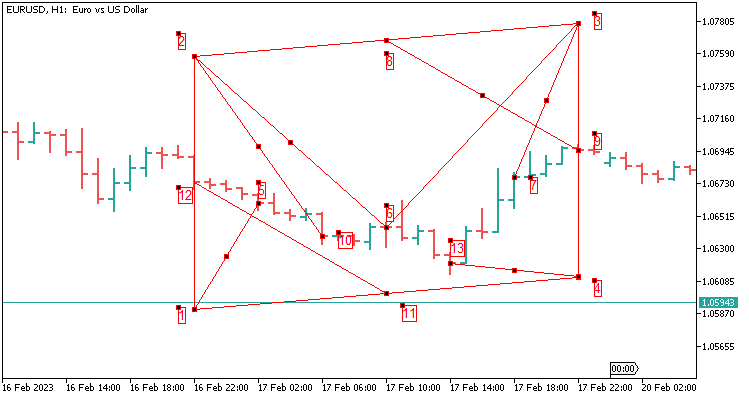
Im Folgenden wird beschrieben, welche Werte wir übergeben:

1. In meinem Fall addieren wir 800 Punkte für fünf Dezimalstellen ab Punkt 9,
2. ziehen 800 Punkte von Punkt 9 ab und erhalte Punkt 4;
3. addieren Sie 800 Punkte von Punkt 12 zu Punkt 2,
4. ziehen Sie 800 Punkte von Punkt 12 bis Punkt 1 ab.
5. Gerundeter Wert von Punkt 8 bis Punkt 9 (Punkt 8 ergibt sich aus der Differenz der Punkte 2 und 3);
6. Gerundeter Wert von Punkt 7 bis Punkt 3;
7. Gerundeter Wert von Punkt 13 bis Punkt 4;
   
8. Gerundeter Wert von Punkt 6 bis Punkt 3;
9. Gerundeter Wert von Punkt 2 bis Punkt 6;
   
10. Gerundeter Wert von Punkt 2 bis Punkt 10;
    
11. Gerundeter Wert von Punkt 12 bis Punkt 11 (Punkt 1 ergibt sich aus der Differenz zwischen den Punkten 4 und 1);
    
12. Gerundeter Wert von Punkt 1 bis Punkt 5;
    

Der Code in Perceptron-EAs:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,5)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   a4 = (int)(a4/100)*100;

   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,17))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,21))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))/2))/Point()) ;
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

So sieht es im Code für EAs aus, die auf der Bibliothek DeepNeuralNetwork.mqh basieren:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,5)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   xInputs[3] = (int)(a4/100)*100;

   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,17))/Point());
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,21))/Point());
   xInputs[6] = (int)(g3/100)*100;
   int b4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))/2))/Point()) ;
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.8 Die Schablone des Parallelogramms mit acht Werten, die sich über 48 Kerzen erstrecken, um eine bessere Abdeckung der Geschichte zu erreichen. Entspricht zwei Tagen auf H1.

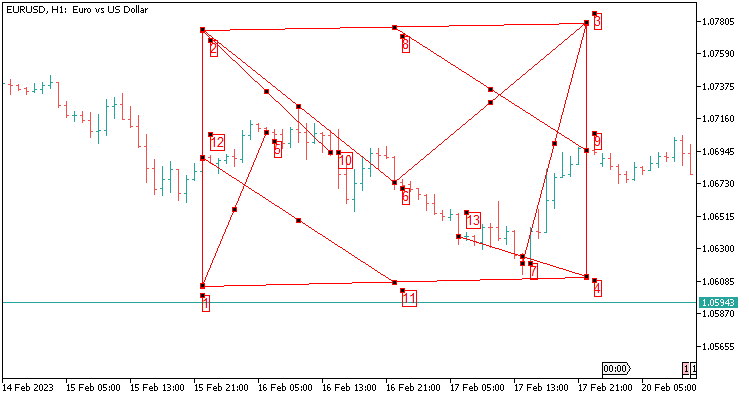
Im Folgenden wird beschrieben, welche Werte wir übergeben:

1. In meinem Fall addieren wir 1200 Punkte für fünf Dezimalstellen ab Punkt 9,
2. ziehen 1200 Punkte von Punkt 9 ab und erhalte Punkt 4,
3. addieren 1200 Punkte von Punkt 12 zu Punkt 2,
4. ziehen Sie 1200 Punkte von Punkt 12 bis Punkt 1 ab.
5. Gerundeter Wert von Punkt 8 bis Punkt 9 (Punkt 8 ergibt sich aus der Differenz der Punkte 2 und 3);
6. Gerundeter Wert von Punkt 7 bis Punkt 3;
7. Gerundeter Wert von Punkt 13 bis Punkt 4;
   
8. Gerundeter Wert von Punkt 6 bis Punkt 3;
9. Gerundeter Wert von Punkt 2 bis Punkt 6;
   
10. Gerundeter Wert von Punkt 2 bis Punkt 10;
    
11. Gerundeter Wert von Punkt 12 bis Punkt 11 (Punkt 1 ergibt sich aus der Differenz zwischen den Punkten 4 und 1);
    
12. Gerundeter Wert von Punkt 1 bis Punkt 5;

Der Code in den Perceptron-EAs:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,17)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,25)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   a4 = (int)(a4/100)*100;

   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,33))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,41))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))/2))/Point()) ;
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

Der Code für die EAs auf der Grundlage von DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   xInputs[0] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,17)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   xInputs[0] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,25)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   xInputs[0] = (int)(a4/100)*100;

   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[0] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,33))/Point());
   xInputs[0] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,41))/Point());
   xInputs[0] = (int)(g3/100)*100;
   int g4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))/2))/Point()) ;
   xInputs[0] = (int)(g4/100)*100;
   
   return(1);

  }

2.9 Die Schablone des Dreiecks mit vier Werten, die sich über 24 Kerzen erstrecken. Sie entspricht einem Tag auf H1.

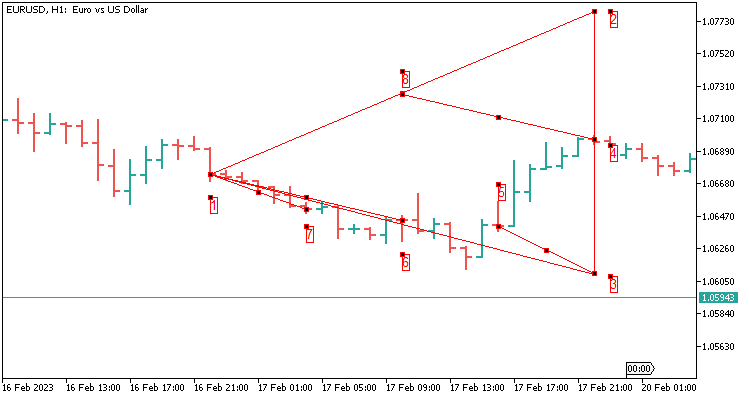
Im Folgenden wird beschrieben, welche Werte wir übergeben:

1. In meinem Fall addieren wir 800 Punkte für fünf Dezimalstellen von Punkt 4 bis Punkt 2,
2. ziehen 800 Punkte von Punkt 4 bis Punkt 3 ab.
3. Gerundeter Wert von Punkt 8 bis Punkt 4 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
4. Gerundeter Wert von Punkt 3 bis Punkt 5;
5. Gerundeter Wert von Punkt 1 bis Punkt 6;
6. Gerundeter Wert von Punkt 1 bis Punkt 7;

Der Code in den Perceptron-EAs:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   a4 = (int)(a4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

Der Code für die EAs auf der Grundlage von DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.10 Die Schablone des Dreiecks mit vier Werten, historische Abdeckung von 48 Kerzen. Zwei Tage auf H1.

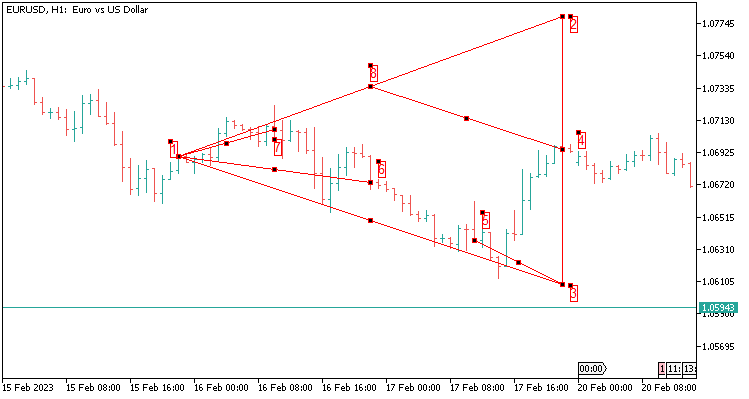
Nachfolgend sind die Werte aufgeführt, die an das Perceptron und das Neuronale Netz übergeben werden:

1. In meinem Fall addieren wir 1200 Punkte für fünf Dezimalstellen von Punkt 4 bis Punkt 2 und
2. ziehen 1200 Punkte von Punkt 4 bis Punkt 3 ab.
3. Gerundeter Wert von Punkt 8 bis Punkt 4 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
4. Gerundeter Wert von Punkt 3 bis Punkt 5;
5. Gerundeter Wert von Punkt 1 bis Punkt 6;
6. Gerundeter Wert von Punkt 1 bis Punkt 7;

Code der Schablone im Perceptron EA:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   a4 = (int)(a4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

Code der Schablone für EAs auf der Grundlage von DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.11 Die Schablone des Dreiecks mit acht Werten, die sich über 24 Kerzen erstrecken. Die historische Erfassung für die Analyse beträgt einen Tag auf H1.

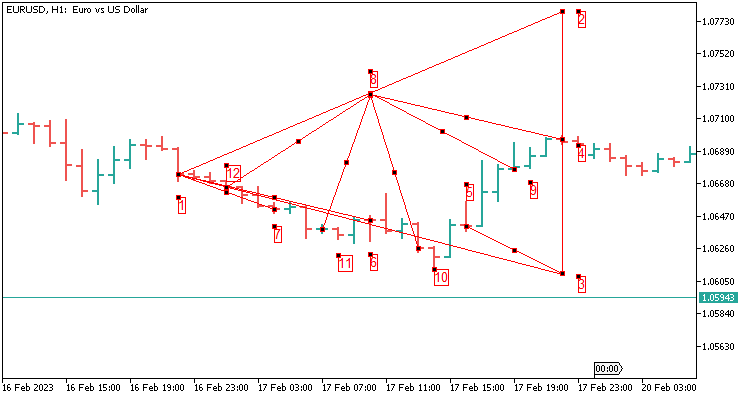
Die bestandenen Werte werden im Folgenden beschrieben:

1. In meinem Fall addieren wir 800 Punkte für fünf Dezimalstellen von Punkt 4 bis Punkt 2,
2. ziehen 800 Punkte von Punkt 4 bis Punkt 3 ab.
3. Gerundeter Wert von Punkt 8 bis Punkt 4 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
4. Gerundeter Wert von Punkt 3 bis Punkt 5;
5. Gerundeter Wert von Punkt 1 bis Punkt 6;
6. Gerundeter Wert von Punkt 1 bis Punkt 7;
7. Gerundeter Wert von Punkt 8 bis Punkt 9 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
   
8. Gerundeter Wert von Punkt 8 bis Punkt 10 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
   
9. Gerundeter Wert von Punkt 8 bis Punkt 11 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
   
10. Gerundeter Wert von Punkt 8 bis Punkt 12 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
    

 

Code der Schablone im Perceptron EA:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point());
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

Code der Schablone für EAs auf der Grundlage von DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point());
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point());
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point());
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point());
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.12 Die Schablone des Dreiecks mit acht Werten, die sich über 48 Kerzen erstrecken. Der historische Erfassungsbereich für die Analyse beträgt zwei Tage auf H1.

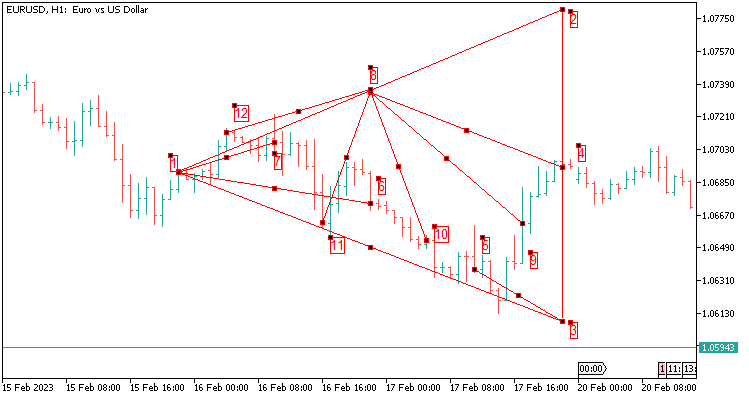
Die bestandenen Werte werden im Folgenden beschrieben:

1. In meinem Fall werden 1200 Punkte für fünf Dezimalstellen von Punkt 4 bis Punkt 2 addiert, der Mehrwert wird um 48 Kerzen erhöht;
2. ziehen 1200 Punkte von Punkt 4 bis Punkt 3 ab.
3. Gerundeter Wert von Punkt 8 bis Punkt 4 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
4. Gerundeter Wert von Punkt 3 bis Punkt 5;
5. Gerundeter Wert von Punkt 1 bis Punkt 6;
6. Gerundeter Wert von Punkt 1 bis Punkt 7;
7. Gerundeter Wert von Punkt 8 bis Punkt 9 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
   
8. Gerundeter Wert von Punkt 8 bis Punkt 10 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
   
9. Gerundeter Wert von Punkt 8 bis Punkt 11 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);
   
10. Gerundeter Wert von Punkt 8 bis Punkt 12 (Punkt 8 ergibt sich aus der Differenz zwischen den Punkten 2 und 1);

Code der Schablone im Perceptron EA:

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,6))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,18))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point());
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

Der Code der Schablone des Dreiecks für EAs auf der Grundlage von DeepNeuralNetwork.mqh:

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,6))/Point());
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,18))/Point());
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point());
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point());
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

3. Expert Advisors

Kommen wir also zum interessantesten Teil, nämlich der Optimierung und dem Testen unserer Schablonen. Wie Sie sich vielleicht erinnern, wurde die Optimierung und das Testen von Expert Advisors auf der Bibliothek DeepNeuralNetwork.mqh mit Standard-MQL5-Tools durchgeführt, ohne die in (Artikel 2) beschriebene Optimierungstechnologie zu verwenden. Es wurde auch festgestellt, dass 20 Durchläufe für diese EAs ein bisschen wenig sind. Ich empfehle Ihnen, die Optimierung selbst mit einer größeren Anzahl von Iterationen durchzuführen. Ich bin sicher, dass dies das Ergebnis verbessern wird. Eine große Anzahl von zu optimierenden Parametern erfordert mehr Zeit, um die besten Ergebnisse zu ermitteln. In diesem Artikel möchte ich nur nicht-standardisierte Methoden zur Übertragung von Daten in einem Neuronalen Netz aufzeigen.

Die auf der Bibliothek DeepNeuralNetwork.mqh basierenden Expert Advisors mit vier Parametern enthalten in der Schablone das 4-4-3-Schema für Neuronale Netze, während bei acht Parametern das Schema 8-4-3 lautet.

Ich habe versucht, jeden der EAs entsprechend seiner Strategie und der für die Analyse verwendeten Schablone zu benennen. Ich denke also, dass es schwer ist, sich zu verirren. Sie können mich jederzeit über das Forum oder über private Nachrichten kontaktieren. 

Die ersten 40 besten Ergebnisse, die bei der Optimierung im Modus „Komplexes Kriterium max“ erzielt wurden, wurden in jedem EA für Vorwärtstests verwendet. Ich werde die Ergebnisse in Form von Optimierungsergebnissen veröffentlichen, und unten sind die Ergebnisse der Vorwärtsprüfung.

In diesem Artikel werde ich EAs auf der Grundlage des Fan-Schablone testen und Schlussfolgerungen über die vorgestellte „technology“ ziehen. Sie können den Rest der Schablonen bei Interesse selbst testen. Ich habe den technischen Teil in Form von vorgefertigten Codes für alle Schablone oben gepostet, sodass ich denke, dass Sie keine Probleme haben werden, die Schablonencodes in den am Ende des Artikels geposteten EAs zu ersetzen und Optimierungen und Tests durchzuführen.

Wenn Sie Schwierigkeiten haben, den Test zu verstehen, lesen Sie Teil 3 der Serie. Dort ist alles detailliert beschrieben.

3.1 Perceptron-basierte EAs

Perceptron Fan 4 SL TP 24 - trade - vier Parameter auf 24 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

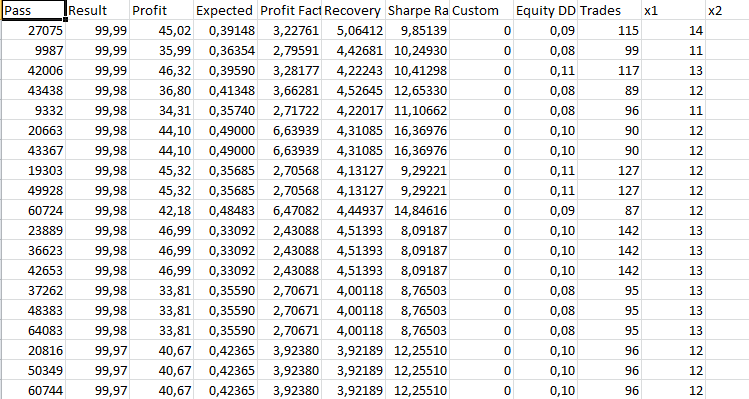
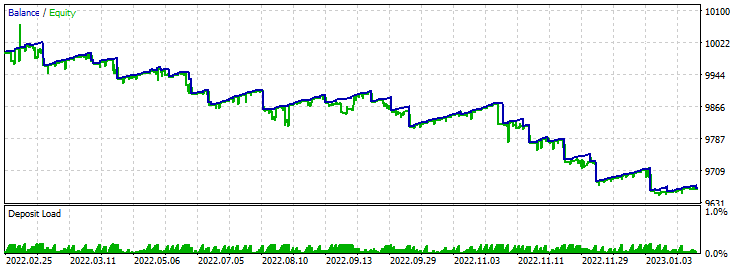
Das Ergebnis der Vorwärtsprüfung ist nicht ermutigend. Es ist ein gleichmäßiges Abschmelzen der Einlage über die gesamte Geschichte hinweg zu beobachten. Der Gewinnfaktor der Testergebnisse ist hoch. Wahrscheinlich hat dies mit dem Verhältnis von Stop-Loss und Take-Profit zu tun.

Take-Profit 230 Stop-Loss 200:

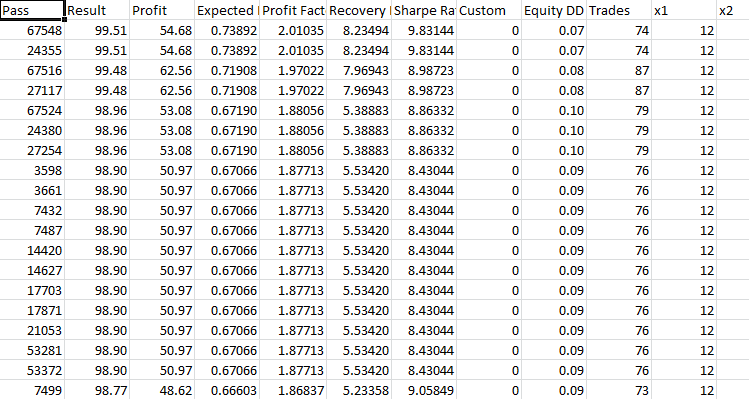
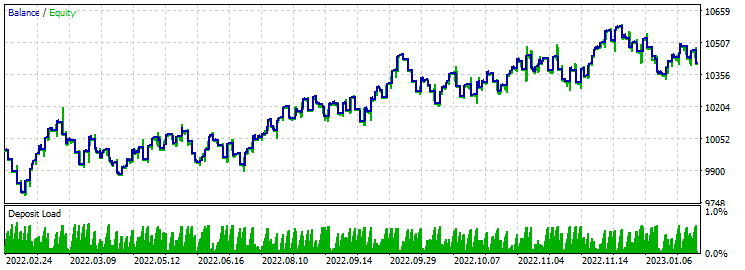
Der Gewinnfaktor übersteigt kaum den Wert von 1,8. Große Einlagenrückgänge sind im gesamten Jahresverlauf zu beobachten. Minimales Saldenwachstum. Wir treten einfach auf der Stelle.

Take-Profit 430 Stop-Loss 200:

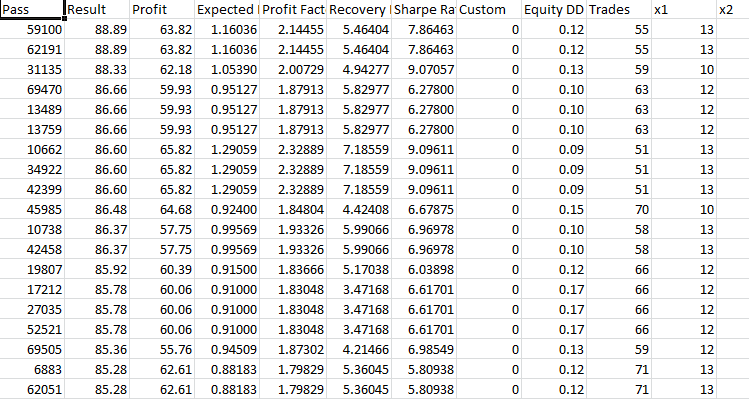
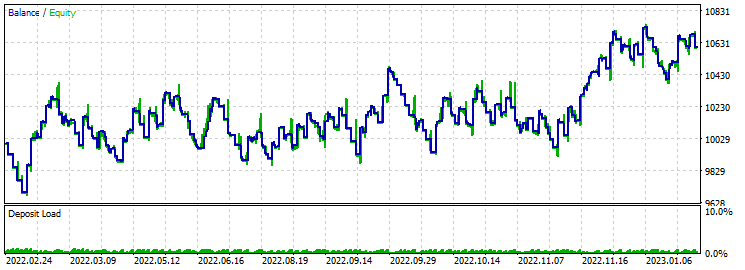
Die Kapitalschwankung ist über den gesamten Bereich des Vorwärtstests zu sehen. Die Gewinne entsprechen den Verlusten, und die Ergebnisse sind unbeständig. Der Gewinnfaktor bei der Optimierung liegt bei etwa 2.

Perceptron fan 4 SL TP 48 - trade - vier Parameter auf 48 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

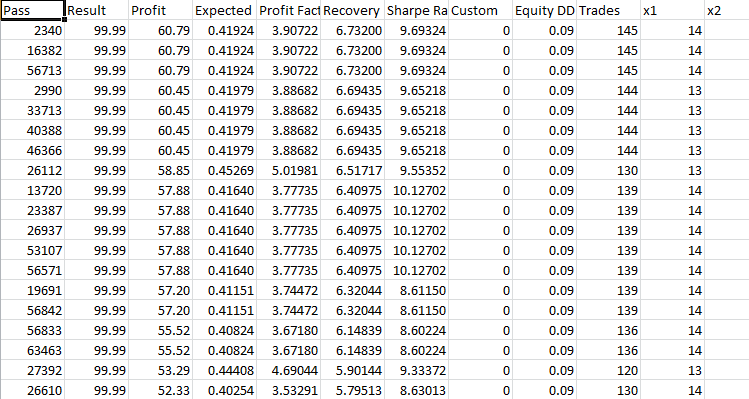
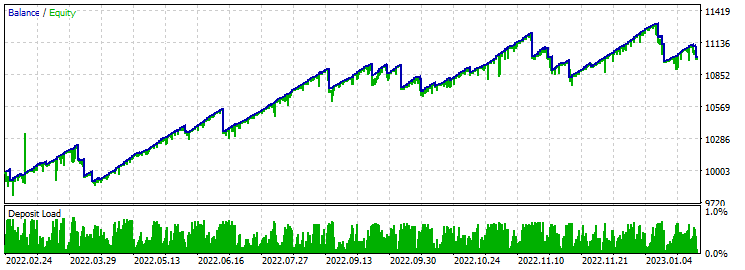
Auf ein stabiles Wachstum der Einlagen in den ersten sechs Monaten folgt ein gewisser Rückgang. Ich glaube, das liegt daran, dass über einen so langen Zeitraum keine zusätzliche Optimierung vorgenommen wurde. Stabilere Ergebnisse werden beobachtet, wenn die Zeit in den übergebenen Parametern erhöht wird. Der Gewinnfaktor ist viel höher als das Ergebnis bei 24 Kerzen. Keine Anzeichen für eine Bindung an das Verhältnis zwischen Stop-Loss und Take-Profit.

Take-Profit 230 Stop-Loss 200:

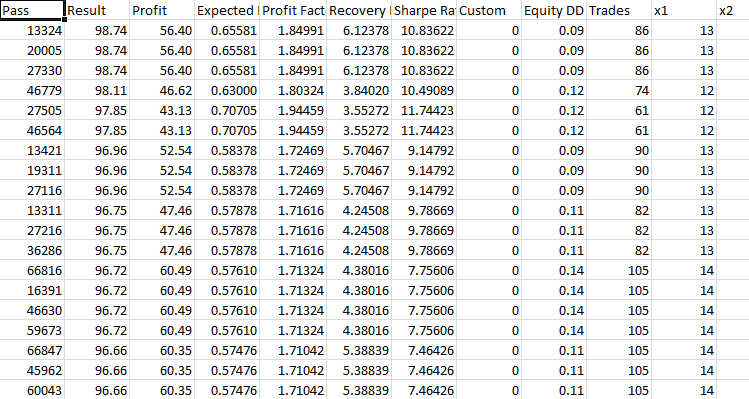
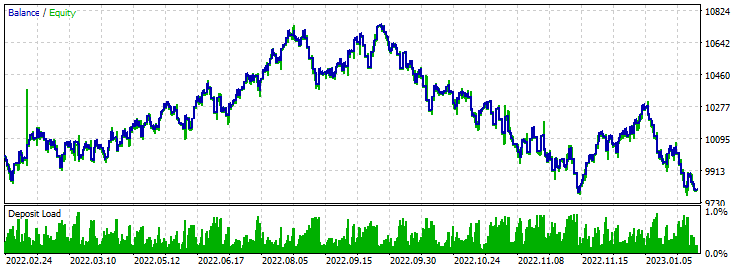
Ein stabiles Wachstum der Einlagen in den ersten fünf Monaten, dann ein Rückgang. Vielleicht hat sich der Markt im Gegensatz zu den im Perceptron gewählten Bedingungen verändert. Die ungleichmäßige Entwicklung in den ersten fünf Monaten deutet immer noch auf die Instabilität des Systems hin.

Take-Profit 430 Stop-Loss 200:

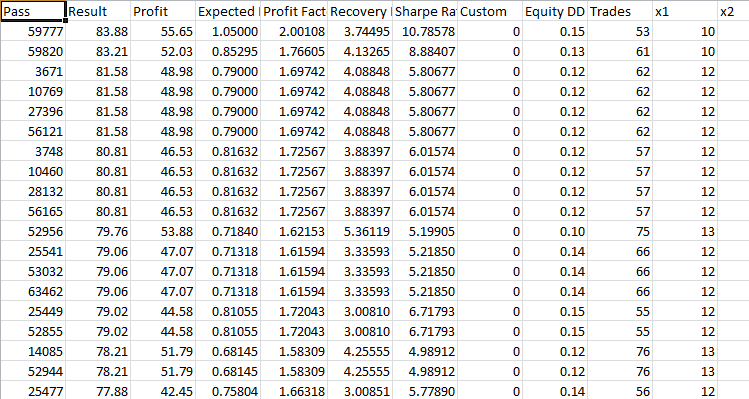
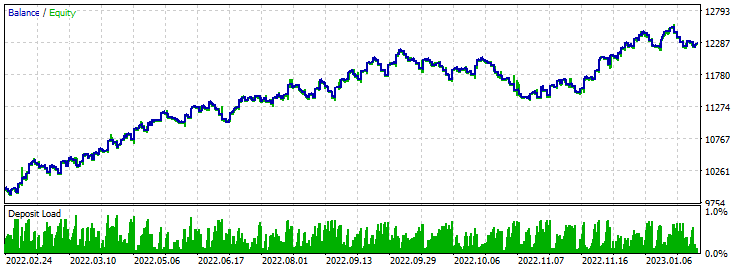
Das stabilste Ergebnis bei den Tests des Perceptrons mit dem Fan-Template. Stetiges Wachstum in den ersten sechs Monaten. Dann ein leichter Rückgang aufgrund der fehlenden Re-Optimierung. Take-Profit mehr als das Doppelte Stop-Loss ergibt ein gutes Ergebnis nach den grundlegenden Handelsregeln. Der Gewinn ist größer als Stopp Loss. Bei der Optimierung liegt der Gewinnfaktor bei 1,6, was meiner Meinung nach angesichts des Verhältnisses von Stop-Loss und Take-Profit normal ist.

 

Perceptron Fan 8 SL TP 24 - trade - acht Parameter auf 24 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

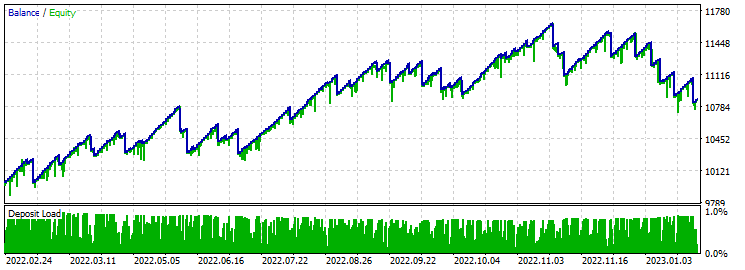
Die Saldenkurve ist recht ungleichmäßig, aber das Ergebnis unterscheidet sich grundlegend von dem EA mit vier Parametern und denselben Take-Profit und Stop-Loss. Nach der ersten Jahreshälfte ist auch ein leichter Rückgang zu verzeichnen. Der durchschnittliche Gewinnfaktor während der Optimierung liegt bei etwa 6, was ziemlich viel ist.

Take-Profit 230 Stop-Loss 200:

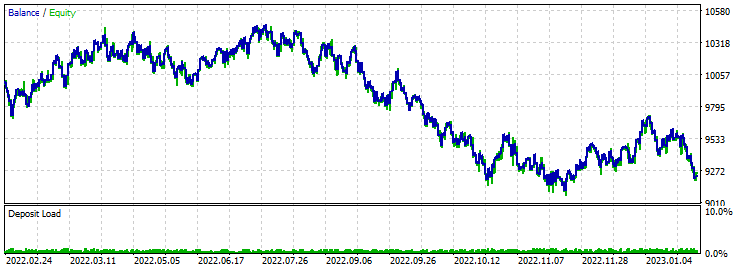
Bei diesem Vorwärtstest kommt es zu einem Totalausfall. Ich denke, dass dies auf das Verhältnis von Take-Profit und Stop-Loss im Verhältnis eins zu eins zurückzuführen ist. Die Optimierung ergab einen Gewinnfaktor von etwa 1,7, aber das konnte die Situation nicht retten.

Take-Profit 430 Stop-Loss 200:

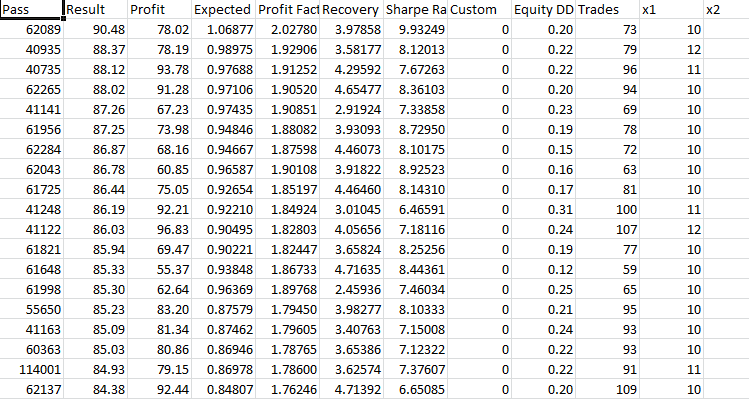
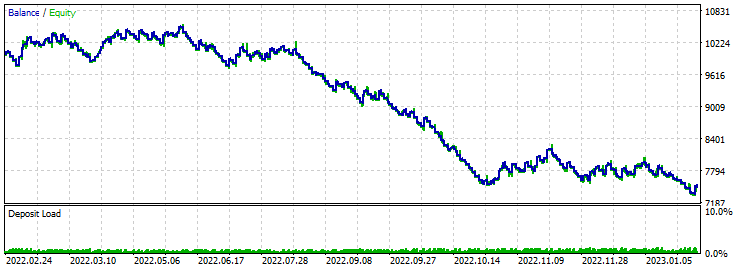
Auch diese Option ist ein völliger Fehlschlag, auch wenn es anfangs einen gewissen Widerstand gibt. Die Optimierung ergab einen Gewinnfaktor von etwa 1,8, aber auch das war nicht hilfreich.

Perceptron fan 8 SL TP 48 - trade - acht Parameter auf 48 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

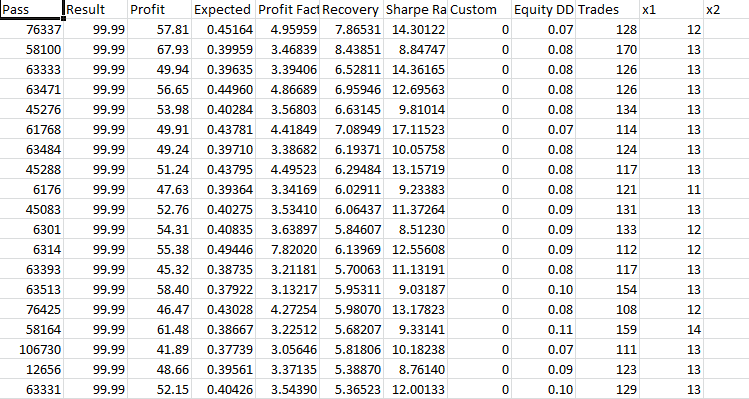
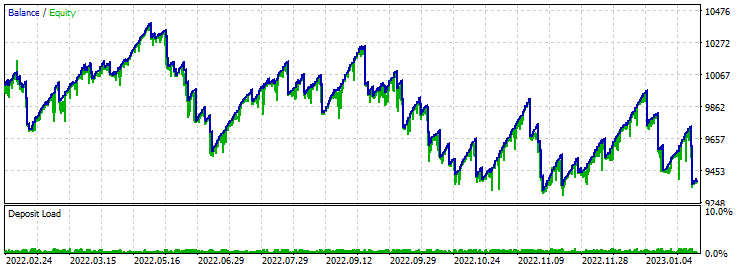
Uneinheitliche Grafik. Unter Berücksichtigung des Verhältnisses von Take-Profit zu Stop-Loss ergibt sich ein Verlust. Die Optimierung ergab einen Gewinnfaktor von etwa 3,5 bis 4, aber die Vorwärtstests ergaben einen Verlust.

Take-Profit 230 Stop-Loss 200:

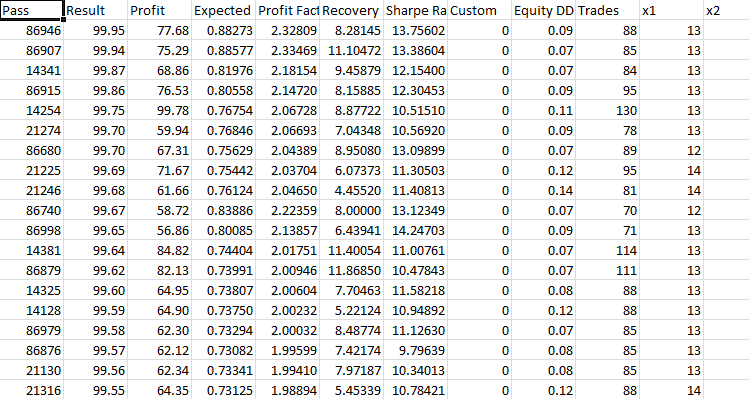
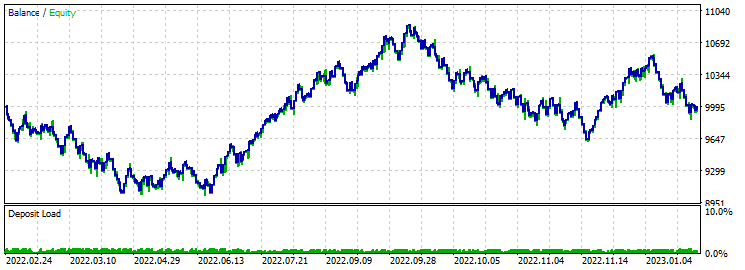
Auch bei dieser Version gibt es an einer Stelle Schwankungen. Merkwürdigerweise tritt die Verschlechterung des Gleichgewichts unmittelbar zu Beginn des Tests auf. Die Optimierung ergab einen Gewinnfaktor von etwa 2.

Take-Profit 430 Stop-Loss 200:

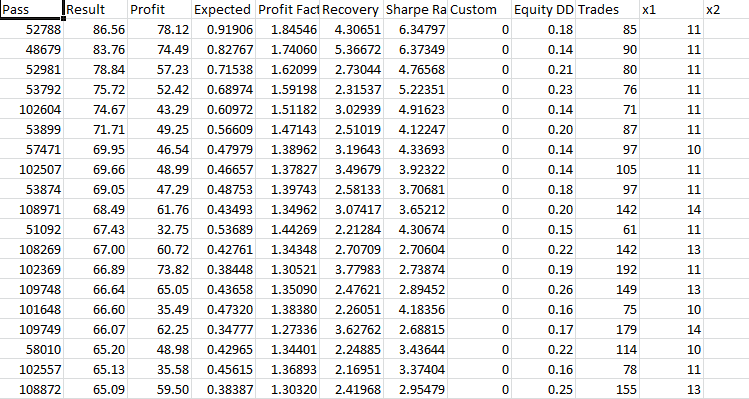
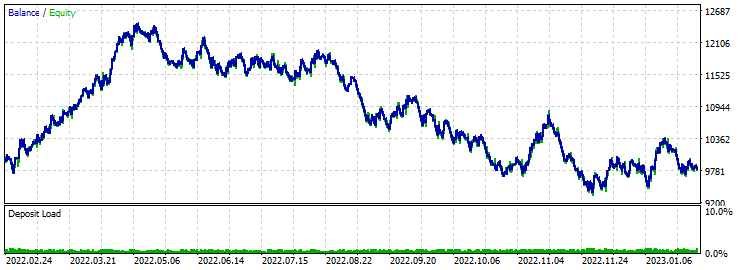
Ein sehr guter Start zu Beginn für etwa die ersten 3 Monate. Dann zeigte sich offenbar der Mangel an neuen Optimierungen. Das Verhältnis von Take-Profit zu Stop-Loss von zwei zu eins konnte die Situation über einen so langen Zeitraum nicht retten. Bei der Optimierung lag der durchschnittliche Gewinnfaktor bei 1,4.

3.2 EAs auf der Grundlage der Bibliothek DeepNeuralNetwork.mqh.

4-4-3 fan 4 SL TP 24 - trade - vier Parameter auf 24 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

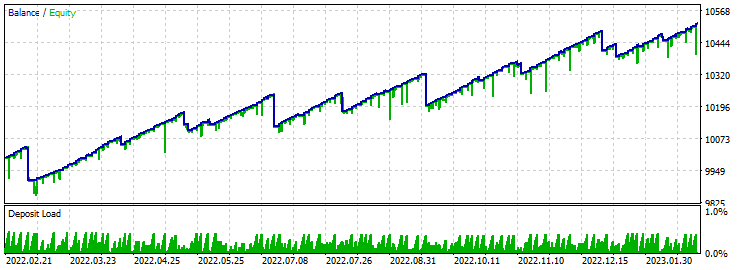
Der Gewinnfaktor 20, das ist eine Menge. Der Vorwärtstest zeigt positive Ergebnisse, aber wir haben große Stop-Losses. Dennoch rettet eine größere Anzahl von kleinen positiven Take-Profits die Situation.

Take-Profit 230 Stop-Loss 200:

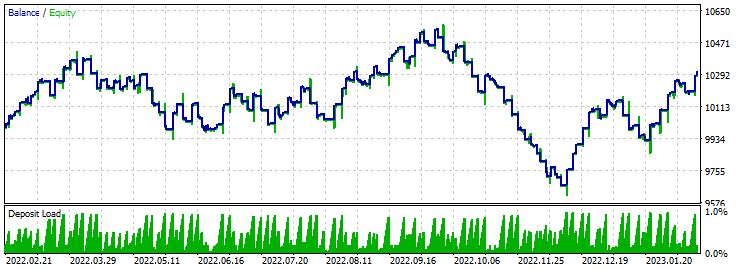
Die Saldenkurve tritt an einer Stelle auf der Stelle. Die Optimierung ergab einen Gewinnfaktor von etwa 1,7.

Take-Profit 430 Stop-Loss 200:

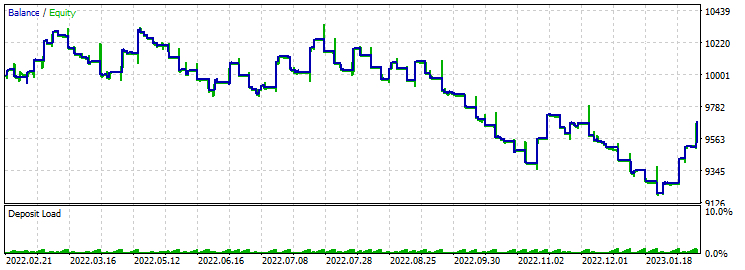
Langsamer, aber sicherer Rückgang. Das Verhältnis von Take-Profit zu Stop-Loss rettet die Situation nicht. Die Optimierung ergab einen Gewinnfaktor von etwa 2.

4-4-3 fan 4 SL TP 48 - trade - vier Parameter auf 48 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

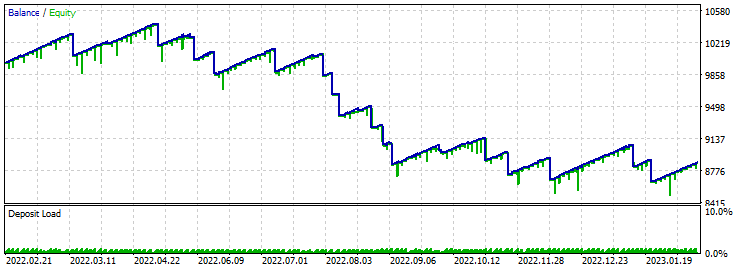
Die Schablone mit 48 Kerzen zeigte kein positives Ergebnis, im Gegensatz zur gleichen Schablone mit 24 Kerzen. Offensichtlich funktioniert eine solche Schablone, die zeitlich so lang ist, nicht gut mit einem solchen Verhältnis von Take-Profit zu Stop-Loss. Die Optimierung ergab einen Gewinnfaktor von etwa 14, was eine ganze Menge ist.

Take-Profit 230 Stop-Loss 200:

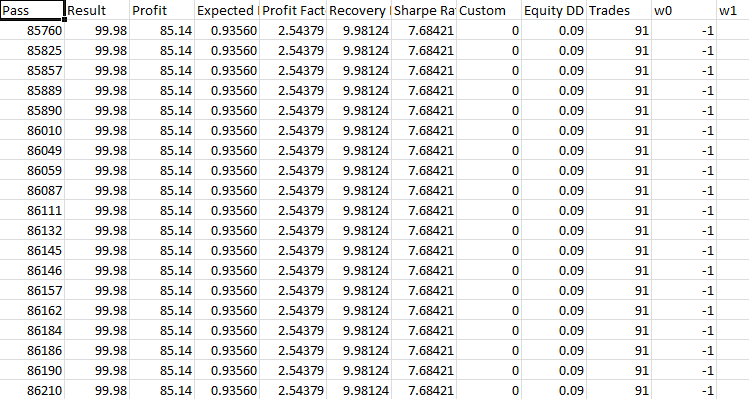
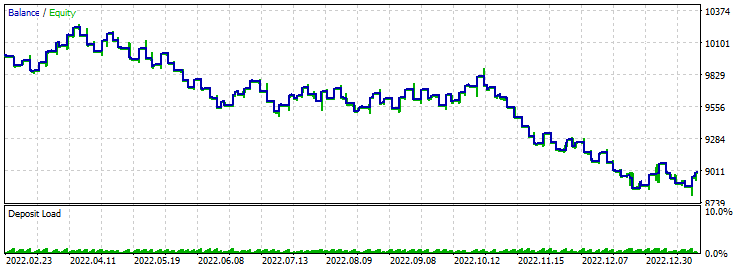
Bei der Optimierung erhalten wir einen Gewinnfaktor von 2,5. Wie wir sehen können, sind Take-Profit 230 Stop-Loss 200 nicht hilfreich. Die Bilanz wird langsam schlechter.

Take-Profit 430 Stop-Loss 200:

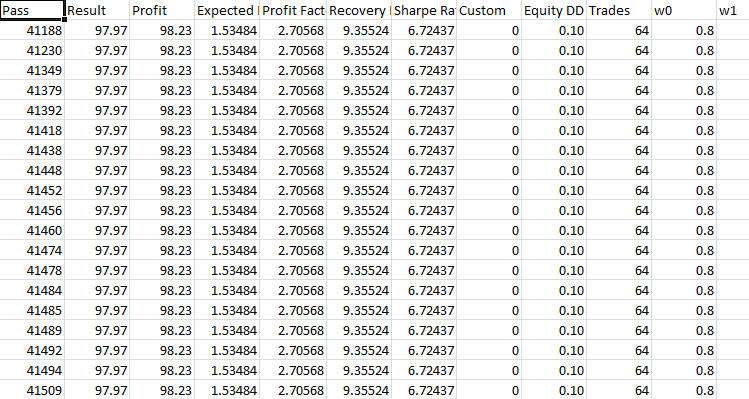
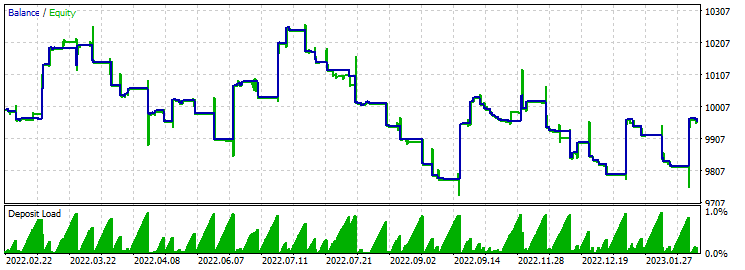
In diesem Fall haben wir keinen Fortschritt. Im Laufe des Jahres fällt und wächst der Saldo. Bei der Optimierung erhalten wir einen Gewinnfaktor von 2,7.

8-4-3 fan 8 SL TP 24 - trade - acht Parameter auf 24 Kerzen, Fächerschablone:

Take-Profit 60 Stop-Loss 600:

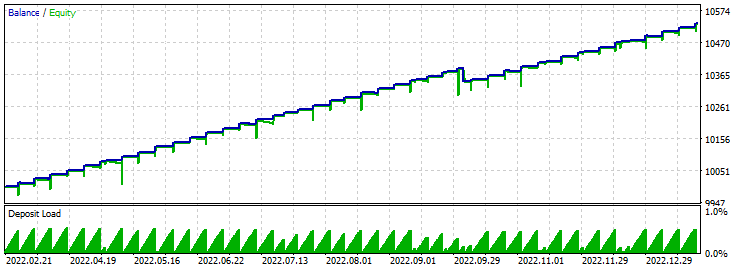
Sehr interessante Ergebnisse, nur ein Stop-Loss in der gesamten Geschichte der Vorwärtstests. Dennoch können die Ergebnisse zufällig sein. Bei der Optimierung geht der Gewinnfaktor bei etwa 29 aus dem Rahmen.

Take-Profit 230 Stop-Loss 200:

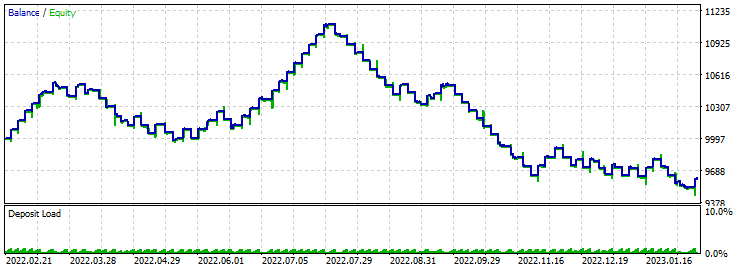
Wie auf dem Screenshot zu sehen ist, gibt es wieder keinen Fortschritt. Bei der Optimierung liegt der Gewinnfaktor bei 2,7, was bei dem aktuellen Verhältnis von Take-Profit zu Stop-Loss eigentlich ausreichen sollte, aber nicht der Fall war. In den ersten sechs Monaten ist ein gewisser Aufschwung zu verzeichnen.

Take-Profit 430 Stop-Loss 200:

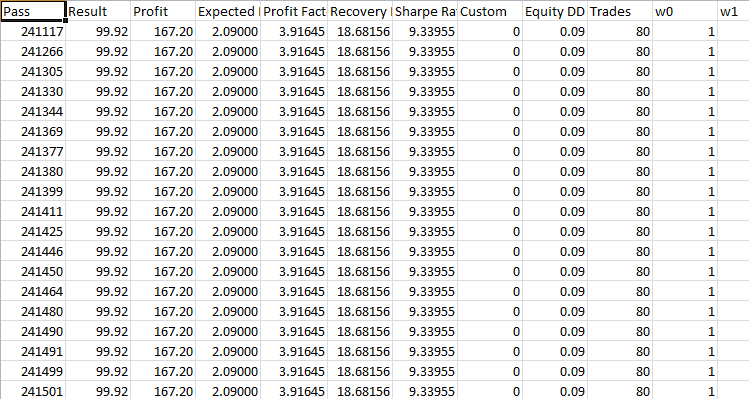
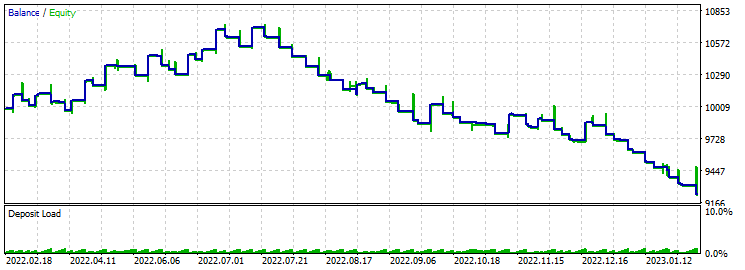
In den ersten zwei oder drei Monaten gab es einen leichten Anstieg, dann änderte sich offenbar die Marktlage, und der EA begann, die Einlage zu verlieren. Offensichtlich ist eine ständige Optimierung noch erforderlich. Bei der Optimierung liegt der Gewinnfaktor bei 3,9.

8-4-3 fan 8 SL TP 48 - trade - acht Parameter auf 48 Kerzen, Fächer-Schablone:

Take-Profit 60 Stop-Loss 600:

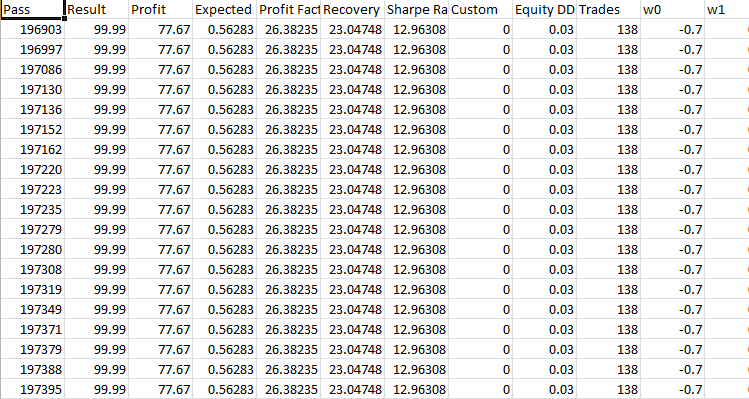
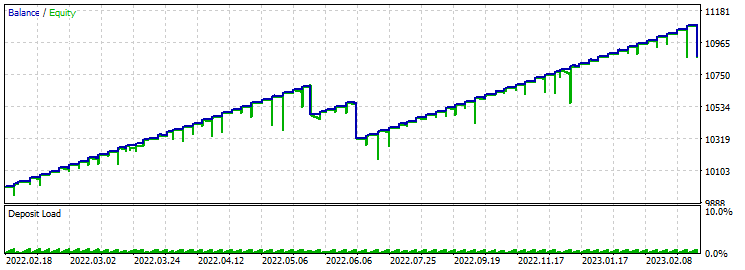
Dieser EA verhält sich ähnlich wie der vorherige EA bei einem 24-Kerzen-Muster. Mehr Verluste. Bei der Optimierung lag der Gewinnfaktor bei 26. Im Falle von 24 Kerzen lag er bei 29.

Take-Profit 230 Stop-Loss 200:

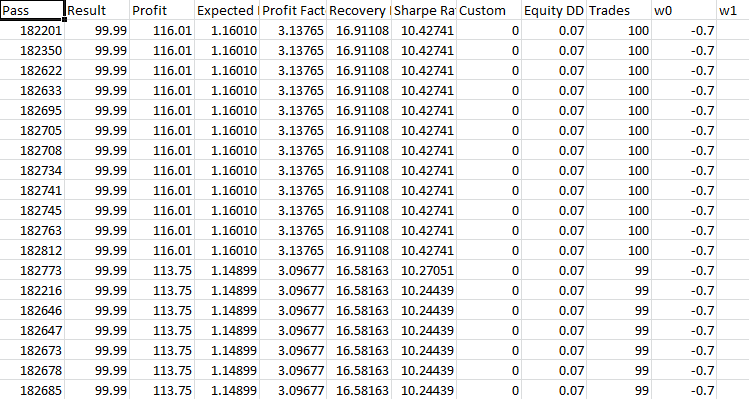
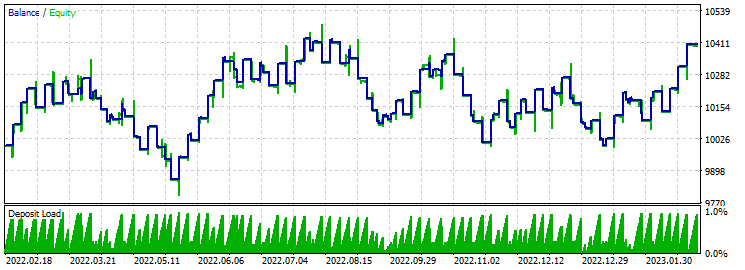
Bei der Optimierung liegt der Gewinnfaktor auf dem Niveau von 3. Der Saldo bleibt gleich. Verluste und Gewinne wechseln sich ab.

Take-Profit 430 Stop-Loss 200:

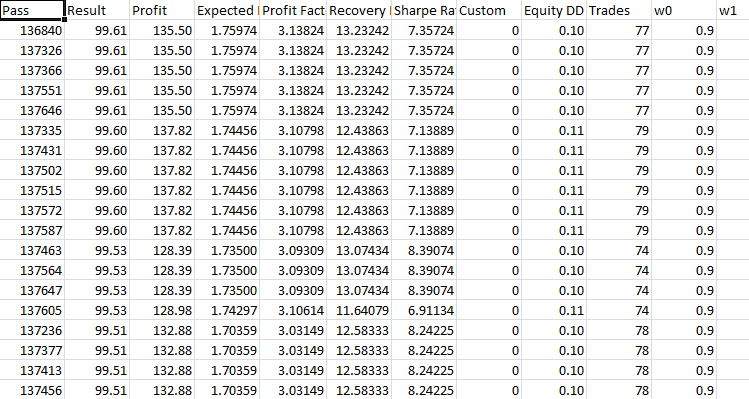
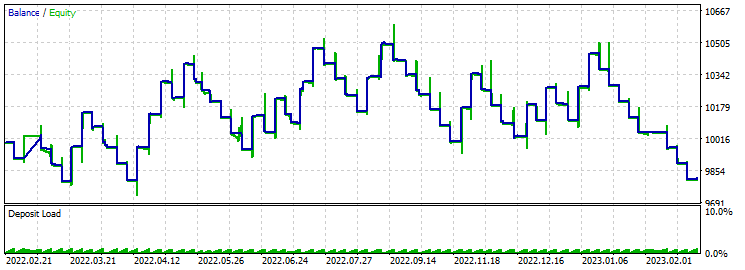
Ein Take-Profit, der doppelt so hoch ist wie der Stop-Loss, führt nicht zu einem positiven Ergebnis. Höchstwahrscheinlich ist das Neuronale Netz nicht in der Lage, einen so hohen Take-Profit vorherzusagen. Bei der Optimierung liegt der Gewinnfaktor auf dem Niveau von 3.

Schlussfolgerung

Wir können sowohl positive als auch negative Schlussfolgerungen aus der geleisteten Arbeit ziehen. Ich werde sie in Form einer kleinen Liste aufführen, damit ich nicht den Faden verliere.

• Was die Skalierung betrifft, so hat sich das System als sehr flexibel erwiesen. Es ist möglich, eine unbegrenzte Anzahl von Schablonen und die Parameter, die wir an sie übergeben, anzuwenden. Denken Sie sich neue Muster aus und beobachten Sie die Ergebnisse, was eine bessere Wirkung auf das Forward Testing hat.
• Es kann notwendig sein, Systeme mit mehreren Perceptrons und unterschiedlichen Templates auszuprobieren, um das Einstiegssignal zu bestimmen.
• Computerleistung ist eindeutig nicht genug. Es werden Systeme mit einer großen Anzahl von Kernen benötigt. Idealerweise ein System mit zwei CPUs mit insgesamt 16 oder mehr Kernen. Wie Sie vielleicht wissen, verwendet der Strategietester nur physische Kerne, keine Threads. Die Möglichkeit, MQL5 Cloud Network zu nutzen, kann die Produktivität unserer Suche erheblich steigern.
• Die Anzahl der weitergegebenen Eingaben erhöht die Belastung eines Perceptrons oder eines Neuronalen Netzes erheblich. Das Runden der Eingabewerte erhöhte die Anzahl der positiven Ergebnisse um etwa das Doppelte.
• Bevor ein System für die weitere Entwicklung ausgewählt wird, müssen einige weitere Optionen für die Übermittlung von Daten an das Perceptron und das Neuronale Netz geprüft werden, nämlich Indikatoren, die sich in einem bestimmten Bereich bewegen, sowie ein so interessantes Phänomen wie die Divergenz. Ich denke, ich werde dies in naher Zukunft tun.

Die Liste der angehängten Dateien:

1. DeepNeuralNetwork - Originalbibliothek;
2. DeepNeuralNetwork2 - modifizierte Bibliothek für das Neuronale Netz mit 4-4-3-Struktur;
3. DeepNeuralNetwork3 - modifizierte Bibliothek für das Neuronale Netz mit 8-4-3-Struktur;
4. perceptron fan 4 SL TP 24 - opt - perceptron-basierter EA zur Optimierung von Fächer-Schablonen mit vier Parametern auf 24 Kerzen;
5. perceptron fan 4 SL TP 48 - opt - perceptron-basierter EA für die Optimierung von Fächer-Schablonen mit vier Parametern auf 48 Kerzen;
6. perceptron fan 8 SL TP 24 - opt - perceptron-basierter EA für die Optimierung von Fächer-Schablonen mit acht Parametern auf 24 Kerzen;
7. perceptron fan 8 SL TP 48 - opt - Perceptron-basierter EA für die Optimierung von Fächer-Schablonen mit acht Parametern auf 48 Kerzen;
8. perceptron fan 4 SL TP 24 - trade (600 60), (200 230), (200 430) - optimierte perceptron-basierte EAs, Fächer-Schablone mit vier Parametern auf 24 Kerzen;
9. perceptron fan 4 SL TP 48 - trade (600 60), (200 230), (200 430) - optimierte perceptron-basierte EAs, Fächer-Schablone mit vier Parametern auf 48 Kerzen;
   
10. perceptron fan 8 SL TP 24 - trade (600 60), (200 230), (200 430) - optimierte perceptron-basierte EAs, Fächer-Schablone für acht Parameter auf 24 Kerzen;
    
11. perceptron fan 8 SL TP 48 - trade (600 60), (200 230), (200 430) - optimierte perceptron-basierte EAs, Fächer-Schablone für acht Parameter auf 48 Kerzen;
    
12. 4-4-3 fan 4 SL TP 24 - opt - bibliotheksbasierte EA für die Optimierung von Fächer-Schablonen mit vier Parametern auf 24 Kerzen;
13. 4-4-3 fan 4 SL TP 48 - opt - bibliotheksbasierte EA für die Optimierung von Fächer-Schablonen mit vier Parametern auf 48 Kerzen;
    
14. 8-4-3 fan 4 SL TP 24 - opt - bibliotheksbasierte EA für die Optimierung von Fächer-Schablonen mit acht Parametern auf 24 Kerzen;
    
15. 8-4-3 fan 4 SL TP 48 - opt - bibliotheksbasierte EA für die Optimierung von Fächer-Schablonen mit acht Parametern auf 48 Kerzen;
    
16. 4-4-3 fan 4 SL TP 24 - trade (600 60), (200 230), (200 430) - optimierte bibliotheksbasierte EAs, Fächer-Schablone mit vier Parametern auf 24 Kerzen;
17. 4-4-3 fan 4 SL TP 48 - trade (600 60), (200 230), (200 430) - optimierte bibliotheksbasierte EAs, Fächer-Schablone mit vier Parametern auf 48 Kerzen;
    
18. 8-4-3 fan 4 SL TP 24 - trade (600 60), (200 230), (200 430) - optimierte bibliotheksbasierte EAs, Fächer-Schablone mit für acht Parameter auf 24 Kerzen;
    
19. 8-4-3 fan 4 SL TP 48 - trade (600 60), (200 230), (200 430) - optimierte bibliotheksbasierte EAs, Fächer-Schablone mit für acht Parameter auf 48 Kerzen;

Vielen Dank für Ihre Aufmerksamkeit!