直觉测试 - 页 13 1...678910111213141516171819 新评论 Alexey Subbotin 2009.11.28 20:12 #121 IlyaA >> : 好的。以下是数据。 我们似乎误解了对方的意思。我对不正常的情绪并不适用于发电机,而是适用于市场。构建第一个增量的分布,自己看一下。 ilyaa 2009.11.28 20:26 #122 Mathemat >> : 那么,对于真空中的球形马来说,即对于保证正态分布来说--是的,这是不可能的。嗯,真正的马不是在真空中的马。有5或6个s.c.e.,甚至10个。 叔叔,请看,现在还有一张1971年的英镑的照片,是日记。可能有一个单一的跛行(顺便说一下,没有一个:),最重要的是它不会成为一个模式。对吗? 自1971年以来的第一次英镑差异。 附上用于检查的数据。 >>S. 也许应该检查他的静止性 :) 附加的文件: data_1.rar 127 kb Alexey Subbotin 2009.11.28 20:28 #123 IlyaA >> : 叔叔,请看,现在还有一张1971年的英镑的照片,是日记。可能有一个单一的跛行(顺便说一下,没有一个:),最重要的是它不会成为一个模式。对吗? 英镑自1971年以来的首次差异 检查的数据附后。 我想用眼睛把它称为拉普拉斯分布。 ilyaa 2009.11.28 20:31 #124 alsu >> : 我把它称为拉普拉斯分布的眼睛 关键是,没有5-6-10个西格玛。否则,是的,但你必须测试它。然而,这可能是可以的。 Sceptic Philozoff 2009.11.28 20:39 #125 伊利亚,这里有一个建议:用正态分布近似这个分布。然后看看真实的直方图和高斯曲线的近似值有多大区别。不要把自己限制在三个西格玛上,至少要查到十个。 另一个微不足道的检查:计算这个分布的第一时刻,并将其与正态分布的时刻进行比较。 金融系列中的肥尾现象早已为人所知。你想向我证明什么? ilyaa 2009.11.28 20:45 #126 Mathemat >> : 伊利亚,这里有一个建议:用正态分布近似这个分布。然后看看真实的直方图和高斯曲线的近似值有多大区别。不要把自己限制在三个西格玛上,至少要查到十个。 另一个微不足道的检查:计算这个分布的第一时刻,并将其与正态分布的时刻进行比较。 金融系列中的肥尾现象早已为人所知。你想向我证明什么? 谈话的内容是5-6-10 RMS。我没有看到他们的外表有什么规律。 Alexey Subbotin 2009.11.28 20:52 #127 IlyaA >> : 关键是,没有5-6-10个西格玛。就像现在这样,是的,但它需要被测试。然而,这可能是正常的。 是非常不可能的事。正态分布通常出现在自然界中,"大 "随机变量是大量以某种方式(但相等)分布的 "小 "随机变量之和。一个最好的例子是布朗运动,在下一个主题中已经用了这么多页来讨论它。就市场而言,价格形成的规律与之相去甚远,因为为了得到一个正常的规律,需要有非常多的外部 "干扰"--它必须是形成分配的主要因素。但我们不认为市场上的定价是噪音,是吗? Sceptic Philozoff 2009.11.28 20:52 #128 在图表上,纯粹从视觉上看,你不会看到那个5-6-10。 在某处,我甚至有一张显示差异的图表。如果你把分布的前两个时刻当作近似正态的时刻,那么频率相差3、4、5等西格玛就很容易计算了。 我不记得具体数字了,但真实的3西格玛偏差频率比高斯的高3-4倍(高斯0.3%,真实的超过1%)。4西格玛偏差在现实中出现的频率比高斯偏差高约15倍。 对于5西格玛,差别是几十倍,甚至几百倍。以此类推。 只要你不评估风险,你就不在乎它是否是高斯的。 P.S. 顺便说一下,根据塔勒布的说法,LTCM的崩溃似乎正是因为低估了风险。10个希格玛的偏差被认为是可以忽略的罕见事件。而这正是所发生的事情。 Alexey Subbotin 2009.11.28 20:54 #129 Mathemat >> : 我不记得具体数字了,但真实的3西格玛偏差频率是高斯的3-4倍(高斯0.3%,真实的超过1%)。4西格玛的偏差在现实中比高斯的偏差多出15倍左右。 对于5西格玛,差别是几十倍。以此类推。 ...这再次成为支持拉普拉斯的证据。 ilyaa 2009.11.28 20:55 #130 Mathemat >> : 只要你不评估风险,你就不在乎它是否是高斯的。 能否请您告诉我如何进行风险评估? 1...678910111213141516171819 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
好的。以下是数据。我们似乎误解了对方的意思。我对不正常的情绪并不适用于发电机,而是适用于市场。构建第一个增量的分布,自己看一下。
那么,对于真空中的球形马来说,即对于保证正态分布来说--是的,这是不可能的。嗯,真正的马不是在真空中的马。有5或6个s.c.e.,甚至10个。
叔叔,请看,现在还有一张1971年的英镑的照片,是日记。可能有一个单一的跛行(顺便说一下,没有一个:),最重要的是它不会成为一个模式。对吗?
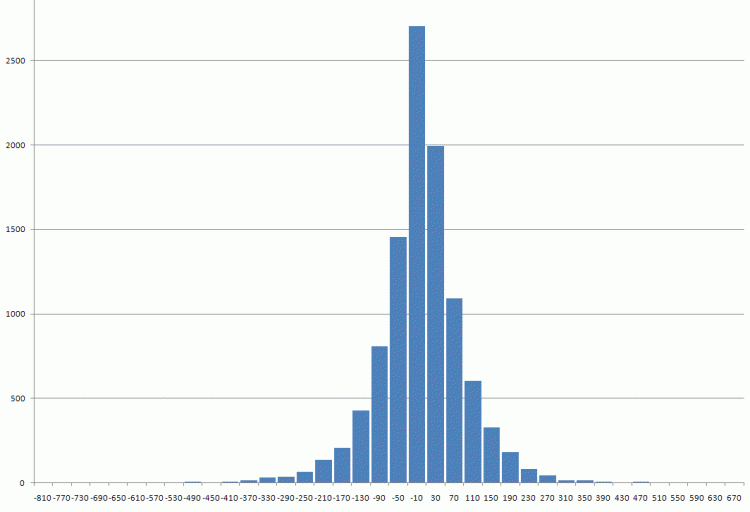
附上用于检查的数据。自1971年以来的第一次英镑差异。
>>S. 也许应该检查他的静止性 :)
叔叔,请看,现在还有一张1971年的英镑的照片,是日记。可能有一个单一的跛行(顺便说一下,没有一个:),最重要的是它不会成为一个模式。对吗?
检查的数据附后。英镑自1971年以来的首次差异
我想用眼睛把它称为拉普拉斯分布。
我把它称为拉普拉斯分布的眼睛
关键是,没有5-6-10个西格玛。否则,是的,但你必须测试它。然而,这可能是可以的。伊利亚,这里有一个建议:用正态分布近似这个分布。然后看看真实的直方图和高斯曲线的近似值有多大区别。不要把自己限制在三个西格玛上,至少要查到十个。
另一个微不足道的检查:计算这个分布的第一时刻,并将其与正态分布的时刻进行比较。
金融系列中的肥尾现象早已为人所知。你想向我证明什么?
伊利亚,这里有一个建议:用正态分布近似这个分布。然后看看真实的直方图和高斯曲线的近似值有多大区别。不要把自己限制在三个西格玛上,至少要查到十个。
另一个微不足道的检查:计算这个分布的第一时刻,并将其与正态分布的时刻进行比较。
金融系列中的肥尾现象早已为人所知。你想向我证明什么?
谈话的内容是5-6-10 RMS。我没有看到他们的外表有什么规律。
关键是,没有5-6-10个西格玛。就像现在这样,是的,但它需要被测试。然而,这可能是正常的。是非常不可能的事。正态分布通常出现在自然界中,"大 "随机变量是大量以某种方式(但相等)分布的 "小 "随机变量之和。一个最好的例子是布朗运动,在下一个主题中已经用了这么多页来讨论它。就市场而言,价格形成的规律与之相去甚远,因为为了得到一个正常的规律,需要有非常多的外部 "干扰"--它必须是形成分配的主要因素。但我们不认为市场上的定价是噪音,是吗?
在图表上,纯粹从视觉上看,你不会看到那个5-6-10。
在某处,我甚至有一张显示差异的图表。如果你把分布的前两个时刻当作近似正态的时刻,那么频率相差3、4、5等西格玛就很容易计算了。
我不记得具体数字了,但真实的3西格玛偏差频率比高斯的高3-4倍(高斯0.3%,真实的超过1%)。4西格玛偏差在现实中出现的频率比高斯偏差高约15倍。 对于5西格玛,差别是几十倍,甚至几百倍。以此类推。
只要你不评估风险,你就不在乎它是否是高斯的。
P.S. 顺便说一下,根据塔勒布的说法,LTCM的崩溃似乎正是因为低估了风险。10个希格玛的偏差被认为是可以忽略的罕见事件。而这正是所发生的事情。
我不记得具体数字了,但真实的3西格玛偏差频率是高斯的3-4倍(高斯0.3%,真实的超过1%)。4西格玛的偏差在现实中比高斯的偏差多出15倍左右。 对于5西格玛,差别是几十倍。以此类推。
...这再次成为支持拉普拉斯的证据。
只要你不评估风险,你就不在乎它是否是高斯的。
能否请您告诉我如何进行风险评估?