
神经网络变得简单(第 75 部分):提升轨迹预测模型的性能
概述
预测即将到来的价格走势的轨迹,或许在为所需规划范围构建交易计划的过程中扮演关键角色之一。这种预测的准确性至关重要。为了提高轨迹预测的品质,我们把轨迹预测模型复杂化。
然而,这个过程也如同硬币的另一面。更复杂的模型需要更多的计算资源。这意味着训练模型及其操作的成本都会增加。模型训练的成本需要加以考虑。然而,就操作成本而言,它们可能更为关键。尤其是在高度波动的市场中使用市价单进行实时交易之时。在这种情况下,我们要查找提高模型性能的方法。理想情况下,这种优化不应影响未来轨迹预测的品质。
我们在最近的文章中讲述的轨迹预测方法是从车辆自动驾驶行业借鉴而来。该领域的研究人员也面临着同样的问题。车速对决策时间提出了更高的要求。采用昂贵的模型来预测轨迹并做出决策,不仅会导致决策时间增加,而且还会增加所用设备的成本,因为这需要安装更昂贵的硬件。在这种情景下,我建议研究文章《自动驾驶中运动预测的有效基线》中提出的思路。其作者设定了构建“轻量级”轨迹预测模型的任务,并强调了以下成就:
- 在运动预测模型的尺度里识别关键挑战,牵涉到资源受约束设备上的实时推理和部署。
- 提出了若干个有效的车辆交通预测基线,即无需明确依赖于对高品质地图情景的详尽分析,而是依赖于先前简单预处理步骤中获得的地图信息,当作预测的指南。
- 使用更少的参数和操作,以更低廉的计算成本达成具有竞争力的性能。
1. 性能提升技术
考虑到分析源数据和模型复杂性之间的平衡,该方法的作者努力运用强大的深度学习技术,包括关注度机制和图形神经网络(GNN),获得局有竞争力的成果。与其它方法相比,这减少了参数和操作的数量。特别是,论文作者使用以下数据作为其模型的输入数据:
- 个体的过去轨迹,及其相应的交互作为社区基准级别模块的唯一输入
- 扩展,用于添加个体冗余区域的简化表示,作为制图数据库的附加输入。
因此,所提出的模型在计算物理情景时,不需要高品质的完全标注地图、或栅格化场景表示。
该方法的作者提议使用一种简单但功能强大的地图预处理算法,其中目标个体的轨迹线性被过滤。然后,它们计算目标个体能够互动的可行区域,仅需考虑地图的几何信息。
社区基线所用的输入,是最明显障碍物的过去轨迹的相对位移,以便馈送到编码器模块。然后使用图神经网络(GNN)计算社区信息。在他们的论文中,该方法的作者使用 CrystalGraph 卷积网络(Crystal-GCN),和多目自关注(MHSA)层来获得个体之间最明显互动。之后,在解码器模块中,使用自回归策略解码这些潜在信息,其中第 i 步的输出取决于前一步。
所提议方法的特点之一是分析与个体的互动,这些个体在涵盖整个时间范围内都有信息 Th = Tobs + Tlen.。同时,减少了复杂交通场景中需要考虑的个体数量。个体 i 的输入是一系列相对位移,替代了所用的绝对 2D 视图:
![]()
该方法的作者未限制或固定序列中的个体数量。为了考虑所有个体的相对位移,使用一个 LSTM-模块,于其中计算序列中每位个体的时态信息。
在按顺序针对每辆车的分析历史进行编码之后,计算个体之间的互动,以便获得最相关的社区信息。为此目的,构造了一个互动图形。Crystal-GCN 层用于构建图形。然后应用 MHSA 来改善对个体-个体互动的学习。
在创建互动机制之前,该方法的作者将时态信息分解为相应的场景。这考虑到每个运动场景可能具有不同数量的个体。互动机制定义为双向全连接图形,其中初始节点特征 v0i 由每辆车 hi,out 的潜在时态信息表示,由运动历史编码器计算得出。另一方面,从节点 k 到节点 l 的边线由绝对坐标中相应个体在某个时间点 tobs,len 之间的距离向量 ek,l 表示:
![]()
给定一个互动图(节点和边线),Crystal-GCN 定义为:
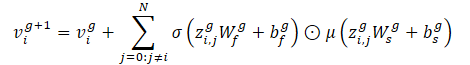
该算子允许我们嵌入边线特征,从而基于车辆之间的距离更新节点特征。该方法的作者使用 2 层 Crystal-GCN,配以 ReLU 及批量常规化,作为层之间的非线性。
σ 和 μ 分别是 sigmoid 和 softplus 的激活函数。此外,zi,j=(vi‖vj‖ei,j) 是 GNN 层中两个节点特征与对应边线的拼接,N 表示场景中的个体总数,W 和 b 是对应层的权重和位移。
遍历互动图形后,每个更新的节点特征 vi 都包含有关个体的时态和社区情景 i 的信息。不过,根据当前位置和过去的轨迹,个体也许需要关注特定的社区信息。为了给这种方法进行建模,该方法的作者使用了具有 4 个眼目的多目自关注机制,其应用于更新的节点特征矩阵 V,其中包含节点 vi 的特征作为字符串。
考虑到盖子下的时态信息,最终社区关注度矩阵 SATT(社区关注度模块的输出,在 GNN 和 MHSA 机制之后)的每一行都代表了个体 i 与周围个体的互动特征。
接下来,该方法的作者使用有关地图的最小信息扩展社区基础模型,从其目标个体的区域 P 离散为 r 个随机选择点的子集 {p0, p1...pr} 围绕合理的中心线(高级和结构化特征),同时参考目标个体在最后一个观察帧中的速度和加速度。这是一个地图预处理步骤,如此模型永远不会看到高分辨率地图。
基于物理定律,该方法的作者将车辆视为刚性结构,在连续时间戳之间运动而不会突然变化。相应地,当描述在道路上行驶的任务时,通常最重要的特征是具体方向(在运动方向上前进)。这允许获得地图的简化版本。
有关轨迹的信息通常包含与实际数据收集过程相关的噪声。为了估算目标个体在最后一个观察帧 tobs,len 中的动态变量,该方法的作者提议首先使用沿每个轴的最小二乘算法过滤目标个体的过去观察。它们假设个体以恒定的加速度移动,并且可以计算目标个体的动态特性(速度和加速度)。然后,它们计算速度向量和加速度的估值。此外,这些向量被汇总为标量,从而获得平滑的估值,为第一次观测分配较少的权重(更高的遗忘因子 λ)。以这种方式,最近的观察结果在判定个体的当前运动状态方面起着关键作用:
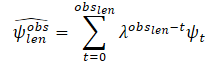
其中
obslen 是观察到的帧数, ψt 是帧 t 中的估算速度/加速度, λ ∈ (0, 1) 是遗忘因子。
在计算运动学状态后,假设物理模型基于在任何时间 t 下具有恒定转弯速度的加速度,从而估算行驶的距离。
然后,这些候选合理车道轨迹经处理后,当作合理的物理信息。首先,它们找到离目标个体的最后一个观察点最近的点,该点将代表合理中心线的起点。然后,它们估算沿原始中心线行进的距离。它们将中心线 m 的端点索引 p 定为累积距离(视为每个点之间的欧几里得距离)大于或等于预先计算的偏差的点。
然后,它们在相应中心线 m 的起点和终点之间执行三次插值,以获取规划范围上的步长。该方法作者进行的实验表明,最佳先验信息,即参考目标个体真实轨迹端点,与经过滤中心线端点之间所覆盖的整个验证集合的平均和中位数距离 L2,是经由参考运动状态下的速度和加速度,并利用最小二乘法过滤输入来达成的。
除了这些高级结构化中心线之外,该方法的作者还提议根据正态分布 N(0, 0.2) 将点变形应用于所有合理的中心线。这会将合理的区域 P 离散化为 r 个随机选择点的子集 {p0, p1...pr} 围绕合理的中心线。从而得到所识别低级特征合理区域的大致了解。该方法的作者使用正态分布 N 作为额外的正则化项,替代正用的车道边界。这将防止编码模块中的过度拟合,类似于先前在轨迹上应用数据增强的方式。
区域和中心线编码器用于计算潜在地图信息。它们分别处理低级和高级地图特征。这些编码器中的每一个都由多层感知器(MLP)表示。首先,它们沿点的维度平滑信息,沿坐标轴交替信息。然后,相应的 MLP(3 层,第一层具有批量常规化、ReLU、和 DropOut)将所解释原点周围的绝对坐标转换为具有代表性的潜在物理信息。静态物理情景(区域编码器的输出)将当作不同模式的常见潜在表示,而具体的物理情景将描绘每种模式的具体地图信息。
未来轨迹解码器代表了所提议的基线模型的第三个分量。该模块由一个 LSTM 模块组成,其按活动历史编码器中学习过去相对运动相同的方式,递归估算未来时间步的相对运动。对于社区基本情况,该模型所用的社区情景由社区互动模块计算,仅关注目标个体的数据。社区情景单独表示场景中的所有流量,表示自回归 LSTM 预测器的输入潜在向量。
从模式 m 的制图基本情况的视角,该方法的作者提议将潜在交通情景识别为社区情景、静态物理情景、和特定物理情景的串联,其将作为 LSTM 解码器的输入隐藏向量。
相对于社区情况下 LSTM 模块的原始数据,它由空间嵌入之后目标个体的已编码的过去 n 次相对运动来表示,而制图基线则加入了目标个体当前绝对位置,与当前中心线之间的已编码距离向量,以及当前标量时间戳 t。在这两种情况(社区和地图)中,LSTM 模块的结果都会使用标准全连接层进行处理。
在获得时间步 t 的相对预测后,我们以这样一种方式平移过去观测值的初始数据,以便将我们最后计算的相对运动带到向量的末尾,并删除第一个数据。
计算多模态预测之后,它们由 MLP 残差连接和处理,从而获得置信度(置信度越高,该区域的可能性越大,越接近真实)。
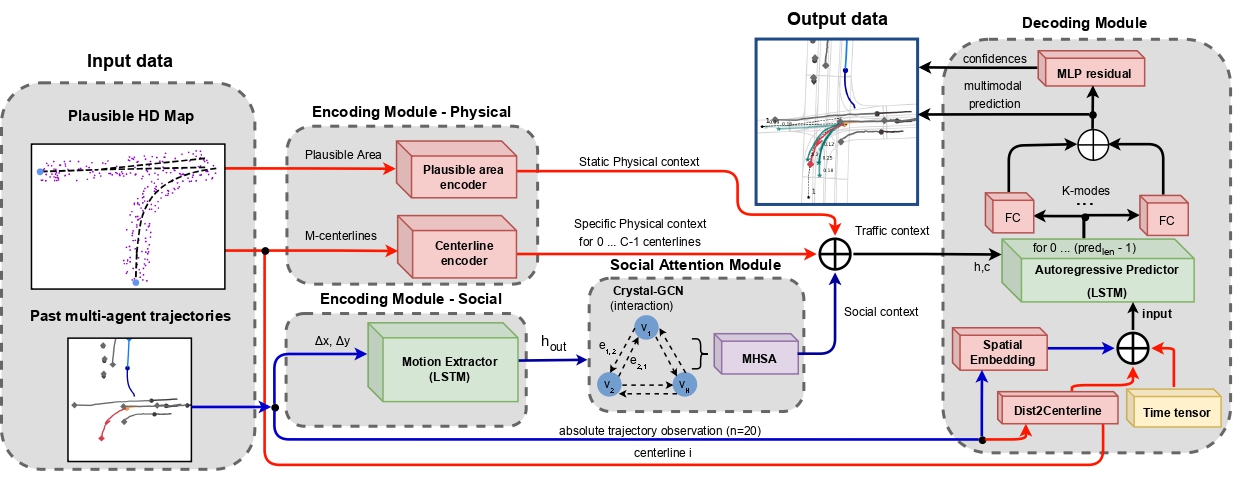
由论文作者所表述方法的原始可视化提供如下。此处,蓝线表示社区信息,红线表示有关地图的信息传输。
2. 利用 MQL5 实现
我们已经研究了所提议方法的理论层面。现在,我们利用 MQL5 实现它。如您所见,该方法的作者将模型划分为多个模块。每个模块使用最少的层数。同时,独立模块架构的简化伴随有关已分析环境的先验信息的额外数据。特别是,地图已预处理,且所传递的轨迹业已过滤。这样,您就可以减少初始数据的噪声和体量,无需丢失构造预测轨迹的品质。
2.1创建 CrystalGraph 卷积网络层
此外,在所提议方法中,我们遇到了以前从未遇到过的图形神经层。相应地,在继续构建所提议算法之前,我们将在我们的函数库中创建一个新层。
该方法作者提出的 CrystalGraph 卷积网络层可以用以下公式表示:
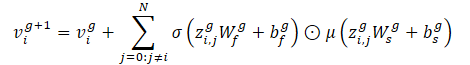
本质上,于此我们看到 2 个全连接层的工作结果的逐个元素相乘。其中一个由 sigmoid 激活,表示图形顶点之间存在连接的可训练二元矩阵。第二层由 SoftPlus 函数激活,它是 ReLU 的软件模拟。
为了实现 CrystalGraph 卷积网络,我们将创建一个新类 CNeuronCGConvOCL,它继承了 CNeuronBaseOCL 的基本功能。
class CNeuronCGConvOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL cInputF; CNeuronBaseOCL cInputS; CNeuronBaseOCL cF; CNeuronBaseOCL cS; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronCGConvOCL(void) {}; ~CNeuronCGConvOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronCGConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
我们的新类会收到一套标准方法用于覆盖,以及来自父类的基本功能。为了实现图形卷积算法,我们将创建 4 个内部全连接层:
- 2 个在反向传播验算期间写入原始数据和误差梯度(cInputF 和 cInputS)
- 2 个执行功能(cF 和 cS)。
我们将创建所有内部静态对象,如此类的构造函数和析构函数将保持 “空”。
在类的初始化方法 Init 中,我们将首先调用父类的相关方法,其针对从外部程序接收的数据实现了所有必要的控制,并初始化所继承对象和变量。
bool CNeuronCGConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false; activation = None;
之后,我们调用它们的初始化方法,按顺序初始化添加的内部对象。
if(!cInputF.Init(numNeurons, 0, OpenCL, window, optimization, batch)) return false; if(!cInputS.Init(numNeurons, 1, OpenCL, window, optimization, batch)) return false; cInputF.SetActivationFunction(None); cInputS.SetActivationFunction(None); //--- if(!cF.Init(0, 2, OpenCL, numNeurons, optimization, batch)) return false; cF.SetActivationFunction(SIGMOID); if(!cS.Init(0, 3, OpenCL, numNeurons, optimization, batch)) return false; cS.SetActivationFunction(LReLU); //--- return true; }
请注意,对于源数据记录的内部层,我们指定了空缺激活函数。对于功能层,我们包括了由所创建层的算法提供的激活函数。CNeuronCGConvOCL 层本身没有激活函数。
初始化对象之后,我们转到创建前馈方法 feedForward。在参数中,该方法接收指向前一个神经层对象的指针,其输出包含初始数据。
bool CNeuronCGConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput() || NeuronOCL.getOutputIndex() < 0) return false;
在方法主体中,我们立即检查接所接收指针的相关性。
成功通过控制模块之后,我们需要将源数据从上一层的缓冲区传输到我们 2 个内部源数据层的缓冲区。不要忘记,我们在 OpenCL 关联环境端执行所有神经层操作。因此,我们还需要将数据复制到 OpenCL 关联环境的内存之中。但我们将更进一步,执行 “复制” 时并不进行物理传输数据。我们将简单地替换指向内层结果缓冲区的指针,并向它们传递指向前一层结果缓冲区的指针。此处我们还要指明前一层的激活函数。
if(cInputF.getOutputIndex() != NeuronOCL.getOutputIndex()) { if(!cInputF.getOutput().BufferSet(NeuronOCL.getOutputIndex())) return false; cInputF.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation()); } if(cInputS.getOutputIndex() != NeuronOCL.getOutputIndex()) { if(!cInputS.getOutput().BufferSet(NeuronOCL.getOutputIndex())) return false; cInputS.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation()); }
因此,当操控内层时,我们可以直接访问前一层的结果缓冲区,而无需物理复制数据。我们以最少的资源实现了数据传输任务。甚至,我们消除了在 OpenCL 关联环境中创建两个额外缓冲区的做法,从而优化了内存占用。
然后我们简单地为内部功能层调用前馈方法。
if(!cF.FeedForward(GetPointer(cInputF))) return false; if(!cS.FeedForward(GetPointer(cInputS))) return false;
作为这些操作的结果,我们得到图形的情景和关系矩阵然后我们执行它们的元素级相乘。为了执行该操作,我们使用 Dropout 内核,我们创建该内核是为了将原始数据逐个元素乘以掩码。在我们的例子中,对于相同的数学运算,我们有不同的背景。
我们将必要的参数和初始数据传递给该内核。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cF.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cS.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
之后,我们将其放入执行队列当中。
下一步是实现反向传播功能。此处,我们从程序的 OpenCL 端创建一个内核开始。要点是,来自前一层的误差梯度的分布,首先根据它们对最终结果的影响,依此转移到内层。为此,我们需要将得到的误差梯度乘以第二个功能层的前馈验算的结果。为了避免两次调用上面所用的元素相乘内核,我们将创建一个新内核,于其中我们将在 1 遍验算中获得两层的误差梯度。
在 CGConv_HiddenGradient 内核参数中,我们将传递指向 5 个数据缓冲区的指针,以及两个层的激活函数类型。
__kernel void CGConv_HiddenGradient(__global float *matrix_g,///<[in] Tensor of gradients at current layer __global float *matrix_f,///<[in] Previous layer Output tensor __global float *matrix_s,///<[in] Previous layer Output tensor __global float *matrix_fg,///<[out] Tensor of gradients at previous layer __global float *matrix_sg,///<[out] Tensor of gradients at previous layer int activationf,///< Activation type (#ENUM_ACTIVATION) int activations///< Activation type (#ENUM_ACTIVATION) ) { int i = get_global_id(0);
我们将根据各层中的神经元数量,在一维任务空间中启动内核。在内核的主体中,我们立即根据线程标识符判定正在分析的元素位于数据缓冲区中的偏移量。
接下来,为了减少访问 GPU 全局内存的 “密集” 操作,我们将分析元素的数据存储在局部变量之中,由此访问速度提高了许多倍。
float grad = matrix_g[i]; float f = matrix_f[i]; float s = matrix_s[i];
此刻,我们拥有计算两层误差梯度所需的所有数据,于是我们计算它们。
float sg = grad * f; float fg = grad * s;
但在把所得数值写入全局数据缓冲区的元素之前,我们需要将找到的误差梯度调整至相应的激活函数。
switch(activationf) { case 0: f = clamp(f, -1.0f, 1.0f); fg = clamp(fg + f, -1.0f, 1.0f) - f; fg = fg * max(1 - pow(f, 2), 1.0e-4f); break; case 1: f = clamp(f, 0.0f, 1.0f); fg = clamp(fg + f, 0.0f, 1.0f) - f; fg = fg * max(f * (1 - f), 1.0e-4f); break; case 2: if(f < 0) fg *= 0.01f; break; default: break; }
switch(activations) { case 0: s = clamp(s, -1.0f, 1.0f); sg = clamp(sg + s, -1.0f, 1.0f) - s; sg = sg * max(1 - pow(s, 2), 1.0e-4f); break; case 1: s = clamp(s, 0.0f, 1.0f); sg = clamp(sg + s, 0.0f, 1.0f) - s; sg = sg * max(s * (1 - s), 1.0e-4f); break; case 2: if(s < 0) sg *= 0.01f; break; default: break; }
在内核操作结束时,我们将操作结果保存到全局数据缓冲区的相应元素之中。
matrix_fg[i] = fg; matrix_sg[i] = sg; }
创建内核之后,我们返回正在工作的类方法。误差梯度分布在 calcInputGradients 方法中实现,在该方法的参数中,我们将传递一个指向前一层对象的指针。在方法主体中,我们立即检查接所接收指针的相关性。
bool CNeuronCGConvOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer || !prevLayer.getGradient() || prevLayer.getGradientIndex() < 0) return false;
接下来,我们需要调用上述内核,以便跨内层分配梯度 CGConv_HiddenGradient。此处我们首先定义任务空间。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = Neurons();
我们将必要的参数传递给内核。
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cF.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cF.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, cS.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, cS.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, cF.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, cS.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
将内核放入执行队列当中。
if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
接下来,我们需要通过内部全连接层传播误差梯度。为此,我们调用它们的相应方法。
if(!cInputF.calcHiddenGradients(GetPointer(cF))) return false; if(!cInputS.calcHiddenGradients(GetPointer(cS))) return false;
在这个阶段,我们得到了原始数据的 2 个内层上的 2 个误差梯度流的结果。我们简单地将它们相加,并将结果传送到前一层的级别。
if(!SumAndNormilize(cF.getOutput(), cS.getOutput(), prevLayer.getOutput(), 1, false)) return false; //--- return true; }
请注意,在这种情况下,我们没有在任何地方明确考虑前一层的激活函数。这对于正确传输误差梯度非常重要。但这里有一个细微差别。我们所有的神经层类都是以这样一种方式构建的,即在将梯度传播到前一层的缓冲区之前,对激活函数的导数进行调整。为此目的,在前馈验算期间,我们为源数据的内层指定了前一层的激活函数。因此,当误差梯度通过我们的内部功能层传播时,我们立即将误差梯度调整为激活函数的导数,这对于两个流的梯度是相同的。在输出中,我们汇总了已经针对激活函数的导数调整的误差梯度。
第二种反向传播方法(更新权重矩阵 updateInputWeights)的算法非常简单。此处我们只调用功能内层的相应方法。
bool CNeuronCGConvOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cF.UpdateInputWeights(cInputF.AsObject())) return false; if(!cS.UpdateInputWeights(cInputS.AsObject())) return false; //--- return true; }
以我的观点,我们实现的 CNeuronCGConvOCL 类的其余方法,并不是特别有趣。我在其中用到了相应方法的常用算法,这些算法在本系列文章中曾多次讲述过。您可以在附件中找到它们。在那里,您还可以找到撰写本文时用到的所有程序的完整代码。现在,我们转到构建模型架构和训练它们时所提议方式的实现。
2.2模型架构
为了创建模型的架构,我们将用到来自之前几篇文章中的模型,同时保持原始数据的结构。这是有意为之的。在 ADAPT 结构中,您还可以选择一个编码器模块,其表示为 特征编码器。它还包括来自多目关注连续层的社区关注模块。可以将端点预测区模块与所提议中心线进行比较。置信度模块类似于预测轨迹概率。这令操控新模型更加有趣。
bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *endpoints, CArrayObj *probability) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!endpoints) { endpoints = new CArrayObj(); if(!endpoints) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
我们从编码器模型开始。我们向模型输入饲喂有关环境状态的原始数据。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
原始源数据在批量数据常规化单元中进行预处理。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
接下来,取代作者提议的 LSTM 模块,我保留了带有位置编码的嵌入层,因为这种方式允许我们保存和分析更深层的历史记录。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {prev_count}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout; if(!encoder.Add(descr)) { delete descr; return false; }
我还在编码器模型中包含一个社区关注度模块。按照原来的方法,它由 2 个连续的图形卷积层组成,由一个批量常规化层分离。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCGConvOCL; descr.count = prev_count * prev_wout; descr.window = descr.count; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count*prev_wout; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCGConvOCL; descr.count = prev_count * prev_wout; descr.window = descr.count; if(!encoder.Add(descr)) { delete descr; return false; }
社区关注度模块的输出使用 1 个多目关注度层。
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLMHAttentionOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = 16; descr.layers = 1; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
我们可以从环境地图中分析得出即将到来的价格走势的一些最可能的选择,然而在我们的例子中,没有环境地图。因此,我们保留端点预测模块,替代中心线。它将使用社区关注度模块的结果作为源数据。
//--- Endpoints endpoints.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (prev_count * prev_wout); descr.activation = None; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
但首先我们需要在一个完全连接层中预处理数据。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
然后我们将使用 LSTM 模块,正如轨迹解码模块方法的作者提议的那样。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronLSTMOCL; descr.count = 3 * NForecast; descr.activation = None; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
在模块的输出端,我们为给定的选项数量生成端点的多模态表示。
预测选择轨迹概率的模型保持不变。我们将前 2 个模型的结果馈送到模型。
//--- Probability probability.Clear(); //--- Input layer if(!probability.Add(endpoints.At(0))) return false; //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = 3 * NForecast; descr.optimization = ADAM; descr.activation = SIGMOID; if(!probability.Add(descr)) { delete descr; return false; }
使用一个全连接层模块处理它们。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NForecast; descr.activation = None; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; }
使用 SoftMax 层将结果转换到概率区域。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = NForecast; descr.step = 1; descr.activation = None; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; } //--- return true; }
与之前的工作一样,我们不会尝试预测价格走势的详细轨迹。我们的主要目标是在金融市场上盈利。因此,我们将训练一个扮演者模型,该模型能够基于预测的价格走势端点生成最优行为策略。
模型架构完全复制自上一篇文章,并在附件文件 “...\Experts\BaseLines\Trajectory.mqh” 中的 CreateDescriptions 方法中呈现。其详细说明在上一篇文章中讲述。
2.3模型训练
从所呈现的模型架构中可以看出,在 EA 中它们与环境交互所用的顺序保持不变。因此,在本文中,我们不会详述收集训练数据和测试训练模型的程序算法。我们直接进入模型训练智能系统。如上一篇文章,所有模型都在一个 EA “...\Experts\BaseLines\Study.mq5” 中训练
在 EA 初始化方法中,我们首先加载一个训练模型的样本数据库。
int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
然后,我们加载预先训练的模型,并在必要时创建新的模型。
//--- load models float temp; if(!BLEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !BLEndpoints.Load(FileName + "Endp.nnw", temp, temp, temp, dtStudied, true) || !BLProbability.Load(FileName + "Prob.nnw", temp, temp, temp, dtStudied, true) ) { CArrayObj *encoder = new CArrayObj(); CArrayObj *endpoint = new CArrayObj(); CArrayObj *prob = new CArrayObj(); if(!CreateTrajNetDescriptions(encoder, endpoint, prob)) { delete endpoint; delete prob; delete encoder; return INIT_FAILED; } if(!BLEncoder.Create(encoder) || !BLEndpoints.Create(endpoint) || !BLProbability.Create(prob)) { delete endpoint; delete prob; delete encoder; return INIT_FAILED; } delete endpoint; delete prob; delete encoder; }
if(!StateEncoder.Load(FileName + "StEnc.nnw", temp, temp, temp, dtStudied, true) || !EndpointEncoder.Load(FileName + "EndEnc.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *endpoint = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); if(!CreateDescriptions(actor, endpoint, encoder)) { delete actor; delete endpoint; delete encoder; return INIT_FAILED; } if(!Actor.Create(actor) || !StateEncoder.Create(encoder) || !EndpointEncoder.Create(endpoint)) { delete actor; delete endpoint; delete encoder; return INIT_FAILED; } delete actor; delete endpoint; delete encoder; //--- }
我们将所有模型传输到单个 OpenCL 关联环境之中。
OpenCL = Actor.GetOpenCL(); StateEncoder.SetOpenCL(OpenCL); EndpointEncoder.SetOpenCL(OpenCL); BLEncoder.SetOpenCL(OpenCL); BLEndpoints.SetOpenCL(OpenCL); BLProbability.SetOpenCL(OpenCL);
以及控制模型的架构。
Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
BLEndpoints.getResults(Result); if(Result.Total() != 3 * NForecast) { PrintFormat("The scope of the Endpoints does not match forecast endpoints (%d <> %d)", 3 * NForecast, Result.Total()); return INIT_FAILED; }
BLEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
在方法结束时,我们创建辅助数据缓冲区,并为启动模型训练生成自定义事件。
if(!bGradient.BufferInit(MathMax(AccountDescr, NForecast), 0) || !bGradient.BufferCreate(OpenCL)) { PrintFormat("Error of create buffers: %d", GetLastError()); return INIT_FAILED; }
if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
在逆初始化方法中,我们保存经过训练的模型,并清除动态对象的内存。
void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); StateEncoder.Save(FileName + "StEnc.nnw", 0, 0, 0, TimeCurrent(), true); EndpointEncoder.Save(FileName + "EndEnc.nnw", 0, 0, 0, TimeCurrent(), true); BLEncoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); BLEndpoints.Save(FileName + "Endp.nnw", 0, 0, 0, TimeCurrent(), true); BLProbability.Save(FileName + "Prob.nnw", 0, 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
模型训练过程在 Train 方法中实现。模型训练过程在 Train 方法中实现。在方法的主体中,我们首先生成一个选择轨迹的概率向量。
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
之后,我们创建局部变量。
vector<float> result, target; matrix<float> targets, temp_m; bool Stop = false; //--- uint ticks = GetTickCount();
创建模型训练循环系统。
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - PrecoderBars - batch)); if(state <= 0) { iter--; continue; }
在外部循环的主体中,我们从来自经验回放缓冲区中的轨迹进行采样,及其学习开始状态。
此处,我们将判定所选轨迹上训练数据包的最后状态,并清除循环数据缓冲区。
BLEncoder.Clear(); BLEndpoints.Clear(); int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
在嵌套循环的主体中,我们从经验回放缓冲区中获取一个环境状态,并运行端点预测模型,及其概率的前馈验算。
for(int i = state; i < end; i++) { bState.AssignArray(Buffer[tr].States[i].state); //--- Trajectory if(!BLEncoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!BLEndpoints.feedForward((CNet*)GetPointer(BLEncoder), -1, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!BLProbability.feedForward((CNet*)GetPointer(BLEncoder), -1, (CNet*)GetPointer(BLEndpoints))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
如您所见,上面讲述的操作与上一篇文章中的操作没有太大区别。但会有变化。它们将特别关注在训练期间把先验知识传送到模型。因为通过使用有关环境的先验知识,该方法的作者努力提高预测的准确性,同时简化模型本身的架构。
事实上,有若干种方式可将先验知识传送到模型。我们可以对原始数据进行预处理以对其进行压缩并使其信息量更大。这个提议是由中心线方法的作者提议。
在训练模型的过程中,我们也可以在生成目标值时使用先验知识。这将有助于模型更多地关注源数据中最明显的对象。当然,也可能同时使用这两种方式。
出于本文目的,我们将使用第二种方法。为了准备端点预测模型训练的目标值,我们将首先从回放缓冲区收集即将到来的价格走势数据。
targets = matrix<float>::Zeros(PrecoderBars, 3); for(int t = 0; t < PrecoderBars; t++) { target.Assign(Buffer[tr].States[i + 1 + t].state); if(target.Size() > BarDescr) { matrix<float> temp(1, target.Size()); temp.Row(target, 0); temp.Reshape(target.Size() / BarDescr, BarDescr); temp.Resize(temp.Rows(), 3); target = temp.Row(temp.Rows() - 1); } targets.Row(target, t); } target = targets.Col(0).CumSum(); targets.Col(target, 0); targets.Col(target + targets.Col(1), 1); targets.Col(target + targets.Col(2), 2);
作为先验知识的一个例子,我们将使用 MACD 指标的信号。我们的主线数据存储在描述环境状态的数组第 7 号元素当中。信号线的数值位于同一数组的第 8 号元素当中。如果信号线高于主线,则我们认为当前趋势看涨。否则,看跌。
int direct = (Buffer[tr].States[i].state[8] >= Buffer[tr].States[i].state[7] ? 1 : -1);
我同意这种方式非常简化,我们可以使用更多的信号和指标来辨别趋势。但恰恰这种简单性将提供一个在本文框架内实施的清晰示例,并允许我们评估该方式的影响。我建议您在项目中采用更综合的方式,从而获得最优结果。
在判定了趋势的方向之后,我们判定在这个方向上的极值。我们按找到的极值,限制即将到来的价格走势的矩阵。
ulong extr=(direct>0 ? target.ArgMax() : target.ArgMin()); if(extr==0) { direct=-direct; extr=(direct>0 ? target.ArgMax() : target.ArgMin()); } targets.Resize(extr+1, 3);
这里需要注意的是,MACD 信号滞后于趋势变化。因此,如果在判定极值时,我们在矩阵的第一行中找到它,我们将趋势的方向更改为相反的方向,并重新定义极值。
通过使用环境的先验知识判定趋势,在一定程度上降低了目标值的随机性,我们之前依据第一根即将到来的蜡烛观察方向。一般来说,这应该有助于我们的模型更正确地判定价格走势的趋势和未来方向。
从即将到来的价格走势的截断矩阵中,我们通过即将到来的价格走势的极值来判定目标值。
if(direct >= 0) { target = targets.Max(AXIS_HORZ); target[2] = targets.Col(2).Min(); } else { target = targets.Min(AXIS_HORZ); target[1] = targets.Col(1).Max(); }
如前,我们从整个多模态终端节点空间判定最准确的模型预测,并在运行反向传播时仅调整选定的预测。
BLEndpoints.getResults(result); targets.Reshape(1, result.Size()); targets.Row(result, 0); targets.Reshape(NForecast, 3); temp_m = targets; for(int i = 0; i < 3; i++) temp_m.Col(temp_m.Col(i) - target[i], i); temp_m = MathPow(temp_m, 2.0f); ulong pos = temp_m.Sum(AXIS_VERT).ArgMin(); targets.Row(target, pos); Result.AssignArray(targets);
以这种方式准备的目标值,允许我们更新端点预测模型,及初始环境状态编码器的参数。
if(!BLEndpoints.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } if(!BLEncoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
此处,我们调整概率预测模型。但是我们不会传送该模型的误差梯度至端点预测模型或编码器。
bProbs.AssignArray(vector<float>::Zeros(NForecast)); bProbs.Update((int)pos, 1); bProbs.BufferWrite(); if(!BLProbability.backProp(GetPointer(bProbs), GetPointer(BLEndpoints))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
下一步是训练扮演者政策。此处,我们首先准备有关账户状态,和持仓的信息。
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
然后我们创建状态和预测端点的嵌入。
//--- State embedding if(!StateEncoder.feedForward((CNet *)GetPointer(BLEncoder), -1, (CBufferFloat*)GetPointer(bAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } //--- Endpoint embedding if(!EndpointEncoder.feedForward((CNet *)GetPointer(BLEndpoints), -1, (CNet*)GetPointer(BLProbability))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
注意,与以前的工作不同,我们使用经过训练的模型之上的前馈验算结果来生成预测端点的嵌入,而不是目标值。这将允许我们根据终端节点预测模型的结果定制扮演者的性能。
准备嵌入后,我们通过扮演者模型执行前馈验算。
//--- Actor if(!Actor.feedForward((CNet *)GetPointer(StateEncoder), -1, (CNet*)GetPointer(EndpointEncoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
前馈验算成功执行后,随后进行后向验算,以遍更新模型参数。此处,在准备训练扮演者模型的目标值时,我们还将加入一些先验知识。特别是,在一个方向或另一个方向开仓交易之前,我们将检查 RSI 和 CCI 指标的数值,它们分别存储在环境状态描述数组的第 4 号和第 5 号元素当中。
if(direct > 0) { if(Buffer[tr].States[i].state[4] > 30 && Buffer[tr].States[i].state[5] > -100 ) { float tp = float(target[1] / _Point / MaxTP); result[1] = tp; int sl = int(MathMax(MathMax(target[1] / 3, -target[2]) / _Point, MaxSL / 10)); result[2] = float(sl) / MaxSL; result[0] = float(MathMax(risk / (value * sl), 0.01)) + FLT_EPSILON; } }
else { if(Buffer[tr].States[i].state[4] < 70 && Buffer[tr].States[i].state[5] < 100 ) { float tp = float((-target[2]) / _Point / MaxTP); result[4] = tp; int sl = int(MathMax(MathMax((-target[2]) / 3, target[1]) / _Point, MaxSL / 10)); result[5] = float(sl) / MaxSL; result[3] = float(MathMax(risk / (value * sl), 0.01)) + FLT_EPSILON; } }
请注意,在这种情况下,我们没有明确检查 MACD 指标信号,因为在判定即将到来的走势方向的指向时,它们已经被考虑在内。
有了这些准备好的目标值,我们就可以通过复合扮演者模型执行反向传播验算。
Result.AssignArray(result); if(!Actor.backProp(Result, (CNet *)GetPointer(EndpointEncoder)) || !StateEncoder.backPropGradient(GetPointer(bAccount), (CBufferFloat *)GetPointer(bGradient)) || !EndpointEncoder.backPropGradient((CNet*)GetPointer(BLProbability)) ) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
我们使用扮演者误差梯度来更新编码器参数,但我们不会更新端点预测模型。
if(!BLEncoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
在循环系统内的操作结束时,我们只需要通知用户训练过程的进度。
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Endpoints", percent, BLEndpoints.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Probability", percent, BLProbability.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
模型训练过程完成后,我们清除图表上的注释字段。将模型训练结果输出到日志中,并启动 EA 终止过程。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Endpoints", BLEndpoints.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Probability", BLProbability.getRecentAverageError()); ExpertRemove(); //--- }
关于实现优化轨迹预测模型的基本方法,我们研究其算法到此结束。您可以在附件中找到此处用到的所有程序的完整代码。
3. 测试
我们已利用 MQL5 实现了优化轨迹预测模型的基本方法。特别是,我们创建了一个图形卷积层,并应用了在模型训练期间设定目标时用到的有关环境的先验知识的方法。这减少了模型中的层数,这应该有降低模型复杂性、并提高其运行速度的潜力。我们在 MetaTrader 5 策略测试器中基于真实数据评估了在训练和测试训练模型的过程中所提出的方法的影响。
如前,模型的训练和测试依据 EURUSD H1 的 2023 年前 7 个月进行。
在构建模型架构时,我们曾提到保留了源数据的结构。这允许我们在训练中使用之前文章中收集的经验回放缓冲区。我们只需将之前收集的数据文件重命名为 BaseLines.bd。如果您要创建新的训练数据集,您可以使用前面讨论的任何方法,即环境交互 EA。
在模型训练过程中生成目标值期间,允许我们使用训练数据集,直到我们获得最优结果,而无需更新和补充它。
然而,训练结果并不像预期的那样有前景。在测试经过训练的模型时,我们将测试周期从 1 个月增加到 3 个月。
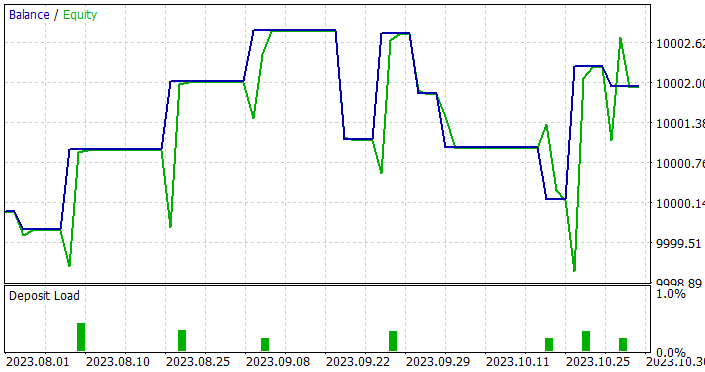
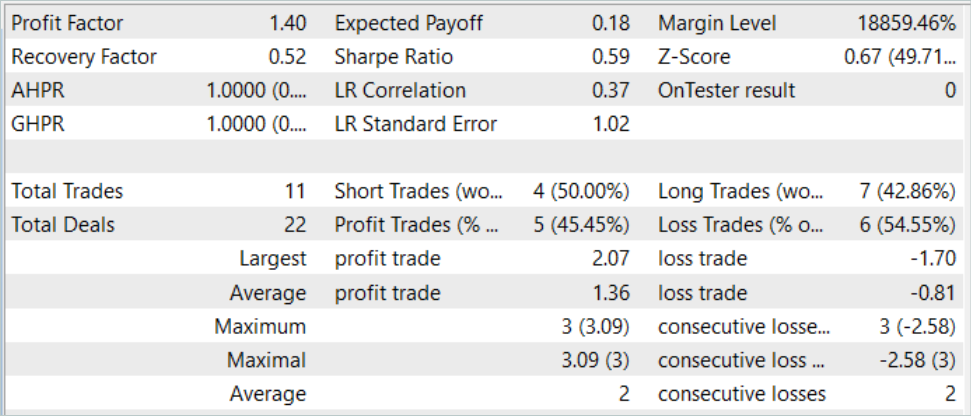
好吧,我们设法获得了一个能够在训练和测试样本上都产生盈利的模型。甚至,所得模型表现出良好的稳定性,盈利因子为 1.4。依据历史数据训练 7 个月后,该模型能够在至少 3 个月里产生盈利。这也许表明该模型能够识别出相当稳定的预测变量。
然而,该模型在交易数量方面相当糟糕。在 11 个月内完成 3 笔交易实在太少了。这不是我们想要达到的结果。
结束语
在本文中,我们研究了优化轨迹预测模型性能的基本方法。所提议方式的实现,令训练模型具备能够识别源数据中真正显要的预测因子的能力。这允许在训练后相当长的时间内稳定运行。
然而,我们的结果表明模型做出的决策具有很强的保守性。这反映在极少数的所做成交当中。如此,这就是我们必须继续研究的方向。
参考
文中所用程序
| # | 已发行 | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | 智能交易系统 | 样本收集 EA |
| 2 | ResearchRealORL.mq5 | 智能交易系统 | 用于使用 Real-ORL 方法收集示例的 EA |
| 3 | Study.mq5 | 智能交易系统 | 模型训练 EA |
| 4 | Test.mq5 | 智能交易系统 | 模型测试 EA |
| 5 | Trajectory.mqh | 类库 | 系统状态定义结构 |
| 6 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 7 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/14187
 自定义指标(第一部份):在MQL5中逐步开发简单自定义指标的入门指南
自定义指标(第一部份):在MQL5中逐步开发简单自定义指标的入门指南
 数据处理的分组方法:在MQL5中实现组合算法
数据处理的分组方法:在MQL5中实现组合算法
 开发回放系统(第 42 部分):图表交易项目(I)
开发回放系统(第 42 部分):图表交易项目(I)
 如何使用抛物线转向(Parabolic SAR)指标设置跟踪止损(Trailing Stop)
如何使用抛物线转向(Parabolic SAR)指标设置跟踪止损(Trailing Stop)