
交易中的神经网络:一种复杂的轨迹预测方法(Traj-LLM)
概述
预测金融市场未来价格走势在交易者的决策过程中起着关键作用。高质量的预测使交易者能够做出更明智的决策并最小化风险。然而,由于市场的混沌和随机性质,预测未来价格轨迹面临着诸多挑战。即使是最先进的预测模型,也常常无法充分考虑影响市场动态的所有因素,例如参与者行为的突然转变或意外的外部事件。
近年来,人工智能的发展,特别是在大型语言模型(LLMs)领域,为解决各种复杂任务开辟了新的途径。LLMs在处理复杂信息和模拟类似人类推理的情景方面展现出了显著的能力。这些模型成功应用于从自然语言处理到时间序列预测的各个领域,使它们成为分析和预测市场走势的有前景的工具。
我想向您介绍论文中描述的Traj-LLM算法(Traj-LLM:用预训练大型语言模型增强轨迹预测的新探索)。Traj-LLM是为了解决自动驾驶领域中的轨迹预测任务而开发的。作者们提出使用LLMs来提高对交通参与者未来轨迹预测的准确性和适应性。
此外,Traj-LLM将大型语言模型的强大功能与创新的时间依赖性和对象间交互建模方法相结合,即使在复杂和动态的条件下,也能实现更准确的轨迹预测。该模型不仅提高了预测的准确性,还提供了分析和理解潜在未来情景的新方法。我们预计,采用作者提出的这种方法能够有效地完成我们的任务,并将提高对未来价格走势预测的质量。
1. Traj-LLM算法
Traj-LLM架构由四个关键组件构成:
- 稀疏上下文联合编码
- 高级交互建模,
- 车道感知概率学习,
- 拉普拉斯多模态解码器。
Traj-LLM方法的作者们建议使用LLM来进行轨迹预测,从而消除了对显式实时特征工程的需求。稀疏上下文联合编码最初将智能体和场景特征转换为LLMs可解释的形式。这些表示随后被输入到预训练的LLMs中以处理高级交互建模。为了模拟类似人类的认知功能,并进一步增强Traj-LLM中的场景理解,通过Mamba模块引入了车道感知的概率学习。最后,使用拉普拉斯多模态解码器来生成可靠的预测。
Traj-LLM的第一步是对场景的时空原始数据进行编码,例如智能体状态和车道信息。对于这些数据中的每一个,使用一个包含循环层和MLP的嵌入模型来提取多维特征。得到的张量hi和fl随后被传递到一个名为Fusion的子模块中,促进智能体状态和车道在局部区域之间的复杂信息交换。此过程使用标记嵌入机制来与LLM架构对齐。
具体而言,融合过程使用多头Self-Attention机制来合并Agent-Agent特征。此外,合并Agent-Lane和Lane-Agent特征包括使用带跳跃连接的多头交叉注意力机制更新智能体和车道视图。该过程的正规表示如下:

随后,hi和fl被组合形成稀疏上下文联合编码gi,直观地捕捉与向量化实体的局部接受域相关的依赖关系。这种编码方法旨在使LLMs能够有效地解释轨迹数据,从而扩展LLM的能力。
轨迹转换遵循由各种场景元素派生的高级约束所控制的模式。为了研究这些交互,作者们探索了LLMs在轨迹预测任务中建模固有依赖关系。尽管轨迹数据与自然语言文本之间存在相似性,但直接使用LLMs处理稀疏上下文联合编码被认为是低效的。因为预训练的LLMs主要针对文本数据进行了优化。一种替代方案是对所有LLMs进行全面再训练。这个过程需要大量的计算资源,导致其在某种程度上不太可行。另一个更有效的解决方案是使用Parameter-Efficient Fine-Tuning方法(PEFT)来微调预训练的LLMs。
Traj-LLM的作者们使用预训练的NLP变换器架构的参数,特别是GPT-2,来进行高级交互建模。他们提议冻结所有预训练的参数,并使用低秩适应技术(LoRA)引入新的可训练参数。LoRA被应用于LLM注意力机制的Query和Key实体。
因此,稀疏上下文联合编码gi被输入到一个由一系列预训练的Transformer块组成的LLM中,这些块通过LoRA进行增强。此过程产生了高级交互表示zi。
![]()
预训练的LLM(大型语言模型)的输出通过一个MLP (多层感知机)进行转换,以匹配gi的维度,从而得到最终的高水平交互状态si。
大多数经验丰富的驾驶员会关注有限数量的相关车道段,这些车道段对他们的未来的行驶有着重要影响。为了复制这种类似人类的认知功能,并进一步提高Traj-LLM(轨迹大型语言模型)中的场景理解能力,该方法的作者使用车道感知概率学习来持续评估运动状态与车道段对齐的可能性。该模型在每个时间步t∈{1,…,tf} 使用Mamba层将目标智能体的轨迹与车道信息进行对齐。作为一个选择性结构化状态空间模型(SSM),Mamba精炼并概括相关信息。这类似于人类驾驶员如何选择性地处理关键环境线索(如潜在车道)来做出选择。
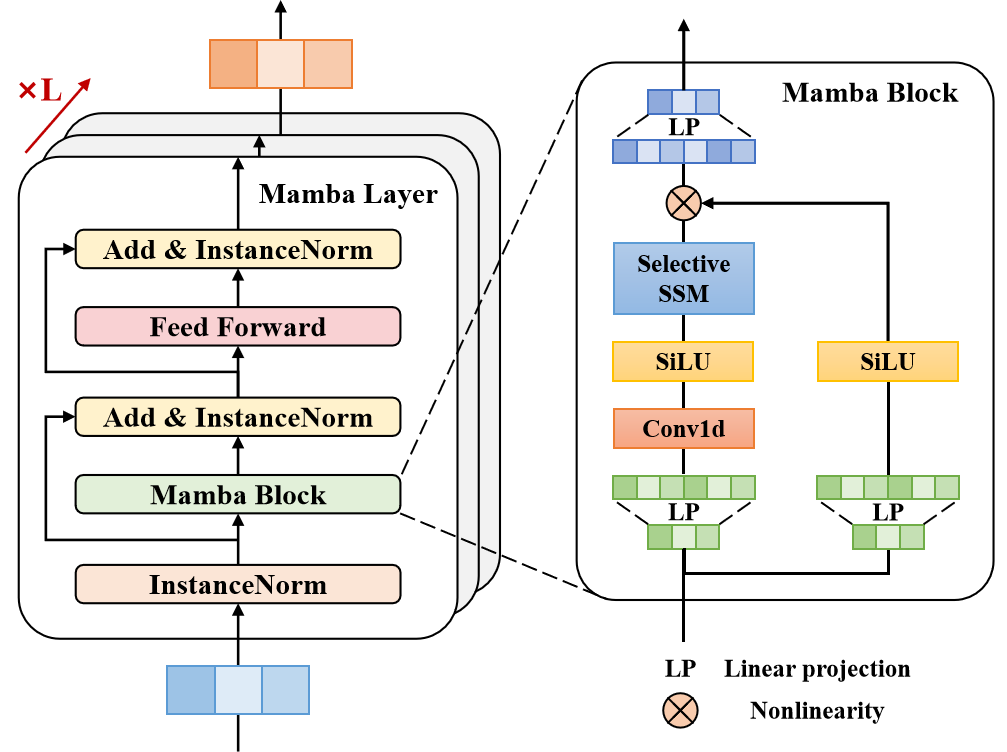
在所提出的架构中,Mamba层包括一个Mamba块、三层归一化和一个位置前馈网络。Mamba块首先通过线性投影扩展维度,为两个并行数据流创建不同的表示。其中一个分支经历卷积和SiLU激活函数,以捕获车道感知的依赖性。其核心在于,Mamba块基于输入数据,包含了一个具有离散参数的选择性状态空间模型。为了提高稳定性,添加了实例归一化和残差连接,从而产生潜在表示。
随后,一个位置前馈网络增强了隐藏维度中车道对齐评估的建模。再次应用实例归一化和残差连接来生成车道感知训练向量,这些向量随后被传递到MLP层。
如前所述,经验丰富的驾驶员会关注关键车道段来做出高效决策。因此,会仔细选择顶级候选车道并将它们组合成一个集合ℳ。
车道感知概率学习被建模为一个分类任务,使用二元交叉熵损失ℒlane来优化概率估计。
作者们对Traj-LLM方法的可视化展示如下:
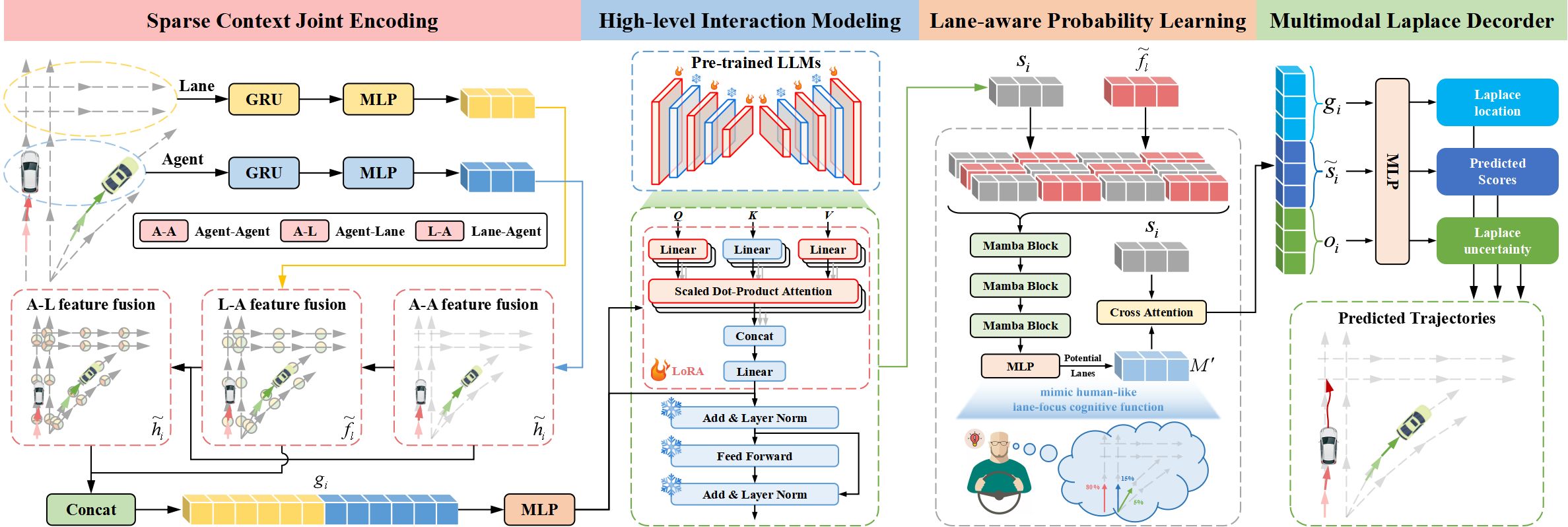
2. 在MQL5中的实现
在探讨了Traj-LLM方法的相关理论之后,我们进入本文的实践部分,在这部分中,我们将使用MQL5实现我们对所提出方法的构想。Traj-LLM算法是一个复杂的框架,它整合了多个架构组件,其中一些我们已经在之前的工作中遇到过。因此,我们在构建算法时可以利用现有的模块。然而,还需要进行额外的修改。
2.1调整LSTM块算法
让我们看一下以上展示的Traj-LLM方法的可视化效果。原始输入数据首先通过稀疏上下文联合编码块,该块包含一个循环层和MLP。我们的库已经包含了循环层CNeuronLSTMOCL。然而,它将输入数据处理为一个统一的环境状态表示。相比之下,该方法的作者们提出了对各个代理和车道状态进行独立编码。因此,我们必须为每个数据通道组织独立编码。我们可以为每个通道实例化一个单独的CNeuronLSTMOCL对象。然而,这将导致内部对象数量无控地增加和按顺序处理,从而对模型性能产生负面影响。
第二个解决方案是修改现有的CNeuronLSTMOCL循环层类。这需要在OpenCL程序方面进行更改。我们循环层的前馈传递是在LSTM_FeedForward内核中实现的。为了在单变量序列内实现操作,我们将不对内核的外部参数进行更改。为了实现对各个单变量序列数据的并行处理,我们将在任务空间中增加一个维度。
__kernel void LSTM_FeedForward(__global const float *inputs, int inputs_size, __global const float *weights, __global float *concatenated, __global float *memory, __global float *output) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); uint id2 = (uint)get_local_id(1); uint idv = (uint)get_global_id(2); uint total_v = (uint)get_global_size(2);
我要提醒您,LSTM块的操作基于四个实体,它们的值由内部层计算得出:
- 遗忘门 — 负责丢弃不相关信息
- 输入门 — 负责引入新信息
- 输出门 — 负责生成输出信号
- 新内容 — 表示用于更新单元状态的候选值
计算这些实体的算法是统一的,并遵循全连接层的结构。唯一的区别在于每个阶段应用的激活函数。因此,在我们的实现中,设计了这些实体的计算过程,以便在工作组内的并行线程中进行处理。为了实现线程之间的数据交换,我们使用了一个分配在本地内存中的数组。
__local float Temp[4];
接下来,我们在全局数据缓冲区中定义偏移常量。
float sum = 0; uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint shift = (inputs_size + total + 1) * (id2 + id);
请注意以下几点。我们实现了具有独立通道的循环块的工作过程。然而,根据Traj-LLM算法的构建逻辑,所有独立的信息通道都包含可比较的数据,无论是关于各种智能体的状态信息还是现有的交通车道信息。因此,使用一个权重矩阵来编码来自不同数据通道的信息是相当合理的,这将使我们能够在输出处获得可比较的嵌入。
因此,通道标识符影响源缓冲区和结果缓冲区中的偏移量。但它不影响权重矩阵中的偏移量。
接下来,我们创建一个循环来计算隐藏状态的加权和。
for(uint i = 0; i < total; i += 4) { if(total - i > 4) sum += dot((float4)(output[shift_out + i], output[shift_out + i + 1], output[shift_out + i + 2], output[shift_out + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += output[shift_out + k] * weights[shift + k]; }
并且我们增加了对输入数据的影响。
shift += total; for(uint i = 0; i < inputs_size; i += 4) { if(total - i > 4) sum += dot((float4)(inputs[shift_in + i], inputs[shift_in + i + 1], inputs[shift_in + i + 2], inputs[shift_in + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += inputs[shift_in + k] * weights[shift + k]; } sum += weights[shift + inputs_size];
我们将相应的激活函数应用于获得的值。
if(isnan(sum) || isinf(sum)) sum = 0; if(id2 < 3) sum = Activation(sum, 1); else sum = Activation(sum, 0);
之后,我们保存操作的结果并同步工作组线程。
Temp[id2] = sum; concatenated[4 * shift_out + id2 * total + id] = sum; //--- barrier(CLK_LOCAL_MEM_FENCE);
现在,我们只需要计算LSTM块的工作结果,这同时也是给定单元的隐藏状态。
if(id2 == 0) { float mem = memory[shift_out + id + total_v * total] = memory[shift_out + id]; float fg = Temp[0]; float ig = Temp[1]; float og = Temp[2]; float nc = Temp[3]; //--- memory[shift_out + id] = mem = mem * fg + ig * nc; output[shift_out + id] = og * Activation(mem, 0); } }
操作的结果被保存在全局数据缓冲区的相应元素中。
我们对反向传播传递内核进行了类似的编辑。其中最重要的修改是在LSTM_HiddenGradient内核中。与前馈内核一样,我们不改变外部参数的组成,只调整任务空间。
__kernel void LSTM_HiddenGradient(__global float *concatenated_gradient, __global float *inputs_gradient, __global float *weights_gradient, __global float *hidden_state, __global float *inputs, __global float *weights, __global float *output, const int hidden_size, const int inputs_size) { uint id = get_global_id(0); uint total = get_global_size(0); uint idv = (uint)get_global_id(1); uint total_v = (uint)get_global_size(1);
所有独立通道都使用同一个权重矩阵。因此,对于权重系数,我们需要从所有独立通道收集误差梯度。每个数据通道都在其自身的线程中运行,我们将这些线程组合成工作组。为了在线程之间交换数据,我们将使用本地内存中的数组。
__local float Temp[LOCAL_ARRAY_SIZE]; uint ls = min(total_v, (uint)LOCAL_ARRAY_SIZE);
接下来,我们在数据缓冲区中定义偏移量。
uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint weights_step = hidden_size + inputs_size + 1;
我们在输入数据的连接缓冲区上创建一个循环。首先,我们只是更新隐藏状态。
for(int i = id; i < (hidden_size + inputs_size); i += total) { float inp = 0; if(i < hidden_size) { inp = hidden_state[shift_out + i]; hidden_state[shift_out + i] = output[shift_out + i]; }
然后,我们确定输入层的误差梯度。
else { inp = inputs[shift_in + i - hidden_size]; float grad = 0; for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - temp) * weights[i + g * weights_step]; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step]; } inputs_gradient[shift_in + i - hidden_size] = grad; }
这里,我们还计算了权重层的误差梯度。首先,我们将本地数组的值重置。
for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE);
确保同步工作组线程的工作。
接下来,我们从所有数据通道收集总的误差梯度。在第一步中,我们将各个值保存在本地数组中。
for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp) * inp; barrier(CLK_LOCAL_MEM_FENCE); }
我们假设在分析的数据中,独立通道的数量相对较少。因此,我们在一个线程中收集数组值的总和,然后将得到的值保存在全局数据缓冲区中。
if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); }
同样地,我们收集新内容权重的误差梯度。
for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - pow(temp, 2.0f)) * inp; barrier(CLK_LOCAL_MEM_FENCE); } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
请注意,在执行主循环操作时,我们忽略了贝叶斯偏差权重因子。为了计算相应的误差梯度,我们根据上述方案实现了附加的操作。
for(int i = id; i < 4 * hidden_size; i += total) { if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); float temp = concatenated_gradient[4 * shift_out + (i + 1) * hidden_size]; if(i < 3 * hidden_size) { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp); barrier(CLK_LOCAL_MEM_FENCE); } } else { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += 1 - pow(temp, 2.0f); barrier(CLK_LOCAL_MEM_FENCE); } } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[(i + 1) * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
应该特别注意线程同步点。它们的数量必须最小限度地确保算法的正确运行。过多的同步点会降低性能并减缓操作速度。此外,放置不当的同步点(并非所有线程都能到达的这些点)可能会导致程序停止响应。
至此,我们完成了对OpenCL代码调整的回顾,这些调整是组织LSTM块在独立数据通道下操作所必需的。至于主程序方面的具体修改,我鼓励您独立进行探索。更新后的CNeuronLSTMOCL类及其所有方法的完整代码已附在附件中。
2.2构建Mamba模块
我们准备工作的下一步是构建Mamba块。这个块的名称是有意让人联想到我们在前一篇文章中讨论过的方法。Traj-LLM的作者们扩展了状态空间模型(SSM)的使用,并提出了一个可以与Transformer编码器相比较的块架构。但在这种情况下,Self-Attention被Mamba架构所取代。
为了实现所提出的算法,我们将创建一个名为CNeuronMambaBlockOCL的新类,其结构如下所示。
class CNeuronMambaBlockOCL : public CNeuronBaseOCL { protected: uint iWindow; CNeuronMambaOCL cMamba; CNeuronBaseOCL cMambaResidual; CNeuronConvOCL cFF[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronMambaBlockOCL(void) {}; ~CNeuronMambaBlockOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMambaBlockOCL; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
核心功能将由基础全连接层类CNeuronBaseOCL继承而来。我们将重写一系列熟悉的虚方法。
在我们新类的结构中,我们可以突出显示一些内部对象,随着我们的方法实现,我们将逐步探索这些对象的功能。所有对象都被声明为静态的。这使我们可以将类的构造函数和析构函数保持“空白”。所有内部对象和变量的初始化都将在Init方法内完成。
正如前面所提到的,Mamba块在架构上类似于Transformer编码器。这种相似性也体现在初始化方法的参数中,这些参数为块的内部架构提供了清晰且结构化的定义。
bool CNeuronMambaBlockOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
在该方法的主体中,我们调用了父类中同名的方法,而该方法已经包含了参数验证和所有继承对象初始化所必需的最小功能模块。
在父类初始化方法成功执行之后,我们将数据分析窗口的大小保存到一个局部变量中,以便后续使用。
iWindow = window;
然后我们继续初始化内部对象。首先,我们初始化Mamba状态空间层。
if(!cMamba.Init(0, 0, OpenCL, window, window_key, units_count, optimization, iBatch)) return false;
接下来是一个全连接层,我们打算使用它的缓冲区来存储带有残差连接的选择性状态空间分析的归一化结果。
if(!cMambaResidual.Init(0, 1, OpenCL, window * units_count, optimization, iBatch)) return false; cMambaResidual.SetActivationFunction(None);
之后,我们添加了一个FeedForward模块。
if(!cFF[0].Init(0, 2, OpenCL, window, window, 4 * window, units_count, 1, optimization, iBatch)) return false; cFF[0].SetActivationFunction(LReLU); if(!cFF[1].Init(0, 2, OpenCL, 4 * window, 4 * window, window, units_count, 1, optimization, iBatch)) return false; cFF[1].SetActivationFunction(None);
然后,我们集中对数据缓冲区指针的替换,以便消除不必要的复制操作。
SetActivationFunction(None); SetGradient(cFF[1].getGradient(), true); //--- return true; }
请注意,这里我们仅替换误差梯度缓冲区的指针。这是因为在前馈过程中,在将结果传递到层输出之前,会组织一个额外的残差连接和对获得结果的归一化处理。
别忘记在每一步监控操作结果。在方法的最后,我们将执行操作的逻辑结果返回给调用程序。
在初始化类对象之后,我们继续构建前馈算法,该算法在feedForward方法中实现。这相当简单。
bool CNeuronMambaBlockOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMamba.FeedForward(NeuronOCL)) return false;
在该方法的参数中,我们接收到来自前一层对象的指针,它向我们传递输入数据。在该方法的主体中,我们立即将接收到的指针传递给状态空间的选择性模型。
在内层的前馈方法操作成功完成后,我们将获得的结果与原始数据相加,然后对值进行归一化。
if(!SumAndNormilize(cMamba.getOutput(), NeuronOCL.getOutput(), cMambaResidual.getOutput(), iWindow, true)) return false;
接下来是FeedForward模块。
if(!cFF[0].FeedForward(cMambaResidual.AsObject())) return false; if(!cFF[1].FeedForward(cFF[0].AsObject())) return false;
我们集中了残差连接,并随后对数据进行归一化处理。
if(!SumAndNormilize(cMambaResidual.getOutput(), cFF[1].getOutput(), getOutput(), iWindow, true)) return false; //--- return true; }
反向传播方法也有一个相当简单的算法,我建议将其留给读者自行研究。在此我提醒一下,在附件中,您将找到这个类及其所有方法的完整代码。
至此,我们完成了准备工作,并开始构建Traj-LLM方法的总体算法。
2.3将独立模块组装成一个连贯的算法
根据以上内容,我们已经完成了准备工作,并为我们的库补充了缺失的“模块构建”,我们将使用这些模块在CNeuronTrajLLMOCL类中构建Traj-LLM算法。新类的结构如下所示。
class CNeuronTrajLLMOCL : public CNeuronBaseOCL { protected: //--- State Encoder CNeuronLSTMOCL cStateRNN; CNeuronConvOCL cStateMLP[2]; //--- Variables Encoder CNeuronTransposeOCL cTranspose; CNeuronLSTMOCL cVariablesRNN; CNeuronConvOCL cVariablesMLP[2]; //--- Context Encoder CNeuronLearnabledPE cStatePE; CNeuronLearnabledPE cVariablesPE; CNeuronMLMHAttentionMLKV cStateToState; CNeuronMLCrossAttentionMLKV cVariableToState; CNeuronMLCrossAttentionMLKV cStateToVariable; CNeuronBaseOCL cContext; CNeuronConvOCL cContextMLP[2]; //--- CNeuronMLMHAttentionMLKV cHighLevelInteraction; CNeuronMambaBlockOCL caMamba[3]; CNeuronMLCrossAttentionMLKV cLaneAware; CNeuronConvOCL caForecastMLP[2]; CNeuronTransposeOCL cTransposeOut; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronTrajLLMOCL(void) {}; ~CNeuronTrajLLMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronTrajLLMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
由此可以看出,在类的结构中,我们重写了相同的虚方法。然而,这个类的特点是内部对象的数量显著更多,这对于如此复杂的架构来说是相当合理的。随着我们逐步实现类的方法,这些声明的对象的用途将会变得清晰。
类的所有内部对象都被声明为静态的。因此,构造函数和析构函数保持为空。所有声明对象的初始化都是在Init方法中完成的。
在该方法的参数中,我们接收将用于初始化嵌套对象的主要常量。在此,我们看到了一些已经熟悉的参数名称。然而,请注意,其中一些参数可能对个别的内部对象具有不同的功能。
bool CNeuronTrajLLMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
按照已经确立的传统,Init方法中的第一步是调用同名的父类方法。正如您所知,该方法已经执行了基本的参数验证以及所有继承对象的初始化。在父类方法成功执行之后,我们继续初始化声明的内部对象。
基于构建以往模型所积累的经验,我们假设输入到模型的是一个描述当前市场状况的矩阵。该矩阵的每一行都包含一组描述单个市场K线的参数,包括所分析指标的相应值。
根据Traj-LLM算法,获得的输入数据首先被传递到稀疏上下文编码器模块,该模块包括智能体编码器和车道编码器。在我们的情况下,这些分别对应于环境状态(单个K线数据)的编码器和所分析参数的历史轨迹(指标)的编码器。
状态编码器将由一个用于分析单个K线的循环模块和两个后续的卷积层构建而成,这两个卷积层将在独立的信息通道中实现MLP操作。
//--- State Encoder if(!cStateRNN.Init(0, 0, OpenCL, window_key, units_count, optimization, iBatch) || !cStateRNN.SetInputs(window)) return false; if(!cStateMLP[0].Init(0, 1, OpenCL, window_key, window_key, 4 * window_key, units_count, optimization, iBatch)) return false; cStateMLP[0].SetActivationFunction(LReLU); if(!cStateMLP[1].Init(0, 2, OpenCL, 4 * window_key, 4 * window_key, window_key, units_count, optimization, iBatch)) return false;
该方法的参数包括用于初始化嵌入对象的主要常量。在此,我们看到了熟悉的参数名称,但需要注意的是,其中一些参数可能对特定的内部对象具有不同的功能。
//--- Variables Encoder if(!cTranspose.Init(0, 3, OpenCL, units_count, window, optimization, iBatch)) return false; if(!cVariablesRNN.Init(0, 4, OpenCL, window_key, window, optimization, iBatch) || !cVariablesRNN.SetInputs(units_count)) return false; if(!cVariablesMLP[0].Init(0, 5, OpenCL, window_key, window_key, 4 * window_key, window, optimization, iBatch)) return false; cVariablesMLP[0].SetActivationFunction(LReLU); if(!cVariablesMLP[1].Init(0, 6, OpenCL, 4 * window_key, 4 * window_key, window_key, window, optimization, iBatch)) return false;
需要指出的是,根据Traj-LLM算法,随后会对智能体(Agents)和车道(Lanes)进行联合分析。因此,编码器的输出会产生向量,这些向量表示序列中各个元素(环境状态或所分析指标的历史轨迹)的维度是相同的。同时,允许序列长度存在差异,因为所分析的环境状态数量通常不等于描述这些状态的分析参数数量。
遵循Traj-LLM算法的下一步,编码器的输出会被传递到Fusion模块,在这里,通过Self-Attention(自注意力)和Cross-Attention(交叉注意力)机制,对各个序列元素之间的相互依赖性进行综合分析。然而,众所周知,为了提高注意力机制的效率,必须在序列元素中添加位置编码标签。为了实现这一功能,我们将引入两个可训练的位置编码层。
//--- Position Encoder if(!cStatePE.Init(0, 7, OpenCL, cStateMLP[1].Neurons(), optimization, iBatch)) return false; if(!cVariablesPE.Init(0, 8, OpenCL, cVariablesMLP[1].Neurons(), optimization, iBatch)) return false;
之后我们才会在自注意力(Self-Attention)模块中分析各个状态之间的依赖关系。
//--- Context if(!cStateToState.Init(0, 9, OpenCL, window_key, window_key, heads, heads / 2, units_count, 2, 1, optimization, iBatch)) return false;
然后我们在接下来的两个交叉注意力(Cross-Attention)模块中进行交叉依赖性分析。
if(!cStateToVariable.Init(0, 10, OpenCL, window_key, window_key, heads, window_key, heads / 2, units_count, window, 2, 1, optimization, iBatch)) return false; if(!cVariableToState.Init(0, 11, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, units_count, 2, 1, optimization, iBatch)) return false;
状态和轨迹的丰富表示被拼接成一个单一的张量。
if(!cContext.Init(0, 12, OpenCL, window_key * (units_count + window), optimization, iBatch)) return false;
之后,数据会经过另一个MLP(多层感知机)。
if(!cContextMLP[0].Init(0, 13, OpenCL, window_key, window_key, 4 * window_key, window + units_count, optimization, iBatch)) return false; cContextMLP[0].SetActivationFunction(LReLU); if(!cContextMLP[1].Init(0, 14, OpenCL, 4 * window_key, 4 * window_key, window_key, window + units_count, optimization, iBatch)) return false;
接下来轮到高级交互建模模块。在此,Traj-LLM方法的作者使用了一个预训练的语言模型,我们将用一个Transformer模块来替换它。
if(!cHighLevelInteraction.Init(0, 15, OpenCL, window_key, window_key, heads, heads / 2, window + units_count, 4, 2, optimization, iBatch)) return false;
接下来是学习后续运动概率的认知模块,该模块会考虑现有的车道情况。这里,我们使用了3个具有相同架构的连续Mamba模块。
for(int i = 0; i < int(caMamba.Size()); i++) { if(!caMamba[i].Init(0, 16 + i, OpenCL, window_key, 2 * window_key, window + units_count, optimization, iBatch)) return false; }
获得的值将在交叉注意力模块中与历史轨迹进行比较。
if(!cLaneAware.Init(0, 19, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, window + units_count, 2, 1, optimization, iBatch)) return false;
最后,我们使用MLP(多层感知机)来预测独立数据通道的后续轨迹。
if(!caForecastMLP[0].Init(0, 20, OpenCL, window_key, window_key, 4 * forecast, window, optimization, iBatch)) return false; caForecastMLP[0].SetActivationFunction(LReLU); if(!caForecastMLP[1].Init(0, 21, OpenCL, 4 * forecast, 4 * forecast, forecast, window, optimization, iBatch)) return false; caForecastMLP[1].SetActivationFunction(TANH); if(!cTransposeOut.Init(0, 22, OpenCL, window, forecast, optimization, iBatch)) return false;
请注意,预测的轨迹张量被转置,以便将信息转换为原始数据的表示形式。
SetOutput(cTransposeOut.getOutput(), true); SetGradient(cTransposeOut.getGradient(), true); SetActivationFunction((ENUM_ACTIVATION)caForecastMLP[1].Activation()); //--- return true; }
我们还使用数据缓冲区指针替换来避免不必要的复制操作。之后,我们将方法操作的逻辑结果返回给调用程序。
在完成类初始化方法的工作之后,我们继续构建前馈传递算法,该算法在feedForward方法中实现。
bool CNeuronTrajLLMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- State Encoder if(!cStateRNN.FeedForward(NeuronOCL)) return false; if(!cStateMLP[0].FeedForward(cStateRNN.AsObject())) return false; if(!cStateMLP[1].FeedForward(cStateMLP[0].AsObject())) return false;
在该方法的参数中,我们接收一个包含初始数据的对象指针,于是立即将其通过状态编码器模块传递。
之后,我们对原始数据进行转置,并对描述环境状态的所分析参数的历史轨迹进行编码。
//--- Variables Encoder if(!cTranspose.FeedForward(NeuronOCL)) return false; if(!cVariablesRNN.FeedForward(cTranspose.AsObject())) return false; if(!cVariablesMLP[0].FeedForward(cVariablesRNN.AsObject())) return false; if(!cVariablesMLP[1].FeedForward(cVariablesMLP[0].AsObject())) return false;
我们对获得的数据添加位置编码。
//--- Position Encoder if(!cStatePE.FeedForward(cStateMLP[1].AsObject())) return false; if(!cVariablesPE.FeedForward(cVariablesMLP[1].AsObject())) return false;
随后,我们通过上下文中的相互依赖关系来丰富数据。
//--- Context if(!cStateToState.FeedForward(cStatePE.AsObject())) return false; if(!cStateToVariable.FeedForward(cStateToState.AsObject(), cVariablesPE.getOutput())) return false; if(!cVariableToState.FeedForward(cVariablesPE.AsObject(), cStateToVariable.getOutput())) return false;
经过丰富化的数据被拼接成一个单一的张量。
if(!Concat(cStateToVariable.getOutput(), cVariableToState.getOutput(), cContext.getOutput(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
然后它被MLP(多层感知机)处理。
if(!cContextMLP[0].FeedForward(cContext.AsObject())) return false; if(!cContextMLP[1].FeedForward(cContextMLP[0].AsObject())) return false;
接下来是高级依赖关系分析模块。
//--- Lane aware if(!cHighLevelInteraction.FeedForward(cContextMLP[1].AsObject())) return false;
以及状态空间模型。
if(!caMamba[0].FeedForward(cHighLevelInteraction.AsObject())) return false; for(int i = 1; i < int(caMamba.Size()); i++) { if(!caMamba[i].FeedForward(caMamba[i - 1].AsObject())) return false; }
然后,我们将历史轨迹与我们的分析结果进行比较。
if(!cLaneAware.FeedForward(cVariablesPE.AsObject(), caMamba[caMamba.Size() - 1].getOutput())) return false;
基于所获得的数据,我们对所分析参数最有可能出现的后续变化进行预测。
//--- Forecast if(!caForecastMLP[0].FeedForward(cLaneAware.AsObject())) return false; if(!caForecastMLP[1].FeedForward(caForecastMLP[0].AsObject())) return false;
之后,我们将预测值转置为输入数据的表示形式。
if(!cTransposeOut.FeedForward(caForecastMLP[1].AsObject())) return false; //--- return true; }
最后,该方法会向调用程序返回一个布尔值,表示所执行操作的成功或失败。
我们工作的下一个阶段是构建反向传播算法。在此,我们必须根据各个对象对最终输出的影响,将误差梯度分配到所有对象中,并随后调整可训练参数,以最小化误差。
虽然更新参数相对简单——因为所有可训练参数都包含在内部(嵌套)对象中,因此只需依次调用这些内部对象的参数更新方法即可——但分配误差梯度却是一个更加复杂且精细的挑战。
误差梯度的分配完全按照前馈传递的算法进行,但顺序相反。这里,需要指出的是,我们的前馈传递并不是那么“向前”的,如果你不介意这个文字描述。在前馈过程中可以识别出几条并行的信息流。而现在,我们必须从所有这些信息流中收集误差梯度。
误差梯度分配算法将在calcInputGradients方法中实现。该方法的参数包括一个指向前一层对象的指针,我们必须将误差梯度传递到该对象中,该梯度是根据初始输入数据对模型最终输出的影响进行分配的。在该方法的开始阶段,我们立即检查接收到的指针的有效性,因为如果指针不正确,那么整个后续过程将变得毫无意义。
bool CNeuronTrajLLMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
需要记住的是,在调用该方法时,当前层的误差梯度已经被存储在其梯度缓冲区中了。这个值是在模型的下一层执行相应方法时写入的。而且,由于我们之前组织的指针替换机制,这个相同的误差梯度也存在于我们内部层的缓冲区中,该内部层负责转置预测结果。因此,我们通过将这个梯度传递给负责预测未来运动的MLP,开始梯度分配过程。
//--- Forecast if(!caForecastMLP[1].calcHiddenGradients(cTransposeOut.AsObject())) return false; if(!caForecastMLP[0].calcHiddenGradients(caForecastMLP[1].AsObject())) return false;
完成上述操作后,我们将误差梯度传播到将所分析参数的历史轨迹与认知分析结果进行对齐的层。
//--- Lane aware if(!cLaneAware.calcHiddenGradients(caForecastMLP[0].AsObject())) return false;
在此,至关重要的是,交叉注意力模块会匹配来自两个独立信息流的数据。相应地,我们必须根据这两个信息流对最终模型输出的影响,将误差梯度分配到这两个流中。
if(!cVariablesPE.calcHiddenGradients(cLaneAware.AsObject(), caMamba[caMamba.Size() - 1].getOutput(), caMamba[caMamba.Size() - 1].getGradient(), (ENUM_ACTIVATION)caMamba[caMamba.Size() - 1].Activation())) return false;
接下来,我们将误差梯度通过状态空间模型传递。
for(int i = int(caMamba.Size()) - 2; i >= 0; i--) if(!caMamba[i].calcHiddenGradients(caMamba[i + 1].AsObject())) return false;
然后,通过高级依赖关系分析模块。
if(!cHighLevelInteraction.calcHiddenGradients(caMamba[0].AsObject())) return false;
通过上下文MLP,我们将误差梯度再传递到更深层——即状态和轨迹的拼接数据缓冲区。
if(!cContextMLP[1].calcHiddenGradients(cHighLevelInteraction.AsObject())) return false; if(!cContextMLP[0].calcHiddenGradients(cContextMLP[1].AsObject())) return false; if(!cContext.calcHiddenGradients(cContextMLP[0].AsObject())) return false;
现在到了最为复杂且关键的部分。这里需要格外小心,避免遗漏任何细节。
在这个阶段,我们需要将拼接缓冲区的梯度拆分为两个独立的流。其本身并不复杂。我们只需运行反拼接方法,并指定适当的数据缓冲区即可。在我们的情况下,是两个交叉注意力层:轨迹到状态(trajectories-to-states)和状态到轨迹(states-to-trajectories)。然而,挑战在于下一步。当我们开始将误差梯度传递通过轨迹到状态的交叉注意力模块时,这个模块也会生成一个需要进一步传递到状态到轨迹的交叉注意力层的梯度。因此,为了确保在这个多步骤过程中不丢失任何梯度信息,我们必须将其保存在一个临时缓冲区中。但在当前类中,即使没有辅助缓冲区,我们也已经创建了许多对象。而在这些对象中,许多还在等待它们的轮次。所以,让我们利用它们来临时存储信息。让我们使用与状态到轨迹的交叉注意力模块相关联的位置编码层作为这个部分梯度的临时存储器。
if(!DeConcat(cStatePE.getGradient(), cVariableToState.getGradient(), cContext.getGradient(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
此外,我们还注意到轨迹的位置编码层的梯度缓冲区已经包含了有用的误差梯度。为了避免丢失这些有价值的信息,我们暂时将其转移到相应编码器的MLP的梯度缓冲区中。
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), 1, false)) return false;
在确保所有必要的梯度信息得以保留之后,我们继续将误差梯度分配到使得轨迹与状态对齐的交叉注意力模块中。
if(!cVariablesPE.calcHiddenGradients(cVariableToState.AsObject(), cStateToVariable.getOutput(), cStateToVariable.getGradient(), (ENUM_ACTIVATION)cStateToVariable.Activation())) return false;
现在,我们可以在将状态与轨迹对齐的交叉注意力模块的层面汇总误差梯度,从两个流中累积。
if(!SumAndNormilize(cStateToVariable.getGradient(), cStatePE.getGradient(), cStateToVariable.getGradient(), 1, false, 0, 0, 0, 1)) return false;
然而,在下一步中,我们需要第三次将误差梯度传回轨迹的位置编码层。因此,我们首先需要从两个数据流中聚合现有的误差梯度。
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesMLP[1].getGradient(), 1, false, 0, 0, 0, 1)) return false;
只有在完成这个聚合之后,我们才会调用将状态与轨迹对齐的交叉注意力模块的梯度分配方法。
if(!cStateToState.calcHiddenGradients(cStateToVariable.AsObject(), cVariablesPE.getOutput(), cVariablesPE.getGradient(), (ENUM_ACTIVATION)cVariablesPE.Activation())) return false;
在这个阶段,我们终于可以在轨迹的位置编码层汇总来自三个不同来源的所有误差梯度。
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesPE.getGradient(), 1, false, 0, 0, 0, 1)) return false;
接下来,我们将误差梯度向下传递到状态的位置编码层。
if(!cStatePE.calcHiddenGradients(cStateToState.AsObject())) return false;
值得注意的是,位置编码层在两个独立且并行的数据流中运行,我们必须将相应的误差梯度向下传递到每个流中对应的编码器。
//--- Position Encoder if(!cStateMLP[1].calcHiddenGradients(cStatePE.AsObject())) return false; if(!cVariablesMLP[1].calcHiddenGradients(cVariablesPE.AsObject())) return false;
接下来,我们将误差梯度通过两个并行的编码器传递,每个编码器都处理相同的原始数据输入张量。这里,我们需要将这两个并行流中的误差梯度合并到一个单一梯度缓冲区。我们再次需要一个辅助数据缓冲区,而我们并没有创建它。此外,在此阶段,我们所有的内部对象都已经被填充了我们无法覆盖的关键数据。
然而,这里有一个微妙但至关重要的细节。我们用来在轨迹编码之前重新排列原始输入数据的数据转置层,不包含任何可训练参数。它的误差梯度缓冲区仅用于将数据传递到前一层。另外,这个缓冲区的大小完全符合我们的需求,因为我们处理的是相同的数据,只是顺序不同。太棒了!我们将误差梯度通过轨迹编码模块进行传递。
//--- Variables Encoder if(!cVariablesMLP[0].calcHiddenGradients(cVariablesMLP[1].AsObject())) return false; if(!cVariablesRNN.calcHiddenGradients(cVariablesMLP[0].AsObject())) return false; if(!cTranspose.calcHiddenGradients(cVariablesRNN.AsObject())) return false; if(!NeuronOCL.FeedForward(cTranspose.AsObject())) return false;
之后我们将获得的误差梯度转移到数据转置层的缓冲区中。
if(!SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getGradient(), cTranspose.getGradient(), 1, false)) return false;
同样地,我们将误差梯度通过状态编码器传递。
//--- State Encoder if(!cStateMLP[0].calcHiddenGradients(cStateMLP[1].AsObject())) return false; if(!cStateRNN.calcHiddenGradients(cStateMLP[0].AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cStateRNN.AsObject())) return false;
随后,我们将来自两个流的误差梯度汇总。
if(!SumAndNormilize(cTranspose.getGradient(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; //--- return true; }
最后,我们将所有操作的逻辑结果返回给调用程序,表明成功与否。
至此,关于CNeuronTrajLLMOCL类算法的描述就结束了。您可以在附件中找到这个类及其所有方法的完整代码。
2.4模型架构
现在,我们可以无缝地将这个类集成到我们的模型中,使用真实的历史数据来评估所提出方法的实际效率。Traj-LLM算法是专门为预测未来轨迹而设计的。我们在环境状态编码器中使用了类似的方法。
请注意,我们对Traj-LLM的实际应用解释是在一个统一的复合模块中实现的。这使得我们能够在不牺牲功能的情况下,保持外部模型结构的简洁和清晰。
像往常一样,描述当前市场状况的原始、未经处理的数据被输入到模型的输入端。
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
主要的数据处理是在批量归一化层中完成的。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
之后,数据会立即被传递到我们新的Traj-LLM模块。很难将这样一种复杂的架构解决方案称为一个神经层。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTrajLLMOCL; descr.window = BarDescr; //window descr.window_out = EmbeddingSize; //Inside Dimension descr.count = HistoryBars; //Units prev_count = descr.layers = NForecast; //Forecast descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
在模块的输出端,已经得到了预测值,我们将原始值的统计参数添加到这些预测值中。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
然后我们在频域中对齐结果。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
其他模型的架构保持不变。所有使用程序的代码也是如此。您可以在文末附加的代码中研究它们。我们现在转入下一阶段。
3. 测试
为了MQL5中实现了Traj-LLM方法,我们已经完成了大量的工作。现在是时候评估实际结果了。我们的目标是在真实的历史数据上训练模型,并在以前未见过的数据集上评估它们的性能。
如前所述,对模型架构的更改并未影响输入数据的结构或其输出的格式。这就使我们能够依赖以前编译的训练数据集进行预训练。
在第一阶段,我们训练环境状态编码器以预测即将到来的价格走势。训练持续进行,直到预测误差稳定在一个可接受的水平。值得注意的是,在这个阶段,我们不会刷新或修改训练数据集。在这个阶段,模型展示了符合预期的结果。它表现出了良好的性能,能够识别即将到来的价格趋势。
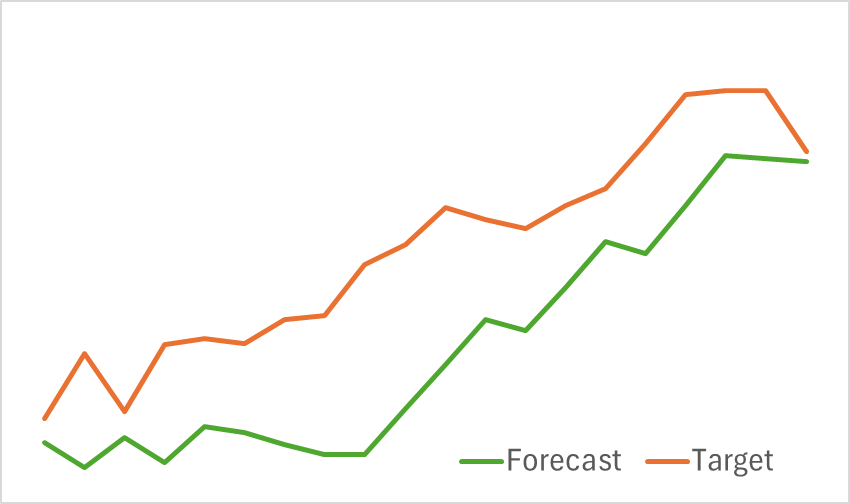
在第二阶段,我们进行Actor的行为策略和Critic的奖励函数的迭代训练。Critic模型的训练起到了辅助作用。它调整了Actor的操作。然而,我们的主要目标是为Actor开发一个能够盈利的策略。为了确保可靠地评估Actor的操作,我们在这一阶段定期更新训练数据集。经过几次迭代后,我们成功开发出一种能够在测试数据集上产生利润的策略。
我要提醒一下,所有模型都是使用2023年EURUSD货币对的历史数据进行训练的,时间框架为H1。测试是在2024年1月的数据上进行的,同时保持所有其他参数不变。
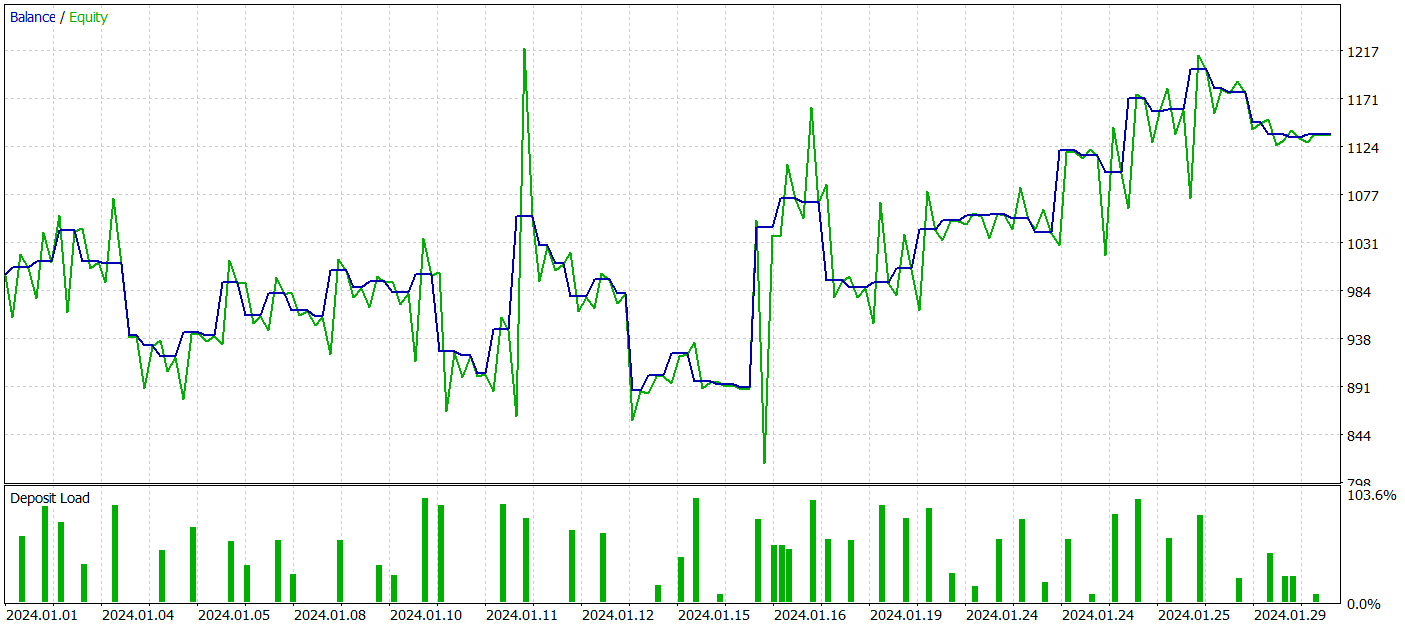
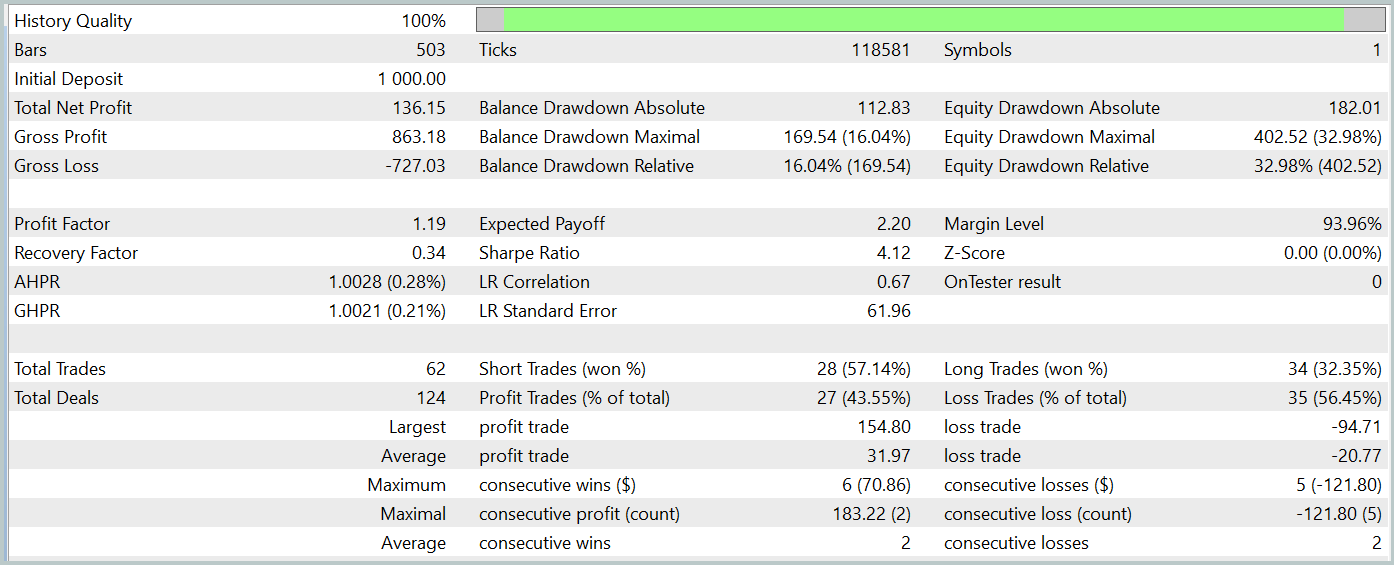
在测试期间,我们的模型共执行了62笔交易,其中27笔(43.55%)以盈利平仓。然而,由于最大盈利交易和平均盈利交易的数值都超过了亏损交易的对应数值的一半,因此在测试期间总体上获得了13.6%的利润。盈利系数为1.19。然而,一个显著的问题是权益回撤,它几乎达到了33%。显然,以目前的形式,该模型还不适合用于实际交易,还需要进一步改进。
结论
在本文中,我们探讨了一种新的Traj-LLM方法,其作者提出了应用大型语言模型(LLMs)的新视角。该方法展示了如何将LLM的能力适应于预测各种时间序列的未来值,从而在不确定性和混沌的条件下实现更准确、更具适应性的预测。
在实践部分,我们实现了对所提出方法的解释,并基于真实的历史数据进行了测试。尽管结果还不尽完美,但仍然令人鼓舞,并显示出进一步优化的潜力。
参考文献
文中所用的程序
| # | Issued to | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | EA | 样本收集EA |
| 2 | ResearchRealORL.mq5 | EA | 使用Real-ORL方法收集示例的 EA |
| 3 | Study.mq5 | EA | 模型训练EA |
| 4 | StudyEncoder.mq5 | EA | 编码器训练EA |
| 5 | Test.mq5 | EA | 模型测试EA |
| 6 | Trajectory.mqh | 类库 | 系统状态定义结构 |
| 7 | NeuroNet.mqh | 类库 | 用于创建神经网络的类库 |
| 8 | NeuroNet.cl | 代码库 | OpenCL程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/15595
 数据科学和机器学习(第 26 部分):时间序列预测的终极之战 — LSTM 对比 GRU 神经网络
数据科学和机器学习(第 26 部分):时间序列预测的终极之战 — LSTM 对比 GRU 神经网络
 威廉·江恩(William Gann)方法(第二部分):创建江恩宫格指标
威廉·江恩(William Gann)方法(第二部分):创建江恩宫格指标
 数据科学和机器学习(第 27 部分):MetaTrader 5 中训练卷积神经网络(CNN)交易机器人 — 值得吗?
数据科学和机器学习(第 27 部分):MetaTrader 5 中训练卷积神经网络(CNN)交易机器人 — 值得吗?
 使用 SMA 和 EMA 自动优化止盈和指标参数的示例
使用 SMA 和 EMA 自动优化止盈和指标参数的示例